Recent Advances in Reinforcement Learning for Chemical Process Control

Abstract

This paper reviews the recent advancements of reinforcement learning (RL) for chemical process control. RL presents a systematic strategy in which the machine learning agent learns a policy of actions based on interactions with the environment. We first provide a brief overview of RL theoretic basis built on Markov decision processes (MDPs) and then move onto its application to process control. With particular interest in chemical processes, we review state-of-the-art research developments on RL for controller tuning and direct control policy learning. This work highlights the importance of safe RL control to incorporate deterministic or probabilistic safety constraints such as constrained MDPs, control barrier functions, etc. We conclude the review with a discussion on some of the outstanding challenges such as sampling efficiency, generalizability, uncertainty, and observability, as well as the emergent and future directions to address these limitations.

1. Introduction

Process control is an integral part of the chemical process industry, which investigates the manipulation of process inputs to ensure the desired output behavior under disturbances while addressing potential constraints and regulations, such as safety requirements and environmental specifications [1,2]. Arguably, the most popular feedback control strategies in chemical processes are proportional-integral-derivative (PID) control and model predictive control (MPC). PID controllers calculate the input values based on the error between the measured output values and their setpoint values for setpoint tracking and disturbance rejection. PID control has been widely adopted in industrial practice, underpinned by extensive theoretical analysis on controller tuning to improve its stability and operational performance [3]. However, optimality is normally not guaranteed for PID control. On the other hand, MPC advances process control by utilizing a mathematical model to predict the process dynamics over a specified time window [4,5] and couples with optimization algorithms to determine the optimal control actions that satisfy both an objective function and possible constraints. Model development (mechanistic/data-driven), online optimization algorithms, and control under uncertainty remain the core areas for MPC research while yet presenting unresolved challenges for practical implementations [6,7].

Belonging to the same optimal control realm, reinforcement learning (RL) offers another promising alternative for process control, given its capability of data-driven control formulation and superior performance in handling system stochasticity. RL is typically deployed for sequential decision-making problems to optimize a defined cumulative reward, especially in scenarios where limited or no prior knowledge about the system exists. As shown in Figure 1, a generic RL setting involves two key entities: an agent and an environment. The environment is the system of interest such as a chemical production process. The state of the system changes in response to the actions taken by the agent. The agent is the decision-making entity, which is trained to take an action based on the current state of the environment. A reward is then received as feedback to the agent after taking a certain action. The objective of the agent is to maximize the cumulative reward, which is termed as the return. Readers of interest are referred to Sutton and Barto [8] for a comprehensive review on RL algorithmic fundamentals.

In the context of process control, an RL algorithm can learn the process dynamics through direct interactions with the process system. The reward to the RL agent can be based on cost, setpoint deviation, safety, etc. By iteratively interacting with the environment and analyzing the reward, RL strives to converge to a policy that can decide the optimal control actions based on the pre-specified optimization objective. Since the observed state affects the actions of the agent, RL problems are intrinsically closed-loop. Using the example of control under uncertainty, Petsagkourakis et al. [9] noted that a deep reinforcement learning (DRL)-based control policy would determine the control actions by considering the future impacts of disturbances in a closed-loop manner. This leads to more robust control actions, which are resilient to disturbances while maximizing the reward function.

Several excellent review papers have been presented on the application of RL in process control. Shin et al. [10] conducted a review on the applications of RL for process control and process decision making. The review covered various RL algorithms together with the major challenges for RL implementation. RL was also compared with conventional mathematical programming-based methods (e.g., MPC) for process control and multi-level decision making. Nian et al. [11] reviewed the fundamental Markov decision process, RL solution algorithms (e.g., dynamic programming, Monte Carlo methods, temporal difference learning) and DRL methods. The authors also discussed the correlation of RL with process control and the comparison with traditional control methods. An illustrating example was presented for the control of an industrial pumping system. Faria et al. [12] discussed the detailed RL implementations in terms of simulation-based offline training, transfer learning for policy deployment, and process demonstrations. A review of RL for process control and fault detection was offered by Dogru et al. [13]. Wang et al. [14] presented a tutorial review using a reactor control example to showcase the efficacy of RL, physics-informed RL, transfer RL, and safe RL. Nievas et al. [15] provided a broader perspective of RL applications in various manufacturing sectors including the power industry, robot automation, etc.

This work differentiates from the aforementioned review papers in the following aspects: (i) we focus on RL for the control of chemical process systems, with a particular interest in the advances over the latest five years; (ii) we emphasize the importance of safe RL for process control and review the recent advances; and (iii) we discuss the potential of emerging algorithms (e.g., large language model-enhanced RL) in overcoming key challenges such as sampling efficiency and generalizability. The remainder of this article is structured as follows: Section 2 introduces the basics of RL including the Markov decision processes and representative DRL methods. Section 3 reviews RL-based process control, i.e., RL for autonomous PID tuning and RL for control policy learning. Section 4 focuses on safe RL using deterministic and probabilistic safety constraints and the applications in process control. Section 5 discusses the limitations, challenges, emergent and future directions on RL development. Section 6 presents concluding remarks.

2. Reinforcement Learning Basics

For the continuity of this paper, this section briefly reviews Markov decision processes and representative RL methods to solve such problems. These methods will be used as the foundation for RL-based control, to be discussed in Section 3. Readers of interest are referred to [10,11] for comprehensive discussions on RL mathematical fundamentals and solution strategies.

2.1. Markov Decision Processes and Useful Definitions

Markov decision processes (MDPs) are used to mathematically model the optimal control problem that the RL algorithms aim to solve [16]. An MDP has four main components: (i) a set of possible states S that characterize the system or environment; (ii) a set of possible actions A taken to manipulate the system; (iii) a probabilistic state transition function $P(s,a,s^{\prime })$ that defines the probability for the system to progress to future state $s^{\prime }$ from current state s, with action a; and (iv) a reward function $R(s,a)$ that represents how desirable it is to take a certain action given a particular state. The state transition function in MDPs is considered to follow the Markov property, i.e., the evolution of the system state only depends on the current state $s_t$ and the action being performed $a_t$. Mathematically, the Markov property is defined in Equation (1).

$$P\left(s_{t+1}\right|s_t,a_t,s_{t-1},a_{t-1},\cdots ,s_0,a_0)=P\left(s_{t+1}\right|s_t,a_t)$$

(1)

where t is discrete time, s is the system state, and a is the action. A conceptual example of the problem framed by an MDP is given in discrete time for an infinite horizon below (Equation (2)).

$$\begin{array}{cc}\hfill J\left(\pi \right)=\underset{\pi }{max}& E\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t)\right|s_0]\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& a_t\sim \pi (·|s_t)\hfill \\ \hfill & s_{t+1}\sim P(·|s_t,a_t)\hfill \end{array}$$

(2)

where $\pi$ is a stochastic policy that maps states to actions, and $a_t\sim \pi (·|s_t)$ means action $a_t$ is sampled from the probability distribution defined by $\pi (·|s_t)$. $\gamma \in [0,1)$ is the discount factor, used to ensure that the sum of future rewards is bounded in infinite time. The solution to this problem gives an optimal policy, ${\pi }^{*}=argmaxJ\left(\pi \right)$, that maximizes the expected sum of discounted future rewards for all time. To solve this problem with RL, it is desirable to define additional functions and parameters. For a given policy $\pi$, a trajectory $\tau$ of system states and actions can be realized from time t to infinity (Equation (3)). The sum of all future rewards based on this trajectory is the return $G_t$ defined as in Equation (4).

$$\tau =[s_t,a_t,s_{t+1},a_{t+1},s_{t+2},a_{t+2},\cdots ]$$

(3)

$$G_t\left(\tau \right)=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots =\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}$$

(4)

A state value function $V_{\pi }\left(s\right)$ is defined by taking the expectation of the return, as given in Equation (5). The state-value function represents the expected return from starting in a state, s, following a policy, $\pi$.

$$V_{\pi }\left(s\right)=E_{\pi }\left[G_t\left(\tau \right)\right|s_t=s]=E_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}\right|s_t=s]$$

(5)

Similarly, an action-value function (Q-function) is defined by Equation (6), which represents the expected value of the return from starting in a state s, performing an action a, and following a policy $\pi$. The finite-time horizon formulations can be derived by bounding the upper limit of k.

$$Q_{\pi }(a,s)=E_{\pi }\left[G_t\left(\tau \right)\right|s_t=s,a_t=a]=E_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}\right|s_t=s,a_t=a]$$

(6)

In certain algorithms, it is useful to use an alternative function called the advantage function, $A_{\pi }(s,a)=Q_{\pi }(s,a)-V_{\pi }\left(s\right)$, which represents how much better one action is over another. Note that the return function can be defined recursively, e.g., $G_t=R_{t+1}+G_{t+1}$, and that an optimal state value function can be achieved by following the optimal policy $V^{*}\left(s\right)={max}_{\pi }{V}_{\pi }\left(s\right)$, which can be derived with the Bellman equation (Equation (7)). Following similar steps, the Bellman optimality equation for the Q-function can also be derived (Equation (8)).

$$V^{*}\left(s\right)=\underset{a}{max}E[R_t+\gamma V^{*}\left(s_{t+1}\right)]$$

(7)

$$Q^{*}(s,a)=E[R_t+\gamma \underset{a_{t+1}}{max}{Q}^{*}(s_{t+1},a_{t+1})]$$

(8)

The optimal advantage function follows as $A^{*}(s,a)=Q^{*}(s,a)-V^{*}\left(s\right)$ and provides critical insight, since if $A^{*}(s,a)=0$, the action is then optimal for the current state. These definitions provide the basis for modern RL algorithms, which often estimate the functions of interest (e.g., $V\left(s\right)$ or $Q(s,a)$) using neural networks (NNs) with the goal to satisfy the optimality equations through time series updates.

The above formulations assume full observability of the system states, and such MDPs are referred to as fully observable Markov decision processes (FOMDPs). In practice, however, the states of the system or processes might not always be fully observable, leading to partially observable Markov decision processes (POMDPs) or hidden Markov decision processes (HMDPs). In these scenarios, state estimation techniques can be incorporated into the RL algorithm for policy training. For example, in POMDP-based RL problems, observations from the system are used to infer the unmeasurable states, typically in the form of probabilistic distributions. Representative techniques to infer the states for the POMDPs include Bayesian methods, Kalman filter approaches, and neural-network-based state estimators. In Bayesian methods, the posterior belief states are computed using Bayes’ rule [17]. Chenna et al. [18] evaluated the performance of the Kalman filter and recurrent neural networks (RNNs) in state estimation. RNNs have also been used in deep reinforcement learning algorithms for solving POMDPs [19,20,21]. The use of these techniques allows one to treat a POMDP as an FOMDP since full state estimates become available. Extended discussions on the observability in RL are provided in Section 5.

2.2. State-of-the-Art RL Algorithms

A summary of the representative RL algorithms is given in

Table 1. RL algorithms—an indicative list.

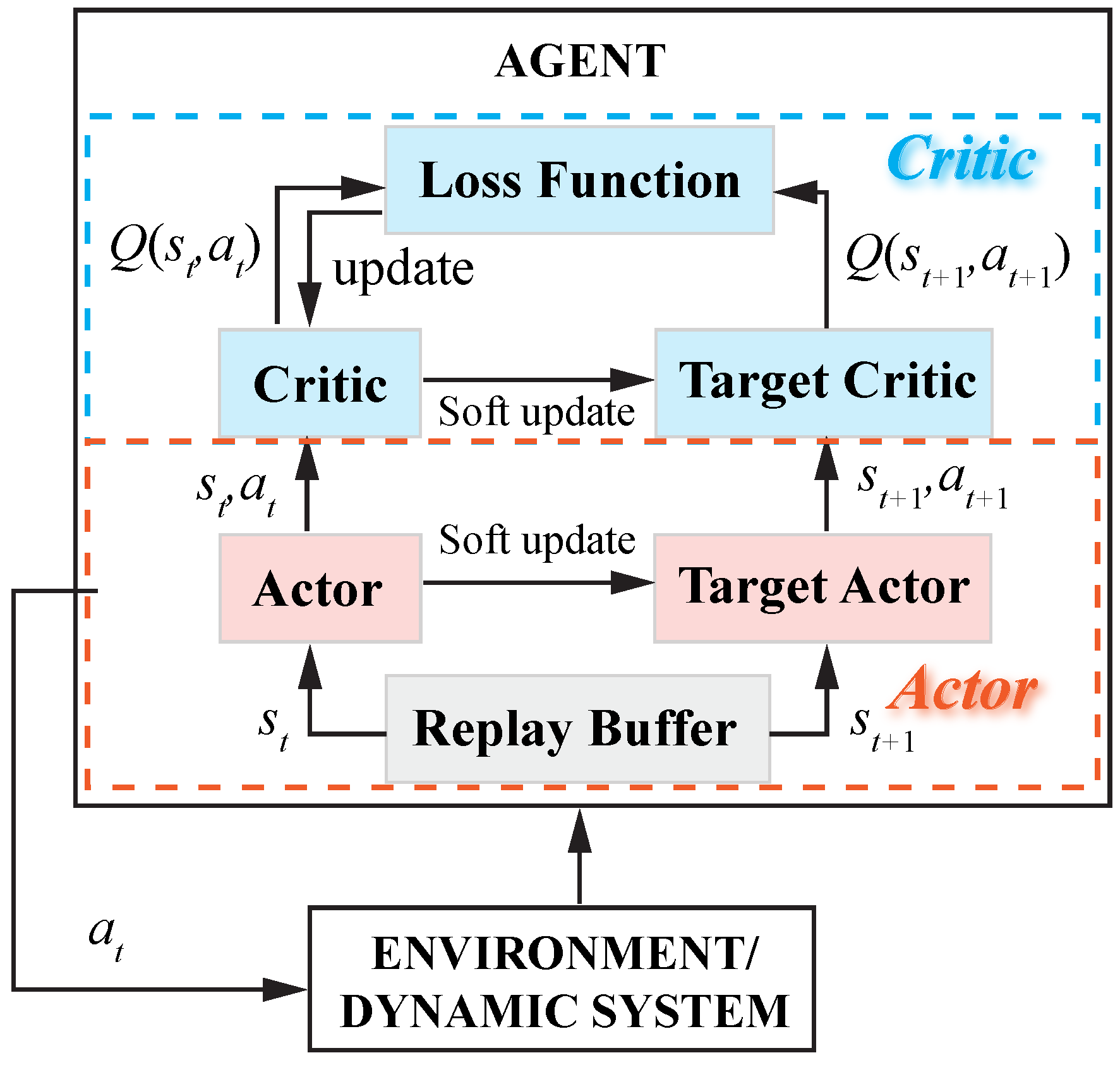
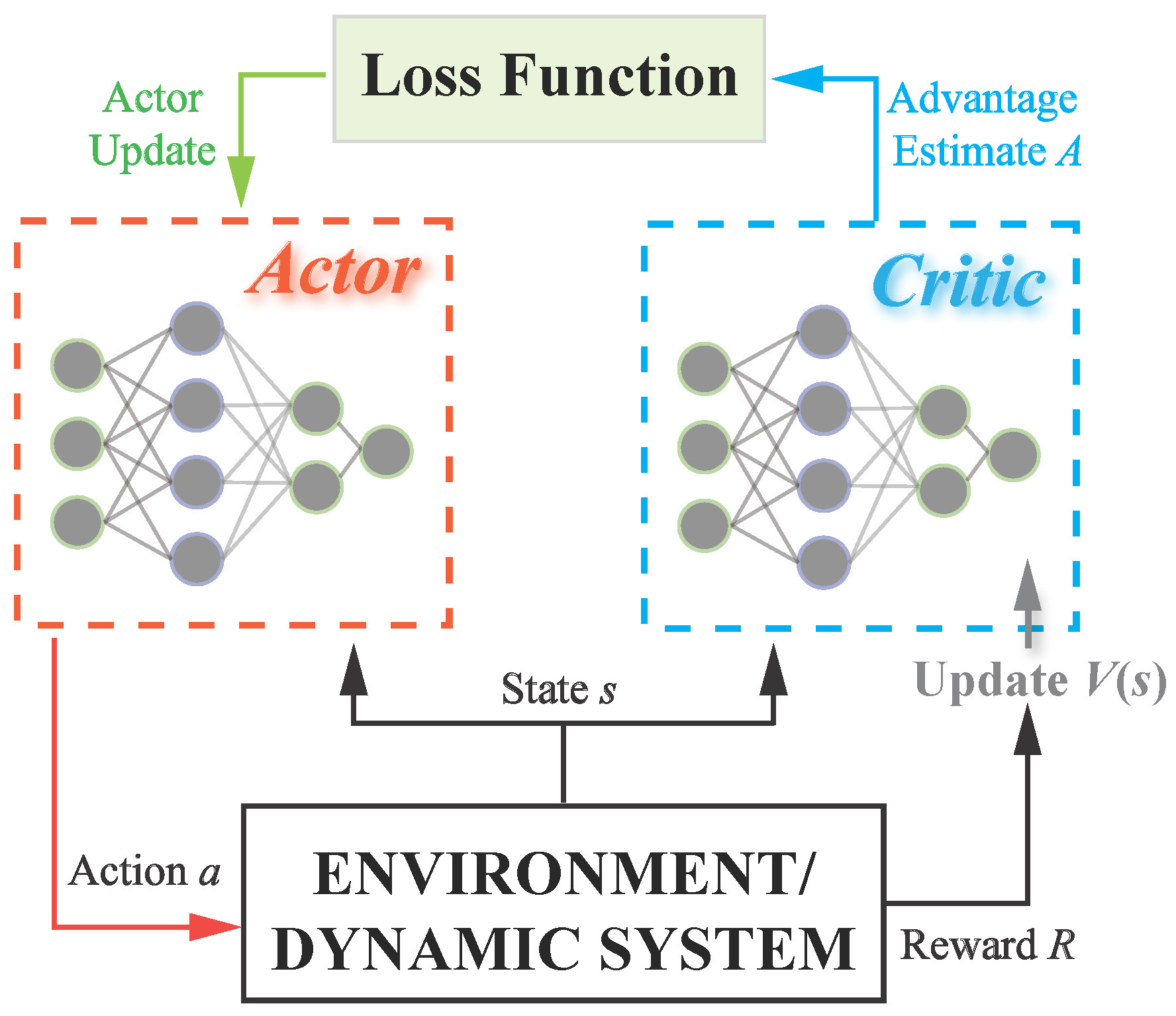
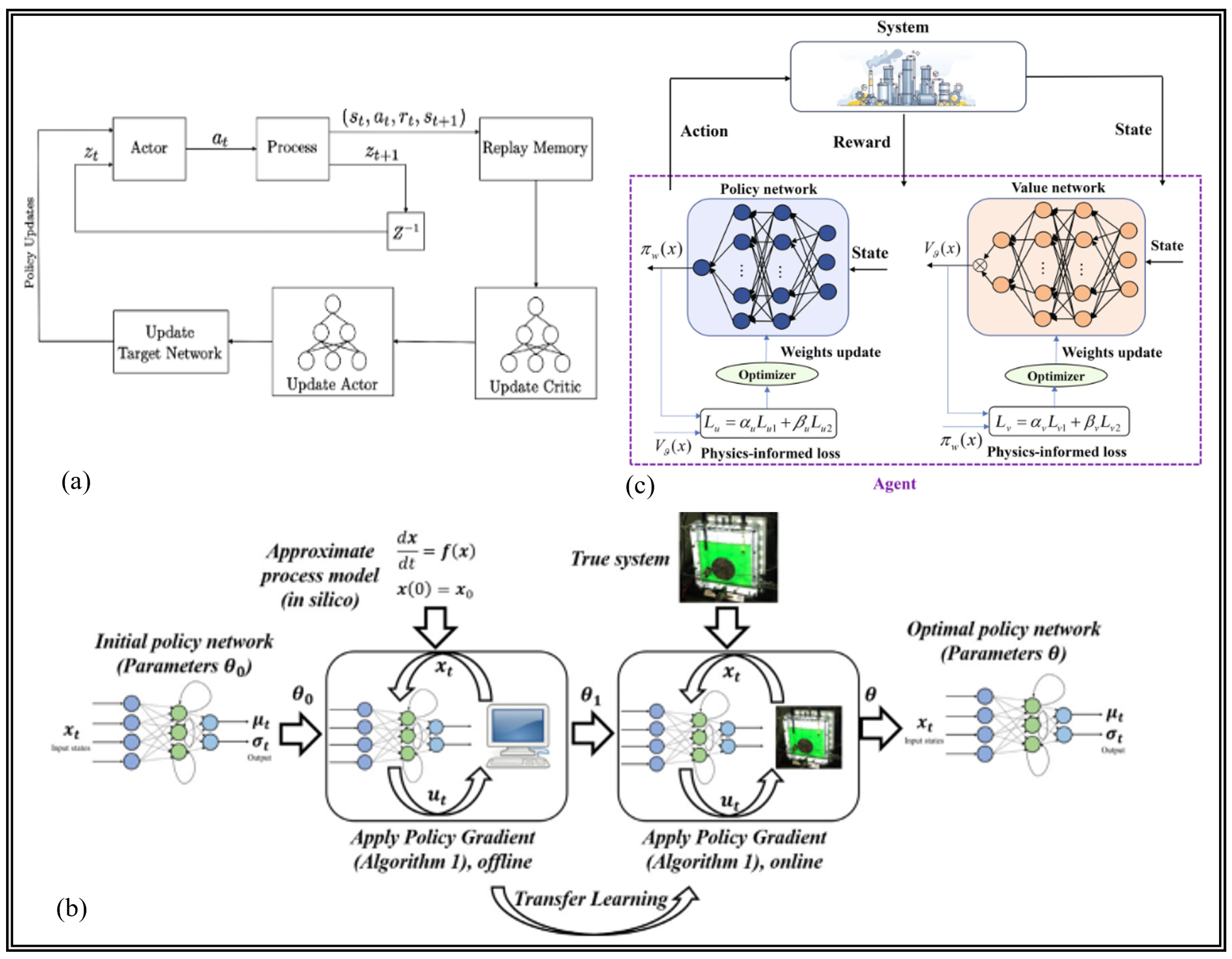
Algorithm	Reference	Key Features	Year
DQN	Mnih et al. [28]	Addressed issues of bias and variance in Q-learning algorithms by introducing target Q-networks and exploiting experience replay	2013
DPG	Silver et al. [29]	A representative departure from stochastic policies that provides the theoretical foundation for deterministic policies in modern RL	2014
DDPG	Lillicrap et al. [30]	Leveraged the tools from DQN to provide a stable and efficient deterministic policy algorithm for continuous action spaces	2015
TRPO	Schulman et al. [31]	Policy update by minimizing the KL-divergence between new and old policies	2015
PPO	Schulman et al. [32]	Clipped surrogate objective to avoid the expensive computation of KL-divergence	2017
TD3	Fujimoto et al. [33]	Twin independent Q-networks, target policy smoothing with clipped noise, delayed policy update	2018
SAC	Haarnoja et al. [34]	Entropy term added for soft Bellman equation, stochastic policy	2018
RND	Burda et al. [35]	Introduces an exploration bonus using the prediction error of a fixed initial neural network for policy improvement	2018
CQL	Kumar et al. [36]	Learns a conservative Q-function to address limitations in standard off-policy RL methods	2020
Distributional SAC	Duan et al. [37], Ma et al. [38]	Leverages distribution function to mitigate Q-value overestimation	2020, 2020
Diffusion-QL	Wang et al. [39]	Represents the policy as a diffusion model to address challenges associated with function approximation on out-of-distribution actions	2023
Offline-to-online RL	Zheng et al. [40]	Considers the difference between offline and online data for adaptive policy learning	2023
PQN	Gallici et al. [41]	Uses LayerNorm to accelerate and simplify temporal difference policy training	2025

, from the classic deep Q-learning algorithm to more recent algorithms such as offline-to-online RL and parallelized Q-network, with a brief overview of each algorithm presented in the following text. Readers of interest are referred to the original research publications for more details. We also refer the readers to review articles on the general topic of RL [22,23,24,25,26,27] for further reading.

• Deep Q-Learning

Q-learning is a classic off-policy method based on temporal difference (TD) learning. The traditional form of Q-learning constructs a table of Q-values for each state–action pair in an exhaustive manner. As the size of the state space increases, this algorithm may become computationally intensive or even intractable. In order to address this issue, deep Q-learning (DQN) is introduced to approximate the Q-function using a deep neural network with weights ($\theta$), i.e., $Q(s,a)\approx Q(s,a,\theta )$.

An important feature of DQN is the use of a second neural network as a target network that computes the target Q-values and is updated less frequently to ensure algorithmic stability. DQN also employs replay buffers (or experience replay), which is a set of all previous experiences that the algorithm has explored. It usually stores these previous experiences in the form of state–action–reward–state tuples. Replay buffers can be very large, storing up to millions of experiences, and are used to train the neural network parameters. The update of the DQN is typically achieved by minimizing the Bellman loss function defined as the mean-squared error between the predicted Q-value of the current state–action pair and the current Q-value (Equation (9)). Gradient descent can be utilized to optimize the loss function and update the weights of the neural network. Additionally, the DQN algorithm adopts an $ϵ$-greedy exploration policy to search the action space. More details can be found in Mnih et al. [28] and Wang et al. [42].

$$L=E\left[{(R+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime },{\theta }^{-})-Q(s,a,\theta ))}^2\right]$$

(9)

where s and a are the current state and action, $s^{\prime }$ and $a^{\prime }$ are the next state and action, $\theta$ are the weights of the main Q-network, and ${\theta }^{-}$ are the weights of the target Q-network. The optimal action can be computed by $a=argmaxQ(s,a,\theta )$, since this algorithm is for discrete action spaces.

• Deterministic Policy Gradient

Deterministic Policy Gradient (DPG) is a policy iteration method where a deterministic policy is developed based on the expected gradient of the action–value function [29]. DPG can be used to map continuous states to continuous actions. It has a Monte Carlo-style of training paradigm. Let ${\mu }_{\theta }$ denote the deterministic policy parametrized with $\theta$. ${\rho }^{\mu }$ defines the discounted state distribution in the deterministic case in analogy to the probabilistic distribution in the stochastic case. The objective is to maximize the expected total discounted reward $J\left({\mu }_{\theta }\right)$, as given in Equation (10). The deterministic policy gradient theorem is formally presented by Equation (11), and can be applied to actor–critic (AC) methods for both on-policy and off-policy learning.

$$J\left({\mu }_{\theta }\right)=E_{s\sim {\rho }^{\mu }}\left[r(s,{\mu }_{\theta }\left(s\right))\right]$$

(10)

$${\mathrm{\nabla }}_{\theta }J\left({\mu }_{\theta }\right)=E_{s\sim {\rho }^{\mu }}\left[{\mathrm{\nabla }}_{\theta }{\mu }_{\theta }\left(s\right){\mathrm{\nabla }}_a{Q}^{\mu }(s,a){|}_{a={\mu }_{\theta }\left(s\right)}\right]$$

(11)

• Deep Deterministic Policy Gradient

Deep Deterministic Policy Gradient (DDPG) [30] presents a seminal actor-critic (AC) algorithm featuring a combination of DQN and DPG. It utilizes the techniques presented in the DQN algorithm (e.g., target networks and experience replay) to provide a more computationally stable algorithm for continuous action space. A schematic of DDPG is illustrated in Figure 2. The algorithm employs the following: (i) a DQN-based critic to estimate the Q-function and (ii) a deterministic policy actor to choose an action based on the current state. Both the actor and critic utilize target networks that are updated using Polyak averaging to avoid aggressive and unstable updates. An actor network is used to estimate the policy for continuous action space, since there is no computationally efficient method to repeatedly compute $a=argmaxQ(s,a,\theta )$, when a is continuous. In this algorithm, the actor network thrives to maximize Q-value approximations and the critic network aims to minimize the Bellman loss.

The DDPG method samples actions in an off-policy manner during training. Instead of adopting the $ϵ$-greedy exploration from DQN, the algorithm uses Ornstein–Ulhenbeck (OU) exploratory noise to explore the continuous action space [43]. Similar to DQN, the use of an experience replay buffer allows the networks to update based on both the current and the past experiences, for a more sampling-efficient learning.

• Trust Region Policy Optimization

Trust Region Policy Optimization (TRPO) is a policy gradient-based RL method introduced in Schulman et al. [31]. It can be characterized as an on-policy method for stochastic policy optimization. TRPO can be applied to both discrete and continuous action spaces. One advantage of TRPO is the guarantee that the updated policies are monotonically improved over the old ones for general classes of stochastic policies. As shown in Equation (12), if a non-negative expected advantage can be achieved for all the states s, namely, ${\sum }_a\tilde{\pi }\left(a\right|s)A_{{\pi }_i}(s,a)\ge 0$, the expected return ($\eta$) of the new policy $\tilde{\pi }$ will be no worse than the old policy $\pi$. Note that ${\rho }_{\pi }\left(s\right)$ is the state visitation density. To relax the calculation of ${\rho }_{\tilde{\pi }}$ as a function of the new policy $\tilde{\pi }$, a local approximation $L\left(\tilde{\pi }\right)$ is normally used in place of $\eta \left(\tilde{\pi }\right)$ (Equation (13)).

$$\eta \left(\tilde{\pi }\right)=\eta \left(\pi \right)+\sum _s{\rho }_{\tilde{\pi }}\left(s\right)\sum _a\tilde{\pi }\left(a\right|s)A_{{\pi }_i}(s,a)$$

(12)

$$L\left(\tilde{\pi }\right)=\eta \left(\pi \right)+\sum _s{\rho }_{\pi }\left(s\right)\sum _a\tilde{\pi }\left(a\right|s)A_{{\pi }_i}(s,a)$$

(13)

A key feature of the practical implementation of TRPO is to take large yet robust steps in the optimization. This is carried out by solving a constrained optimization problem to determine a new set of weights and biases for a parameterized stochastic policy $\left({\pi }_{\theta }(·|s)\right)$, as given in Equation (14).

$$\begin{array}{cc}\hfill \underset{{\theta }_{new}}{max}& L_{{\theta }_{old}}\left({\theta }_{new}\right)\hfill \\ \hfill s.t.& {\overline{D}}_{KL}^{\rho {\theta }_{old}}({\theta }_{old},{\theta }_{new})\le \delta \hfill \end{array}$$

(14)

where ${\overline{D}}_{KL}^{\rho {\theta }_{old}}({\theta }_{old},{\theta }_{new})$ is the average Kullback–Leibler (KL) divergence between the two stochastic policies parameterized by ${\theta }_{old}$ and ${\theta }_{new}$, which are bounded by a hyperparameter $\delta$. The constraint on the average KL divergence does not hold the strong theoretical guarantees across the full state space, but it addresses the solvability issue with imposing constraints on each individual point. This average-based constraint provides heuristic confidence that, on average, the policy is improving or at worst, would stay the same, at each update. In practice, this optimization problem can still be complex to implement as it requires a second-order optimization solver to repeatedly compute the Hessian of the KL divergence constraint.

• Proximal Policy Optimization

Proximal Policy Optimization (PPO) is built on the same motivation as TRPO, i.e., to make large and robust improvements in the policy while ensuring a stable convergence. Built upon TRPO, Schulman et al. [32] introduced PPO as a more generalized AC-based approach with first-order optimization to simplify the implementation and reduce sampling complexity while retaining the same stability benefits. A schematic of PPO is illustrated in Figure 3. While TRPO implements the KL divergence criterion as a hard constraint, PPO uses a clipped surrogate objective to avoid the expensive Hessian computation of the KL divergence altogether. The clipped surrogate objective is represented in Equation (15). A hyperparameter $ϵ$ is used to develop a special clipping in the objective function that effectively eliminates aggressive and unstable policy updates. This clipped objective removes the incentive for the ratio of the new policy to the old policy (i.e., ${\displaystyle \frac{{\pi }_{\theta }\left(a\right|s)}{{\pi }_{{\theta }_k}\left(a\right|s)}}$) to move out of the range of $[1-ϵ,1+ϵ]$. The objective can be maximized using minibatch stochastic gradient descent.

$${\mathcal{L}}^{CLIP}\left(\theta \right)={\mathbb{E}}_t\left[\min \left({\displaystyle \frac{{\pi }_{\theta }\left(a\right|s)}{{\pi }_{{\theta }_k}\left(a\right|s)}}{A}^{{\pi }_{{\theta }_k}}(s,a),\mathrm{clip}({\displaystyle \frac{{\pi }_{\theta }\left(a\right|s)}{{\pi }_{{\theta }_k}\left(a\right|s)}},1-ϵ,1+ϵ)A^{{\pi }_{{\theta }_k}}(s,a)\right)\right]$$

(15)

• Twin Delayed Deep Deterministic Policy Gradient

Twin Delayed Deep Deterministic Policy Gradient (TD3) is an extension of the DDPG proposed by Fujimoto et al. [33]. This algorithm aims to reduce the Q-function overestimation bias caused by DQN and DDPG. Like DDPG, TD3 is also an off-policy algorithm for continuous action spaces utilizing replay buffers. TD3 has three key modifications that have contributed to improved performances over DDPG: clipped double Q-learning, delayed policy updates, and target policy smoothing.

For clipped double Q-learning, two independent critic networks are used with their Q-functions (denoted by $Q_{{\theta }_1}$ and $Q_{{\theta }_2}$ in Equation (16)). The algorithm uses the smaller value of the two to make the actor updates. By choosing this smaller, or more “pessimistic” Q-value, TD3 could achieve reduced overestimation of the Q-function.

$$y_1(r,s^{\prime })=r+\gamma \underset{i=1,2}{\min }{Q}_{{\theta }_i}(s^{\prime },{\pi }_{{\varphi }_1}\left(s^{\prime }\right))$$

(16)

where ${\theta }_1$ and ${\theta }_2$ are the weights of the twin critic networks representing the independent value functions, and ${\varphi }_1$ is the weight of the actor network.

The delayed policy update feature ensures that the policy is not updated as frequently as the critic, usually at a ratio of two critic updates for every one policy update. The update of the policy network is performed at least until the Q-values have converged, i.e., the value error is as small as possible. As for target policy smoothing, a clipped zero-mean noise $ϵ$ with a variance $\sigma$ is added to the target actions (Equations (17) and (18)). This addresses the shortcoming of DDPG that, due to Q-function overestimation in certain areas of the action and state spaces, random peaks may develop, and these local maxima are quickly exploited by the policy. Using the noise within the target policy ensures that similar states and actions have similar Q-values, essentially smoothing the peaks within the Q-estimates.

$$y=r+\gamma \underset{i=1,2}{\min }{Q}_{{\theta }_i}(s^{\prime },{\pi }_{{\varphi }_1}\left(s^{\prime }\right)+ϵ)$$

(17)

$$ϵ\sim clip\left(\mathcal{N}\right(0,\delta ),-c,c)$$

(18)

• Soft Actor–Critic

Soft Actor–Critic (SAC), originally proposed by Haarnoja et al. [34], aims to improve sampling efficiency and to learn a stochastic policy. SAC is an AC-based off-policy method based on maximum entropy learning. Similar to TD3, SAC utilizes the mean squared Bellman error as the loss function to train the critic networks. SAC also trains two independent critics using a shared target value and then uses the clipped double-Q methodology of choosing the smaller Q-value to make updates. In contrast to TD3, the target includes an entropy term, making use of a modified version called a soft Bellman equation.

Another major difference is the use of the current policy instead of the target policy to choose actions for the future states. The loss function of critic networks is formulated as Equation (19). The target value (y) can be described as Equation (20). The objective for the actor network training is to maximize the expected future return and the expected entropy, as shown in Equation (21).

$$L({\theta }_i,\mathcal{D})={\mathbb{E}}_{(s,a,r,s^{\prime })\sim \mathcal{D}}[(Q_{{\theta }_i}(s,a)-y{(r,s^{\prime })}^2]$$

(19)

$$y(r,s^{\prime })=r+\gamma (\underset{j=1,2}{\min }{Q}_{{\theta }_{target,j}}(s^{\prime },a^{\prime })-\alpha log{\pi }_{\theta }\left(a^{\prime }\right|s^{\prime }))$$

(20)

$$V^{\pi }\left(s\right)=\underset{a\sim \pi }{\mathbb{E}}\left[Q^{\pi }(s,a)\right]-\alpha log\pi \left(a\right|s)$$

(21)

where $i=\{1,2\}$ indicates the independent critic networks, ${\theta }_i$ is the weight of the networks, y is the target value, $a^{\prime }$ is the future action corresponding to the future state $s^{\prime }$ sampled from the policy for the target calculation.

• Random Network Distillation

The random network distillation (RND) algorithm is an exploration method introduced to deal with the parallel processing of large numbers of samples in RL agent training [35]. The central idea of the RND method is to use prediction errors of networks trained on the agent’s past experience to quantify the novelty of the new experience. The algorithm is composed of two neural networks: a fixed and randomly initialized target network that converts an observation into an embedding, and a predictor neural network that is trained by gradient descent to minimize the expected prediction mean squared error. The RND prediction error can be viewed as a special case of a previously proposed uncertainty quantification method in Osband et al. [44] that quantifies the uncertainty in predicting the constant zero function in the following minimization, with regression targets $y_i$ = 0:

$$\theta =arg\underset{\theta }{min}{\mathbb{E}}_{(x_i,y_i)\sim \mathcal{D}}{∥f_{\theta }\left(x_i\right)+f_{{\theta }^{*}}\left(x_i\right)-y_i∥}^2+\mathcal{R}\left(\theta \right)$$

(22)

where $D=\{x_i,y_i\}$ is the data distribution, $f_{\theta }$ is the mapping of the neural network parameters $\theta$, and R is a regularization term from the prior. For detailed description and demonstration on study cases, we refer the readers to Burda et al. [35].

• Conservative Q-Learning

Introduced by Kumar et al. [36], the Conservative Q-learning (CQL) algorithm aims to address the overestimation issue associated with standard value-based off-policy RL algorithms on out-of-distribution actions, with a conservative estimate of the value function. The algorithm targets estimating the value $V\left(s\right)$ of a target policy $\pi$ given a dataset $\mathcal{D}$, generated from a behavior policy ${\pi }_{\beta }$. The penalty is formulated to minimize the expected Q-function ($\widehat{Q}$) under a particular distribution of state–action pairs, $\mu (s,a)$, as in:

$${\widehat{Q}}^{k+1}\leftarrow arg\underset{Q}{min}\alpha {\mathbb{E}}_{s\sim \mathcal{D},a\sim \mu \left(a\right|s)}\left[Q(s,a)\right]+{\displaystyle \frac{1}{2}}{\mathbb{E}}_{s,a\sim \mathcal{D}}\left[{\left(Q(s,a)-{\mathcal{B}}^{\pi }{\widehat{Q}}^k(s,a)\right)}^2\right]$$

(23)

where $\mathcal{B}$ is the Bellman operator. By setting $\mu (s,a)=d^{{\pi }_{\beta }}\left(s\right)\mu \left(a\right|s)$ to match the state-marginal in the dataset, it can be proven that the Q-function can provide a lower bound at all $(s,a)$ pairs. To tighten the bound, the authors introduced an additional Q-value maximization term to formulate a new iterative update as:

$$\begin{array}{c}\hfill {\widehat{Q}}^{k+1}\leftarrow arg\underset{Q}{min}\alpha ·\left({\mathbb{E}}_{s\sim \mathcal{D},a\sim \mu \left(a\right|s)}\left[Q(s,a)\right]-{\mathbb{E}}_{s\sim \mathcal{D},a\sim {\widehat{\pi }}_{\beta }\left(a\right|s)}\left[Q(s,a)\right]\right)\\ \hfill +{\displaystyle \frac{1}{2}}{\mathbb{E}}_{s,a,s^{\prime }\sim \mathcal{D}}\left[{\left(Q(s,a)-{\mathcal{B}}^{\pi }{\widehat{Q}}^k(s,a)\right)}^2\right]\end{array}$$

(24)

To utilize the Q-value lower bound in policy optimization, the authors then formulated a family of optimization problems over $\mu \left(a\right|s)$ to approximate the policy that maximizes the current Q-function iteration, with a particular choice of regularizer $R\left(\mu \right)$, as in the following [36]:

$$\begin{array}{c}\hfill \underset{Q}{min}\underset{\mu }{max}\alpha \left({\mathbb{E}}_{s\sim \mathcal{D},a\sim \mu \left(a\right|s)}\left[Q(s,a)\right]-{\mathbb{E}}_{s\sim \mathcal{D},a\sim {\widehat{\pi }}_{\beta }\left(a\right|s)}\left[Q(s,a)\right]\right)\\ \hfill +{\displaystyle \frac{1}{2}}{\mathbb{E}}_{s,a,s^{\prime }\sim \mathcal{D}}\left[{\left(Q(s,a)-{\mathcal{B}}^{{\pi }_k}{\widehat{Q}}^k(s,a)\right)}^2\right]+R\left(\mu \right)\end{array}$$

(25)

• Distributional SAC

To mitigate Q-value overestimations, Duan et al. presented a distributional soft actor–critic algorithm for continuous control settings in [37]. Specifically, the algorithm first learns a distribution function of state–action results and then embeds the return distribution function into maximum entropy RL for mitigated Q-value overestimation. The algorithm was developed with a general entropy-augmented objective with a policy entropy term $\mathcal{H}$ to augment the reward J.

$$J_{\pi }={\mathbb{E}}_{(s_i\ge t,a_i\ge t)\sim {\rho }_{\pi },r_i\ge t\sim R(·|s_i,a_i)}\left[\sum _{i=t}^{\infty }{\gamma }^{i-t}\left[r_i+\alpha \mathcal{H}\left(\pi (·|s_i)\right)\right]\right]$$

(26)

where

$$\begin{array}{cc}\hfill \mathcal{H}\left(\pi \right(·\left|s\right))& =-{\int }_{a\in \mathcal{A}}\pi \left(a\right|s)log\pi \left(a\right|s)da\hfill \\ \hfill & ={\mathbb{E}}_{a\sim \pi (·|s)}\left[-log\pi \left(a\right|s)\right]\hfill \end{array}$$

(27)

The expected soft return for selecting action $a_t$ in state $s_t$ with policy $\pi$ with the soft Q-value of policy $\pi$ is then defined as:

$$Q^{\pi }(s_t,a_t)={\mathbb{E}}_{r\sim R(·|s_t,a_t)}\left[r\right]+\gamma {\mathbb{E}}_{\begin{array}{c}(s_i>t,a_i\ge t)\sim {\rho }_{\pi },\\ r_i>t\sim R(·|s_i,a_i)\end{array}}\left[G_{t+1}\right]$$

(28)

where the return $G_t$ is calculated as $G_t={\sum }_{i=t}^{\infty }{\gamma }^{i-t}\left[r_i-\alpha log\pi \left(a_i\right|s_i)\right]$, with $\alpha$ being the discount factor. The maximum entropy RL is then extended to distributional learning by directly modeling the distribution of the soft returns $Z^{\pi (s,a)}$, $\tilde{Z}\left(Z^{\pi (s,a)}\right|s,a)$, where $Z^{\pi (s,a)}$ is defined as: $Z^{\pi }(s_t,a_t)=r_t+\gamma G_{t+1}{|}_{(s_i>t,a_i>t)\sim {\rho }_{\pi },r_i\ge t\sim R(·\mid s_i,a_i)}$.

The distributional variant of the Bellman operator (${\mathcal{T}}_D^{\pi }$) in the maximum entropy framework is defined as:

$${\mathcal{T}}_D^{\pi }{Z}^{\pi }(s,a)\stackrel{D}{=}r+\gamma \left(Z^{\pi }(s^{\prime },a^{\prime })-\alpha log\pi \left(a^{\prime }\right|s^{\prime })\right)$$

(29)

and the Bellman operator can be implemented as a loss function defined as the following:

$${\tilde{Z}}_{\mathrm{new}}=arg\underset{Z}{min}{\mathbb{E}}_{(s,a)\sim {\rho }_{\pi }}\left[d\left({\mathcal{T}}_D^{\pi }{\tilde{Z}}_{\mathrm{old}}(·|s,a),\tilde{Z}(·|s,a)\right)\right]$$

(30)

where $\tilde{Z}$ is the soft state–action return distribution or the distributional value function. Theoretical analysis and case study demonstration are given in [37]. Other notable examples with distributional SAC algorithms include [38], for example.

• Diffusion Q-Learning

Diffusion Q-Learning was introduced by Wang et al. [39] to use diffusion models for policy regularization to address the inaccurate function approximation issue with standard offline RL algorithms with out-of-distribution actions. The RL policy is represented as the reverse process of a conditional diffusion model as:

$${\pi }_{\theta }(\mathit{a}\mid s)=p_{\theta }(a^{0:N}\mid s)=\mathcal{N}(a^N;0,\mathit{I})\prod _{i=1}^N{p}_{\theta }(a^{i-1}\mid a^i,s)$$

(31)

where $P_{\theta }$ is parameterized as a noise prediction model with covariance matrix ${\Sigma }_{\theta }({\mathit{a}}^i,\mathit{s},i)={\beta }_i\mathit{I}$ and mean constructed as ${\mu }_{\theta }({\mathit{a}}^i,\mathit{s},i)={\displaystyle \frac{1}{\sqrt{{\overline{\alpha }}_i}}}\left({\mathit{a}}^i-{\displaystyle \frac{{\beta }_i}{\sqrt{1-{\overline{\alpha }}_i}}}{ϵ}_{\theta }({\mathit{a}}^i,\mathit{s},i)\right)$, with $a^N$ sampled from $\mathcal{N}(0,\mathit{I})$ to form the reverse diffusion chain parameterized by $\theta$:

$${\mathit{a}}^{i-1}\mid {\mathit{a}}^i={\displaystyle \frac{{\mathit{a}}^i}{\sqrt{{\alpha }_i}}}-{\displaystyle \frac{{\beta }_i}{\sqrt{{\alpha }_i(1-{\overline{\alpha }}_i)}}}{ϵ}_{\theta }({\mathit{a}}^i,\mathit{s},i)+\sqrt{{\beta }_i}\mathit{ϵ},\mathit{ϵ}\sim \mathcal{N}(0,\mathit{I}),\mathrm{for}i=N,\dots ,1.$$

(32)

The conditional model is then trained with a simplified objective function ${\mathcal{L}}_d\left(\theta \right)$:

$${\mathcal{L}}_d\left(\theta \right)={\mathbb{E}}_{i\sim \mathcal{U},\mathit{ϵ}\sim \mathcal{N}(0,\mathit{I}),(s,\mathit{a})\sim \mathcal{D}}\left[{∥\mathit{ϵ}-{ϵ}_{\theta }\left(\sqrt{{\overline{\alpha }}_i}\mathit{a}+\sqrt{1-{\overline{\alpha }}_i}\mathit{ϵ},\mathit{s},i\right)∥}^2\right]$$

(33)

and the final policy-learning objective is given as a combination of policy regularization and policy improvement, as:

$$\pi =arg\underset{{\pi }_{\theta }}{min}\mathcal{L}\left(\theta \right)={\mathcal{L}}_d\left(\theta \right)+{\mathcal{L}}_q\left(\theta \right)={\mathcal{L}}_d\left(\theta \right)-\alpha ·{\mathbb{E}}_{\mathit{s}\sim \mathcal{D},{\mathit{a}}^0\sim {\pi }_{\theta }}\left[Q_{\varphi }(\mathit{s},{\mathit{a}}^0)\right]$$

(34)

where the Q-value can be solved by minimizing the Bellman operator.

• Offline-to-Online RL

In [40], Zheng et al. introduced an offline-to-online algorithm to address the challenge of online learning in obtaining large amounts of data for policy training, and the issue with offline learning where the performance can be poor if the offline data do not represent well the online interactions. The underlying idea of the algorithm is to use an optimistic online RL update strategy to emphasize more the real situation of the policy, and a pessimistic offline RL update strategy to also leverage offline data for policy training. The idea can be represented in the following general formalization:

$$C^{k+1}\leftarrow \mathcal{F}\left(\mathbb{A}\left(C^k\right)+\mathcal{W}(\mathit{s},\mathit{a})\mathbb{B}\left(C^k\right)\right)$$

(35)

where C represents a policy or value function for policy-based or value-based methods. $\mathbb{A}\left(C\right)$ is the optimistic update strategy, such as the Bellman error for value-based methods, and $\mathbb{B}\left(C\right)$ is the pessimistic update strategy as a penalty to make the learned agent take actions close to the dataset or take conservative actions. $\mathcal{W}(\mathit{s},\mathit{a})$ is the weight function to the penalty term $\mathbb{B}\left(C\right)$ that enables adaptive learning of the policy, and $\mathcal{F}$ is the general updating operator, such as $argmin$ or $argmax$. Demonstration with value-based and policy-based methods is provided in [40].

• Parallelized Q-network

Proposed in Gallici et al. [41], the parallelized Q-learning (PQN) algorithm seeks to address the stabilization issue in training with TD algorithms with off-policy data, with a simplified version of DQN. The basis of the algorithm is to use LayerNorm and $L^2$ regularization for TD stabilization with the following Q-function approximator:

$$Q_{\varphi }^k\left(x\right)=w^{\top }{\sigma }_{\mathrm{Post}}\circ {\mathrm{LayerNorm}}^k\left[{\sigma }_{\mathrm{Pre}}\circ Mx\right]$$

(36)

where $\varphi =[w^{\top },\mathrm{Vec}{\left(M\right)}^{\top }]$ is the parameter vector, $M\in {\mathbb{R}}^{k\times d}$ is a $k\times d$ matrix, $w\in {\mathbb{R}}^k$ is a vector of the final layer weights, and ${\sigma }_{Pre}$ and ${\sigma }_{Post}$ are element-wise $C^2$ continuous activations with bounded 2nd order derivatives [41]. The author further assumes ${\sigma }_{Post}$ is $L_{Psot}$–Lipschitz with ${\sigma }_{Post}\left(0\right)=0$. The LayerNorm is defined as:

$${\mathrm{LayerNorm}}_i^k\left[f\left(x\right)\right]:={\displaystyle \frac{1}{\sqrt{k}}}·{\displaystyle \frac{f_i\left(x\right)-\frac{1}{k}{\sum }_{j=0}^{k-1}{f}_j\left(x\right)}{\sqrt{\frac{1}{k}{\sum }_{i=0}^{k-1}{\left(f_i\left(x\right)-\frac{1}{k}{\sum }_{j=0}^{k-1}{f}_j\left(x\right)\right)}^2+ϵ}}}$$

(37)

where $ϵ$ is a small constant for numerical stability. The authors then demonstrated that with $\lambda$-returns, which is a parallelized variant of a previously proposed approach in Daley and Amato [45], an exploration policy can then be rolled out: starting with $R_{i+T}^{\lambda }={max}_{a^{\prime }}{Q}_{\varphi }(s_{i+T},a^{\prime })$, and computed recursively back in time from $R_{i+T-1}^{\lambda }$ to $R_i^{\lambda }$ for the targets, using $R_t^{\lambda }=r_t+\gamma \left[\lambda R_{t+1}^{\lambda }+(1-\lambda ){max}_{a^{\prime }}{Q}_{\varphi }(s_{t+1},a^{\prime })\right]$.

3. Implementations for Process Control

Since its advent, RL has received increasing applications for chemical process control. In terms of applications on control strategy development, RL has been mainly used for controller tuning and direct policy learning, while in terms of processes, RL has been widely applied from molecular design, to materials, to chemical reaction optimization, and to process design and optimization etc. In this section, we review the latest advances on these research fronts. While RL-based controller tuning can generally be carried out on fixed-parameter controllers, such as PID, lead-lag, linear quadratic regulator (LQR), and gain scheduling controllers, etc., here, we will primarily focus on PID tuning, given its popularity, and give a brief summary on some of the other types of controllers. While most of the references in this review are chemical process-related, a brief summary on some of the specific fields in chemical processes that have benefited from and are seeing increasing applications with RL is also given at the end of this section.

3.1. RL-Based PID Tuning

A generic proportional-integral-derivative (PID) formulation is given in Equation (38):

$$u\left(t\right)=K_pϵ\left(t\right)+K_I{\int }_0^Tϵ\left(t\right)dt+K_D\dot{ϵ}\left(t\right)$$

(38)

$ϵ\left(t\right)$ is the deviation from the set-point of the controlled variable at any given time t. $K_p$, $K_I$, and $K_D$ are the proportional gain, integral gain, and derivative gain as the tunable parameters, respectively. PID tuning is conventionally performed offline under a certain set of operating conditions [46]. These approaches can be categorized as (i) rule-based, such as Ziegler–Nichols methods and Cohen–Coon etc., and (ii) model-based, such as internal model control (IMC). However, these tuning methods might require knowledge on the system dynamics, time-consuming fine tuning, and might not offer satisfactory performance for complex systems with nonlinearity, stochasticity, and unknown dynamics due to the lack of real-time response to time-varying uncertainties [47]. To improve the applicability of PID controllers, researchers have referred to RL for (1) automation, where tuning the parameters can be efficiently performed by interacting with the environment in an autonomous manner; (2) real-time adaptivity, where the controller dynamically tunes the parameters to adapt to changes or disturbances in the process; and (3) optimality, where multiple optimization objectives and constraints can be incorporated in designing the controller parameters for optimal performance.

One of the first efforts on this front is credited to Howell and Best [48], where PID tuning is automated using RL for a Ford Motors Zetec engine. The parameters were initialized with the Ziegler–Nichols tuning rule, and the authors applied a continuous action reinforcement learning automata (CARLA) algorithm to tune the controller, and achieved reduced process operating cost as compared to using the baseline PID parameters. As depicted in Figure 4, the RL agent was designed with several CARLA modules, each of which represents a variable for one PID parameter. In this way, three CARLA modules were used to tune one single PID controller. The performance metric was evaluated each time, based on which action the agent chose to optimize the controller tuning parameter. This approach, however, would come at a very high computational cost for the training process, as the process scale increases with more controllers, a large number of CARLA modules may be required.

The advent of DRL has further transformed the use of RL for autonomous PID tuning. Nian et al. [11] provided an excellent literature review on the early advances in the implementation of DRL algorithms for PID tuning (before 2020). Over the last few years, AC-algorithms have been increasingly used to design the RL agents, as they overcome the shortcomings of the value-based and policy-based methods.

Table 2. Methods for RL-based PID tuning — an indicative list.

Publication	Algorithm	Key features	Year
Dogru et al. [49]	Contextual bandit	Constrained-RL; Offline training using approximate step-response model; Online fine tuning	2022
Lakhani et al. [50]	DPG	PID tuning with stability consideration; Episodic tuning; Layer normalization	2022
Fujii et al. [51]	Policy-gradient-type AC	MIMO process; Complex process with input coupling and input–output lag	2021
Mate et al. [52]	DDPG	Single DRL agent used to tune multiple PID controllers; Inverting gradients to integrate interval constraints on tuning parameters	2023
Wang and Ricardez-Sandoval [47]	Modified IDDPG	Nonlinear MIMO; Time-varying uncertainty	2024
Li and Yu [53]	TGSL-TD3PG	Multiple agents trained via imitation learning and curriculum learning	2021
Li and Yu [54]	FSSL-TD3	Improved exploration using fittest survival strategy	2021
Lawrence et al. [55]	Modified TD3	Implementation in a real physical process; Software-hardware interplay; Interpretability	2022
Chowdhury et al. [56]	EMTD3	Entropy-maximizing stochastic actor for environment exploration, followed by deterministic actor for local exploitation	2023
Veerasamy et al. [57]	TD3 and SAC	Comparison of discrete and Gaussian reward functions; Nonlinear process	2024
Shuprajhaa et al. [58]	Modified PPO	Unstable processes with unbounded output; Action repeat; Early stopping	2022

presents a list of recent methods for RL-based PID tuning, followed by detailed discussions of the representative works.

Mate et al. [52] presented the PID tuning of a plant-wide control framework involving multiple single-input single-output (SISO) PID controllers. A DDPG algorithm was used to simultaneously tune these PID controllers to account for interactions between different control loops. A challenge for the proposed algorithm was that it required a massive amount of real-time operating data to train the RL agent, which required the development of, e.g., a high-fidelity digital twin to enable online deployment. Interval constraints were enforced on the tuning parameters to ensure safe plant operations. These constraints were integrated within the RL algorithm via the inverting gradients approach [59], as illustrated in Figure 5a. Namely, if a parameter reached the constraint bound, the sign of its gradient would be inverted. This inverting gradients approach is widely applied in many RL-based PID tuning methods, as can be noted from the following discussions.

For multi-input multi-output (MIMO) systems, Fujii et al. [51] developed a self-tuning PI control system for a thin film production process using an AC-based DRL algorithm. One challenge was the spatial mechanical coupling in this production process, where there existed inter-dependencies among the various inputs. This was addressed by introducing a spatial coefficient that can be tuned to compensate the degree of interaction between inputs. A better performance was observed in terms of film thickness control as compared to a conventional PI controller tuned with Ziegler–Nichols method. However, transient oscillation was also observed in the spatial root mean squared error, suggesting further improvement was needed. Wang and Ricardez-Sandoval [47] modified the inverted DDPG algorithm to further account for time-varying uncertainty in nonlinear MIMO systems. The widely used PID tuning criterion, integral of the time-weighted absolute errors (ITAEs), was used as the reward function. The algorithm was tested for a MIMO CSTR system by simulating time-varying uncertainty in two different ways: catalyst deactivation and regeneration. While conventionally-tuned controllers failed to address the uncertainty and led to notable offsets and ITAEs, the RL-based ITAE optimization algorithm provided significantly better performance with >90% reduction in ITAE mean and standard deviation.

Dogru et al. [49] introduced a constrained RL algorithm using a contextual bandit agent that does not require the assumption of Markovian state transitions. The authors also developed a training and deployment strategy to minimize online tuning. As shown in Figure 5b, The agent was initially trained offline on an approximate step-response model of the process to determine an initial set of tuning parameters. On this basis, the agent would be fine tuned when implemented online to interact with the real process under sensory noise. The online computational complexity was significantly reduced as part of the training shifted offline. The approach was successfully showcased on a pilot-scale experimental process involving a multi-model tank system.

Li and Yu [53] proposed the two-stage training strategy twin delayed deep determination policy gradient (TGSL-TD3PG) approach as a large-scale DRL algorithm, as shown in Figure 5c. This algorithm leveraged imitation and curriculum learning to train the agent. The resultant algorithm was reported to improve the robustness, adaptability, and constraint consideration compared to conventional PID control. It was applied to optimize the PID controller parameters to regulate the output voltage of a solid oxide fuel cell (SOFC). The optimal tuning parameters led to a 45.2% reduction of output voltage setting time and 30% less overshoot in the output voltage. Li and Yu [54] further addressed the consideration of fuel utilization constraints in addition to output voltage control. The authors investigated the tuning of a fractional order PID controller in SOFC using a modified fittest survival strategy large-scale twin delayed deep deterministic policy gradient (FSSL-TD3) algorithm. FSSL-TD3 showed improved exploration efficiency as the use of fittest survival strategy and imitation learning provided higher robustness and adaptivity for tuning.

Also addressing the implementation of RL in actual physical systems, Lawrence et al. [55] proposed an algorithm where the policy was directly parametrized by PID parameters. This also led to enhanced interpretability of the RL controller. A modified TD3 algorithm was designed using the OpenAI Gym environment. Herein, a human machine interface (HMI) was developed in Matlab to connect with the tank system. HMI also recorded process data and sent them to the RL agent periodically. The RL agent would convert the data into state–action–reward–transition series ($s,a,r,s^{\prime }$) and construct a replay buffer. The reward function was formulated based on the tracking error for output variables as well as the change in manipulating variables at two successive time steps. To ensure safe operations, input constraints were enforced using the inverse gradient approach (Figure 5a). The authors compared the results with the Skogstad internal model control (SIMC) tuning method and the Honeywell Accutune III relay auto-tuning algorithm. The RL algorithm demonstrated better performance in terms of nominal performance, robustness, disturbance rejection, and satisfaction of input constraints. However, the RL algorithm used 30–50 min for training while Accutune III used around 10 min.

Closed-loop stability under noisy system measurements remains an open research question for RL-based control. The parameters chosen for autonomous RL-based PID tuning should be ensured to maintain stability of the system. To this purpose, Lakhani et al. [50] presented a stability-preserving RL-based algorithm for autonomous PID tuning based on DPG. Layer normalization was implemented for the actor and critic networks to prevent policy saturation and to ensure the convergence to the optimal PID parameters. An episodic tuning method was developed in which the parameters in the DPG networks were updated at the end of each episode. In this way, the PID parameters stayed the same for each episode to gain a thorough evaluation of the entire closed-loop performance. The reward function was set based on tracking error. A supervisor mechanism was applied to update the tuning parameters if better tracking performance was achieved or, otherwise, switch back to the baseline values to ensure stable closed-loop operation. The efficacy of the proposed method was demonstrated using a second-order plus dead-time (SOPDT) process.

Sampling efficiency presents another outstanding challenge for RL. As mentioned earlier, a large amount of data is required for RL agent training over many episodes. The low sample efficiency caused by the inefficient exploration strategies also could lead to sub-optimal policies and sub-optimal parameters. To address this challenge, Chowdhury et al. [56] developed an entropy-maximizing TD3 (EMTD3) approach for autonomous PID tuning (Figure 5d). To improve exploration, the algorithm started with an entropy-maximizing stochastic actor to obtain the knowledge on the environment, followed by a deterministic actor for local exploitation to accelerate convergence. This algorithm was showcased using a SOPDT process and a nonlinear CSTR system. The EMTD3 algorithm was shown to provide superior performance compared to the traditional TD3 and SAC algorithms in terms of sample efficiency, convergence speed, and stability. However, this algorithm required a good selection of hyperparameters to ensure satisfactory control performance.

3.2. Application of RL on Other Controllers

RL algorithms are also used to facilitate gain scheduling controller and LQR design. In [60], the authors presented a gain-scheduled PI controller design with a proximal policy optimization approach to simultaneously target three design objectives: quick initial response, minimized overshoot, and fast settling and minimal steady state error. Specifically, the control task is divided into three segments, with one RL-based controller for each segment to target one of the three specific objectives. Each RL-based controller will output a set of PI controller design parameters, and the scheduling of the switch among different parameters is dictated by the error band between the target and the process output. Simulation results with a second-order system and a steam turbine system demonstrated significant improvement over other popular approaches considered in the work [60]. Other related works include [61,62]. In [63], Rizvi et al. incorporated RL for a model-free solution to a continuous-time LQR problem. In their work, a filter-based observer was first implemented to parameterize the state vector for output feedback, and they investigated both policy and value iterations in searching for the optimal solution to the time-continuous LQR problem. Theoretical analysis and simulation results demonstrated that the proposed RL-based solution to the LQR problem can overcome limitations from exploration bias, with improved stability. Interested readers are also referred to the classic work by Bradtke [64] on this topic.

The application of RL on model predictive control (MPC) has also received wide attention over the years. MPC stands as one of the most popular controllers in industrial application and enjoys advantages such as safety constraint handling and real-time adaptability, etc. However, the performance of MPC is heavily dependent on the underlying model, which can be challenging to identify. RL can then be used to learn and adapt to a new environment for predictions to be used in the MPC setup, potentially improving the stability of the closed-loop MPC control. For example, in [65], the authors combined economic MPC (EMPC) with RL to form an optimal control framework, where RL is used to estimate the bounded parameters of the underlying nonlinear model for an accurate prediction of the system dynamics, while the optimal control actions are calculated with EMPC. Theoretical analysis suggests the achievement of practical stability and recursive feasibility under certain assumptions, and implementation on a catalytic oxidation of ethylene to ethylene oxide process in a continuous stirred-tank reactor demonstrated improved accuracy in model parameter estimation, as well as in the resulting control performance. In [66], Oh et al. proposed a double-deep Q-network to learn the action–value function in an off-policy manner to assign the terminal cost used in the MPC objective function. It was claimed by the authors that the proposed control framework could improve the control policy with smaller amounts of data, with less sensitivity to the Q-network hyperparameters, and can enable explicit incorporation of state constraints. Simulated testing results on an industrial-scale penicillin product bioreactor showed that, the proposed method improved the control policy with smaller amounts of data compared to DDQN and DDPG, and it also outperformed DDP by overcoming the model–plant mismatch. Other related research works and review articles on this topic include [67,68,69,70,71], to name a few.

3.3. RL for Control Policy Learning

In addition to tuning the control parameters, RL has been applied to directly learn the control policy.

Table 3. RL methods for control policy learning—an indicative list.

Publication	Algorithm	Key Features	Year
Spielberg et al. [72]	AC	Discrete-time SISO, MIMO, and nonlinear processes; Set-point tracking and disturbance rejection	2019
Goulart & Pereira [73]	AC	Particle swarm optimization for RL hyperparameter tuning	2020
Petsagkourakis et al. [9]	REINFORCE	Batch process with plant-model mismatch; Offline training followed by transfer learning and online deployment	2020
Bangi and Kwon [74]	DDPG	Principal component analysis for dimensionality reduction; Transfer learning for online deployment	2021
Siraskar [75]	DDPG	Graded learning technique; MATLAB (R2019a) RL Toolbox and Simulink	2021
Panjapornpon et al. [76]	DDPG	Multi-agent RL with gated recurrent unit layer; Grid search for hyperparameter tuning	2022
Patel [77]	DDPG	Problem formulation with domain knowledge	2023
Bao et al. [78]	DDACP	Immediate reward to provide gradient information to actor; Expectation form of policy gradient	2021
Elmaz et al. [79]	PPO	Combining two separate process phases; Constraints implemented via logarithmic barrier functions	2023
Hong et al. [80]	DDPG	DRL-PID cascade control	2024
Beahr et al. [81]	TD3	RL-PID in parallel	2024
Wang and Wu [82]	Physics-informed RL	Integrating Lyapunov stability and policy iteration convergence conditions	2024
Faridi et al. [83]	Model-based DRL	Deep NN to learn process dynamics	2024
Croll et al. [84]	–	Comparison of DQN; ppO, TD3, etc.	2023
Oh [85]	–	Comparison of data-driven MPC using N4SID, NNARX, LSTM vs. model-free RL control using DDPG, TD3, SAC	2024

presents a list of recent methods for RL control, followed by detailed discussions of representative works.

The motivation of Spielberg et al. [72] was to develop model-free control that could learn a dynamic data-driven control policy as a replacement to the interruptive model re-identification procedures used in the current practice. The authors successfully implemented an AC-style algorithm to develop a DRL-based controller (Figure 6a) for set-point tracking of discrete-time SISO, MIMO, and nonlinear processes with dynamic disturbances. Case studies were presented for a paper-making machine, a distillation column, and a heating, ventilation, and air conditioning process. Alves Goulart and Dutra Pereira [73] developed an AC-based pH controller to handle the wastewater from the electroplating industry. A key aspect of the controller was that the tuning of the RL hyperparameters was automated by adapting the particle swarm optimization (PSO) algorithm. Using a conventional PID controller, oscillatory responses were observed due to the highly nonlinear process dynamics, with an offset of at least 12.6% for the servo operation. Testing with the RL controller demonstrated a smooth control performance with no offsets, in contrast. As hyperparameter tuning was key to RL, the authors compared the algorithm with or without the PSO-based tuning, and found that the superior control performance was only achieved when the hyperparameters were well-tuned.

As briefly discussed in the Introduction section, Petsagkourakis et al. [9] implemented a policy-gradient-based REINFORCE algorithm for batch bioprocesses with plant–model mismatch. The batch process was characterized with complex nonlinear dynamics and stochastic behaviors. As depicted in Figure 6b, the agent was initially trained offline using a state-space representation of the process model. Transfer learning was then implemented for online deployment. Part of the policy network would be kept frozen to retain the knowledge learned offline, while the last hidden layers or the newly added layers would be trained using the real-time data. The offline training time was reported to be 3 h on CPU while the online implementation required merely 0.002 s. The performance was compared with that of a nonlinear MPC. Transfer learning was also leveraged by Bangi and Kwon [74] for online learning using real-time data. In this work, a DDPG-based RL control strategy was developed for a hydraulic fracturing process. A key feature of this algorithm was using principal component analysis to reduce the dimensionality of the RL state before actor and critic learning, thus achieving faster learning. A reduced-order model was developed using the multivariate output error state space algorithm, based on which the agent was trained offline. The use of transfer learning was also observed to reduce the online computational time. A cumulative reward function was designed that comprised three separate terms to, respectively, minimize tracking error, enforce constraints on control inputs, and incorporate prior process knowledge.

Panjapornpon et al. [76] discussed a multi-agent DDPG-based RL strategy for the coupled control of pH and liquid level in an acid–base reaction process. A gated recurrent unit (GRU) layer was used for the actor and critic networks. A grid search technique was also implemented for the efficient tuning of hyperparameters such as the number of training episodes and the number of hidden layers. The reward function was designed separately for the pH and the liquid level control, accounting for tracking error and output constraints. The algorithm was compared to the performance of SISO PI controllers, showcasing superior set-point tracking speed with less oscillation and lower error metrics.

Bao et al. [78] developed the deep deterministic actor critic predictor (DDACP) architecture to enhance the learning process for dynamic control. The process dynamics were assumed to follow Gaussian distribution. The action–value function was then separated into (i) immediate reward that provided the actor with gradient at the early stages and (ii) next state’s value function for policy gradient estimation in the expectation form. The control performance of the DDACP algorithm was compared with that of DDPG, TD3, and model-based action gradient estimation methods (e.g., MAGE-DDPG and MAGE-TD3). The DDACP method achieved more stable convergence and higher total reward after learning 10,000 episodes, and also showed superior control performance in comparison with PID control for SISO systems and MPC for MIMO systems.

Several works have also explored the integrated use of RL control and conventional process control techniques. Hong et al. [80] presented a PID-DRL cascade control scheme. A DDPG-based architecture was used to model the DRL controller. The states of the RL environment were designed as a PID-control inspired observation vector containing three values: (i) the current value of the output variable, (ii) the error value that denotes the current deviation of the output variable from its set point, and (iii) an error integral to capture the accumulated error accounting for historical behavior. The reward function was designed to both reward the smaller deviations using the reciprocal of their absolute values, and penalize the larger deviations using the square root of their absolute values. This PID-DRL cascade control was then compared with PID-PID cascade control, and demonstrated a >50% reduction in terms of the integral absolute errors. Beahr et al. [81] developed a control scheme which operated RL control and PID in parallel. The RL agent could learn from the PID control actions to enable safe and efficient online training. By continuously evaluating the online performance of both control strategies, the process system could transition from PID to RL if the agent decision making was improved, or vice versa if stability should be attained via the PID controller. Even when paired with suboptimal PID, the RL agent derived near-optimal control policies without significant performance degradation.

In the context of process control, data-driven methods (e.g., systems identification, neural networks) can be applied to “learn the model”, while reinforcement learning can be applied to directly “learn the value”. To quantitatively compare their efficacy, Oh [85] studied six methods: (i) three data-driven MPC approaches using N4SID, NNARX, long short term memory (LSTM) to learn the model, and (ii) three model-free RL approaches based on DDPG, TD3, and SAC to learn the value. Three dynamic process case studies were investigated, including continuous stirred tank reactor, slow moving bed, and a semi-batch Penicillin bioreactor. The general conclusion from this work was that data-driven MPC presented lower cost variances and better data efficiency, while RL-based control performed better at capturing complex process dynamics (e.g., the periodic SMB process). The recent impetus of physics-informed machine learning also opens up new opportunities for process modeling and control [86,87]. As RL is essentially a black-box approach, the infusion of physics-based knowledge can also address the challenge of interpretability. As an example toward this direction, Wang and Wu [82] introduced an AC-based physics-informed RL algorithm to provide optimal control with input constraints. The knowledge of Lyapunov stability and policy iteration convergence conditions were incorporated to the value and policy networks, as shown in Figure 6c.

Reinforcement learning has benefited a variety of research fields in chemical process control. While it is impossible to cover all the related applications, here, we provide a brief summary on some of the notable areas with recent original research publications and/or review articles: drug design [88,89,90], crystallization [91,92,93,94,95,96,97], polymerization [98,99], material self-assembly [100,101,102,103,104,105], water treatment [106,107,108,109,110,111,112], chemical process monitoring and fault detection [113,114], autonomous operation [12,65,115], chemical reaction optimization [116,117,118,119,120,121,122], real-time chemical process design and optimization [123,124,125,126,127,128,129]. Other notable review articles include: [10,11,13,77,130].

4. Safe Reinforcement Learning

For chemical systems, it is imperative to satisfy process constraints to ensure operational safety. While input constraints can be relatively easier to be integrated to RL problems by defining the action space accordingly, it is not trivial to enforce path constraints (e.g., on state variables). The low interpretability of RL as a black box also presents formidable challenges, hindering the practical implementations of RL-based control. Hence, safe RL has emerged as a relatively new field of study where the agents are designed to incorporate safety considerations. This section provides a discussion on the general theoretic algorithms for safe RL and their applications to chemical process control.

4.1. General Basics

A key review paper is offered by Garcıa and Fernández [131] on the advances of safe RL before 2015. The authors formally defined safe RL as the process to learn policies that can maximize the expectation of the return while ensuring system performance and/or safety constraints during the learning/deployment processes. They also classified the existing safe RL approaches into the two categories: (i) modifying the optimization criterion to integrate the risk concept (e.g., worst case criterion, risk-sensitive criterion) and (ii) modifying the exploration process to avoid unsafe situations (e.g., incorporating external knowledge, risk-direction exploration). Brunke et al. [132] also discussed the three levels of safety that can be posed via different constraint formulation: (a) Safety Level I—which encourages constraint satisfaction (or in other words, allows possible minimal violations). This can be posed via soft constraints such as adding penalty terms and constraining the expected value. (b) Safety Level II—which requires no violations to happen at high probability. This can be posed via probabilistic constraints, and (c) Safety Level III—which requires no violations to be posed via hard constraints. These safety constraints can be applied to assure safe operating states, input actions, stability guarantee, etc.

A number of safe RL approaches have been developed, such as safe exploration, safe optimization, safety critic, constrained MDP-based RL, etc. A brief overview is presented in the following, and comprehensive discussions can be found in [131,132]. In safe exploration, the safety layer presents an example that can be utilized to transform an optimal but potentially unsafe action to the nearest action satisfying the safety constraints. Safe optimization refers to the “safe” sampling of actions to optimize the cost function (i.e., to eliminate actions that exceed safety thresholds or violate constraints). These approaches typically leverage Gaussian process (GP) models. Safety critic is another technique within the broader category of Safe RL algorithms. Similar to conventional critics, a safety critic is learned based on a safe action–value function ($Q_{safe}^{\pi }$) that determines whether the given action leads to unsafe states. Several works have used safety critics to determine safe alternative inputs in case the agent encounters uncertainties.

Constrained MDPs (CMDPs) are also widely used for safe RL. CMDPs are an extension of the conventional MDPs subject to a set of constraints $\mathcal{C}={\{C_i,b_i\}}_{i=1}^m$, where $c_i$ are the costs and $b_i$ are the bounds for safety constraints. Incorporating this to RL, the cost value functions $V_{\pi }^{c_i}\left(s\right)$ can be defined as in Equation (39). The corresponding action–value function and advantage function can be formulated in a similar way. On this basis, the cost function can be calculated via Equation (40).

$$V_{\pi }^{c_i}\left(s\right)={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^t{c}_i(s_t,a_t)\right|s_0=s]$$

(39)

$$C_i\left(\pi \right)={\mathbb{E}}_{s\sim {\rho }_0(·)}\left[V_{\pi }^{c_i}\left(s\right)\right]$$

(40)

The goal is thus to maximize the reward while ensuring safety (Equation (41)), and this can be achieved with the Constrained policy optimization (CPO) method, proposed by Achiam et al. [133].

$$\underset{\pi \in {\mathrm{\Pi }}_S}{\max }J\left(\pi \right)\mathrm{s}.\mathrm{t}.C_i\left(\pi \right)⪯b_i$$

(41)

On the basis of safe RL theory, Gu et al. [134] summarized five fundamental questions for RL safety:

• Safety Policy: How to find an optimal policy that is also compliant with the safety constraints (i.e., to avoid adversary attacks, undesirable situations, reduce risks).
• Safety Complexity: How many training samples are required to arrive at the safe policy? Sample complexity is a key issue, as pointed out in many works [135,136].
• Safety Applications: What are the latest advances for the applications?
• Safety Benchmarks: What benchmarks can be used to examine safe RL performance in a fair and holistic manner?
• Safety Challenges: What are the challenges for the research of safe RL?

4.2. Safe RL Approaches in Chemical Process Control

Safety-aware chemical process control more often refers to the integration between chemical process safety and control [137,138,139]. A formal correlation between process safety and safe RL control presents a key yet untapped research question. Safe RL also presents a relatively under-explored research area for chemical processes, and the aforementioned approaches (e.g., safe exploration, CMDPs) are oriented from the perspective of safety reinforcement learning. In the specific context of safe RL for process control, the approaches can be broadly classified as (i) constraint tightening with backoffs, (ii) control barrier functions, and (iii) control invariant sets. A list of works is summarized in

Table 4. Safe RL methods for process control—an indicative list.

Publication	Safety Additions	Key Features	Year
Savage et al. [140]	Constraint tightening with backoffs	GPs to approximate action–value function; Analytical uncertainty; GP-based backoffs	2021
Pan et al. [141]	Constraint tightening with backoffs	“Oracle”-assisted constrained Q-learning; Self-tuning backoffs using Broyden’s method	2021
Petsagkourakis et al. [142]	Constraint tightening with Backoffs	Chance constrained policy optimization; GP-based backoffs for policy gradient algorithm	2022
Kim and Oh [143]	Backoffs and control barrier function	GP-based backoffs; Plant-model mismatches and stochastic disturbances	2024
Kim and Lee [144]	Control Lyapunov functions	Value function restricted to control Lyapunov function; Asymptotic stability	2022
Wang and Wu [145]	Control Lyapunov-barrier functions	Value network trained to approximate the control Lyapunov-barrier function; Input constraints	2024
Bo et al. [146]	Controlled invariant sets	CIS-based initial state sampling, reward design, state reset; Safety supervisor algorithm for online training	2023
Wang et al. [147]	Controlled invariant sets & Lyapunov functions	Lyapunov neural network trained using data from controlled invariant sets; Transfer learning	2024

, with detailed discussions following.

• Constraint Tightening with Backoffs

In the constraint tightening with backoffs approaches, the constraints are tightened by adding backoffs, which would reduce the perceived size of the feasible region to improve chance constraint satisfaction [143]. These methods have been successfully applied for integrated design and control problems, e.g., Ricardez-Sandoval et al. [148,149]. For process control, Bradford et al. [150] applied the technique to a stochastic data-driven nonlinear MPC. Therein, Gaussian-process-based sampling was utilized to derive state-space representations based on input/output data. Explicit backoffs were used to tighten the constraints based on closed-loop simulations. Petsagkourakis et al. [142] developed a chance constrained policy optimization approach that used adaptive GP-based backoffs for constraint tightening to the policy-gradient-based REINFORCE algorithm. The goal of the algorithm was to find the least conservative backoffs that could satisfy the joint chance constraints at the desired probability and confidence interval. Kim and Oh [143] presented a model-based safe RL approach that used determined GP-based adaptive backoffs for constraint tightening under plant–model mismatches and stochastic disturbances. This work was built on the authors’ prior work utilizing control barrier function to enforce state and input constraints, as well as Sontag’s formula to improve system stability. Savage et al. [140] developed another strategy utilizing GPs in a model-free safe RL algorithm for discrete actions in time. Instead of using neural networks as in many other works, the action–value function was designed via GPs. The analytical uncertainty was determined from the standard deviation calculated from the GP posterior probability distribution. On this basis, Bayesian optimization was then leveraged to improve the balance of exploration and exploitation. The probabilistic constraint violation modeled via GP was adopted as a constraint tightening backoff to encourage safe exploration.

• Control Barrier Functions

Barrier functions are commonly used in constrained optimization problems, which are augmented to the objective function to account for inequality constraints and to ensure constraint satisfaction. The barrier functions are designed to approach infinity at the boundaries of the feasible region, thus ensuring the system remains within the feasible region. Control barrier functions (CBFs) are the counterpart in the control theory [151]. CBFs use the concepts of barrier certificates in a control-theoretic perspective to guarantee safety along the manipulated dynamic system trajectory [152,153]. In their simplest definition, CBFs restrict the control actions within a safe set. It takes the current state as an input and, in most cases, outputs a finite real number. However, if the process progresses toward a boundary of the safe set, the CBF usually approaches an infinite value. A CBF constraint typically has the form $\dot{h}(x,u)\le \alpha h\left(x\right)$, where $h\left(x\right)$ is the CBF defined on states x, which must be satisfied when determining the control action $\left(u\right)$. In this way, CBFs can be used to design controllers with safety guarantees by guiding the system away from the unsafe boundaries [154].

Kim and Lee [144] presented a model-based RL control strategy for a nonlinear optimal control problem with asymptotic stability guarantees. The value function was restricted to CLF, and a Lyapunov neural network was adopted for this purpose. The policy was updated based on a modified Sontag formula. Kim and Kim [155] extended this approach to include input and state constraints by introducing a barrier function. The applicability was also extended to general nonlinear systems beyond control-affine systems. Wang and Wu [145] developed a safe RL algorithm for the optimal control of nonlinear systems with input constraints, which featured a performance index function based on control Lyapunov-barrier functions (CLBFs) to achieve closed-loop stability and safety, with the CLBF-based value function approximated with neural networks. Demonstrated by the authors, the CLBFs can simultaneously provide the theoretical properties of both CLFs and CBFs.

• Control Invariant Sets

Positive invariant set [156] for dynamic systems refers to a subset of the state space where once the system enters the set it will stay in it. Using the concept of “energy” from Lyapunov theory for dynamic systems, the boundaries of positive invariant sets can be formed by the level surfaces of a Lyapunov function. Considering a dynamic system, the initial states belong to a certain admissible set defined by the state constraints. The dynamic trajectories might take the system out of the admissible set of states. However, if the admissible states are included within the positive variant set, safe trajectories are guaranteed without constraint violations. Extending this concept to control theory, a control invariant set (CIS) can be formally defined as: a set $\mathcal{X}\subseteq {\mathbb{R}}^n$ is control invariant for a dynamic system $x^{+}=f(x,u)$, if for all states in the set $x\in \mathcal{X}$, there exists a control action u that guarantees the system states would remain in the set $x^{+}\in \mathcal{X}$. Note, n is the dimension of the state space. The same definition can be extended to a robust CIS in the presence of disturbances and/or uncertainties.

Bo et al. [146] developed a CIS-enhanced safe RL algorithm that used an explicit form of the CIS for RL training. The training was performed both offline and online. Offline training leveraged CIS for (i) the design of RL reward function—to penalize the actions that led the system states to move outside the CIS, (ii) sampling of the initial state—as starting from an initial state within the CIS ensured the RL to determine control actions which could stabilize the system, and (iii) reset of the state—in the cases when the trajectory caused the current state to be outside the CIS. The controller was then deployed online with additional training to account for possible new unexplored operating conditions. The trained agent was allowed to operate on policy until it encountered a new state detected by the safety supervisor algorithm. The system was then reset and retrained. The agent was expected to keep retraining during the safety supervisor algorithm until an action was found that could keep the system within the CIS, or until the maximum iterations were reached. In the latter case, a backup table was used to provide safe actions.

Wang et al. [147] presented a safe transfer RL framework that combined the use of CIS and Lyapunov functions. The transfer RL algorithm leveraged knowledge from pre-trained source RL tasks to learn new, related tasks faster with better data efficiency. The critic network was developed as a Lyapunov NN. However, instead of using barrier functions, safety guarantees were provided during training by using data from the CIS. Analogous to the discussion of transfer RL in Section 3, the weights of the critic network of the source task were then transferred identically to the target network with an additional layer with weights initialized to the identity. Then the weights of the target critic network were fine tuned by training in a similar fashion as the source network training. This would allow new models with data scarcity to be developed for new tasks by using knowledge from the source datasets. A theoretical error bound was also derived to quantify the difference between the source and the target tasks.

5. Limitations, Emerging and Future Explorations

As discussed in the previous sections, RL provides a promising strategy for process control with reduced errors, enhanced adaptability to stochastic systems, and better handling of complex non-linear dynamics. However, key open challenges remain on algorithmic interpretability, sampling efficiency, performance evaluation, etc. In this section, we discuss some of the limitations and challenges in RL and chemical process control, as well as the emerging and future directions of research in this field.

5.1. Environments for RL Design and Benchmark

Many online environments have been developed that provide attractive tools to design and benchmark RL algorithms such as Gymnasium [157] and OpenAI’s Gym [158]. However, OpenAI Gym lacks parallelization on GPUs. Some vectorized environments use JAX to implement parallelization. These include Gymnax [159], Brax [160], Jumanji [161], and PGX [162]. For a specific environment for process control implementations, PC-Gym has been developed by Bloor et al. [163], which is an open-source tool to develop and evaluate RL algorithms for chemical process control. PC-Gym can be used as the environment within the general RL framework, and agents can be trained using DDPG, ppO, or SAC frameworks. PC-Gym is also designed to include constraint handling abilities. Tools are included for reward function design, disturbance generation, visualization, etc. Benchmark with nonlinear MPC-based “oracle” is also supported to evaluate the performance of RL-based control. PC-Gym is built in Python with discrete-time representations using CASADi or JAX vectorization for numerical integration.

5.2. Data Efficiency

Data efficiency is a widely recognized challenge for RL. A large amount of data is required for RL agent training over many episodes. Model-free RL algorithms typically start with the action–values initialized as zero, and hence, even the most trivial tasks would take a lot of samples to be learned. To give a more intuitive idea: OpenAI Five [164], a scaled-up PPO-based agent for game playing, was trained on approximately 45,000 years worth of real-time experience over the course of 10 months. OpenAI Rubik’s cube agent [165] required 13,000 years worth of compressed real-time simulation for training. Swan et al. [166] commented that the reliance on sampled rewards may be intrinsically not safe for RL training and application in real-world processes. The limitation in sampling efficiency is also related to other key challenges such as RL scalability [11] and generalizability [167].

Extensive efforts have been made to improve the sampling efficiency of RL and DRL frameworks. Experience replay has been used to improve the sampling efficiency of DQN [168] and DDPG [29]. As discussed in Section 2.2, experience replay stores previous interactions in the form of tuples $<s,a,r,s^{\prime }>$ collected via exploration. Prioritized experience replay Schaul et al. [169] presents an enhanced version that prioritized the transitions causing high temporal difference error instead of uniformly sampling all experiences. This leads to a higher expected progress during agent learning. However, to prevent the loss of diversity in experiences, a stochastic prioritization is implemented, along with importance sampling to reach a balance between prioritization and uniform sampling. Prioritized experience replay was shown to improve the DQN learning speeds at 41 out of 49 Atari 2600 games.

Transfer learning is considered a promising method to improve data efficiency and generalizability of RL algorithms. The underlying hypothesis of using transfer learning to address data efficiency issues in RL is that, knowledge learned from different yet related environments can compensate information scarcity of the target environment, that using both limited information of the target system and knowledge from related environments can lead to efficient and reliable policy learning. Different approaches can facilitate such knowledge transfer, such as with regularization techniques to avoid overfitting on the source system, with domain randomization to introduce variations in the source system in training the RL algorithm such that it could treat information in the target system as a variant of the source system [170], or to partially retrain the RL algorithm with information from the new system, etc. Using the Deep RL as an example, the knowledge about the environment is embedded in the weights of the neural network, learned from interacting with the environment. When transferring to a new environment with data deficiency, instead of learning the large number of the NN weights for the new environment from scratch, transfer learning algorithms seek to adapt the NN previously trained from a related system by further training with data collected from the new system for weights tailored for the new environment. Taylor and Stone [171], Lazaric [172], Zhu et al. [173], Ada et al. [174] provide a comprehensive survey on transfer learning for RL for the past several decades. Notable applications of transfer learning for data efficiency span from process design to control and to autonomous manufacturing. For example, in [175], the authors deployed transfer learning into a RL framework to achieve process design with an 8% higher revenue and a reduced learning time by a factor of 2. In [176], the authors demonstrated the application of transfer learning in learning the manufacturing process parameters to autonomously fabricate photonic crystals, which can function as an acoustic filter. The authors first trained a source RL algorithm with a first-principle-based model and then learned a probabilistic model based on the source RL algorithm to approximate the reward function in the target system. The authors demonstrated that with transfer learning, the agent can identify the optimal state with as few as 25 artifacts, whereas traditional design approaches would require 144 artifacts, significantly reducing the amount of training data needed. For applications on process control, transfer learning can be used in different ways, such as approximating the process model for model-based RL control, approximating the reward function, or learning the new control policy directly, such as the previously mentioned work in [9]. Other notable examples include [177], where the authors used offline apprenticeship learning for preliminary policy parameterization and then fine-tuned the policy with online training. We refer the readers to review articles [12,178,179] for a more comprehensive survey on how TL can benefit RL in terms of process control.

Meta-reinforcement learning is another attractive alternative for data efficiency and generalizability of RL. Similar, yet different from TL, meta-learning aims at leveraging knowledge previously learned from a wide range of tasks (meta-data), to learn quickly the solution of an unseen system. In meta-RL, the agent learns “how to learn” based on experiences with different systems, thus gaining the capability of adapting to changing and/or unseen environment, such as learning the update rules for the RL agent parameters, as shown in [180]. In [180], the authors proposed a meta-learning architecture, named the learned policy gradient (LPG), to learn both what to predict and how to improve the policy. The LPG is a backward LSTM network that produces as the output how to update the policy and the prediction from the trajectory of the agent. The architecture is trained by considering a comprehensive improvement of a population of agents interacting with different environments for improved generalization to a specific environment. The authors reported that by training the architecture only on toy environments, it gained satisfactory generalizability to complex Atari games, showing the potential of meta-learning in improving RL generalizability. In [181], the authors presented a context-based meta-learning RL method for offline PI controller tuning to improve the online tuning sample efficiency. Specifically, the authors developed an RNN to capture the system context and to enable the agent to adapt to changes in the process dynamics. The controller was then trained offline by exposing the actor–critic agent to a broad distribution of different dynamics generated from a first-order plus time delay system model (FOPTD), where the model parameters were uniformly sampled from a range to generate a distribution of different environments. Application of the meta-learning tuned PI controller on a nonlinear two-tank system, which can be approximated with the FOPTD models, demonstrated its capability of rapidly finding the reasonable PI parameters for the new system with noise added to the measurement, further justifying the efficacy of meta-learning in addressing the sample efficiency issue in process control. Other notable works on generalization improvement include [182,183], and review article [184].

5.3. Uncertainty-Aware RL Algorithms

One direction for continued efforts can be the development of uncertainty-aware RL algorithms. Uncertainty is ubiquitous. In reinforcement learning, especially model-based reinforcement learning, uncertainties can come from training the model, inheriting uncertainties native to model development, and also from interacting with the environment. Neglecting these uncertainties can result in ineffective performance for practical implementation. Being aware of this, studies on uncertainty measuring, assessing, and uncertainty-aware RL development have started to gain attentions. In [185], the author classified uncertainties as either aleatoric, which are inherent to the system and typically unavoidable, or epistemic, which are due to modeling and can be mitigated. In RL, aleatoric uncertainties could come from stochastic rewards, stochastic observations, and stochastic actions. Although they cannot be reduced, measuring and quantifying these uncertainties can help improve the performance of the control. Addressing epistemic uncertainty has been prominently considered in exploration, either implicitly, such as with the count method, where the underlying rationale is to increase training samples to reduce uncertainty, or explicitly. Common methods on explicitly estimating and handling epistemic uncertainties in RL include bootstrapping Q-networks, Monte Carlo Dropout, and variants based off these two fundamental concepts. In [185], Lockwood provided an excellent review on contemporary development in uncertainty estimate and handling in RL, with references to representative works [185]. Other notable works include [186], where the authors proposed an opinion inference algorithm using subjective logic to selectively emphasize more on the critical uncertainties in training the RL algorithm; [187], where the authors developed an action-conditioned ensemble model capable of assessing uncertainty to represent the environment and then proposed an adaptive truncation approach-based RL method for learning efficiency and improved performance; and [188], where an action-conditioned model was developed to assess the uncertainty in an application of an autonomous driving scenario. In addition to the aforementioned works, other methods also include Bayesian neural networks [189,190,191,192,193], or the Dempster–Shafer theory [194,195,196,197], etc.

5.4. State Observability

Observability is essential in ensuring an effective control. While most of the RL-algorithms have assumed observability of the system with fully observable MDPs, partially observable processes (POMDPs) are prevalent in real applications, limiting the application of RL. Dealing with partially observable processes is notoriously challenging, as training the algorithm would require an exponentially large number of samples. Therefore, RL-algorithms that account for state observability present another invaluable research direction. Current efforts on this topic include (1) state estimation-based RL, such as observable operator models [198], belief state estimation, and world models [199,200,201] for compressed or abstracted representation of the environment, to facilitate decision making. Examples include [202], where the authors proposed an object-centric belief model with sequential Monte Carlo inference to provide multiple object-centric scene hypotheses, to improve the performance of RL in an application to a POMDP. In [201], the authors proposed a transformer-based world model agent, named TransDreamer, to use a transformer state-space model to predict process dynamics to train the RL agent. Testing on visual RL tasks that required long-range memory access showed outstanding performance. Other notable works include [187,203,204,205], to name a few. (2) RL with function approximation. In [206], the authors introduced a partially observable bilinear framework and proposed an actor–critic style algorithm to perform agnostic policy learning. Leveraging both memory-based policies and a value function class that incorporates both memory and future observations as the inputs, the authors achieved satisfactory performance. In [207], Uehara et al. developed a model-free off-policy algorithm by introducing future-dependent value functions as conditional moment equations to use history proxies as instrumental variables. With a minimax learning method, the authors presented close to the true policy value with the proposed approach. Other important works include [208,209,210,211,211], to name a few.

5.5. RL Enhanced by Large Language Models

There has been a recent impetus in the development of large language models (LLMs). LLMs are trained on terabytes worth of data, containing billions of parameters [212]. Notable examples of these include GPT-3 [213], which was trained with 175 billion parameters and demonstrated that scaling up the language model can greatly improve task-agnostic, few-shot performance; LLaMA [214], which showed the possibility of training foundation language models with parameters ranging from 7 B to 65 B with publicly available datasets, without resorting to proprietary and inaccessible datasets, for competitive performance compared to benchmark models; and GPT-4 [215], which possesses the capability of solving a wide range of novel and difficult problems with strikingly close to human-level performance that often vastly outperforms prior LLMs such as ChatGPT. These models possess excellent natural language (NL) and computer vision (CV) parsing abilities and can master a wide range of tasks such as language generation and knowledge correlation. Emergent capabilities of LLMs have also been developed such as in-context learning, reasoning, and generalization [216]. These capabilities are defined as abilities that are not present in smaller-scale models but are present in large-scale models that cannot be predicted by simply extrapolating the performance improvements on smaller-scale models, due to the scaling up of the language models. However, how the LLMs gained such capabilities is yet to be explored. Additionally, while step-by-step tasks are complex for smaller models, LLMs can use sophisticated prompting strategies to structure the algorithm in a much more articulate manner, enabling LLMs to output sequences that reflect the progression of thoughts or actions. Such prompting strategies include: Chain of Thought (CoT) [217], which allows the model to decompose multi-step problems into intermediate natural language reasoning to formulate solutions to the overall problem; Tree of Thought (ToT) [218], which builds upon CoT by incorporating multiple different reasoning paths and self-evaluating choices at each intermediate steps, for deliberate decision making; and Graph of Thought (GoT) [219], which is further built upon ToT, and models the information as an arbitrary graph, where the “thoughts” are the vertices, and the edges represent the dependencies between the vertices, to form synergistic outcomes, distill the essence of the thoughts, and/or to enhance the thoughts with feedback loops.

Incorporation of the multimodal data (e.g., NL- and CV-based image data) into the RL structure has also been a challenge [220,221]. It increases the sampling inefficiency as the agent not only has to learn a policy but also needs to parse the multimodal data. The advances in LLMs provide instrumental capabilities not only to handle the multimodal data, but also to handle the inherent challenges posed by the conventional RL paradigm. Pre-trained LLMs such as generative pre-trained transformer (GPT) models posses a vast amount of world knowledge. Cao et al. [222] presented a survey in which they introduced the term LLM-enhanced RL, which was defined as “the methods that utilize the multimodal information processing, generating, reasoning, and other high-level cognitive capabilities of pre-trained, knowledge-inherent LLM models to assist the RL paradigm”. The sampling inefficiency of RL can be improved by providing contextually valid predictions or suggestions by using a framework of LLMs, thereby reducing the required number of interactions between the agent and the environment. LLMs have also been used for a more informed reward design, as showcased in Li et al. [223]. Notable works on this topic include: Chakraborty et al. [224], which presented a framework for language-based feedback to improve RL generalization; Pang et al. [225], which used LLMs to translate NL-based instructions to task-specific language within RL; and Vyas and Mercangöz [226], which proposed the use of an agentic system comprising LLM-agents for autonomous control with adaptivity to unforeseen disturbances. Detailed discussions on the potential and challenges of LLM-enhanced RL can be found in Cao et al. [222].

In addition to the aforementioned topics, we also note other directions such as convergence, reachability, stability, interpretability [227], and multi-agent control [228,229], etc., and refer the readers to review articles [25,230,231,232,233] on the limitations, challenges, and opportunities of RL for further reading.

6. Concluding Remarks

This article provides a literature review on the recent advances in RL for chemical process control. The article first introduces the concept of RL and how it intersects with process control. We then review RL basics including the fundamentals of MDPs and state-of-art RL algorithms (e.g., DQN, DDPG, TD3, SAC). The article also surveys the recent implementations of RL within process control from the aspects of RL-based controller tuning and RL for control policy learning. Various methods of safe RL are presented with examples on how they have been implemented for process control. The article further discusses the limitations, challenges, and opportunities offered by the emerging computing algorithms (e.g., transfer learning, meta learning, and large language models) to enhance RL-based control toward practical implementations.