Operational Risk Assessment of Power Imbalance for Power Systems Considering Wind Power Ramping Events
Abstract
1. Introduction
- (1)
- A conventional generator outage model incorporating temporal correlations is developed, in which two key factors—the outage time and outage probability—are introduced. The temporal characteristics of generator outages are sampled using a non-sequential Monte Carlo method.
- (2)
- An operational risk index that accounts for the economic losses associated with both load shedding and wind power curtailment is proposed. Based on the index, an optimal power flow model is formulated with the objective of minimizing the total combined loss.
- (3)
- Based on the dynamic frequency response process of the power system, two types of dynamic frequency security constraints—the initial rate of change of frequency constraint and the maximum frequency deviation constraint—are derived and incorporated into the optimal power flow model.
2. Operation Risk Assessment Principle of Wind Power Ramp Events
2.1. Operational Risk Assessment Indicators
2.2. Probabilistic Modeling of Wind Power and Load Level
2.3. Conventional Unit Outage Model Considering Time-Series Characteristics
3. Optimal Power Flow Model Considering Dynamic Frequency Constraints
3.1. Frequency Dynamic Response Process and Dynamic Frequency Security Constraints
- (1)
- RoCoF
- (2)
- Δfnadir
3.2. Optimal Power Flow Model
- Objective function
- 2.
- Constraint condition
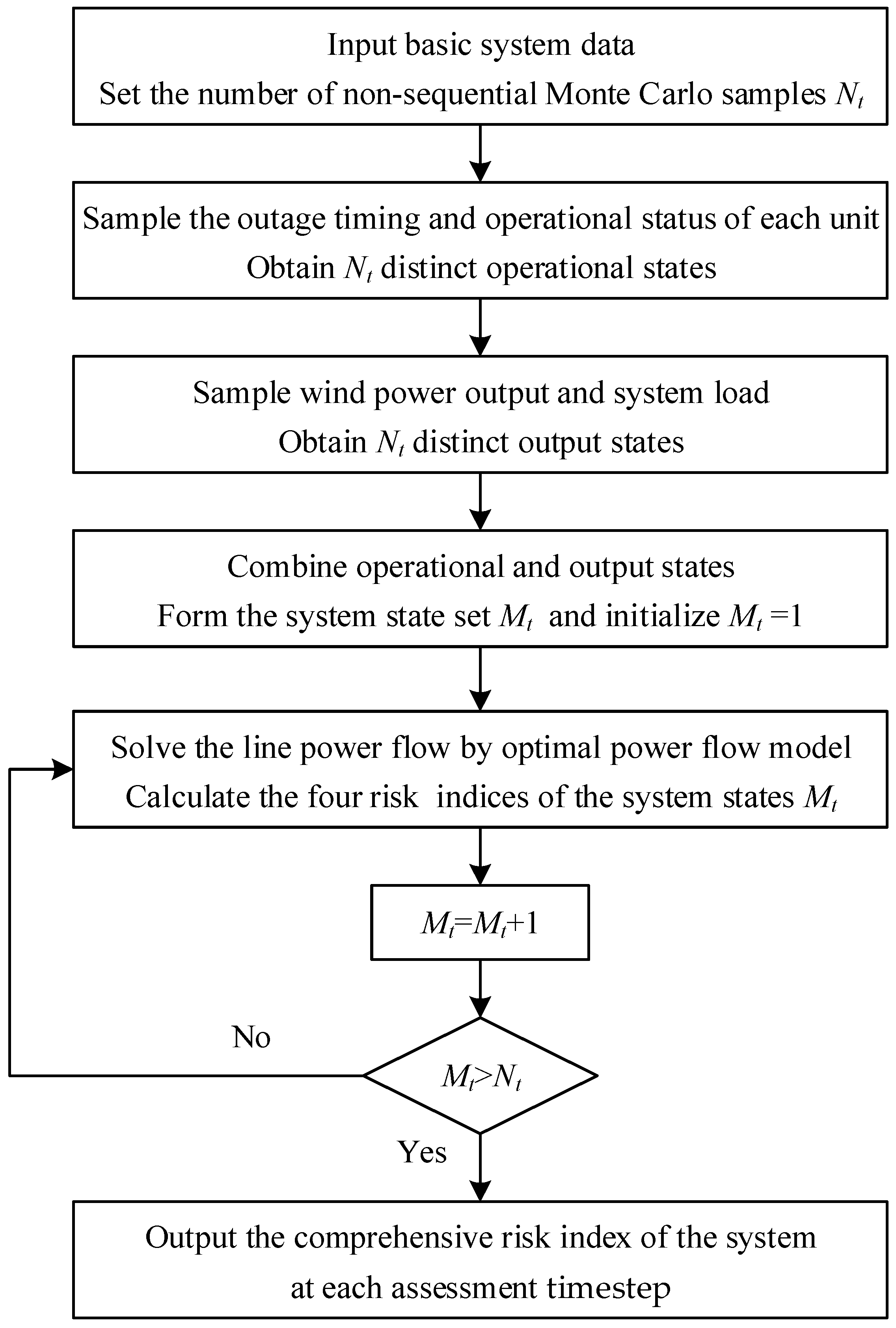
4. Process of Operational Risk Assessment for Power Systems Under Wind Power Ramping Events
- (1)
- Input basic system data, including conventional unit generation schedules, wind power, and load day-ahead forecast outputs; set the number of non-sequential Monte Carlo samples Nt.
- (2)
- Perform non-sequential Monte Carlo sampling. Sample the outage timing and operational status of each unit based on the time-series outage model of conventional units, obtaining Nt distinct operational states throughout the entire assessment period.
- (3)
- Simultaneously, sample wind power output using ramping event characterization parameters and forecast errors during non-ramping periods, along with system load forecast errors, yielding Nt distinct output states.
- (4)
- Combine operational and output states to form system states for the entire assessment period, assign a system state index Mt, and initialize Mt = 1.
- (5)
- Solve the line power flow, load shedding amount, and wind curtailment for system state Mt using the optimal power flow model. Substitute these results into the operational risk index severity formula to calculate the four operational risk index values at each time step under scenario Mt.
- (6)
- Increment Mt = Mt + 1, compare Mt with Nt. If Mt > Nt, output the comprehensive risk index of the system at each assessment time step; otherwise, return to Step 5.
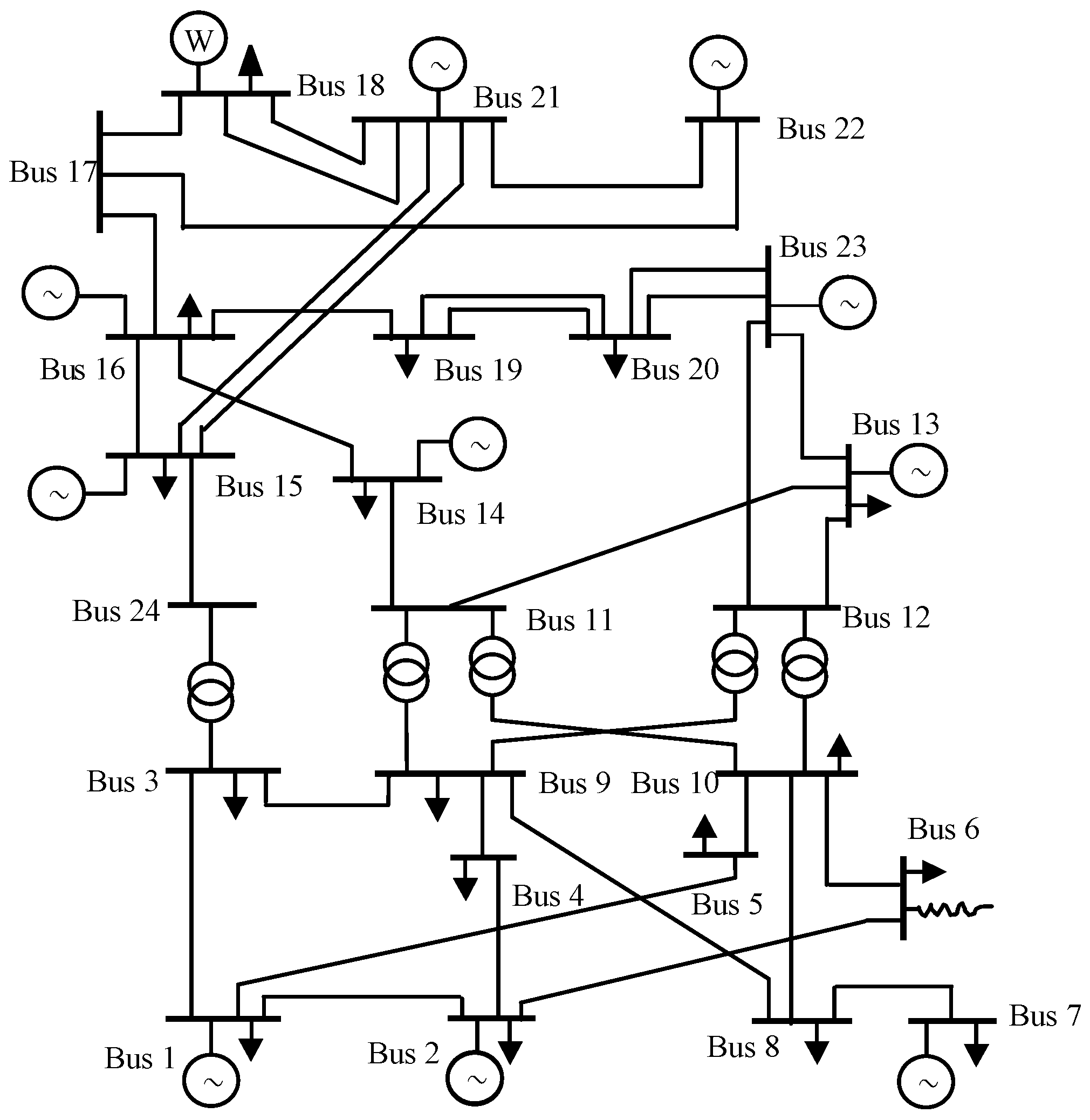
5. Case Study
5.1. Parameter Settings
5.2. Assessment Results
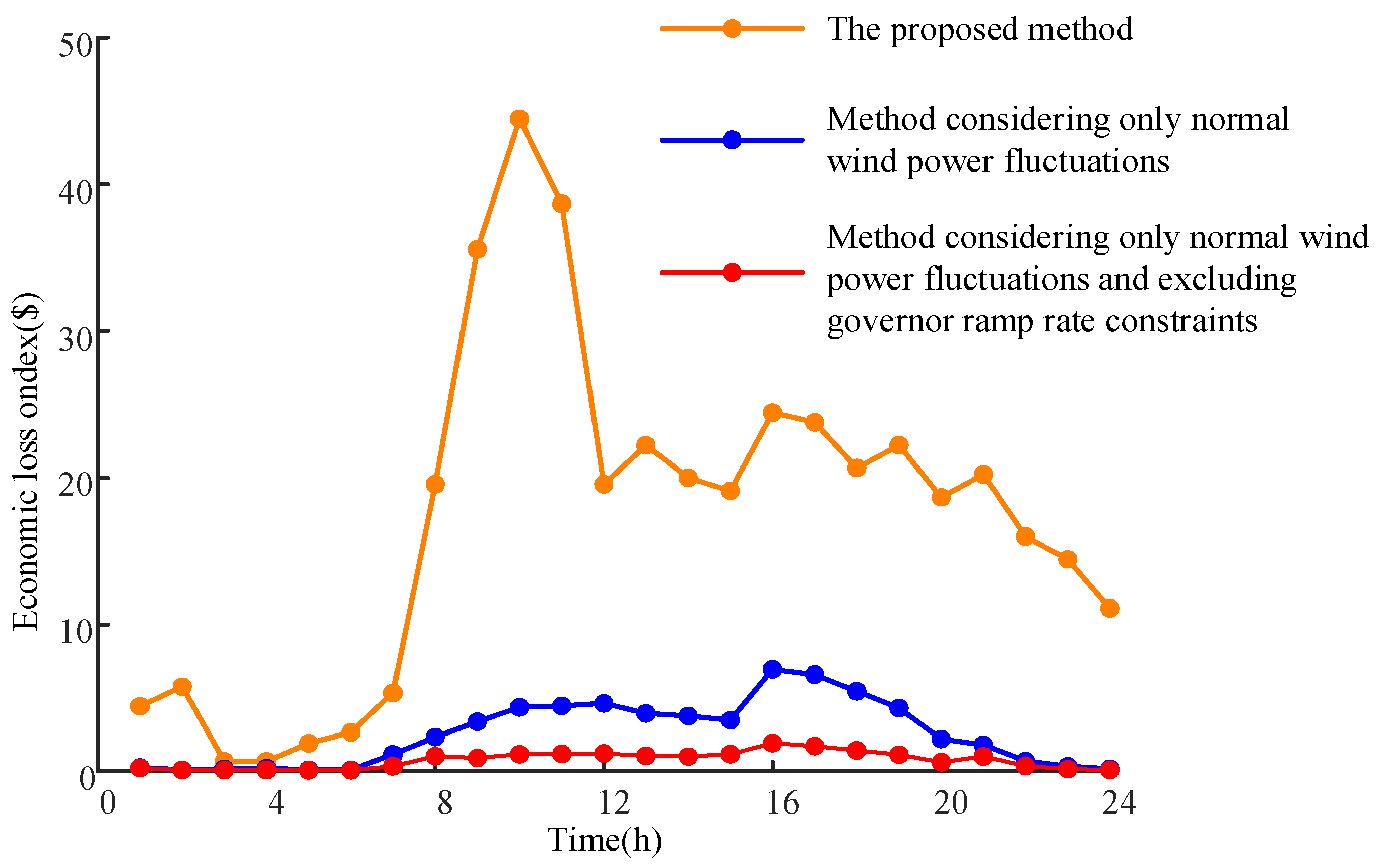
- Comparison of the results of different methods
- 2.
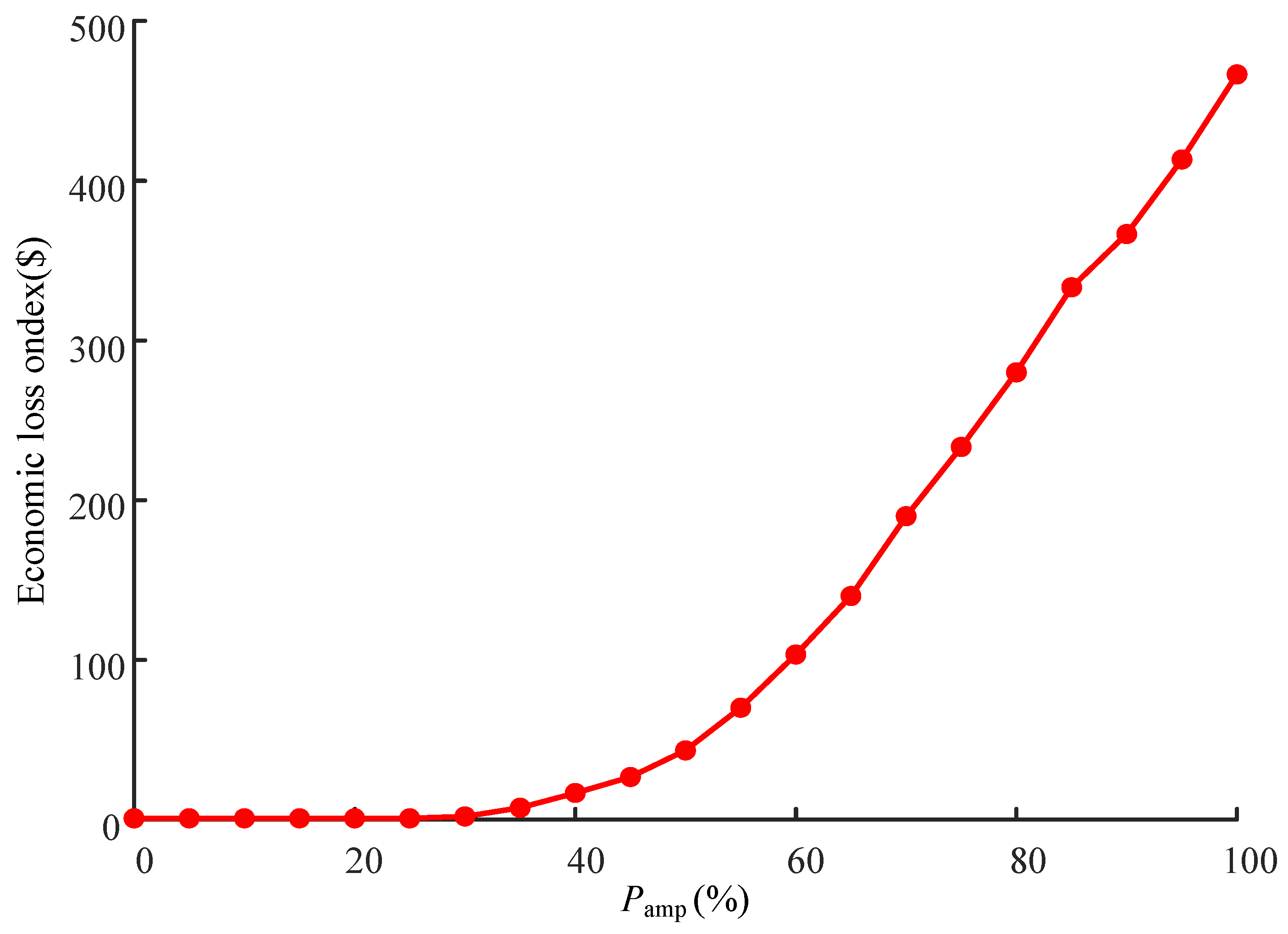
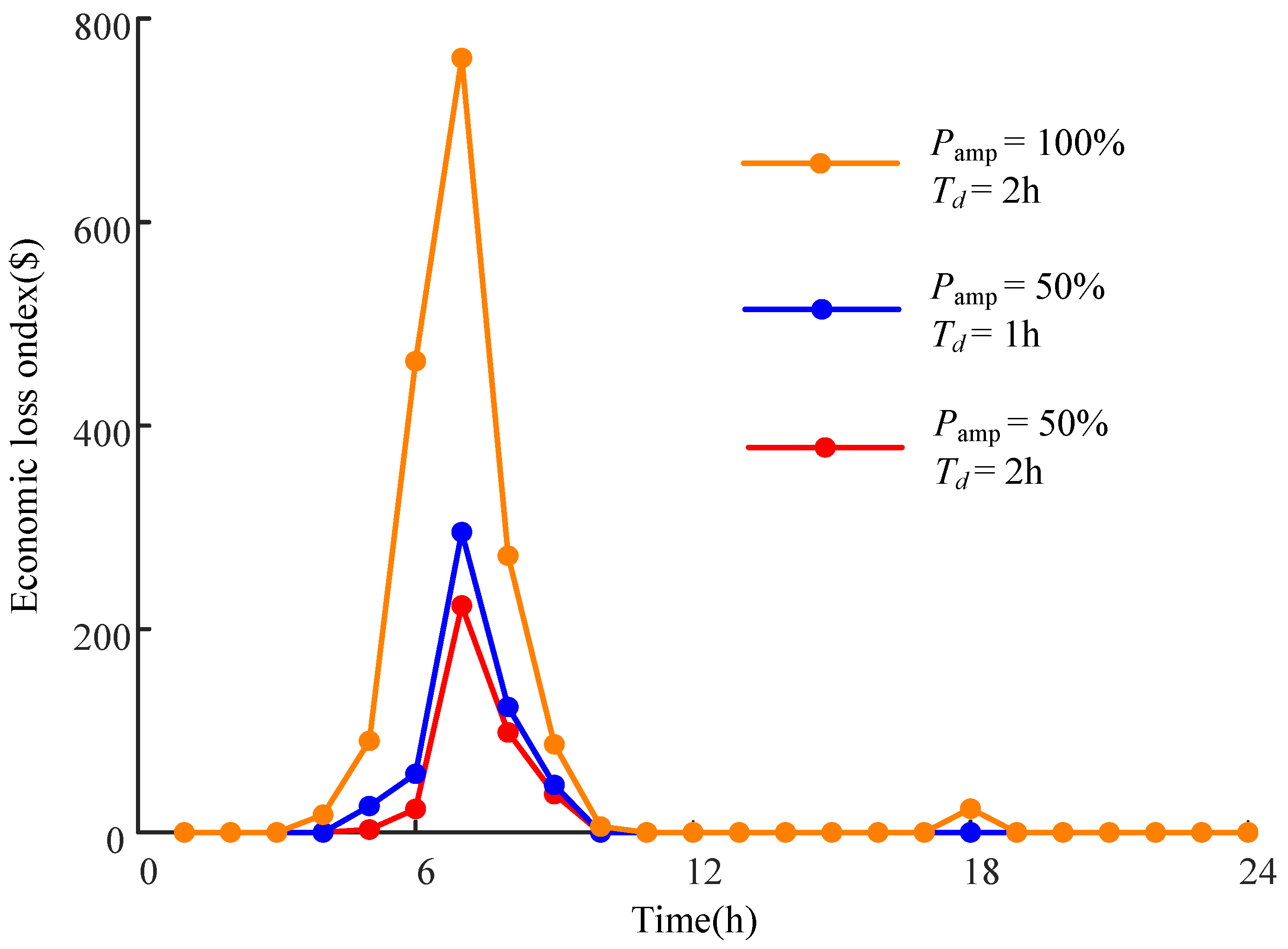
- Impact of magnitude, duration, and start time of wind power ramping events on system risk indices.
- (a)
- Pamp = 50%, Td = 2 h;
- (b)
- Pamp = 50%, Td = 1 h;
- (c)
- Pamp = 100%, Td = 2 h.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| risk value of the power system at time t | |
| system operating state at time t | |
| p() | probability of the system operating state occurring at time t |
| system output state at time t | |
| p() | probability of the system output state at time t |
| S() | risk severity under the operating state and output state at time t |
| Re | comprehensive loss risk index |
| Se | severity function corresponding to Re |
| ag,i | output adjustment cost coefficient for conventional generators at node i |
| b | wind curtailment cost coefficient |
| c | load shedding cost coefficient |
| NG | total number of nodes connected to conventional generators |
| NW | total number of nodes connected to wind turbines |
| ND | total number of nodes connected to loads |
| post-frequency-response output of the conventional unit at node i | |
| load shedding at node i | |
| wind curtailment at node i | |
| Ts | start time of wind power ramping events |
| Td | duration of wind power ramping events |
| Pamp | magnitude of wind power ramping events |
| actual wind power output at time | |
| forecast actual wind power output at time | |
| forecast wind power at ramping start time | |
| forecast error of wind power at time t under non-ramping conditions | |
| actual active load at node i at time t | |
| forecast load at node i at time t | |
| load forecast error | |
| probability of conventional unit at node i being in outage state at time t | |
| pg,i,up | startup success rate of unit |
| λg,i | failure rate of unit |
| tg,i | cumulative operating duration of unit up to time t |
| tg,i,on | scheduled startup time of unit |
| tg,i,off | scheduled outage time of unit |
| ti | possible outage timing of conventional units |
| probability that an outage event occurs at time ti after unit is committed | |
| outage probability of unit i at time t | |
| ug,i(tg,i,on) | binary operational status indicator of unit i |
| Hsys | system inertia |
| Δf(t) | frequency deviation |
| PFR(t) | primary frequency regulation output adjustment of conventional units |
| ΔPim | active power imbalance under the given system state |
| ΔfDB | frequency deadband |
| tDB | time from power imbalance onset to frequency reaching the deadband |
| Csys | system-wide primary frequency regulation response rate |
| binary variable denoting unit i’s primary frequency response participation at time t | |
| cg,i | governor’s maximum ramp rate of unit i |
| TD | system’s primary frequency regulation response time |
| RoCoF | rate of change of frequency |
| Δfnadir | maximum frequency deviation |
| RoCoF,max | maximum allowable initial rate of change of frequency for the system |
| ΔfT,max | system’s maximum allowable dynamic frequency deviation |
| active power transmitted on line l at time t | |
| total active power sent from node i at time t | |
| total active power received at node i at time t | |
| Pg,i,max | upper limits of active power output of unit at node i |
| Pg,i,min | lower limits of active power output of unit at node i |
| Pl,max | maximum allowable active power transmission capacity of line l |
| Nt | number of non-sequential Monte Carlo samples |
| Mt | system state index under Monte Carlo sampled scenario |
References
- Shi, J.; Qin, J.; Li, H.; Li, Z.; Ge, Y.; Liu, B. Probabilistic Power and Energy Balance Risk Scheduling Method Based on Distributed Robust Optimization. Energies 2024, 17, 4894. [Google Scholar] [CrossRef]
- Li, J.; Fang, J.; Wen, I.; Pan, Y.; Ding, Q. Optimal Trade-off between Regulation and Wind Curtailment in the Economic Dispatch Problem. CSEE J. Power Energy Syst. 2015, 1, 37–45. [Google Scholar] [CrossRef]
- Kamath, C. Associating Weather Conditions with Ramp Events in Wind Power Generation. In Proceedings of the 2011 IEEE/PES Power Systems Conference and Exposition, Phoenix, AZ, USA, 20–23 March 2011. [Google Scholar]
- Li, J.; Wang, X.; Liu, B. Event-Based Deep Reinforcement Learning for Smoothing Ramp Events in Combined Wind-Storage Energy Systems. IEEE Trans. Ind. Inform. 2024, 20, 7871–7882. [Google Scholar] [CrossRef]
- Garip, S.; Özdemir, Ş.; Altin, N. Power System Reliability Assessment—A Review on Analysis and Evaluation Methods. J. Energy Syst. 2022, 6, 401–419. [Google Scholar] [CrossRef]
- Chang, Y.; Liu, C.; Huang, S.; Liu, W.; Liu, Z.; Shao, J.; Li, R.; Lv, Y. Risk Assessment of Generation and Transmission Systems Considering Wind Power Penetration. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018. [Google Scholar]
- Dai, Y.; Preece, R.; Panteli, M. Risk Assessment of Cascading Failures in Power Systems with Increasing Wind Penetration. Electr. Power Syst. Res. 2022, 211, 108392. [Google Scholar] [CrossRef]
- Tomasson, E.; Soder, L. Generation Adequacy Analysis of Multi-Area Power Systems with a High Share of Wind Power. IEEE Trans. Power Syst. 2018, 33, 3854–3862. [Google Scholar] [CrossRef]
- Li, H.; Lu, Z.; Qiao, Y.; Wang, W. Risk Assessment of Power System with High Penetration of Wind Power Considering Negative Peak Shaving and Extreme Weather Conditions. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014. [Google Scholar]
- Yang, X.; Yang, Y.; Liu, Y.; Deng, Z. A Reliability Assessment Approach for Electric Power Systems Considering Wind Power Uncertainty. IEEE Access 2020, 8, 12467–12478. [Google Scholar] [CrossRef]
- Li, X.; Wang, H. Operation Risk Assessment of Wind Farm Integrated System Influenced by Weather Conditions. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Negnevitsky, M.; Nguyen, D.H.; Piekutowski, M. Risk Assessment for Power System Operation Planning with High Wind Power Penetration. IEEE Trans. Power Syst. 2015, 30, 1359–1368. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Negnevitsky, M.; Piekutowski, M. A Risk Assessment Approach for Power System with Significant Penetration Levels of Wind Power Generation. In Proceedings of the 2013 Australasian Universities Power Engineering Conference (AUPEC), Hobart, TAS, Australia, 29 September–3 October 2013. [Google Scholar]
- Deng, W.; Ding, H.; Zhang, B.; Lin, X.; Bie, P.; Wu, J. Multi-period Probabilistic-scenario Risk Assessment of Power System in Wind Power Uncertain Environment. IET Gener. Transm. Distrib. 2016, 10, 359–365. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Li, Y.; Feng, C.; Chen, P. Risk Assessment of Power Imbalance for Power Systems with Wind Power Integration Considering Governor Ramp Rate of Conventional Units. Electr. Power Syst. Res. 2023, 217, 109111. [Google Scholar] [CrossRef]
- Sevlian, R.; Rajagopal, R. Detection and Statistics of Wind Power Ramps. IEEE Trans. Power Syst. 2013, 28, 3610–3620. [Google Scholar] [CrossRef]
- Cui, Y.; He, Y.; Xiong, X.; Chen, Z.; Li, F.; Xu, T.; Zhang, F. Algorithm for Identifying Wind Power Ramp Events via Novel Improved Dynamic Swinging Door. Renew. Energy 2021, 171, 542–556. [Google Scholar] [CrossRef]
- He, C.; Tang, Q.; Yang, J. Risk Assessment of Power System with Large-Scale Wind Power Connected Considering the Time-Sequence Characteristic of Wind Power Ramp Event. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018. [Google Scholar]
- Xu, C.; Wei, Z.; He, C.; Wang, H. Risk Assessment of Wind Power Ramp Event Considering Time-Sequence Characteristic. In Proceedings of the 2014 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Hong Kong, China, 7–10 December 2014. [Google Scholar]
- Qiu, W.; Huang, Y.; Zhai, X.; Ma, J.; Zhang, T.; Liu, S.; Lin, Z. Operational Risk Assessment on Power System Based on Weather Regionalization Considering Power Ramp of Renewable Energy Generation. Energy Rep. 2023, 9, 396–408. [Google Scholar] [CrossRef]
| Time | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Wind Power Forecast (p.u) | 0.76 | 0.80 | 0.98 | 1.00 | 0.95 | 0.93 | 0.85 | 0.68 | 0.57 | 0.58 | 0.52 | 0.50 |
| Time | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Wind Power Forecast (p.u) | 0.44 | 0.38 | 0.34 | 0.36 | 0.42 | 0.51 | 0.47 | 0.48 | 0.44 | 0.53 | 0.63 | 0.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Xiong, X.; Yang, D.; Wang, S.; Dong, X. Operational Risk Assessment of Power Imbalance for Power Systems Considering Wind Power Ramping Events. Processes 2025, 13, 1779. https://doi.org/10.3390/pr13061779
Wang W, Xiong X, Yang D, Wang S, Dong X. Operational Risk Assessment of Power Imbalance for Power Systems Considering Wind Power Ramping Events. Processes. 2025; 13(6):1779. https://doi.org/10.3390/pr13061779
Chicago/Turabian StyleWang, Weikun, Xiaofu Xiong, Di Yang, Song Wang, and Xinyi Dong. 2025. "Operational Risk Assessment of Power Imbalance for Power Systems Considering Wind Power Ramping Events" Processes 13, no. 6: 1779. https://doi.org/10.3390/pr13061779
APA StyleWang, W., Xiong, X., Yang, D., Wang, S., & Dong, X. (2025). Operational Risk Assessment of Power Imbalance for Power Systems Considering Wind Power Ramping Events. Processes, 13(6), 1779. https://doi.org/10.3390/pr13061779





