Impact of High Temporal Resolution Data on Water Quality Modeling: Insights from Erhai Case Study

Abstract

Lake monitoring is essential for sustaining aquatic ecosystems, and accurate estimation/prediction of water quality parameters is crucial to this effort. Despite its importance, the performance of predictive models built on varying temporal resolutions remains underexplored systematically. This study used daily and 4 h high temporal resolution (HTR) datasets to assess the performance of multiple machine learning models—namely, Support Vector Regression (SVR), Random Forest (RF), Extreme Gradient Boosting (XGBoost), and Long Short-Term Memory (LSTM) networks—under consistent data scales. The results indicate that dissolved oxygen (DO) exhibits pronounced sensitivity to temporal resolution, while total nitrogen (TN), total phosphorus (TP), and ammonia nitrogen (NH₃-N) show distinct, parameter-specific response patterns that align with the temporal characteristics of their underlying biogeochemical processes. This research helps to deepen the understanding of how temporal data resolution influences model performance in water quality prediction, offering valuable insights for selecting optimal data resolutions and modeling techniques to enhance lake monitoring and protection strategies.

1. Introduction

The protection of aquatic environments has become an urgent global priority, as intensified human activities and accelerating climate change continue to increase the frequency and severity of water pollution incidents [1,2]. Studies have shown that the implementation of water treatment strategies could potentially alleviate approximately 20% of global economic water scarcity risks, which surged from USD 116 billion to USD 380 billion between 1995 and 2010; during the same period, risks specifically related to water quality increased from 20% to 30% [3]. The resulting influx of contaminants and heightened hydrological variability threaten the ecological integrity of freshwater systems and undermine essential ecosystem services. In this context, effective water quality monitoring is essential for the timely detection of pollution events, assessment of environmental trends, and informed decision-making.

However, the intrinsic fluctuations of key water parameters—arising from diverse biogeochemical processes such as nutrient cycling, phytoplankton dynamics, and contaminant transport—occur across a wide range of temporal scales [4,5]. While traditional methods such as biomonitoring techniques offer valuable ecological insights by capturing cumulative impacts and subtle environmental changes through biological responses [6], they often struggle to provide real-time data for rapid pollution events and can be labor-intensive. Similarly, advanced tools like single-molecule detection techniques and Atomic Force Microscopy (AFM), while providing highly detailed physicochemical information about individual aquatic microorganisms and biomolecules [7], primarily focus on highly specific, discrete analyses rather than broad-spectrum, continuous monitoring of multiple water quality parameters. These dynamic processes require monitoring strategies with frequencies tailored to their specific temporal characteristics to accurately capture both rapid events and gradual changes. Such considerations highlight the necessity for adaptive, high-resolution monitoring frameworks that can address the growing complexity of aquatic environments and support sustainable water resource management.

Traditional water quality monitoring has primarily relied on field sampling and laboratory analysis, which typically produce low-frequency datasets at daily, weekly, or longer intervals [8,9,10]. While such approaches are useful for identifying baseline conditions and long-term trends, they often fail to capture the sudden, short-duration, and high-impact pollution events that increasingly threaten aquatic systems, especially in regions with complex environmental dynamics and multiple pollution sources [11]. To address these shortcomings, high-frequency monitoring technologies—such as multi-parameter ultra-spectral sensors, automated in situ platforms, and unmanned aerial vehicles (UAVs)—have emerged as powerful alternatives, providing near-continuous measurements of key water quality parameters on timescales of minutes to hours [12,13]. Moreover, the wealth of high-resolution data generated by these modern systems aligns well with recent advancements in machine learning and other data-driven methods, which excel at uncovering complex patterns, identifying anomalies, and forecasting future water quality states [14,15,16]. For example, Zhang et al. [17] developed attention mechanism-based deep learning models using data sampled at 2 h intervals for wastewater treatment plant monitoring, consistently outperforming baseline models in predicting parameters like total nitrogen, total phosphorus, and chemical oxygen demand. Rodriguez-Perez et al. [18] developed a method for detecting technical anomalies in high-frequency water quality data using artificial neural networks (ANNs), utilizing turbidity and conductivity data collected by automated in situ sensors in riverine and estuarine environments, achieving effective detection of sudden and long-term anomalies through semi-supervised and supervised classification, with models calibrated via Bayesian multi-objective optimization. Huang et al. [19] developed a Self-Attentive LSTM (SA-LSTM) model integrated with LOADEST, using weekly/monthly sampled data from Dongting Lake, achieving Nash–Sutcliffe Efficiency (NSE) scores of 0.71 for COD Mn and 0.57 for NH₃-N, and reducing RMSE by 20–30% compared to standalone machine learning models.

While high-resolution water quality data offer significant potential to advance the efforts of data-driven models, their use might introduce additional challenges as well. For example, high-frequency datasets are not only more susceptible to noise, but also introduce substantial computational complexity [20]. Furthermore, the acquisition of long-term, continuous high-frequency datasets remains difficult, and even when available, these datasets demand rigorous quality control due to increased variability from frequent sampling. Systematic studies exploring the trade-offs between temporal data resolution and predictive accuracy remain scarce, especially given the substantial resources required for deploying and maintaining high-frequency monitoring networks. The prevailing assumption that simply increasing sampling frequency leads to better model performance has left the true value and limitations of high-frequency data underexplored [21], highlighting the critical need for systematic investigations into how temporal resolution influences predictive modeling in water quality monitoring.

This study aims to fill such a research gap by investigating the impact of temporal resolution on water quality prediction model performance. Using Erhai Lake as a pilot region, we systematically evaluated four representative machine learning models (SVR, RF, XGBoost, and LSTM) across two temporal resolutions (4-hourly and daily) for four critical water quality parameters, namely, total nitrogen, total phosphorus, ammonia nitrogen, and dissolved oxygen. This multifaceted analytical approach provides insights into the complex relationships between temporal resolution, model architecture, and water quality parameter characteristics, contributing to more efficient and effective monitoring and prediction systems. Our main contributions include characterizing the statistical differences between daily average and high temporal resolution water quality data and quantitatively evaluating the performance of popular machine learning models across different temporal resolutions for various water quality parameters. The results provide a scientific basis for optimizing monitoring strategies and model selection in monitoring and managing the water environment.

The remainder of this study is organized as follows: Section 2 introduces the materials, methods, and experimental design employed in this research. Section 3 presents the results regarding the data characteristics and model performance, and Section 4 further discusses insights behind the findings. The final conclusions are then presented in Section 5.

2. Materials and Methods

2.1. Study Area

Erhai Lake (see Figure 1), located in the northwestern part of Yunnan Province, Southwestern China, lies at an elevation of 1972 m above sea level. As one of the country’s largest freshwater lakes, it spans an area of approximately 249.8 km² and has an average depth of 10.2 m. Although there have been efforts to improve and protect the lake, it continues to suffer from eutrophication, pollution, and habitat degradation. These issues are primarily driven by rapid urban growth, tourism, and the intensification of agriculture. The water quality of the lake has been fluctuating between Class II and Class III standards [22], with significant algal blooms occurring since 1996, with particularly severe episodes in 2003–2004 and again after 2013.

2.2. Datasets

We collected 4 h water quality data from the Erhai Huxin monitoring site, a national key water quality assessment section located at the Erhai Lake. This site served as the sole monitoring location that provided consistent high temporal resolution data for a wide-spectrum of water quality parameters over the study period. We selected ten key parameters in freshwater systems as input features, including water temperature (WT), pH, dissolved oxygen (DO), permanganate index (IMn), electrical conductivity (EC), turbidity (NTU), ammonia nitrogen (NH₃-N), total nitrogen (TN), total phosphorus (TP), and chlorophyll a (Chla). After excluding outliers and filling in a small amount of missing data, we obtained a dataset of 7994 records covering the period from 5 March 2020 to 25 December 2023.

2.3. Models and Evaluation Matrix

This section introduces the predictive models adopted in the study and the evaluation metrics used to quantify their performance.

2.3.1. Machine Learning Models for Water Quality Predictions

(1)

Support Vector Regression (SVR)

Support Vector Regression (SVR) [23] is an extension of Support Vector Machines (SVMs) for regression tasks. SVR aims to find a function that deviates from the training data by a value no greater than a predetermined margin ε, while remaining as flat as possible. An SVR optimization problem can be formulated as follows:

$$\underset{\mathrm{w},\mathrm{b},\mathrm{\xi },{\mathrm{\xi }}^{*}}{\min }{\displaystyle \frac{1}{2}}{‖\mathrm{w}‖}^2+C{\sum }_{i=1}^n\left({\mathrm{\xi }}_i+{\mathrm{\xi }}_i^{\mathrm{*}}\right)$$

(1)

Subject to the following:

$${\mathrm{y}}_{\mathrm{i}}-{\mathrm{w}}^{\mathrm{T}}\mathrm{\varphi }\left({\mathrm{x}}_{\mathrm{i}}\right)-\mathrm{b}\le \mathrm{\epsilon }+{\mathrm{\xi }}_{\mathrm{i}}$$

(2)

$${\mathrm{w}}^{\mathrm{T}}\mathrm{\varphi }\left({\mathrm{x}}_{\mathrm{i}}\right)+\mathrm{b}-{\mathrm{y}}_{\mathrm{i}}\le \mathrm{\epsilon }+{\mathrm{\xi }}_{\mathrm{i}}^{*}$$

(3)

$${\mathrm{\xi }}_i,{\mathrm{\xi }}_i^{\mathrm{*}}\ge 0,\mathrm{i}=1,\dots ,\mathrm{n}$$

(4)

where $\mathrm{w}$ is the weight vector, $b$ is the bias term, ${\mathrm{x}}_{\mathrm{i}}$ and ${\mathrm{\xi }}_{\mathrm{i}}^{\mathrm{*}}$ are slack variables, $C$ is the regularization parameter, and $\mathrm{\varphi }\left(\mathrm{x}\right)$ is a kernel function that maps the input features to a higher-dimensional space. SVR is effective for handling non-linear relationships in data with moderate dimensionality.

(2)

Random Forest (RF)

Random Forest [24] is an ensemble learning method that constructs multiple decision trees during training and outputs the average prediction of the individual trees for regression tasks. Each tree is built from a bootstrap sample of the training data, and at each node, a random subset of features is considered for splitting. The prediction function can be expressed as follows:

$${\mathrm{f}}_{\mathrm{R}\mathrm{F}}\left(\mathrm{x}\right)={\displaystyle \frac{1}{\mathrm{B}}}{\sum }_{\mathrm{b}=1}^{\mathrm{B}}{\mathrm{T}}_{\mathrm{b}}\left(\mathrm{x}\right)$$

(5)

where $\mathrm{B}$ is the number of trees in the forest and ${\mathrm{T}}_{\mathrm{b}}\left(\mathbf{x}\right)$ is the prediction of the $\mathrm{b}$-th tree. Random Forest reduces overfitting through its ensemble nature and feature randomization, making it robust for environmental modeling where data may contain complex interactions and noise.

(3)

Extreme Gradient Boosting (XGBoost)

XGBoost [25] is an advanced implementation of gradient boosting that sequentially builds decision trees, with each new tree trained to correct the errors of the ensemble of existing trees. The objective function being optimized in XGBoost is as follows:

$$\mathcal{L}\left(\mathrm{\varphi }\right)={\sum }_{\mathrm{i}=1}^{\mathrm{n}}\mathrm{l}\left({\mathrm{y}}_{\mathrm{i}},\widehat{y_i}\right)+\sum \mathrm{k}=1^{\mathrm{K}}\mathrm{\Omega }\left({\mathrm{f}}_{\mathrm{k}}\right)$$

(6)

where $\mathrm{l}$ is a differentiable convex loss function, $\widehat{y_i}$ is the prediction, and $\mathrm{\Omega }\left(\mathrm{f}\right)=\mathrm{\gamma }\mathrm{T}+{\displaystyle \frac{1}{2}}\mathrm{\lambda }{\left|\mathrm{w}\right|}^2$ is a regularization term that penalizes the complexity of the model. XGBoost incorporates sophisticated regularization techniques and a system for handling sparse data, making it highly effective for water quality prediction where relationships may be complex and data often contain missing values.

(4)

Long Short-Term Memory (LSTM)

LSTM [25] is a specialized recurrent neural network architecture designed to learn long-term dependencies in sequential data. Unlike traditional neural networks, LSTM contains memory cells with gates that regulate the flow of information, allowing the network to capture temporal patterns across different timescales. The core equations of an LSTM cell are as follows:

$${\mathrm{f}}_{\mathrm{t}}=\mathrm{\sigma }\left({\mathrm{W}}_{\mathrm{f}}\cdot \left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}}\right]+{\mathrm{b}}_{\mathrm{f}}\right){\mathrm{i}}_{\mathrm{t}}=\mathrm{\sigma }\left({\mathrm{W}}_{\mathrm{i}}\cdot \left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}}\right]+{\mathrm{b}}_{\mathrm{i}}\right)$$

(7)

$$\tilde{\mathrm{C}}t=\tanh \left(W_C\cdot \left[h\mathrm{t}-1,{\mathrm{x}}_{\mathrm{t}}\right]+{\mathrm{b}}_{\mathrm{C}}\right)$$

(8)

$${\mathrm{C}}_{\mathrm{t}}={\mathrm{f}}_{\mathrm{t}}\times {\mathrm{C}}_{\mathrm{t}-1}+{\mathrm{i}}_{\mathrm{t}}\times \tilde{\mathrm{C}}t$$

(9)

$$o_t=\mathrm{\sigma }\left(W_o\cdot \left[h\mathrm{t}-1,{\mathrm{x}}_{\mathrm{t}}\right]+{\mathrm{b}}_{\mathrm{o}}\right)$$

(10)

$${\mathrm{h}}_{\mathrm{t}}={\mathrm{o}}_{\mathrm{t}}\times \tanh \left({\mathrm{C}}_{\mathrm{t}}\right)$$

(11)

where ${\mathrm{f}}_{\mathrm{t}}$, ${\mathrm{i}}_{\mathrm{t}}$, and $o_t$ are the forget, input, and output gates, respectively, ${\mathrm{C}}_{\mathrm{t}}$ is the cell state, ${\mathrm{h}}_{\mathrm{t}}$ is the hidden state, $W$ and $\mathrm{b}$ are the weight matrices and bias vectors, and $\mathrm{\sigma }$ is the sigmoid function. LSTM networks are suitable for water quality prediction as they capture complex temporal dependencies in environmental time series data, including seasonal patterns and irregular fluctuations.

2.3.2. Wavelet Component Analysis

The Wavelet Component Analysis [26] was performed using the Daubechies 4 (db4) mother wavelet with a decomposition level of 4. This method decomposes signals into approximate and detail coefficients, enabling multi-scale feature extraction. The db4 wavelet is selected for its balance between smoothness and compact support, while level 4 decomposition optimizes noise reduction and frequency localization. The discrete wavelet transform (DWT) with Daubechies 4 (db4) at level 4 was applied.

2.3.3. SHapley Additive exPlanations (SHAP)

SHapley Additive exPlanations (SHAP) is a unified framework for interpreting machine learning models by quantifying the contribution of each input feature to the model’s output [27,28]. Grounded in cooperative game theory, SHAP values represent the average marginal contribution of a feature across all possible coalitions.

2.3.4. Evaluation Matrix

The following four matrices were used to evaluate model performance, with each highlighting a different aspect of prediction quality, including accuracy, variability, and reliability.

(1)

MAPE—Mean Absolute Percentage Error

$$\mathrm{MAPE}={\displaystyle \frac{100\%}{n}}{\sum }_{i=1}^n\left|{\displaystyle \frac{y_i-\widehat{y_i}}{y_i}}\right|$$

(12)

MAPE measures the average absolute percentage difference between predicted values ($\widehat{y_i}$) and actual values $y_i$. It expresses the prediction error as a percentage, which makes it easy to interpret across different scales.

(2)

rRMSE—Relative Root Mean Square Error

$$\mathrm{rRMSE}={\displaystyle \frac{\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}}{\overline{y}}}\times 100\%$$

(13)

Relative RMSE is the Root Mean Square Error normalized by the mean observed values ($\overline{y}$). It expresses the RMSE as a percentage of the mean, helping to compare performance across different datasets or models.

(3)

R²—Coefficient of Determination

$${\mathrm{R}}^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$$

(14)

R² indicates how well the model explains the variability of the observed data. A value of 1 means perfect prediction, while zero means that the model performs no better than the mean of the observed values.

(4)

Kling–Gupta efficiency

The modified Kling–Gupta efficiency ($KGE$) [29] and its three components ($\mathrm{\beta }$, $\mathrm{\alpha }$, $\mathrm{\rho }$) were used to evaluate model performance [30,31]. The theoretical version of the modified $KGE$ metrics is

$$KGE=1-\sqrt{{\left(\mathrm{\beta }-1\right)}^2+{\left(\mathrm{\alpha }-1\right)}^2+{\left(\mathrm{\rho }-1\right)}^2}$$

(15)

$$\mathrm{\beta }={\displaystyle \frac{\overline{S}}{\overline{O}}}$$

(16)

$$\mathrm{\alpha }={\displaystyle \frac{{\mathrm{\sigma }}_S}{{\mathrm{\sigma }}_O}}$$

(17)

$$\mathrm{\rho }={\displaystyle \frac{\mathrm{Cov}\left(S,O\right)}{{\mathrm{\sigma }}_S{\mathrm{\sigma }}_O}}$$

(18)

where $\mathrm{\beta }$ (Bias) measures the ratio of the mean of the simulated values ($\overline{S}$) to the mean of the observed values ($\overline{O}$). $\mathrm{\alpha }$ (Variability) measures the ratio of the standard deviation of the simulated values (${\sigma }_S$) to the standard deviation of the observed values (${\sigma }_O$). $\mathrm{\rho }$ (Correlation) measures the Pearson correlation coefficient between the simulated values ($S$) and the observed values ($O$).

2.4. Experiment Design

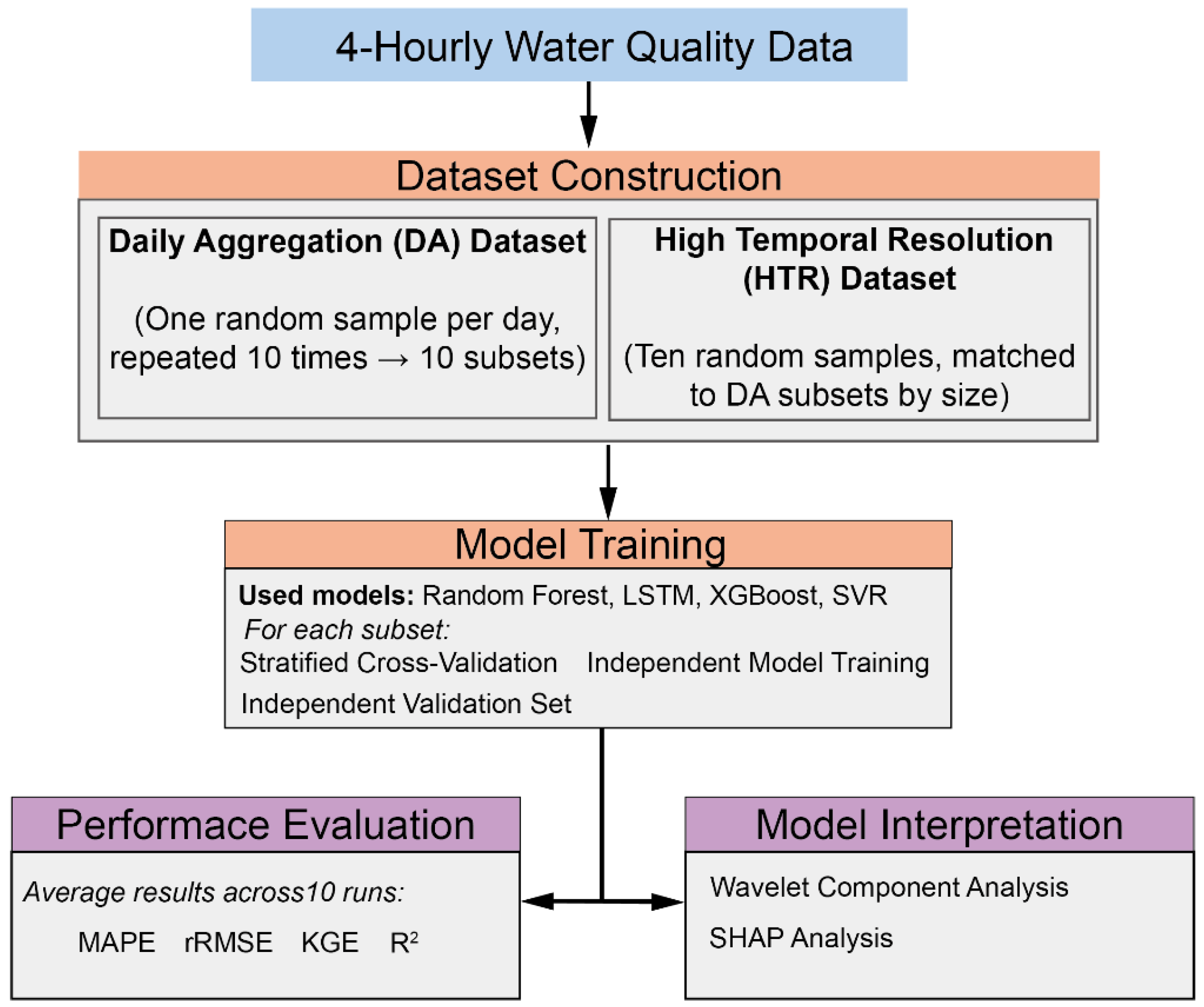
The experiments (see Figure 2) use 4-hourly water quality monitoring data from the Erhai watershed to create two distinct datasets: a low-frequency daily aggregation (DA) dataset and a high-frequency 4 h high temporal resolution (HTR) dataset. We generated the DA dataset through a specific method: for each calendar day, we randomly selected one observation from the raw dataset as the representative value. This sampling process was repeated ten times to create ten DA data subsets.

To address potential bias from sample size differences, we performed ten independent random samplings on the HTR data, with each sample strictly matching the corresponding DA subset’s sample size. We then averaged the ten results to minimize sampling randomness. We applied stratified cross-validation for model training, building prediction models independently for each data subset. The final performance metrics were calculated as the arithmetic mean of the ten modeling results. We also established independent validation sets to ensure the statistical reliability of our evaluation conclusions. Our evaluation framework includes four complementary metrics: Mean Absolute Percentage Error (MAPE) to measure prediction bias; coefficient of determination (R²) to assess how well the model explains water quality variations; relative Root Mean Square Error (rRMSE) to evaluate prediction error fluctuations; and the Kling–Gupta efficiency (KGE), helping identify parameters sensitive to temporal resolution. This approach reveals how temporal resolution affects model accuracy, stability, and timeliness. Finally, Wavelet Component Analysis and SHAP (SHapley Additive exPlanations) were employed to interpret the underlying drivers of the model predictions, providing insights into how different temporal components and input variables contribute to the model’s performance across varying time resolutions.

The research addresses two key questions: (1) how changes in temporal resolution directionally impact model performance indicators, and (2) whether different water quality parameters (such as dissolved oxygen and ammonia nitrogen) respond differently to changes in temporal scale.

3. Results

3.1. Statistical Characterization of Data

We analyze the distributional characteristics between the original 4 h resolution data and the daily mean (DM) values, as presented in

Table 1. Summary of basic statistics for high temporal resolution (HTR) and daily mean (DM) observations of various water quality parameters.

Parameter	Mean		Std		Min		25%		50%		75%		Max		SNR
	HTR	DM	HTR	DM	HTR	DM	HTR	DM	HTR	DM	HTR	DM	HTR	DM	HTR	DM
Temp	17.43	17.30	4.25	4.56	8.28	8.53	13.91	13.36	18.23	17.72	21.17	21.62	26.89	25.25	4.10	3.80
pH	8.52	8.56	0.20	0.19	5.75	6.74	8.37	8.46	8.54	8.57	8.66	8.68	9.27	9.13	41.73	45.78
IMn	4.21	4.19	0.84	0.80	2.61	3.17	3.87	3.87	4.10	4.06	4.40	4.35	20.97	20.97	5.01	5.22
DO	7.65	7.75	1.02	0.95	2.46	4.20	7.02	7.06	7.59	7.77	8.36	8.45	13.77	10.92	7.54	8.14
NH3-N	0.03	0.03	0.01	0.01	0.01	0.03	0.03	0.03	0.03	0.03	0.03	0.03	0.18	0.16	2.32	2.45
TP	0.02	0.02	0.01	0.01	0.01	0.01	0.02	0.02	0.02	0.02	0.02	0.03	0.09	0.07	3.44	3.73
TN	0.33	0.32	0.08	0.08	0.09	0.10	0.27	0.26	0.32	0.31	0.38	0.37	0.83	0.55	4.04	4.10
EC	292.61	290.75	24.28	25.40	154.85	154.94	288.57	287.05	295.59	293.44	303.50	302.27	320.08	319.88	12.05	11.45
NTU	4.41	4.75	11.72	10.49	0.27	0.41	2.13	2.04	2.68	3.11	4.25	4.66	342.58	184.33	0.38	0.45
chla	0.01	0.01	0.02	0.02	0.00	0.00	0.00	0.00	0.01	0.01	0.01	0.01	0.40	0.28	0.61	0.69

HTR = high temporal resolution; DM = daily mean. Statistical terms: std = standard deviation, SNR = signal-to-noise ratio. Percentiles (25%, 50%, 75%) refer to 25th, 50th (median), and 75th percentiles.

. According to Table 1, both daily and HTR datasets exhibit similar water quality characteristics. The daily dataset shows a mean temperature of 17.30 °C (standard deviation 4.56 °C) and a mean pH value of 8.56 (standard deviation 0.20), indicating stable alkaline conditions. The permanganate index averages 4.20 mg/L (standard deviation 0.86), while dissolved oxygen averages 7.78 mg/L (standard deviation 1.03), suggesting adequate oxygenation with moderate fluctuations. Ammonia nitrogen concentrations remain low (mean 0.03 mg/L), with total phosphorus and total nitrogen averaging 0.02 mg/L and 0.32 mg/L, respectively. Electrical conductivity averages 290.75 μS/cm (standard deviation 25.40). Notably, turbidity shows a mean value of 4.75 but with a high standard deviation of 10.49 and a maximum value of 262.25, indicating significant outliers. Chlorophyll-a concentrations average merely 0.01 mg/m³, reflecting low algal growth levels. Regarding signal-to-noise ratio (SNR), which is calculated by dividing the mean of the signal by the standard deviation (std) of the noise, the daily dataset demonstrates consistently higher values across parameters, such as dissolved oxygen (8.14) and temperature (45.78), both exceeding those of the HTR dataset, suggesting superior signal quality in the daily measurements.

The HTR dataset presents largely comparable parameters to the daily dataset: temperature averages 17.43 °C (standard deviation 4.25 °C), pH averages 8.52 (standard deviation 0.20), permanganate index averages 4.21 mg/L (standard deviation 0.84), and dissolved oxygen averages 7.65 mg/L (standard deviation 1.02). Ammonia nitrogen maintains a mean of 0.03 mg/L (standard deviation 0.01). Total phosphorus and total nitrogen average 0.02 mg/L and 0.32 mg/L, respectively, while electrical conductivity averages 290.69 μS/cm (standard deviation 24.28). Interestingly, turbidity shows a mean of 4.41 (standard deviation 11.72) with a maximum value of 184.33, higher than in the daily dataset. Chlorophyll-a concentrations remain consistent with the daily dataset at 0.01 mg/m³. In terms of SNR, the HTR dataset demonstrates slightly lower values overall compared to the daily dataset, with dissolved oxygen at 7.54, temperature at 41.73, and pH at 5.01, all lower than their daily counterparts, indicating greater data variability in specific parameters within the HTR measurements.

The parameter distribution characteristics are shown in Figure 3. In the HTR data, the distribution of standardized values for water quality parameters shows a multimodal pattern: temperature (Temp) forms a steep unimodal peak near zero, IMn forms a broad peak around 0.50, extending into the 1.00 range, and NH3_N and TN show primary peaks at 0.00 and 0.20, respectively, with TN exhibiting a slight right skew in the range above 0.4 (Figure 3a). In comparison, the daily average parameters demonstrate a more concentrated distribution pattern: pH and chla form sharp peaks near the origin, with DO showing a prominent peak at 0.4 and a notable right skew, EC displays a broad peak around 0.3, and TP shows a rapid decay in the right tail (right plot). The differences in kurtosis among the parameter distributions indicate that the HTR data have a wider range of variability compared to the daily average data, with IMn and EC exhibiting the broadest distribution spans across both timescales.

3.2. Model Performance of DA and HTR Datasets

We compared the predictive performance of four models—SVR, RF, XGBoost, and LSTM—across two temporal scales (4 h HTR and daily) for four water quality parameters (TN, TP, NH3_N, and DO). The results revealed significant differences in model performance across different water quality parameters (

Table 2. Performance comparison of four machine learning models under high temporal resolution (HTR) and daily aggregation (DA) timescales for water quality prediction.

Model	Index	MAPE		rRmse		R2
		HTR	DA	HTR	DA	HTR	DA
SVR	TN	12.04	18.59	14.39	20.76	0.00	0.27
	TP	36.55	100.10	35.90	91.44	−4.08	−9.79
	NH3_N	71.04	228.92	65.05	203.71	−5.87	−27.75
	DO	2.14	3.59	3.20	5.21	0.91	0.80
RF	TN	4.60	9.80	7.23	13.70	0.76	0.68
	TP	6.17	8.96	9.81	14.18	0.66	0.75
	NH3_N	3.60	8.04	8.29	18.41	0.90	0.77
	DO	1.73	3.37	2.66	5.05	0.94	0.81
XGBoost	TN	4.75	10.01	7.31	14.25	0.75	0.66
	TP	6.38	9.26	9.85	14.30	0.65	0.75
	NH3_N	3.60	8.83	8.15	19.93	0.90	0.73
	DO	1.71	3.38	2.61	5.01	0.94	0.81
LSTM	TN	5.98	9.38	8.45	12.62	0.66	0.70
	TP	12.08	14.15	16.21	22.56	0.09	0.40
	NH3_N	9.91	14.16	15.56	29.90	0.61	0.56
	DO	2.50	5.44	3.56	8.27	0.88	0.61

). The RF and XGBoost models demonstrated strong predictive capabilities for most water quality parameters, while SVR showed limited effectiveness except for DO predictions. The RF model achieved superior performance for TN prediction with HTR and daily MAPE values of 4.60% and 10.81%, rRMSE values of 7.23% and 14.93%, and R² values of 0.76 and 0.62, respectively. Similarly, for TP prediction, RF maintained strong performance with HTR and daily MAPE values of 6.17% and 10.73%, rRMSE values of 9.81% and 18.02%, and R² values of 0.66 and 0.62. For NH3-N, both RF and XGBoost models achieved identical HTR MAPE values of 3.60%, with RF maintaining slightly better daily performance (MAPE 9.30% versus 10.07%). For DO prediction, all models performed relatively well, with XGBoost achieving the lowest HTR MAPE of 1.71% (rRMSE 2.61%, R² 0.94), closely followed by RF with MAPE 1.73% (rRMSE 2.66%, R² 0.94).

Overall, tree-based models (RF and XGBoost) demonstrated superior and more consistent predictive capabilities compared to SVR and LSTM, particularly when handling variations in temporal resolution. SVR consistently underperformed across most parameters, often failing to capture concentration patterns effectively. LSTM, despite its strengths in sequential data, showed mixed results and did not consistently outperform the tree-based algorithms.

Surprisingly, LSTM did not outperform the tree-based models despite its theoretical advantages in handling sequential data. LSTM showed poor performance in TP prediction, with HTR and daily MAPE values of 12.08% and 16.23%, rRMSE values of 16.21% and 24.43%, and R² values of only 0.09 and 0.36, respectively. The SVR model consistently underperformed across most parameters, with inferior results for TP (HTR MAPE 36.55%, daily MAPE 104.86%) and NH3-N (HTR MAPE 71.04%, daily MAPE 200.92%), and negative R² values indicating a complete failure to capture concentration patterns.

Our analysis indicates that TN, NH3-N, and DO are relatively easier to predict than TP, which presents significant challenges across all models. This pattern was consistent in both temporal resolutions. For instance, even the best-performing RF model achieved HTR and daily MAPE values of 6.17% and 10.73% for TP, compared to 3.60% and 9.30% for NH3-N. The DO prediction task yielded the best results across all models, with the lowest MAPE values ranging from 1.71% to 2.50% for HTR predictions and 4.31% to 5.20% for daily predictions.

The benefit of using high temporal resolution data varied by parameter. Using HTR data consistently yielded better model performance for TN, NH3-N, and DO predictions than daily aggregated data. For example, RF’s MAPE for TN improved from 10.81% (daily) to 4.60% (HTR), and for NH3-N, it from 9.30% (daily) to 3.60% (HTR). The improvement was also notable for DO, with RF’s MAPE decreasing from 4.31% (daily) to 1.73% (HTR). However, for TP prediction, the improvement from high-frequency data was less pronounced, with RF’s MAPE decreasing from 10.73% (daily) to 6.17% (HTR). These variable benefits across parameters suggest that the added value of high-frequency monitoring may depend on the specific water quality parameter’s inherent characteristics and fluctuation patterns.

4. Discussion

4.1. Insights from Model Performance with Different Temporal Data

In this section, we discussed the temporal scaling effects using the Kling–Gupta efficiency metric and its components. The KGE measures the model performance by considering the bias, correlation, and variability between the prediction and observation. The results are shown in Figure 4. Among the prediction models, SVR exhibits the lowest KGE scores in predicting TN, TP, and NH3-N. The consistently poor performance (KGE = 0.42–0.56 for TN, approximately 0.00 for both TP and NH3-N) stems from inadequate correlation metrics and extreme bias amplification (bias ratios of 1.02–1.28 for TN, 1.28–1.87 for TP, and 1.58–3.00 for NH3-N), indicating fundamental limitations in capturing temporal patterns of target variables.

RF, XGBoost, and LSTM models demonstrate superior capability, achieving positive KGE scores across all target variables. For TN prediction, tree-based models (RF and XGBoost) notably benefit from high temporal resolution (HTR) data, enabling better temporal pattern capture, though with slight performance variations. XGBoost achieved the most stable TN simulations across temporal resolutions (Daily KGE = 0.83, HTR KGE = 0.75), driven by robust variability correlation (0.89 daily, 0.84 HTR) and minimal bias (1.00). While RF exhibited comparable daily performance (KGE = 0.80), its HTR KGE declined to 0.70 due to reduced correlation (0.75 vs. 0.84 daily). Similar enhancement effects from HTR data are observed for RF and XGBoost in predicting NH3-N and DO, where XGBoost consistently emerged as the most reliable model (NH3-N: Daily KGE = 0.92, HTR KGE = 0.83; DO: Daily KGE = 0.96, HTR KGE = 0.88).

An exception occurs in TP prediction, where HTR data result in worse performance than daily aggregated (DA) data. RF and XGBoost maintained relatively stable KGE across scales (RF: 0.72–0.81; XGBoost: 0.73–0.84) with balanced bias ratios (1.00) and strong variability correlations (0.80–0.95), but the performance degradation with HTR data might be attributed to the low signal-to-noise ratio (SNR) of TP measurements. This suggests that high noise components introduced in HTR datasets might degrade model performance instead of enhancing it [32]. Therefore, assessing the quality of monitoring data in terms of signal and noise components is crucial before implementing high-frequency monitoring systems.

The LSTM model achieved better performance with HTR data in predicting NH3-N and DO, with improvement observed in DO prediction. Surprisingly, LSTM demonstrated an inverse pattern for TN with superior HTR KGE (0.81) compared to daily (0.74), reflecting its capacity to leverage sequential dependencies in high-frequency data. Such behavior might be related to the recurrent mechanism of LSTM design, which is specifically engineered to capture long-term dependencies in sequential data [33]. Another interesting observation is that using HTR data for TP prediction with LSTM significantly enhanced the model’s ability to capture temporal variability, but correlation performance worsened (HTR KGE = 0.53 vs. daily KGE = 0.55). This dichotomy suggests that LSTM’s temporal advantage is conditional on parameter-specific dynamic characteristics rather than universally applicable [34,35].

Overall, the impact of temporal resolution varied significantly by model architecture. Tree-based methods (RF, XGBoost) showed inherent robustness to temporal scaling, experiencing only moderate performance degradation when moving from daily to HTR data (Average ΔKGE = 0.09). SVR’s structural limitations led to extreme sensitivity and poor performance across resolutions. LSTM, conversely, displayed non-linear temporal effects—excelling in TN HTR predictions but struggling with DO and NH₃-N at finer resolutions, exhibiting the largest temporal sensitivity for DO (ΔKGE = 0.21 between daily 0.91 and HTR 0.70). This highlights challenges in modeling oxygen fluctuations against complex biochemical interactions at finer resolutions [35].

4.2. SHAP Interpretability Analysis for Main Driving Factors

We first applied SHAP analysis to identify key features that influence model predictivity. This helps to study the relationships among model performance, dominant features, and the temporal characteristics of water quality parameters (Figure 5 and Figure 6).

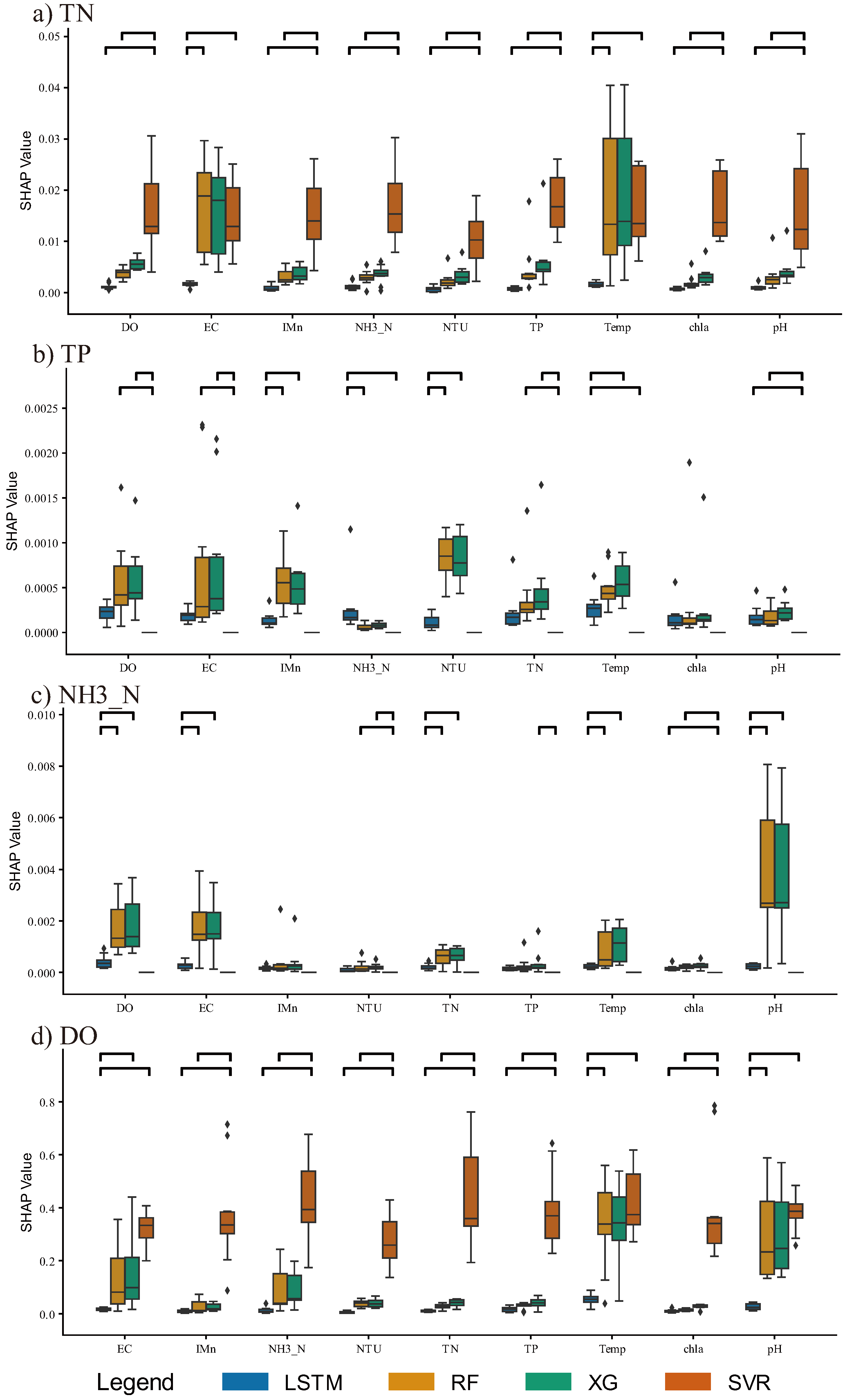
Statistical analysis revealed significant differences in SHAP values between models across all water quality parameters. For TN prediction, SHAP analysis revealed that DO and temperature were the primary influencing factors. The SVR model showed higher dependency on DO, EC, and temperature (SHAP values 0.04–0.05) compared to the RF and XGBoost models (SHAP values < 0.02). This pattern of feature importance might explain why RF and XGBoost achieved better HTR performance (KGE = 0.80–0.83) compared to daily aggregation (KGE = 0.70–0.75), as these models possibly better captured sub-daily variations (variability correlation 0.84–0.89 vs. 0.75–0.84 daily). The relationship between environmental factors and nitrogen dynamics has been well-documented in previous studies [36,37].

For TP prediction, SHAP analysis identified TN as the most critical feature (SHAP value approximately 0.0015 in LSTM), with temperature also playing a significant role across traditional machine learning models. The complex interactions between these factors possibly contribute to the universally poorer predictions for TP (best RF daily KGE = 0.81) compared to other parameters. High-frequency noise may have degraded model accuracy at finer temporal resolutions (ΔKGE = −0.09 for RF), suggesting why daily aggregation improved model stability through smoothing of high-frequency components [38].

For NH3-N prediction, SHAP analysis indicated that DO was the dominant feature (SHAP value approximately 0.0055 in LSTM), while pH showed abnormally high importance in the SVR model (SHAP value around 0.008). This feature importance pattern might explain XGBoost’s optimal daily performance (KGE = 0.92) compared to HTR (KGE = 0.83), as daily aggregation potentially better aligned with the parameter’s intrinsic variations. RF’s 11% degradation in HTR performance further evidences possible limitations in resolving high-frequency fluctuations present in NH3-N signals [39].

For DO prediction, SHAP analysis identified temperature as the primary driver, with SHAP values ranging from 0.05 in the LSTM model to approximately 0.5 in the SVR model, substantially exceeding the contribution of other features. This finding aligns with established knowledge of temperature-driven oxygen dynamics in aquatic systems [40]. The strong relationship between temperature variation patterns and DO explains the excellent performance across all models (HTR XGBoost KGE = 0.96, HTR RF KGE = 0.94), with only marginal improvements from high temporal resolution data (ΔKGE = 0.08–0.10). This feature–response relationship supports the stable variability correlations (0.93–0.97) observed across temporal resolutions.

The integration of SHAP analysis with model performance metrics provides compelling evidence that prediction accuracy is maximized when model architecture and temporal sampling align with the dominant processes influencing water quality parameters. Parameters with strong temperature dependence (DO) achieved consistent performance across models and temporal scales, while parameters with complex multi-factor dynamics (TP) present inherent prediction challenges regardless of model sophistication. Parameters influenced by slower environmental processes (NH3-N) might perform better with daily aggregation, while those with significant sub-daily components (TN) could benefit from high temporal resolution monitoring [41].

This analysis demonstrates that the predictability of water quality parameters is potentially linked to the alignment among feature importance patterns, model architecture capabilities, and the inherent temporal characteristics of the target parameters.

4.3. Wavelet Decomposition for Temporal Variability Components

The previous analysis implied that the benefit of using high temporal data is not univocal. Both model structure and SNR of the data may play a role in the final performance. In this section, by analyzing wavelet decomposition, we further delve into the temporal characteristics of water quality measurements to explore the predictability of target water quality parameters. Under a 4 h sampling interval, the D1–D4 decomposition levels correspond to timescales of 8 h, 16 h, 32 h, and 64 h, respectively, thereby providing a comprehensive characterization of dynamic processes from intra-daily fluctuations to inter-weekly variations (Figure 7).

The results showed that, for lake water temperature, pH, DO, and TN, the sub-daily component (D2) appears as the dominant energy. Specifically, DO exhibited primary energy (99.57%) with D2 dominance in residual energy (47.40% at 16 h scale), aligning with diurnal photosynthetic cycles [42]. Similarly, TN showed D2-scale dominance (41.57% at 16 h) alongside the possibility of intermittent high-frequency influences related to rainfall events. Such results may link to the fact that these variables are sensitive to daily environmental cycles, such as sunlight and air temperature changes.

The presence of strong diurnal patterns in these parameters might explain their good predictability, as shown in previous model performance results. For DO, this mesoscale regularity explains why all models achieved satisfying daily predictions (XGBoost KGE = 0.96, RF = 0.94) with only marginal improvements from high temporal resolution data (ΔKGE = 0.08–0.10). The balanced energy distribution across sub-daily scales enabled comparable performance between temporal resolutions, as reflected in stable variability correlations (0.93–0.97) [42]. For TN, this temporal characteristic explains RF and XGBoost’s good HTR performance (KGE = 0.80–0.83 vs. daily 0.70–0.75) through enhanced capture of sub-daily variations (variability correlation 0.84–0.89 vs. 0.75–0.84 daily).

For IMn, NH3-N, EC, and NTU, the D4 component appears to be the dominant. NH3-N demonstrated D4 dominance (38.93% at 64 h) aside from primary energy, which is consistent with slow sediment-exchange processes. EC showed extreme low-frequency dominance (99.99% trend), explaining its minimal temporal resolution sensitivity [43]. NTU exhibited multi-scale energy distribution (54.85% trend), correlating with known sensitivity to disturbance events. These components correspond to longer-period fluctuations that might be mainly driven by slower biogeochemical processes or multi-day weather conditions [16,44]. XGBoost’s optimal daily performance for NH3-N (KGE = 0.92 vs. HTR = 0.83) aligns with this low-frequency control, while RF’s 11% HTR degradation reveals possible limitations in resolving residual high-frequency fluctuations.

Interestingly though, TP shows no dominant component, displaying balanced multi-scale energy (D1–D4: 24.77–27.79%) aside from the primary energy. This implies that the variation in TP in Erhai Lake could involve multiple processes operating at different timescales as well as irregular external inputs, reflecting complex interactions from rapid runoff (D1) to weekly sediment processes. This spectral complexity corresponds with TP’s universally poor predictions (best RF daily KGE = 0.81) compared to other parameters, particularly in HTR mode where high-frequency noise potentially degrades performance (ΔKGE = −0.09 for RF). The energy distribution explains why daily aggregation improved model stability through high-frequency smoothing [45,46].

Variables with strong cyclic patterns such as TN and DO might benefit from HTR datasets due to their distinct temporal signatures. For instance, LSTM’s inverse temporal pattern for TN (HTR KGE = 0.81 > daily 0.74) suggests a unique capacity to leverage sequential dependencies despite shared D2 dominance [47,48,49]. On the other hand, the prediction of TP will likely be more challenging even with the HTR dataset, as its strong variability originates from complex biogeochemical processes operating across multiple timescales. An alternative for improving the predictability of TP could be to enlarge the spectrum of input variables.

Supplementary analysis confirmed these general patterns: Chla revealed D3–D4 dominance beside primary energy (46.43%), aligning with algal growth cycles [50]. The spectral analysis suggests that models achieve optimal performance when their architectural design corresponds with the prevailing scale characteristics of the underlying processes, while high-frequency complexities (as in TP) may inherently limit prediction accuracy regardless of temporal resolution [51].

4.4. Implications for Water Quality Monitoring and Modeling

This study integrates machine learning models with SHAP value analysis to uncover the driving mechanisms behind dynamic changes in water quality parameters. Our results provide practical implications for designing effective monitoring strategies across different temporal resolutions.

For routine water quality monitoring programs, our findings demonstrate that daily resolution data generally satisfy prediction requirements for most parameters. Tree-based machine learning models like RF and XGBoost achieve satisfactory prediction performance (KGE > 0.80 for most parameters) using daily aggregated data, which meets the basic needs of lake water quality monitoring while minimizing resource investment. This finding is relevant for resource-constrained monitoring programs where high-frequency sensor deployment may not be feasible.

However, parameter-specific temporal dependencies suggest that differentiated monitoring strategies might be optimal. Temperature-sensitive parameters like DO benefit from high-resolution monitoring that captures diurnal fluctuations (HTR XGBoost KGE = 0.96 vs. daily KGE = 0.88), while parameters with complex multi-scale dynamics like TP present inherent prediction challenges regardless of temporal resolution or model sophistication. For specialized lake types, such as phosphorus-limited eutrophic lakes, precise TP monitoring remains critical. Our analysis reveals that despite the challenges in TP prediction, daily aggregated data provide more stable model performance than high-resolution data (RF daily KGE = 0.81 vs. HTR KGE = 0.72), possibly due to the smoothing of high-frequency noise components that might otherwise degrade model accuracy [52].

Comparative model analysis demonstrates that non-linear models (i.e., LSTM, RF, XGBoost) exhibit notable advantages in capturing the interactions of features across different temporal patterns [53]. LSTM models show particular promise for parameters with strong sequential dependencies, as evidenced by their superior performance for TN prediction using high temporal resolution data (HTR KGE = 0.81 vs. daily KGE = 0.74). This suggests that advanced modeling frameworks could compensate for limitations in monitoring frequency when deployed appropriately [54].

For implementation in water resource management, we recommend a tiered monitoring approach where routine parameters are monitored at daily intervals using cost-effective traditional machine learning models, while critical parameters for specific lake systems receive targeted high-frequency monitoring coupled with specialized modeling techniques. Such an approach would optimize resource allocation while ensuring accurate water quality assessment and prediction capabilities [55,56]. This strategy holds the potential to enhance water quality prediction performance and provide more reliable spatiotemporal dynamics for watershed management decision-making.

5. Conclusions

This study comprehensively investigates the impact mechanism of temporal resolution on water quality prediction models through a multi-scale analysis approach, providing a robust theoretical basis for optimizing monitoring strategies. The results indicate significant differences in the sensitivity of water quality parameters to temporal resolution: DO exhibits relatively consistent performance across temporal scales in all models, with XGBoost achieving optimal results at both daily (KGE = 0.96) and HTR (KGE = 0.88) resolutions through exceptional correlation (0.97 daily, 0.94 HTR) and variability reproduction. This temporal stability aligns closely with DO’s pronounced diurnal cycle driven by photosynthesis (47.40% of energy at the 16 h scale). In contrast, TN, TP, and NH₃-N demonstrate parameter-specific response patterns, reflecting the unique temporal scale characteristics of different biogeochemical processes. For instance, NH₃-N shows a dominant characteristic at the 64 h scale (38.93% of energy), explaining why XGBoost emerged as the most reliable model for NH₃-N simulation (Daily KGE = 0.92, HTR KGE = 0.83), supported by near-ideal bias ratios (1.00–1.01) and superior variability tracking (0.94 both scales).

Model comparison analysis further reveals that tree-based methods (RF, XGBoost) demonstrate moderate HTR performance degradation (Average ΔKGE = 0.09), suggesting their inherent robustness to temporal scaling. In contrast, SVR displayed systematic limitations, particularly in HTR variability correlation and excessive bias (1.28–3.00), resulting in failures for TP and NH₃-N predictions (KGE = 0.00). LSTM exhibited non-linear temporal effects—excelling in TN HTR predictions (HTR KGE = 0.81 > daily KGE = 0.74) but struggling with DO and NH₃-N at finer resolutions (ΔKGE = 0.21 for DO). Feature importance analysis based on SHAP values further elucidates the temporal scale effects of environmental driving factors. Temperature is identified as the most significant factor influencing DO variations, with a strong correlation at the 16 h scale, confirming the dominant role of the diurnal photosynthesis cycle. These findings provide scientific support for developing parameter-specific monitoring strategies: high-frequency monitoring (≤1 h) is beneficial for parameters with significant sub-daily components like TN, while parameters dominated by low-frequency processes (NH₃-N) perform adequately with daily aggregation. The “parameter-scale-model” matching framework established in this study not only deepens the understanding of water quality dynamics but also provides methodological guidance for the optimization of intelligent monitoring system design.

This study highlights the influence of temporal resolution on water quality model performance, revealing distinct sensitivities across parameters. DO showed stable predictive accuracy across scales, driven by its diurnal pattern, while nutrient indicators such as TN, TP, and NH₃-N exhibited scale-dependent behaviors reflecting varied biogeochemical dynamics. XGBoost consistently outperformed other models for DO and NH₃-N, while tree-based methods demonstrated general robustness to resolution changes. In contrast, SVR showed notable degradation at high temporal resolution, and LSTM displayed mixed results depending on the parameter. SHAP analysis further confirmed scale-specific feature importance, particularly the role of temperature in sub-daily DO variation.

This study, while contributing valuable insights, has several limitations that warrant attention. First, the current analysis focuses exclusively on Erhai Lake, which might constrain its generalizability to other regions with different climatic, hydrological, and socio-economic characteristics. Second, it is important to acknowledge that only the water quality data from a single long-term monitoring site were used in the analysis. This limits our ability to assess the spatial variability and gradients of water quality parameters across the entire lake, given that the Erhai watershed is characterized by strong heterogeneous hydrological and environmental conditions which might influence the contaminant distribution in Erhai Lake. Future research might explore spatial patterns of lake water quality and include other variables besides water quality parameters in prediction models to further enhance the generalizability.