Micro-Pore Structure and Fractal Characteristics of Shale Reservoir in Jiyang Depression
Abstract
1. Introduction
2. Experimental Method and Procedure
2.1. Experimental Materials
2.2. Experimental Procedures
2.2.1. Nitrogen Adsorption Test
2.2.2. Scanning Electron Microscope Experiment
2.2.3. Fracturing Fluid Damage Experiments
2.2.4. Contact Angle Experiment
3. Results
3.1. Electron Microscope Scanning Experiment
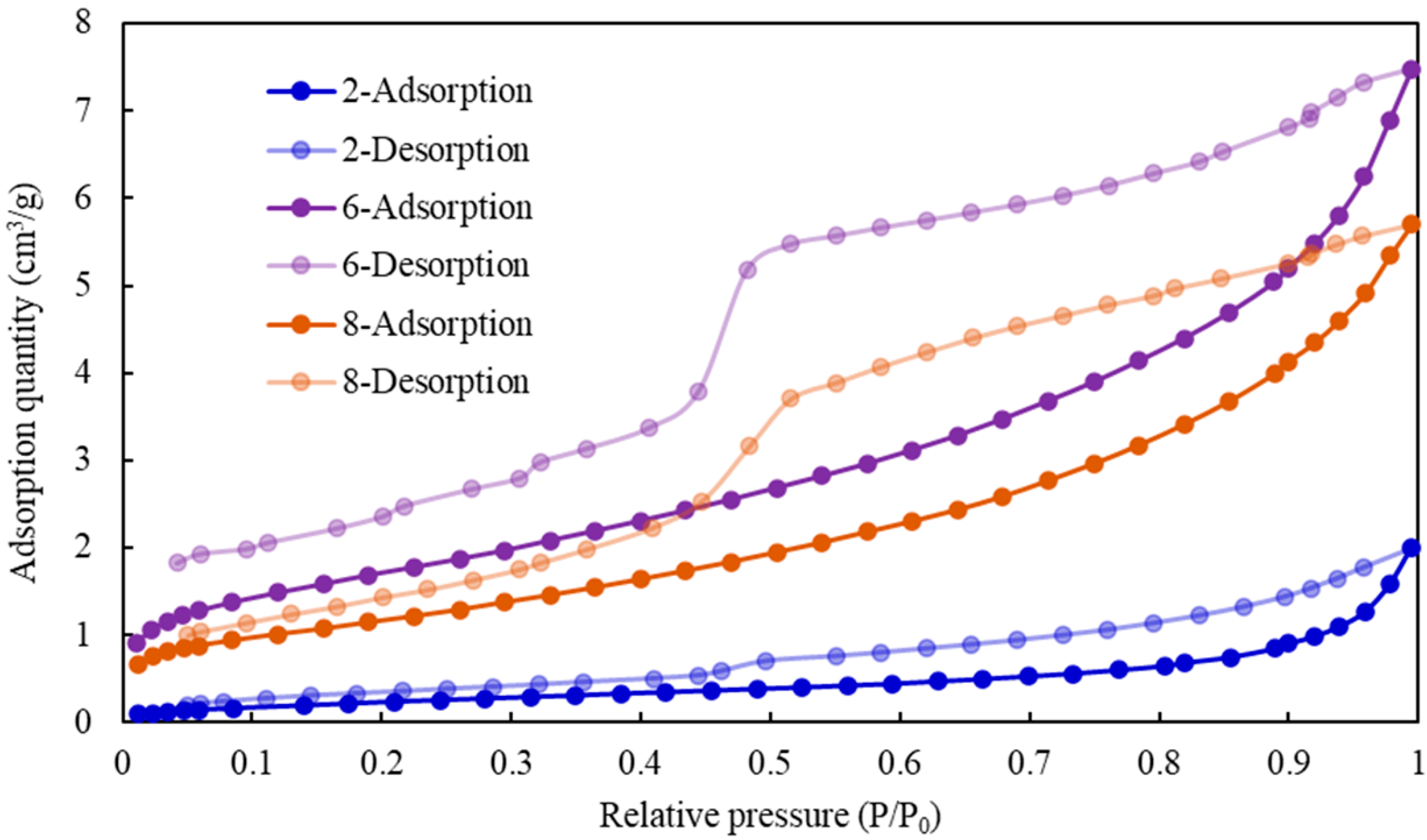
3.2. Nitrogen Adsorption Experiment
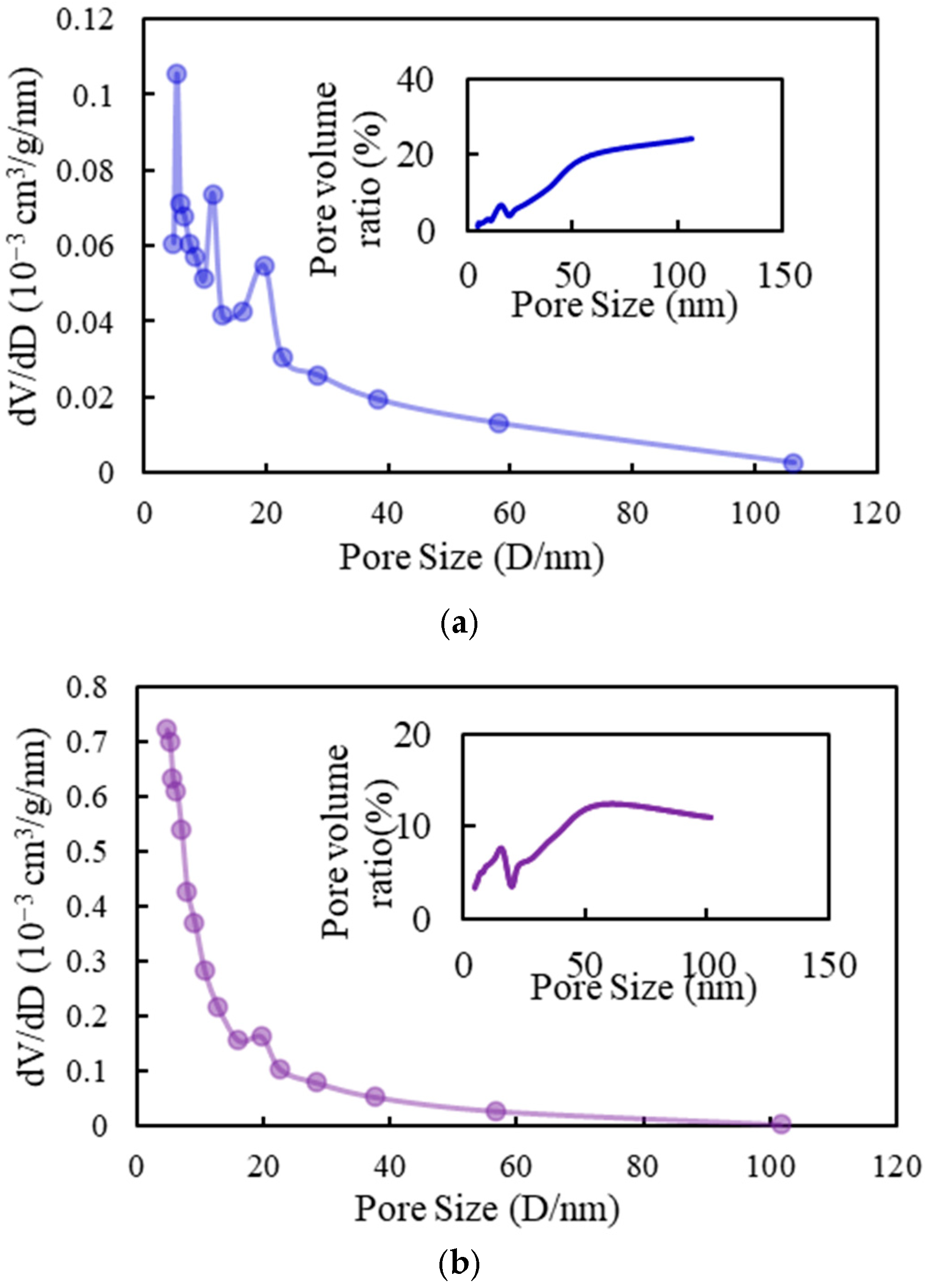
3.3. Pore Size Distribution Characteristics
3.4. Rock Physical Property Evaluation Experiment
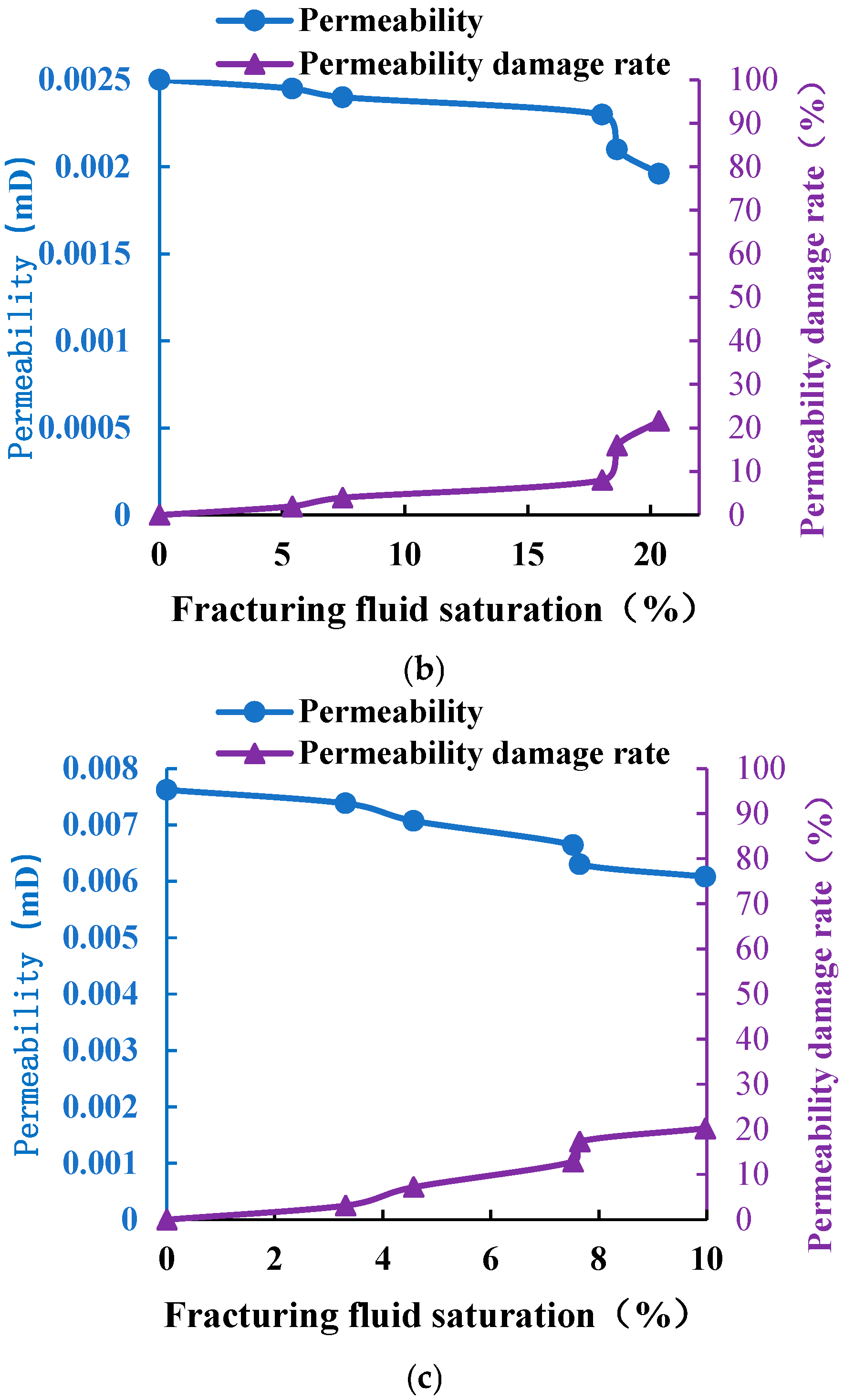
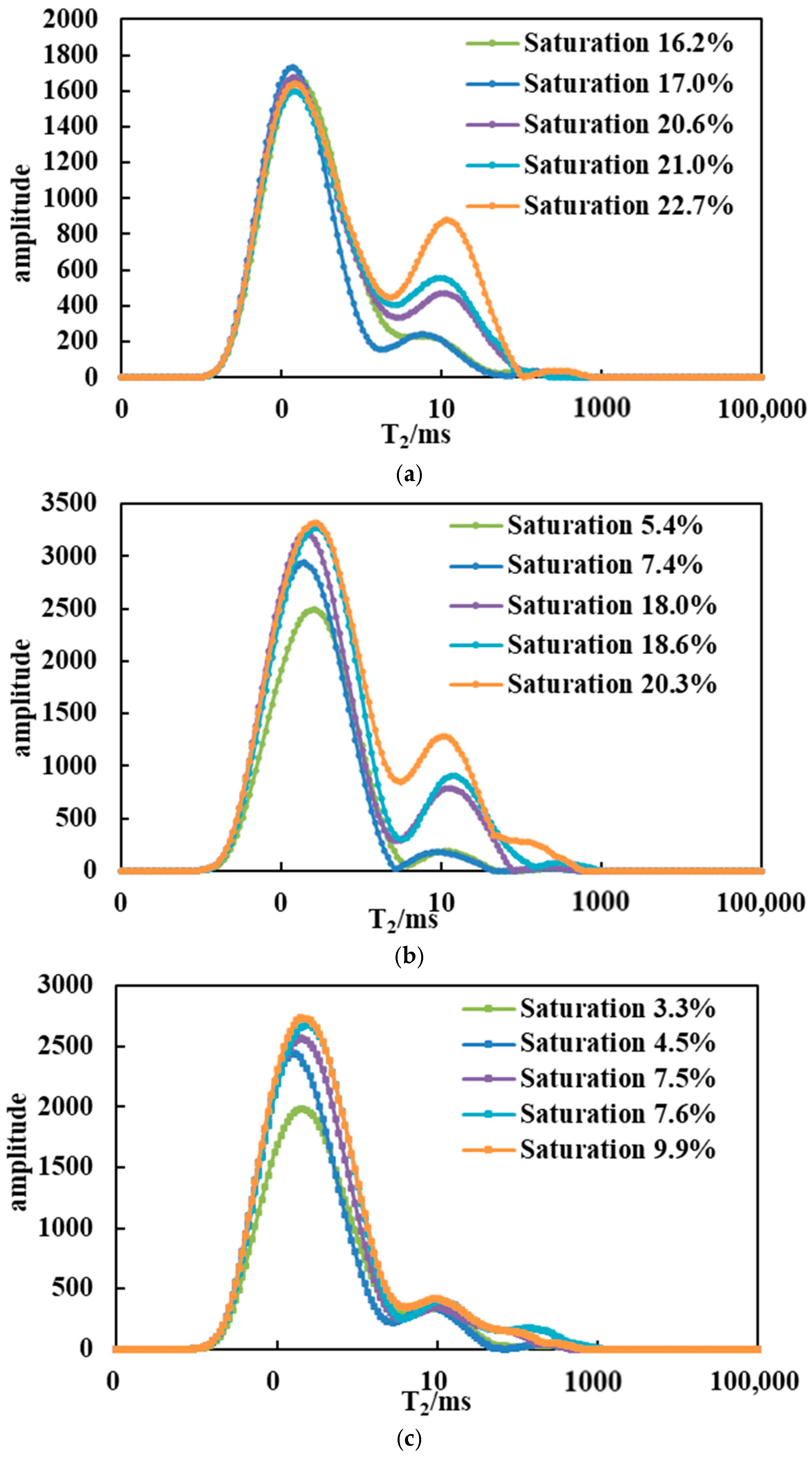
3.4.1. Permeability Damage Experiment
3.4.2. Shale Permeability Damage Evaluation
3.4.3. Contact Angle Analysis
4. Discussion
4.1. Quantitative Evaluation of Pore Structure
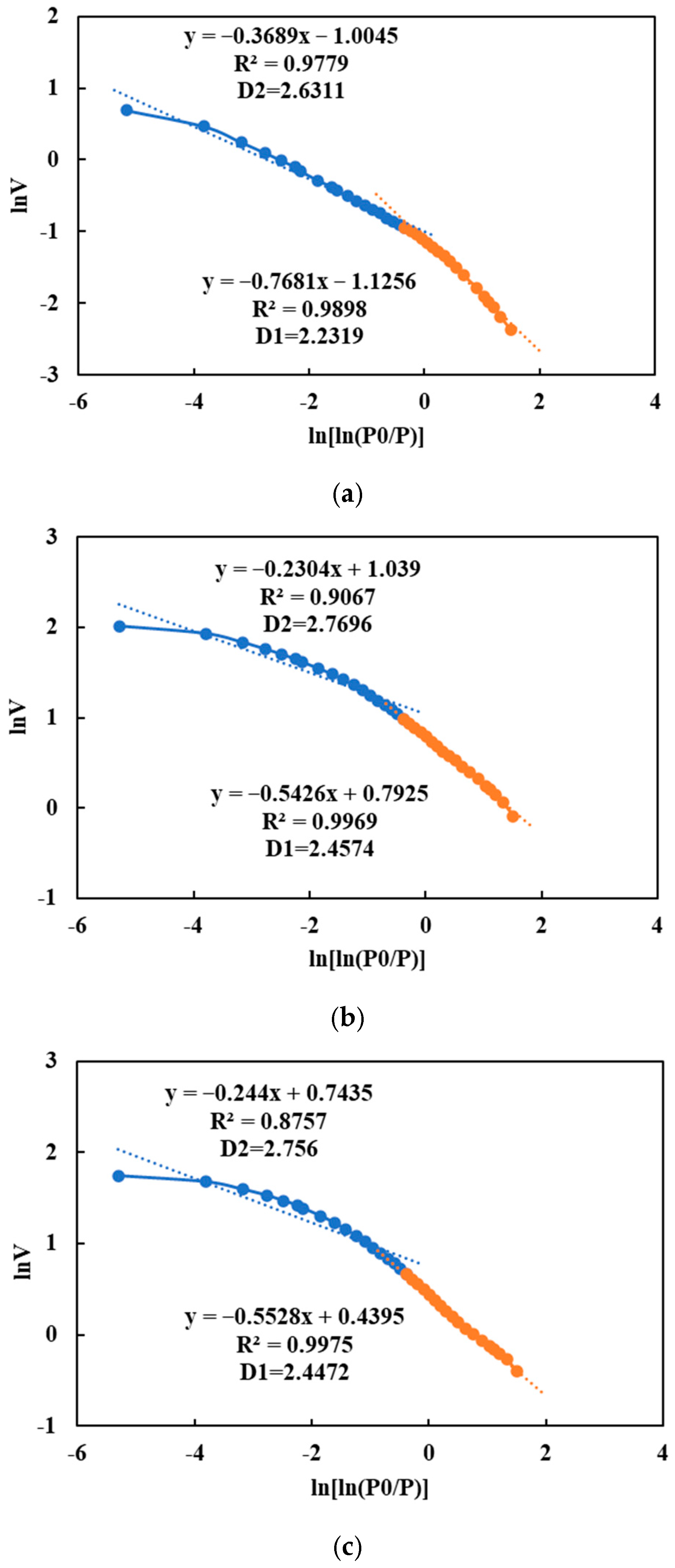
4.2. Calculation of Fractal Dimension
4.3. Relationship Between Fractal Dimension and Pore Structure Parameters
5. Conclusions
- (1)
- The dominant pore structure observed in the shale reservoirs of Jiyang Depression primarily consists of inorganic pores, with a lesser occurrence of micro-fractures and organic pores. Inorganic pores mainly include intergranular pores developed around minerals and intragranular pores developed inside minerals. Fractures are mainly developed between mineral particles or organic matter or between mineral particles and organic matter. The organic matter pores are mainly distributed in or between organic matter and are partially surrounded by clay minerals.
- (2)
- There is a strong correlation between the equivalent diameter of pores and the parameters describing their structure in shale reservoirs. The distribution of pore sizes varies significantly among different types of pore structures found in shale formations. A unimodal distribution of changes in pore volume indicates that medium and large pores dominate the composition of shale rock samples. Conversely, a scattered distribution with multiple peaks suggests that rock samples are distributed across various pore sizes.
- (3)
- By utilizing the FHH model, we computed the fractal dimensions of various pore sizes using a relative pressure threshold of 0.5 to distinguish between regions with high and low pressures. The average value of the fractal dimension, which characterizes the surface properties and small pores, was determined to be 2.3788. Furthermore, we obtained an average fractal dimension of 2.7189 for medium-sized pores. A smaller deviation from a fractal dimension of 2 indicates enhanced homogeneity in pore surface characteristics and regularity in pore structure.
- (4)
- Both fractal dimension and fractal dimension are correlated with specific surface area, total pore volume, and average pore diameter. However, the correlation of fractal dimension is better, which can more intuitively characterize the development in the pore interior, indicating that when is closer to 3, the specific surface area and pore volume are larger, and the internal structure of the pore is more complex.
- (5)
- The permeability curve of the core continues to decline with the increase in the slippery water saturation; the contact Angle of cores in the three blocks of Y depression decreases with the increase in the action time of slippery water. After the slippery water enters the core, it erodes clay minerals, and the surface hydrophilicity gradually increases, while the wetting Angle gradually decreases.
Research Contributions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, C.; Zhu, R.; Wu, S.; Yang, Z.; Tao, S.; Yuan, X.; Hou, L.; Yang, H.; Xu, C.; Li, D.; et al. Types, characteristics, genesis and prospects of conventional and unconventional hydrocarbon accumulations:taking tight oil and tight gas in China as an instance. Acta Pet. Sin. 2012, 33, 173–187. [Google Scholar]
- Zou, C.N.; Zhang, G.S.; Yang, Z.; Tao, S.Z.; Hou, L.H.; Zhu, R.K.; Yuan, X.J.; Ran, Q.Q.; Li, D.H.; Wang, Z.P. Geological concepts, characteristics, resource potential and key techniques of unconventional hydrocarbon: On unconventional petroleum geology. Pet. Explor. Dev. 2013, 40, 385–399. [Google Scholar] [CrossRef]
- Wang, H.; Shi, Y.; Xu, D.; Chen, X.; Li, C. Unconventional reservoir pore structure characterization techniques and progress. Pet. Geol. Recovery 2019, 26, 21–30. [Google Scholar] [CrossRef]
- Yang, Z.; Zou, C.; Wu, S.; Lin, S.; Pan, S.; Niu, X.; Men, G.; Tang, Z.; Li, G.; Zhao, J.; et al. Formation, distribution and resource potential of the “sweet areas (sections)” of continental shale oil in China. Mar. Pet. Geol. 2019, 102, 48–60. [Google Scholar] [CrossRef]
- Brunauer, S.; Deming, L.S.; Deming, W.E.; Teller, E. On a theory of the van der waals adsorption of gases. J. Am. Chem. Soc. 1940, 62, 1723–1732. [Google Scholar] [CrossRef]
- Chen, K.; Liu, X.; Liu, J.; Zhang, C.; Guan, M.; Zhou, S. Lithofacies and pore characterization of continental shale in the second member of the Kongdian Formation in the Cangdong Sag, Bohai Basin, China. J. Pet. Sci. Eng. 2019, 177, 154–166. [Google Scholar] [CrossRef]
- Yu, L.; Lu, J. The Fundamental Principles and Applications of Scanning Electron Microscopy. Exp. Sci. Technol. 2019, 17, 85–93. [Google Scholar]
- Bao, F.; Yu, L.; Rui, X.; Zhang, Q.; Fan, M.; Ma, Z. Microstructure and SEM-Raman study of organic matter pore heterogeneity in shale. Pet. Geol. Exp. 2021, 43, 871–879. [Google Scholar]
- Zhang, W.K.; Shi, Z.J.; Tian, Y.M.; Xie, D.; Li, W.J. The combination of high-pressure mercury injection and rate-controlled mercury injection to characterize the pore-throat structure in tignt sandstone reservoirs. Fault-Block Oil Gas Field 2021, 28, 14–20. [Google Scholar]
- Li, T.; Jiang, Z.; Su, P.; Zhang, X.; Chen, W.; Wang, X.; Ning, C.; Wang, Z.; Xue, Z. Effect of laminae development on pore structure in the lower third member of the Shahejie Shale, Zhanhua Sag, Eastern China. Interpretation 2020, 8, T103–T114. [Google Scholar] [CrossRef]
- Pszonka, J.; Sala, D. Application of the mineral liberation analysis (MLA) for extraction of grain size and shape measurements in siliciclastic sedimentary rocks. E3S Web Conf. 2018, 66, 02002. [Google Scholar] [CrossRef]
- Pszonka, J.; Schulz, B. SEM Automated Mineralogy applied for the quantification of mineral and textural sorting in submarine sediment gravity flows. Gospod. Surowcami Miner.—Miner. Resour. Manag. 2022, 38, 105–131. [Google Scholar] [CrossRef]
- Huang, W.; Ma, X.; Zhou, X.; Liu, J.; He, T.; Tao, H.; Li, S.; Hao, L. Characteristics and controlling factors of pore structure of shale in the 7th member of Yanchang Formation in Huachi area, Ordos Basin, China. J. Nat. Gas Geosci. 2023, 8, 319–336. [Google Scholar] [CrossRef]
- Yasin, Q.; Liu, B.; Sun, M.; Sohail, G.M.; Ismail, A.; Majdanski, M.; Golsanami, N.; Ma, Y.; Fu, X. Automatic pore structure analysis in organic-rich shale using FIB-SEM and attention U-Net. Fuel 2024, 358, 130161. [Google Scholar] [CrossRef]
- Wang, G.; Chen, X.; Wang, G.; Zhang, H.; Wang, J.; Xu, H. Accurate structural characterization of nanopores in coal by cryo-FIB-SEM. Adv. Geo-Energy Res. 2024, 14, 187–200. [Google Scholar] [CrossRef]
- Ding, C.; He, J.; Wu, H.; Zhang, X. Nanometer Pore Structure Characterization of Taiyuan Formation Shale in the Lin-Xing Area Based on Nitrogen Adsorption Experiments. Minerals 2021, 11, 298. [Google Scholar] [CrossRef]
- He, H.; Liu, P.; Xu, L.; Hao, S.; Qiu, X.; Shan, C.; Zhou, Y. Pore structure representations based on nitrogen adsorption experiments and an FHH fractal model: Case study of the block Z shales in the Ordos Basin, China. J. Pet. Sci. Eng. 2021, 203, 108661. [Google Scholar] [CrossRef]
- Zapata, Y.L.; Sakhaee-Pour, A. Modeling adsorption–desorption hysteresis in shales: Acyclic pore model. Fuel 2016, 81, 557–565. [Google Scholar] [CrossRef]
- Wu, X.; Cai, M.; Zhu, Y.; Guo, Q.; Wang, P.; Dong, J. An experimental study on the fractal characteristics of the effective pore structure in granite by thermal treatment. Case Stud. Therm. Eng. 2023, 45, 102921. [Google Scholar] [CrossRef]
- Song, W.; Wang, D.; Yao, J.; Li, Y.; Sun, H.; Yang, Y.; Zhang, L. Multiscale image-based fractal characteristic of shale pore structure with implication to accurate prediction of gas permeability. Fuel 2019, 241, 522–532. [Google Scholar] [CrossRef]
- Sheng, G.; Su, Y.; Zhao, H.; Liu, J. A unified apparent porosity/permeability model of organic porous media: Coupling complex pore structure and multi-migration mechanism. Adv. Geo-Energy Res. 2020, 4, 115–125. [Google Scholar] [CrossRef]
- Li, K.; Kong, S.; Xia, P.; Wang, X. Microstructural characterisation of organic matter pores in coal-measure shale. Adv. Geo-Energy Res. 2020, 4, 372–391. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. On the geometry of homogeneous turbulence with stress on the fractal dimension of the iso-surfaces of scalars. J. Fluid Mech. 1975, 72, 401–416. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Passoja, D.E.; Paullay, A.J. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Hansen, J.P.; Skjeltorp, A.T. Fractal pore space and rock permeability implications. Phys. Rev. B 1988, 38, 2635–2638. [Google Scholar] [CrossRef]
- Heister, K. The measurement of the specific surface area of soils by gas and polar liquid adsorption methods-limitations and potentials. Geoderma 2014, 216, 75–87. [Google Scholar] [CrossRef]
- Yan, J.; He, X.; Geng, B.; Li, X.; Guo, H. Models based on fractal theory to assess pore structure of low permeability sand reservoirs. Well Logging Technol. 2017, 41, 345–352. [Google Scholar]
- Brooks, R. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Huang, J.L.; Dong, D.Z.; Li, J.; Hu, J.; Wang, Y. Reservoir fractal characteristics of continental shale: An example from Triassic Xujiahe Formation shale, Sichuan Basin, China. Nat. Gas Geosci. 2016, 27, 1611. [Google Scholar]
- Li, K. Analytical derivation of Brooks-Corey type capillary pressure models using fractal geometry and evaluation of rock heterogeneity. J. Pet. Sci. Eng. 2010, 73, 20–26. [Google Scholar] [CrossRef]
- Liu, L.L.; Zhao, Z.P.; Li, L.; Chen, W.L.; He, Y.A. Application of the variable scale fractal technique in fracture prediction and reservoir evaluation. Oil Gas Geol. 2008, 29, 31–37. [Google Scholar]
- Wood, D.A. Techniques used to calculate shale fractal dimensions involve uncertainties and imprecisions that require more careful consideration. Adv. Geo-Energy Res. 2021, 5, 153–165. [Google Scholar] [CrossRef]
- He, W.; Zhong, F.; He, C.; Feng, W. Fractal texture research on the pores in reservoir rocks and its application. Nat. Gas Ind. 2000, 20, 67–70. [Google Scholar]
- Shen, J.; Zhang, C. Study on the heterogeneity of the pore structure of Chang6 reservoir in ZJ oilfield, Ordos Basin using fractal theory. J. Xi’an Shiyou Univ. Nat. Sci. Ed. 2008, 23, 19–23. [Google Scholar]
- Ji, F.; Zhang, Y. Application of fractal geometry in description of heterogeneity. J. Univ. Pet. China Ed. Nat. Sci. 1994, 18, 161–168. [Google Scholar]
- He, Y.; Wu, N. A new method for determining fractal dimension of pore structure. Exp. Pet. Geol. 1999, 21, 372–375. [Google Scholar]
- Liu, K.; Ostadhassan, M. The impact of pore size distribution data presentation format on pore structure interpretation of shales. Adv. Geo-Energy Res. 2019, 3, 187–197. [Google Scholar] [CrossRef]
- Feng, K.; Liu, G.; Zhang, Z.; Liu, H.; Lv, R.; Wang, X.; Chang, P.; Lin, J.; Barakos, G. Fractal Strategy for Improving Characterization of N2 Adsorption–Desorption in Mesopores. Fractal Fract. 2024, 8, 617. [Google Scholar] [CrossRef]
- Ji, C.; Liu, T.; Chen, Y.; Wang, Q.; Sun, P.; Sun, L.; He, T. Nanoscale pore structure and fractal characteristics of lacustrine shale: A case study of the Upper Cretaceous Qingshankou shales, Southern Songliao Basin, China. PLoS ONE 2024, 19, e0309346. [Google Scholar] [CrossRef]
- Zhao, C.; Bao, Z.; Li, Z.; Qi, Y.; Chen, L.; Wang, H.; Zhang, Y.; Fang, F. Characterization and fractal characteristics of nano-scale pore structure in shale gas reservoirs: A case study of the deep Longmaxi Formation, Zigong region, Southern Sichuan Basin, China. Front. Earth Sci. 2024, 12, 1410437. [Google Scholar] [CrossRef]
- Zheng, N. Evaluation of Micro-Damage and Fluidity of Slickwater on Shale Reservoir; Northeast Petroleum University: Daqing, China, 2023. [Google Scholar]
- An, C.; Liu, G.; Sun, M. Analysis of shale pore structure characteristics based on nitrogen adsorption experiment and fractal FHH model. Pet. Geol. Sci. Exp. 2023, 45, 576–586. [Google Scholar]
- Feng, X.; Zhu, H. Micro-pore structure and fractal characteristics of the Xiashihezi Formation tight sandstone reservoirs in Sulige area, Ordos Basin. Geol. Sci. Technol. Inf. 2019, 38, 147–156. [Google Scholar]
- Zhang, C.M.; Chen, Z.B.; Zhang, Z.S.; Li, J.; Ling, H.S.; Sun, B.D. Fractal characteristics of reservoir rock pore structure based on NMR T2 distribution. J. Oil Gas Technol. 2007, 29, 80–86. [Google Scholar]
- Liang, L.; Xiong, J.; Liu, X. Fractal characteristics of pore structure of longmaxi formation shale in south of Sichuan Basin, China. J. Chengdu Univ. Technol. Sci. Technol. Ed. 2015, 42, 700–708. [Google Scholar]
- Zhang, Q.; Wu, W.; Liu, L. Pore structure and fractal characteristics of ultra-low permeability reservoirs in Yanchang Formation in Zhenbei area, Ordos Basin. Pet. Geol. Recovery Effic. 2020, 27, 20–31. [Google Scholar]
- Zhang, B.; Wang, H.; Sun, B.; Ouyang, Z.; Dou, W.; Wang, B.; Lai, P.; Hu, Z.; Luo, B.; Yang, M.; et al. Pore Size Distribution and Fractal Characteristics of Deep Coal in the Daning–Jixian Block on the Eastern Margin of the Ordos Basin. ACS Omega 2024, 9, 32837–32852. [Google Scholar] [CrossRef]











| Numbering | Porosity (%) | Permeability (mD) | Specific Surface Area (m2/g) | Total Pore Volume (10−3 cm3/g) | Average Pore Size (nm) |
|---|---|---|---|---|---|
| 2 | 4.47 | 0.014 | 0.5038 | 2.73 | 21.68 |
| 6 | 5.83 | 0.00021 | 2.7513 | 8.921 | 12.97 |
| 8 | 4.41 | 0.00015 | 2.3049 | 6.553 | 11.37 |
| Numbering | Length/cm | Diameter/cm | Porosity/% | Permeability/mD |
|---|---|---|---|---|
| B8 | 2.091 | 2.53 | 18.21% | 0.0025 |
| N9 | 4.922 | 2.424 | 9.45% | 0.00115 |
| F13 | 4.941 | 2.47 | 16.25% | 0.00762 |
| Pore Type | Pore Diameter (nm) | ||
|---|---|---|---|
| Pore Size Distribution | Average Pore Size | ||
| Intergranular pore | 2 | 653 | 263 |
| Intra-granular pore | 3 | 853 | 106 |
| Organic matter pore | 21 | 1835 | 245 |
| Numbering | K1 | P/P0 < 0.5 D1 = K1 + 3 | R2 | K2 | P/P0 > −0.5 D2 = K2 + 3 |
|---|---|---|---|---|---|
| 2 | −0.7681 | 2.2319 | 0.9898 | −0.3689 | 2.6311 |
| 6 | −0.5426 | 2.4574 | 0.9969 | −0.2304 | 2.7696 |
| 8 | −0.5528 | 2.4472 | 0.9975 | −0.244 | 2.7560 |
| Parameter | Regression Equation | R2 |
|---|---|---|
| Specific Surface Area vs. Total Pore Volume | y = 2.5731x + 1.2992 | 0.9605 |
| Average Pore Size vs. Total Pore Volume | y = −0.4848x + 13.505 | 0.7414 |
| Average Pore Size vs. Fractal Dimension () | y = −0.0226x + 2.7249 | 0.9663 |
| Average Pore Size vs. Fractal Dimension () | y = −0.0134x + 2.9242 | 0.9463 |
| Total Pore Volume vs. Fractal Dimension () | y = 0.0383x + 2.1463 | 0.8833 |
| Total Pore Volume vs. Fractal Dimension () | y = 0.0233x + 2.5772 | 0.9129 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, Q.; Lu, M.; Zhong, A.; Yang, F.; He, W.; Li, L. Micro-Pore Structure and Fractal Characteristics of Shale Reservoir in Jiyang Depression. Processes 2025, 13, 1704. https://doi.org/10.3390/pr13061704
Qian Q, Lu M, Zhong A, Yang F, He W, Li L. Micro-Pore Structure and Fractal Characteristics of Shale Reservoir in Jiyang Depression. Processes. 2025; 13(6):1704. https://doi.org/10.3390/pr13061704
Chicago/Turabian StyleQian, Qin, Mingjing Lu, Anhai Zhong, Feng Yang, Wenjun He, and Lei Li. 2025. "Micro-Pore Structure and Fractal Characteristics of Shale Reservoir in Jiyang Depression" Processes 13, no. 6: 1704. https://doi.org/10.3390/pr13061704
APA StyleQian, Q., Lu, M., Zhong, A., Yang, F., He, W., & Li, L. (2025). Micro-Pore Structure and Fractal Characteristics of Shale Reservoir in Jiyang Depression. Processes, 13(6), 1704. https://doi.org/10.3390/pr13061704






