Three-Dimensional Geomechanical Modeling and Hydraulic Fracturing Parameter Optimization for Deep Coalbed Methane Reservoirs: A Case Study of the Daniudi Gas Field, Ordos Basin
Abstract
1. Introduction
2. Geological Setting Area
3. Three-Dimensional Geological and Mechanical Modeling
3.1. Geological Facies Modeling
3.2. Geological Property Modeling
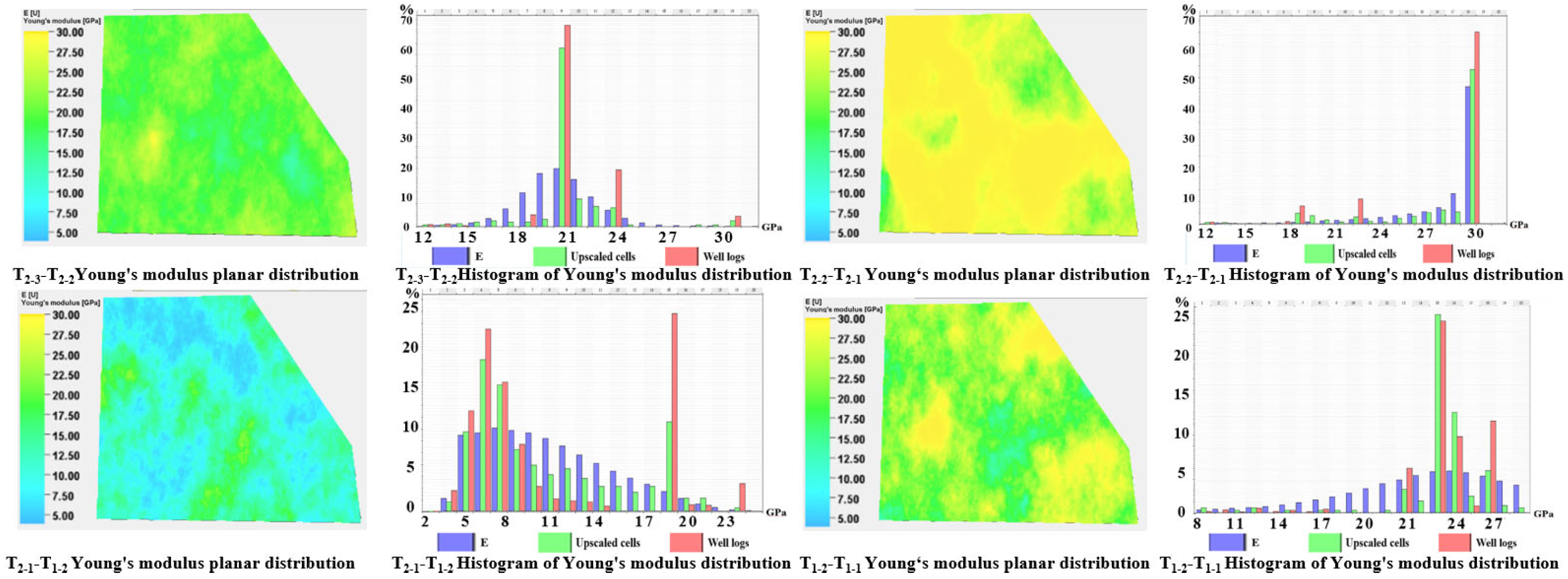
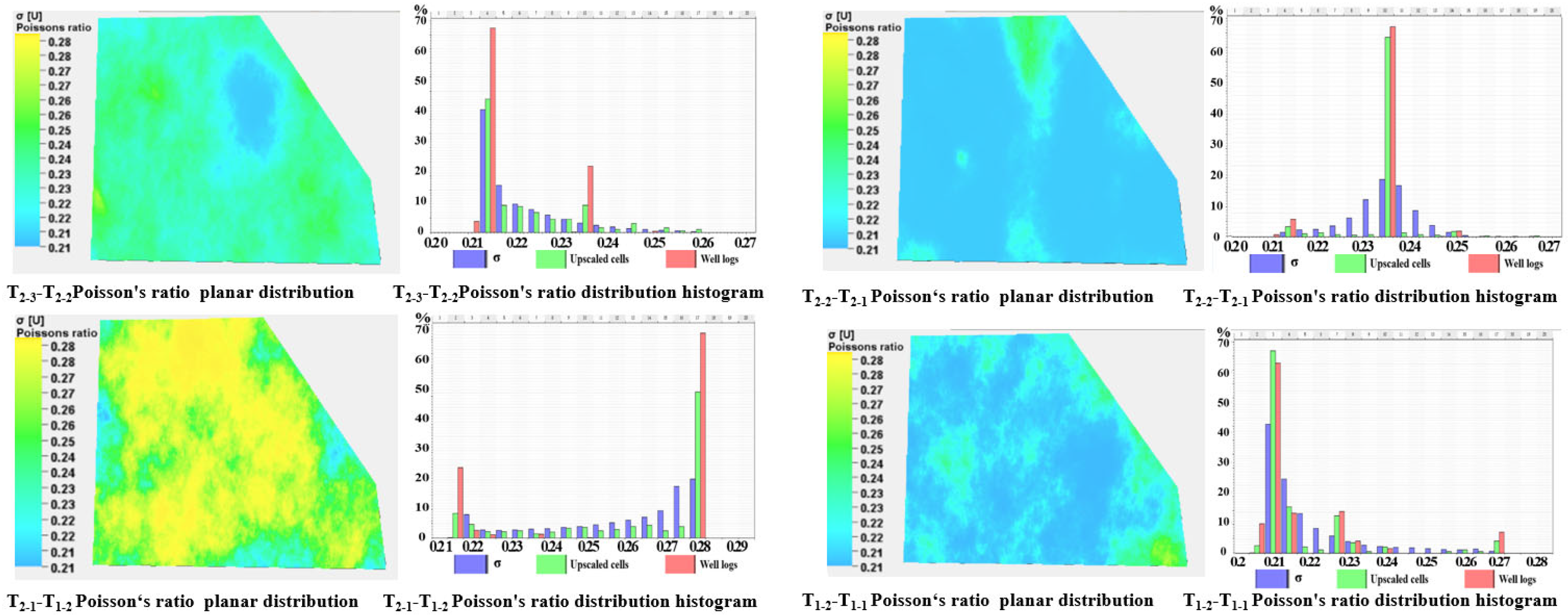
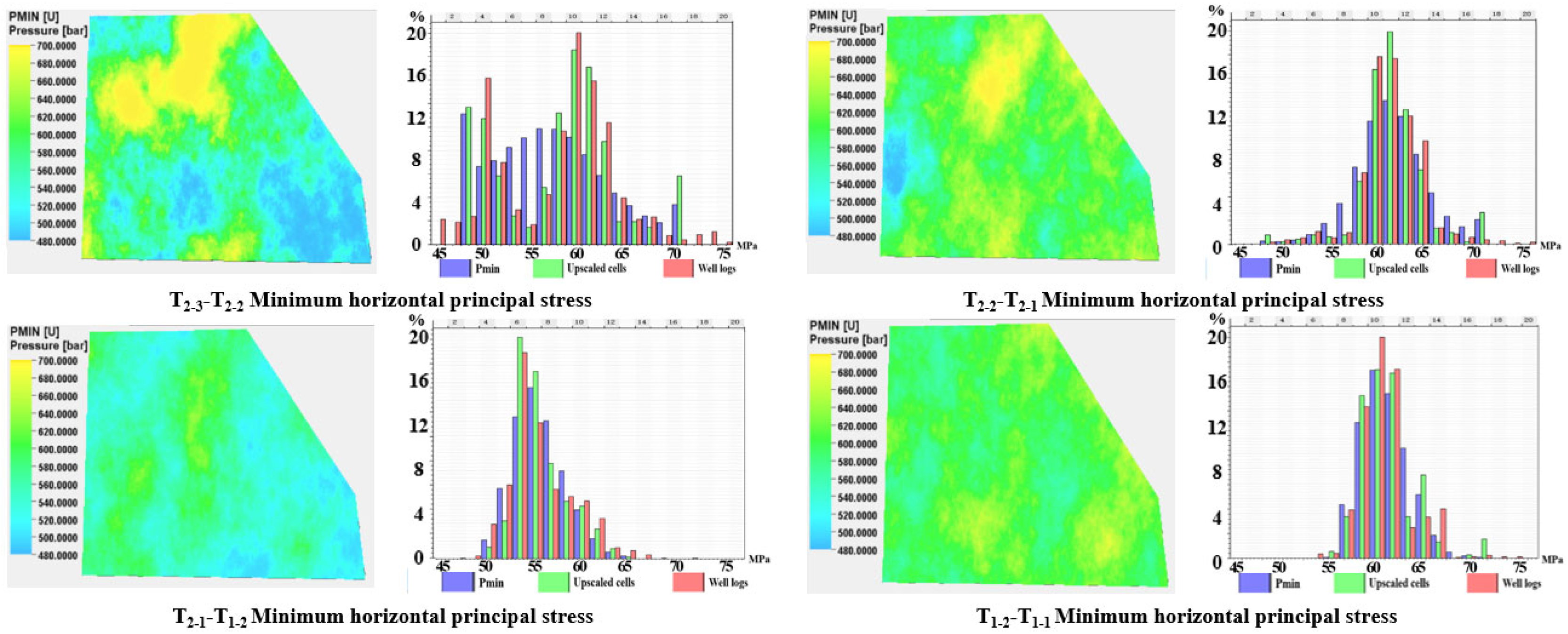
3.3. Rock Mechanics and Stress Modeling
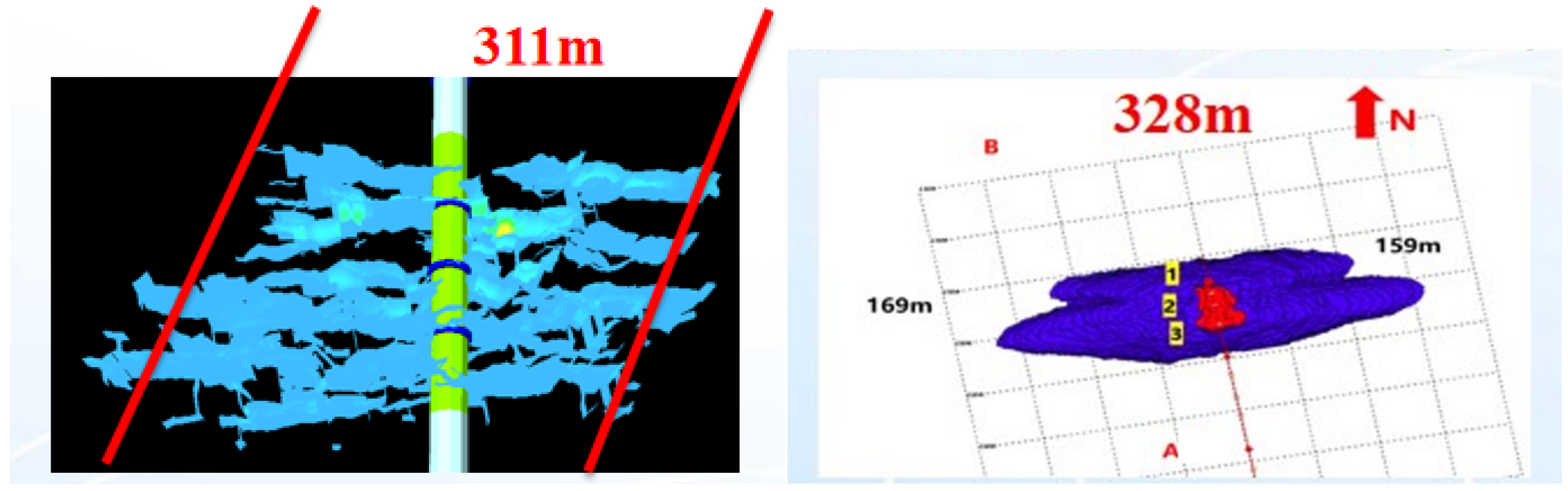
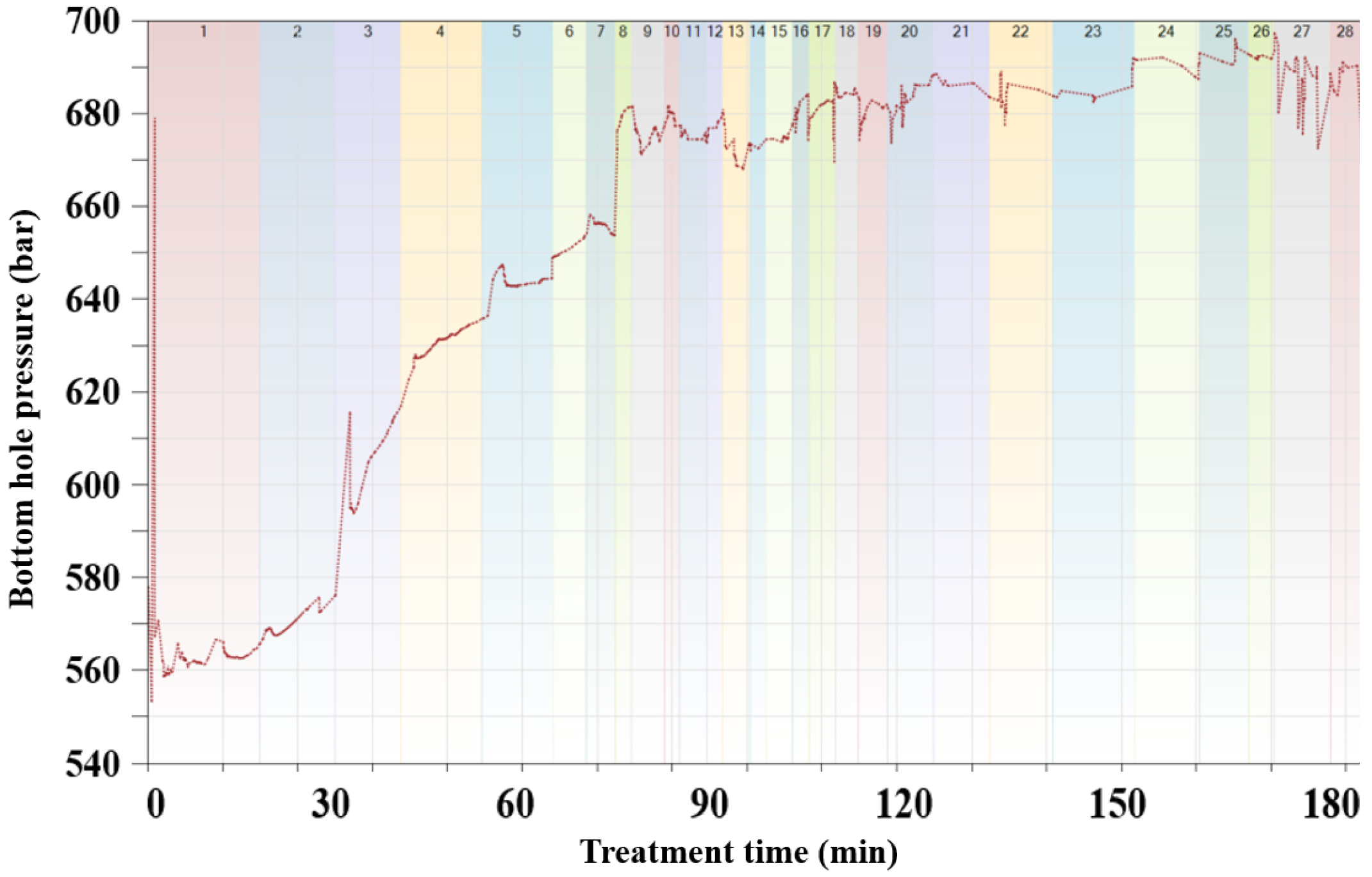
3.4. Establishment and Calibration of Hydraulic Fracturing Model for Deep Coal Reservoirs
4. Fracturing Parameter Optimization
4.1. Single Well Fracturing Parameter Optimization
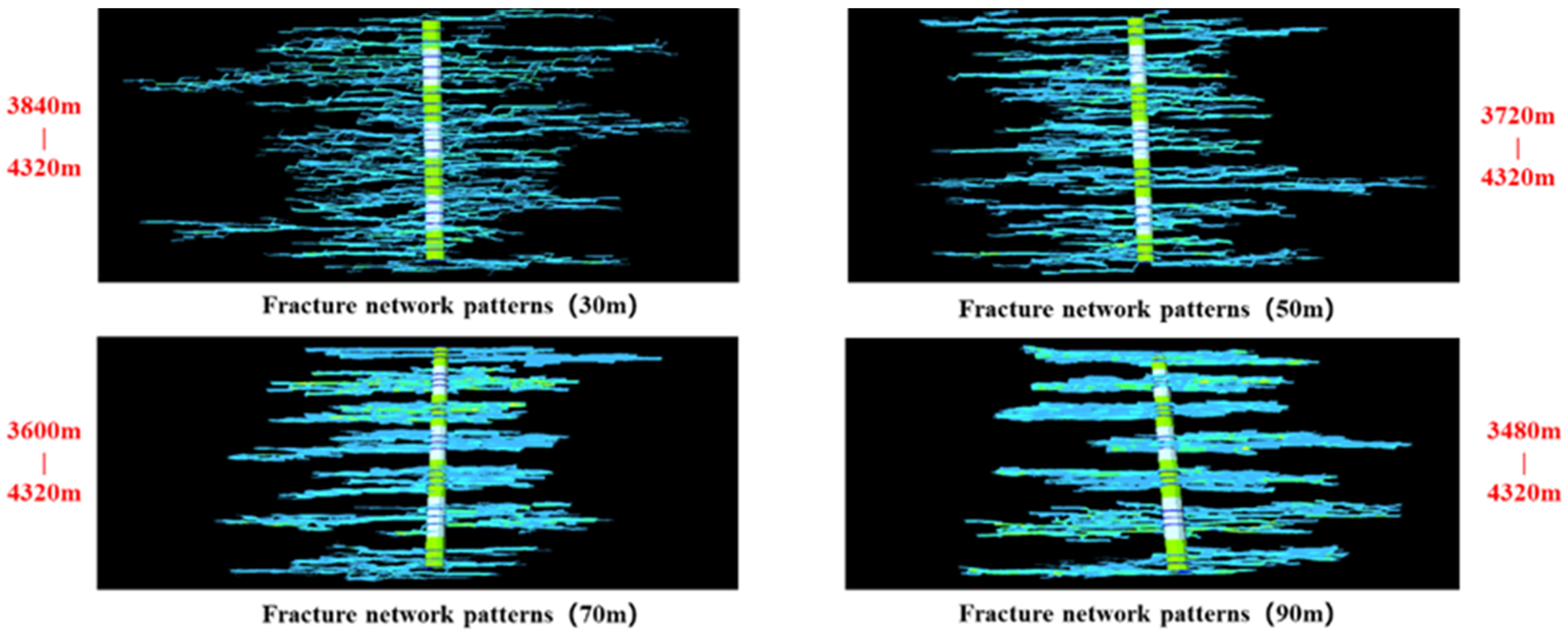
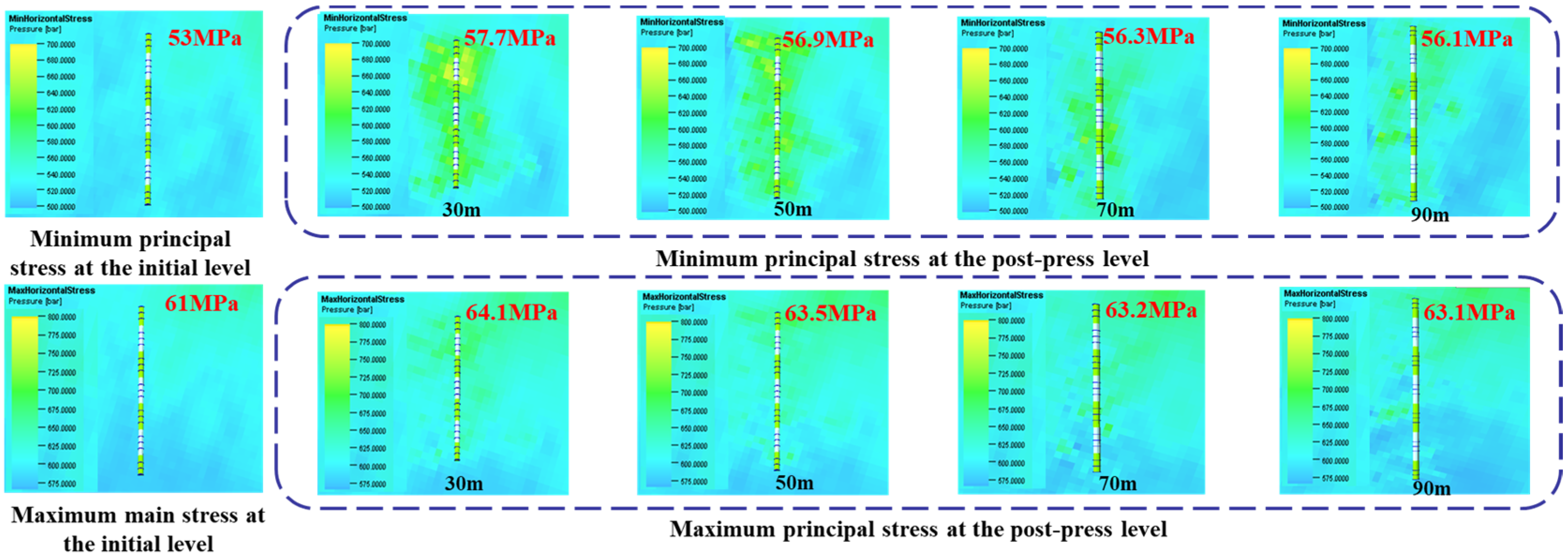
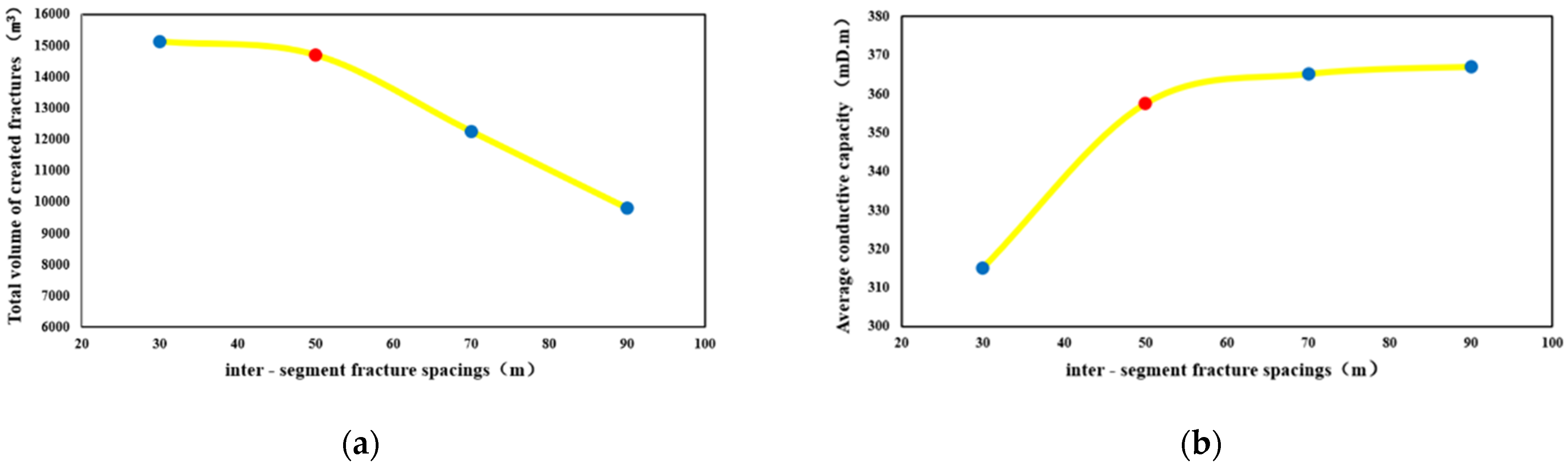
4.1.1. Inter-Stage Fracture Spacing
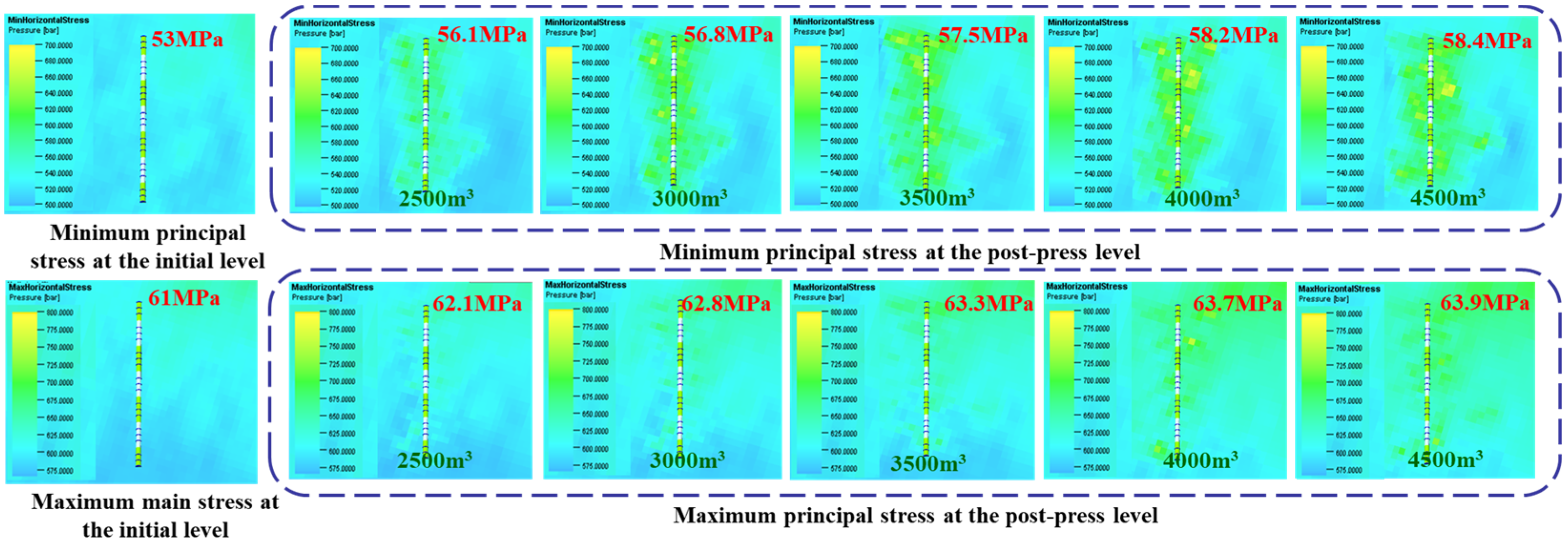
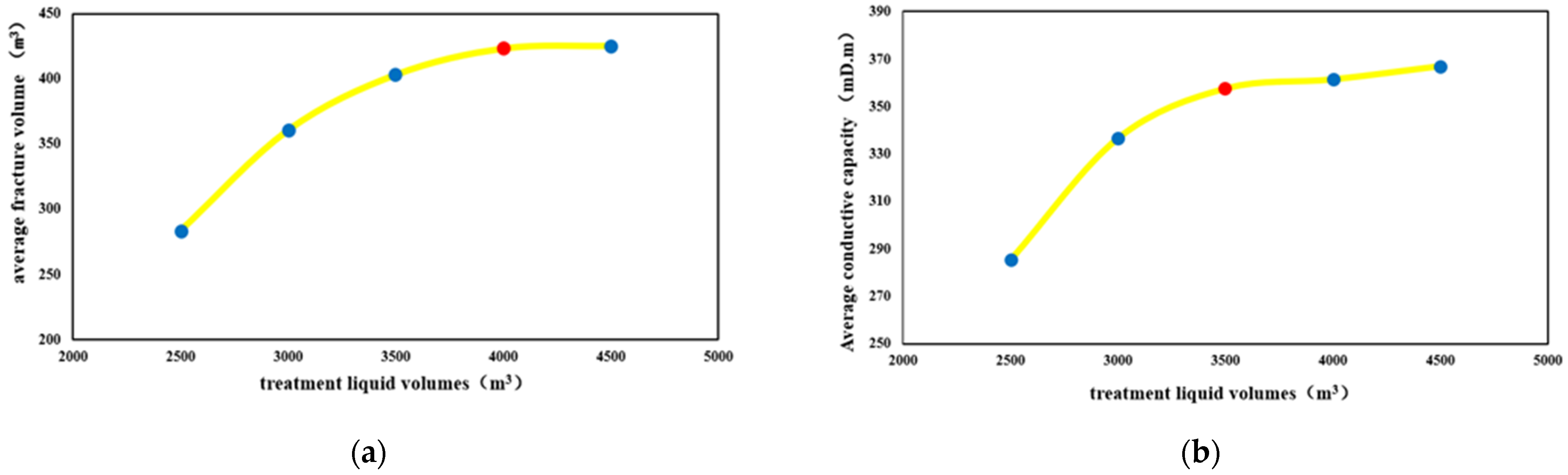
4.1.2. Fracturing Liquid Volume
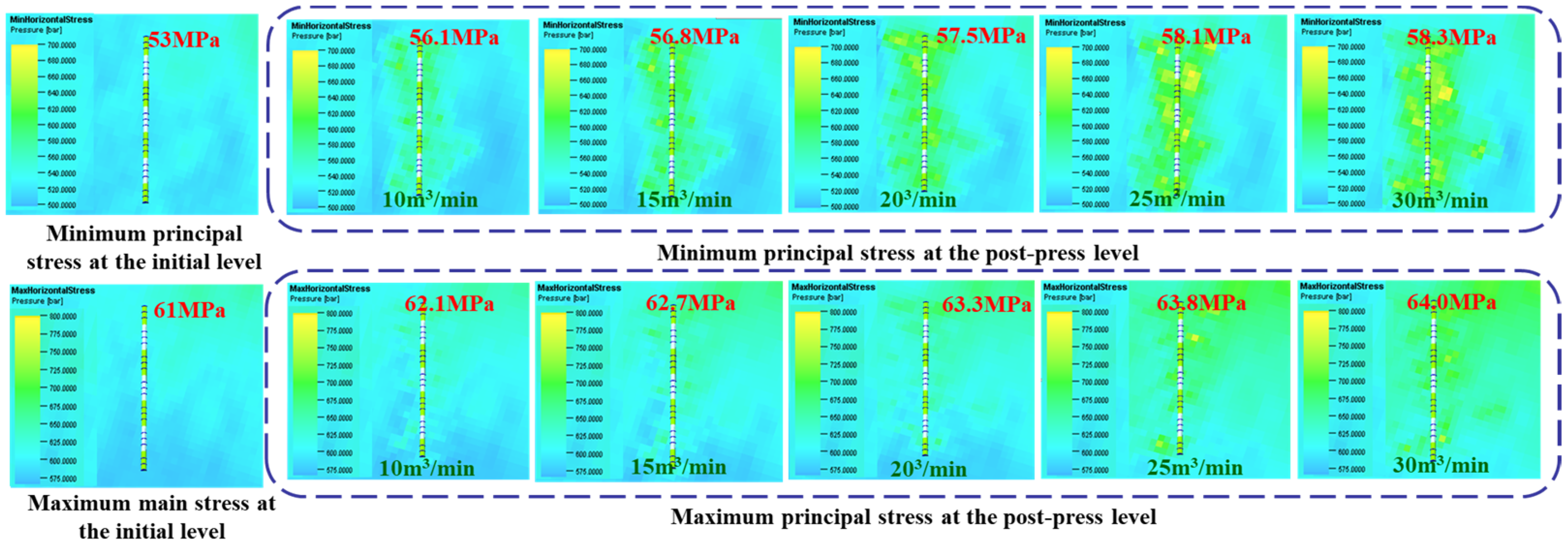
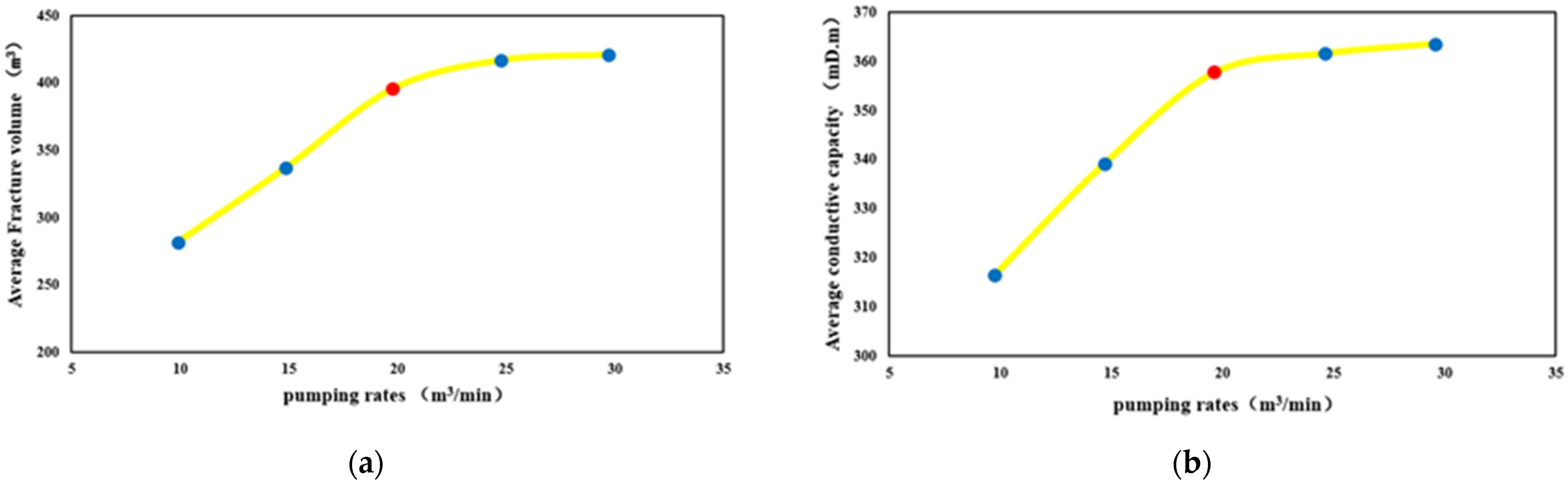
4.1.3. Pumping Rate
4.2. Well Group Fracturing Parameter Optimization
4.2.1. Inter-Stage Fracture Spacing
4.2.2. Fracturing Liquid Volume
4.2.3. Pumping Rate
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pang, X.Q.; Jia, C.Z.; Wang, W.Y. Petroleum geology features and research developments of hydrocarbon accumulation in deep petroliferous basins. Pet. Sci. 2015, 12, 1–53. [Google Scholar] [CrossRef]
- Xu, C.G.; Zhu, G.H.; Ji, H.Q. Exploration progress and reserve increase strategy of onshore natural gas of CNOOC. China Pet. Explor. 2024, 29, 32–46. [Google Scholar]
- Zhang, Q.; Jiang, W.P.; Jiang, Z.B. Present situation and technical research progress of coalbed methane surface development in coal mining areas of China. Coal Geol. Explor. 2023, 51, 139–158. [Google Scholar]
- Qing, S.R.; Cun, Z.; Guang, W. Hydraulic fracture initiation and propagation in deep coalbed methane reservoirs considering weak plane: CT scan testing. Gas Sci. Eng. 2024, 125, 205286. [Google Scholar]
- Zhou, D.H.; Chen, G.; Chen, Z.L. Exploration and development progress, key evaluation parameters and prospect of deep CBM in China. Nat. Gas Ind. 2022, 42, 43–51. [Google Scholar]
- Xie, H.P.; Gao, F.; Ju, Y. Research and exploration of deep rock mass mechanics. Chin. J. Rock Mech. Eng. 2015, 34, 2161–2178. [Google Scholar]
- Xiong, D.; He, J.Y.; Ma, X.F. Fracturing simulation with different perforation positions atdeep coal seam and roof/floor rock—case study at the No.8 deep coal seam of a gas-field in the Ordos basin. J. China Coal Soc. 2024, 49, 4897–4914. [Google Scholar] [CrossRef]
- Lei, N.Z. Predication and Stochastic Modeling of Coalbed Methane Reservoir Properties in Luling Well Field. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2012. [Google Scholar]
- Qu, L.C. Geological Modeling Technology and Application of Coalbed Methane. Ph.D. Thesis, China University of Geosciences (Beijing), Beijing, China, 2013. [Google Scholar]
- Huai, Y.C.; Zhang, M.; Yang, L.W. 3D geological modeling of coalbed methane reservoirs based on facies control. J. Earth Sci. Environ. 2017, 39, 275–282. [Google Scholar]
- Ma, P.H.; Shao, X.J.; Huo, M.Y. Geological modeling ideas and methods for coal reservoirs. Pet. Geol. Oilfield Dev. Daqing 2018, 39, 601–610. [Google Scholar]
- Chen, B.; Tang, D.Z.; Zhang, Y.P. Logging inversion and 3D geological modeling of coal body structure. Coal Sci. Technol. 2019, 47, 88–94. [Google Scholar]
- Liu, W.; Zhang, S.A.; Peng, C. Research on pressure drawdown characteristics during coalbed methane drainage. Coal Technol. 2019, 38, 18–21. [Google Scholar]
- Li, Y.; Jiang, Z.B.; Liu, Y.H. Analysis of production characteristics of coalbed methane wells based on 3D geological modeling. Coal Mine Saf. 2020, 51, 190–194. [Google Scholar]
- Lü, J.T.; Zhang, M.; Huai, Y.C. Wang Dianao Coal Reservoir Logging Analysis and Fine Geological Modeling Technology: A Case Study of Coalbed Methane Area in Surat Basin, Australia. J. China Coal Soc. 2020, 45, 1824–1834. [Google Scholar]
- Zhou, Y.; Zhang, S.H.; Tang, S.H. 3D modeling of gas content in coalbed methane reservoirs. Coal Geol. Explor. 2020, 48, 96–103. [Google Scholar]
- Xiang, L.W.; Jie, N.P.; Yi, J. Morphology and propagation of supercritical carbon dioxide-induced fractures in coal based on a non-destructive surface extraction method. Fuel 2025, 384, 133948. [Google Scholar]
- An, Q.; Yang, F.; Yang, R.Y. Volume fracturing practice and understanding of deep coalbed methane in the Shenfu area, Ordos Basin. J. Coal Sci. Eng. 2024, 49, 2376–2393. [Google Scholar]
- Li, B.; Yang, F.; Zhang, H.J. Research on efficient development technology of deep coalbed methane in the Shenfu area. Coal Geol. Explor. 2024, 52, 57–68. [Google Scholar]
- Yang, F.; Li, B.; Wang, Q.J. Large-scale limit volume fracturing technology for deep coalbed methane horizontal wells. Pet. Explor. Dev. 2024, 51, 389–398. [Google Scholar]
- Liu, X. Comparison of fracture network morphology in coal reservoirs under different fracturing scales. Reserv. Eval. Dev. 2024, 14, 510–518. [Google Scholar]
- Xiong, X.Y.; Zhen, H.B.; Li, S.G. Multi-round turn fracturing technology and application for deep coalbed methane in the Da Ning-Ji County area. Coal Geol. Explor. 2024, 52, 147–160. [Google Scholar]
- Zhong, Z.T.; Zhuang, X.; Yu, H.W. Numerical simulation of fracture propagation in deep coalseam reservoirs. Energy Sci. Eng. 2023, 11, 3559–3574. [Google Scholar]
- Zhi, H.Z.; Tian, Y.W.; Jian, C.G. Study on the Spatial and Temporal Evolution Law of Large-Size Fracture Propagation in Deep Coalbed Based on Acoustic Emission Technology. Rock Mech. Rock Eng. 2025, 58, 3799–3814. [Google Scholar] [CrossRef]

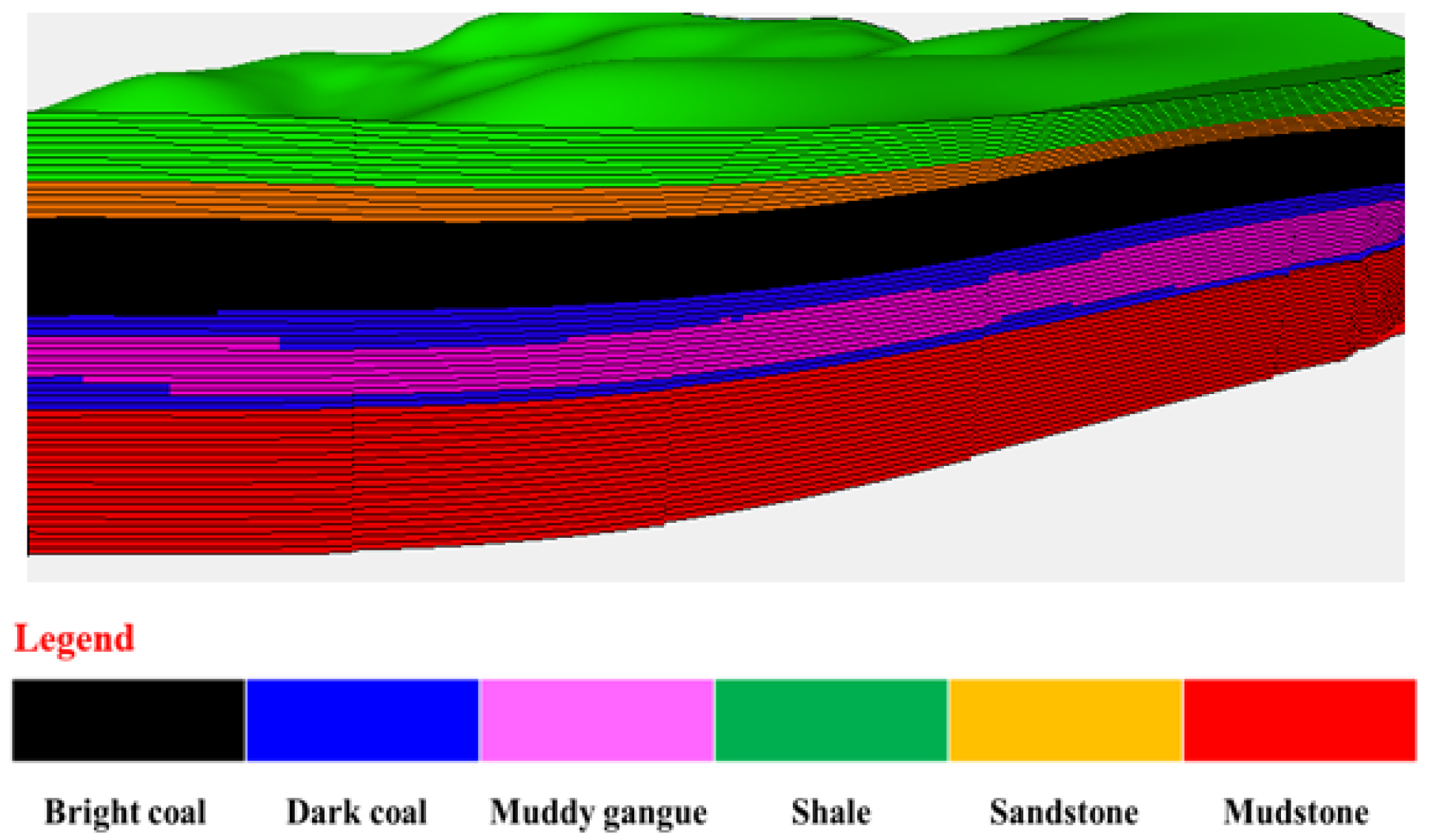

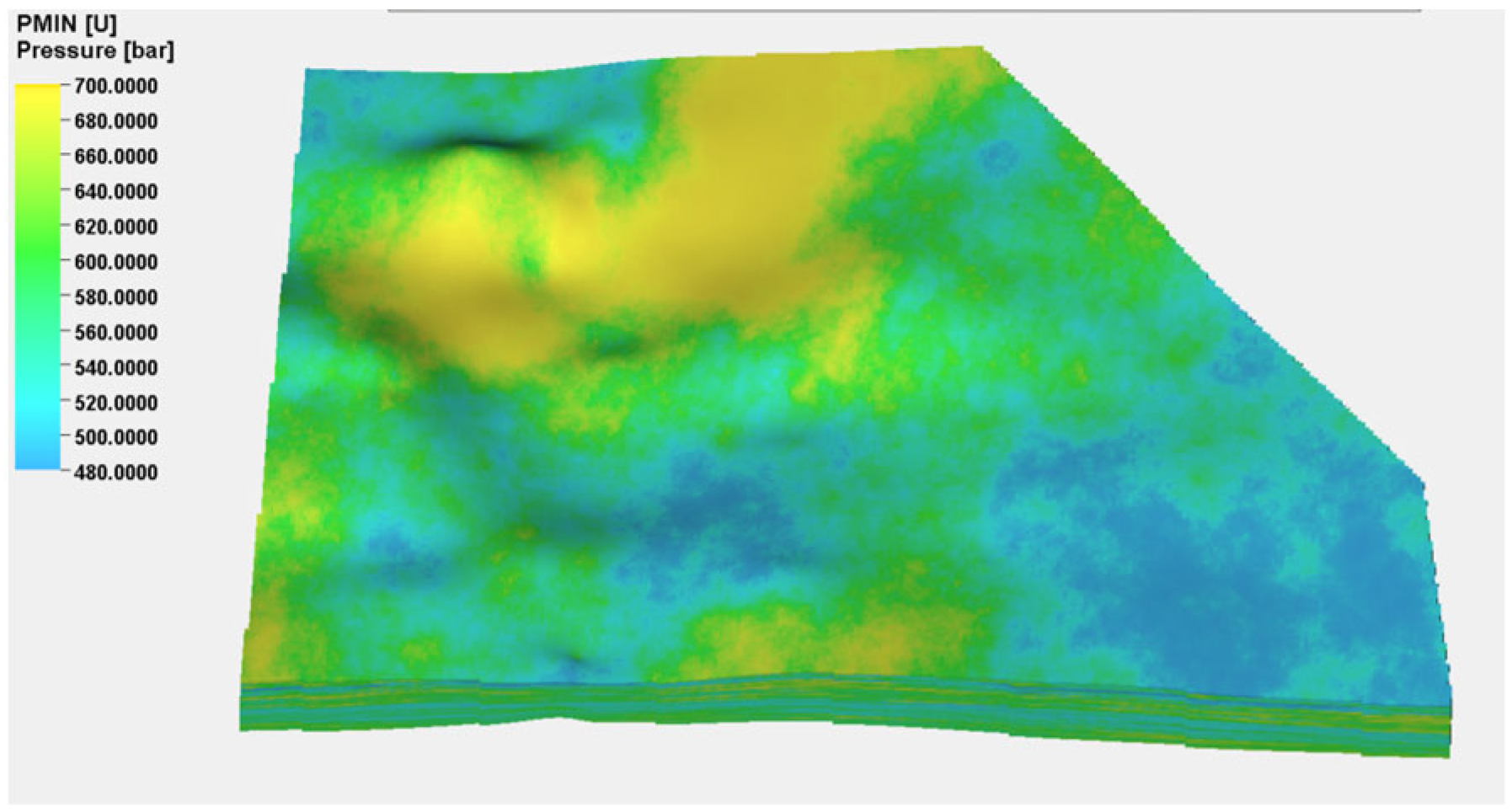

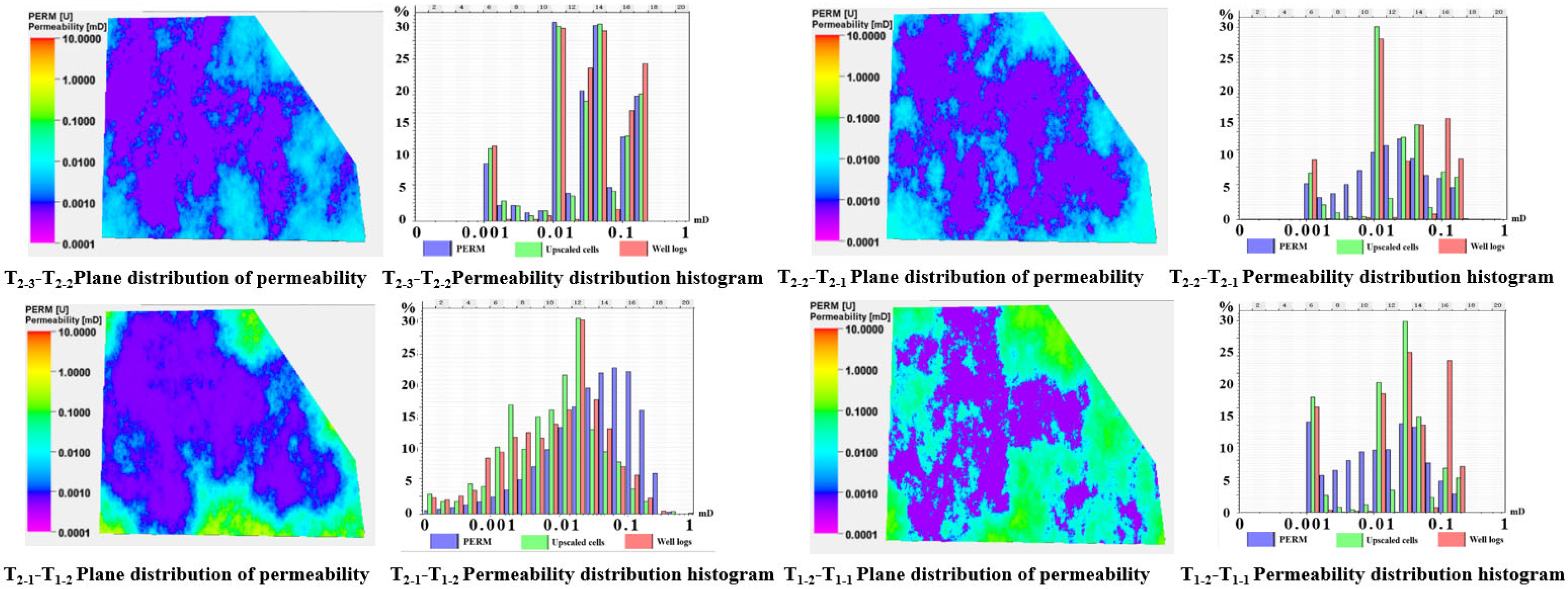
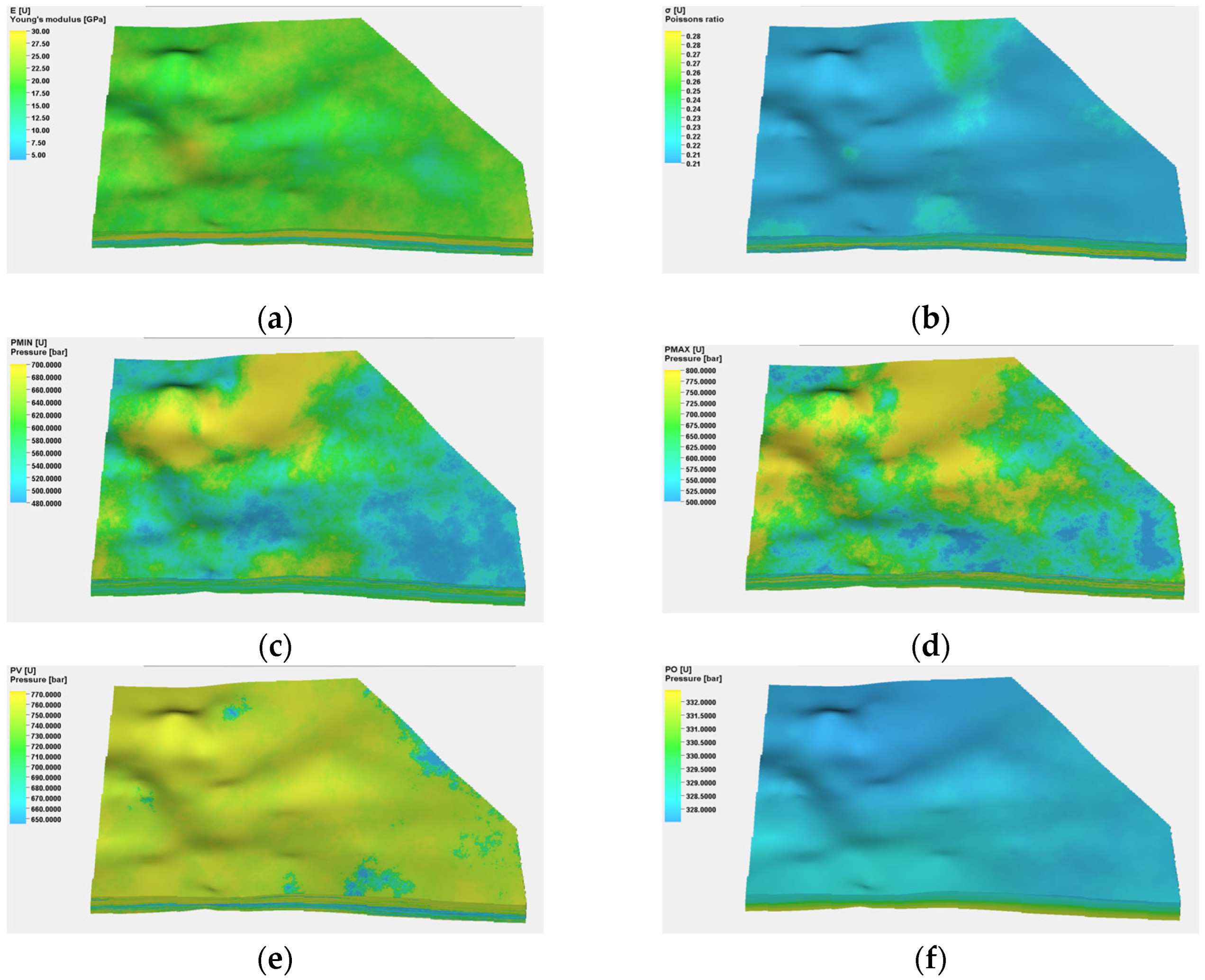






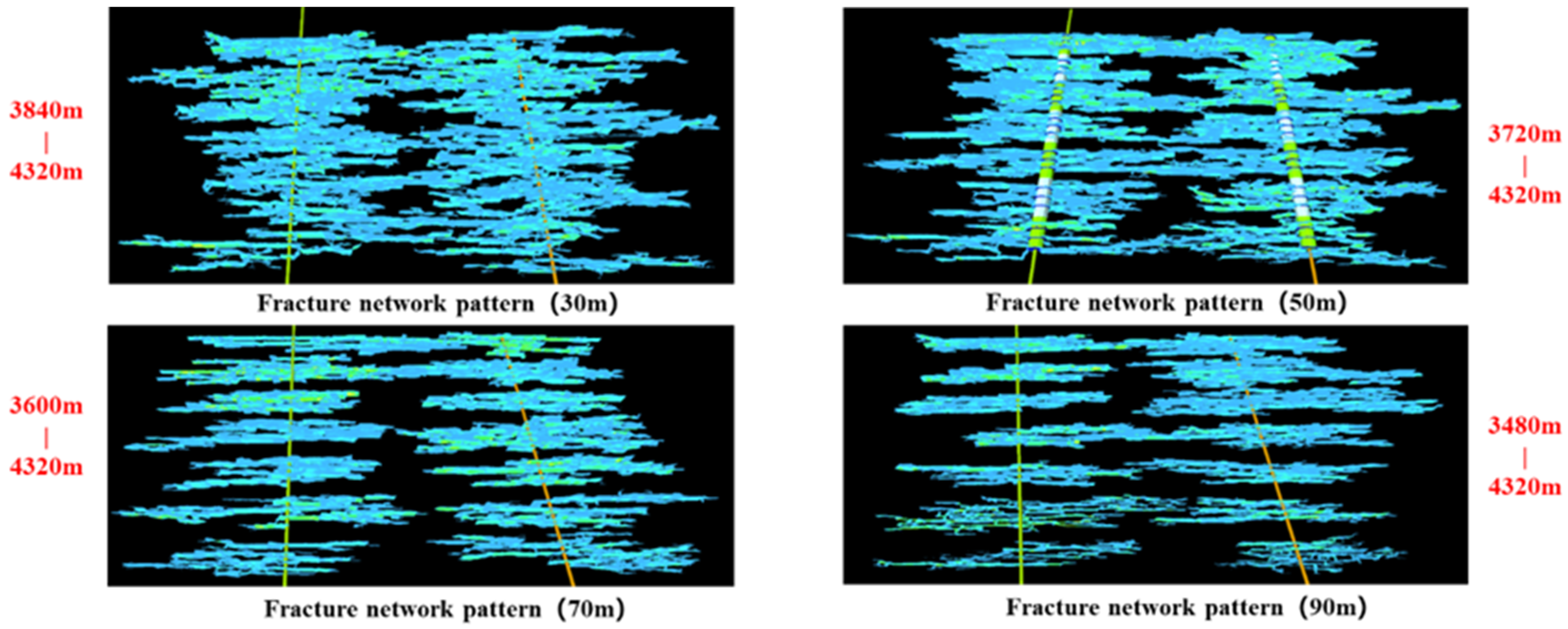
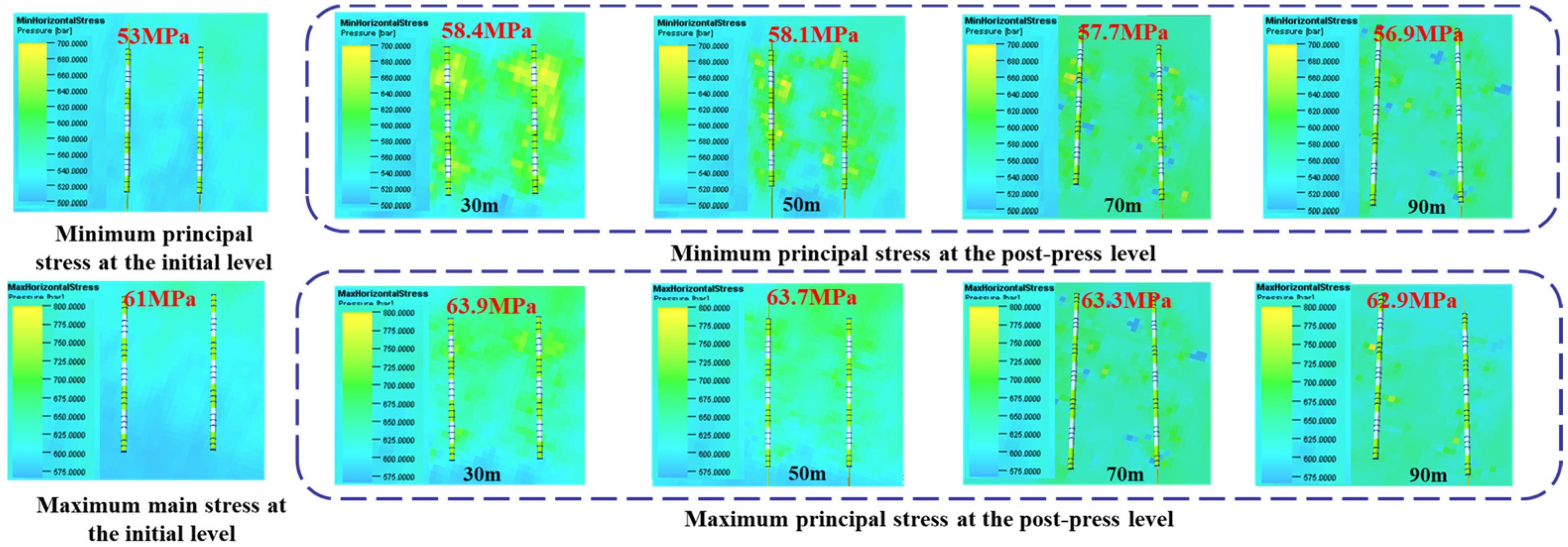

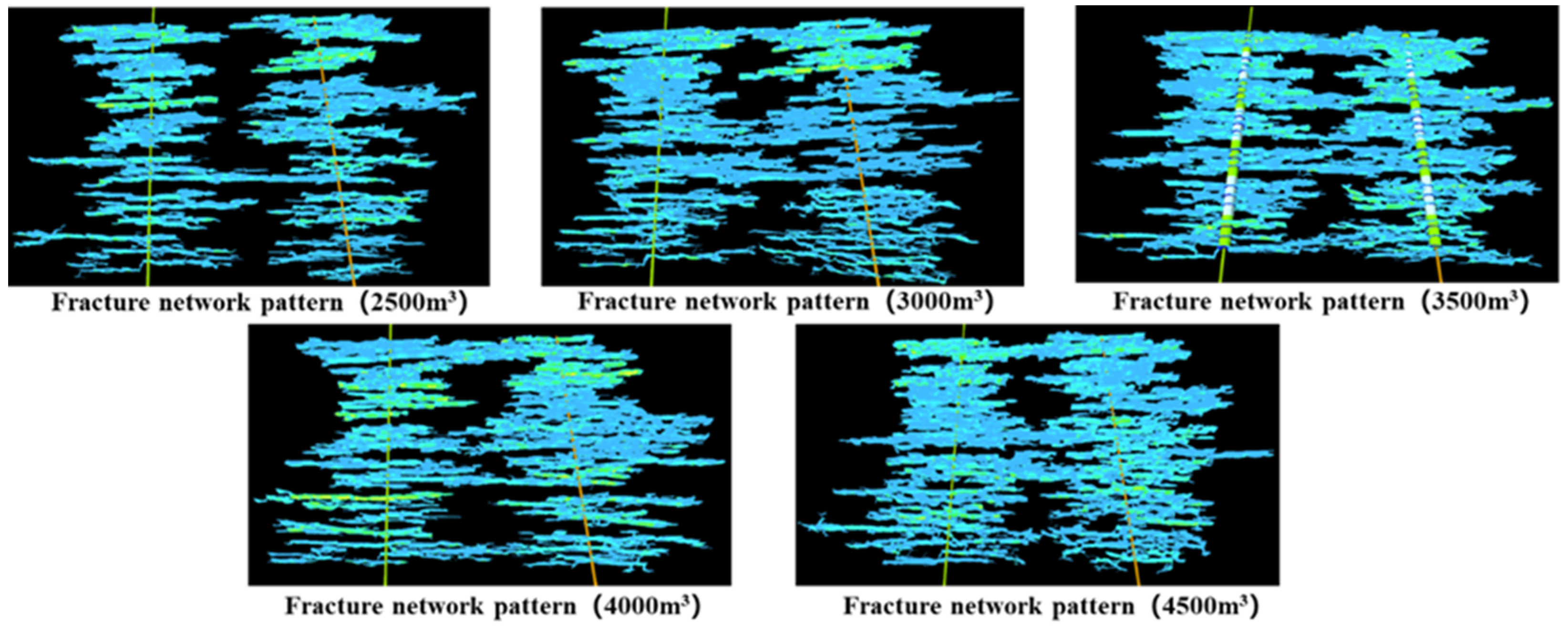



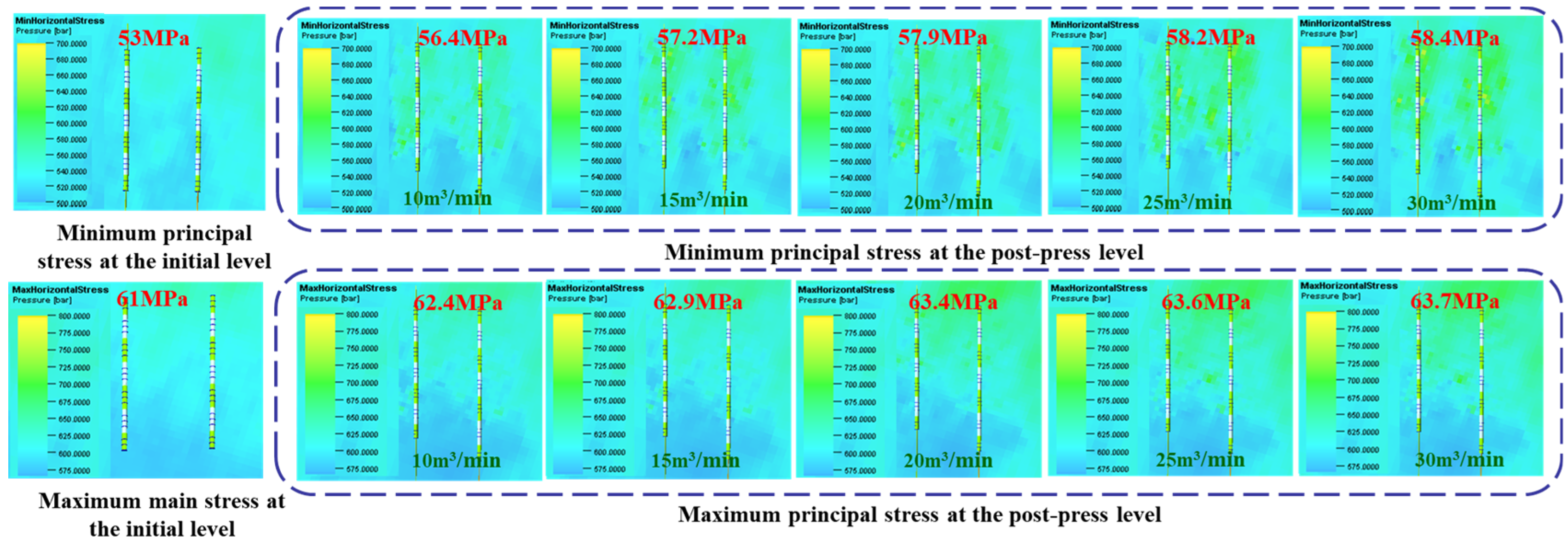
| Layer Number | Measuring Depth (m) | Visual Thickness (m) | Vertical Depth (m) | Porosity (%) | Permeability (mD) | Gas Saturation (%) | Interpret Conclusions |
|---|---|---|---|---|---|---|---|
| 1 | 2798.5–2801.7 | 3.2 | 2738.75–2741.85 | 5.6 | 0.29 | 26.4 | Gas-bearing layer |
| 2 | 2806.8–2811.9 | 5.1 | 2746.79–2751.74 | 7.7 | 0.57 | 33.8 | Differential gas layer |
| 3 | 2830.2–2834.2 | 4 | 2769.47–2773.34 | 4.8 | 0.19 | 28.3 | Gas-bearing layer |
| 4 | 2836.8–2838.5 | 1.7 | 2775.85–2777.50 | 7 | 0.42 | 28.9 | Gas-bearing layer |
| 5 | 2850.7–2855.1 | 4.4 | 2789.31–2793.57 | 7.7 | 0.54 | 46.3 | Differential gas layer |
| 6 | 2862.0–2865.4 | 3.4 | 2800.25–2803.54 | 5.2 | 0.02 | 12.4 | Carbonaceous mudstone |
| 7 | 2869.3–2870.7 | 1.4 | 2807.31–2808.67 | 6.7 | 0.35 | 22.3 | Coal |
| 8 | 2880.1–2882.0 | 1.9 | 2817.77–2819.61 | 7.2 | 0.32 | 27.8 | Coal |
| 9 | 2884.8–2897.1 | 12.3 | 2822.33–2834.25 | 4.6 | 0.19 | 22.1 | Dry layer |
| 10 | 2897.9–2904.6 | 6.7 | 2835.02–2841.52 | 5.9 | 0.42 | 31.3 | Coal |
| 11 | 2904.6–2909.4 | 4.8 | 2841.52–2846.17 | 2.8 | 0.71 | 17.4 | Dry layer |
| 12 | 2909.4–2911.5 | 2.1 | 2846.17–2848.21 | 4.5 | 0.04 | 11.2 | Carbonaceous mudstone |
| Lithofacies | Truncated Value |
|---|---|
| Bright coal | GR ≤ 60GAPI, DEN ≤ 1.6 g/cm3, LLD > 3000 Ω.cm |
| Semi-bright coal | 60 < GR < 100GAPI, DEN ≤ 1.6 g/cm3, LLD > 3000 Ω.cm |
| Semi-dark coal | 100 ≤ GR < 120GAPI, 1.6 < DEN ≤ 1.85 g/cm3, LLD > 500 Ω.cm |
| Dull coal | 120 ≤ GR < 140GAPI, 1.6 < DEN ≤ 1.85 g/cm3, LLD > 500 Ω.cm |
| Gangue | GR < 140GAPI, DEN ≤ 2 g/cm3 |
| Limestone | GR < 60GAPI, DEN > 2 g/cm3, CNL ≤ 7% |
| Semi-dark coal | 100 ≤ GR < 120GAPI, 1.6 < DEN ≤ 1.85 g/cm3, LLD > 500 Ω.cm |
| Dull coal | 120 ≤ GR < 140GAPI, 1.6 < DEN ≤ 1.85 g/cm3, LLD > 500 Ω.cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wang, X.; Chen, F.; Zhu, X.; Mao, Z.; Liu, X.; Ma, H. Three-Dimensional Geomechanical Modeling and Hydraulic Fracturing Parameter Optimization for Deep Coalbed Methane Reservoirs: A Case Study of the Daniudi Gas Field, Ordos Basin. Processes 2025, 13, 1699. https://doi.org/10.3390/pr13061699
Liu X, Wang X, Chen F, Zhu X, Mao Z, Liu X, Ma H. Three-Dimensional Geomechanical Modeling and Hydraulic Fracturing Parameter Optimization for Deep Coalbed Methane Reservoirs: A Case Study of the Daniudi Gas Field, Ordos Basin. Processes. 2025; 13(6):1699. https://doi.org/10.3390/pr13061699
Chicago/Turabian StyleLiu, Xugang, Xiang Wang, Fuhu Chen, Xinchun Zhu, Zheng Mao, Xinyu Liu, and He Ma. 2025. "Three-Dimensional Geomechanical Modeling and Hydraulic Fracturing Parameter Optimization for Deep Coalbed Methane Reservoirs: A Case Study of the Daniudi Gas Field, Ordos Basin" Processes 13, no. 6: 1699. https://doi.org/10.3390/pr13061699
APA StyleLiu, X., Wang, X., Chen, F., Zhu, X., Mao, Z., Liu, X., & Ma, H. (2025). Three-Dimensional Geomechanical Modeling and Hydraulic Fracturing Parameter Optimization for Deep Coalbed Methane Reservoirs: A Case Study of the Daniudi Gas Field, Ordos Basin. Processes, 13(6), 1699. https://doi.org/10.3390/pr13061699







