Integrated Modeling of Time-Varying Permeability and Non-Darcy Flow in Heavy Oil Reservoirs: Numerical Simulator Development and Case Study
Abstract
1. Introduction
2. Flow Mechanism Characterization
2.1. Time-Varying Mechanism
2.1.1. Characterization Method
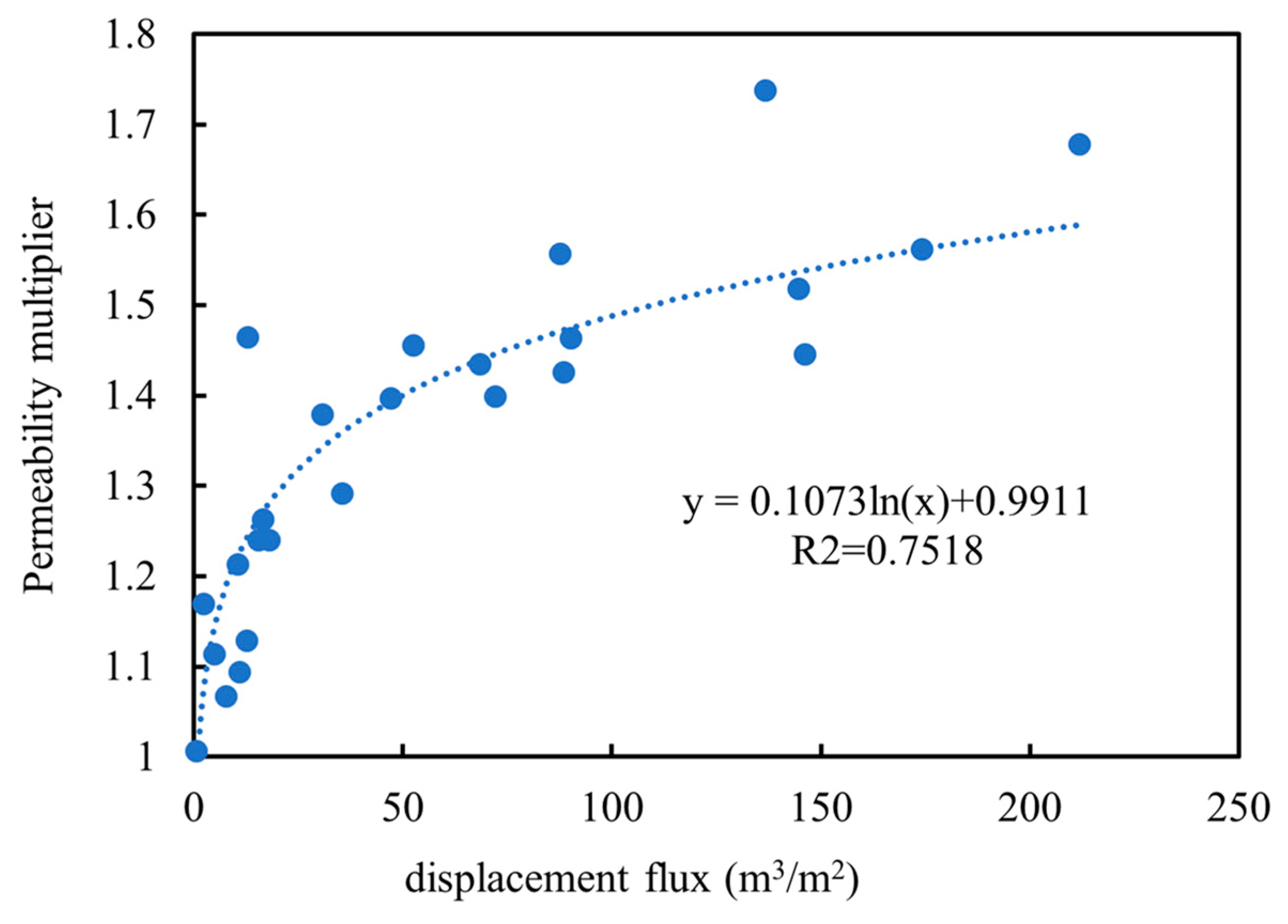
2.1.2. Time-Varying Permeability
2.2. Water-Flooding-Dependent Threshold Pressure Gradient
3. Mathematical Modeling and Numerical Simulator Development
3.1. Model Assumptions
- (1)
- Flow is under isothermal reservoir conditions;
- (2)
- Flow is oil-water two phases;
- (3)
- Nonlinear seepage is considered solely in the oil phase;
- (4)
- Time-varying permeability and water-flooding-dependent threshold pressure gradient are incorporated.
3.2. Mathematical Model
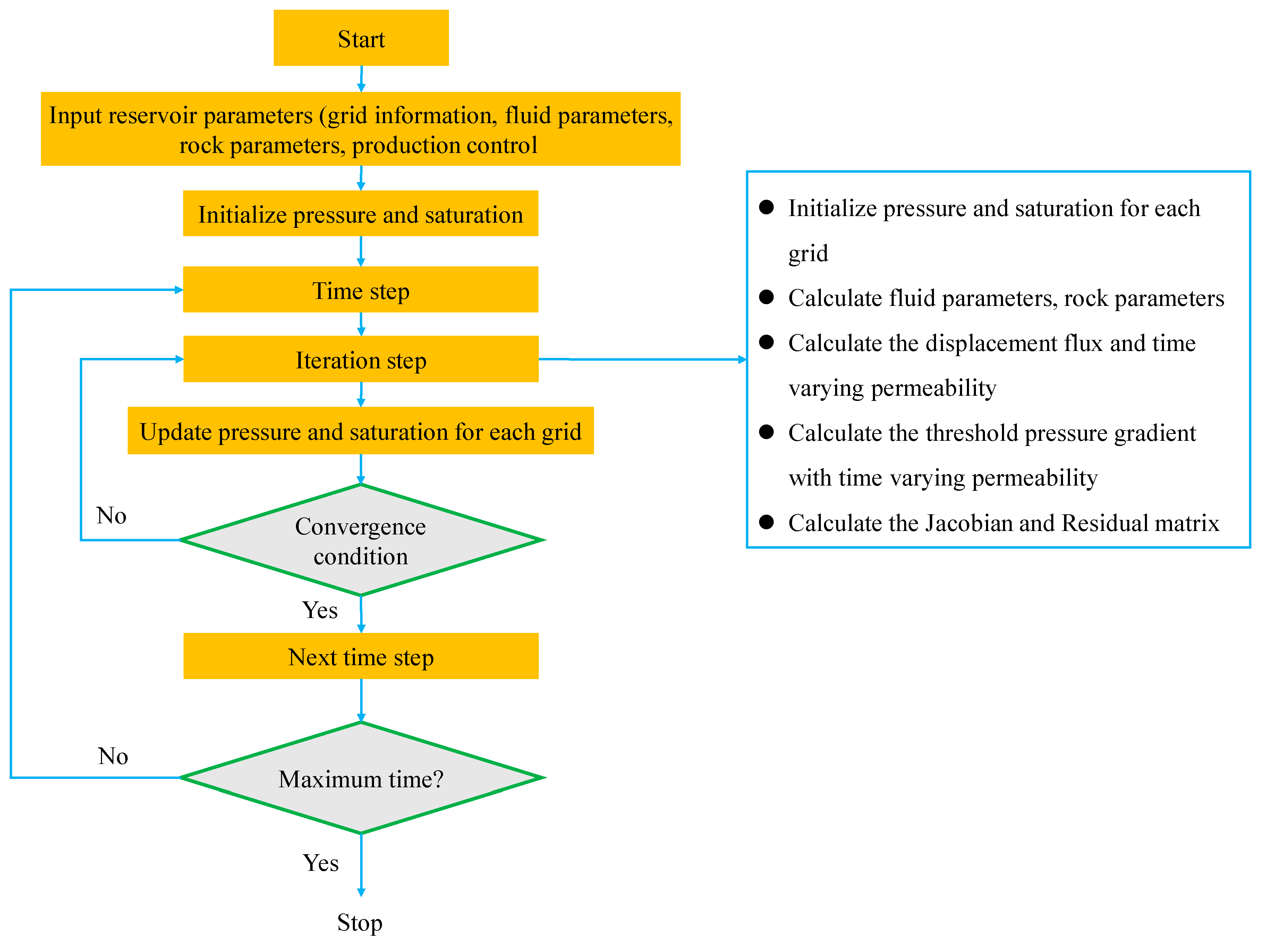
3.3. Simulator Development
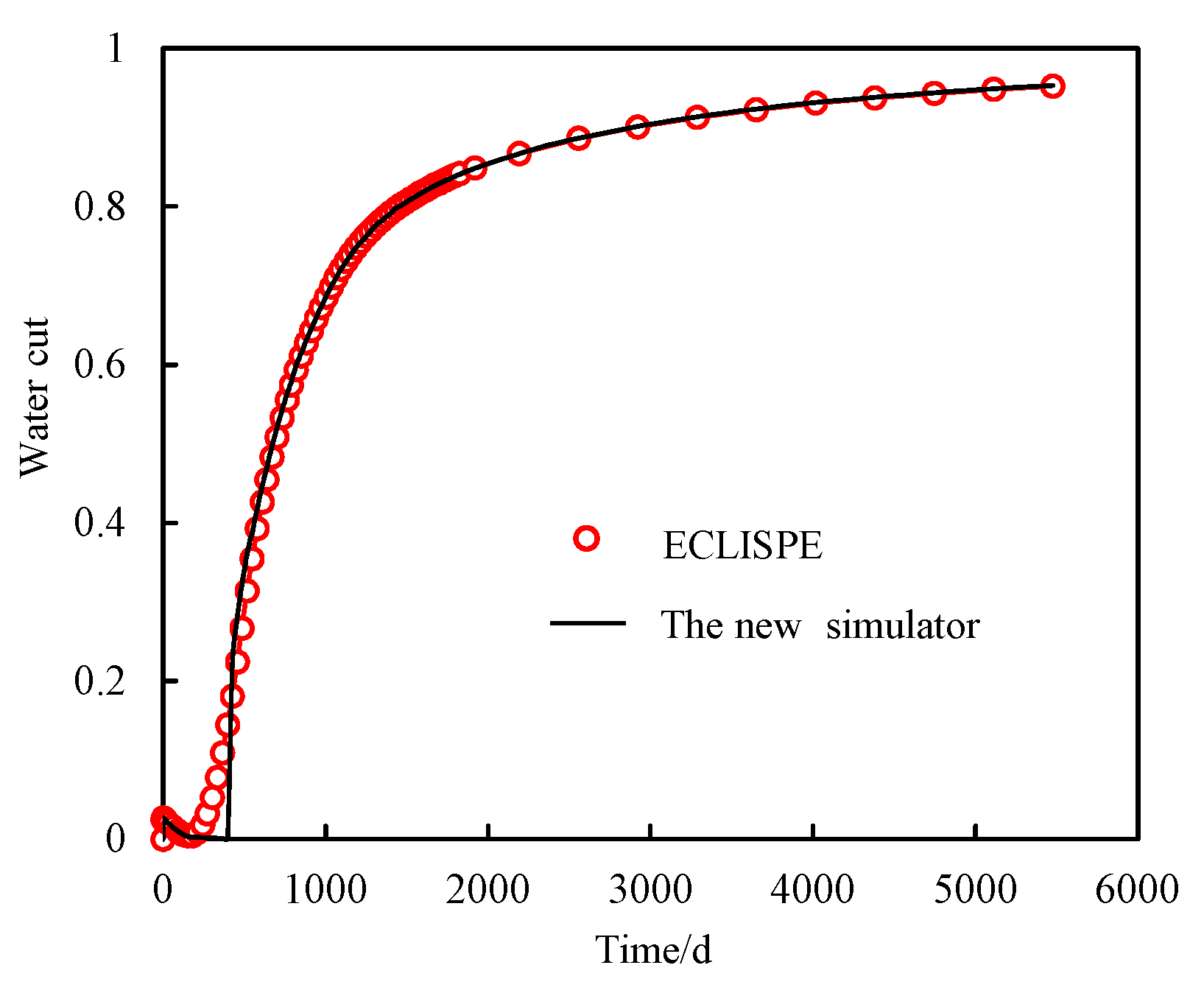
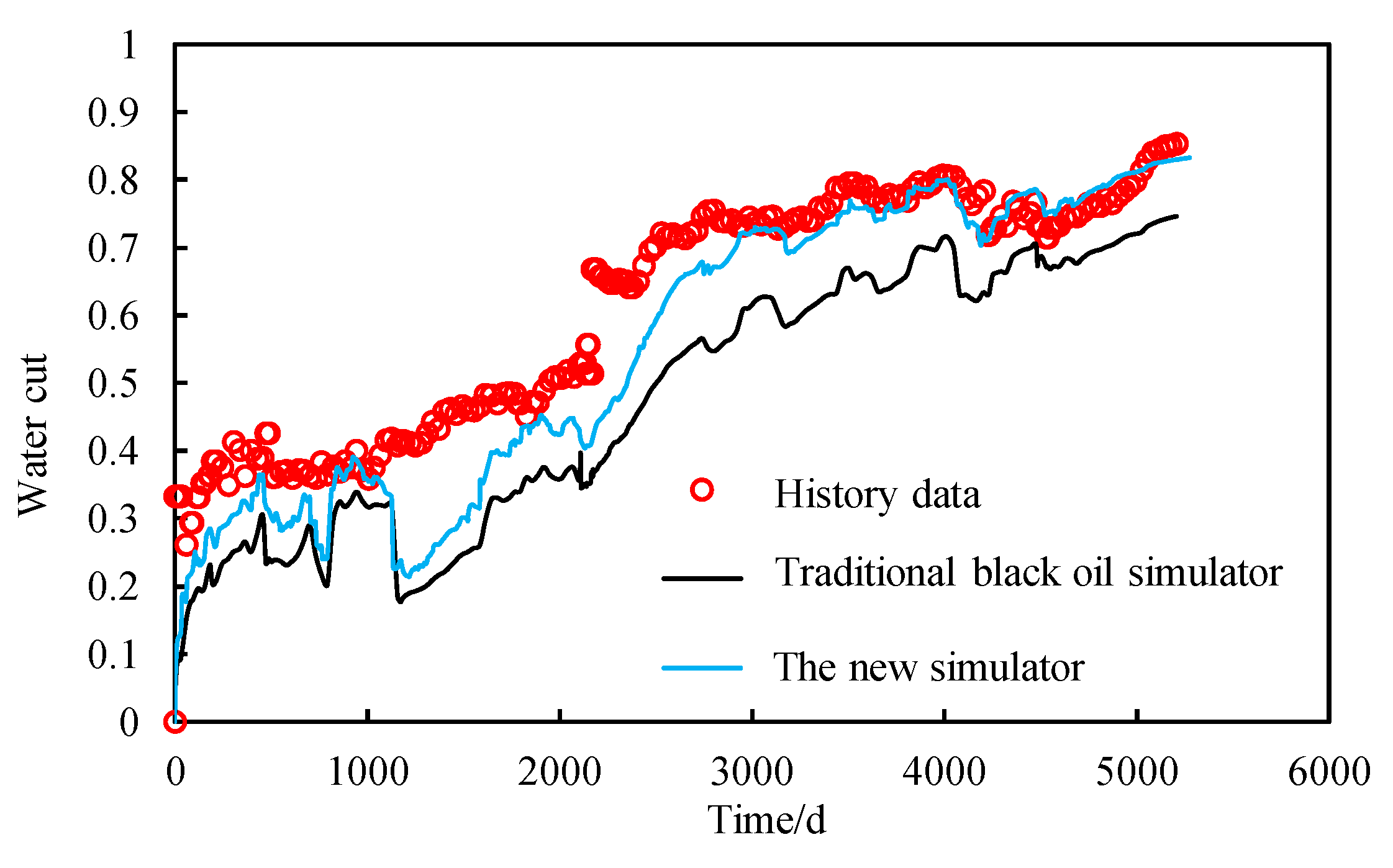
3.4. Validation
4. Sensitivity Analysis and Field Application
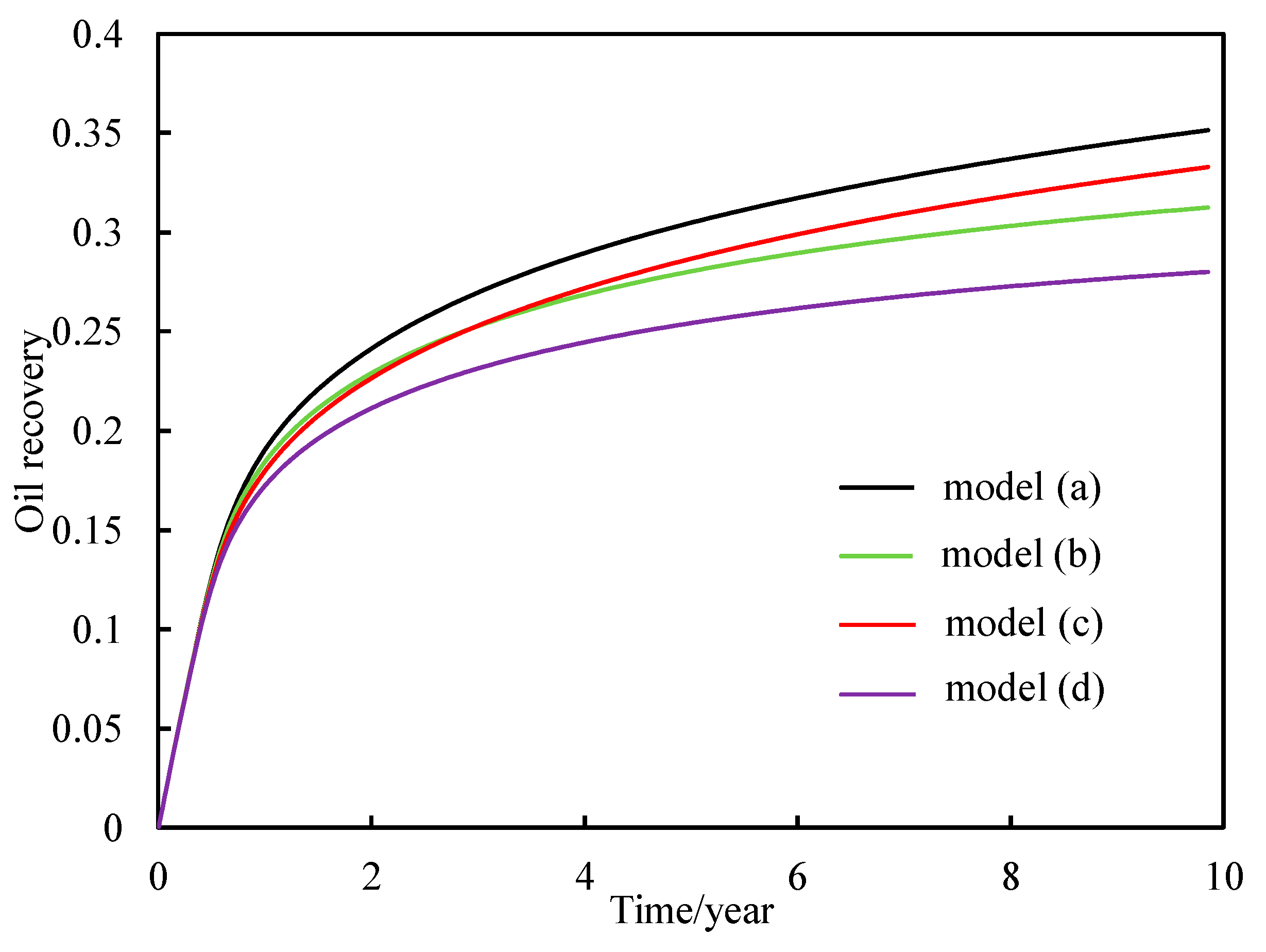
4.1. Sensitivity Analysis
- (1)
- The influence of time-varying permeability
- (2)
- The influence of threshold pressure gradient
- (3)
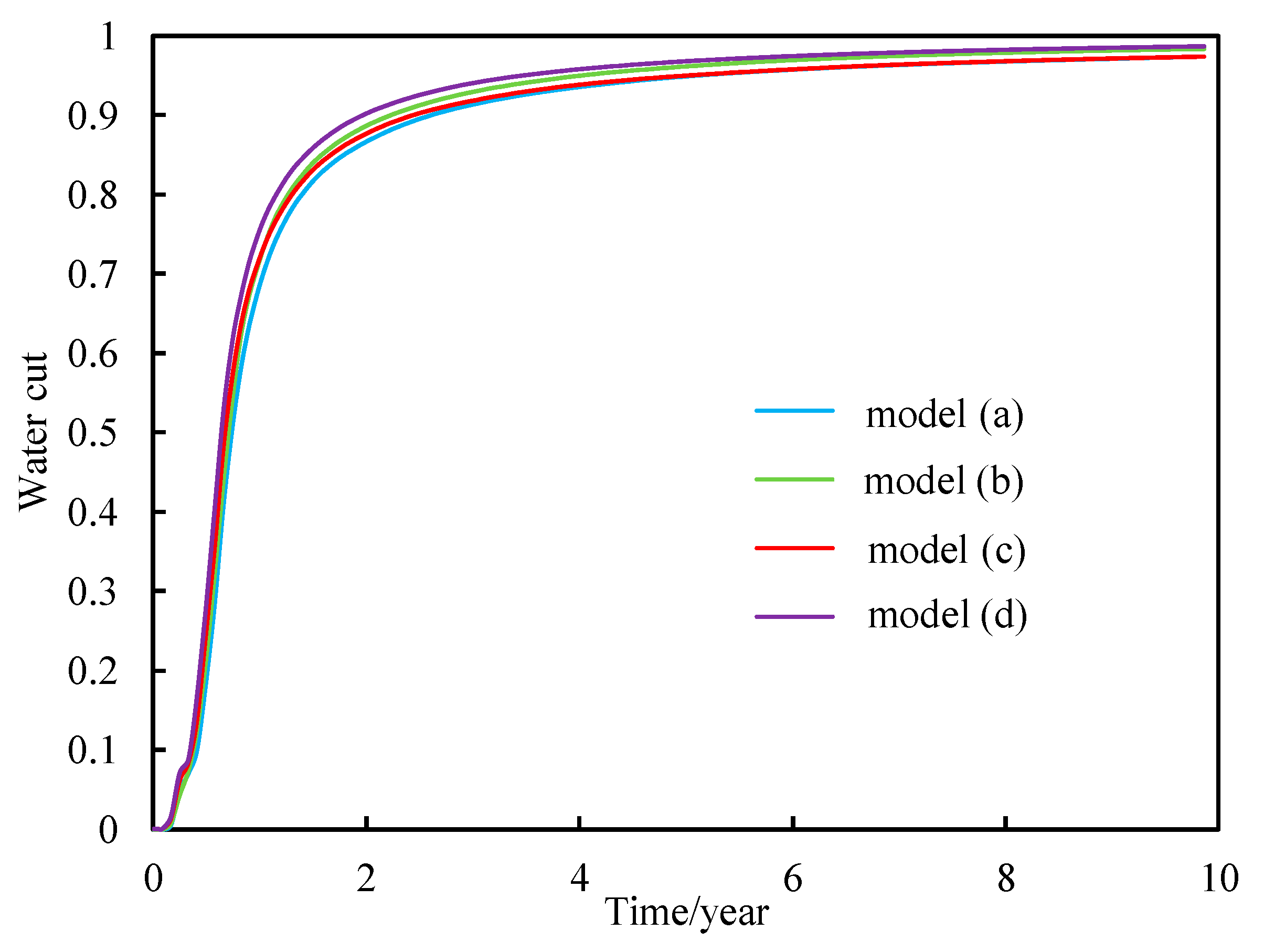
- The comprehensive influence of permeability time variation and threshold pressure gradient
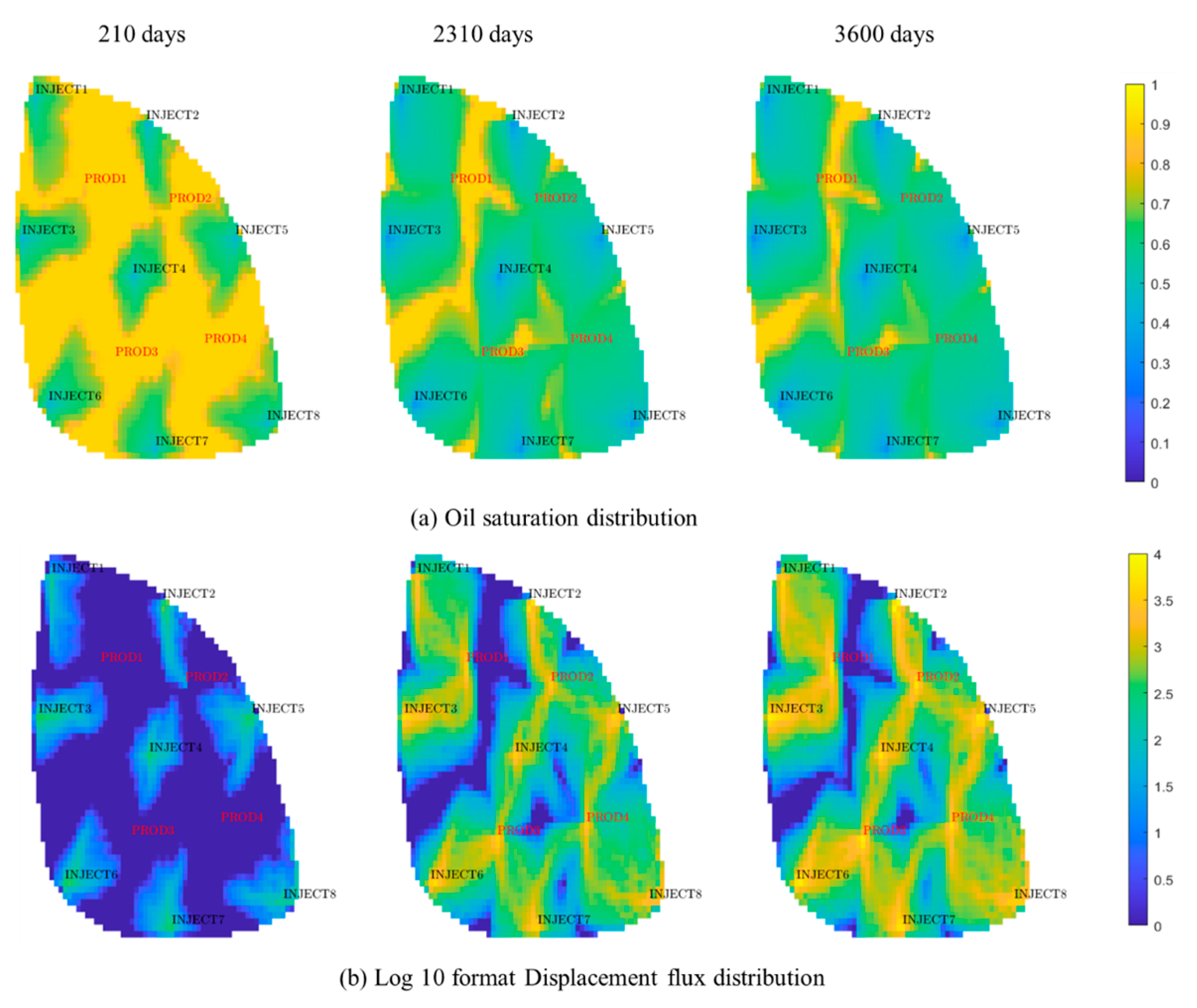
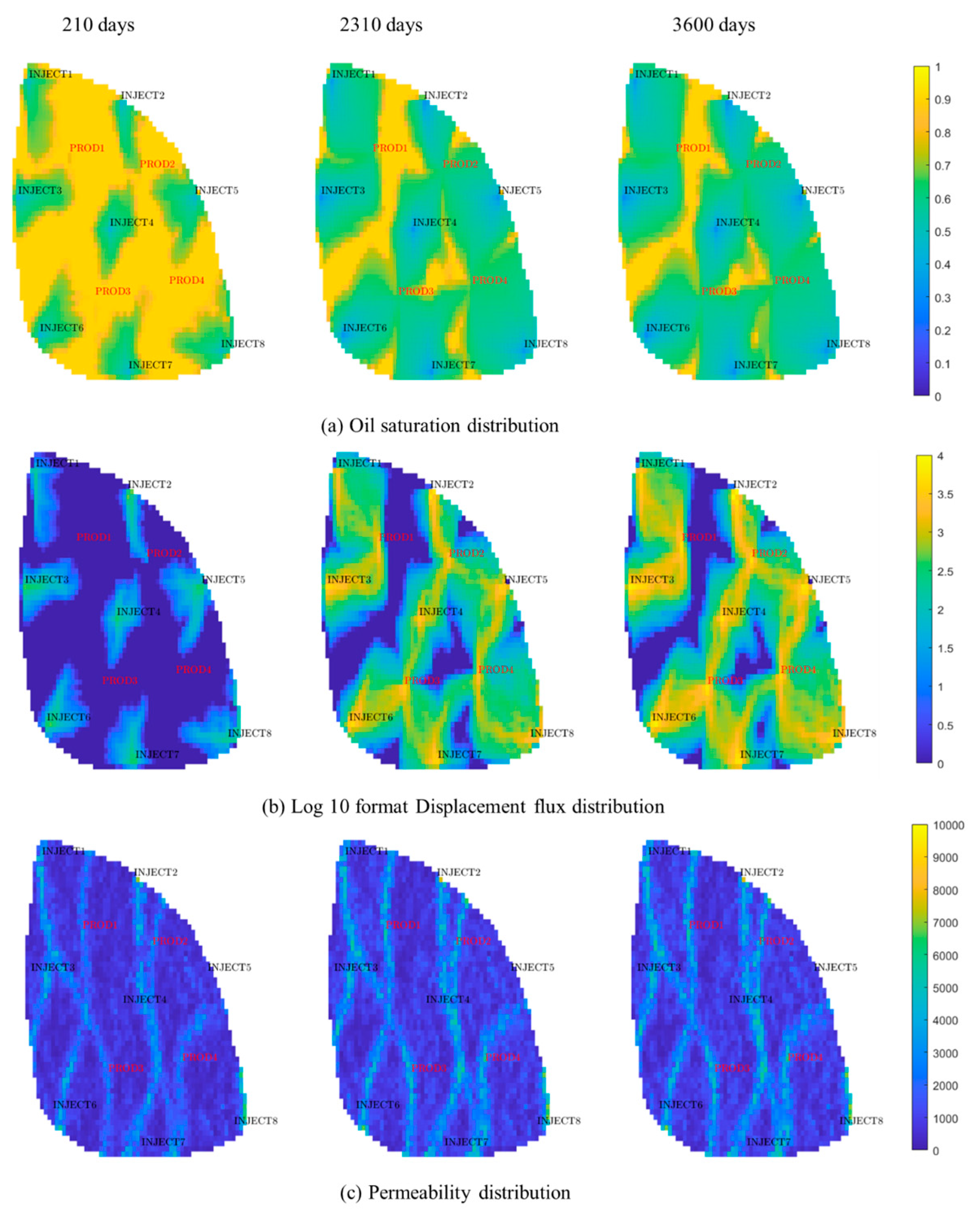
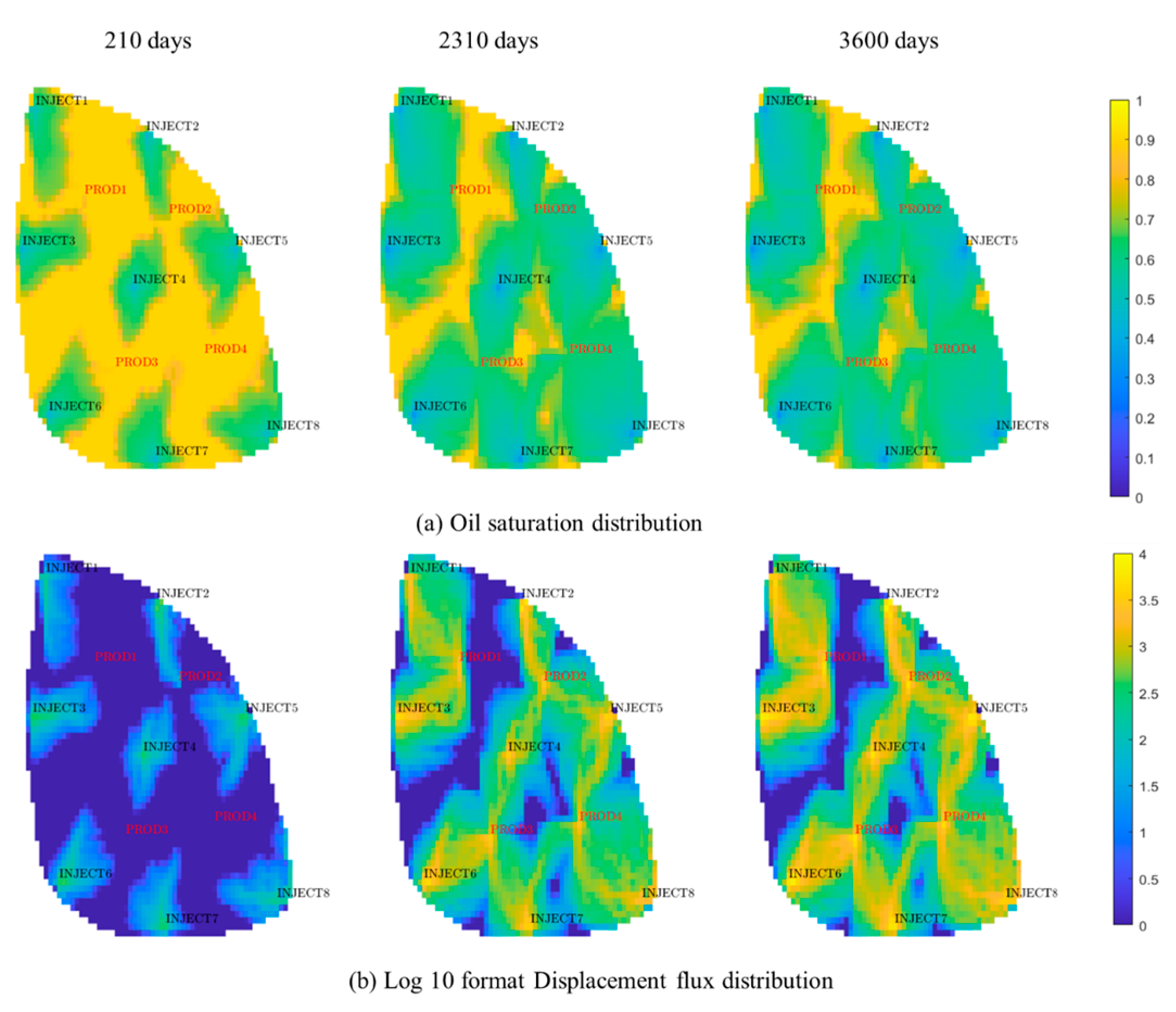
4.2. Field Application
5. Conclusions
- (1)
- The novel oil–water two-phase numerical simulator simultaneously accounts for time-varying permeability and the water-flooding-dependent threshold pressure gradient based on the traditional black oil model. The water-flooding-dependent threshold pressure gradient is first proposed by integrating permeability time variation. The new simulator can achieve a more reasonable and accurate numerical simulation.
- (2)
- The complex flow mechanisms significantly influence production performance. The synergistic consideration of time-varying permeability and threshold pressure gradient results in the lowest oil recovery. The presence of the threshold pressure gradient imposes additional resistance to oil flow and reduces the sweep region since production. Consequently, the permeability of the mainstream region increases markedly, and the threshold pressure gradient decreases during production with more significant flux. This phenomenon further amplifies flow heterogeneity and reduces oil recovery. Without considering the complex flow mechanisms, the simulation results can lead to large errors.
- (3)
- The newly developed simulator can improve the history matching of water flooding in heavy oil reservoirs by comprehensively considering permeability time variation and threshold pressure gradient, thereby enhancing the reliability of production forecasting.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yin, H.; Yu, J.; Qu, H.; Yin, S. A Novel Approach to Waterflooding Optimization in Irregular Well Patterns Using Streamline Simulation and 3D Visualization. Processes 2025, 13, 1114. [Google Scholar] [CrossRef]
- Yang, R. Further study on oil/water relative permeability ratio model and waterflooding performance prediction model for high water cut oilfields sustainable development. J. Pet. Explor. Prod. Technol. 2024, 14, 1297–1309. [Google Scholar] [CrossRef]
- Zhong, H.; Shi, B.; Bi, Y.; Cao, X.; Zhang, H.; Yu, C.; Tang, H. Interaction of elasticity and wettability on enhanced oil recovery in viscoelastic polymer flooding: A case study on oil droplet. Geoenergy Sci. Eng. 2025, 250, 213827. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, Q.; Huang, Z.; Zhao, K.; Zhao, H.; Guo, L.; Wang, Y. Core flooding experimental study on enhanced oil recovery of heavy oil reservoirs with high water cut by sub-and supercritical water. Geoenergy Sci. Eng. 2024, 242, 213208. [Google Scholar] [CrossRef]
- Khormali, A.; Ahmadi, S. Synergistic Effect Between Oleic Imidazoline and 2-Mercaptobenzimidazole for Increasing the Corrosion Inhibition Performance in Carbon Steel Samples. Iran. J. Chem. Chem. Eng. 2023, 42, 321–336. [Google Scholar]
- Song, K.; Wang, D.; Yang, E.; Wu, X.; Dong, C.; Sun, P. A novel method to identify preferential flow paths by considering the time-varying effect of petrophysical parameters in ultra-high water-cut reservoirs. Geoenergy Sci. Eng. 2024, 241, 213172. [Google Scholar] [CrossRef]
- Fu, H.; Song, K.; Ma, Z.; Zhao, Y.; Liang, L.; Guo, H. An accurate identification and spatial characterization method for the development degree of preferential flow paths in water-flooded reservoir. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 141. [Google Scholar] [CrossRef]
- Nie, R.S.; Wang, Y.M.; Kang, Y.L.; Jia, Y.L. Modeling the characteristics of Bingham porous-flow mechanics for a horizontal well in a heavy oil reservoir. J. Pet. Sci. Eng. 2018, 171, 71–81. [Google Scholar] [CrossRef]
- Balhoff, M.T.; Thompson, K.E. Modeling the steady flow of yield-stress fluids in packed beds. AIChE J. 2004, 50, 3034–3048. [Google Scholar] [CrossRef]
- Lowman, J.; Abukhdeir, N.M.; Ioannidis, M.A. Predictive multiphysics model of vapor extraction (VAPEX) for the in-situ recovery of heavy oil and bitumen. Fuel 2025, 381, 133408. [Google Scholar] [CrossRef]
- Dong, X.; Liu, H.; Wang, Q.; Pang, Z.; Wang, C. Non-Newtonian flow characterization of heavy crude oil in porous media. J. Pet. Explor. Prod. Technol. 2013, 3, 43–53. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Q.; Dong, Y.; Chen, Z.; Duan, Y.; Sun, H.; Yan, X. Analytical and numerical studies on a moving boundary problem of non-Newtonian Bingham fluid flow in fractal porous media. Phys. Fluids 2022, 34, 023101. [Google Scholar] [CrossRef]
- Gao, Y.; Ma, K.; Liu, J.; Ling, D.; Yang, B. Considering Shear Dilution and Threshold Pressure Gradient Heavy Oil Reservoir Nonlinear Numerical Simulation and Residual Oil Characterization. In Proceedings of the International Petroleum Technology Conference, Dhahran, Saudi Arabia, 12–14 February 2024; p. IPTC-23459-EA. [Google Scholar]
- Civan, F. Non-isothermal permeability impairment by fines migration and deposition in porous media including dispersive transport. Transp. Porous Med. 2010, 85, 233–258. [Google Scholar] [CrossRef]
- Zhu, L.; Du, Q.; Li, Z.J.; Yu, H.; Song, X. Variation of physical characteristics and wettability of the reservoir at high water-cut stage. Pet. Explor. Dev. 2004, 31 (Suppl. S1), 82–84. [Google Scholar]
- Hu, J.I.; Zhang, R.; Xianbo, L.U.; Zili, Z.H.; Lu, Y.A. Nuclear magnetic resonance experiments on the time-varying law of oil viscosity and wettability in high-multiple waterflooding sandstone cores. Pet. Explor. Dev. 2024, 51, 394–402. [Google Scholar]
- Beckingham, L.E. Evaluation of macroscopic porosity-permeability relationships in heterogeneous mineral dissolution and precipitation scenarios. Water Resour. Res. 2017, 53, 10217–10230. [Google Scholar] [CrossRef]
- Kamal, M.M.; Morsy, S.; Suleen, F.; Pan, Y.; Dastan, A.; Stuart, M.R.; Mire, E.; Zakariya, Z. Determination of in-situ reservoir absolute permeability under multiphase-flow conditions using transient well testing. SPE Reserv. Eval. Eng. 2019, 22, 336–350. [Google Scholar] [CrossRef]
- Duan, J.; Zhu, L.; Luo, W. Establishment and application of a novel four-dimensional model for simulation of a natural water flooding reservoir—A case study of Nanpu No. 2 structure in the BHW basin. Processes 2023, 11, 189. [Google Scholar] [CrossRef]
- Wang, S.C.; Zhang, N.; Tang, Z.H.; Zou, X.F.; Sun, Q.; Liu, W. Time-dependent model for two-phase flow in ultra-high water-cut reservoirs: Time-varying permeability and relative permeability. Pet. Sci. 2024, 21, 2536–2553. [Google Scholar] [CrossRef]
- Ju, B.S.; Fan, T.L.; Zhang, J.C.; Wang, X.D. Oil viscosity variation and its effects on production performance in water drive reservoir. Shiyou Kantan Yu Kaifa (Pet. Explor. Dev.) 2006, 33, 99–102. [Google Scholar]
- Chuanzhi, C.; Kaikai, L.; Yong, Y.; Yingsong, H.; Qi, C. Identification and quantitative description of large pore path in unconsolidated sandstone reservoir during the ultra-high water-cut stage. J. Pet. Sci. Eng. 2014, 122, 10–17. [Google Scholar] [CrossRef]
- Xu, J.; Guo, C.; Jiang, R.; Wei, M. Study on relative permeability characteristics affected by displacement pressure gradient: Experimental study and numerical simulation. Fuel 2016, 163, 314–323. [Google Scholar] [CrossRef]
- Jiang, R.; Zhang, W.; Zhao, P.; Jiang, Y.; Cai, M.; Tao, Z.; Zhao, M.; Ni, T.; Xu, J.; Cui, Y.; et al. Characterization of the reservoir property time-variation based on ‘surface flux’and simulator development. Fuel 2018, 234, 924–933. [Google Scholar] [CrossRef]
- Zhao, P.; Shen, Z.; Cai, M. Comprehensive time-varying numerical simulation of reservoir physical properties based on effective displacement flux and its application. J. China Univ. Pet. 2022, 46, 89–96. [Google Scholar]
- Sun, Z.; Li, Y.; Ma, K.; Xu, J.; Zhang, G.; Jiang, R.; Pan, S. A novel method to characterise time-variation of reservoir properties: Experimental study, simulator development and its application in Bohai Bay oilfield. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Bali, Indonesia, 29–31 October 2019; p. SPE-196282-MS. [Google Scholar]
- Lin, J.; Jiang, R.; Shen, Z.; Wang, Q.; Cui, Y.; Ni, Q.; Zhang, F. Comprehensive characterization investigation of multiple time-varying rock-fluid properties in waterflooding development. J. Energy Resour. Technol. 2022, 144, 073001. [Google Scholar] [CrossRef]
- Zhou, Z.; Jia, H.; Zhang, R.; Ding, B.; Geng, X. Three dimensional time-variation simulator for water flooding reservoir based on “effective water flux”. Phys. Fluids 2024, 36, 103101. [Google Scholar] [CrossRef]
- Xin, X.; Yu, G.; Chen, Z.; Wu, K.; Dong, X.; Zhu, Z. Effect of non-newtonian flow on polymer flooding in heavy oil reservoirs. Polymers 2018, 10, 1225. [Google Scholar] [CrossRef]
- Xin, X.; Liu, S.; Yu, G.; Ma, R.; Xu, P. Quantitative Characterization of Heavy Oil Threshold Pressure Gradient in Porous Media. In Proceedings of the SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, UAE, 24–26 January 2023; p. D031S017R002. [Google Scholar]
- Xin, X.; Li, Y.; Yu, G.; Wang, W.; Zhang, Z.; Zhang, M.; Ke, W.; Kong, D.; Wu, K.; Chen, Z. Non-Newtonian Flow Characteristics of Heavy Oil in the Bohai Bay Oilfield: Experimental and Simulation Studies. Energies 2017, 10, 1698. [Google Scholar] [CrossRef]
- Ruizhong, J.; Qingdong, N.; Chunguang, Z.; Fengbo, Z.; Yihua, G.; Jingqi, L. Research on seepage model and numerical simulation of variable starting pressure gradient for heavy oil reservoirs based on pressure sensitive effect. Pet. Geol. Recovery Effic. 2021, 28, 54–62. [Google Scholar]
- Jianchun, X.; Baojiang, S.; Bailian, C. A hybrid embedded discrete fracture model for simulating tight porous media with complex fracture systems. J. Pet. Sci. Eng. 2019, 174, 131–143. [Google Scholar]
- Liu, X.; Cheng, S.; Cui, Y.; Wang, Y.; Wei, C. A dynamic Pre-Darcy model and its application in the numerical simulation of enhanced geothermal system. Geoenergy Sci. Eng. 2024, 241, 213193. [Google Scholar] [CrossRef]
- Chen, Z. Formulations and numerical methods of the black oil model in porous media. SIAM J. Numer. Anal. 2000, 38, 489–514. [Google Scholar] [CrossRef]
- Jansen, J.D.; Fonseca, R.M.; Kahrobaei, S.; Siraj, M.M.; Van Essen, G.M.; Van den Hof, P.M. The egg model–a geological ensemble for reservoir simulation. Geosci. Data J. 2014, 1, 192–195. [Google Scholar] [CrossRef]


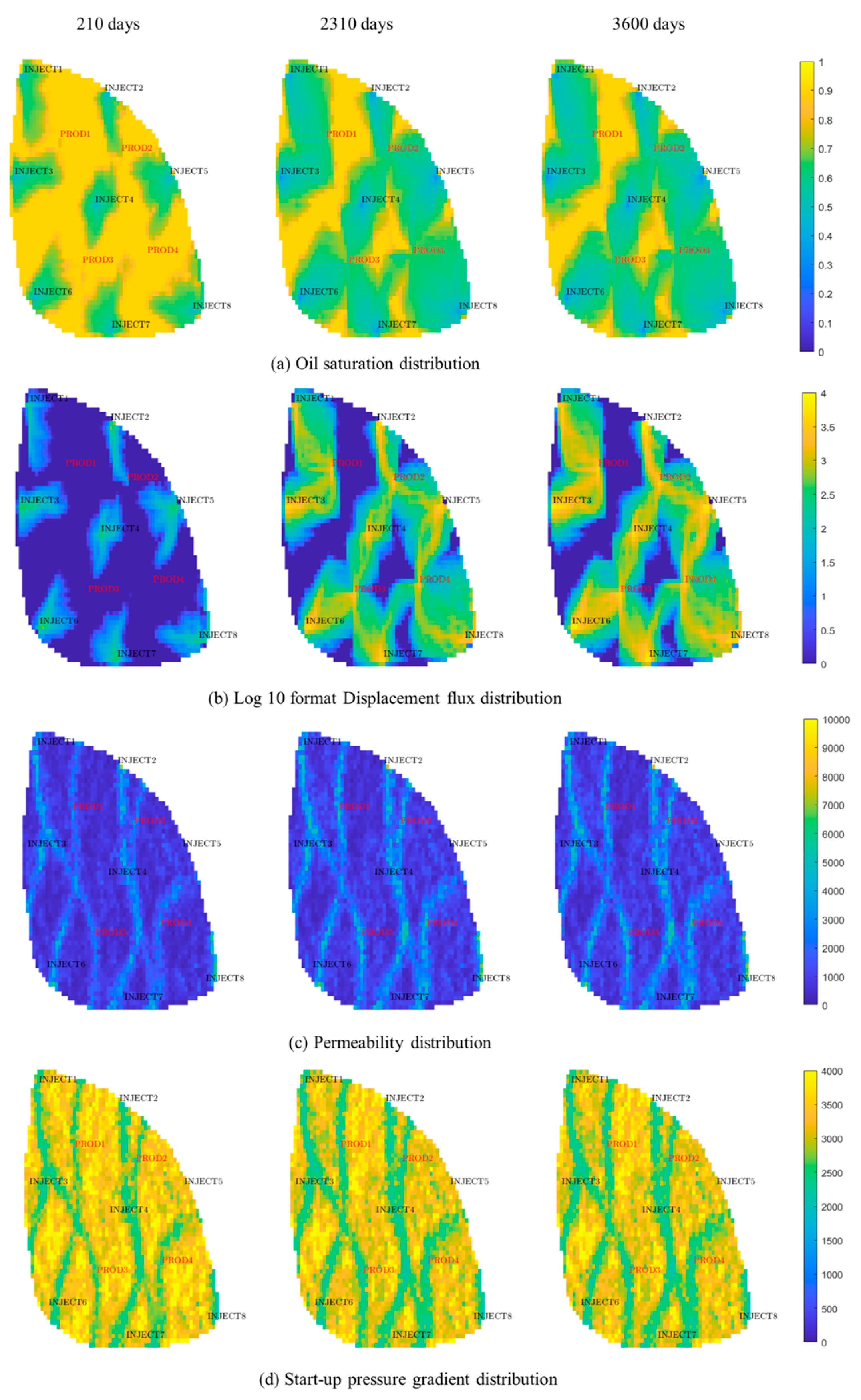
| Parameters | Value |
|---|---|
| Grid number | 31 × 31 × 5 |
| Grid number/m | 5 × 5 × 5 |
| Porosity | 0.4 |
| Permeability/mD | 100 × 100 × 6 |
| Initial formation pressure/MPa | 13.5 |
| Model | Model Description |
|---|---|
| (a) | Traditional black oil |
| (b) | Incorporation of time-varying permeability only |
| (c) | Considering threshold pressure gradient effect only |
| (d) | Comprehensively considering the threshold pressure gradient and time-varying permeability |
| Model | (a) | (b) | (c) | (d) |
|---|---|---|---|---|
| Oil recovery | 0.35 | 0.31 | 0.33 | 0.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Zhou, W.; Liu, C. Integrated Modeling of Time-Varying Permeability and Non-Darcy Flow in Heavy Oil Reservoirs: Numerical Simulator Development and Case Study. Processes 2025, 13, 1683. https://doi.org/10.3390/pr13061683
Cui Y, Zhou W, Liu C. Integrated Modeling of Time-Varying Permeability and Non-Darcy Flow in Heavy Oil Reservoirs: Numerical Simulator Development and Case Study. Processes. 2025; 13(6):1683. https://doi.org/10.3390/pr13061683
Chicago/Turabian StyleCui, Yongzheng, Wensheng Zhou, and Chen Liu. 2025. "Integrated Modeling of Time-Varying Permeability and Non-Darcy Flow in Heavy Oil Reservoirs: Numerical Simulator Development and Case Study" Processes 13, no. 6: 1683. https://doi.org/10.3390/pr13061683
APA StyleCui, Y., Zhou, W., & Liu, C. (2025). Integrated Modeling of Time-Varying Permeability and Non-Darcy Flow in Heavy Oil Reservoirs: Numerical Simulator Development and Case Study. Processes, 13(6), 1683. https://doi.org/10.3390/pr13061683





