Development of a Pump Characteristic Curve Prediction Model Using Transfer Learning

Abstract

With the advancement of intelligent industrial equipment and the growing demand for system digitalization, parametric modeling of pump operational states has become increasingly important. This is especially true for large pumps, where real-time monitoring remains a major challenge. This paper proposes a pump characteristic curve prediction method based on transfer learning. By leveraging characteristic curve data from small, easily testable source domains for pre-training, the learned features are transferred as initial conditions for training performance models of other pump types. The test results show that neural network models pre-trained with transfer learning achieve faster prediction speeds and lower error rates. Transfer learning also demonstrates strong adaptability to characteristic curve data from various pump categories. Under varying volumes of target data, prediction accuracy improves significantly. Notably, when data are limited, the transfer learning approach achieves a prediction error of 5.2%, compared to 48.1% for direct deep learning modeling. Moreover, the proposed method effectively reduces prediction range beyond the scope of the original data.

1. Introduction

To achieve energy conservation, cost reduction, and enhanced production efficiency, the intelligentization of industrial equipment has become a critical development trend. Centrifugal pumps, widely used in sectors such as petrochemical processing and urban water supply, are central to this transformation [1,2]. Globally, pump loads account for a significant portion of energy consumption. For example, in industrial applications, approximately 21% of the total annual power generation in industrial applications [3]. Efforts to optimize pump systems for energy efficiency generally focus on three areas: motor upgrades, pump design improvements, and efficient regulation of operation. Among these, permanent magnet synchronous motors have gained prominence due to their superior energy efficiency, often exceeding 97%, making them a key technology for enhancing overall pump unit performance [4,5]. While years of extensive research have led to diminishing returns in hydraulic efficiency through design optimization, operational regulation still offers substantial energy-savings potential. For instance, Hieninger et al. [6] reported that effective regulating of pump systems can yield average energy savings of up to 30%. In specific industrial contexts, such as crude oil extraction, water injection into wells is necessary to maintain reservoir pressure and improve oil recovery [7]. However, substantial seasonal fluctuations in injection volumes are typically managed by adjusting outlet valves. This approach often results in pumps operating inefficiently, leading to a mismatch between system capacity and actual demand, and creating considerable waste of energy and water [8]. Similar inefficiencies are prevalent across pump–pipeline systems in various industries. To address these challenges, intelligent regulation and industrial digital transformation have become essential for upgrading aging pump systems [9,10]. However, the complexity of existing facility layouts and the limited on-site space often hinder the installation of monitoring equipment. This makes it difficult to directly measure critical parameters such as pump head, system efficiency, and motor efficiency. To overcome these limitations, parametric modeling of pump performance has become a vital solution. By predicting key operational parameters in real time, these models enable efficient system monitoring and intelligent control across diverse industrial applications [11].

Traditional methods for predicting pump characteristics primarily rely on computational fluid dynamics (CFD) simulations and empirical formulas. While CFD can capture the complexities of internal flow fields, it is both computationally expensive and time-consuming. Empirical formulas, on the other hand, are computationally efficient but generally applicable only to specific pump types. When the impeller geometry deviates from the main design conditions, the prediction errors for head values often exceed 5% [12]. For parametric modeling of pump characteristic curves [10], techniques such as polynomial fitting [13], response surface methodology [14], and machine learning algorithms [15] have been utilized. In recent years, artificial intelligence (AI) methods have seen widely applied in areas including pump performance prediction [16], target recognition [17], and fault diagnosis [18]. Compared with traditional numerical simulations and experimental approaches, artificial neural networks (ANNs) offer clear advantages in hydraulic performance evaluation of centrifugal pumps, including faster prediction cycles and less cost, hence presenting a promising alternative. Wang et al. [19] proposed a method that combines ANNs with the particle swarm optimization (PSO) algorithm to improve the centrifugal pump efficiency at the design point. The deviation between predicted and simulated efficiency was only 1.05%, and the optimized pump exhibited a 0.12% improvement in efficiency. Moreover, flow separation on the pressure side of the blades was eliminated, significantly reducing hydraulic losses. The effectiveness of this method was validated by numerical simulations. Yu et al. [20] developed a machine learning-based model that uses the pump’s specific speed and partial Suter curve data to predict the full characteristic curve of centrifugal pumps, demonstrating the potential of machine learning in pump performance modeling. Han et al. [12] utilized a backpropagation (BP) neural network and the Levenberg–Marquardt algorithm. Using multidimensional inputs like specific speed, flow rate, rotational speed, and impeller geometric parameters, they accurately predicted hydraulic performance. The outputs, including head and efficiency, provided valuable insights during the design process. Wu et al. [21] applied a genetic algorithm-optimized backpropagation neural network (GA-BPNN) model to predict the centrifugal pump flow rate. This method significantly enhanced prediction accuracy under low-flow conditions, with most relative errors remaining below 5%. Their approach supports the development of flow sensor-free monitoring and control technologies for centrifugal pumps, offering a new direction for improving energy efficiency. Such techniques are particularly relevant in systems where the installation of high-precision flow meters is not feasible due to large pipeline diameters and limited available space, leading to a lack of direct flow measurement. Collectively, these studies indicate the effectiveness of using ANN-based approaches for centrifugal pump performance prediction.

These modeling methods typically require large amounts of labeled data to effectively train the models [22]. However, in practical applications, especially for large-scale pumps, it is often difficult to obtain sufficient operational data through experiments. Moreover, input variables such as the impeller geometric parameter, commonly used in the aforementioned literature, are usually unavailable at the time of pump delivery. The limited availability of characteristic data makes accurate modeling challenging. Additionally, the hydraulic designs of pumps are often proprietary and considered trade secrets by manufacturers, further restricting access to detailed model specifications. This issue is particularly evident in older pumps that require retrofitting, where only basic information such as the rated speed may be available. For engineering applications, the essential data needed to control pump operation typically includes characteristic curves that describe the relationships among speed, flow rate, head, and efficiency. However, conducting characteristic curve tests for large pumps is often impossible due to space, time, and cost constraints, leading to insufficient data for accurate predictive modeling. To address these limitations, transfer learning has emerged as promising approach.

Transfer learning is a significant branch of machine learning research, with its core principle centered on transferring knowledge and features representations learned in a source domain to a related target domain [23,24]. As machine learning becomes increasingly widespread, traditional supervised learning methods—though effective—typically rely on large amounts of labeled data. However, data labeling is often labor-intensive and costly, especially in fields such as image processing. In many cases, pre-trained models (e.g., transfer application of pre-trained models of ImageNet) are frequently used in transfer learning approaches. This approach offers a promising solution for addressing the challenge of pump characteristic prediction under small-sample conditions. By combining deep learning with transfer learning, models can more effectively adapt to target domains or tasks, particularly when labeled data are scarce or when there is a correlation between the source and target domains or tasks. This combination not only enhances model performance but also reduces the dependency on extensive training datasets. In the context of pump characteristic prediction, the source domain can be composed of pump groups with sufficient characteristic curve data, such as small centrifugal pumps that are easy to test. The target domain refers to large-scale pumps operating under special conditions, where characteristic data are limited. This concept is analogous to the pump similarity theory in hydraulic machinery, which maintains key dimensionless parameters such as the specific speed and efficiency. While pump similarity theory preserves key criteria characteristics across different pump scales, transfer learning facilitates performance modeling by extracting and transferring relevant features from source pump characteristic curves. Recent advancements in transfer learning have shown significant success in various domains, including image processing, speech recognition, and natural language processing [25,26,27]. It has been applied to areas such as fault diagnosis of rotating machinery [28] and wastewater flow prediction [29]. However, studies specifically targeting pump characteristic prediction remain limited, highlighting a valuable opportunity for further research and development in this area.

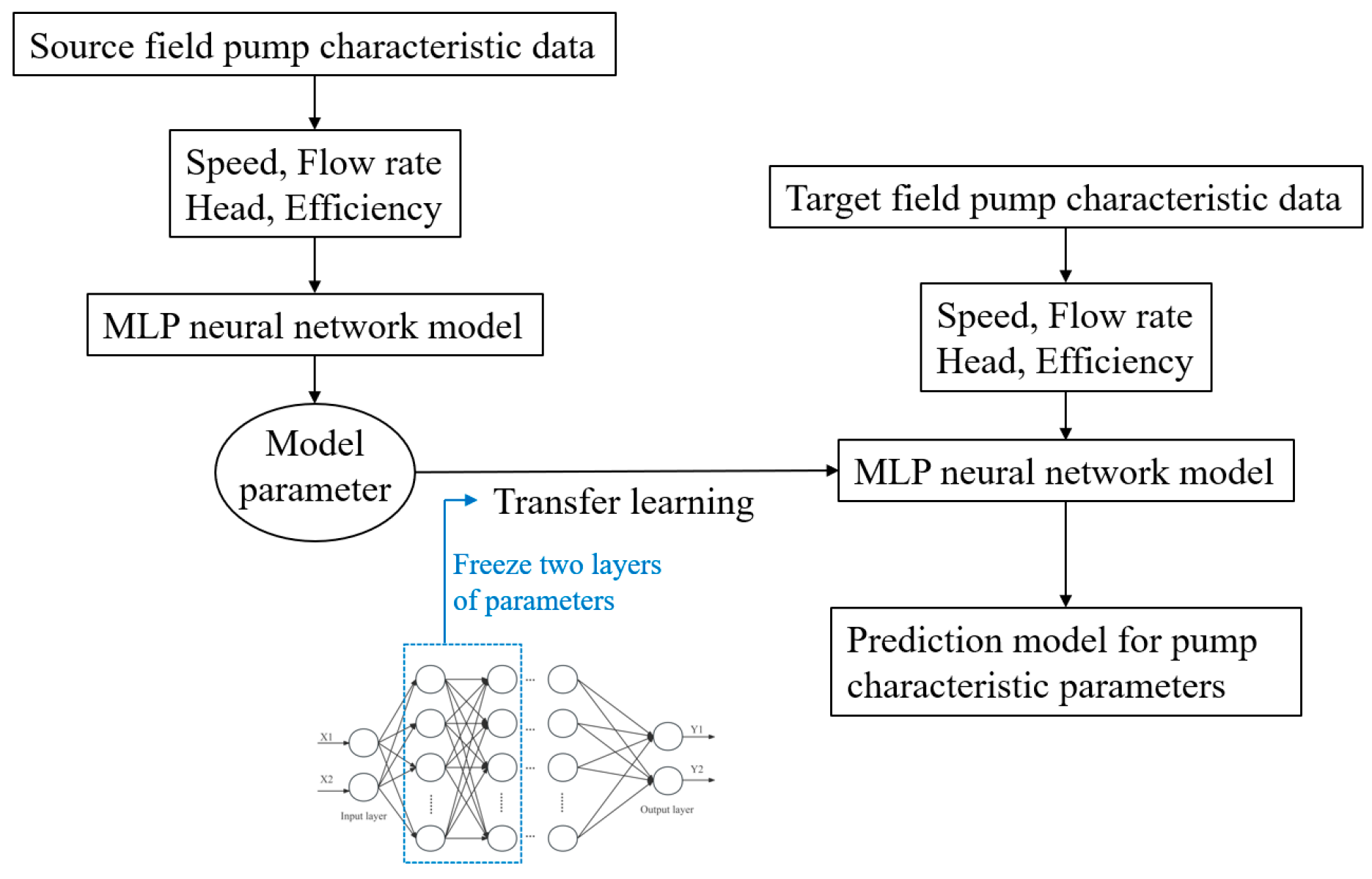
This study focuses on engineering applications such as the retrofitting of injection pumps on deep-sea oil platforms. Due to the complexity of the pump system’s piping and the limited space, it is impractical to install additional monitoring devices such as flow meters. To monitor the operational status, it is necessary to model the system’s running conditions in advance. By utilizing measurable data, such as rotational speed and pressure, the flow rate can be predicted. However, there are insufficient data available for modeling. This is especially true for older pump equipment that requires retrofitting, where only the rated rotational speed might be available. Therefore, this study considers using transfer learning to address the issue of insufficient pump data for modeling. In this study, easily testable and simulated small, single-stage centrifugal pumps were selected to conduct pump characteristic experiments under multiple operating speeds. The performance data obtained from these tests serves as source domain knowledge, forming a transfer learning database based on single-stage centrifugal pump data. These data are used to train models, which are subsequently applied to other pump types to enhance the accuracy of characteristic curve predictions. To evaluate the effectiveness of transfer learning, the study incorporates experimental data from multistage submersible pumps and simulation data from high-pressure injection pumps as target domain datasets. Both datasets are modeled to assess the adaptability of the trained models. In scenarios of limited data availability and when predictive inputs fall outside the range of the original training dataset, the study compares the prediction accuracy of conventional deep learning models with that of models enhanced through transfer learning. This investigation examines the cross-domain transferability of transfer learning techniques across different pump types, offering valuable insights into their practical effectiveness in real-world engineering scenarios. A novel solution is provided for the neural network modeling problem when pump characteristic data are insufficient.

2. Model Principle

2.1. Principle of Deep Learning Model

Deep learning is a specialized branch of machine learning method inspired by the way the human brain processes information. It employs ANNs to automatically learn and extract complex patterns from data. These networks consist of multiple layers of interconnected neurons, each capable of transforming input signals data using adjustable parameters known as weights and biases. In this study, the deep learning model is constructed based on pump characteristic curves, which exhibit unique data patterns and features. The model utilizes a Multi-Layer Perceptron (MLP), also known as an Artificial Neural Network (ANN), which is a type of Fully Connected Neural Network (FCN). An MLP consists of a minimum of three layers: an input layer that receives the initial data, one or more hidden layers that perform intermediate processing, and an output layer that produces the final prediction.

The MLP imposes no fixed constraints on the number of hidden layers or the number of neurons in the output layer; these can be configured based on specific modeling requirements. In an MLP, the neurons in each hidden layer are fully connected to the neurons in the preceding layer. If the input layer is represented by a vector X, the output of the hidden layer can be expressed as:

$$\mathrm{f}({\mathrm{W}}_1\mathrm{X} +{\mathrm{b}}_1)$$

(1)

where W₁ denotes the weight matrix, b₁ the bias vector, and f the activation function, commonly chosen as the Sigmoid function, denoted by S. The connection between the hidden layer and the output layer typically involves multi-class logistic regression, also known as Softmax regression. Therefore, the output of the output layer can be formulated as follows:

$$\mathrm{S}({\mathrm{W}}_2{\mathrm{X}}_1+{\mathrm{b}}_2)$$

(2)

where X₁ is the output of the hidden layer f(W₁X + b₁). In summary, the operations of a three-layer MLP can be mathematically represented as follows:

$$\mathrm{y}=\mathrm{S}({\mathrm{b}}_2+{\mathrm{W}}_2\left(\mathrm{f}\right({\mathrm{b}}_1+{\mathrm{W}}_1\mathrm{X}\left)\right))$$

(3)

All parameters of the MLP consist of the connection weights and biases between layers, specifically including W₁, b₁, W₂, and b₂.

During the training process, several hyperparameters that critically influence the performance of deep learning models must be carefully adjusted. These include batch size, number of training iterations, activation functions, and loss functions. The number of training iterations directly affects both the duration of the training process and the accuracy of prediction results. To improve computational efficiency, training samples can be divided into smaller subsets (known as batches) and processed sequentially. Activation functions play a crucial role in introducing nonlinearity into the network, thereby enhancing the model’s capacity to learn and solve complex problems. Common activation functions include Sigmoid, Tanh, and ReLU, among others.

In this study, the ReLU (Rectified Linear Unit) function is adopted due to its simplicity and effectiveness. It consists of two simple linear functions and is mathematically expressed in Equation (4):

$${\mathrm{f}}_{\mathrm{ReLU}}\left(\mathrm{x}\right)=\left\{\begin{array}{cc}\mathrm{x}& \mathrm{x} > 0\\ 0& \mathrm{x} \ge 0\end{array}\right.$$

(4)

When the input x > 0, the derivative of the function is 1; otherwise, it is 0. The ReLU function effectively mitigates the vanishing gradient problem, which can hinder the training of deep networks. During the training process, data normalization is required. The normalization function is as follows:

$$\mathrm{x}={\displaystyle \frac{\mathrm{x} -{ \mathrm{x}}_{\min }}{{\mathrm{x}}_{\max } -{ \mathrm{x}}_{\min }}}$$

(5)

where x represents the parameter value. The characteristic parameters of the pump can all be normalized using this method, scaling the parameters to the range of [0, 1]. The Mean Square Error (MSE) is the most commonly used loss function for regression tasks. It is defined as the mean of the square difference between the predicted values x and the true target values y as shown in formula (6):

$$\mathrm{MSE}={\displaystyle \frac{\sum _1^{\mathrm{n}}(\mathrm{f}\left(\mathrm{x}\right) - \mathrm{y}{)}^2 }{\mathrm{n}}}$$

(6)

This study selects MSE as the loss function, primarily due to the regression nature of pump characteristic prediction tasks. To ensure robustness, comparative tests were conducted with other commonly used regression loss functions. The results are presented in

Table 1. The impact of using different loss functions on errors.

Loss Functions	Mean Squared Error (m2)	Mean Absolute Error (m)
MSE	0.27	0.41
MAE	0.25	0.43
Huber	0.39	0.49

. As shown in the table, all three loss functions achieve relatively high prediction accuracy. The Huber loss exhibits slightly larger prediction errors compared to MSE and Mean Absolute Error (MAE). The choice of MSE as the final loss function is driven by its squared term, which applies stronger penalties to larger prediction errors, making it more effective at capturing steep variations in the characteristic curves.

Backpropagation is a widely used algorithm for training ANNs and is applicable across various neural network models. It enables the model to optimize parameters using algorithms such as gradient descent by propagating the simulated gradients backward through the network. During this process, the network’s parameter is iteratively adjusted based on the error values, with the objective of minimizing the loss function. Through this iterative training and optimization, backpropagation allows the model to converge toward an optimal solution, thereby improving prediction accuracy and overall performance.

2.2. Principle of Transfer Learning

Transfer learning is a machine learning strategy that allows models to utilize knowledge gained from one task or domain. For example, it uses small pump model parameters to assist with another related task or domain, such as multistage submersible pump model parameters. This approach improves learning efficiency and boosts overall performance. This approach often relies on pre-trained neural networks, which are trained on large datasets. These datasets include extensive characteristic curve data gathered from experiments on small pumps. These networks learn general and transferable features, which can then serve as a solid starting point for new tasks, eliminating the need to train a model from scratch. This approach significantly reduces training time and improves model performance, particularly in scenarios where the target task domain has limited available data. In this study, a MLP is used, and the structure of the neural network model trained on the source data is illustrated in Figure 1. The model employs a seven-layer architecture with 16 nodes in each hidden layer. The input variables are speed and flow rate, while the output variables are head and efficiency, collectively forming a neural network model for predicting pump characteristic curves.

In the transfer learning process, the parameters learned by the small pump characteristic model are transferred to the model designed for the target task involving large pumps. Training then continues using data from the large pump. During this process, the parameters of certain layers—transferred from the source domain model—are frozen, meaning they remain unchanged, while the parameters of other layers are fine-tuned to adapt to the new task. Since the model from the source task has already captured general features, the aim is to preserve these features, adjusting only the final layers to suit the new task. This process is illustrated in Figure 2, where the parameters from the source domain neural network model (based on the pump characteristic curve) are copied to the target domain neural network model. This helps retain some features from the source data and accelerates the training process.

3. Model Training

3.1. Dataset Construction

To construct a dataset of characteristic curves for different pumps, data are obtained through experimental testing or numerical simulations. In this study, the characteristic curve data of a small single-stage pump is selected as the source domain dataset. For the target domain, two types of pumps are selected: a multistage submersible pump and a ten-stage high-pressure pump (BB3 pump). These pumps differ significantly in terms of geometry and structure, allowing for an assessment of model transferability between different pump types.

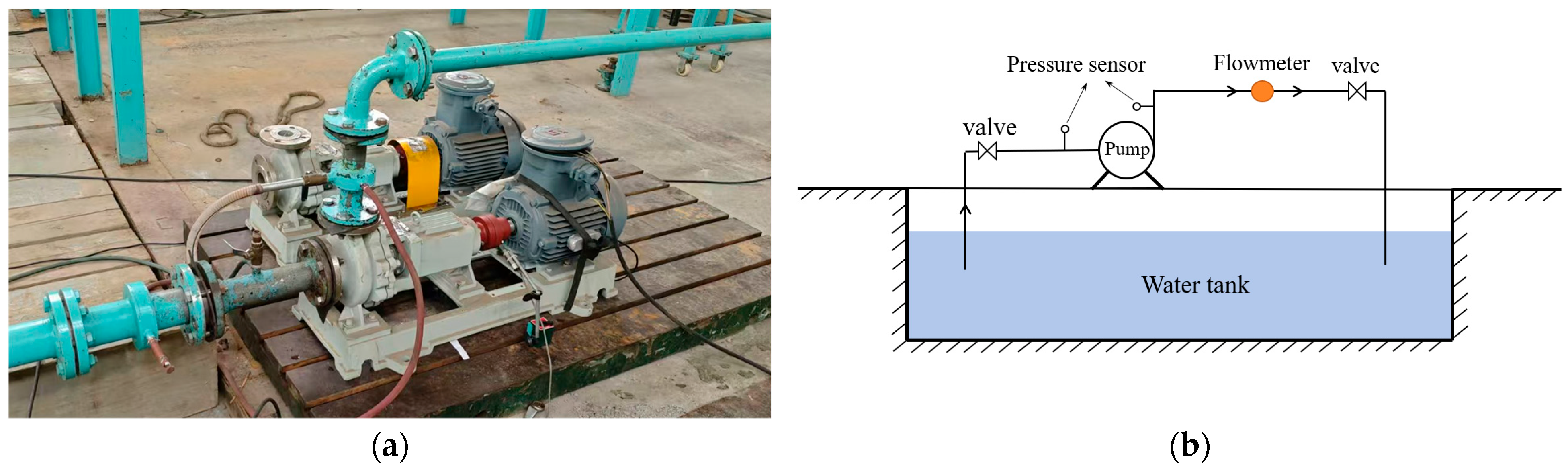
The performance parameters for the source domain model are obtained through pump experimental testing. Characteristic curve tests are conducted on a small single-stage centrifugal pump, which is relatively easy to test. The test pump has a rated flow of 25 m³/h, a head of 32 m, and a rated speed of 2980 rpm. The schematic diagram of the experimental platform is shown in Figure 3.

This experimental platform is designed to measure the hydraulic performance of the test pump and to record its characteristic parameters. The system primarily consists of inlet and outlet valves, the test pump, inlet and outlet pipelines, a turbine flow meter, inlet and outlet pressure sensors, a speedometer, and an electrical control cabinet. Pump characteristic curves at different rotational speeds are measured, including flow-head curves and flow-efficiency curves. To ensure comprehensive data collection, the speed range for the source domain is extended beyond that of the target data. The target data speed range corresponds to the practical applications of the pump. Since the operating speed and flow rate typically do not deviate significantly from their rated values, this extended range helps preserve more characteristic features for model transfer. Generally, the operational speed deviates by no more than 10% from the rated speed. For the test pump with a rated speed of 2980 rpm driven by a 50 Hz motor, the pump speed is adjusted using a frequency converter between 42 and 56 Hz. At each speed setting, the outlet flow valve is adjusted from fully closed to fully open, with measurements taken at more than twelve points, and the recorded parameters include inlet and outlet pressures, flow rate, rotational speed, and efficiency.

A multistage submersible pump is selected as one of the target domains models. It has a rated flow of 50 m³/h, a head of 52 m, and a rated speed of 2850 rpm. The operational data of this pump are also obtained through experimental tests using the same method as for the source domain. The only difference lies in the calculation of inlet pressure, which is derived based on the vertical distance between the liquid surface and the pump inlet. The characteristic curve data measured at different rotational speeds constitute the target dataset for transfer learning.

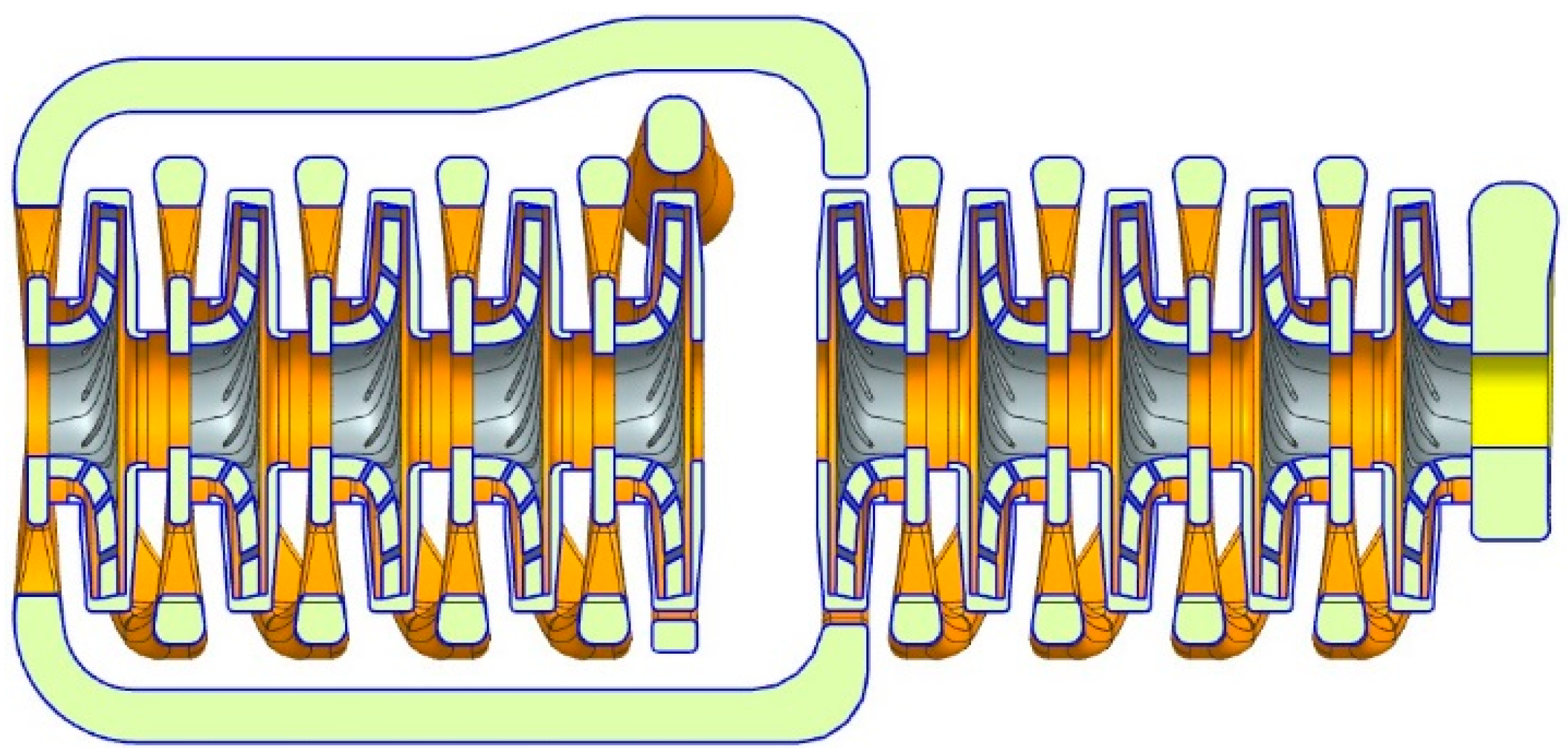
To further study model transferability, a high-pressure water injection pump is selected as another target domain. This pump has a rated flow of 120 m³/h, a head of 1450 m, and a rated speed of 2980 rpm. It belongs to the category of large-scale pumps, which are difficult to measure experimentally, as noted in the introduction. Therefore, 3D modeling software (NX1980) is used to model key components including the impeller, suction chamber, transition channel, low-pressure and high-pressure final-stage pressurized water chambers, etc. The internal fluid domain of the pump is shown in Figure 4. ICEM CFD 2024 R1 software is used for mesh generation. To accurately simulate fluid behavior near the wall surface, the Y+ value of the boundary layer mesh is controlled to remain below 200. Figure 5 shows the Y+ distribution cloud map for the twisted blades. As this study does not require high-precision analysis, the selected simulation accuracy is sufficient to obtain reliable pump characteristic curves. The simulations are carried out using CFX to generate characteristic curves of the pump at different speeds.

3.2. Deep Learning Model Training

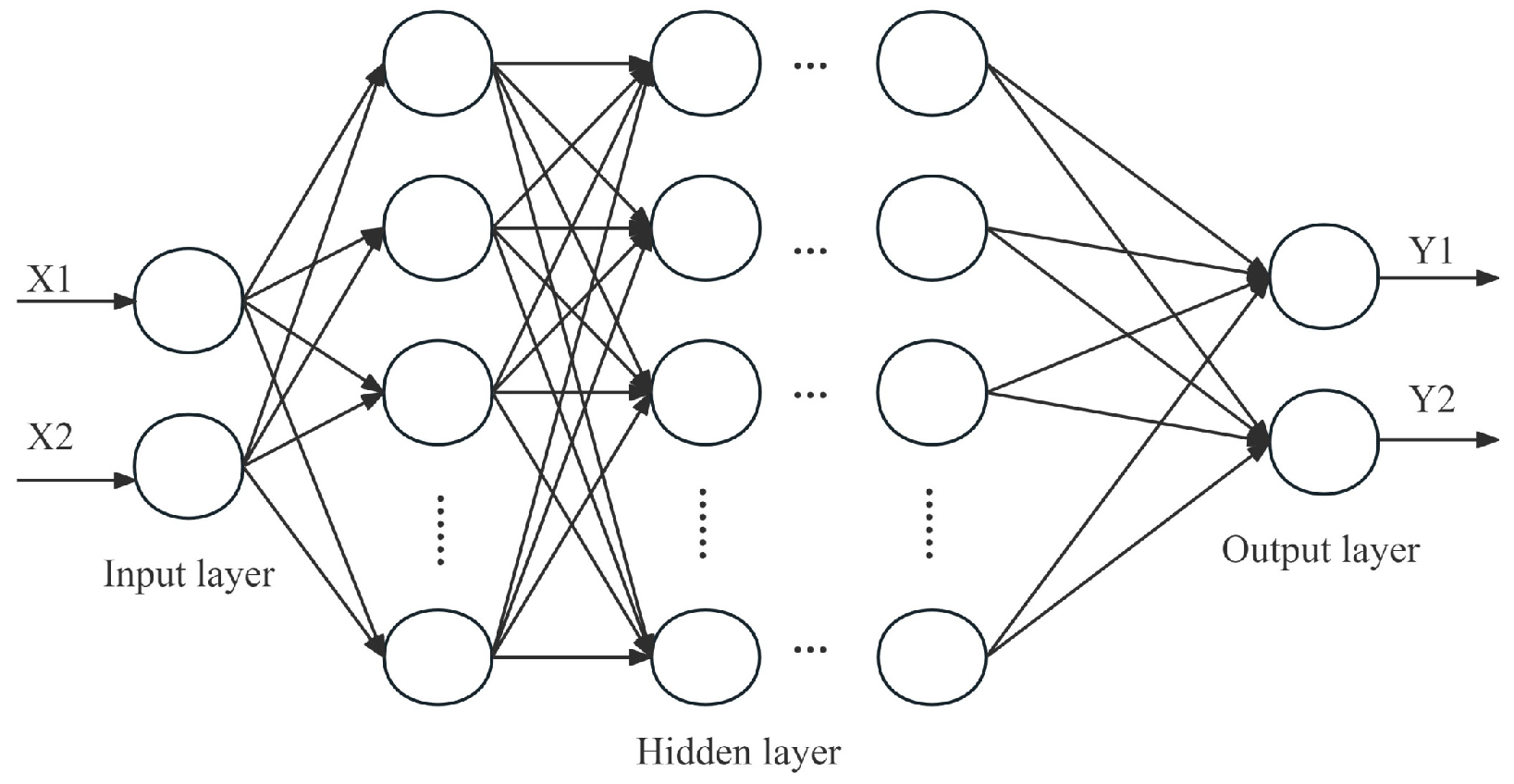
A pre-trained neural network model was developed using data collected from a small single-stage centrifugal pump. The implementation was carried out using Python 3.9 and PyTorch 1.12.0. The model was trained on an AMD Ryzen 7 3700X CPU (AMD, Santa Clara, CA, USA) with 32 GB of memory. Model parameters were initialized using the Kaiming uniform distribution, and the initialization parameters for transfer learning were set as the pre-trained model’s parameters. The parameter settings for deep learning and transfer learning were consistent. During the training phase, a batch size of 16 was used, and the model was optimized with the popular Adam optimizer, featuring a learning rate of 0.01. ReLU was employed as the activation function for all hidden layers. The model’s input consisted of rotational speed and flow rate, while the output included head and efficiency, enabling the construction of a neural network model for pump characteristic curves. Tests were conducted on models with varying numbers of hidden layers, and the results are shown in

Table 2. The influence of the number of hidden layers in neural networks.

Number of Hidden Layers	Mean Squared Error (m2)	Mean Absolute Error (m)
3	1.67	0.85
4	2.2	1.19
5	0.27	0.41
6	0.59	0.73

. A five-layer hidden structure in the MLP neural network was found to achieve high prediction accuracy, with each hidden layer consisting of 16 nodes. The loss function used was Mean Squared Error (MSE). Due to the small number of model parameters, the training time was short, and the time required for training did not impact either the model’s development or its engineering applications. Therefore, the effect of training time was not considered in this study.

The pump characteristic parameter prediction model, trained on small pump data, is applied in transfer learning framework to predict the characteristic curves of other pumps using a smaller portion of data. In this study, a multistage submersible pump is selected as the target model, with a rated flow of 50 m³/h, a head of 52 m, and a rated speed of 2850 rpm. Operational data obtained through testing is used as the target dataset for transfer learning. To demonstrate the ability of transfer learning to adapt data knowledge from single-stage pumps to other types of pumps, not only are physically measured characteristic curve parameters used, but so are data obtained from numerical or experimental simulations. In addition, simulation data from a deep-sea oil extraction ten-stage high-pressure injection pump is employed as another target dataset. This pump has a rated flow of 105 m³/h, a head of 1221 m, and a rated speed of 2980 rpm. Considering the difficulties of testing large pumps, this study develops a deep learning model specifically designed to operate under limited data conditions. Additionally, it establishes a second model using transfer learning, based on a pre-trained MLP model of small pumps. Both methods are trained, and their prediction accuracies are compared to evaluate performance.

4. Results and Analysis

As shown in Figure 6a, model was trained using the loss function on characteristic data from 40 sets of multi-stage submersible pumps, with 80% of the data used for training and 20% for testing. Both deep learning and transfer learning approaches were applied. The parameter settings for transfer learning are identical to those used in the training of the small single-stage centrifugal pump model described in the previous section. The initialization parameters are taken from the pre-trained small pump model. Transfer learning requires freezing certain hidden layers of the model. These layers directly reuse the pre-trained parameters from the source domain (small pump). During training in the target domain, the parameters of these frozen layers remain unchanged, preserving the general characteristics shared across different pump types. To determine the optimal number of layers to freeze, predictive results were compared across models with varying numbers of frozen layers, as shown in

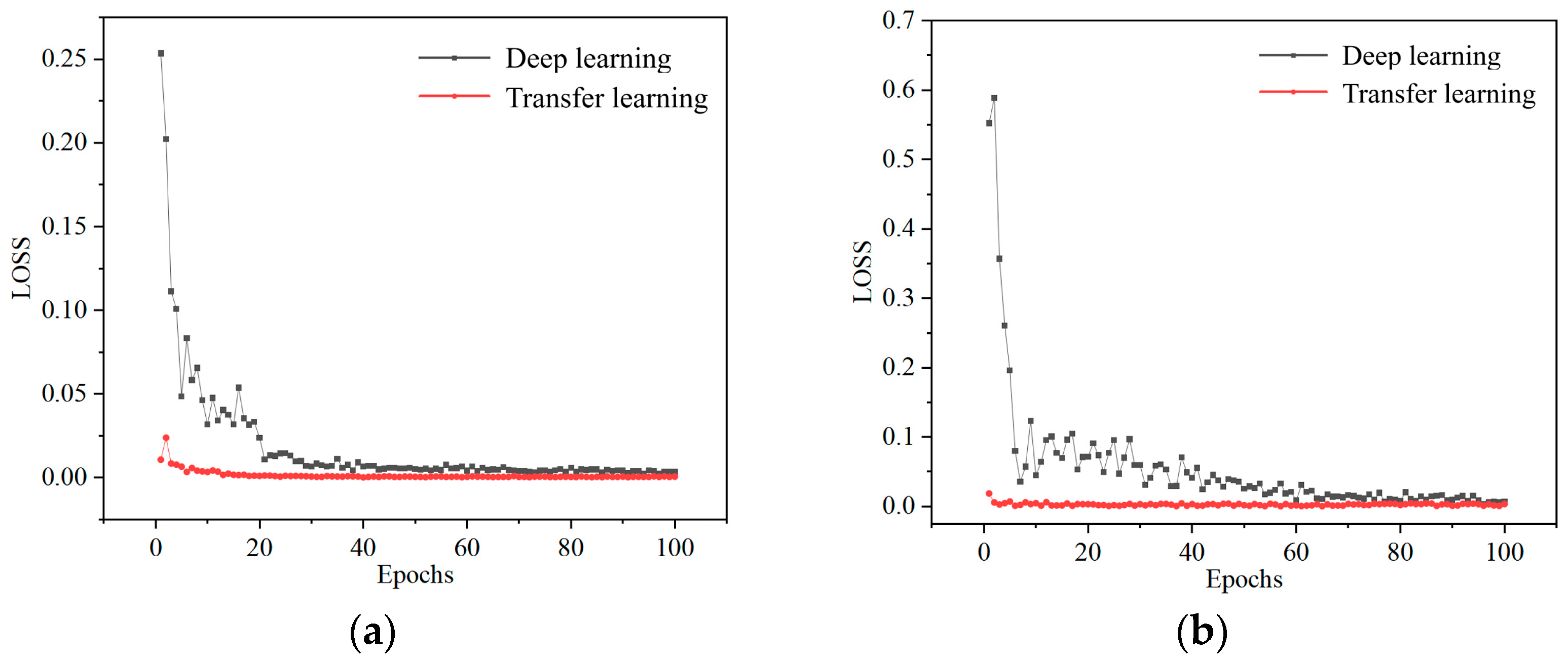
Table 3. The impact of freezing layers on the prediction of transfer learning models.

Freezing Layers	Mean Squared Error (m2)	Maximum Error (%)
1	5.9	6.2
2	2.4	4.4
3	68.9	28.5

. The maximum relative error between the predicted values of two models and the true values is calculated by selecting five points near the rated flow point and selecting the maximum error. The results indicate that freezing two layers yields the smallest prediction error. Therefore, this study chooses to freeze two layers for subsequent research. When three layers are frozen, the error increases sharply due to the excessive retention of source domain features, which severely impacts the target domain. Therefore, it is crucial to validate the fixed parameters during transfer learning. This ensures that the desired characteristics are maintained while minimizing the impact of source domain features on the target domain. In this study, freezing two layers was chosen for subsequent research. The loss functions during the training process of both deep learning and transfer learning are illustrated in Figure 6. Following pre-training with the initial dataset, transfer learning allows the model to achieve a low loss value from the outset. In contrast, direct deep learning begins with a significantly higher initial loss. Although the loss gradually decreases and stabilizes after 15 training steps, it remains higher than that achieved through transfer learning. This clearly highlights the substantial improvements in both training accuracy and speed offered by transfer learning.

Considering that the inputs are rotational speed and flow rate, and the outputs are head and efficiency, a neural network model was constructed to represent the pump characteristic curves. Different control strategies are applied based on the operational requirements of various pump systems. For example, in the case of water injection pumps, the operating conditions are determined by the required flow rate and pressure. Without accounting for valve opening, the necessary rotational speed and corresponding efficiency can be calculated to meet the demands.

To adapt to varying operating conditions, another model was developed with flow rate and pressure as inputs, and rotational speed and efficiency as outputs. The was similarly trained using the same loss function as the 40 sets of pump characteristic data from multi-stage submersible pumps, with 80% of the data used for training and 20% for testing. Both deep learning and transfer learning approaches were utilized. The training results, illustrated in Figure 6b, closely mirror those in Figure 6a, demonstrating that the relationships among flow rate, pressure, speed, and efficiency can be effectively defined. This allows the model to flexibly accommodate the requirements of various operating conditions. The model was validated with inputs of speed and flow rate and outputs of head and efficiency, to assess its predictive capability. Similarly to the evaluation of the loss function, MSE is also used for prediction error analysis. For the intuitive display of engineering applications, relative errors were also calculated. The relative error was defined as the maximum relative difference between the predicted and the experimental values for five points near the rated flow point. The predicted results are shown in

Table 4. Comparison of deep learning and transfer learning results of different data volumes of multi-stage submersible pumps.

Sample Size	Data Point Distribution	Deep Learning		Transfer Learning
		MSE (m2)	Maximum Error (%)	MSE (m2)	Maximum Error (%)
10	Centralized distribution	364.2	48.1	4.3	5.2
	Uniform distribution	30.3	11.7	6.3	4.7
20	Uniform distribution	17.9	6.9	6.0	5.8
40	Uniform distribution	12.9	4.4	2.4	4.4
40 (efficiency)	Uniform distribution	12.7	8.1	1.8	3.2

. Using the transfer learning model, predictions were made with a dataset of 40 samples. The maximum relative error in head prediction is 4.4%, and the efficiency prediction error is 3.2%. The MSE values are 2.4 m² and 1.8 m², respectively. With the pump’s rated head being 52 m, the overall prediction error remains relatively small. This indicates that the model, which uses speed and flow rate as inputs and head and efficiency as outputs, achieves sufficient prediction accuracy for engineering applications.

To further investigate the effect of sample size, the study focuses on the model with speed and flow rate as inputs and head and efficiency as outputs. Although speed, when used as an output, differs from inputs like flow rate and head, the functional relationships are mathematically equivalent. For instance, with a known flow rate and speed, head can be determined, and vice versa. The mapping relationships in these two cases are equivalent at a mathematical level. The effectiveness of the proposed transfer learning was validated by varying the sample size and distribution in the target dataset.

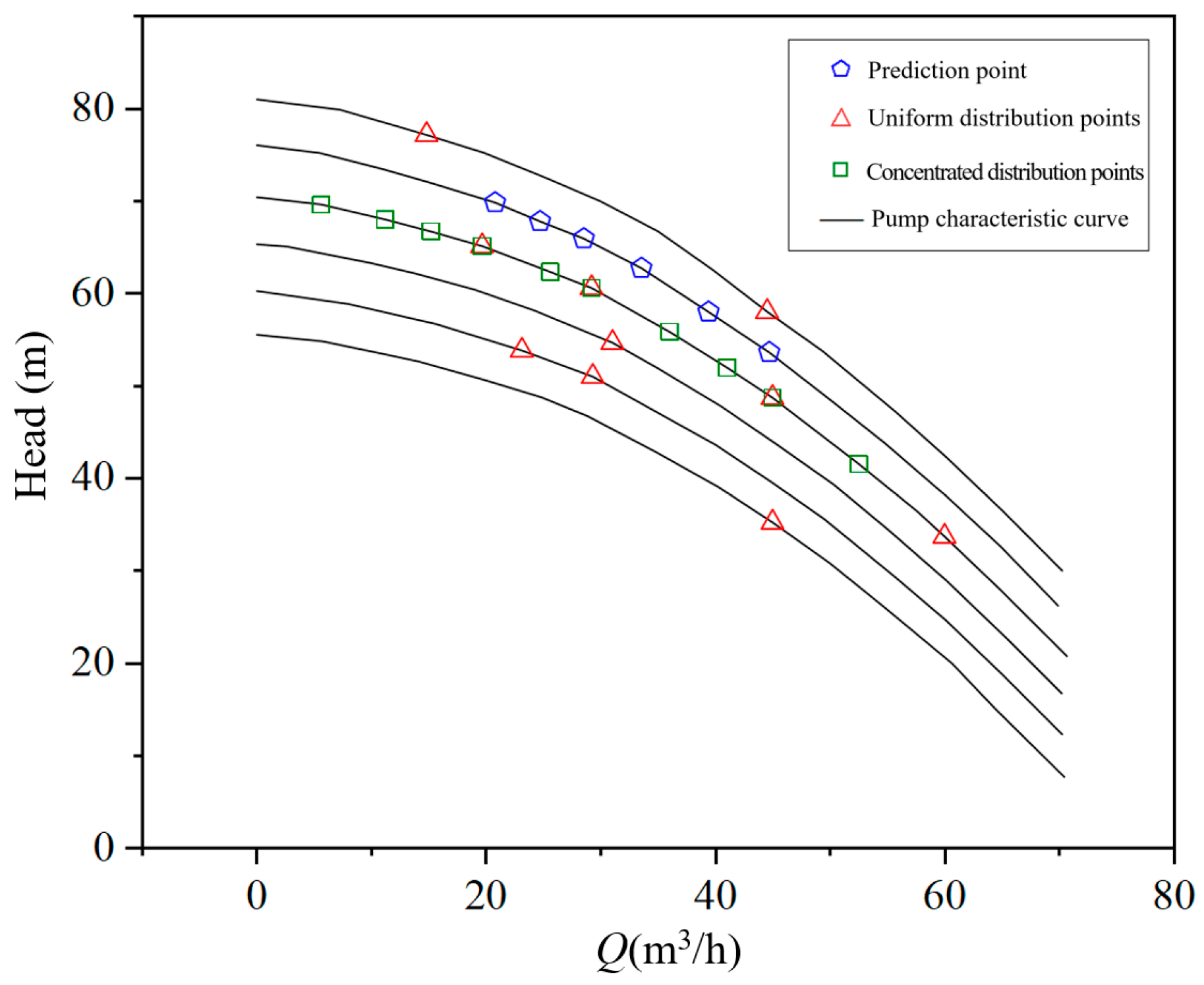
As shown in Figure 7, six background curves represent experimentally measured flow-head curves at different speeds. Five prediction points were chosen from the target dataset’s flow rate values corresponding to experimental measurements. Prediction results are shown in Table 4. The prediction error refers to the maximum relative error between the head prediction results of the two models and the experimental head values, calculated separately for five points with the maximum error selected. Typically, during pump testing, only the characteristic curve at the rated speed is measured. To assess the prediction accuracy of deep learning models with limited data, neural network training was performed using only ten data points at a single speed. This approach reflects the real-world conditions of engineering tests. The concentrated distribution points in Figure 7 represent the performance points on the characteristic curve at the rated speed. To compare the performance of transfer learning, a separate set of randomly distributed data points across multiple speeds was selected, as shown by the evenly distributed points in Figure 7. When using only ten data points for prediction, the results presented in Table 4. The model prediction results show a maximum relative error of 48.1%, whereas, under the same data conditions, transfer learning reduces the error to only 5.2%. The MSE values are 364 m² and 4.3 m², respectively. Relative to the pump’s rated head of 52 m, the deep learning prediction results are not usable. When training directly using multiple speed data points (ten evenly distributed data points), the error for deep learning remains at 11.7%, whereas the error for transfer learning is only 4.7%. This demonstrates that transfer learning can achieve relatively accurate predictive models even with very limited pump characteristic data.

During training, datasets of 10, 20, and 40, data points were applied to evaluate deep learning and transfer learning performance. Predictions were made for head under various operating conditions at 2736 rpm (0.96 times the rated speed), a common engineering regulation range (within 5%). Table 4 shows the maximum prediction relative error for head. The data indicate that even with very limited input data, transfer learning yields a relatively low prediction error. For instance, when only 10 data points are used, the prediction error for deep learning reaches as high as 48.1%, making them unsuitable for accurate predictions. In contrast, transfer learning achieves an error of just 5.2%, which is acceptable for certain less demanding engineering applications. As the number of data points increases, both deep learning and transfer learning methods show a significant reduction in prediction errors. When 40 sets of data were used, the maximum prediction error of the model built directly using deep learning is the same as that of the transfer learning model. However, the MSE of deep learning is relatively larger, indicating that the overall prediction error of the deep learning model is higher.

The cross-domain migration test was carried out on a ten-stage high-pressure injection pump, with a flow rate of 120 m³/h and a head of 1450 m. Despite the significant structural differences between this target pump and the single-stage centrifugal pump as the source domain; the results demonstrate that the transfer learning-based prediction model exhibits strong adaptability. This highlights the model’s ability to effectively manage substantial variations in pump design across domains effectively. As shown in

Table 5. Comparison of deep learning and transfer learning results of different data volumes of high-pressure injection pumps.

Sample Size	Maximum Relative Error of Deep Learning (%)	Maximum Relative Error of Transfer Learning (%)
10	40.1	7.3
20	19.0	6.3
40	3.1	5.4

, transfer learning was implemented using data from a single-stage centrifugal pump as the source domain. The simulation data from the ten-stage high-pressure water injection pump served as the target domain. With only 10 data samples, the transfer learning model achieves a head prediction relative error of 7.3%, significantly lower than the 40.1% error observed in the deep learning model. When 40 sets of data were used, deep learning achieved slightly better accuracy than transfer learning model. This discrepancy is because transfer learning retains some characteristics from the source domain, which may limit performance in the target domain.

However, the overall relative prediction error is slightly higher compared to the results for multi-stage submersible pumps. This suggests that differences in data characteristics between the source and target domains can affect model performance. This finding also suggests that both experimental and simulation data can be effectively used as target domain datasets, given their similar characteristics. In situations where experimental data are limited, a combination of both experimental and simulation data for pump characteristic curves can be employed to develop the model. A small amount of experimental data can serve to validate the simulation results, ensuring that the simulation data accurately reflects the actual operating conditions of the pump. Similarly, simulation data can also be utilized in the source domain, as it provides a useful dataset for pre- learning key data features that support model development for the target domain. Since simulation data inherently includes characteristic parameters of the pumps, it is suitable as training data for the source domain. Due to the fact that the ten-stage pump model in this study is optimized for hydraulic performance, its characteristic curve does not show a hump. This feature may influence the algorithm’s behavior, and further research is needed to study the impact of hump-shaped characteristic curves on model performance.

Transfer learning effectively expands the applicability of models and offers significant advantages in addressing prediction tasks beyond the range of the training data. In modeling the characteristic curves of submersible pumps, data within the speed range of 2622–3078 rpm was used for training. To evaluate the model’s performance outside the input range, the characteristic curve at 2508 rpm was predicted. As shown in

Table 6. Prediction errors outside the dataset.

Objectives and Tasks	Type	Prediction Relative Error Within the Dataset (%)	Prediction Relative Error Out of Dataset (%)
Multi-stage Submersible pump	Deep learning	1.3	28.8
	Transfer learning	1.5	8.7
High pressure water-Injection pump	Deep learning	3.1	13.6
	Transfer learning	5.4	9.6

, the deep learning model trained directly produced a prediction relative error of 28.8%. In contrast, the model assisted by transfer learning achieved a significantly lower relative error of just 8.7%. This indicates that the ability of transfer learning to considerably reduce prediction errors for data outside the training set. The improvement is mainly due to the larger source dataset used to build the transfer learning model. This advantage becomes particularly evident when the target domain data are limited. Therefore, in this study, the source dataset for transfer learning included pump characteristic curves within a broader speed range of 2400–3500 rpm. By covering a wider operating range than that target domain, the model gains improved generalization capabilities. Transfer learning enhances the model’s generalization capability, mitigating underfitting issues caused by insufficient data outside the training range.

5. Conclusions

This paper proposes a pump parameter identification method based on deep learning and transfer learning, suitable for large high-pressure pumps and other types of pumps that are difficult to simulate or test experimentally. The method reduces the cost of experiments and numerical simulations, requiring only a small amount of experimental data to train a pump performance identification model that meets engineering requirements. For parameters such as flow rate, pressure, rotational speed, and efficiency parameters of pump characteristics, the input–output relationships can be adjusted to accommodate different operating conditions. Based on algorithm analysis, the following conclusions are drawn:

Compared with pure deep learning, models incorporating transfer learning significantly enhance training speed and reduce prediction errors for pump head and efficiency during training. Even with limited pump characteristic curve data, this method achieves high prediction accuracy. Model error analysis shows that when the performance model of a high-pressure water injection pump is used as the target domain, reducing the data volume from 40 groups to 10 groups causes the relative error of traditional deep learning models to increase sharply (from 8.1% to 48.1%). In contrast, the error of transfer learning models remains stable within 10%, demonstrating the method’s engineering applicability under data-scarce scenarios. When constructing the source domain dataset, it is important to appropriately expand the data coverage, especially the range of rotational speeds. This significantly reduces prediction errors for data outside the training range and effectively prevents underfitting caused by limited target data.

This paper successfully transfers the single-stage centrifugal pump model to both multi-stage submersible pumps and high-pressure injection pumps. These results verify the proposed method’s cross-domain transfer capability across different types of pump equipment. The prediction accuracy surpasses that of models built using traditional deep learning directly based on pump characteristics. In scenarios where experimental data are insufficient, sufficient simulation data can be used to build the pump characteristic curve model. A small amount of experimental data can validate the simulation results, ensuring alignment with the pump’s actual operating parameters.

This study establishes a reusable pump modeling framework, providing a new approach for the digital design of large pump equipment. However, further research is needed to assess the adaptability of this method to axial piston pumps and other types of positive displacement pumps. Future work will focus on the transferability of the method across various pump types. Additionally, integrating more pump and motor parameters could enable comprehensive modeling of the entire pump–motor system and support the development of an online transfer learning mechanism within a digital twin framework.