Scheduling Strategy of Virtual Power Plant Alliance Based on Dynamic Electricity and Carbon Pricing Using Master–Slave Game
Abstract
1. Introduction
2. Energy Transaction Structure of VPPA
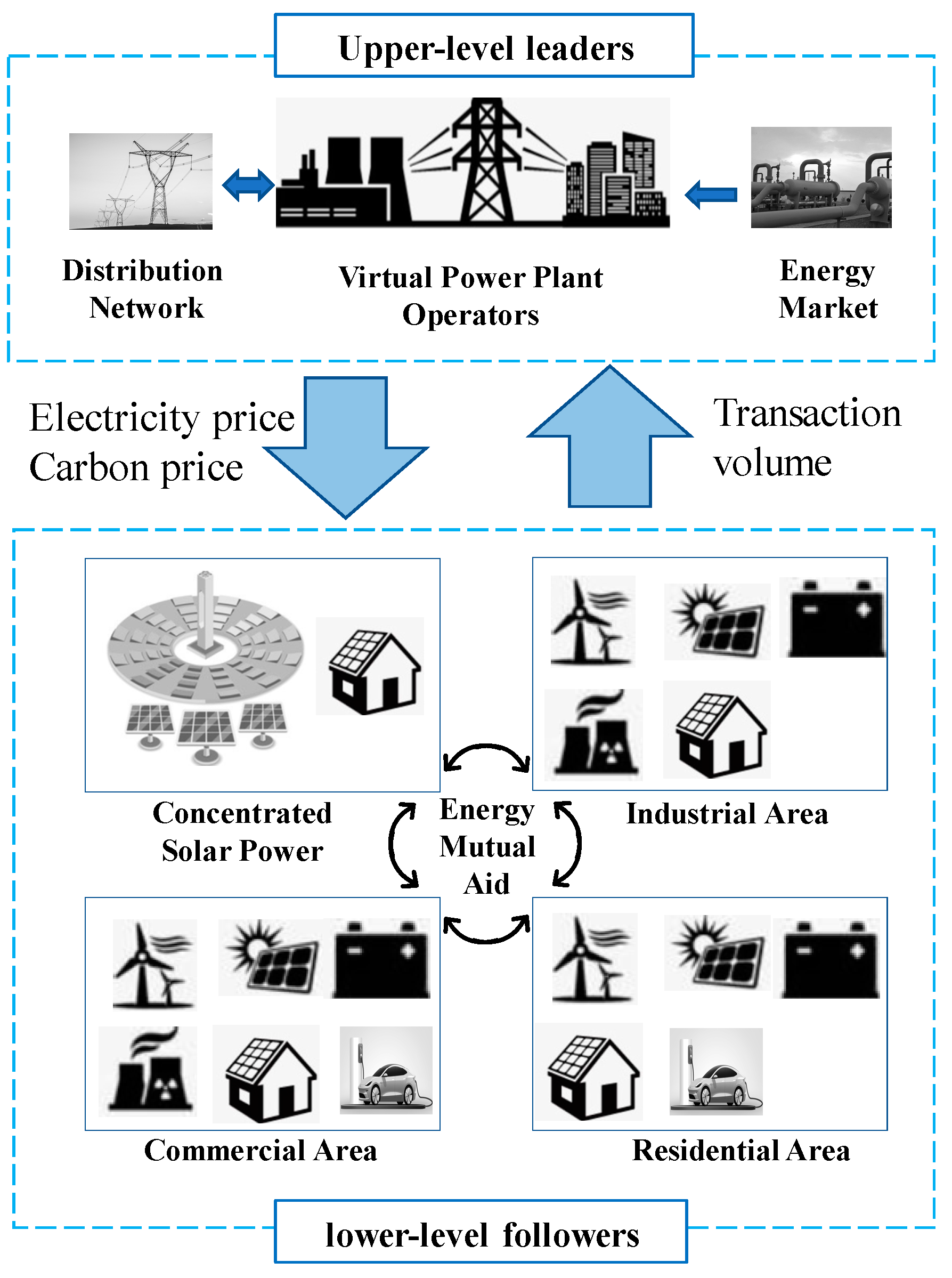
2.1. Operation Structure of VPPA
2.2. Types of Graphics
2.2.1. Mathematical Model of CSP Station
2.2.2. The Mathematical Model of the Energy Storage System
2.2.3. Mathematical Model of Electric Vehicle
2.2.4. Mathematical Model of Other Equipment
3. Master–Slave Game Model
3.1. Interaction Mechanism of Master–Slave Game
3.2. Scheduling Model of Alliance Operator
3.2.1. Objective Function
3.2.2. Power Transmission Constraint
3.3. C. Scheduling Model of VPP User Entity
3.3.1. Objective Function
- Operation and maintenance cost:
- 2.
- Gas purchase cost:
- 3.
- Electricity energy interaction cost:
- 4.
- Environmental cost:
- 5.
- Electric and thermal demand response cost:
3.3.2. Power Transmission Constraint
- Operation and maintenance cost:
- 2.
- Energy balance constraint:
- 3.
- Electric and thermal integrated demand response constraint:
4. VPPA Scheduling Model Based on IGDT
4.1. Opportunity Model of VPPA
4.2. Robustness Model of VPPA
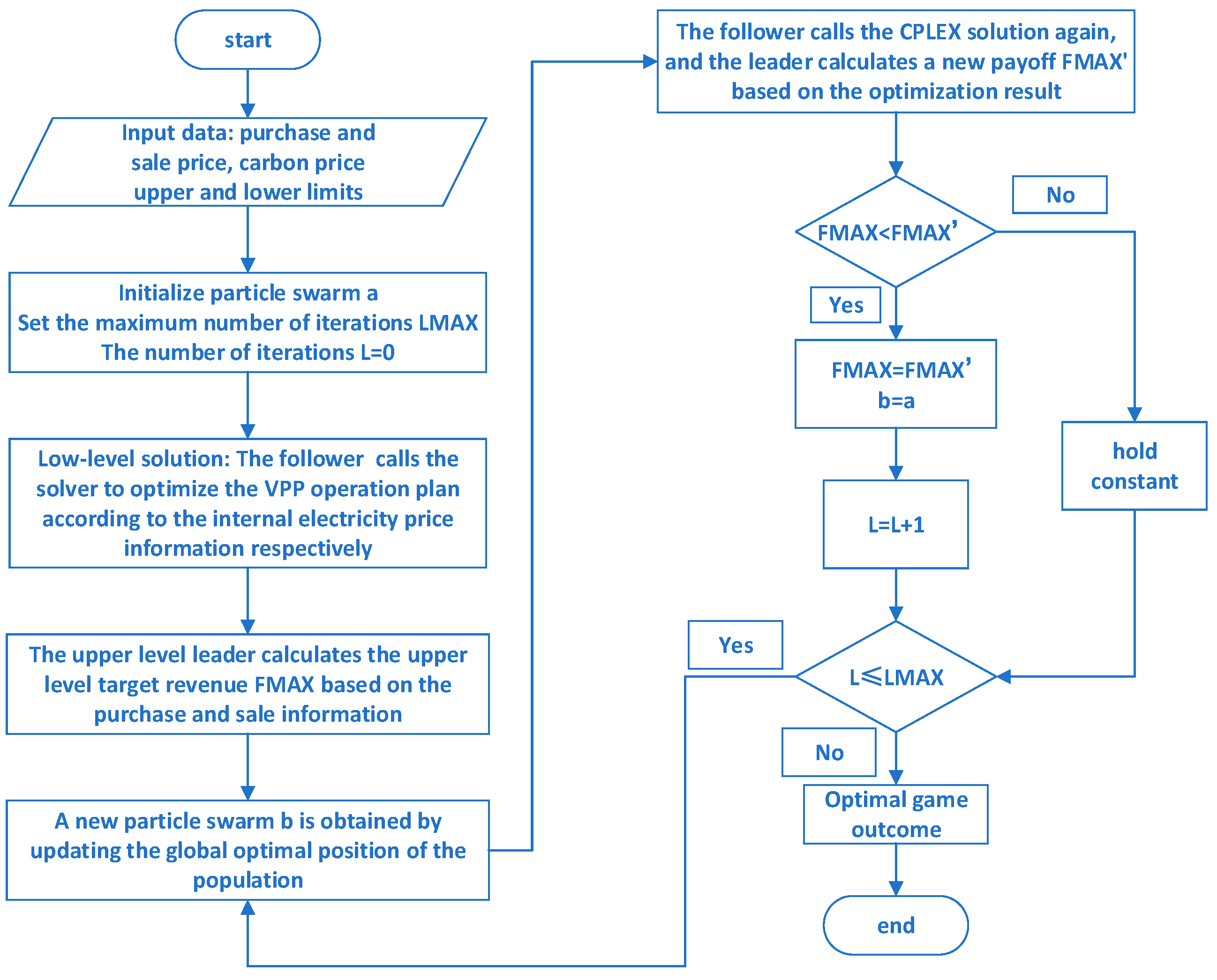
5. Solution Process
6. Comparative Analysis of Numerical Examples
6.1. An Analysis of the Conclusions of the Master–Slave Game
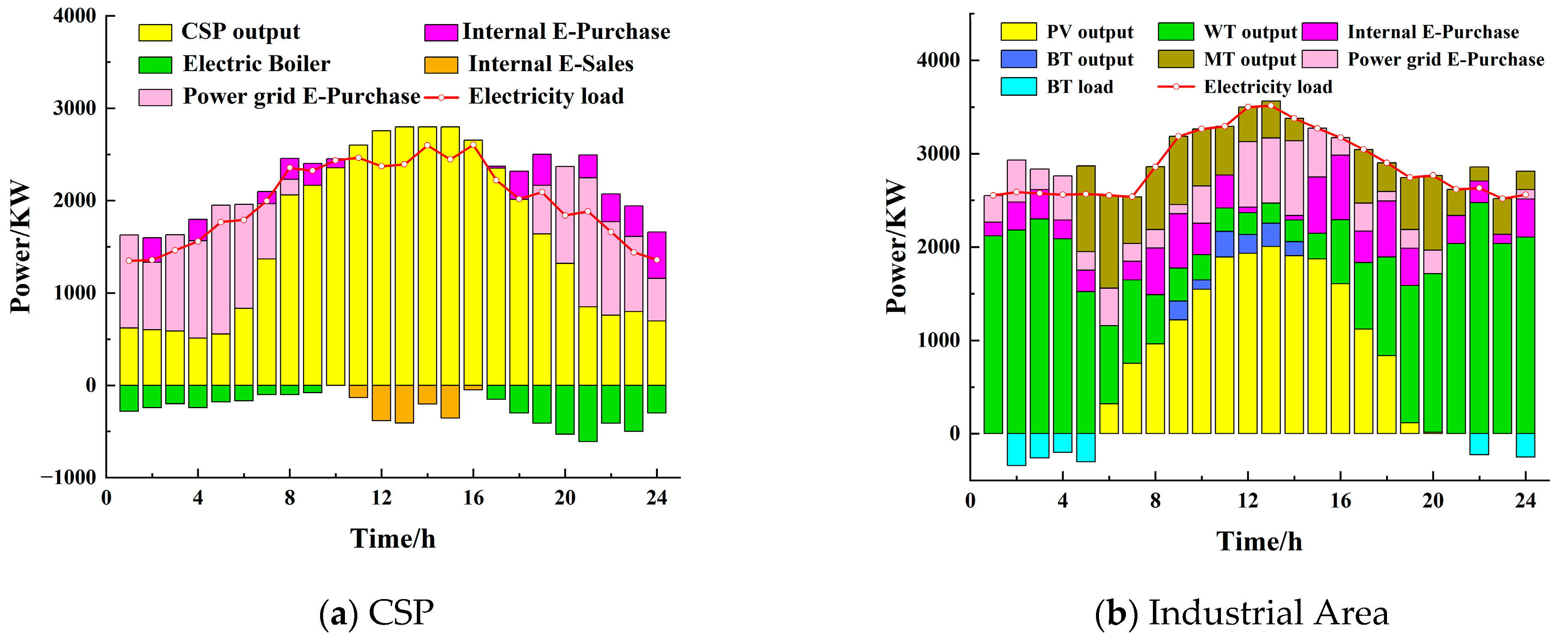
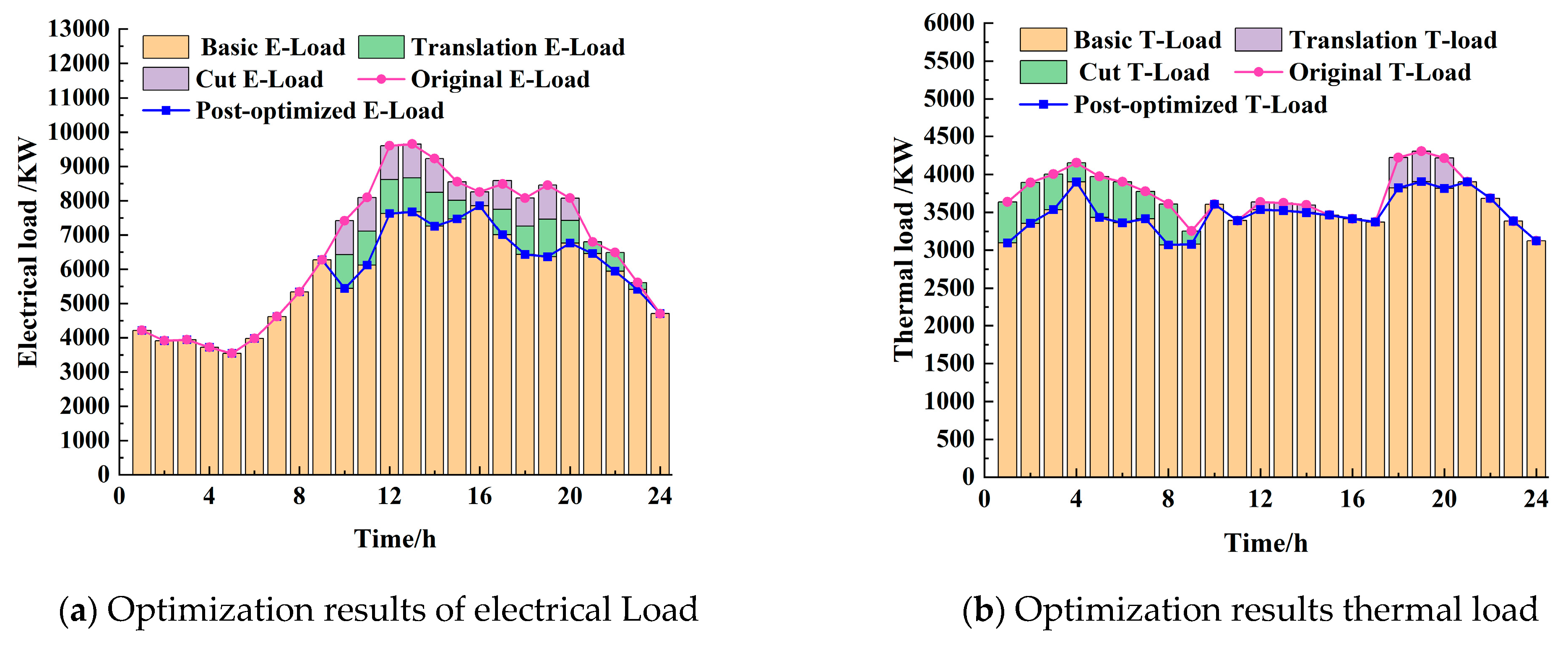
6.2. Analysis of Optimization Scheduling Results
6.3. Analysis of Source–Load Interaction
6.4. Comparative Analysis of Different Schemes
6.5. Analysis of VPPA Scheduling Results Based on IGDT
7. Conclusions
- An optimal scheduling strategy for the VPPA based on the Master–Slave game considering electricity energy interaction and source–load interaction is proposed. It can increase the energy consumption cost of users, increase the amount of electricity energy interaction among VPPs by 67.04%, promote the absorption of distributed energy, and have a significant peak shaving and valley filling effect.
- The alliance operator guides the transactions of a VPP user entity by formulating dynamic electricity and carbon prices, which not only realizes energy interaction among VPPs and meets the load demand, but also increases the alliance operator’s revenue by 35.34% and reduces carbon emissions by 16.17%, with strong economic and environmental protection performance.
- The IGDT of the RM and OM is used to deal with the source–load uncertainty. The optimization scheduling results show that the RM strategy has higher carbon emissions and lower benefits but has a strong tolerance for uncertainty; the OM strategy makes full use of uncertainty to obtain benefits. Decision-makers can choose between the two strategies according to their own expectations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VPP | Virtual power plant |
| VPPA | Virtual power plant alliance |
| IGDT | Information gap decision theory |
| CSP | Concentrated solar power |
| V2G | Vehicle-to-grid |
| EES | Electrical energy storage |
| TES | Thermal energy storage |
| EV | Electric vehicle |
| WT | Wind turbine |
| PV | Photovoltaic |
| GT | Gas turbines |
| GB | Gas boilers |
| OM | Opportunity model |
| RM | Robustness model |
Appendix A
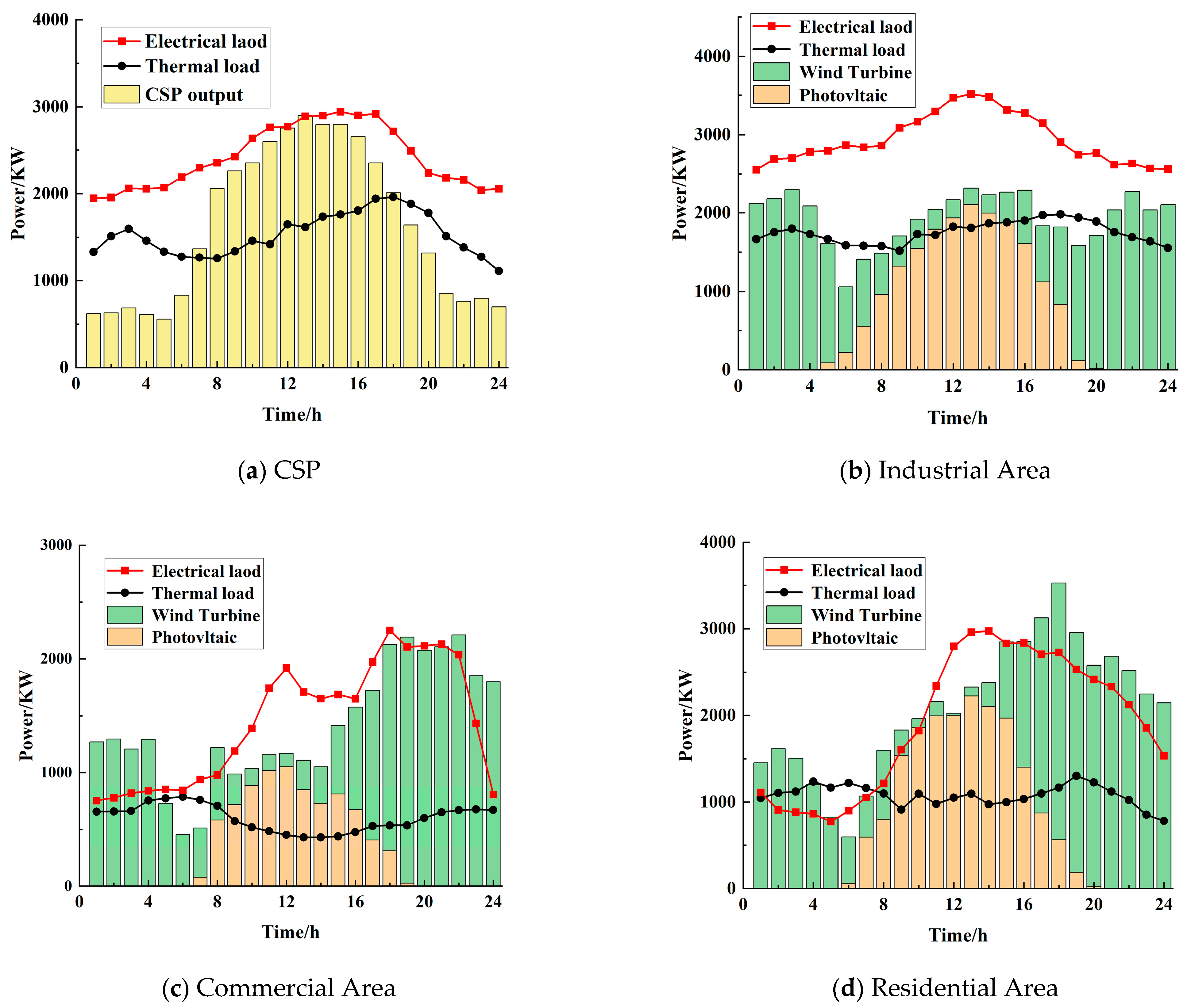
Appendix B
| Equipment | Parameter | Industrial Area | Commercial Area | Residential Area |
|---|---|---|---|---|
| PV | 0.02 | 0.02 | 0.02 | |
| WT | 0.02 | 0.02 | 0.02 | |
| EES (KW) | 1200 | 600 | 800 | |
| 400 | 200 | 200 | ||
| 200 | 200 | 300 | ||
| 350 | 200 | 200 | ||
| 350 | 200 | 200 | ||
| 0.95 | 0.95 | 0.95 | ||
| 0.95 | 0.95 | 0.95 | ||
| 0.001 | 0.001 | 0.001 | ||
| 0.02 | 0.02 | 0.02 | ||
| TES (KW) | 285 | 475 | 475 | |
| 120 | 200 | 200 | ||
| 120 | 200 | 200 | ||
| 150 | 250 | 250 | ||
| 0.95 | 0.95 | 0.95 | ||
| 0.95 | 0.95 | 0.95 | ||
| 0.001 | 0.001 | 0.001 | ||
| 285 | 475 | 475 | ||
| 0.02 | 0.02 | 0.02 | ||
| CSP | 0.4 | |||
| 0.4 | ||||
| 0.98 | ||||
| 0.98 | ||||
| 0.031 | ||||
References
- Cao, W.; Wang, S.; Xu, M. Optimal scheduling of virtual power plant based on Latin hypercube sampling and improved Clara clustering algorithm. Processes 2022, 10, 2414. [Google Scholar] [CrossRef]
- Peng, D.; Shui, J.; Wang, D.; Zhao, H. Review of virtual power plant under the background of “dual carbon”. Power Gener. Technol. 2023, 44, 602. [Google Scholar]
- Ruan, G.; Qiu, D.; Sivaranjani, S.; Awad, A.S.; Strbac, G. Data-driven energy management of virtual power plants: A review. Adv. Appl. Energy 2024, 14, 100170. [Google Scholar] [CrossRef]
- Sun, S.; Xing, J.; Cheng, Y.; Yu, P.; Wang, Y.; Yang, S.; Ai, Q. Optimal Scheduling of Integrated Energy System Based on Carbon Capture–Power to Gas Combined Low-Carbon Operation. Processes 2025, 13, 540. [Google Scholar] [CrossRef]
- Cao, J.; Yang, D.; Dehghanian, P. Cooperative operation for multiple virtual power plants considering energy-carbon trading: A Nash bargaining model. Energy 2024, 307, 132813. [Google Scholar] [CrossRef]
- Chen, Y.; He, S.; Wang, W.; Yuan, Z.; Cheng, J.; Cheng, Z.; Fan, X. Optimization strategy for shared energy storage operators-multiple microgrids with hybrid game-theoretic energy trading. Processes 2024, 12, 218. [Google Scholar] [CrossRef]
- Cao, J.; Zheng, Y.; Han, X.; Yang, D.; Yu, J.; Tomin, N.; Dehghanian, P. Two-stage optimization of a virtual power plant incorporating with demand response and energy complementation. Energy Rep. 2022, 8, 7374–7385. [Google Scholar] [CrossRef]
- Qi, L.; Gao, Y.; Ai, Q. Virtual Power Plant and Multi-prosumer Hybrid Game Strategy Based on Energy Sharing. Electr. Power Constr. 2025, 46, 1–13. [Google Scholar]
- Duan, M.; Cheng, H.; Fang, K.; Huang, Y.; Lu, S.; Chen, L. Research on Stackelberg game strategy for virtual power plant considering time-of-use electricity and carbon coupled price. Electr. Meas. Instrum. 2024, 61, 1–11. [Google Scholar]
- Yue, M.; Hong, L. Economic Optimization Scheduling Of Multi-Microgrid System Based On Master-Slave Game Under Multi-Agent Technology. Acta Energiae Solaris Sin. 2024, 45, 574–582. [Google Scholar]
- Wang, L.; Xu, Z.; Yang, C.; Yuan, G.; Tang, L.; Wang, X. Modeling and Solving Method of Electricity-Carbon Joint Optimization for Multi-Virtual Power Plants. Autom. Electr. Power Syst. 2024, 48, 29–40. [Google Scholar]
- Li, P.; Wu, D.; Li, Y.; Yin, Y.; Fang, Q.; Chen, B. Multi-objective Union Optimal Configuration Strategy for Multi-microgrid Integrated Energy System Considering Bargaining Games. Power Syst. Technol. 2020, 44, 3680–3690. [Google Scholar]
- Zhou, J.; Liang, C.; Shi, L.; Li, Y.; Yi, W. Optimal Scheduling of Integrated Energy System Considering The Ladder-type Carbon Trading Mechanism. Electr. Power 2025, 58, 77–87. [Google Scholar]
- Gao, Y.; Xu, Y.; Zhang, T.; Song, W.; Wang, P.; Xi, L.; Mi, L. Multi-microgrid system optimization scheduling including Electric vehicle coordinated charging and reward and punishment ladder carbon trading. Electr. Power Constr. 2025, 46, 174–188. [Google Scholar]
- Zhang, N.; Jia, J.; Li, B.; Shi, Z. Study on optimization of operation strategy of electric-gas coupling virtual power plant considering carbon trading. Electr. Meas. Instrum. 2024, 61, 20–28. [Google Scholar]
- Li, Y.; Yang, Y.; Zhang, F.; Li, Y. A Stackelberg game-based approach to load aggregator bidding strategies in electricity spot markets. J. Energy Storage 2024, 95, 112509. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, Z.; Liang, J.; Li, Z.; Dinavahi, V.; Liang, J. Low-carbon optimal scheduling of park-integrated energy system based on bidirectional Stackelberg-Nash game theory. Energy 2024, 305, 132342. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, G.; Yue, S.; Yao, X.; Song, Y.; Liu, J. Study on Master Slave Interaction Model Based on Stackelberg Game in Distributed Environment. Symmetry 2020, 12, 232. [Google Scholar] [CrossRef]
- Liu, X. Research on optimal dispatch method of virtual power plant considering various energy complementary and energy low carbonization. Int. J. Electr. Power Energy Syst. 2022, 136, 107670. [Google Scholar] [CrossRef]
- Yuan, G.; Zhong, F.; Zhang, R.; Zhou, T. Combined heat and power scheduling optimization for virtual power plants considering carbon capture and demand response. Power Syst. Technol. 2023, 47, 4458–4467. [Google Scholar]
- Li, X.; Ai, X.; Hu, J.; Zhou, B.; Lin, Z. Three-stage combined peak regulation strategy for nuclear-thermal-virtual power plant considering carbon trading mechanism. Power Syst. Technol. 2019, 43, 2460–2470. [Google Scholar]
- Zhang, L.; Dai, G.; Nie, Q.; Tong, Z. Economic dispatch model of virtual power plant considering electricity consumption under a carbon trading mechanism. Power Syst. Prot. Control 2020, 48, 154–163. [Google Scholar]
- Zhu, S.; Ji, J.; Huang, Q.; Li, S.; Ren, J.; He, D.; Yang, Y. Optimal scheduling and trading in joint electricity and carbon markets. Energy Strategy Rev. 2024, 54, 101426. [Google Scholar] [CrossRef]
- Ge, S.; Cheng, X.; Liu, H. Market design of P2P electricity carbon coupling transaction among multi-microgrids in the zone. High Volt. Eng. 2023, 49, 1341–1349. [Google Scholar]
- Qiu, D.; Xue, J.; Zhang, T.; Wang, J.; Sun, M. Federated reinforcement learning for smart building joint peer-to-peer energy and carbon allowance trading. Appl. Energy 2023, 333, 120526. [Google Scholar] [CrossRef]
- Shui, J.; Peng, D.; Zeng, H.; Song, Y.; Yu, Z.; Yuan, X.; Shen, C. Optimal scheduling of multiple entities in virtual power plant based on the Master-Slave game. Appl. Energy 2024, 376, 124286. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, Q.; Qin, W.; Qu, G.; Kong, Y.; Zhang, X. Source-Grid-Load-Storage Synergistic Planning Considering Electricity-Carbon Coupling and Flexible Supply-Demand Balance. Electr. Power Constr. 2025, 46, 116–127. [Google Scholar]
- Ding, Y.; Tan, Q.; Wei, Y.; Shan, Z. Collaborative Optimization of Wind—Photovoltaic—Thermal Power Operation Based on Low—Carbon Sustainable under the Coupling of Electricity—Carbon Market. Syst. Eng.-Theory Pract. 2025, 1–14. [Google Scholar]
- Dong, L.; Li, Y.; Chen, S.; Qian, J.; Pu, T. Multi-Microgrid Cooperative Game Optimization Scheduling Considering Multiple Uncertainties and Coupled Electri-ci-ty-Carbon Transactions. Trans. China Electrotech. Soc. 2024, 39, 2635–2651. [Google Scholar]
- Li, J.; Cheng, J.; Zhou, B.; Liu, J.; Mao, T.; Zhao, W.; Wang, T.; Huang, G.; Xu, Y. Stochastic Optimal of Integrated Energy System in Low-Carbon Parks Considering Carbon Capture Storage and Power to Hydrogen. Electr. Power 2024, 57, 149–156. [Google Scholar]
- Wei, B.; Qiao, S.; Meng, R.; Li, J. Two-stage Robust Optimization Scheduling of Microgrids Based on Data-driven Uncertain Sets. High Volt. Eng. 2025, 51, 852–863. [Google Scholar]
- Li, J.; Liu, Y.; Wang, X. Green Certificate Real-time Pricing Based on Information Gap Decision Theory. Power Syst. Prot. Control 2024, 52, 32–43. [Google Scholar]



| Iteration Number | Operating Cost (CNY) | Carbon Emissions (kg) | Electric Energy Interaction Volume (KW) | Revenue of VPPA (CNY) |
|---|---|---|---|---|
| 10 | 18,280 | 38,635 | 5684 | 1258 |
| 20 | 17,672 | 31,213 | 5306 | 3005 |
| 30 | 14,672 | 26,625 | 7185 | 2521 |
| 40 | 15,435 | 28,726 | 8963 | 2849 |
| 50 | 15,435 | 28,726 | 8963 | 2849 |
| Scheme | Operating Cost (Yuan) | Carbon Emissions (kg) | Electric Energy Interaction Volume (KW) | Revenue of VPPA (Yuan) |
|---|---|---|---|---|
| Scheme 1 | 15,435 | 28,726 | 8693 | 2849 |
| Scheme 2 | 17,962 | 34,269 | 5423 | 2105 |
| Scheme 3 | 29,524 | 38,120 | / | 1608 |
| Scheme 4 | 17,264 | 34,328 | 5204 | 2197 |
| 0 | 0.02 | 0.04 | 0.06 | 0.08 | 0.10 | |
|---|---|---|---|---|---|---|
| 0 | 0.035 | 0.068 | 0.098 | 0.131 | 0.172 | |
| Profit (CNY) | 2843 | 2784 | 2731 | 2680 | 2629 | 2579 |
| 0 | 0.02 | 0.04 | 0.06 | 0.08 | 0.10 | |
|---|---|---|---|---|---|---|
| 0 | 0.030 | 0.062 | 0.091 | 0.134 | 0.167 | |
| Profit (CNY) | 2843 | 2892 | 2961 | 3002 | 3060 | 3102 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Ma, S.; Jin, F.; Li, J.; Zhao, R.; Liang, Z.; Ren, X. Scheduling Strategy of Virtual Power Plant Alliance Based on Dynamic Electricity and Carbon Pricing Using Master–Slave Game. Processes 2025, 13, 1658. https://doi.org/10.3390/pr13061658
Zhang Q, Ma S, Jin F, Li J, Zhao R, Liang Z, Ren X. Scheduling Strategy of Virtual Power Plant Alliance Based on Dynamic Electricity and Carbon Pricing Using Master–Slave Game. Processes. 2025; 13(6):1658. https://doi.org/10.3390/pr13061658
Chicago/Turabian StyleZhang, Qiang, Shangang Ma, Fubao Jin, Jiawei Li, Ruiting Zhao, Zengyao Liang, and Xuwei Ren. 2025. "Scheduling Strategy of Virtual Power Plant Alliance Based on Dynamic Electricity and Carbon Pricing Using Master–Slave Game" Processes 13, no. 6: 1658. https://doi.org/10.3390/pr13061658
APA StyleZhang, Q., Ma, S., Jin, F., Li, J., Zhao, R., Liang, Z., & Ren, X. (2025). Scheduling Strategy of Virtual Power Plant Alliance Based on Dynamic Electricity and Carbon Pricing Using Master–Slave Game. Processes, 13(6), 1658. https://doi.org/10.3390/pr13061658





