1. Introduction
Amid the global transition toward low-carbon energy restructuring, unconventional natural gas resources such as shale gas and tight gas, with their clean and low-carbon characteristics, have emerged as strategic priorities for ensuring energy security and achieving carbon neutrality targets [
1]. China possesses vast reserves of unconventional gas resources with extensive geographical distribution, demonstrating enormous exploration and development potential [
2]. However, the inherent low porosity and permeability characteristics of unconventional reservoirs render conventional extraction techniques ineffective for obtaining industrial-scale production. Hydraulic fracturing technology has evolved into a pivotal technique for efficient unconventional reservoir development [
3]. This method utilizes pressurized fluids to induce rock deformation and fracture initiation, creating artificial fracture networks within reservoirs. Such artificial fractures effectively reduce the seepage distance from matrix fluids to wellbores while enhancing overall reservoir permeability. In homogeneous reservoirs under ideal conditions, hydraulic fractures predominantly propagate perpendicular to the minimum horizontal principal stress direction, forming simple bi-wing fracture geometries [
4,
5]. Nevertheless, the presence of geological discontinuities such as natural fractures and bedding planes significantly alters hydraulic fracture propagation paths, substantially increasing fracture network complexity [
6]. The intricate interaction behaviors between hydraulic and natural fractures, including crossing, slippage, opening, and capture, exhibit strong dependence on multiple factors: in-situ stress regimes, fracture morphology, mechanical properties of weak planes, and fluid viscosity [
7]. These complexities necessitate the development of comprehensive discrimination models to elucidate fracture interaction mechanisms.
Significant advancements have been achieved in both experimental and numerical investigations of hydraulic-natural fracture interaction mechanisms. Experimental studies employing true triaxial hydraulic fracturing systems have systematically characterized interaction behaviors under various geological and operational parameters [
8]. Key controlling factors identified include natural fracture approach angle, cementation strength, and stress differential [
9,
10]. Blanton’s seminal work demonstrated that hydraulic fractures preferentially cross natural fractures under high-stress differentials and large approach angles, whereas low-stress differentials and small approach angles promote interfacial slippage [
11]. Operational parameters such as injection rate, duration, and fracturing fluid viscosity further modulate interaction modes [
12,
13]. Elevated injection rates and high-viscosity fluids enhance fracture-crossing tendencies, while lower rates and reduced viscosities favor natural fracture activation and complex network development [
14,
15]. Numerical simulations employing fluid–solid coupling models have replicated interaction processes using diverse computational approaches: finite element method (FEM) [
16], extended finite element method (XFEM) [
17,
18], discrete element method (DEM) [
19], and boundary element method (BEM) [
20]. These models particularly emphasize how cementation strength, approach angle, stress differential, and fluid viscosity govern fracture propagation patterns [
21]. Simulation results confirm that strong cementation, high-stress differentials, and steep approach angles collectively drive direct fracture crossing. Conversely, weak cementation, low-stress differentials, and shallow angles induce fracture capture and bifurcation, generating intricate network geometries [
16,
22].
Building upon clarified hydraulic-natural fracture interaction mechanisms, researchers have established multi-dimensional theoretical criteria to quantitatively predict fracture propagation paths. Blanton pioneered a criterion incorporating stress intensity factors and approach angles, proposing hydraulic fracture crossing occurs when the fluid pressure at the fracture tip surpasses the combined natural fracture normal stress and rock tensile strength [
23]. Warpinski and Teufel developed criteria for determining natural fracture slippage versus opening, simultaneously considering the effects of natural fracture permeability, fluid leak-off on fracture-tip stress fields, and hydraulically induced stress field interactions [
24]. Renshaw and Pollard formulated a crossing criterion for orthogonal hydraulic fractures intersecting frictionless interfaces based on linear elastic fracture mechanics [
25], subsequently extended by Gu and Weng to non-orthogonal scenarios [
26,
27]. Sarmadivaleh further refined these models by incorporating cohesive strength and adhesive forces within natural fractures [
28]. Recent advancements employ energy balance principles to establish discrimination criteria for post-interaction fracture behaviors. Griffith’s foundational concept of surface energy in solid materials established that system-released energy partially converts to surface energy during fracturing [
29]. Irwin subsequently defined the energy release rate as the energy liberated per unit area during fracture propagation [
30]. Yao and Wang developed an interaction criterion based on Griffith’s theory, quantitatively characterizing critical conditions for hydraulic fracture crossing, natural fracture opening, and slippage under far-field stress state [
31].
Based on the Griffith energy balance principle and considering the influence of fracture fluid in hydraulic fracture on the stress field, this study establishes an interaction discrimination model between hydraulic fractures and natural fractures. By analyzing energy transformation during fracture interaction, the critical pressure conditions for hydraulic fracture crossing, natural fracture opening, and slippage are derived. The propagation behaviors under different geological parameters are systematically investigated, providing theoretical guidance for optimizing fracturing parameters in naturally fractured reservoirs.
2. Model Establishment
According to the Griffith linear fracture hypothesis, a three-dimensional elliptical linear fracture with a thickness of
δ and a half-length of
l continuously propagates within an infinite plane, as illustrated in
Figure 1.
When the fracture propagates a distance of Δ
l, the fracture width along the length direction can be expressed as follows [
32]:
The incremental fracture volume is given by the following:
In the formula, Pf is the fluid pressure inside the fracture, MPa; l is the fracture length, m; E′ is the plane-strain Young’s modulus, GPa; δ is the linear fracture thickness, m.
When a hydraulic fracture propagates along its path and intersects a natural fracture, the approach angle between the hydraulic fracture and the natural fracture is denoted as
θ. The interaction is governed by the maximum horizontal principal stress (
σH) and the minimum horizontal principal stress (
σh). A two-dimensional interaction model illustrating this scenario is presented in
Figure 2.
Under the combined effects of the in-situ stress field and the fluid stress field within the hydraulic fracture, the stress field around the natural fracture is expressed as follows:
When only the far-field in-situ stress is considered for its effect on the natural fracture, the normal and shear stresses acting on the natural fracture are given by the following:
In the formula, KI represents the mode-I stress intensity factor, MPa·m0.5; is the maximum horizontal principal stress, MPa; is the minimum horizontal principal stress, MPa; r is the distance from the hydraulic fracture tip to the natural fracture, m; is the normal stress acting on the natural fracture surface, MPa; τ is the shear stress on the natural fracture surface, MPa.
- (1)
Critical condition of natural fracture slip
Under the combined influence of the stress concentration at the hydraulic fracture tip and far-field in-situ stresses, natural fractures may experience slip before being intersected by hydraulic fractures. Alternatively, when hydraulic fractures connect with natural fractures, continuous fluid leak-off reduces the pore pressure within natural fractures below the normal stress acting on their surfaces, leading to slip initiation. According to the Mohr–Coulomb criterion, the following can be established:
Critical pressure of natural fracture slip:
In the formula, kf represents the friction coefficient of the natural fracture surface (dimensionless). C represents the cohesion of natural fractures, MPa.
- (2)
Critical condition of hydraulic fracture crossing
According to Griffith’s fracture stability theory, during hydraulic fracturing, the injected fluid continuously drives the fracture to propagate forward. Part of the work conducted by the fluid pressure is transformed into the deformation of the rock matrix, which shows as stored elastic energy; part of it is transformed into dissipated surface energy generated by new fractures; and the other part is transformed into heat energy through friction. Accordingly, the principle of conservation of energy is as follows [
29]:
In the formula, ΔWp represents work conducted by the pressure of the injected fluid, J; ΔWela represents the elastic energy of rock, J; γ is the surface energy of materials, J/m2; 2γδΔl represents the surface energy dissipated by the generation of new fractures, J; Q stands for dissipated heat energy, J.
In view of the hydraulic fracture propagation process, the hydraulic fracture is subjected to both fluid pressure and in-situ stress, and the hydraulic fracture is essentially driven by net pressure. When heat dissipation is neglected, Equation (7) is expressed as follows:
The work conducted by injecting fluid pressure into hydraulic fracture is the product of fluid pressure and the increased volume of hydraulic fracture, which is expressed as follows:
In-situ stress work is the product of far-field stress perpendicular to the direction of fracture propagation and the increased volume of hydraulic fracture. This is expressed as follows:
The elastic energy stored in rocks is expressed as follows:
The net pressure in the hydraulic fracture is the following:
The net pressure work in the hydraulic fracture is the product of the net pressure and the increased volume of the hydraulic fracture, which is expressed as:
The increased volume of hydraulic fracture can be corrected as follows:
According to the theory of fracture mechanics, the energy release rate of hydraulic fracture propagation is as follows:
The hydraulic fracture propagation process belongs to mode-I fracture propagation. The energy release rate can be expressed as follows:
When hydraulic fracture propagates, the mode-I stress intensity factor is equal to the fracture toughness of the rock. At this time, the critical fluid pressure of hydraulic fracture passing through natural fracture can be calculated as follows:
In the formula, KIc represents the mode-I fracture toughness of the reservoir rock matrix, MPa·m0.5.
- (3)
Critical condition of natural fracture opening
When the hydraulic fracture communicates with the natural fracture, the fluid enters the natural fracture, and the natural fracture continues to expand under the net pressure. When heat dissipation is neglected, the work conducted by the net pressure in natural fractures can be expressed as follows:
The net pressure on a natural fracture is the difference between the fluid pressure in the fracture and the normal stress on the wall, which can be expressed as follows:
In the formula, Pnet′ represents the net pressure in natural fracture, MPa; Pf′ represents the fluid pressure in natural fracture, MPa; γ′ represents the surface energy of cement in natural fracture, J/m2.
The stored elastic energy is the following:
The increased volume of natural fractures is the following:
According to the theory of fracture mechanics, the energy release rate g of natural fracture propagation is the following:
When the mode-I stress intensity factor of the cement in the natural fracture is equal to the fracture toughness, the natural fracture opens, and at this time, the critical minimum fluid pressure of the natural fracture opening can be calculated. This is expressed as follows:
In the formula, KI′ represents the mode-I stress intensity factor of cement in natural fracture, MPa·m0.5; KIc′ represents the fracture toughness of cement in natural fracture, MPa·m0.5; η represents the bond strength ratio of natural fractures.
4. Results and Discussion
The interaction behaviors between hydraulic and natural fractures are governed not only by their mechanical properties but also by critical factors, including horizontal stress difference and approach angles. This section systematically analyzes the effects of five governing parameters on hydraulic-natural fracture interaction mechanisms: hydraulic fracture length, mode-I fracture toughness, frictional properties of natural fractures, horizontal stress difference, and approach angles. The input parameters employed in the computational framework are summarized in
Table 2.
4.1. Hydraulic Fracture Length
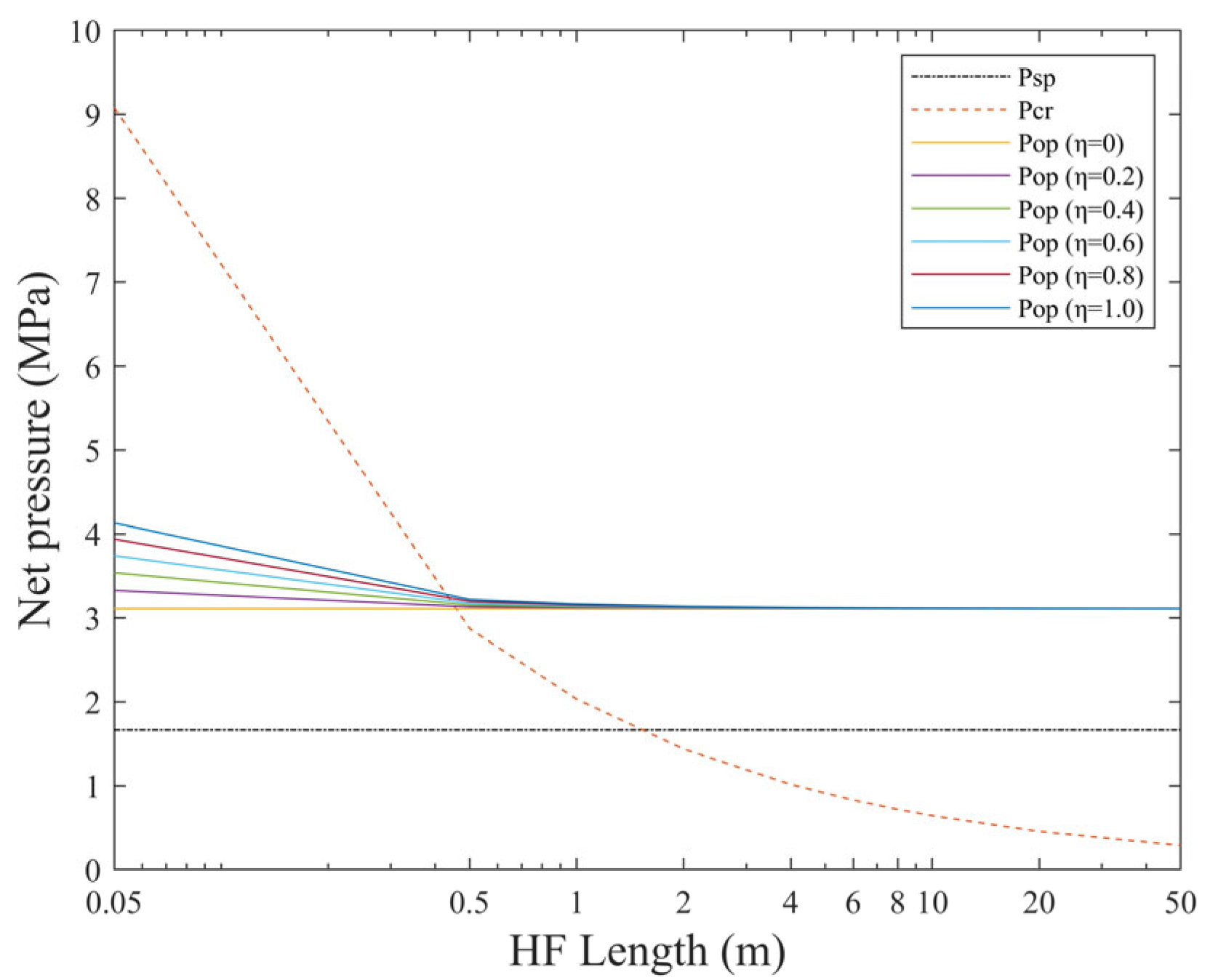
Figure 3 illustrates the influence of hydraulic fracture length on interaction behaviors. The results demonstrate that hydraulic fracture length exhibits no correlation with the critical pressure required for natural fracture slip. As hydraulic fracture length increases, the critical crossing pressure required for hydraulic fracture crossing through natural fractures progressively decreases, making crossing states more favorable. When hydraulic fracture length is less than 0.5 m, the fluid pressure difference required to satisfy opening conditions under varying
η values becomes increasingly pronounced. Conversely, for hydraulic fracture lengths exceeding 0.5 m, variations in
η exhibit negligible effects on the minimum fluid pressure required for opening conditions.
Hydraulic fracture length exhibits distinct threshold effects on interaction behaviors at 0.5 m and 1.5 m. These thresholds represent critical values for the transition of early-stage propagation behaviors during the interaction between hydraulic fractures and natural fractures. When the length is below 0.5 m, natural fractures undergo slip initiation first, resulting in hydraulic fracture arrest. This induces pressure accumulation within the fracture system, leading to progressive elevation of fluid pressure. Once the internal fluid pressure surpasses the normal stress acting on fracture walls, natural fracture opening occurs, triggering hydraulic fracture reorientation along natural fracture trajectories. For fracture lengths between 0.5 m and 1.5 m, natural fracture slip still causes hydraulic fracture arrest. Subsequent fluid pressure escalation eventually reaches critical crossing conditions, enabling hydraulic fracture crossing through natural fractures. When hydraulic fracture length exceeds 1.5 m, direct crossing behavior dominates post-interaction. The absence of sustained pressure accumulation after crossing prevents the achievement of critical slip conditions for natural fractures. Consequently, interaction mechanisms transition progressively from natural fracture opening to direct hydraulic fracture crossing with increasing fracture length.
4.2. Fracture Toughness
Figure 4 demonstrates the influence of fracture toughness on interaction behaviors. The results reveal that the fracture toughness of reservoir rock exhibits no correlation with the critical pressure for natural fracture slip. Notably, the critical slip pressure consistently remains below the critical opening pressure for natural fractures. Increasing fracture toughness elevates the critical fluid pressure required for hydraulic fracture crossing through natural fractures, thereby reducing the crossing likelihood. When fracture toughness is below 1.5 MPa·m
0.5, variations in
η exert negligible influence on the critical fluid pressure for natural fracture opening. Conversely, above 1.5 MPa·m
0.5, distinct critical opening pressures emerge under different
η values, demonstrating progressive pressure escalation with increasing
η.
Fracture toughness manifests threshold effects at 1 MPa·m0.5 and 2 MPa·m0.5. Below 1 MPa·m0.5, direct crossing behavior dominates post-interaction. Between 1–2 MPa·m0.5, the system prioritizes slip initiation (lowest critical slip pressure), resulting in hydraulic fracture arrest. Subsequent net pressure buildup within fractures eventually reaches critical crossing thresholds, enabling through-cutting propagation. Above 2 MPa·m0.5, initial slip transitions to fracture reorientation along natural fractures when net pressure attains critical opening thresholds. Thus, increasing fracture toughness progressively shifts interaction mechanisms from hydraulic fracture crossing to natural fracture opening dominance.
4.3. Horizontal Stress Difference and Cohesion of Natural Fractures
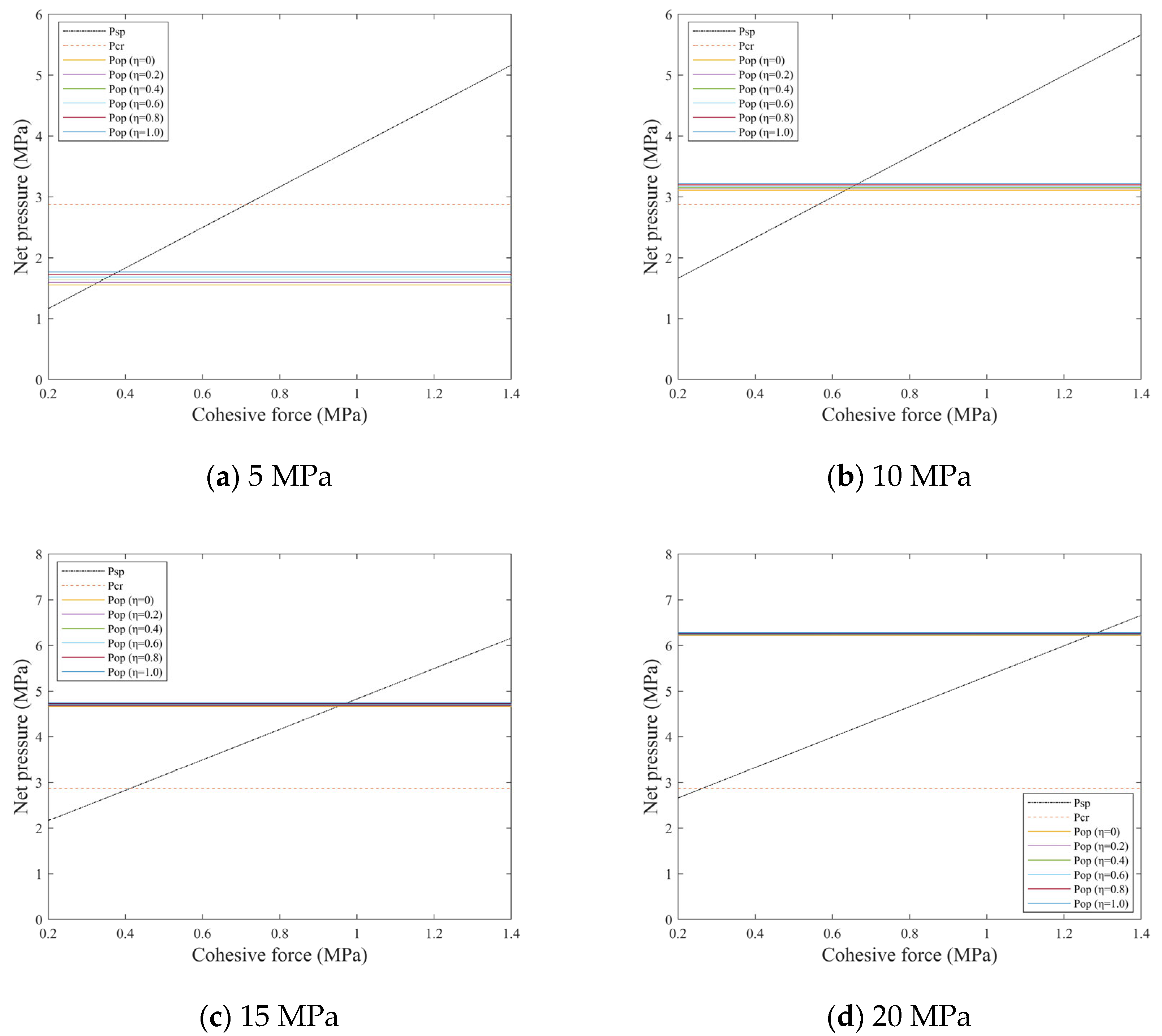
Figure 5 illustrates the influence of horizontal stress differences and cohesion of natural fractures on interaction behaviors. The results demonstrate that the critical hydraulic fracture crossing pressure shows no dependence on either horizontal stress difference or cohesion, whereas the critical natural fracture opening pressure maintains independence from cohesion but exhibits a positive correlation with horizontal stress difference. With increasing horizontal stress difference and cohesion, the critical natural fracture slip pressure progressively rises, making fracture slip more difficult to initiate. As horizontal stress difference increases, the influence of η variation on the critical fluid pressure for natural fracture opening gradually diminishes, while cohesion changes show negligible effects on η.
Cohesion demonstrates a distinct threshold effect on interaction behaviors. Under low horizontal stress difference conditions (≤5 MPa), the critical natural fracture opening pressure consistently remains lower than the critical hydraulic fracture crossing pressure, prioritizing natural fracture opening over hydraulic fracture crossing. Taking a stress difference of 5 MPa as an example, threshold effects emerge at cohesion values of 0.37 MPa and 0.71 MPa. When cohesion is less than 0.37 MPa, natural fractures initially undergo slip. The subsequent increase in net pressure to the critical opening pressure triggers natural fracture opening, followed by hydraulic fracture crossing upon reaching the critical crossing pressure. For cohesion between 0.37 MPa and 0.71 MPa, natural fractures first open and subsequently slip as net pressure reaches the critical slip condition, with hydraulic fracture crossing occurring at higher net pressures. When cohesion exceeds 0.71 MPa, natural fractures open first, and hydraulic fracture crossing occurs before achieving slip conditions due to pressure release post-crossing. Under high horizontal stress difference conditions (≥10 MPa), only a single cohesion threshold exists. At 15 MPa stress difference, the threshold occurs at 0.4 MPa cohesion. Below 0.4 MPa, the initial natural fracture slip transitions to hydraulic fracture crossing without achieving natural fracture opening conditions. Above 0.4 MPa, the minimized crossing pressure enables direct hydraulic fracture crossing upon reaching critical pressure. The analysis reveals that increasing natural fracture cohesion universally promotes hydraulic fracture crossing through natural fractures. Horizontal stress difference modulates both the sequence of interaction behaviors and the magnitude of cohesion thresholds.
4.4. Horizontal Stress Difference and Friction Coefficient of Natural Fractures
Figure 6 illustrates the influence of horizontal stress differences and natural fracture friction coefficients on interaction behaviors. The results indicate that the friction coefficient shows no correlation with either the critical natural fracture opening pressure or critical hydraulic fracture crossing pressure. With increasing friction coefficient, the critical natural fracture slip pressure progressively rises, while the influence of η on the critical opening pressure remains relatively insignificant. As horizontal stress difference increases, both critical opening and slip pressures of natural fractures gradually increase, while the impact of η on critical opening pressure diminishes correspondingly.
Similar to the cohesion effect, the friction coefficient exhibits distinct threshold effects on interaction behaviors under varying horizontal stress difference conditions. Under low horizontal stress difference (≤5 MPa), two friction coefficient thresholds emerge. Taking a 5 MPa stress difference as an example, threshold effects occur at friction coefficients of 0.35 and 0.58. When the friction coefficient is less than 0.35, the interaction sequence progresses from natural fracture slip to opening, followed by hydraulic fracture crossing as net pressure increases. For friction coefficients between 0.35 and 0.58, natural fractures first open, subsequently slip, and finally experience hydraulic fracture crossing. When the friction coefficient exceeds 0.58, natural fractures open initially, followed directly by hydraulic fracture crossing. Under high horizontal stress difference conditions (≥10 MPa), only a single friction coefficient threshold exists. Below this threshold, natural fracture slip precedes hydraulic fracture crossing after reaching critical crossing pressure. Above the threshold, hydraulic fractures penetrate directly upon achieving critical pressure. Increasing natural fracture friction coefficients universally promotes hydraulic fracture crossing through natural fractures. Horizontal stress difference governs both the sequence of interaction behaviors and the magnitude of friction coefficient thresholds.
4.5. Horizontal Stress Difference and Approach Angle
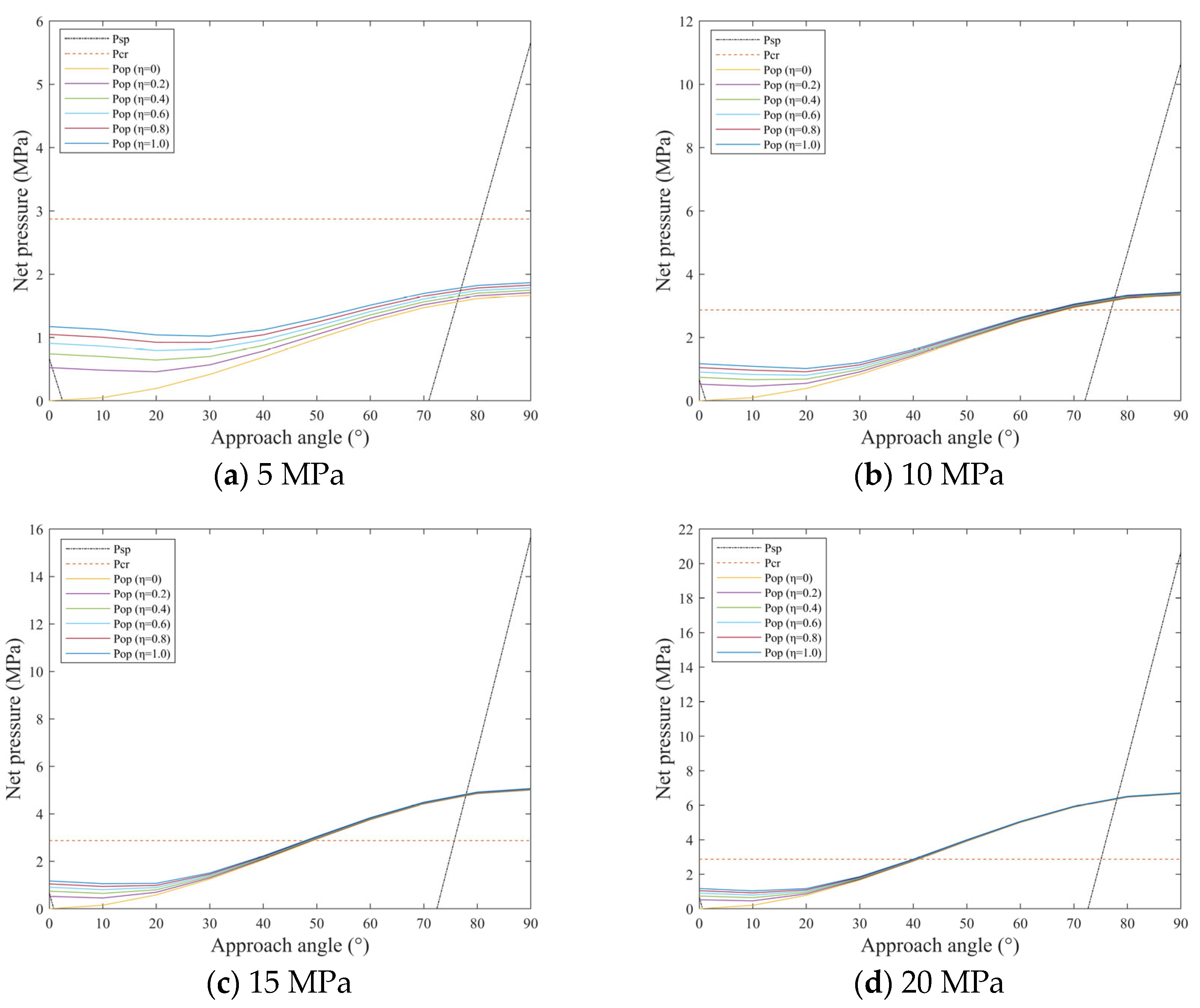
Figure 7 illustrates the influence of horizontal stress difference and approach angle on interaction behaviors. The results demonstrate that the critical crossing pressure of hydraulic fractures crossing through natural fractures remains independent of both horizontal stress difference and approach angle. With increasing approach angle, the critical opening pressure of natural fractures gradually rises, while the influence of
η on this critical opening pressure diminishes progressively. When the approach angle exceeds 70°, the critical slip pressure of natural fractures increases linearly with the approach angle, and its growth rate accelerates with a higher horizontal stress difference. Increasing horizontal stress difference elevates both the critical opening and slip pressures of natural fractures, amplifies the impact of approach angle on these critical pressures, and reduces
η’s influence on the critical opening pressure.
Under low horizontal stress difference conditions (≤5 MPa), the critical opening pressure of natural fractures remains consistently lower than the critical crossing pressure of hydraulic fractures. Following the interaction between hydraulic and natural fractures, natural fractures preferentially open, causing hydraulic fractures to reorient and propagate along the natural fracture paths. As hydraulic fractures extend to the tips of natural fractures, pressure gradually accumulates within the fractures. Upon reaching the critical crossing pressure, hydraulic fractures cross through the natural fracture tips and continue propagating along the direction of the maximum horizontal principal stress. At high horizontal stress differences (≥10 MPa), a critical approach angle governs the interaction behavior. When it is below this critical value, the natural fracture opening pressure remains lower than the hydraulic fracture crossing pressure, leading to the fracture opening upon interaction. Crossing occurs only after sufficient pressure accumulation, which enables breakthroughs at the natural fracture tips. Conversely, when the approach angle exceeds this critical value, the natural fracture opening pressure surpasses the crossing threshold, resulting in direct hydraulic fracture crossing through natural fractures. The critical approach angle progressively decreases with increasing horizontal stress difference. For approach angles exceeding 70°, the interaction initiates with natural fracture slip, followed by hydraulic fracture crossing once the critical pressure threshold is achieved through continued pressure accumulation. Consequently, as horizontal stress difference and approach angle increase, the interaction mechanism transitions from a sequential process of natural fracture opening followed by crossing to direct crossing dominance.