The Impact of the Feed Rate and the Binder Concentration on the Morphology of Spray-Dried Alumina–Polymer Nanocomposites
Abstract
1. Introduction
2. Material and Methods
2.1. Feed Material Particle System
2.2. Spray-Drying Experimental Setup
2.3. Conducted Spray-Drying Experiments
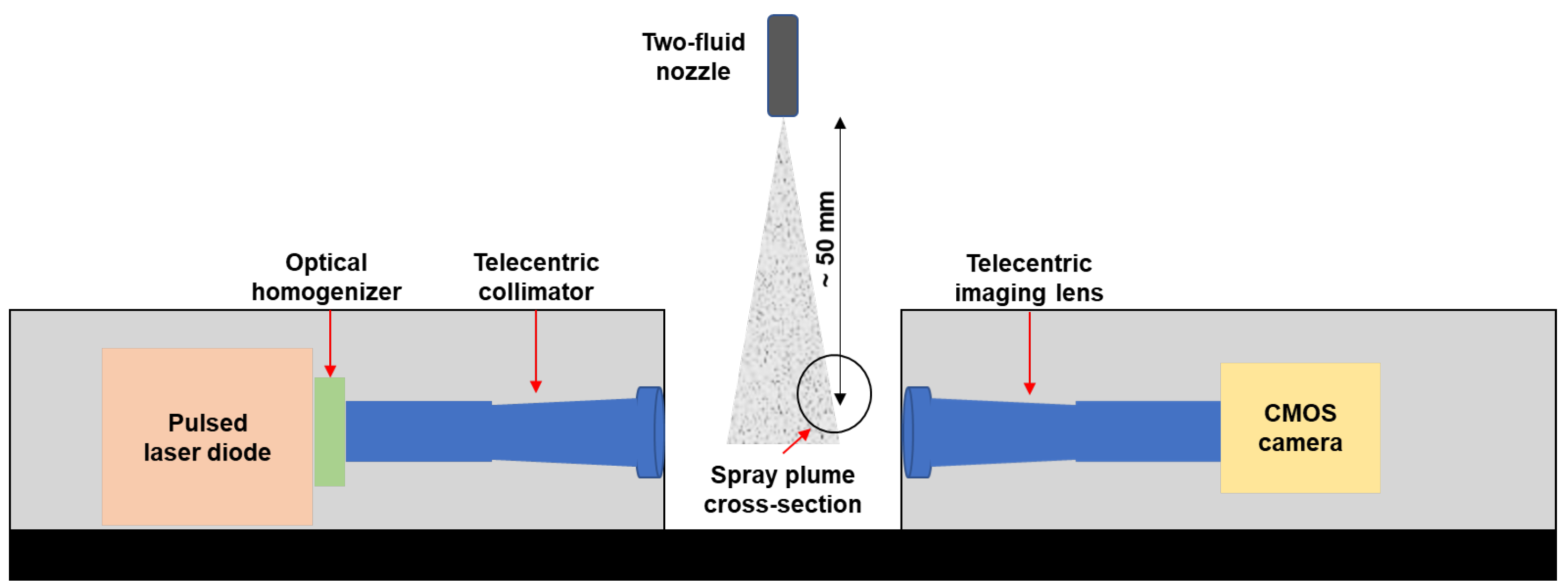
2.4. Offline Droplet Imaging Setup
2.5. Inline Granule Imaging Setup
2.6. Size and Shape Descriptors of Granules
- Maximum Feret diameter ()—the longest distance between two parallel lines tangential to the 2D silhouette of the granule as observed in the imaging plane. It provides an estimate of the granule’s largest dimension in the image plane. Formally, it is defined aswhere represents the distance between two distinct parallel lines at an angle to the x-axis that are tangents of the granule’s 2D silhouette.
- Aspect ratio ()—the aspect ratio is defined as the ratio of the minimum Feret diameter to the maximum Feret diameter () of the granule, where the minimum Feret diameter is given via Equation (1), by substituting with . Then, the aspect ratio, , is given byNote that the aspect ratio is a dimensionless number between 0 and 1 that indicates the compactness or elongation. An aspect ratio of 1 indicates a compact shape (equal length and width), whereas values significantly less than 1 indicate an elongated 2D silhouette. The real minimum Feret diameter was used instead of the Feret diameter perpendicular to to ensure robustness and orientation-independent calculations of the granule shape.
2.7. Parametric Modeling and Prediction of Descriptor Distributions
3. Results
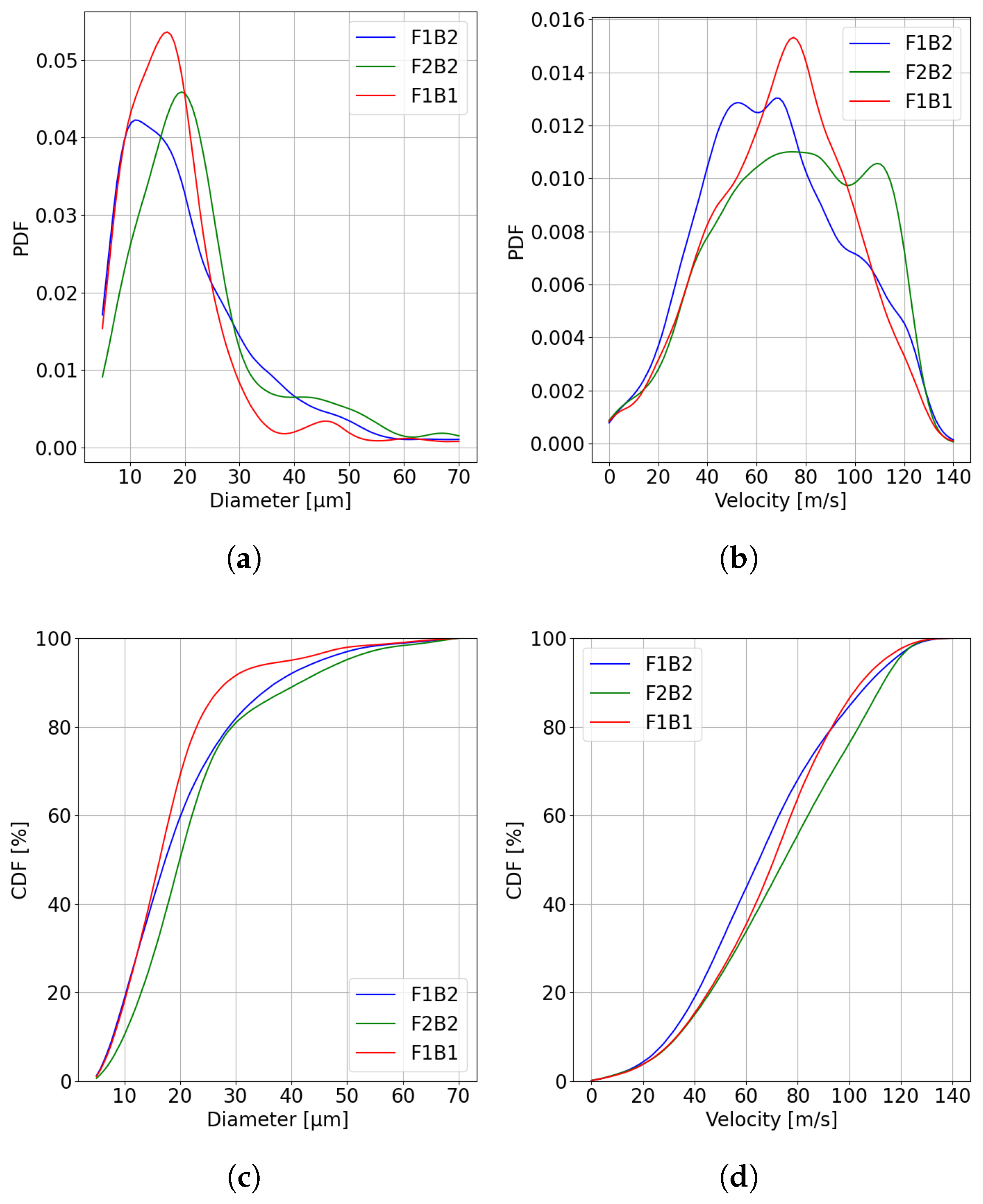
3.1. Droplet Size and Velocity Distributions
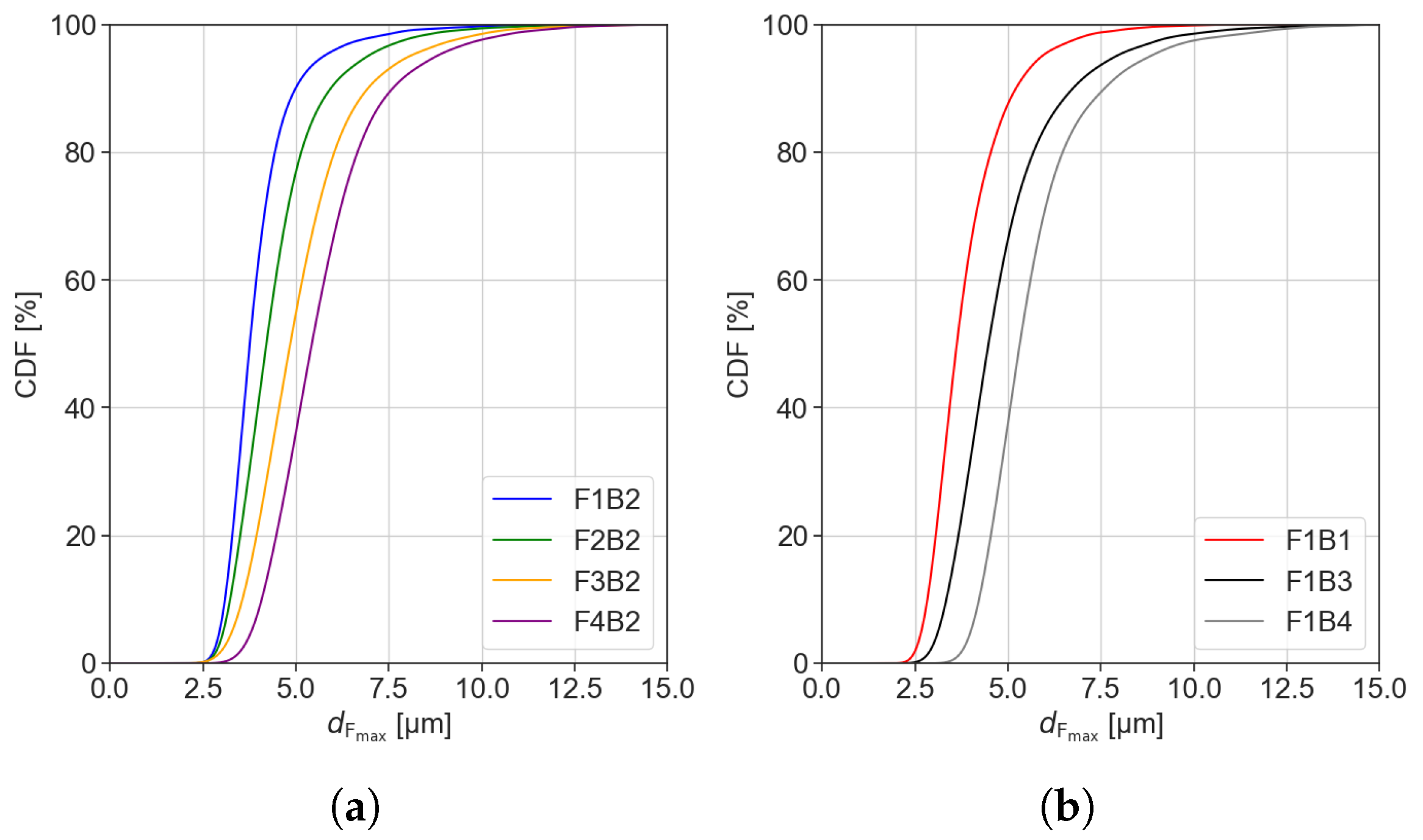
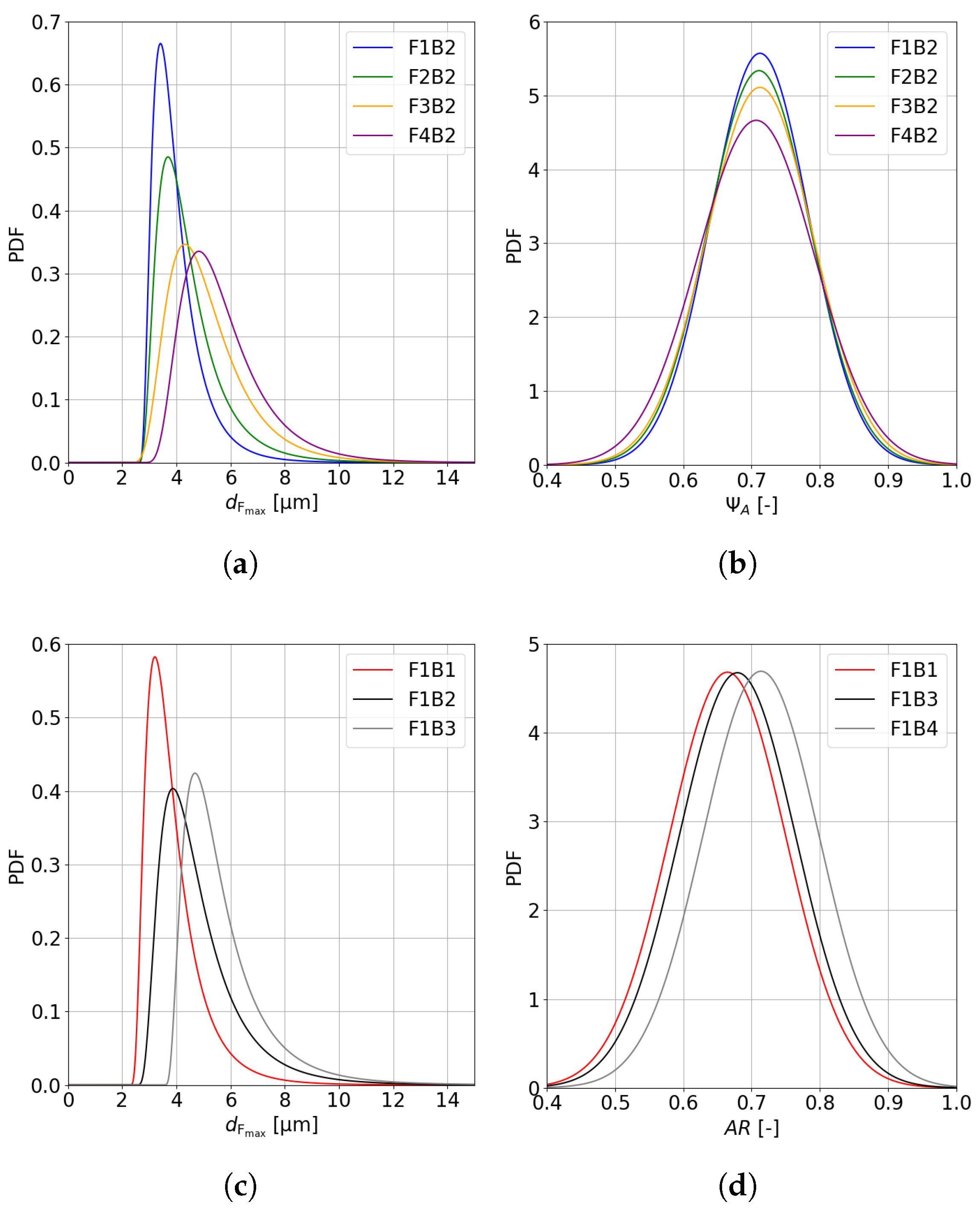
3.2. Granule Size and Shape Distributions
3.3. SEM Imaging of Dried Granules
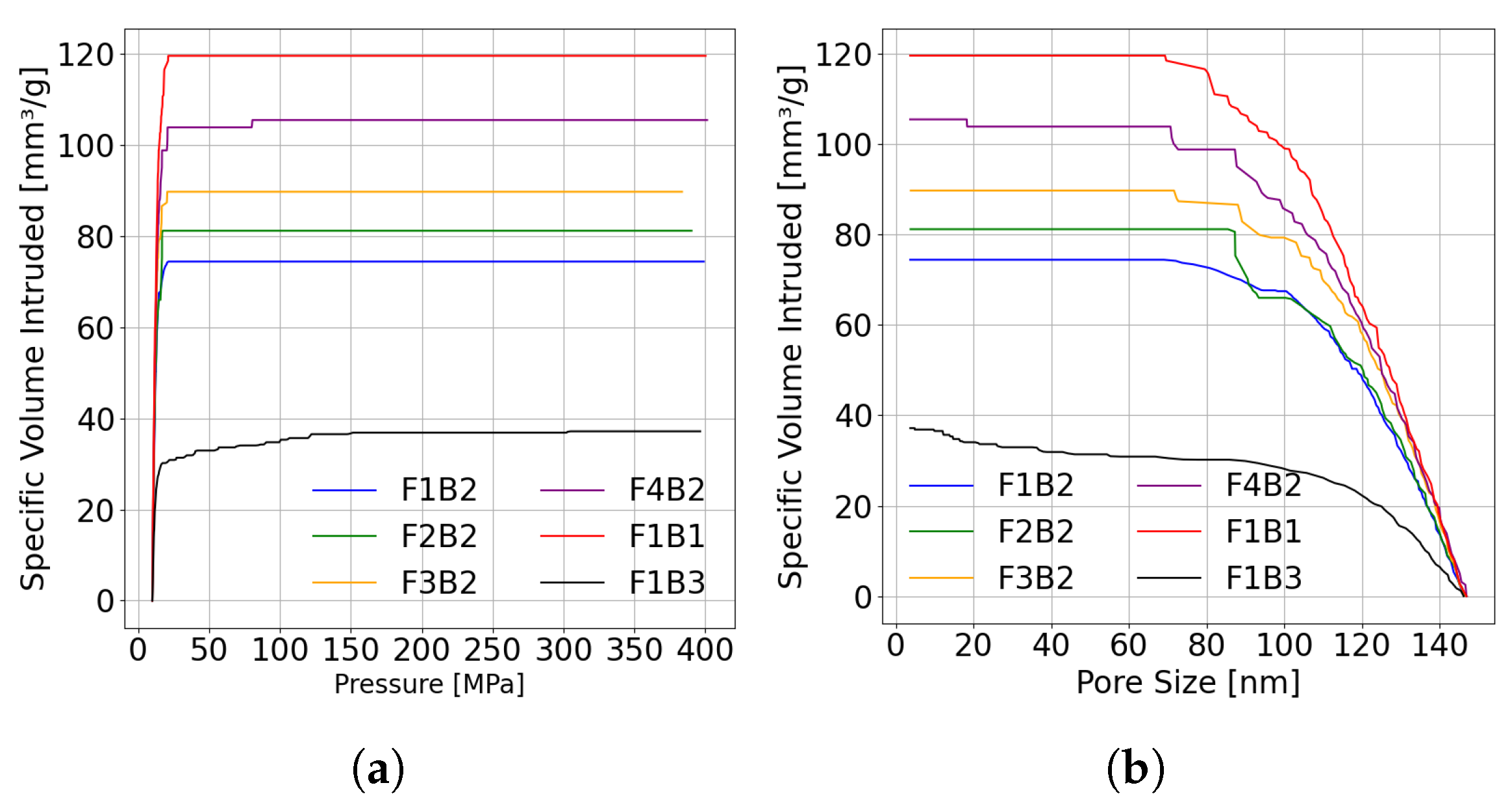
3.4. Granule Porosity Analysis
4. Discussion
4.1. Influence of Process Parameters on Droplet Characteristics
4.2. Impact of Droplet Characteristics on Granule Morphology
4.3. Parametric Modeling and Process Optimization
4.4. Microstructural Insights and Implications
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, X.D.; Zhang, S.C.; Huebner, W.; Ownby, P.D.; Gu, H. Effect of the solvent on the particle morphology of spray dried PMMA. J. Mater. Sci. 2001, 36, 3759–3768. [Google Scholar] [CrossRef]
- Schwarzer, H.C.; Peukert, W. Experimental Investigation into the Influence of Mixing on Nanoparticle Precipitation. Chem. Eng. Technol. 2002, 25, 657. [Google Scholar] [CrossRef]
- Iskandar, F.; Gradon, L.; Okuyama, K. Control of the morphology of nanostructured particles prepared by the spray drying of a nanoparticle sol. J. Colloid Interface Sci. 2003, 265, 296–303. [Google Scholar] [CrossRef]
- Banert, T.; Peuker, U.A. Production of highly filled Fe3O4/PMMA nanocomposites by the spraying process. Chem. Ing. Tech. 2005, 77, 224–227. [Google Scholar] [CrossRef]
- Ciprari, D.; Jacob, K.; Tannenbaum, R. Characterization of Polymer Nanocomposite Interphase and Its Impact on Mechanical Properties. Macromolecules 2006, 39, 6565–6573. [Google Scholar] [CrossRef]
- Dallas, P.; Georgakilas, V.; Niarchos, D.; Komninou, P.; Kehagias, T.; Petridis, D. Synthesis, characterization and thermal properties of polymer/magnetite nanocomposites. Nanotechnology 2006, 17, 2046–2053. [Google Scholar] [CrossRef]
- Castrillo, P.; Olmos, D.; Amador, D.; González-Benito, J. Real dispersion of isolated fumed silica nanoparticles in highly filled PMMA prepared by high energy ball milling. J. Colloid Interface Sci. 2007, 308, 318–324. [Google Scholar] [CrossRef]
- Srivastava, S.; Haridas, M.; Basu, J.K. Optical properties of polymer nanocomposites. Bull. Mater. Sci. 2008, 31, 213–217. [Google Scholar] [CrossRef]
- Gyergyek, S.; Huskić, M.; Makovec, D.; Drofenik, M. Superparamagnetic nanocomposites of iron oxide in a polymethyl methacrylate matrix synthesized by in situ polymerization. Colloids Surfaces A Physicochem. Eng. Asp. 2008, 317, 49–55. [Google Scholar] [CrossRef]
- Rudolph, M.; Peuker, U.A. Coagulation and stabilization of sterically functionalized magnetite nanoparticles in an organic solvent with different technical polymers. J. Colloid Interface Sci. 2011, 357, 292–299. [Google Scholar] [CrossRef]
- Rudolph, M.; Turan, C.; Kirchberg, S.; Ziegmann, G.; Peuker, U. Nanoparticles in Organic Solvents with Polymers—Stability and Consequences upon Material Synthesis through Spray Drying and Melt Moulding. In NanoFormulation; Tiddy, G., Tan, R., Eds.; The Royal Society of Chemistry: London, UK, 2012; pp. 177–187. [Google Scholar] [CrossRef]
- Darwish, M.S.A.; Peuker, U.; Kunz, U.; Turek, T. Bi-layered polymer–magnetite core/shell particles: Synthesis and characterization. J. Mater. Sci. 2011, 46, 2123–2134. [Google Scholar] [CrossRef]
- Santos, D.; Maurício, A.C.; Sencadas, V.; Santos, J.D.; Fernandes, M.H.; Gomes, P.S. Spray Drying: An Overview. In Biomaterials—Physics and Chemistry—New Edition; InTech: Rijeka, Croatia, 2018. [Google Scholar] [CrossRef]
- de Souza Lima, R.; Ré, M.I.; Arlabosse, P. Drying droplet as a template for solid formation: A review. Powder Technol. 2020, 359, 161–171. [Google Scholar] [CrossRef]
- Rudolph, M.; Peuker, U.A. Phase transfer of agglomerated nanoparticles: Deagglomeration by adsorbing grafted molecules and colloidal stability in polymer solutions. J. Nanoparticle Res. 2012, 14, 990. [Google Scholar] [CrossRef]
- Perecin, C.; Cerize, N.; Chitta, V.; Gratens, X.; Léo, P.; de Oliveira, A.; Yoshioka, S. Magnetite Nanoparticles Encapsulated with PCL and Poloxamer by Nano Spray Drying Technique. Nanosci. Nanotechnol. 2016, 6, 68–73. [Google Scholar] [CrossRef]
- Rothberg, H.; Pietsch-Braune, S.; Spahr, L.; Kanina, Y.; Heinrich, S. Production of magnetite-polyvinyl butyral composites using a Nano Spray Dryer. Powder Technol. 2021, 394, 394–402. [Google Scholar] [CrossRef]
- Johnson, P.E.; Muttil, P.; MacKenzie, D.; Carnes, E.C.; Pelowitz, J.; Mara, N.A.; Mook, W.M.; Jett, S.D.; Dunphy, D.R.; Timmins, G.S.; et al. Spray-Dried Multiscale Nano-biocomposites Containing Living Cells. ACS Nano 2015, 9, 6961–6977. [Google Scholar] [CrossRef]
- Lefrançois Perreault, L.; Colò, F.; Meligrana, G.; Kim, K.; Fiorilli, S.; Bella, F.; Nair, J.R.; Vitale-Brovarone, C.; Florek, J.; Kleitz, F.; et al. Spray-Dried Mesoporous Mixed Cu-Ni Oxide@Graphene Nanocomposite Microspheres for High Power and Durable Li-Ion Battery Anodes. Adv. Energy Mater. 2018, 8, 1802438. [Google Scholar] [CrossRef]
- Sen, D.; Spalla, O.; Belloni, L.; Charpentier, T.; Thill, A. Temperature Effects on the Composition and Microstructure of Spray-Dried Nanocomposite Powders. Langmuir 2006, 22, 3798–3806. [Google Scholar] [CrossRef] [PubMed]
- Sen, D.; Melo, J.S.; Bahadur, J.; Mazumder, S.; Bhattacharya, S.; Ghosh, G.; Dutta, D.; D’Souza, S.F. Buckling-driven morphological transformation of droplets of a mixed colloidal suspension during evaporation-induced self-assembly by spray drying. Eur. Phys. J. E 2010, 31, 393–402. [Google Scholar] [CrossRef]
- Sen, D.; Bahadur, J.; Mazumder, S.; Bhattacharya, S. Formation of hollow spherical and doughnut microcapsules by evaporation induced self-assembly of nanoparticles: Effects of particle size and polydispersity. Soft Matter 2012, 8, 10036. [Google Scholar] [CrossRef]
- Sen, D.; Bahadur, J.; Mazumder, S.; Verma, G.; Hassan, P.A.; Bhattacharya, S.; Vijai, K.; Doshi, P. Nanocomposite silicasurfactant microcapsules by evaporation induced self assembly: Tuning the morphological buckling by modifying viscosity and surface charge. Soft Matter 2012, 8, 1955–1963. [Google Scholar] [CrossRef]
- Sen, D.; Ghosh, A.; Mazumder, S.; Bindal, R.; Tewari, P. Novel polysulfone–spray-dried silica composite membrane for water purification: Preparation, characterization and performance evaluation. Sep. Purif. Technol. 2014, 123, 79–86. [Google Scholar] [CrossRef]
- Guo, Z.; Pereira, T.; Choi, O.; Wang, Y.; Hahn, H.T. Surface functionalized alumina nanoparticle filled polymeric nanocomposites with enhanced mechanical properties. J. Mater. Chem. 2006, 16, 2800. [Google Scholar] [CrossRef]
- Mallakpour, S.; Khadem, E. Recent development in the synthesis of polymer nanocomposites based on nano-alumina. Prog. Polym. Sci. 2015, 51, 74–93. [Google Scholar] [CrossRef]
- Pinto, D.; Bernardo, L.F.A.; Amaro, A.; Lopes, S. Mechanical Properties of Epoxy Nanocomposites Using Alumina as Reinforcement—A Review. J. Nano Res. 2015, 30, 9–38. [Google Scholar] [CrossRef]
- Xu, J.; Wang, A.; Wang, X.; Su, D.; Zhang, T. Synthesis, characterization, and catalytic application of highly ordered mesoporous alumina-carbon nanocomposites. Nano Res. 2010, 4, 50–60. [Google Scholar] [CrossRef]
- Hakamy, A.; Abd-Elnaiem, A.M. Porous alumina–lithium composites for novel lithium-ion batteries. J. Appl. Electrochem. 2024, 54, 1463–1471. [Google Scholar] [CrossRef]
- Pourmadadi, M.; Farokh, A.; Rahmani, E.; Shamsabadipour, A.; Eshaghi, M.M.; Rahdar, A.; Ferreira, L.F.R. Porous alumina as potential nanostructures for drug delivery applications, synthesis and characteristics. J. Drug Deliv. Sci. Technol. 2022, 77, 103877. [Google Scholar] [CrossRef]
- Zhou, L.; Luo, X.; Li, J.; Ma, L.; He, Y.; Jiang, Y.; Yin, L.; Gao, L. Meso-molding three-dimensionally ordered macroporous alumina: A new platform to immobilize enzymes with high performance. Biochem. Eng. J. 2019, 146, 60–68. [Google Scholar] [CrossRef]
- Tadic, M.; Panjan, M.; Tadic, B.V.; Kralj, S.; Lazovic, J. Magnetic properties of mesoporous hematite/alumina nanocomposite and evaluation for biomedical applications. Ceram. Int. 2022, 48, 10004–10014. [Google Scholar] [CrossRef]
- Huntington, D.H. The Influence of the Spray Drying Process on Product Properties. Dry. Technol. 2004, 22, 1261–1287. [Google Scholar] [CrossRef]
- Nandiyanto, A.B.D.; Okuyama, K. Progress in developing spray-drying methods for the production of controlled morphology particles: From the nanometer to submicrometer size ranges. Adv. Powder Technol. 2011, 22, 1–19. [Google Scholar] [CrossRef]
- Homayoonfal, M.; Malekjani, N.; Baeghbali, V.; Ansarifar, E.; Hedayati, S.; Jafari, S.M. Optimization of spray drying process parameters for the food bioactive ingredients. Crit. Rev. Food Sci. Nutr. 2022, 64, 5631–5671. [Google Scholar] [CrossRef] [PubMed]
- Höhne, S.; Gaukel, V. Impact of the drying rate on product properties of spray dried emulsions to enable a targeted product design. Dry. Technol. 2024, 42, 2080–2086. [Google Scholar] [CrossRef]
- Nicklas, J.; Peuker, U. Agglomeration of fine hydrophobic particles: 1D and 2D characterization by dynamic image analysis of in-line probe data. Powder Technol. 2023, 426, 118685. [Google Scholar] [CrossRef]
- Eiermann, N.; Furat, O.; Nicklas, J.; Peuker, U.A.; Schmidt, V. Quantitative characterization of hydrophobic agglomeration at different mixing intensities using a copula-based probabilistic modeling approach. Powder Technol. 2025, 460, 120907. [Google Scholar] [CrossRef]
- Allen, T. Mercury porosimetry. In Particle Size Measurement; Springer: Berlin/Heidelberg, Germany, 1990; pp. 653–681. [Google Scholar] [CrossRef]
- Dobry, D.E.; Settell, D.M.; Baumann, J.M.; Ray, R.J.; Graham, L.J.; Beyerinck, R.A. A Model-Based Methodology for Spray-Drying Process Development. J. Pharm. Innov. 2009, 4, 133–142. [Google Scholar] [CrossRef]
- Petersen, L.N.; Poulsen, N.K.; Niemann, H.H.; Utzen, C.; Jørgensen, J.B. Comparison of three control strategies for optimization of spray dryer operation. J. Process Control 2017, 57, 1–14. [Google Scholar] [CrossRef]
- Schmitt, J.M.; Baumann, J.M.; Morgen, M.M. Predicting Spray Dried Dispersion Particle Size Via Machine Learning Regression Methods. Pharm. Res. 2022, 39, 3223–3239. [Google Scholar] [CrossRef]
- Petersen, L.N.; Poulsen, N.K.; Niemann, H.H.; Utzen, C.; Jørgensen, J.B. Comparison of Linear and Nonlinear Model Predictive Control for Optimization of Spray Dryer Operation. IFAC-PapersOnLine 2015, 48, 218–223. [Google Scholar] [CrossRef]
- Muñoz López, C.A.; Peeters, K.; Van Impe, J. Data-Driven Modeling of the Spray Drying Process. Process Monitoring and Prediction of the Particle Size in Pharmaceutical Production. ACS Omega 2024, 9, 25678–25693. [Google Scholar] [CrossRef] [PubMed]
- Neumann, M.; Gräfensteiner, P.; Santos de Oliveira, C.; Martins de Souza e Silva, J.; Koppka, S.; Enke, D.; Huber, P.; Schmidt, V. Morphology of nanoporous glass: Stochastic 3D modeling, stereology and the influence of pore width. Phys. Rev. Mater. 2024, 8, 045605. [Google Scholar] [CrossRef]
- Furat, O.; Masuhr, M.; Kruis, F.E.; Schmidt, V. Stochastic modeling of classifying aerodynamic lenses for separation of airborne particles by material and size. Adv. Powder Technol. 2020, 31, 2215–2226. [Google Scholar] [CrossRef]
- Ishiduki, K.; Esumi, K. Adsorption Characteristics of Poly(acrylic acid) and Poly(vinyl pyrrolidone) on Alumina from Their Mixtures in Aqueous Solution. J. Colloid Interface Sci. 1997, 185, 274–277. [Google Scholar] [CrossRef]
- Ishiduki, K.; Esumi, K. The Effect of pH on Adsorption of Poly(acrylic acid) and Poly(vinylpyrrolidone) on Alumina from Their Binary Mixtures. Langmuir 1997, 13, 1587–1591. [Google Scholar] [CrossRef]
- Koivuluoto, H.; Matikainen, V.; Larjo, J.; Vuoristo, P. Novel Online Diagnostic Analysis for In-Flight Particle Properties in Cold Spraying. J. Therm. Spray Technol. 2018, 27, 423–432. [Google Scholar] [CrossRef]
- Silverman, B. Density Estimation for Statistics and Data Analysis; Routledge: London, UK, 2018. [Google Scholar] [CrossRef]
- Shao, J. Mathematical Statistics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; John Wiley & Sons: Hoboken, NJ, USA, 1995; Volume 2. [Google Scholar]
- Smirnov, S.; Vlassiouk, I.; Takmakov, P.; Rios, F. Water Confinement in Hydrophobic Nanopores. Pressure-Induced Wetting and Drying. ACS Nano 2010, 4, 5069–5075. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Biswas, P.; Sen, D.; Mazumder, S.; Doshi, P. Controlling sphere to doughnut transformation during quick drying of colloidal micrometric droplets. AIP Conf. Proc. 2017, 1832, 140009. [Google Scholar] [CrossRef]
- Siemons, I.; Politiek, R.; Boom, R.; van der Sman, R.; Schutyser, M. Dextrose equivalence of maltodextrins determines particle morphology development during single sessile droplet drying. Food Res. Int. 2020, 131, 108988. [Google Scholar] [CrossRef]
- Fan, X.; Li, S.; Wu, Y.; Niu, L. Large-scale preparation of macro-porous silica microspheres via sol–gel composite particles and a spray drying process. RSC Adv. 2017, 7, 56081–56086. [Google Scholar] [CrossRef]
- Faure, B.; Sæderup Lindeløv, J.; Wahlberg, M.; Adkins, N.; Jackson, P.; Bergström, L. Spray drying of TiO2 nanoparticles into redispersible granules. Powder Technol. 2010, 203, 384–388. [Google Scholar] [CrossRef]
- Prabhakaran, K.; Beigh, M.; Lakra, J.; Gokhale, N.; Sharma, S. Characteristics of 8molby spray drying process. J. Mater. Process. Technol. 2007, 189, 178–181. [Google Scholar] [CrossRef]
- Wang, X.; Wang, P.; Liu, S.; Crouse, J.; Gardner, D.J.; Via, B.; Gallagher, T.; Elder, T.; Peng, Y. Material properties of spray-dried cellulose nanocrystal reinforced homopolymer polypropylene composites. Polym. Compos. 2023, 46, 1177–1191. [Google Scholar] [CrossRef]






| Process Parameters | F Series | B Series | |||||
|---|---|---|---|---|---|---|---|
| F1B2 | F2B2 | F3B2 | F4B2 | F1B1 | F1B3 | F1B4 | |
| Atomization pressure [bar] | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| Spray gas flow rate [L h−1] | 742 | 742 | 742 | 742 | 742 | 742 | 742 |
| Inlet temperature [°C] | 220 | 220 | 220 | 220 | 220 | 220 | 220 |
| Drying gas flow rate [m3 h−1] | 35 | 35 | 35 | 35 | 35 | 35 | 35 |
| Feed flow rate [mL min−1] | 11 | 14 | 17 | 20 | 11 | 11 | 11 |
| PVP-30 concentration [wt%] | 0.8 | 0.8 | 0.8 | 0.8 | 0.4 | 1.6 | 3.2 |
| Image format | Monochromatic 8-bit |
| Image dimensions [pixels × pixels] | 2464 × 2056 |
| Frame rate [ | 20 |
| Conversion factor [ | 0.2464 |
| Focus position [ | 99.8629 |
| Strobe intensity [%] | 100 |
| Exposure time [ | 6400 |
| Reflector distance [ | 1000 |
| F Series | B Series | ||||||
|---|---|---|---|---|---|---|---|
| F1B2 | F2B2 | F3B2 | F4B2 | F1B1 | F1B3 | F1B4 | |
| [ | 3.11 | 3.26 | 3.57 | 4.07 | 2.87 | 3.36 | 4.26 |
| [ | 3.77 | 4.23 | 4.85 | 5.42 | 3.65 | 4.49 | 5.35 |
| [ | 5.16 | 6.06 | 6.97 | 7.69 | 5.34 | 6.84 | 7.82 |
| CV [-] | 0.25 | 0.29 | 0.31 | 0.28 | 0.27 | 0.32 | 0.30 |
| F1B2 | 0.19 | 0.59 | 2.56 | 0.71 | 0.07 |
| F2B2 | 0.52 | 0.58 | 2.49 | 0.71 | 0.08 |
| F3B2 | 1.03 | 0.46 | 2.03 | 0.71 | 0.08 |
| F4B2 | 1.04 | 0.47 | 2.57 | 0.71 | 0.09 |
| F1B1 | 0.32 | 0.60 | 2.25 | 0.67 | 0.09 |
| F1B3 | 0.69 | 0.59 | 2.48 | 0.68 | 0.09 |
| F1B4 | 0.58 | 0.65 | 3.52 | 0.71 | 0.09 |
| F series | a | 0.10 | −0.02 | −0.01 | 0.00 | 0.00 |
| b | −0.89 | 0.77 | 2.64 | 0.72 | 0.05 | |
| B series | a | 0.09 | 0.02 | 0.47 | 0.02 | 0.00 |
| b | 0.38 | 0.58 | 1.94 | 0.66 | 0.09 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitra, R.; Fuchs, L.; Furat, O.; Sinnwell, Y.; Antonyuk, S.; Schmidt, V.; Peuker, U.A. The Impact of the Feed Rate and the Binder Concentration on the Morphology of Spray-Dried Alumina–Polymer Nanocomposites. Processes 2025, 13, 1643. https://doi.org/10.3390/pr13061643
Mitra R, Fuchs L, Furat O, Sinnwell Y, Antonyuk S, Schmidt V, Peuker UA. The Impact of the Feed Rate and the Binder Concentration on the Morphology of Spray-Dried Alumina–Polymer Nanocomposites. Processes. 2025; 13(6):1643. https://doi.org/10.3390/pr13061643
Chicago/Turabian StyleMitra, Rahul, Lukas Fuchs, Orkun Furat, Yannik Sinnwell, Sergiy Antonyuk, Volker Schmidt, and Urs Alexander Peuker. 2025. "The Impact of the Feed Rate and the Binder Concentration on the Morphology of Spray-Dried Alumina–Polymer Nanocomposites" Processes 13, no. 6: 1643. https://doi.org/10.3390/pr13061643
APA StyleMitra, R., Fuchs, L., Furat, O., Sinnwell, Y., Antonyuk, S., Schmidt, V., & Peuker, U. A. (2025). The Impact of the Feed Rate and the Binder Concentration on the Morphology of Spray-Dried Alumina–Polymer Nanocomposites. Processes, 13(6), 1643. https://doi.org/10.3390/pr13061643








