A Study on the Crack Propagation Behavior of Cement Sheath Interfaces Considering Bond Strength
Abstract
1. Introduction
2. Cement Sheath Interface Bond Strength Testing
2.1. Experimental Methods and Procedures
2.1.1. Sample Preparation
2.1.2. Experimental Apparatus and Procedure
- (1)
- Normal Bond Strength
- (2)
- Shear Bond Strength
2.1.3. Data Processing
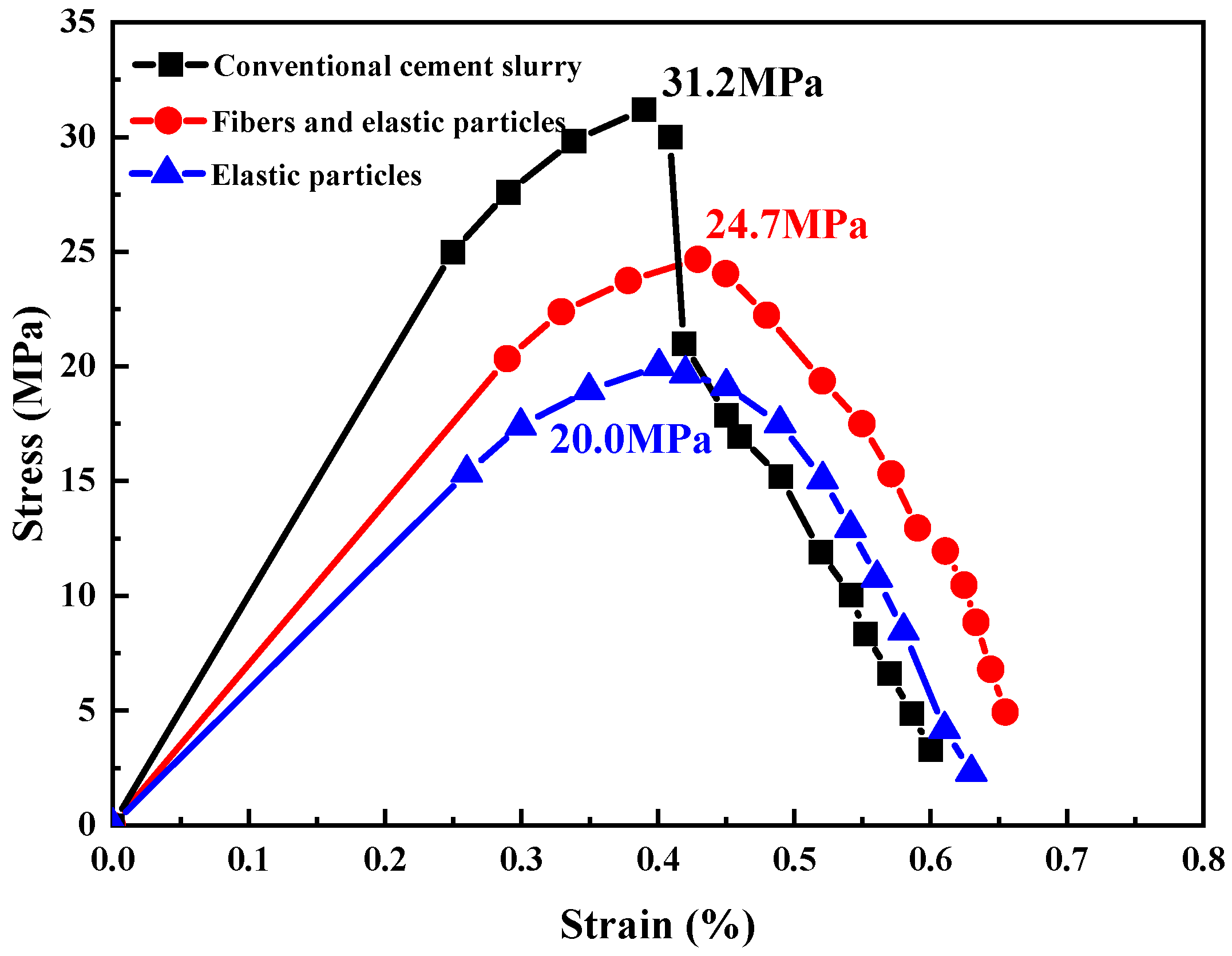
2.2. Experimental Results
3. Cement Sheath Interface Crack Propagation Mechanism
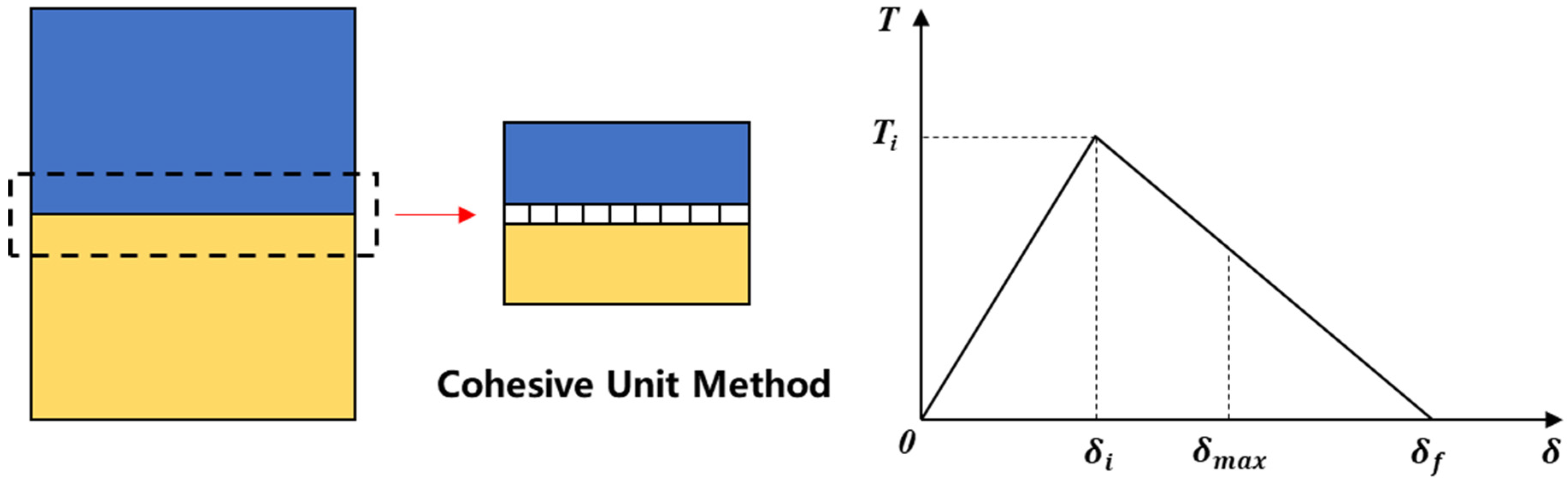
3.1. Interface Crack Damage Evolution
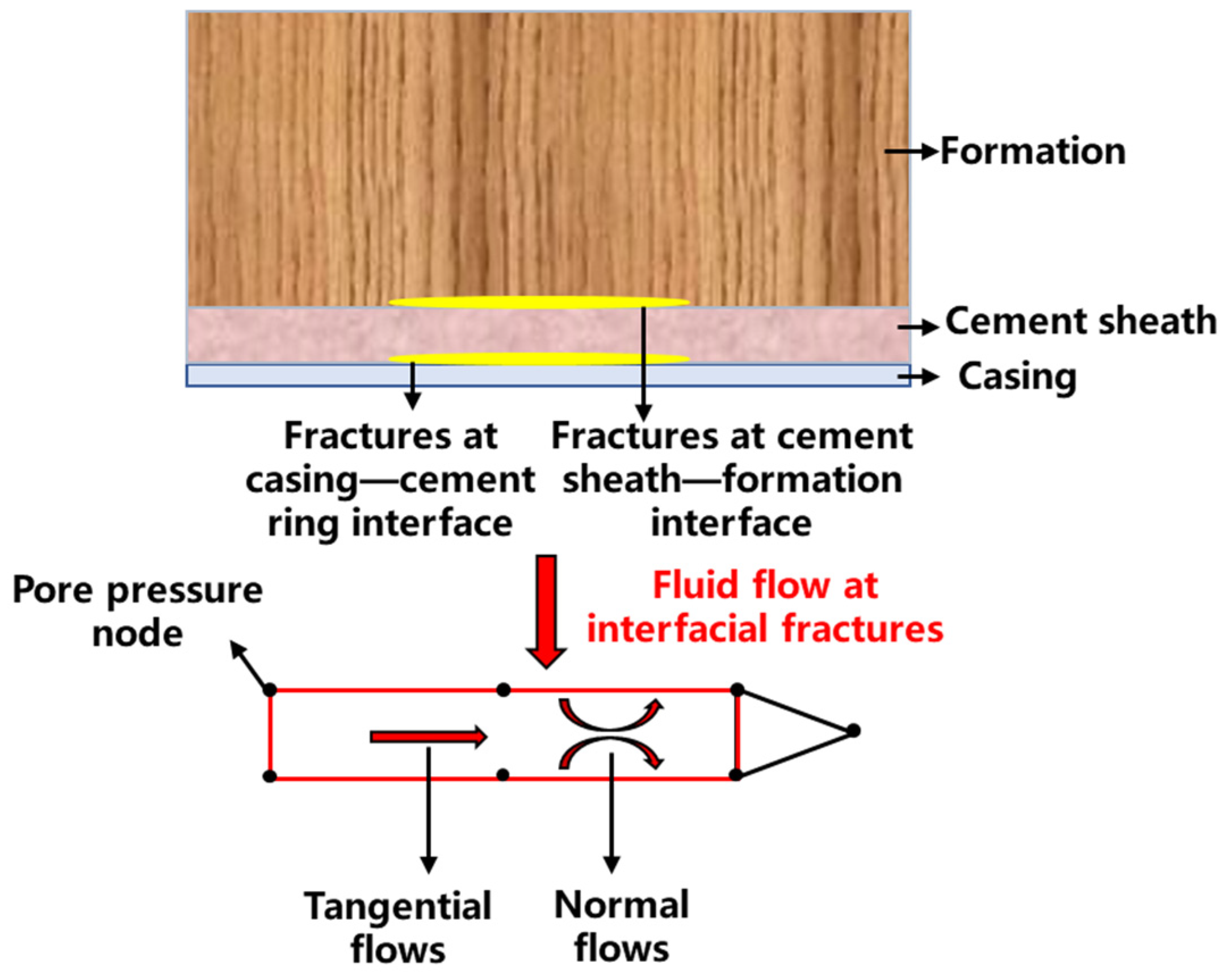
3.2. Fluid Flow in Cement Sheath Interface Cracks
4. Cement Sheath Interface Crack Propagation Numerical Model
4.1. Geometric Model and Meshing
4.2. Boundary Conditions and Parameter Setting
4.3. Model Applicability Statement
- (1)
- Interfacial Roughness: The interface was modeled using zero-thickness cohesive elements, which do not explicitly represent surface roughness. However, as described in Section 2, the normal and shear bonding strengths of the cement stone–casing and cement stone–shale interfaces were determined through Brazilian splitting and direct shear tests, respectively. The obtained values were used to define the parameters of the cohesive elements, thereby partially capturing the influence of different interfacial geometries on mechanical response.
- (2)
- Thermal Effects and Fluid Flow Characteristics: The model primarily focused on the mechanical evolution of interfacial cracks in the cement sheath during hydraulic fracturing. Thermal stresses caused by temperature differences between the fracturing fluid and the wellbore, as well as the influence of cement sheath permeability on pore pressure transmission, were not considered at this stage.
- (3)
- Parameter Selection Range: In the parameter sensitivity analysis, key parameters such as the elastic modulus and Poisson’s ratio of the cement sheath, as well as internal casing pressure, were investigated. The crack toughness and interface thickness were held constant.
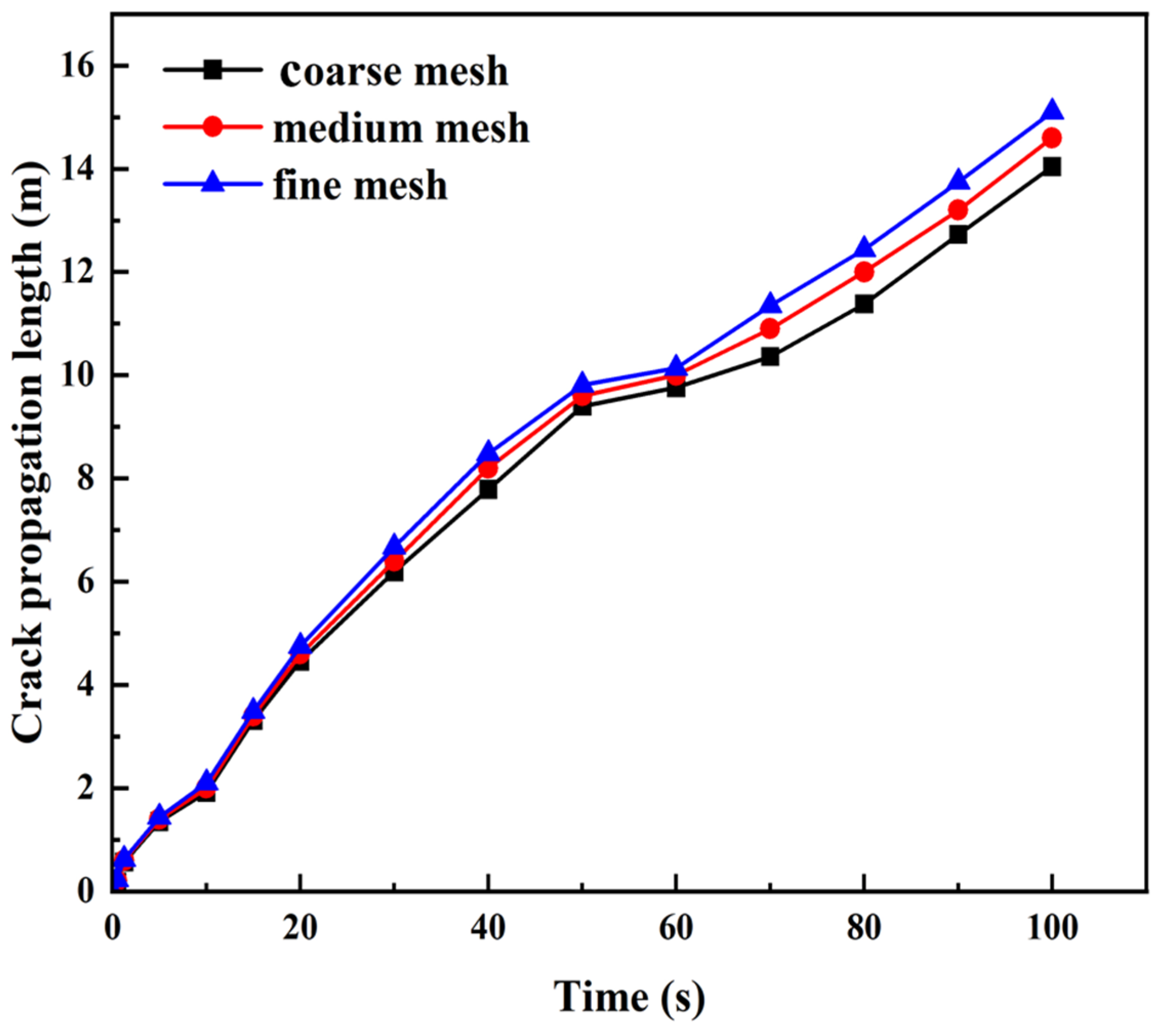
4.4. Mesh Sensitivity Analysis
5. Results and Discussion
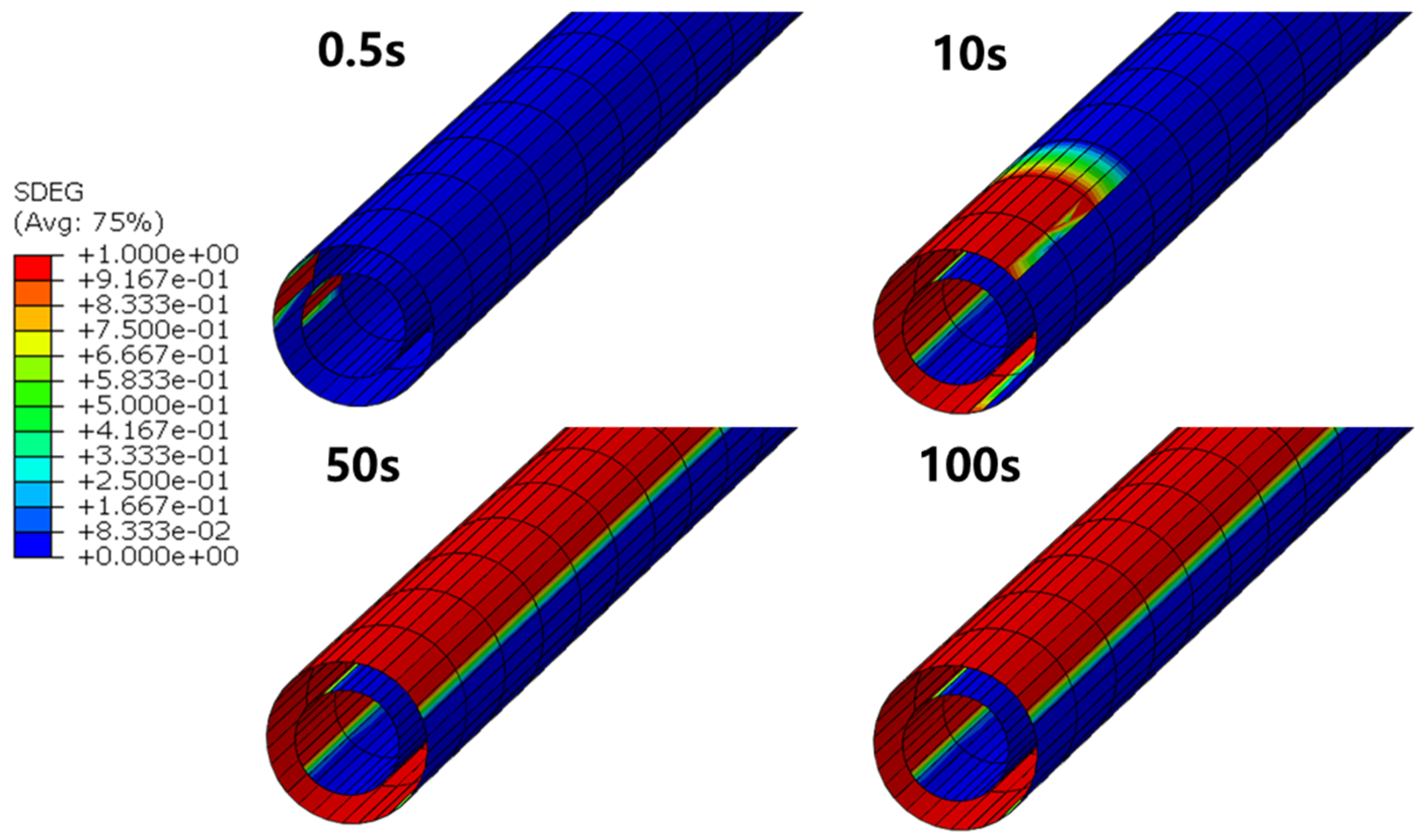
5.1. Cement Sheath Interface Crack Propagation Characteristics
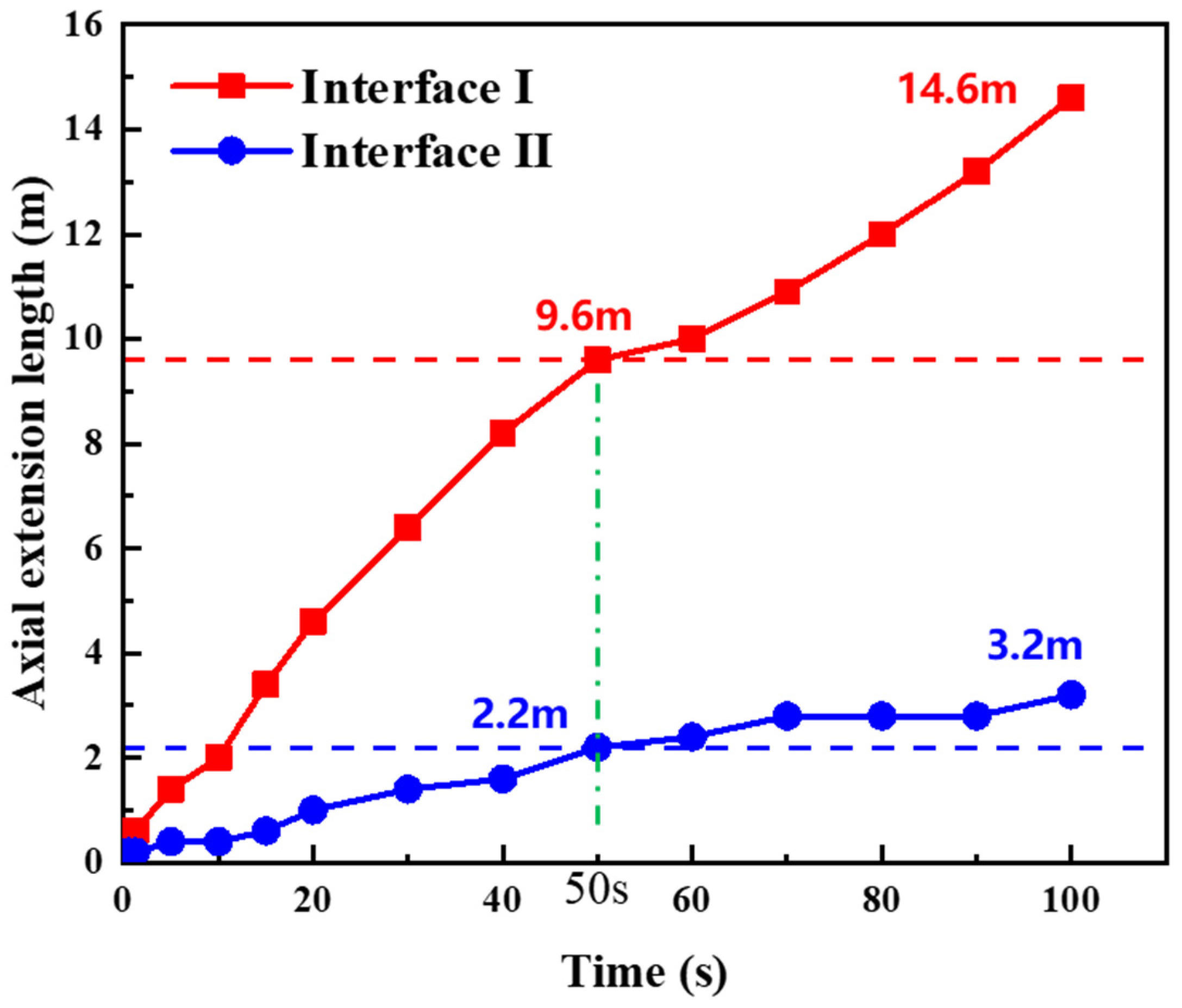
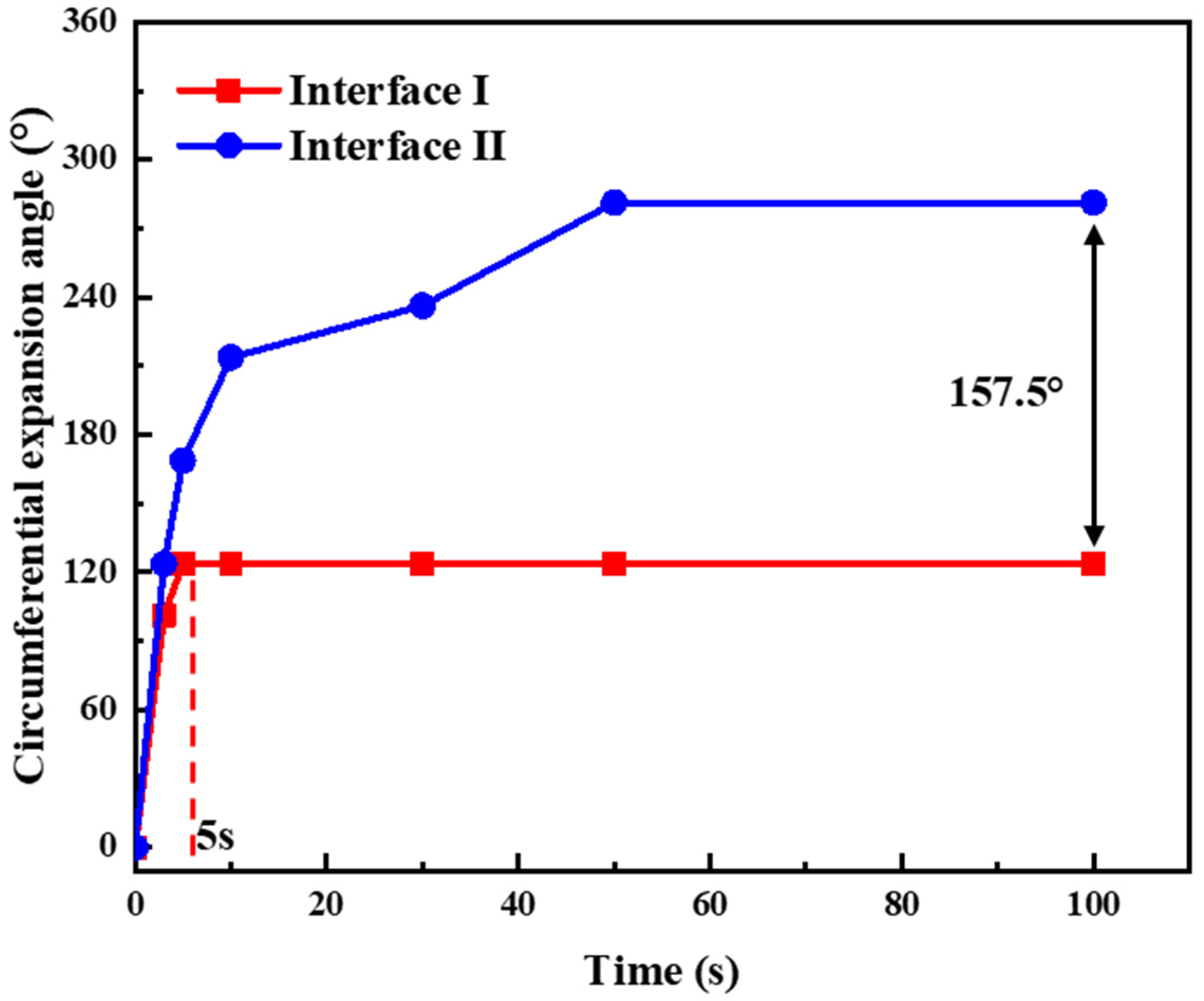
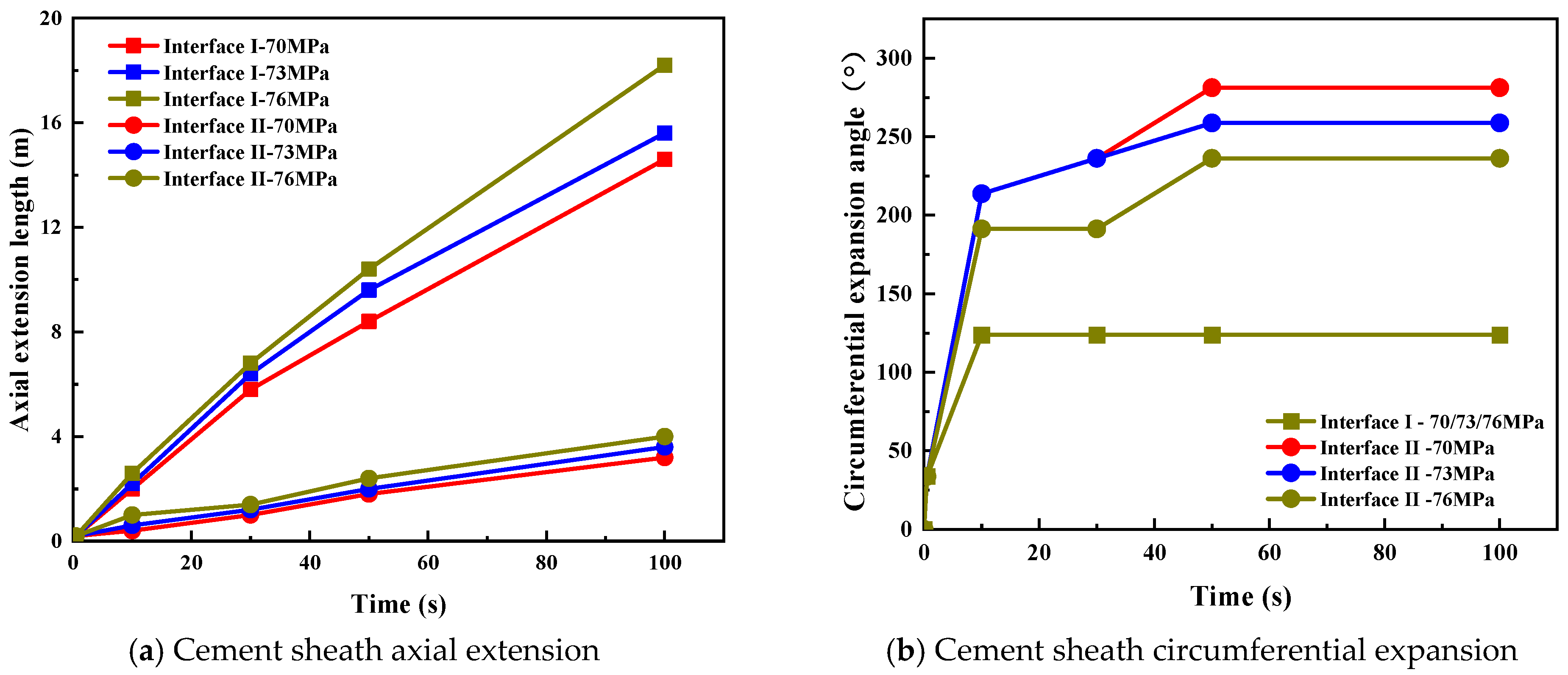
5.2. Cement Sheath Interface Crack Propagation Law
5.3. Sensitivity Analysis
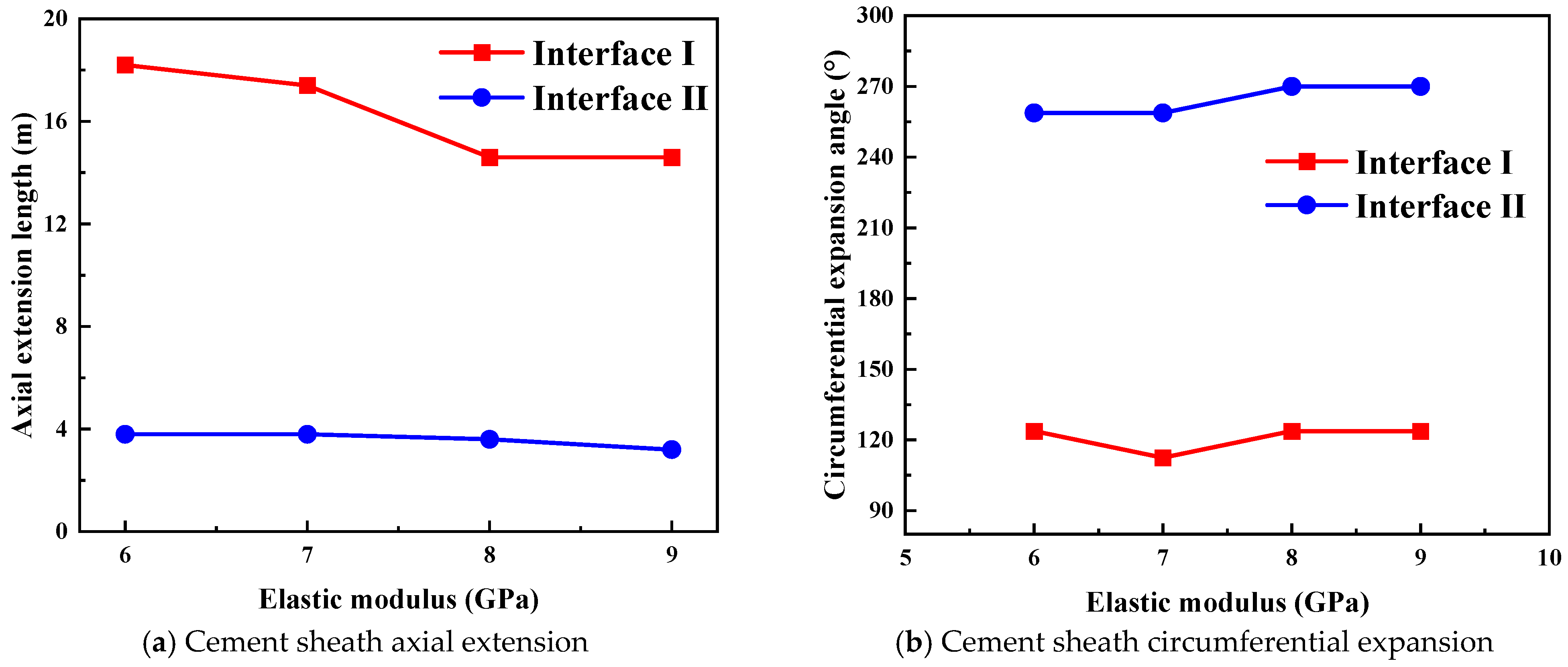
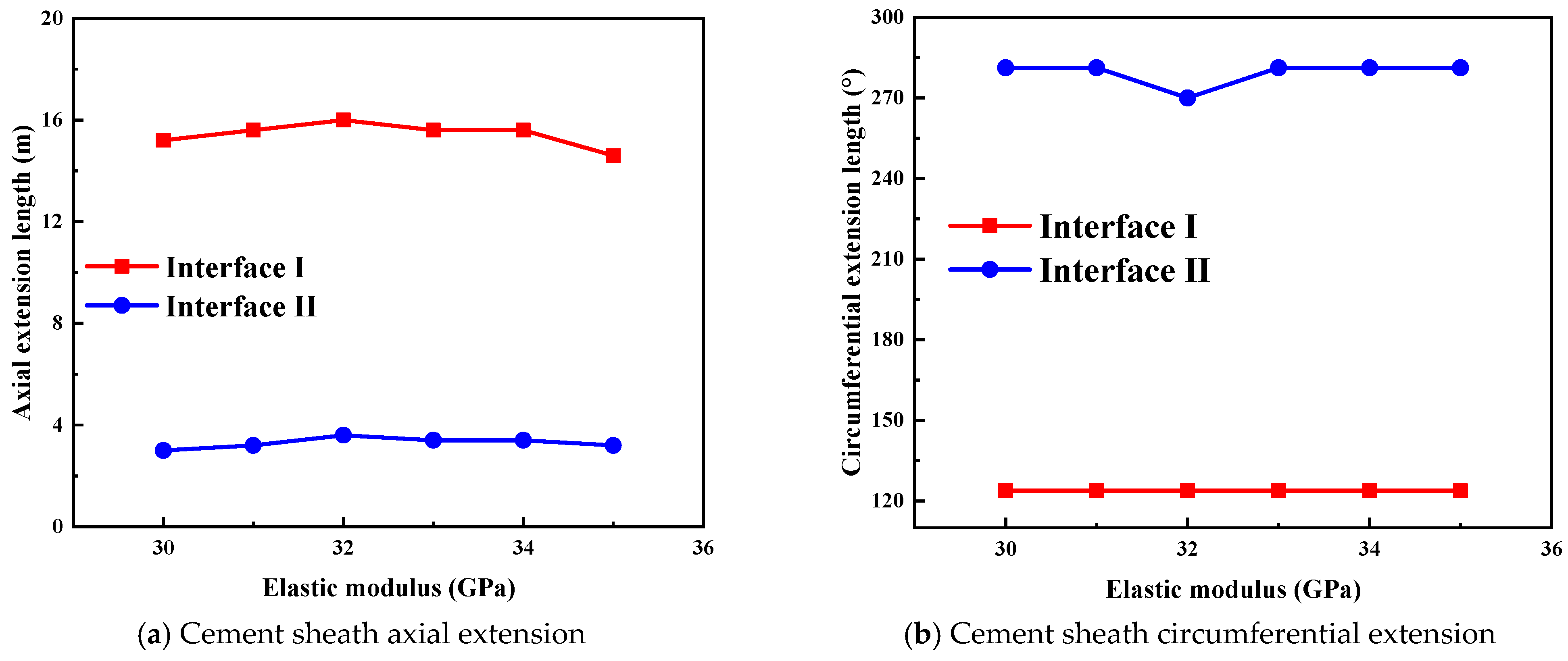
5.3.1. Mechanical Properties of Cement Sheath
- (1)
- Elastic Modulus
- (2)
- Poisson’s Ratio
5.3.2. Casing Pressure
5.3.3. Formation Elastic Modulus
6. Future Work
7. Conclusions
- (1)
- The normal and tangential bonding strengths at interfaces I and II of the cement sheath were quantified. Due to the differences in the properties of shale and casing materials, as well as their bonding degree with the cement slurry, the normal bonding strength at interface II was higher, while the tangential bonding strength was lower.
- (2)
- The interface bonding strength significantly affects crack propagation at the cement sheath interface. The crack propagation rate and length at interface I are both greater than at interface II in the axial direction. However, cracks at interface II are more likely to propagate circumferentially, with the propagation angle increasing rapidly in a short time.
- (3)
- Increasing the elastic modulus of the cement sheath helps to mitigate the axial crack propagation length at the interface. However, the impact of the elastic modulus on crack propagation, micro-annular gaps at the interface, and the tensile failure of the cement sheath should be considered comprehensively. It is recommended to control the elastic modulus of the cement sheath in the range of 7 to 8 GPa.
- (4)
- During hydraulic fracturing, appropriately reducing the construction pump pressure to lower the casing internal pressure can reduce the axial crack propagation length in the cement sheath and mitigate the risk of crossflow between stages and clusters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Zhang, Y.; Liao, W.; Yang, B.; Yang, L.; Zhou, D. The Diffusion Law of Salt Ions in Shale Reservoirs and Its Application in Hydraulic Fracture Network Diagnostics. Xinjiang Oil Gas 2025, 21, 41–49. [Google Scholar]
- Chen, X.; Zhang, Y.; Luo, W.; Cai, Z.; Yu, W. Prediction Method and Prevention Measures for Casing Deformation of Horizontal Well in Volume Fracturing. Xinjiang Oil Gas 2025, 21, 61–68. [Google Scholar]
- Tian, Z.; Shi, L.; Qiao, L. Research of and countermeasure for wellbore integrity of shale gas horizontal well. Nat. Gas Ind. 2015, 35, 70–76. [Google Scholar]
- Zeng, D.; Yu, Z.; He, Q.; Liu, Q.; Shi, T. Research on safety assessment technology of sustained casing pressure in shale gas. J. Southwest Pet. Univ. (Sci. Technol. Ed.) 2019, 41, 146–154. [Google Scholar]
- Li, J.; Chen, M.; Liu, G.; Zhang, H. Elastic-plastic analysis of casing-concrete sheath-rock combination. Acta Pet. Sin. 2005, 26, 99–103. [Google Scholar]
- Chen, Z.; Cai, Y. Study on casing load in a casing-stratum system by elastoplastic theory. Pet. Explor. Dev. 2009, 36, 242–246. [Google Scholar]
- Li, Y.; Liu, S.; Wang, Z.; Yuan, J.; Qi, F. Analysis of Cement Sheath Coupling Effects of Temperature and Pressure in Non-Uniform in-situ Stress Field. In Proceedings of the SPE International Oil and Gas Conference and Exhibition in China SPE 2010, Beijing, China, 8–10 June 2010; p. 131878. [Google Scholar]
- Xu, H.; Zhi, Z.; Shi, T.; Xiong, J. Stress analysis of the cement sheath under both pressure and temperature. Pet. Drill. Tech. 2014, 42, 45–48. [Google Scholar]
- Nabipour, A.; Joodi, B.; Sarmadivaleh, M. Finite Element Simulation of Downhole Stresses in Deep Gas Wells Cements. In Proceedings of the SPE Deep Gas Conference and Exhibition SPE 2010, Manama, Bahrain, 24–26 January 2010; p. 132156. [Google Scholar]
- De Andrade, J.; Sangesland, S. Cement sheath failure mechanisms: Numerical estimates to design for long-term well integrity. J. Pet. Sci. Eng. 2016, 147, 682–698. [Google Scholar] [CrossRef]
- Arjomand, E.; Salimzadeh, S.; Mow, W.S.; Movassagh, A.; Kear, J. Geomechanical modelling of ground surface deformation induced by CO2 injection at In Salah, Algeria: Three wells, three responses. Int. J. Greenh. Gas Control 2024, 132, 104034. [Google Scholar] [CrossRef]
- Patel, H.; Salehi, S. Development of an advanced finite element model and parametric study to evaluate cement sheath barrier. J. Energy Resour. Technol. 2019, 141, 092902. [Google Scholar] [CrossRef]
- Boukhelifa, L.; Moroni, N.; James, S.G.; Le Roy–Delage, S.; Thiercelin, M.J.; Lemaire, G. Evaluation of Cement Systems for Oil and Gas Well Zonal Isolation in a Full-Scale Annular Geometry. In Proceedings of the SPE/IADC Drilling Conference and Exhibition SPE 2004, Kuala Lumpur, Malaysia, 13–15 September 2004; p. 87195. [Google Scholar]
- Li, J.; Li, Z.; Tang, S.; Sun, J.; Wu, H.; Su, D.; Chen, W. Mechanism for the promotional effect of a novel solidifiable spacer fluid system on the cementation quality of cement sheath/formation interface. Energy Sci. Eng. 2020, 8, 4212–4221. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, H.; Wei, Y.; Bu, Y.; Jing, S.; Zhou, P. Integrity and Failure Analysis of Cement Sheath Subjected to Coalbed Methane Fracturing. Fluid Dyn. Mater. Process. 2023, 19, 329–344. [Google Scholar] [CrossRef]
- Chu, W.; Shen, J.; Yang, Y.; Li, Y.; Gao, D. Calculation of micro-annulus size in casing-cement sheath-formation system under conditions internal casing pressure change. Pet. Explor. Dev. 2015, 42, 379–385. [Google Scholar] [CrossRef]
- Liu, S.; Li, D.; Yuan, J.; Qi, F.; Shen, J.; Guo, M. Cement sheath integrity of shale gas well: A case study from the Sichuan Basin. Nat. Gas Ind. 2017, 5, 76–82. [Google Scholar] [CrossRef]
- Zeng, Y.; Liu, R.; Li, X.; Zhou, S.; Tao, Q.; Lu, P. Cement sheath sealing integrity evaluation under cyclic loading using large-scale sealing evaluation equipment for complex subsurface settings. J. Pet. Sci. Eng. 2019, 176, 811–820. [Google Scholar] [CrossRef]
- Xi, Y.; Jin, J.; Fan, L.; Guo, X.; Shen, J.; Li, J. Research on the establishment of gas channeling barrier for preventing SCP caused by cyclic loading-unloading in shale gas horizontal wells. J. Pet. Sci. Eng. 2022, 208, 109640. [Google Scholar] [CrossRef]
- Xi, Y.; Yao, Y.; Guo, X.; Li, J.; Tian, Y.; Liu, G. Failure evaluation mechanism of cement sheath sealing integrity under casing eccentricity during multistage fracturing. Pet. Sci. 2024, 21, 3428–3445. [Google Scholar] [CrossRef]
- Zhao, X.; Guan, Z.; Shi, Y.; Li, T.; Liao, H.; Jiang, J.; Sun, B. An assessment method for occurrence of micro-annular fractures on cementing interfaces of oil and gas well casing. J. China Univ. Pet. 2017, 41, 94–101. [Google Scholar]
- Guo, X.; Bu, Y.; Li, J.; Shen, Z.; Li, G.; Guo, A. The effect of mud cake on the bond strength of the second interface under varied temperatures. Drill. Fluid Complet. Fluid 2010, 27, 55–57+92. [Google Scholar]
- Plank, J.; Tiemeyer, C.; Buelichen, D.; Echt, T. A Study of Cement/Mudcake/Formation Interfaces and Their Impact on the Sealing Quality of Oilwell Cement. In Proceedings of the IADC/SPE Asia Pacific Drilling Technology Conference and Exhibition, SPE 2014, Bangkok, Thailand, 25–27 August 2014; p. 170452. [Google Scholar]
- Xu, B.; Lu, X.; Xie, Y. A new bonding strength measurement method for oil well cement sheath under high temperatures and high pressures. Nat. Gas Ind. 2016, 36, 65–69. [Google Scholar]
- Maagi, M.T.; Pin, G.; Jun, G. Influence of nano-TiO2 on the wellbore shear bond strength at cement-formation interface. Upstream Oil Gas Technol. 2020, 5, 100016. [Google Scholar] [CrossRef]
- Liu, H.; Bu, Y.; Liang, Y.; Guo, S.; Wang, Y. Device and method for evaluating the cementation property of cement-formation interface under disturbance. Res. Explor. Lab. 2020, 39, 78–83. [Google Scholar]
- Gu, J.; Yang, H.; Qin, W.; Zhang, Y.; Gao, Y. Evaluation method for isolation ability of cement-formation interface. Acta Pet. Sin. 2008, 29, 451–454. [Google Scholar]
- Guo, X.; Shen, Z.; Bu, Y.; Li, J. Research development of Cement Microannular and its solving methods. Drill. Prod. Technol. 2009, 32, 1–3+124. [Google Scholar]
- Opedal, N.; Todorovic, J.; Torsæter, M.; Vrålstad, T.; Mushtaq, W. Experimental study on the cement-formation bonding. In Proceedings of the SPE International Conference and Exhibition on Formation Damage Control SPE 2014, Lafayette, LA, USA, 26–28 February 2014; p. D021S010R006. [Google Scholar]
- Lecampion, B.; Bunger, A.; Kear, J.; Quesada, D. Interface debonding driven by fluid injection in a cased and cemented wellbore: Modeling and experiments. Int. J. Greenh. Gas Control 2013, 18, 208–223. [Google Scholar] [CrossRef]
- Feng, Y.; Li, X.; Gray, K.E. Development of a 3D numerical model for quantifying fluid-driven interface debonding of an injector well. Int. J. Greenh. Gas Control 2017, 62, 76–90. [Google Scholar] [CrossRef]
- Williams, H.; Khatri, D.; Keese, R.; Le Roy-Delage, S.; Roye, J.; Leach, D.; Rodriguez, J. Flexible, Expanding Cement System (FECS) Successfully Provides Zonal Isolation Across Marcellus Shale Gas Trends. In Proceedings of the SPE Canada Unconventional Resources Conference SPE 2011, Calgary, AB, Canada, 15–17 November 2011; p. 149440. [Google Scholar]
- Kim, J.; Moridis, G.J.; Martinez, E.R. Investigation of possible wellbore cement failures during hydraulic fracturing operations. J. Pet. Sci. Eng. 2016, 139, 254–263. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Jin, J.; Jiang, L.; Ding, F.; Yuan, X. Cement ring interface crack propagation under volume fracturing in shale gas well. Acta Pet. Sin. 2017, 38, 105–111. [Google Scholar]
- Lian, W.; Li, J.; Liu, G.; Tao, Q. Numerical simulation of cement-to-formation interface debonding during hydraulic fracturing of shale gas wells. J. Adhes. Sci. Technol. 2020, 34, 917–935. [Google Scholar] [CrossRef]
- Wang, W.; Taleghani, A.D. Three-dimensional analysis of cement sheath integrity around Wellbores. J. Pet. Sci. Eng. 2014, 121, 38–51. [Google Scholar] [CrossRef]
- Wang, D.; Li, J.; Zhang, W.; Lian, W. Performance Evaluation of the Cement Sheath in Jimsar Shale Oil Wells. Xinjiang Oil Gas 2023, 19, 49–55. [Google Scholar]
- Turon, A.; Camanho, P.P.; Costa, J.; Dávila, C.G. A damage model for the simulation of delamination in advanced composites under variable-mode loading. Mech. Mater. 2006, 38, 1072–1089. [Google Scholar] [CrossRef]
- Hagoort, J.; Weatherill, B.D.; Settari, A. Modeling the propagation of waterflood-induced hydraulic fractures. Soc. Pet. Eng. J. 1980, 20, 293–303. [Google Scholar] [CrossRef]
- Wang, W.; Taleghani, A.D. Impact of hydraulic fracturing on cement sheath integrity; A modelling approach. J. Nat. Gas Sci. Eng. 2017, 44, 265–277. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Fan, M.; Chen, X.; Jin, D.; Gao, F.; Wang, Q. Rule of Propagation of Fractures through the Bonding Interfaces of Cement Sheath in Horizontal WellFracturing. Drill. Fluid Complet. Fluid 2022, 39, 761–766+775. [Google Scholar]
- Yan, X.I.; Jun, L.I.; Liu, G.; Qian, T.; Wei, L. A new numerical investigation of cement sheath integrity during multistage hydraulic fracturing shale gas wells. J. Nat. Gas Sci. Eng. 2018, 49, 331–341. [Google Scholar] [CrossRef]
- Guo, X.; Song, Y.; Bu, Y.; Guo, S.; Liu, H.; Wang, C. Simulation of seal integrity of cement sheath under variable internal casing pressure based on damage mechanics. Acta Pet. Sin. 2020, 41, 1425–1433. [Google Scholar]







| Normal Cementation Strength | Tangential Cementation Strength | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | Destructive Load (KN) | Destructive Displacement | Tensile Strength (MPa) | Average Value (MPa) | Standard Deviation | Number | Destructive Load (KN) | Destructive Displacement | Tensile Strength (MPa) | Average Value (MPa) | Standard Deviation |
| N-1 | 0.211 | 0.77 | 0.36 | 0.413 | 0.041 | S-1 | 1.855 | 1.03 | 0.468 | 0.464 | 0.0026 |
| N-2 | 0.248 | 0.81 | 0.42 | S-2 | 1.815 | 0.92 | 0.463 | ||||
| N-3 | 0.266 | 0.75 | 0.46 | S-3 | 1.817 | 1.31 | 0.462 | ||||
| Normal Cementation Strength | Tangential Cementation Strength | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | Destructive Load (KN) | Destructive Displacement | Tensile Strength (MPa) | Average Value (MPa) | Standard Deviation | Number | Destructive Load (KN) | Destructive Displacement | Tensile Strength (MPa) | Average Value (MPa) | Standard Deviation |
| N-11 | 0.316 | 1.78 | 0.55 | 0.577 | 0.025 | S-11 | 1.215 | 1.18 | 0.306 | 0.187 | 0.0246 |
| N-12 | 0.345 | 1.41 | 0.57 | S-12 | 1.003 | 1.27 | 0.252 | ||||
| N-13 | 0.358 | 1.05 | 0.61 | S-13 | 1.199 | 1.21 | 0.30 | ||||
| Name | Outer Diameter (mm) | Inside Diameter (mm) | Elastic Modulus (GPa) | Poisson’s Ratio | Internal Friction Angle (°) | Cohesive Force (MPa) |
|---|---|---|---|---|---|---|
| Casing | 139.7 | 118.62 | 210 | 0.3 | - | - |
| Cement sheath | 215.9 | 139.7 | 8 | 0.17 | 15.1 | 21 |
| Formation | - | - | 35 | 0.25 | 30 | 59 |
| Density (g/cm3) | Toughened Materials | Elasticity Modulus (GPa) |
|---|---|---|
| 1.88 | None | 9.96 |
| 1.84 | Fibers and elastic particles | 7.02 |
| 1.81 | Elastic particles | 5.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Wang, X.; Xie, S.; Wu, Y.; Li, Y.; Shu, Z.; Zhang, X.; Lian, W.; Yuan, D. A Study on the Crack Propagation Behavior of Cement Sheath Interfaces Considering Bond Strength. Processes 2025, 13, 1631. https://doi.org/10.3390/pr13061631
Wu J, Wang X, Xie S, Wu Y, Li Y, Shu Z, Zhang X, Lian W, Yuan D. A Study on the Crack Propagation Behavior of Cement Sheath Interfaces Considering Bond Strength. Processes. 2025; 13(6):1631. https://doi.org/10.3390/pr13061631
Chicago/Turabian StyleWu, Jiwei, Xuegang Wang, Shiyuan Xie, Yanxian Wu, Yilin Li, Zhenhui Shu, Xiaojun Zhang, Wei Lian, and Dandan Yuan. 2025. "A Study on the Crack Propagation Behavior of Cement Sheath Interfaces Considering Bond Strength" Processes 13, no. 6: 1631. https://doi.org/10.3390/pr13061631
APA StyleWu, J., Wang, X., Xie, S., Wu, Y., Li, Y., Shu, Z., Zhang, X., Lian, W., & Yuan, D. (2025). A Study on the Crack Propagation Behavior of Cement Sheath Interfaces Considering Bond Strength. Processes, 13(6), 1631. https://doi.org/10.3390/pr13061631





