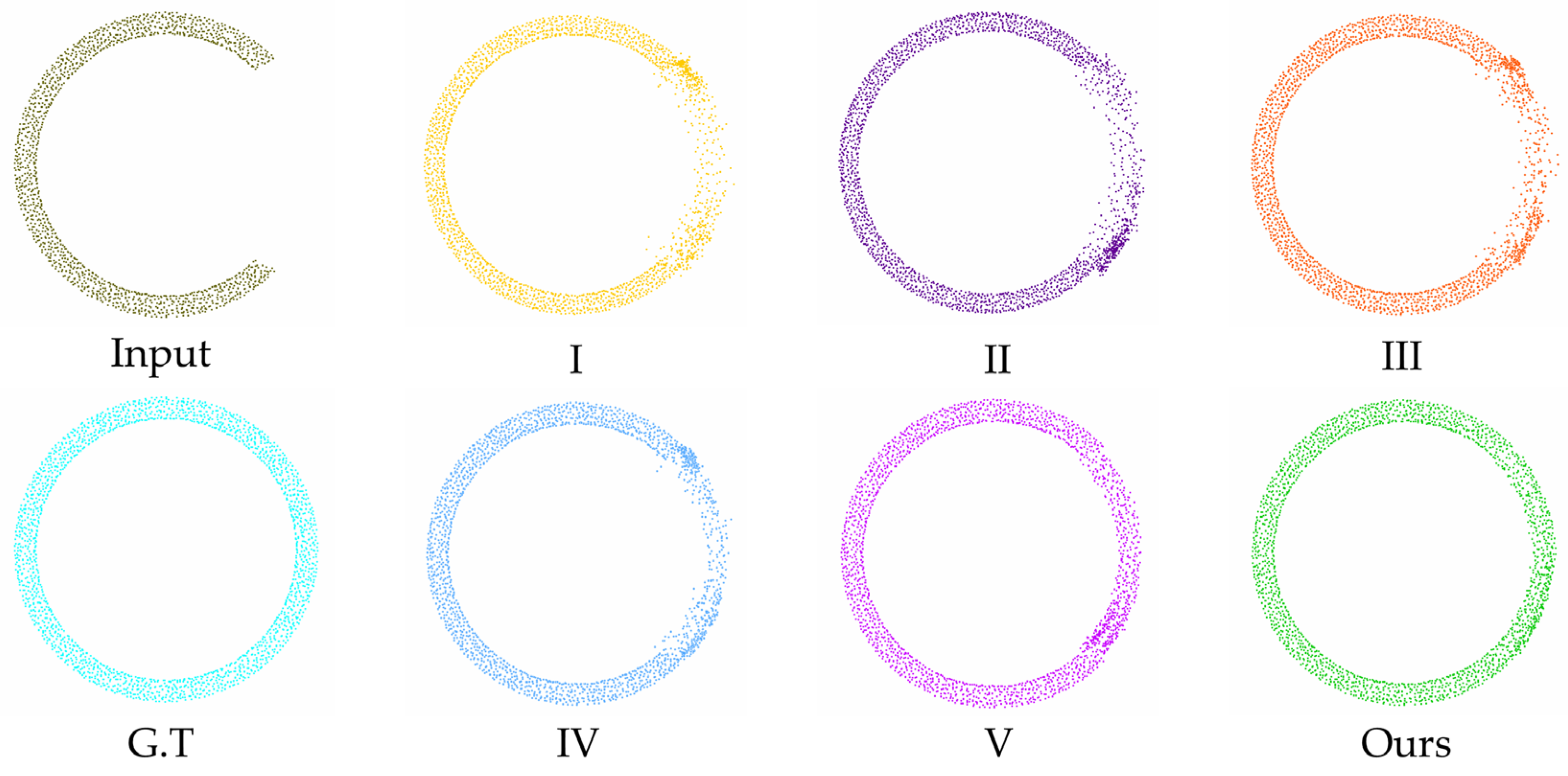1. Introduction
As a critical component in engines, the assembly quality of oil seal rings significantly impacts engine performance. Consequently, assessing the assembly quality of oil seal rings is an essential step in the engine production process. Traditional detection methods rely on manual measurements, which are inefficient and time-consuming. Moreover, two-dimensional vision techniques, lacking depth information, fail to capture the spatial structural details of the components [
1].
With the ongoing advancement of industrial manufacturing, the demand for industrial automation has steadily increased, driving widespread attention to three-dimensional (3D) vision technologies in industrial applications [
2]. As the primary data representation in 3D vision, point clouds offer significant advantages in non-contact inspection, precision measurement, intelligent assembly, and robot navigation. This is due to their ability to accurately and intuitively capture the spatial morphology, geometric features, and surface details of objects. Nevertheless, in the process of acquiring point clouds, elements such as weather conditions, resolution limitations, occlusion, and viewing angles [
3] often result in incomplete data with varying degrees of missing information. Consequently, efficiently completing missing point cloud data to reconstruct complete 3D information has emerged as a critical research direction in 3D vision applications. By integrating geometric knowledge with deep learning techniques, point cloud completion technology not only compensates for acquisition deficiencies but also provides more comprehensive and precise 3D data, enhancing production efficiency and quality in industrial settings. Leveraging advancements in computational technology, a series of deep learning-based algorithms have emerged, markedly advancing point cloud completion and substantially enhancing its accuracy. Nevertheless, these methods typically depend on extensive training data and often exhibit sub-optimal performance in small-sample scenarios, where data scarcity is common due to the complexities of industrial data acquisition [
4,
5,
6,
7].
To address these challenges, we propose a novel point cloud completion network built upon the PF-Net framework, integrating dynamic multi-scale feature fusion and Transformer enhancements to achieve robust performance under limited data conditions. The main contributions are as follows:
We introduce a multi-scale dynamic weighted fusion point cloud completion model with robust feature extraction capabilities, outperforming most state-of-the-art methods in comprehensive performance on small-sample data.
We develop an EdgeConv [
8]-integrated multi-layer perceptron (ECMLP), enhancing the model’s ability to capture local geometric features in point clouds.
We design a multi-scale dynamic weighted fusion (MS-DWF) module, enabling adaptive feature integration across scales and preserving critical information for effective synthesis.
We propose a Transformer-enhanced multi-layer perceptron (TRMLP) module, strengthening the interplay between global and local features to improve the precision of missing region predictions.
We present a custom oil seal ring point cloud dataset and validate our model’s superior completion performance on this dataset, particularly under small-sample conditions.
2. Related Work
Existing point cloud completion methods can be broadly classified into traditional approaches and deep learning-based techniques [
9]. Traditional methods primarily rely on geometric features [
10] or model databases [
11]. Geometric feature-based approaches, such as surface reconstruction [
12] and symmetry-based methods [
13], depend on assumptions of shape smoothness or symmetry. These are effective for scenarios with minor data loss but struggle with large-scale missing regions. Model database-based methods—including direct retrieval, partial retrieval [
14], deformation [
15,
16], and geometric tuple techniques [
17]—perform completion via shape matching. However, their reliance on extensive databases limits flexibility and generalization, particularly in complex scenarios. Overall, traditional methods exhibit constraints in adaptability and completion quality.
The rapid rise of deep learning has shifted the research focus toward deep learning-based point cloud completion, leveraging its superior feature learning and adaptability to handle complex shapes and significant data loss. These methods extract global and local features directly from point cloud data, capturing geometric and topological information to produce high-quality completions, thereby overcoming the limitations of traditional approaches and improving accuracy, adaptability, and computational efficiency.
Early deep learning methods, however, were not designed to process unstructured point clouds directly, which are inherently disordered and complex, often containing additional attributes like intensity, color, and timestamps [
18]. Initial approaches converted point clouds into 3D meshes for processing with 3D convolutional networks [
19] or projected them into 2D multi-view images for 2D convolutional analysis [
20]. These techniques suffered from inefficiencies, loss of geometric detail, and inadequate feature representation. In 2017, Qi et al. introduced PointNet [
21], a pioneering model capable of directly processing point clouds, addressing their irregularity and disorder. To enhance local feature extraction, PointNet++ [
22] was proposed, incorporating a hierarchical feature extraction structure with feature aggregation. Yuan et al. [
23] developed PCN, utilizing PointNet as an encoder and FoldingNet [
24] as a decoder for coarse-to-fine completion. TopNet [
25] introduced a hierarchical tree decoder for layer-by-layer point cloud generation, while PF-Net [
26] employed a multi-resolution encoder and pyramid-style recursive decoder to improve completion accuracy progressively. GRNet [
27] excelled in handling large-scale missing regions and complex shapes through geometry-aware mechanisms, residual learning, and multi-scale feature fusion.
The advent of the Transformer model [
28] further advanced point cloud processing due to its alignment invariance and robust global modeling capabilities [
29]. PoinTr [
30] first integrated a Transformer into point cloud completion, designing a Transformer-based encoder. AdaPoinTr [
31] built on this by introducing adaptive feature learning, enhancing adaptability to diverse missing patterns, and boosting accuracy. Similarly, Xiang et al. [
32] proposed SnowflakeNet, featuring a snowflake point deconvolution layer and skip-transformer module to simulate point generation, significantly improving completion precision through iterative refinement.
Although the aforementioned deep learning-based approaches have made remarkable progress in point cloud completion, these methods were not originally designed for few-shot point cloud completion scenarios. Consequently, they heavily rely on large-scale point cloud data for training. However, given the high complexity and susceptibility to noise inherent in point cloud data, collecting sufficient high-quality training data is extremely time-consuming and labor-intensive. Therefore, learning effective point cloud models from limited training data has emerged as a critical challenge in the field of point cloud understanding.
3. Methods
The architectural framework of our model is illustrated in
Figure 1. The model comprises three primary components: a multi-scale feature encoder, a pyramid decoder, and a discriminator.
Initially, the input incomplete point cloud undergoes two iterations of Iterative Farthest Point Sampling (IFPS) to generate three downsampled point clouds of varying densities. Compared to other sampling methods, IFPS offers higher efficiency, uniform sampling, and better preservation of the point cloud’s geometric structure. These multi-density point clouds are then processed by the multi-scale feature encoder, where feature extraction is performed using the ECMLP, yielding latent vectors at three distinct scales. Subsequently, the MS-DWF assigns learnable weights to these multi-scale features (latent vectors), which are then concatenated and fused to produce a comprehensive multi-scale feature map (fusion vector). This feature map is further refined by the Transformer multi-layer perceptron (TRMLP) module to extract the final feature vector.
The final feature vector is fed into the pyramid decoder, where three fully connected layers generate feature vectors corresponding to the missing regions. These vectors are decoded and hierarchically fused to produce three predicted point clouds aligned with the ground truth (real point cloud). A discriminator then evaluates the similarity between the generated and real point clouds, computing a loss that is fed back to the network. This feedback loop iteratively optimizes the model’s parameters, enhancing the quality of point cloud completion.
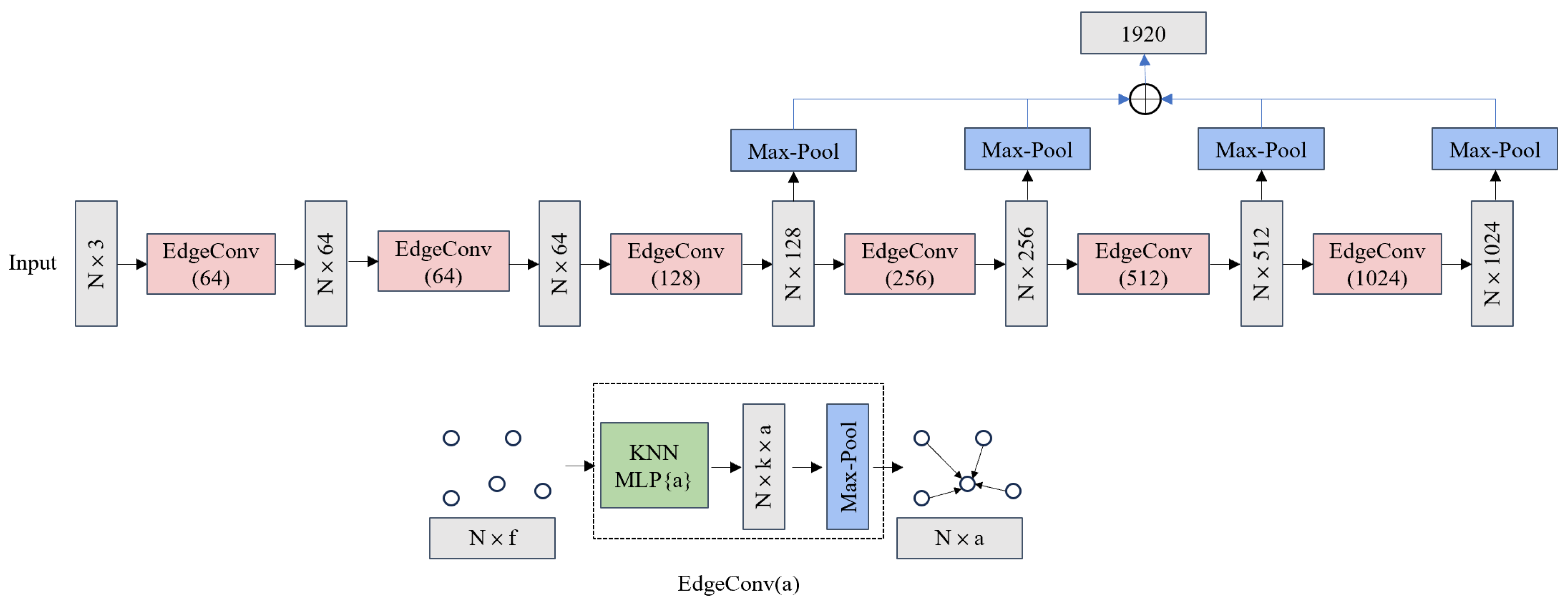
3.1. ECMLP Feature Extraction Module
In small-sample oil seal ring scenarios, point cloud completion faces challenges due to limited training data, which often leads to the insufficient capture of local geometric details, such as edges and fine structures, critical for accurate reconstruction. The EdgeConv multi-layer perceptron (ECMLP) module is designed to address these issues by enhancing the extraction of local geometric features, ensuring precise representation of oil seal ring structures despite data scarcity.
The structure of the EdgeConv multi-layer perceptron (ECMLP) is depicted in
Figure 2. Built around EdgeConv as its core, this module is designed to efficiently extract both local geometric features and global structural information from point cloud data. The input to the module consists of an N × 3 point cloud, where N represents the number of points and 3 denotes the 3D coordinates (x, y, z) of each point. Within the EdgeConv framework, the input point cloud is first processed by constructing local neighborhoods using k-nearest neighbors (k-nn), which establishes correlations between each point and its k-nearest neighbors. Subsequently, a multi-layer perceptron (MLP) extracts feature relationships with these neighboring points, and a max-pooling (MaxPool) operation aggregates the features to derive the local geometric characteristics and global structural information for each point.
The ECMLP module comprises six stacked EdgeConv layers, progressively encoding the input into feature vectors of increasing dimensionality: {64, 64, 128, 256, 512, 1024}. To capture multi-scale global information, the feature vectors from the last four layers ({128, 256, 512, 1024}) are concatenated after MaxPool, yielding a multi-scale feature vector with 1920 dimensions (i.e., 128 + 256 + 512 + 1024 = 1920). This layer-by-layer refinement of local features, combined with the fusion of multi-scale information, significantly enhances the robustness and discriminative power of the point cloud feature representation, making it well suited for point cloud completion tasks. Furthermore, this design enables the encoder to effectively gather both local spatial structures and global features, thereby improving the model’s ability to handle complex geometric relationships. By improving the capture of local geometric details, ECMLP ensures high-quality point cloud completion for small-sample oil seal rings, supporting more precise quality evaluation in industrial applications.
3.2. MS-DWF Feature Fusion Module
In small-sample oil seal ring scenarios, point cloud completion faces challenges due to varying missing rates. Traditional feature fusion strategies rely on static weight mechanisms, which fail to adaptively handle feature extraction from different missing regions and consequently lose critical geometric structure details, thereby hindering accurate completion. To address this, we propose the Multi-Scale Dynamic Weighted Fusion (MS-DWF) module, which dynamically optimizes multi-scale feature extraction and integration according to the missing data degree to ensure geometric accuracy.
To overcome the limitations of fixed weight allocation in multi-scale feature fusion, we propose a Multi-Scale Dynamic Weighted Fusion (MS-DWF) module. By introducing learnable weight parameters, this module dynamically optimizes the integration of multi-scale features based on their varying importance, thereby enhancing the robustness and discriminative power of point cloud feature representations.
The MS-DWF module utilizes features extracted by the ECMLP module from point cloud data at different densities, denoted as
, where
i indexes the feature scale. To achieve dynamic weighted fusion, a set of learnable weights
is defined for each scale’s features. These weights are initialized to 1, ensuring equal contributions from all scales at the start of training. During training,
is adaptively adjusted to assign greater values to features with higher contributions. The feature-weighted fusion is formulated in Equation (1).
where
represents the fused multi-scale feature map, and
denotes element-by-element multiplication.
This module adaptively adjusts the weights of multi-scale features to achieve optimal feature integration. Enhancing the model’s ability to consolidate information, enables more effective extraction of useful features from limited data, ultimately improving the point cloud completion performance. By enhancing the robustness of feature integration across different missing rates, MS-DWF improves the accuracy of oil seal ring point cloud completion, enabling more reliable geometric assessment in industrial quality control.
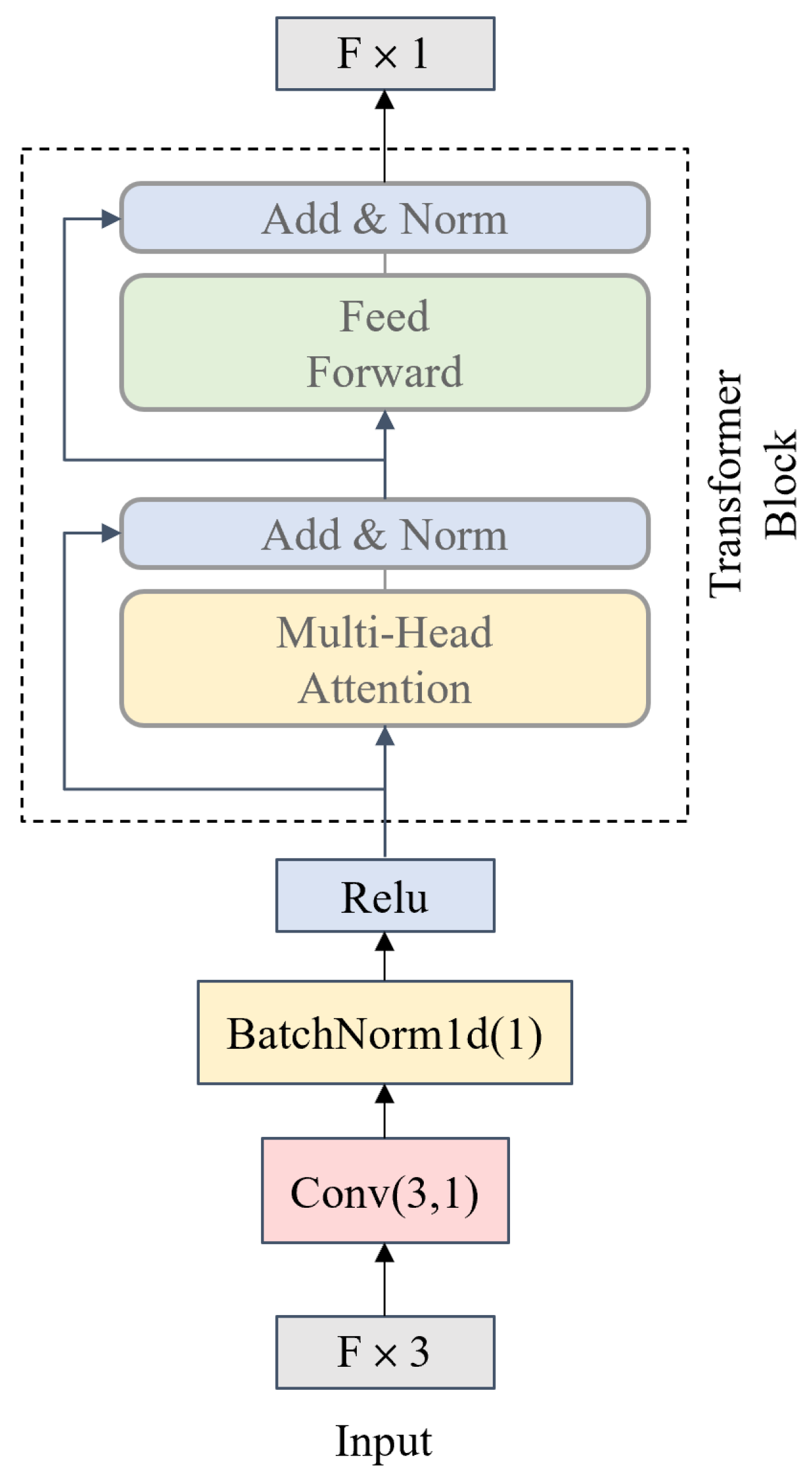
3.3. TRMLP Feature Enhancement Module
In small-sample oil seal ring scenarios, point cloud completion often struggles to balance global and local features, leading to geometric inconsistencies in the reconstructed point cloud, which can affect the accuracy of quality inspection. The Transformer multi-layer perceptron (TRMLP) module is designed to address these challenges by strengthening the connection between global and local features, ensuring geometric consistency in the completed point cloud despite limited data.
The Transformer multi-layer perceptron (TRMLP) module, with its structure illustrated in
Figure 3, is designed to strengthen the global contextual modeling of point cloud features, overcoming the limitations of local-only feature extraction. Utilizing a multi-head attention approach, this module adeptly identifies extended-range relationships between points within the point cloud, while residual connections and a feed-forward network enhance feature expressiveness, producing representations with richer information content.
The module first processes input point cloud features through dimensionality reduction and normalization. Each feature, originally in three dimensions (N × 3), is compressed to one dimension (N × 1) via a Conv(3,1) convolutional operation, reducing computational complexity. Batch normalization and a ReLU activation function then normalize and non-linearly transform these downscaled features, ensuring stability and enhancing the expressiveness of the feature distribution. The processed features are subsequently fed into the feature enhancement layer, which comprises two core components: a multi-head attention mechanism and a feed-forward network.
The multi-head attention mechanism simultaneously models long-range dependencies across all points, generating contextual features enriched with global relationships. A two-layer feed-forward network further refines these features through mapping and non-linear transformation. To ensure training stability and optimization efficiency, residual connections and normalization operations (Add and Norm) are applied after each sub-component. The final output is a fused global feature vector of dimensions of F × 1, combining global structural information and localized geometric features of the point cloud. By enhancing the quality and consistency of point cloud completion, TRMLP supports the more accurate quality assessment of oil seal rings in industrial applications.
3.4. Pyramid Decoder
In small-sample oil seal ring scenarios, point cloud completion faces challenges in reconstructing missing regions with high fidelity, as limited data often result in coarse or incomplete representations of critical geometric structures, impacting the accuracy of quality inspection. The pyramid decoder is designed to address these issues by employing a hierarchical recovery strategy, progressively refining the point cloud to achieve high-fidelity reconstruction of oil seal ring structures.
The structure of the pyramid decoder is illustrated in
Figure 1. The final feature vector input to the decoder is processed through three fully connected layers, yielding three distinct feature representations: detailed features, key features, and core features. Each feature layer is tasked with predicting and generating point clouds for missing regions at different resolutions. Specifically, core features produce a coarse point cloud, key features generate the primary structure, and detailed features refine the output into a high-resolution point cloud. The decoder employs a hierarchical recovery strategy, initially generating a low-resolution coarse point cloud. Subsequently, higher-resolution features are introduced layer by layer to progressively refine the predictions, transforming the coarse point cloud into a fine, detailed one. This layer-by-layer processing ensures the gradual reconstruction of missing regions, with each layer’s output building upon the previous layer’s results while incorporating additional detail to enhance the precision of the completion. By delivering a high-quality and detailed point cloud, the pyramid decoder enhances the reliability of oil seal ring reconstruction for industrial quality evaluation.
3.5. Discriminator
In small-sample oil seal ring scenarios, point cloud completion faces significant challenges due to limited training data, often resulting in generated point clouds that lack realism and fail to accurately represent the true geometric structures, such as edges and surfaces, critical for quality inspection. The discriminator in our model is designed to address these issues by enhancing the realism of the generated point clouds through adversarial training, ensuring high-fidelity reconstruction that aligns with the real geometry of oil seal rings.
The structure of the discriminator is depicted in
Figure 1. It takes as input both generated and real point clouds and adopts an autoencoder-like architecture. Feature extraction is performed using a multi-layer perceptron (MLP), followed by multiple fully connected layers, culminating in a sigmoid classifier that determines whether the input point cloud is real or generated. The discriminator’s primary role is to guide the generator in optimizing the point cloud generation process by distinguishing between real and synthetic outputs. During training, it assesses the similarity between the generated and real point clouds, providing feedback to the generator to improve the realism of its outputs. Through adversarial training, the generator iteratively enhances the accuracy and fidelity of the completed point cloud, ultimately achieving high-quality point cloud reconstruction. By ensuring the generated point clouds closely match the real geometric features of oil seal rings, the discriminator improves the overall quality of completion, supporting more reliable quality assessment and defect detection in industrial applications.
4. Loss Function
The loss function (
) comprises two components: a multi-stage completion loss (
) and an adversarial loss (
), and it is formulated in Equation (2).
measures the discrepancy between the real point cloud and the generated point cloud in missing regions across multiple resolution stages. It is formulated in Equation (3).
where
,
, and
denote the predicted detailed, coarse, and primary point clouds, respectively, generated by the pyramid decoder.
represents the real point cloud with a point count matching
, while
and
are
downsampled via IFPS to correspond to
and
, respectively. The Chamfer Distance (CD) measures the geometric difference between point cloud sets, assessing the similarity between generated and real point clouds, and is formulated in Equation (4).
Here, and represent the real and generated point clouds, respectively.
optimizes the encoder and decoder to enhance the quality of the generated point clouds, aligning their distribution more closely with that of the real point clouds. It is formulated in Equation (5).
represents the output of the generator, i.e., the predicted missing point cloud; is the discriminator, tasked with distinguishing whether an input point cloud originates from real data or is produced by the generator; and denote the real point cloud and the input point cloud, respectively; and is the total number of training samples.
The final loss function integrates the completion loss and the adversarial loss through weighted summation to achieve joint optimization, where the weights and satisfy .
5. Experiments
5.1. Datasets
This research utilizes two datasets to assess the effectiveness of the proposed model. The first is an industrial oil seal ring point cloud dataset, comprising 156 point cloud models of industrial oil seal rings with seven distinct specifications and shapes. To construct this dataset, we started with 156 three-dimensional models of industrial oil seal rings, representing 7 different models and sizes, sourced from industrial design specifications. These 3D models were imported into CloudCompare 2.14, a 3D point cloud processing software, where they were converted into point cloud models by sampling the surface vertices of each model. To meet the input requirements of the model and ensure uniformity, Iterative Farthest Point Sampling (IFPS) was applied to standardize the number of points in each point cloud to 2048, preserving the geometric integrity of the oil seal rings. The size information of these oil seal rings is summarized in
Table 1, where d represents the inner diameter, D represents the outer diameter, and T represents the thickness.
The second is a small-sample subset derived from ShapeNet, consisting of 16 categories, each containing no more than 100 samples. ShapeNet-Part is a widely used public dataset for 3D shape analysis, containing 17,775 point cloud models across 16 categories, such as chairs, tables, and airplanes. To create a small-sample subset suitable for our research, for each category, we randomly sampled a maximum of 100 point cloud models to simulate small-sample conditions, resulting in a total of 1466 point cloud models. This sampling process was designed to balance the dataset while ensuring diversity across categories, with the number of samples per category ranging from 62 to 100 based on availability.
For both datasets, 70% of the data are allocated for training and 30% for testing. Prior to model input, all data undergo normalization and centering preprocessing.
5.2. Experimental Settings
The experiments are conducted on an Ubuntu 18.04 operating system, utilizing the PyTorch 1.12 framework for training on an NVIDIA TITAN RTX GPU. To generate incomplete point clouds, a spherical cropping method is applied to complete point clouds, with a default missing rate of 25%. Specifically, additional experiments with 50% and 75% missing rates are conducted on the industrial oil seal ring dataset to evaluate the model’s performance under conditions of large-scale regional missing data. For fair evaluation, the input and output point counts of all models are standardized: at a 25% missing rate, the input point cloud contains 1536 points and the output point cloud contains 2048 points; at a 50% missing rate, the input contains 1024 points and the output contains 2048 points; at a 75% missing rate, the input contains 512 points and the output contains 2048 points. The parameter configurations of the baseline models (AdaPoinTr, FoldingNet, GRNet, PCN, PF-Net, TopNet, and SnowflakeNet) follow their original papers, while our model employs the Adam optimizer (with an initial learning rate of 0.0001 and a weight decay of 0.001), combined with a StepLR scheduler that reduces the learning rate to 0.2 times its previous value every 40 epochs, a batch size of 10, and training for 200 epochs. All comparative models are re-implemented by this study and trained on the aforementioned two datasets to obtain their pre-trained weight files. Based on these weight files, the incomplete input point clouds are processed to infer complete point clouds with 2048 points. All point cloud files are visualized using MeshLab 2023.12 software.
5.3. Evaluation Metrics
The effectiveness of point cloud completion is evaluated through three criteria: Chamfer Distance (CD), as formulated in Equation (4). Earth Mover’s Distance (EMD), and Maximum Mean Discrepancy (MMD), as formulated in Equation (7). These metrics evaluate the similarity between generated and real point clouds by computing distance-based measures, where smaller values indicate better completion quality. Among these, CD is selected as the primary evaluation metric due to its proven effectiveness in point cloud completion research, while EMD and MMD serve as secondary metrics.
EMD measures the minimum matching distance between the generated point cloud and the real point cloud, where
denotes the real point cloud,
denotes the generated point cloud, and
represents a bijective mapping between the two point clouds. The computation is formulated in Equation (6).
MMD evaluates the distributional difference between two point sets, where
and
represent the real and generated point clouds, respectively, and
is a Gaussian kernel used to compute the similarity between point sets. The computation is formulated in Equation (7).
5.4. Evaluation on the Oil Seal Ring Dataset
To validate the performance of our proposed model, we conducted qualitative and quantitative comparisons with seven representative point cloud completion models: AdaPoinTr, FoldingNet, GRNet, PCN, PF-Net, TopNet, and SnowflakeNet.
Table 2 presents the performance of various models across three metrics—CD, EMD, and MMD—under missing rates of 25%, 50%, and 75%.
Figure 4 visualizes the completion results of these models on the industrial oil seal ring dataset for 25% missing rates. The experimental outcomes reveal that our approach delivers superior effectiveness across all three evaluation measures. Specifically, compared to AdaPoinTr, our model reduces CD by 33%; compared to SnowflakeNet, it reduces EMD by 24%; and compared to PCN, it reduces MMD by 60%.
The visualization in
Figure 4 further highlights the differences. AdaPoinTr produces point clouds with partial completion but exhibits uneven density, local gaps, and unsmooth edges. This is primarily attributed to its feature extraction process, which prioritizes global features while neglecting local details. Consequently, it fails to effectively balance local detail fidelity with global shape consistency, ultimately resulting in non-uniform density distributions and the formation of local voids. FoldingNet yields severely distorted results, significantly deviating from the target shape This distortion originates from its folding-based decoding strategy, which folds a two-dimensional grid into a three-dimensional point cloud through deformation. Under few-shot conditions, the features learned by FoldingNet are insufficient to support it in performing multiple folding transformations to generate a three-dimensional point cloud, thus leading to severe distortion in the output. GRNet generates point clouds with a relatively complete overall structure, yet the distribution is chaotic, with uneven local density, indistinct boundaries, and a lack of the smoothness and detail present in real point clouds. This is attributed to the fact that GRNet first converts the point cloud into a voxel grid during point cloud completion and then transforms the completed voxel grid back into point cloud data. However, the voxelization process leads to the loss of local details, resulting in blurred boundaries and a disordered distribution of the completed point cloud. PCN’s outputs are sparse, forming only a rough shape that fails to approach the density of real point clouds. The primary reason lies in the fact that PCN employs a single-scale feature extraction strategy, resulting in insufficient feature extraction capability. Furthermore, during the decoding stage, PCN utilizes a folding-based decoding strategy similar to FoldingNet, which leads to the generation of poor-quality point clouds. PF-Net results in uneven point distributions with noticeable clustering. Although PF-Net utilizes multi-scale feature extraction, it directly concatenates the extracted multi-scale features. This simple feature fusion method cannot adaptively balance local and global features, leading to local clustering artifacts in the generated point cloud. TopNet roughly restores shapes but struggles with uneven distribution, particularly in local completion regions, appearing sparse and fragmented, with limited detail recovery and a coarse overall effect. The primary reason lies in the fact that TopNet also employs single-scale feature extraction. This approach struggles to extract sufficient feature information under few-shot conditions, ultimately leading to poor quality in the generated point clouds. SnowflakeNet closely approximates the real point cloud shape but suffers from local holes and discontinuities. This model extracts both global and local features, enabling it to possess a strong feature extraction capability. However, it utilizes skip connections to fuse multi-scale features, which is a static fusion strategy with insufficient dynamic adaptability, making it difficult to fully guarantee the consistency between global and local information. In contrast, our method can not only consider the feature extraction of both global and local information but also perform adaptive dynamic fusion of them, enabling a generated point cloud with uniform density, closely matching the real point cloud’s shape, featuring smooth edges and strong continuity.
When the missing rate is 50%, the proposed model achieves optimal performance in both the CD and EMD metrics, with reductions of 28% and 26%, respectively, compared to the sub-optimal AdaPoinTr model. Although the MMD metric is not the best, the overall performance remains superior.
Figure 5 visualizes the completion results of these models on the industrial oil seal ring dataset for 50% missing rates.
At a 75% missing rate, the proposed model again outperforms others in CD and EMD, with CD decreasing by 30% compared to the sub-optimal AdaPoinTr and EMD decreasing by 47% compared to the sub-optimal TopNet; however, its performance in MMD is relatively weaker.
Figure 6 visualizes the completion results of these models on the industrial oil seal ring dataset for 75% missing rates.
Analysis of the output results across different missing rates reveals that as the missing rate increases, the difficulty of point cloud completion escalates, leading to a corresponding decline in completion quality. This trend is consistently reflected in the quantitative metrics (CD, EMD, and MMD) and visually corroborated by the progressive degradation observed in
Figure 4,
Figure 5 and
Figure 6.
To more comprehensively evaluate our model, we designed a complexity analysis experiment, the results of which are shown in
Table 3. In the table, FLOPs represents floating-point operations, and Params represents the number of parameters. These data were calculated with a batch size of 1 to ensure a fair comparison of the computational resource consumption of different models. Additionally, to comprehensively assess model performance, this paper also provides the average CD (Chamfer distance) values of the completion results of different models under varying degrees of missingness. The data in the table indicate that our model’s computational cost is at a moderate level, while its storage cost is relatively high. However, it achieves the best completion performance. Overall, our model strikes an effective balance between computational cost and completion performance.
5.5. Evaluation on the Small-Sample ShapeNet Sub-Dataset
To more comprehensively evaluate the adaptability and stability of our model, we performed experimental tests on the constructed small-sample ShapeNet sub-dataset.
Table 4,
Table 5 and
Table 6 present the performance of various models across the CD, EMD, and MMD metrics, respectively, with the best results highlighted in bold. Overall, our model demonstrates superior performance across all three metrics. In terms of CD, our model achieves the best results for all categories except “earphone”, while it consistently outperforms all competing methods across all categories for both EMD and MMD.
We also visualized the completion results for selected categories in
Figure 7. Analysis reveals that our model generates point clouds of the highest quality, as exemplified by categories such as “car” and “motor”, which exhibit uniform point distributions and smoother boundaries. Furthermore, our model effectively covers entire missing regions, as observed in “car” and “laptop”, whereas other models produce point clouds with varying degrees of shrinkage in these areas, failing to fully reconstruct the missing regions and exhibiting significant distortion. These advantages underscore our model’s ability to effectively integrate global and local information, resulting in generated point clouds that closely resemble the true shapes.
5.6. Ablation Study
To more thoroughly evaluate the influence of our proposed modules on the model’s effectiveness, we performed an ablation analysis on the oil seal ring dataset.
Table 7 records the effects of different modules on the CD, EMD, and MMD metrics, with the best results highlighted in bold. In the table, A, B, and C denote our three proposed modules: MS-DWF, TRMLP, and ECMLP, respectively. Model I represents the baseline (PF-Net) without any modules, Model II uses only A, Model III uses only B, Model IV combines A and B, Model V uses only C, and ours incorporates all three modules (A + B + C). The results demonstrate that each module provides a beneficial enhancement to the model’s effectiveness, with ours achieving the best outcomes across CD, EMD, and MMD. Specifically, our model achieves significant improvements over PF-Net, reducing CD by 46%, EMD by 49%, and MMD by 74%. We also visualized the completion results of each model variant, as shown in
Figure 8, where ours exhibits the most uniform point cloud distribution.
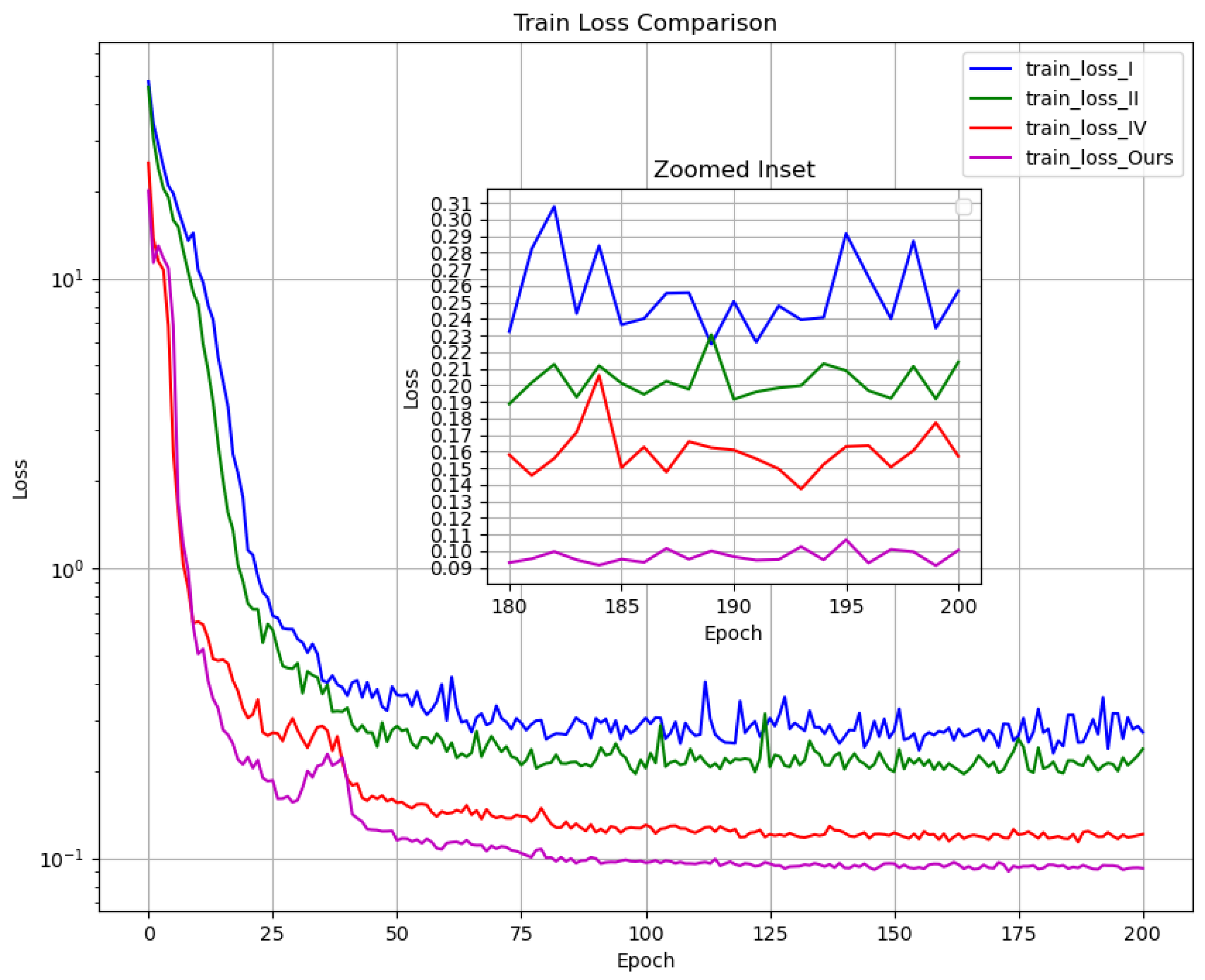
Additionally, we plotted the training and validation loss curves for Models I, II, IV, and ours, as presented in
Figure 9 and
Figure 10. The curves reveal that Model I exhibits a slower initial decline in both training and validation losses, with significant oscillations in later stages, indicating limited optimization capability and stability. Model II shows a reduced loss value after stabilization, with noticeably smaller oscillations. Model IV demonstrates a markedly faster loss reduction, achieving a lower final loss, though it retains considerable oscillations. Ours combines the strengths of the preceding models, exhibiting the fastest loss convergence, the lowest final loss value, and the smallest oscillation amplitude.
7. Conclusions
To address the challenges of structural degradation and uneven point cloud distribution in existing point cloud completion models under limited training data, we introduce a Multi-Scale Dynamic Weighted Fusion Point Cloud Completion Model tailored for small-sample scenarios. This model integrates three innovative modules—ECMLP, MS-DWF, and TRMLP—which collectively enhance feature extraction capabilities. Experiments on a custom oil seal ring dataset validate its superior performance, reducing CD by 46%, EMD by 49%, and MMD by 74% compared to PF-Net under a 25% missing rate. Further studies on the small-sample ShapeNet sub-dataset demonstrate that our model also exhibits strong generalization capabilities.
The proposed method not only achieves high-fidelity point cloud completion in small-sample scenarios but also delivers high-quality completion results when addressing large-scale regional missing data. This capability enables the accurate reconstruction of critical geometric features, such as edges and surfaces, even under severe data limitations (e.g., a 75% missing rate). This is particularly crucial for evaluating the structural integrity of oil seal rings—essential components in industrial machinery. By providing precise digital representations, the method facilitates detailed geometric analysis, thereby supporting the assessment of oil seal ring designs and their performance under diverse operating conditions. This is especially valuable in industrial contexts where small-sample data are prevalent, and traditional methods often struggle to maintain accuracy, ultimately enhancing the design optimization and reliability evaluation of oil seal rings.
Our current emphasis is on encoding-phase feature extraction;, future work will explore advanced decoding strategies to further refine completion quality. Additionally, we aim to extend this approach to diverse, complex industrial components, amplifying its practical impact.