Abstract
In the Chengdao–Zhuanghai area, there are few core samples of Mesozoic clastic rocks but abundant logging data. It is difficult to establish a fracture model of clastic rocks directly based on core samples and relevant tests. In this study, triaxial compression tests are conducted on Mesozoic clastic rock samples to reveal the failure mechanism of clastic rocks. A statistical model based on logging data is utilized to calculate dynamic rock mechanical parameters, and theoretical relationships between static and dynamic mechanical parameters are derived. A failure model for clastic rocks is established using logging data and the minimum energy consumption principle by applying the principle of minimum energy consumption and adopting the unified energy yield criterion of rocks as the energy consumption constraint. This research study shows that a linear relationship exists between the static and dynamic mechanical parameters of Mesozoic clastic rocks, and the correlation coefficient can reach 85%. The core aspect of clastic rock failure is energy dissipation. As confining pressure increases, more energy must be dissipated during the failure of clastic rocks. Upon failure, the releasable elastic energy accumulated within the clastic rocks clearly reflects the confining pressure effect. A higher initial confining pressure leads to a greater release of elastic energy and results in a more severe failure degree. The developed rock failure model effectively represents the nonlinear mechanical behavior of Mesozoic clastic rocks in the Chengdao–Zhuanghai area under complex stress conditions. It is suitable for investigating the fracture distribution of Mesozoic clastic rocks and addresses the challenge of understanding the failure mechanism of these rocks in the Chengdao–Zhuanghai region.
1. Introduction
Since the Mesozoic era, the Chengdao–Zhuanghai area in the Jiyang Depression has undergone the Yanshan Movement and the Himalayan Movement. Multiple phases of tectonic activity have contributed to the extensive development of Mesozoic faults and fractures in clastic rocks. Clarifying the failure mechanism of clastic rocks provides a critical foundation for examining the fracture distribution of Mesozoic clastic rocks in the Chengdao–Zhuanghai area. At present, many scholars have conducted in-depth investigations into rock fracturing mechanisms using a range of theories, high-resolution imaging techniques such as acoustic emission and ultrasonic emission, and various numerical simulation approaches [1,2,3,4]. Chai [5], utilizing moment tensor theory in combination with particle flow theory, analyzed the failure mechanisms of intact rocks under both uniaxial and triaxial compression conditions. Liang [6] performed hydraulic and pneumatic fracturing experiments on different types of reservoir rocks and proposed a novel fractal criterion for crack initiation and propagation during rock fracturing under fluid or gas pressure. Peng [7] examined the mechanical properties and failure mechanisms of coarse-grained and fine-grained sandstones with prefabricated through-fractures of various structural types under complex stress conditions, including uniaxial, biaxial, conventional triaxial, and true triaxial loading. Tan [8] conducted a series of laboratory tests coupling compression and tension on red sandstone specimens. The study systematically clarified the deformation and failure characteristics, fracturing mechanisms, and energy evolution patterns under different unloading rates and confining pressures during compression-tension coupling tests by employing 3D laser scanning and SEM microscopy for fracture morphology characterization. Fan [9] developed a novel tensile testing device and conducted comprehensive investigations into rock tensile performance assessment methods and mesoscale fracturing mechanisms through integrated laboratory testing and numerical simulation techniques. Gong et al. [10] unveiled micromechanical fracturing mechanisms in shale through an integrated methodology incorporating X-ray diffraction, triaxial compression testing, micro-CT scanning, and scanning electron microscopy. Their findings indicated that increased confining pressure favors the formation of intragranular fractures within mineral grains, enhancing fracture development in shale formations. These methods can analyze the fracture mechanism of rocks under different stress states. However, they all rely on an ample number of core samples, as well as testing and analysis. For study areas with few core samples but abundant logging data, it is difficult to directly obtain the mechanical parameters of rocks from core samples and related tests. Moreover, different series of logging data can reflect various types of geological information. Some scholars have established statistical models of dynamic rock mechanical parameters by using compressional wave transit time, shear wave transit time, and formation density logging data [11,12,13]. Therefore, logging data should be taken into account in the study of the rock fracture mechanism. Wang et al. [14] investigated the impact of fracture inclination angles and confining pressures on the mechanical properties and failure modes of fractured sandstone using a combined approach of triaxial compression tests and numerical modeling. Yang [15] and Li [16] employed laboratory mechanical testing and discrete element numerical simulations to analyze the mechanical response patterns of the microscopic rock structure under external forces and the failure evolution process. Gui [17] developed a three-dimensional finite element numerical model based on uniaxial compression, conventional triaxial compression, and confining pressure unloading tests of marble, revealing the mechanical behavior, energy evolution characteristics, and fracture mechanisms of marble under true triaxial loading and unloading scenarios. Liu et al. [18] proposed a rock fragmentation simulation method based on the coupling of a Voronoi diagram and discretized the virtual internal bond. This method can simply and efficiently simulate the fragmentation of rocks containing blocks. Based on the rock fragmentation simulation method, Liu et al. [19,20] further developed a three-dimensional hydromechanical coupled element partition method. This method allows fractures to penetrate rock elements and can correctly simulate the propagation of three-dimensional hydraulic fractures, the interaction between hydraulic fractures and natural fractures, and the influence of in situ stress. These methods are capable of simulating the fracture process of rocks under different states. However, they all rely on an abundant supply of core samples, specific mechanical theories, and rock models. The principle of minimum energy consumption, which is grounded in fundamental physical principles such as thermodynamics and the conservation of energy, can demonstrate that materials will fracture along the path that minimizes the total energy consumption of the system during the process of being stressed. This is consistent with the law of fracture development in rocks under the action of loads. Therefore, the principle of minimum energy consumption can be applied to the study of the rock fracture mechanism.
In view of the fact that there are few core samples of Mesozoic clastic rocks and abundant logging data in the Chengdao–Zhuanghai area, it is difficult to establish a clastic rock fracture model directly based on the core samples and relevant tests. This study performs triaxial compression tests on Mesozoic clastic rocks in the Chengdao–Zhuanghai area under varying confining pressures and analyzes the energy conversion relationships at different stages of clastic rock failure. Static rock mechanical parameters are determined based on triaxial rock tests, while dynamic rock mechanical parameters are obtained using the statistical model derived from logging data. Then, the theoretical relationship between static and dynamic rock mechanical parameters is derived. A rock failure model based on logging data and the minimum energy consumption principle is established by applying the principle of minimum energy consumption from an energy perspective and considering the unified energy yield criterion of rocks as the energy dissipation constraint. This model clarifies the failure mechanism of Mesozoic clastic rocks in the Chengdao–Zhuanghai area and is utilized in the analysis of fracture distribution in the study area.
2. Geological Background
The Chengdao–Zhuanghai area is located in the offshore region of the northeastern Jiyang Depression and is structurally bounded by the Chengdao Heave, Chengdong Heave, and Changdi Heave. It is connected to the Chengdong Heave in the west by the NNE-striking Chengdong Fault, to the Chengbei Heave in the north by the Chengbei Fault, to the Changdi Heave in the east by the approximately NS-trending Changdi Fault, and to the Gudao Heave in the south by the nearly EW-oriented Gubei Fault (Figure 1a). The Chengdao–Zhuanghai area has undergone intense tectonic activity since the Mesozoic, leading to extensive fault development. The intersection and interaction of faults with different orientations and characteristics have resulted in a distinctive structural pattern featuring northward divergence, southward convergence, and a reticulated fault distribution (Figure 1b). During the Mesozoic period in the Chengdao–Zhuanghai area, braided river alluvial plain facies, meandering river facies, and delta facies were predominantly developed. The Mesozoic strata include residual Jurassic and Cretaceous systems, with lithologies mainly consisting of clastic rocks (pebbly sandstone, sandstone) and mudstone (Figure 1c). Influenced by multi-phase tectonic events, including the Yanshanian and Himalayan orogenies, the Mesozoic clastic rocks in the Chengdao–Zhuanghai area primarily developed shear fractures and compressional fractures, with shear cracks and compaction seams as the dominant fracture types. The fracture density ranges from 0.8 to 4.7 fractures per meter, with apertures between 0.5 mm and 2 mm (Figure 2).
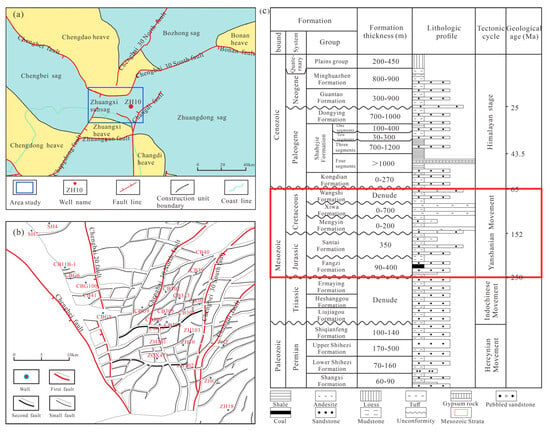
Figure 1.
(a) Tectonic location map of Chengdao–Zhuanghai area; (b) tectonic unit division of Chengdao–Zhuanghai area; (c) lithologic columnar section of Chengdao–Zhuanghai area.

Figure 2.
Fracture properties of different cores.
3. Database and Methods
The logging data used in this study include shear wave logging data (Δts), compressional wave logging data (Δtp), and density logging data (ρb) from boreholes penetrating the Mesozoic strata in the Chengdao–Zhuanghai area (Table 1). The logging data have a sampling interval of 0.125 m.

Table 1.
SH7 well logging data (part).
The samples used for testing were collected from pebbly sandstone without developed fractures within the Mesozoic strata of the Chengdao–Zhuanghai area. In accordance with the standards of the International Society for Rock Mechanics (ISRM) [21], the rock samples were ground into standard cylindrical specimens with a diameter × height of 25 mm × 50 mm. The uniformity and integrity of the selected specimens conform to the test specifications, and the rock specimens are shown in Figure 3.

Figure 3.
Sandstone sample and confining pressure.
A total of 9 rock samples representing different lithologies, taken from 5 wells and labeled as BH-1, BH-2, BH-3, BH-4, BH-5, BH-6, BH-7, BH-8, and BH-9, were used for triaxial compression testing. Based on the burial depths (ranging from 2248 m to 4580 m) of the Mesozoic clastic rock samples, conventional triaxial compression tests were performed under confining pressures of 32 MPa, 34 MPa, and 36 MPa. Three parallel tests were conducted for each confining pressure. The conventional triaxial compression tests were conducted at China University of Petroleum (East China), using an electro-hydraulic servo-controlled triaxial testing system (TAW-1000). Following the axial displacement control method, the tests began by applying confining pressure under hydrostatic conditions until the predefined values were reached. After stabilizing the confining pressure, axial deviatoric stress was applied at a constant rate of 0.02 mm/min until specimen failure occurred. Throughout the loading process, the servo-controlled testing system automatically recorded the applied axial load. Axial and radial deformations were simultaneously monitored using two high-precision linear variable differential transformers (LVDTs) mounted on the base of the pressure chamber and one strain measurement ring attached to the specimen. The test was terminated upon achieving the predefined control objectives.
4. Test Results
According to the above test scheme, taking into account the formation pressure gradient of the Jiyang Depression and the existing rock samples, setting a specific confining pressure for the rock samples at a fixed depth is more in line with the actual stress conditions of the underground rock samples. Based on this, triaxial compression tests were carried out on the Mesozoic clastic rocks in the Chengdao–Zhuanghai area. Table 2 lists the coring locations of the nine representative rock samples, the confining pressure settings, and the compressive strength test results. It indicates that the compressive strength increases with the rise in confining pressure, indicating that higher initial confining pressure gradually closes the micro-cracks within the rock sample and densifies the particle skeleton, enhancing the compressive strength of the clastic rock.

Table 2.
Compressive strength of clastic rocks under different confining pressures.
Figure 4 shows the relationship curves of the measured deviatoric stress (σ1–σ3) versus axial strain (ε1), radial strain (ε3), and volumetric strain (εv) of the clastic rock samples under confining pressures of 32 MPa, 34 MPa, and 36 MPa, respectively. Figure 5 illustrates the relationship curves of the measured volumetric strain (εv) versus axial strain (ε1) under different confining pressures.
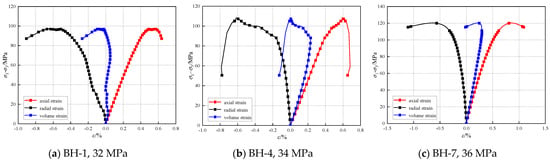
Figure 4.
Relationship between deviatoric stress and strain for breccia lava under different confining pressures.
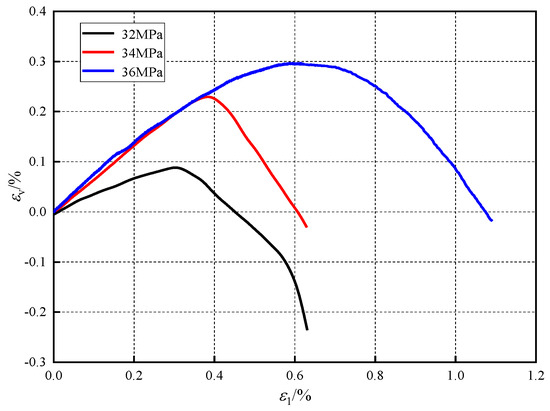
Figure 5.
Relationship between the volume strain and axial strain of the rock sample.
Based on the deviatoric stress–strain relationship describing the failure of clastic rocks in Figure 4, the failure process of the Mesozoic clastic rocks in the Chengdao–Zhuanghai area can be broadly categorized into five stages [22,23,24]: (1) Compaction stage: The initially open structural planes within the clastic rocks gradually close, and the infilling materials become compacted [22,23,24]. The compressive deformation exhibits nonlinear characteristics. Deformation during this stage is primarily influenced by the initial internal structural features of the clastic rocks and the properties of the infilling materials. (2) Elastic deformation stage: Following compaction, the clastic rocks transition from a discontinuous medium to a quasi-continuous one and enter the elastic deformation stage [22,23,24]. In this stage, the deviatoric stress–strain curve is approximately linear, and the deformation is fully recoverable. The extent of the curve in this stage depends on the hardness of the clastic rocks. (3) Stable fracturing stage: As the load increases, the clastic rocks shift from linear elastic deformation to nonlinear deformation [22,23,24]. When the yield point (elastic limit) is surpassed, micro-fractures begin to form within the clastic rocks and gradually propagate as the stress differential increases. If stress remains constant, fracture development ceases. Due to the emergence of micro-fractures, the volumetric compression rate of the rock sample rises, and both the axial and lateral strain rates increase to some degree. (4) Unstable failure stage: A qualitative change in micro-fracture development marks this stage [22,23,24]. Due to stress concentration effects, even if the stress remains unchanged or slightly fluctuates, fractures continue to evolve. The weakest part of the clastic rock fails, leading to stress redistribution, which causes the next weakest section to fail, eventually failing the entire clastic rock. During this stage, volumetric strain transitions from compression to expansion, and both the axial and lateral strain rates rise sharply. (5) Complete failure stage: The internal fracture surfaces of the clastic rock evolve into continuous, through-going fractures [22,23,24]. The strength of the rock sample declines rapidly, and deformation persists until the sample disintegrates into separate blocks.
Based on the relationship between the volumetric strain and axial strain of the clastic rock samples under various confining pressures shown in Figure 5, the variation patterns of volumetric strain under different confining pressures are generally consistent. Specifically, the clastic rocks overall exhibit a trend of initial compression followed by expansion. When the axial strain is relatively small, the slope of the curve increases with higher confining pressure. In addition, the stationary point of the volumetric strain–axial strain curve corresponds to the initial yield point [25,26], which rises with an increase in confining pressure (Figure 5).
5. Rock Fracture Model and Fracture Mechanism
5.1. Derivation of Rock Fracture Model
Based on the laws of thermodynamics, rock fracture is fundamentally a process in which the thermodynamic equilibrium of the system is initially disrupted and subsequently re-established [27,28,29]. When fractures occur within a rock, the equilibrium of the thermodynamic system is broken. As energy dissipation stabilizes, the system transitions to a new thermodynamic equilibrium state. Based on this principle, Xie et al. [30] introduced the concepts of dissipated energy of rock elements, releasable strain energy, strength loss, and overall failure. They proposed that in a conventional triaxial stress system that is closed and thermally insulated, the dissipated energy Wd of rock elements satisfies Formulas (1)–(3) [30].
where W is the total strain energy of the rock element; We is the releasable elastic strain energy of the rock element; E is the unloading elastic modulus of the failed rock; μ is the nominal Poisson’s ratio of the material before failure; σi (i = 1, 2, and 3) is the nominal stress of the rock element; εi (i = 1, 2, and 3) is the nominal strain of the rock element; ε0 is the initial strain in the initial compaction stage.
Based on the concepts of dissipated energy of rock elements and overall failure, Sun et al. [31] integrated the principle of minimum energy consumption, took the unified energy yield criterion of rock as the constraint condition for energy consumption, and established the rock failure Equation (4), which can be found in Ref. [31].
where , , , , ; σi (i = 1, 2, and 3) is the nominal stress of the rock element; εi (i = 1, 2, and 3) is the nominal strain of the rock element; E0 is the initial elastic modulus of the rock before failure. E = E0 is taken to simplify the numerical analysis; μ is the nominal Poisson’s ratio of the material before failure; ε10 is the failure threshold strain; K1 is the test loading parameter, and λ* and c0 are determined by deriving from the results of the triaxial compression test.
The establishment of the rock fracture equation based on the principle of minimum energy consumption is supported by an adequate number of core samples, along with comprehensive testing and analysis. However, core samples of Mesozoic clastic rocks in the Chengdao–Zhuanghai area are limited, making it challenging to obtain rock mechanical parameters through core sampling and testing. Based on elastic wave theory, the elastic parameters of rocks are closely associated with rock density and the propagation velocity of acoustic waves within the rock [11,32]. In this study, the logging data of compressional wave slowness (Δtp), shear wave slowness (Δts), and formation density (ρb) are employed. Based on the physical properties of rock elastomechanics, the dynamic elastic modulus and dynamic Poisson’s ratio of Mesozoic clastic rocks are calculated using Formulas (5) and (6) [11,32].
where Ed is the dynamic elastic modulus; μd is the dynamic Poisson’s ratio; ρb is the density logging data; Δts is the shear wave slowness log data; Δtp is the compressional wave slowness log data.
Static elastic parameters of Mesozoic clastic rocks are obtained through triaxial mechanical testing. Regression fitting is performed between the static elastic parameters and the dynamic elastic parameters derived from the logging data. The static and dynamic elastic parameters satisfy Formulas (7) and (8) [33].
where Es is the static elastic modulus and E0 = Es; μs is the static Poisson’s ratio; μ = μs; m, n, p, and q are conversion coefficients, which are related to the mechanical properties of clastic rocks and the stress environment.
Substitute Equations (7) and (8) into Equation (4) to obtain the rock fracture equation based on logging data and the principle of minimum energy consumption:
The unified energy yield criterion of rock is adopted as the evaluation criterion for the failure threshold, and it satisfies Formulas (10)–(12) [25].
where α and β are material parameters; ws is the shear strain energy; wv is the volume strain energy.
The internal friction angle and elastic parameters are determined through triaxial compression testing of clastic rocks and then substituted into Equations (11) and (12) to calculate the shear strain energy and volume strain energy under different confining pressures (Figure 6). A linear relationship exists between the shear strain energy and the volume strain energy, and it is applicable to the yield criterion of Mesozoic clastic rocks in the Chengdao–Zhuanghai area. Based on Equation (13), α = −0.941 and β = 36.862, and the linear correlation coefficient between the shear strain energy and the volume strain energy can reach 92%.
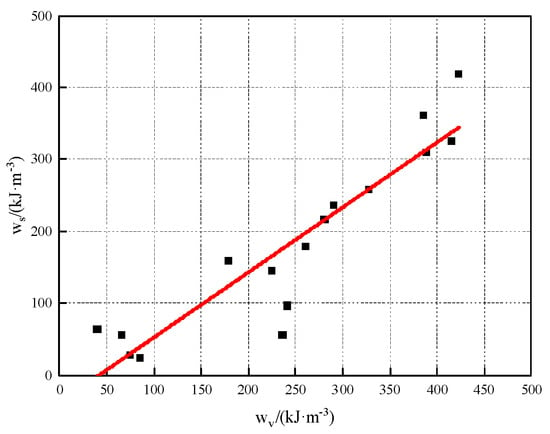
Figure 6.
Relationship between ws and wv when the rock sample yields.
The degree of rock failure differs under different confining pressures. In this study, the stress (σs), axial strain (ε1s), and radial strain (ε3s) at the peak points of the stress–strain curves of the rock under confining pressure are considered. The strengths at the peak points of the rock stress–strain curves are utilized to determine the model parameters λ* and c0, and the model parameters satisfy Formulas (14) and (15) [31].
Table 3 lists the dynamic and static rock mechanical parameters of Mesozoic clastic rocks under varying confining pressures. As the confining pressure increases, the dynamic elastic modulus, static elastic modulus, and static Poisson’s ratio all increase, whereas the variation trend of the dynamic Poisson’s ratio remains unclear. The dynamic elastic modulus is greater than the static elastic modulus, and there is no consistent relationship between the magnitudes of the dynamic Poisson’s ratio and the static Poisson’s ratio.

Table 3.
Dynamic and static parameters of rock mechanics.
A linear relationship is evident between the dynamic and static elastic mechanical parameters based on the analysis of the crossplot between the dynamic and static elastic moduli and between the dynamic and static Poisson’s ratios in Figure 7. The parameters are identified from Equations (16) and (17) as m = 0.460, n = 2.164, p = −5.391, and q = 1.378, and the linear correlation coefficient of the dynamic and static elastic mechanical parameters can reach 85%. Cohesion and internal friction angles are inherent properties of the rock samples. This study determines cohesion c, a fixed value of 16.58 MPa, and the internal friction angle φ, a fixed value of 32.5°.
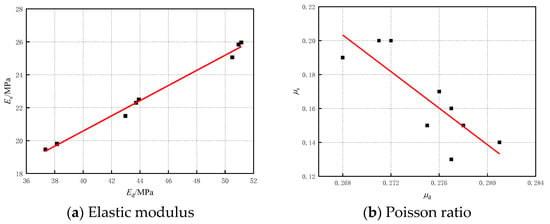
Figure 7.
Relationship diagram of dynamic and static parameters of rock mechanics.
The theoretical curve of the clastic rock failure model is calculated using Equation (9) to verify the rationality of the failure model, as illustrated in Figure 8. The theoretical and test curves align closely under different confining pressures by comparing the theoretical curve with the indoor triaxial test curve. This consistency indicates that the rock failure model, based on logging data and the principle of minimum energy consumption, can accurately simulate the stress–strain relationship of clastic rocks at various stages before the peak during loading in a complex stress environment. In addition, it demonstrates a strong simulation capability regarding the nonlinear mechanical properties of clastic rocks in the post-yield stage.
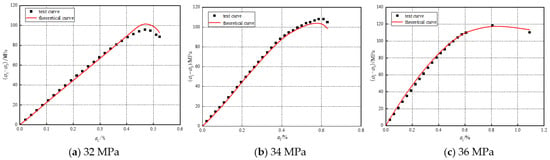
Figure 8.
Comparison between experimental curve and theoretical curve of damage model.
5.2. Analysis of the Fracture Mechanism of Clastic Rocks
The curves of energy variation with axial strain during the compression and failure process of clastic rocks under different confining pressures are plotted (Figure 9) using the above numerical calculation formula for energy. From an energy perspective, the compression and failure process of clastic rocks can be divided into four stages: (1) Initial inelastic stage: In the early stage of loading, the external load performs work by compressing the clastic rocks. The work is primarily utilized to close internal pores within the material and to elastically deform the particle skeleton. At this stage, the growth rate of the elastic energy that the clastic rock units can release is relatively slow. (2) Linear elastic stage: The clastic rocks convert the work performed by the external load into releasable elastic potential energy and store it. Both the total energy absorbed by the clastic rocks and the releasable elastic energy increase rapidly, while the growth rate of dissipated energy remains relatively low. During this stage, the pre-existing fractures within the clastic rocks are fully closed, the stress and strain maintain a linear relationship, and the particle skeleton exhibits linear elastic deformation. (3) Fracture development stage: The growth rate of releasable elastic energy gradually slows and reaches a maximum at the peak stress. Simultaneously, the dissipated energy increases rapidly, and the total strain energy of the clastic rock units is consumed in forms such as plastic and thermal energy. In this stage, micro-cracks within the clastic rocks propagate rapidly, resulting in plastic deformation. As fracture development progresses, the strength of the clastic rocks begins to gradually decline, exhibiting nonlinear mechanical behavior. (4) Complete failure stage after the peak: When energy accumulation reaches the level of dissipated energy required for failure, the energy is released rapidly, causing the overall failure of the clastic rocks. At this point, internal cracks continue to propagate and interconnect, eventually forming a macroscopic fracture surface.
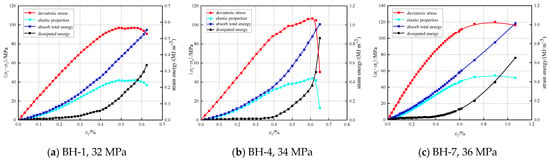
Figure 9.
Energy evolution during triaxial compression test.
Through analysis of the energy evolution law governing clastic rock failure, energy dissipation serves as the internal driving force behind the failure of clastic rocks. A positive correlation exists between the initial confining pressure endured by the clastic rocks and the amount of energy dissipated during the failure process. In the failure development stage, higher confining pressure corresponds to a greater proportion of dissipated energy relative to the total strain energy. Under high confining pressure conditions, the releasable elastic energy stored within the clastic rocks increases significantly at failure, resulting in a more severe failure degree.
6. Discussion
Based on previous numerical simulations of the Mesozoic tectonic stress field in the Chengdao–Zhuanghai area [34,35], this study incorporates inverted mechanical parameter volumes derived from 3D seismic data, combined with dynamic–static rock mechanical parameter relationships and Mesozoic clastic rock fracture equations. This study combined a fractal dimension-based quantitative characterization method with variance body coherence slices to analyze the fracture distribution patterns in Mesozoic clastic formations (Figure 10). Previous studies indicated that the Chengdao–Zhuanghai area has experienced Yanshanian and Himalayan tectonic events since the Mesozoic. During the Yanshanian period, the maximum principal stress showed an increasing trend from northwest to southeast, with stress minima located in the northern and southwestern parts of the study area. The entire region experienced tensile stresses surpassing the fracture strength of the Mesozoic clastic rocks, leading to fracturing primarily in structural highs adjacent to the Chengbei Fault and southern Chengbei 20 Fault zones. During the Himalayan period, the area continued to be subject to tensile stress regimes, particularly in the northeastern sector, where stress intensities slightly exceeded the tensile strength of the clastic rocks, resulting in increased fracturing near the Chengbei 30 North Fault, Chengbei 30 South Fault, and Changdi Fault systems [34,35]. According to Figure 10, in the local area of the southern part of the Chengbei 20 fault, the rising plate of the Chengbei fault, the southern part of the Chengbei 30 fault, the Changdi fault, and the western part of the Chengbei 30 north fault, the fractal dimension is relatively large, the variance value is relatively high, and the cracks are relatively developed. This is consistent with the distribution characteristics of Mesozoic clastic rock fractures in the Chengdao–Zhuanghai area presented by the superposition of two tectonic stress fields, indicating that the fracture mechanism of Mesozoic clastic rocks is applicable to the study of the distribution of fractures in Mesozoic clastic rocks.
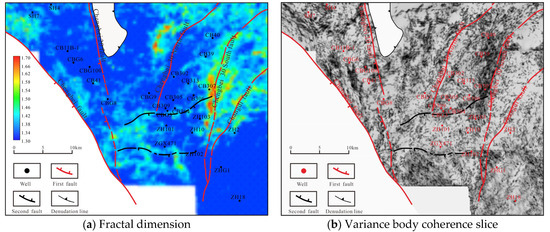
Figure 10.
Prediction of the fracture development of Mesozoic clastic rocks in the Chengdao–Zhuanghai area.
7. Conclusions
(1) Based on the triaxial mechanical tests of Mesozoic clastic rocks in the Chengdao–Zhuanghai area and the statistical model derived from logging data, the theoretical relationships between static and dynamic rock mechanical parameters are deduced. A model is established based on both the logging data and the principle of minimum energy consumption by incorporating the logging data into the failure model of clastic rocks. This approach addresses the limitations posed by the limited availability of core samples of Mesozoic clastic rocks and the challenges in investigating their failure mechanisms.
(2) Numerical calculations are conducted using the developed failure model of clastic rocks. It is demonstrated that the model effectively reflects the stress–strain behavior of Mesozoic clastic rocks under varying confining pressures by comparing the theoretical calculation results with the experimental data. This validates the applicability of the failure model in analyzing the failure mechanisms of Mesozoic clastic rocks.
(3) The fracture of Mesozoic clastic rocks essentially constitutes a process of energy dissipation. During the failure development stage, as the confining pressure increases, the proportion of dissipated energy within the total strain energy progressively rises, requiring greater energy dissipation during rock failure. At the point of failure, the releasable elastic energy stored within the clastic rocks exhibits a pronounced confining pressure effect. Higher initial confining pressure leads to the release of greater elastic energy, resulting in a more severe degree of failure.
(4) The fracture mechanism of Mesozoic clastic rocks in the Chengdao–Zhuanghai area is applicable to analyzing the distribution of fractures in these rocks. A positive correlation exists between the degree of fracture development and the extent of rock failure. In addition, the development of fractures in Mesozoic clastic rocks is influenced by the primary controlling faults, with more intensive fracture development observed in proximity to these faults.
Author Contributions
Conceptualization, S.M. and S.Y.; methodology, S.M.; validation, S.M.; formal analysis, S.M.; investigation, S.M., D.H., and Y.Z.; data curation, S.M. and Y.W.; writing—original draft preparation, S.M.; writing—review and editing, S.M. and S.Y.; visualization, S.M.; supervision, S.Y.; project administration, S.Y.; funding acquisition, S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the China National Science and Technology Major Project (grant number 2017ZX05009001) and the Innovation Fund of the China University of Petroleum (East China) supported by the Fundamental Research Funds for the Central Universities (grant number 27RA2301006).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors appreciate Shengli Oilfield Company for providing the core samples, dataset, and permission for publication. The authors would like to thank the editors and reviewers for their help with this research.
Conflicts of Interest
Author Yanjia Wu was employed by the company SINOPEC. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The SINOPEC had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
| Δts | Shear wave slowness log data |
| Δtp | Compressional wave slowness log data |
| ρb | Density logging data |
| σ1-σ3 | Deviatoric stress |
| ε1 | Axial strain |
| ε3 | Radial strain |
| εv | Volumetric strain |
| W | Total strain energy of the rock element |
| We | Releasable elastic strain energy of the rock element |
| Wd | Dissipated energy |
| E | Unloading elastic modulus of the failed rock |
| μ | Nominal Poisson’s ratio of the material before failure |
| σi (i = 1, 2, and 3) | Nominal stress of the rock element |
| εi (i = 1, 2, and 3) | Nominal strain of the rock element |
| ε0 | Initial strain in the initial compaction stage |
| E0 | Initial elastic modulus of the rock before failure |
| ε10 | Failure threshold strain |
| K1 | Test loading parameter |
| λ∗ | Relevant parameters characterizing the material properties |
| Relevant parameters characterizing the material properties | |
| c0 | Relevant parameters characterizing the material properties |
| K | Bulk modulus |
| K1 | Test loading parameter |
| G | Shear modulus |
| σ1t | Axial deviatoric stress |
| A1 | Relevant parameters characterizing the material properties |
| A2 | Relevant parameters characterizing the material properties |
| B1 | Relevant parameters characterizing the material properties |
| B2 | Relevant parameters characterizing the material properties |
| Ed | Dynamic elastic modulus |
| μd | Dynamic Poisson’s ratio |
| Es | Static elastic modulus |
| μs | Static Poisson’s ratio |
| m | Conversion coefficients |
| n | Conversion coefficients |
| P | Conversion coefficients |
| q | Conversion coefficients |
| α | Material parameters |
| β | Material parameters |
| ws | Shear strain energy |
| wv | Volume strain energy |
| φ | Internal friction angle |
| c | Cohesion |
| σs | The stress at the peak point |
| ε1s | The axial strain at the peak point |
| ε3s | The radial strain at the peak point |
References
- Tang, C.A.; Liu, H.; Lee, P.K.K.; Tsui, Y.; Tham, L.G. Numerical studies of the influence of microstructure on rock failure in uniaxial compression—Part I: Effect of heterogeneity. Int. J. Rock Mech. Min. Sci. 2000, 37, 555–569. [Google Scholar] [CrossRef]
- Tang, C.A.; Tham, L.G.; Lee, P.K.K.; Tsui, Y.; Liu, H. Numerical studies of the influence of microstructure on rock failure in uniaxial compression—Part II: Constraint, slenderness and size effect. Int. J. Rock Mech. Min. Sci. 2000, 37, 571–583. [Google Scholar] [CrossRef]
- Blair, S.C.; Cook, N.G.W. Analysis of compressive fracture in rock using statistical techniques: Part I. a non-linear rule-based model. Int. J. Rock Mech. Min. Sci. 1998, 35, 837–848. [Google Scholar] [CrossRef]
- Blair, S.C.; Cook, N.G.W. Analysis of compressive fracture in rock using statistical techniques: Part II. effect of microscale heterogeneity on macroscopic deformation. Int. J. Rock Mech. Min. Sci. 1998, 35, 849–861. [Google Scholar] [CrossRef]
- Chai, J.F. Study on Fracture Mechanism of Brittle Rock Based on Moment Tensor Theory. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2017. [Google Scholar]
- Liang, X. Study on Fractal Fracture Mechanism of Rocks Under Water & Gas Fracturing and Fractal Discrete Fracture Networks. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2019. [Google Scholar]
- Peng, S.L. Research on Mechanical Properties and Fracture Mechanism of Flawed Coarse & Fine Sandstone. Ph.D. Thesis, ChongQing University, Chongqing, China, 2021. [Google Scholar]
- Tan, G.X. Experimental Study on Failure Mechanism and Energy Evolution of Red Sandstone Under Triaxial Extension. Master’s Thesis, Central South University, Changsha, China, 2022. [Google Scholar]
- Fan, Q.H. Development of Rock Direct Tensile Centring Device and Study on the Micro Fracture Mechanism of Rock Stretching. Master’s Thesis, Shandong University, Jinan, China, 2023. [Google Scholar]
- Gong, X.; Jin, Z.J.; Ma, X.H.; Liu, Y.Y.; Li, G.F.; Liao, W. Mechanical properties of the silurian longmaxi formation shale, southern Sichuan basin and its microfracturing mechanisms. Oil Gas Geol. 2024, 45, 1447–1455. [Google Scholar]
- Yan, S.W. The method of calculating rock strength with logging data. Well Log Technol. 1979, 1979, 10–19. [Google Scholar]
- Liu, Z.D. On calculating method of the rock poisson ratio using well logging data. Well Log Technol. 2024, 2024, 508–510+566. [Google Scholar]
- Wu, Y.L. Geomechanical parameters and in-situ stress in a block, xushen gasfield, songliao basin. Nat. Gas Explor. Dev. 2020, 43, 54–63. [Google Scholar]
- Wang, X.; Liu, X.Y.; Yuan, C.; Ma, Z.M. Study on the damage and rupture mechanism of red sandstone under the influence of fracture type and dip angle. Metal Mine 2025, 2025, 1–13. [Google Scholar]
- Yang, X.W. Experimental and Numerical Study on Failure Mechanism of Bedded Rocks. Master’s Thesis, Wuhan University, Wuhan, China, 2021. [Google Scholar]
- Li, J.R. Study on Mechanical Response and Microcosmic Failure Mechanism Ender Different Confining Pressures. Master’s Thesis, Shandong University, Jinan, China, 2023. [Google Scholar]
- Gui, X. Research on Energy Characteristics and Fracture Mechanism of Deep Marble Under True Triaxial Loading and Unloading Conditions. Master’s Thesis, Xihua University, Chengdu, China, 2022. [Google Scholar]
- Liu, S.; Zhang, Z.N. Modeling rock fragmentation by coupling voronoi diagram and discretized virtual internal bond. Theor. Appl. Mech. Lett. 2020, 10, 321–326. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Z.N.; Huang, Z.W. Three-dimensional hydraulic fracture simulation with hydromechanical coupled-element partition method. Int. J. Geomech. 2021, 21, 04021162. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Z.Y.; Zhang, Z.N. Numerical study on hydraulic fracture-cavity interaction in fractured-vuggy carbonate reservoir. J. Pet. Sci. Eng. 2022, 213, 110426. [Google Scholar] [CrossRef]
- Ulusay, R. The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring: 2007–2014; Springer International Publisher: Cham, Switzerland, 2014; Volume 15, pp. 47–48. [Google Scholar]
- Gao, Y.; Guo, P.; Li, X.; Li, Y.Y.; Xu, D.S.; Zhou, Z.Y.; Qin, J.H.; Shi, G.X.; Li, S.D. Investigation of triaxial compression failure and acoustic emission characteristics of different reservoir rocks. J. Eng. Geol. 2022, 30, 1169–1178. [Google Scholar]
- Zhang, Q.; Zhang, X.P.; Chang, X.; Liu, C.Y. Study on energy evolution characteristics at pre-peak and post-peak stages and brittleness evaluation of rock. J. Eng. Geol. 2024, 32, 2110–2119. [Google Scholar]
- Zhao, Z.Y.; Yan, C.L.; Xue, J.C.; Cheng, Y.F.; Han, Z.Y.; Zhang, Z.; Sun, B.; Zhou, G.X. Study on the rock mechanical properties and anisotropy of Paleocene Huxiang reservoirs: A case study of the Shahejie Formation in the southeastern Bohai Bay Basin. Prog. Geophys. 2025, 40, 0806–0816. [Google Scholar]
- Zhou, H.; Li, Z.; Zhu, G.J.; Li, Y.; Lu, J.J.; Zhang, D.D. Unified energy yield criterion of rock. Chin. J. Rock Mech. Eng. 2016, 32, 2170–2184. [Google Scholar]
- Cao, W.G.; Zhao, H.; Zhang, L.; Zhang, Y.J. Damage statistical softening constitutive model for rock considering effect of damage threshold and its parameters determination method. Chin. J. Rock Mech. Eng. 2008, 27, 1148–1154. [Google Scholar]
- Liu, X.; Ning, J.G.; Tan, Y.L.; Gu, Q.H. Damage constitutive model based on energy dissipation for intact rock subjected to cyclic loading. Int. J. Rock Mech. Min. Sci. 2016, 85, 27–32. [Google Scholar] [CrossRef]
- Guo, J.Q.; Liu, X.R.; Wang, J.H.; Yu, Y. Damage constitutive model of rock salt based on energy principles. J. Cent. South Univ. (Sci. Technol.) 2013, 44, 5045–5050. [Google Scholar]
- Liu, X.M.; Xiong, L.; Liu, J.H.; Zhao, M.H. Slacking mechanism of red sandstone based on energy dissipation principle. J. Cent. South Univ. (Sci. Technol.) 2011, 42, 3143–3149. [Google Scholar]
- Xie, H.P.; Ju, Y.; Li, L.Y. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles. Chin. J. Rock Mech. Eng. 2005, 24, 3003–3010. [Google Scholar]
- Sun, M.C.; Xu, W., Y.; Wang, S.S.; Wang, R.B.; Wang, W. Study on damage constitutive model of rock based on principle of minimum dissipative energy. J. Cent. South Univ. (Sci. Technol.) 2018, 49, 2067–2075. [Google Scholar]
- Wang, X.; Xiao, Y.L.; Zhang, P.S. Application of logging technology in evaluation and analysis of rock mechanical properties in Qidong mine in northern Anhui. J. Shandong Univ. Sci. Technol. (Nat. Sci.) 2015, 34, 30–35. [Google Scholar]
- Zheng, J.K. Fracture Distribution Research of Igneous Reservoir in the West Flank of Chepaizi Uplift. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2019. [Google Scholar]
- Li, L.; Dai, J.S. Numerical simulation of tectonic stress field and fracture distribution of Mesozoic and Paleozoic erathem in Chengdao area. J. China Univ. Petrol. (Nat. Sci. Ed.) 2000, 24, 6–9. [Google Scholar]
- Chang, B.T. Petroleum Migration and Accumulation in Zhuanghai Buried Hill, Shengli Oilfield. Ph.D. Thesis, Tongji University, Shanghai, China, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).