Particle Motion and Gas–Solid Heat Exchange Enhancement in Rotary Drums with Aligned/Separated Flight
Abstract
1. Introduction
2. Numerical Procedure
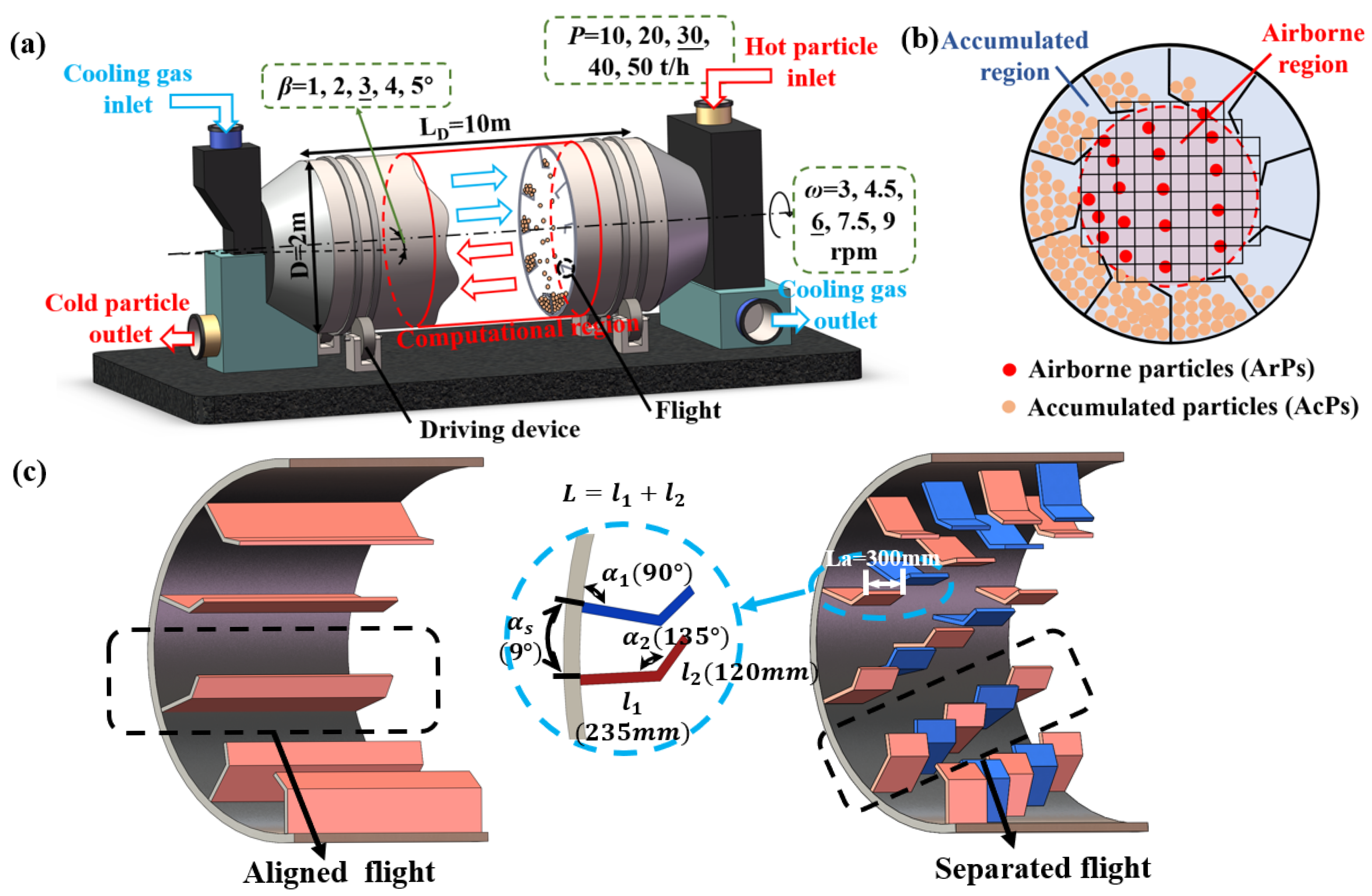
2.1. Physical Model
2.2. Discrete Element Method
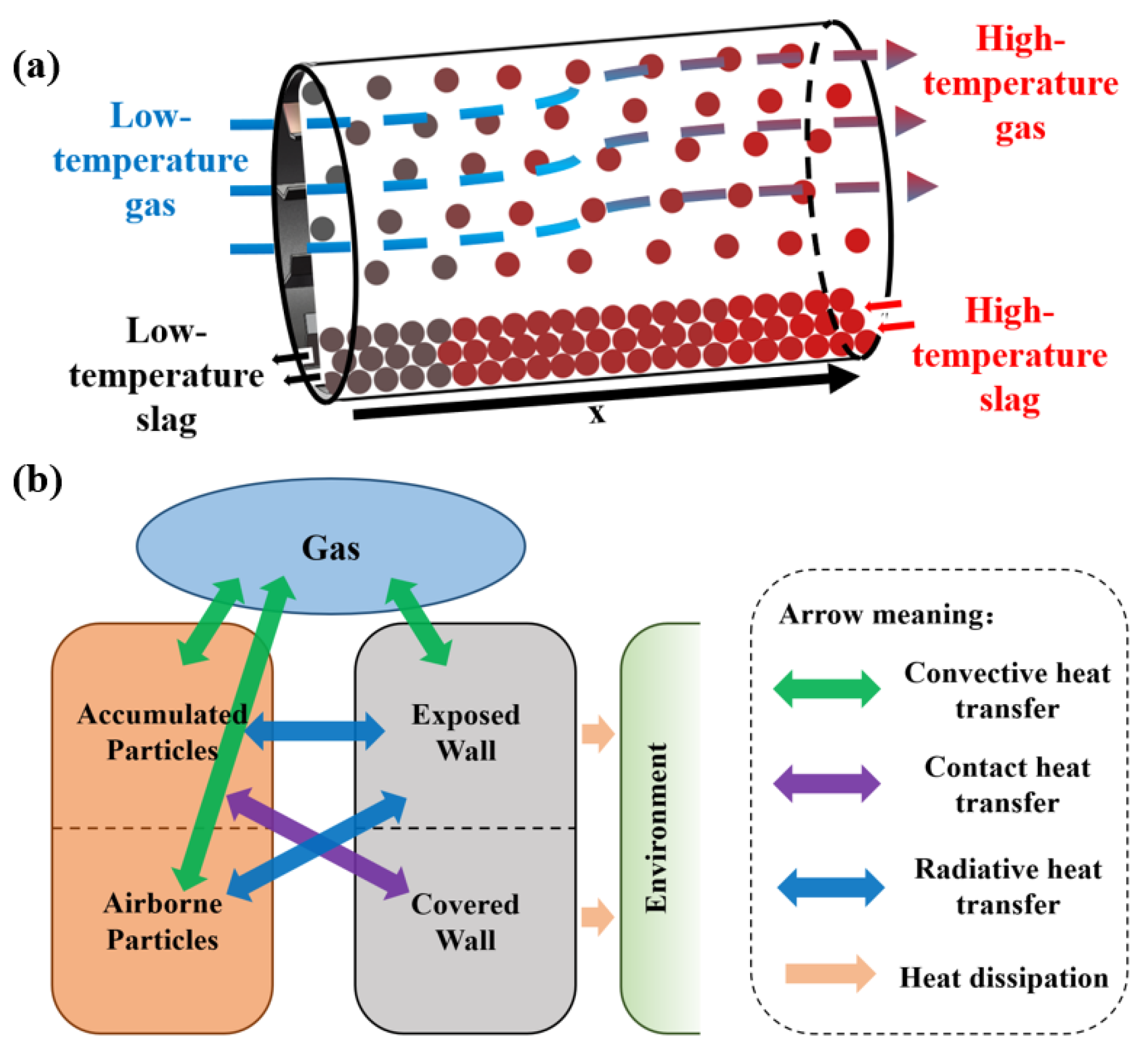
2.3. Gas–Solid Heat Exchange Model
2.4. Data Processing
2.5. Simulation Conditions
3. Result and Discussion
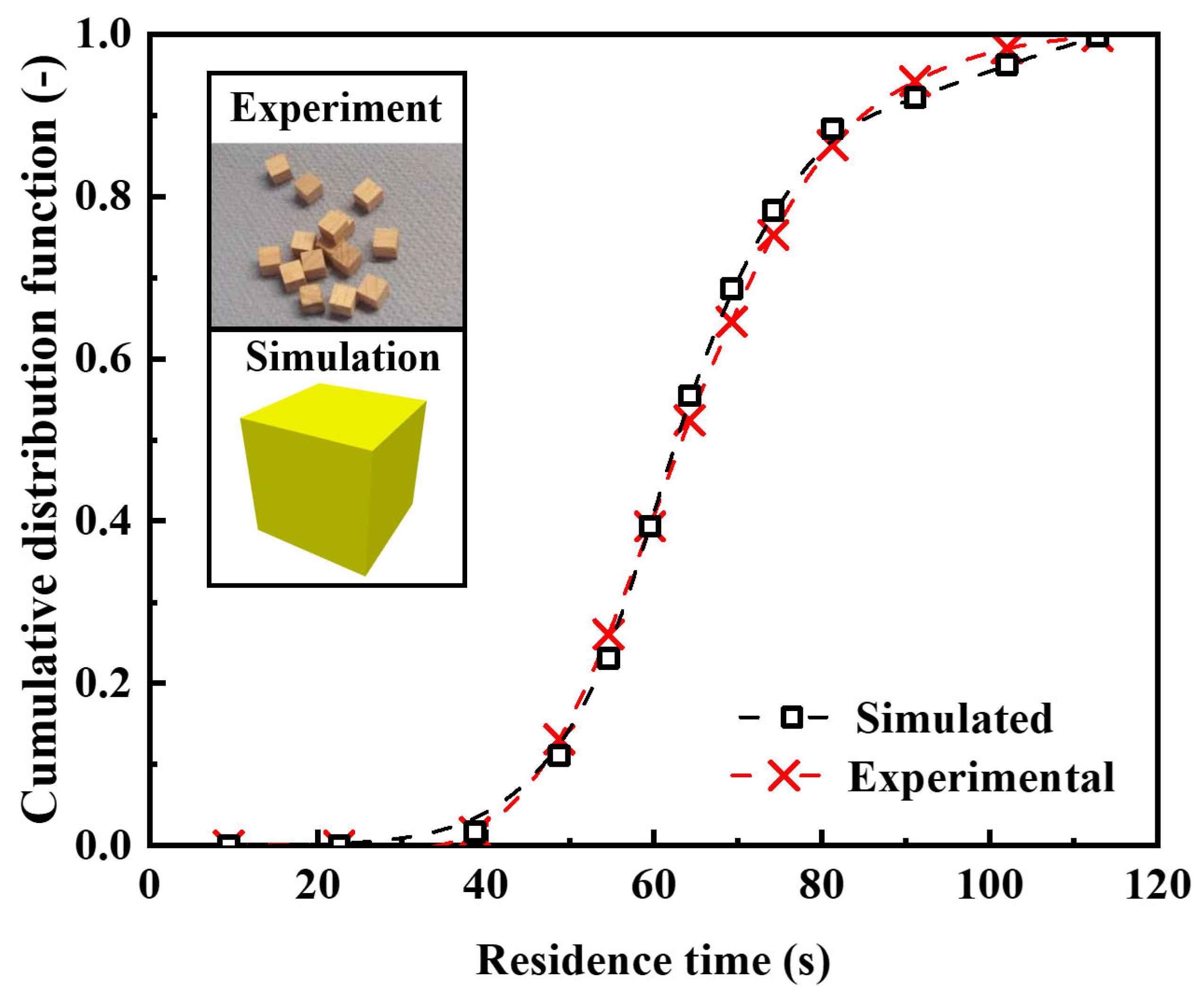
3.1. Model Validation
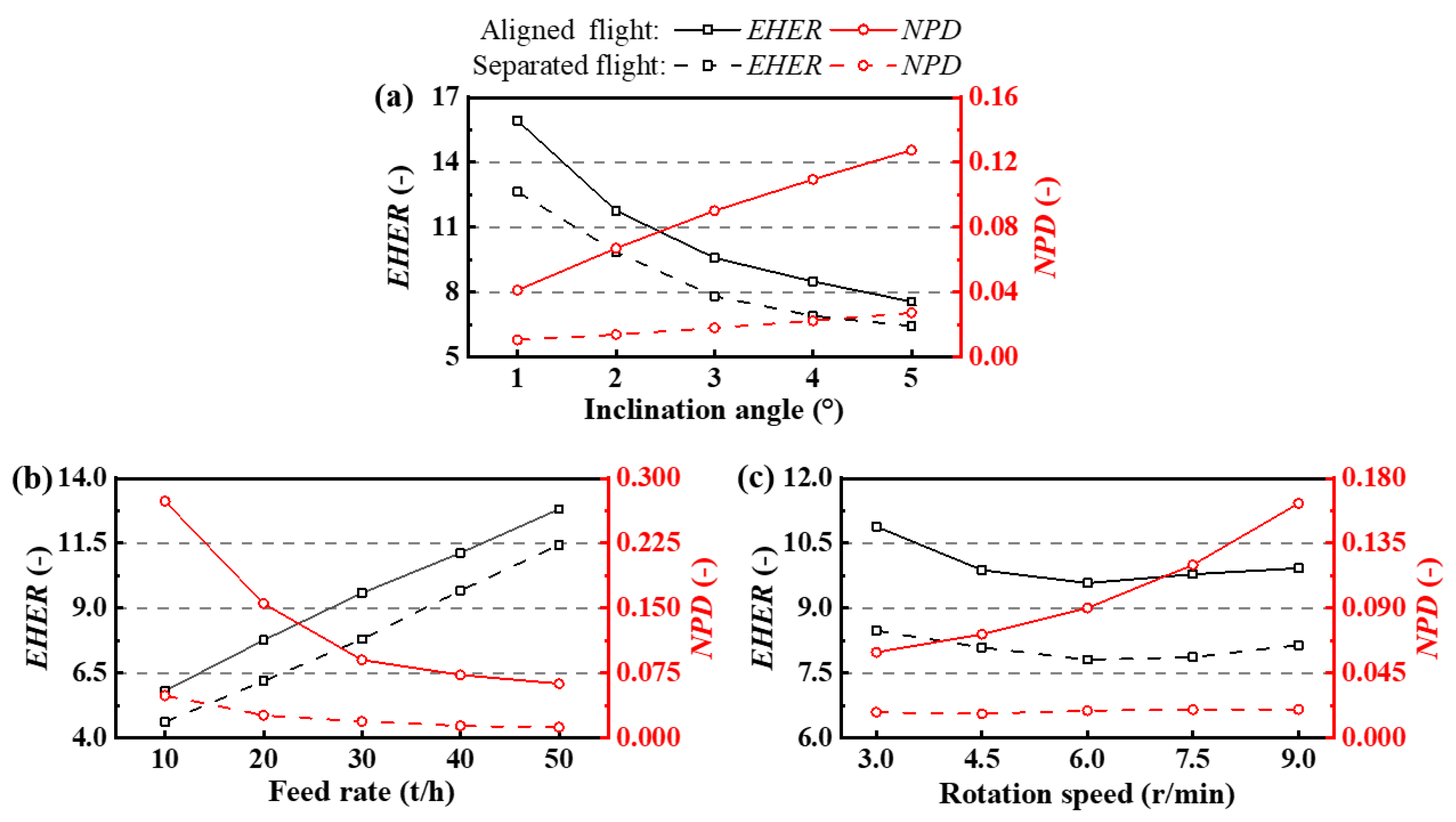
3.2. Effect of Operating Variables on Particle Motion
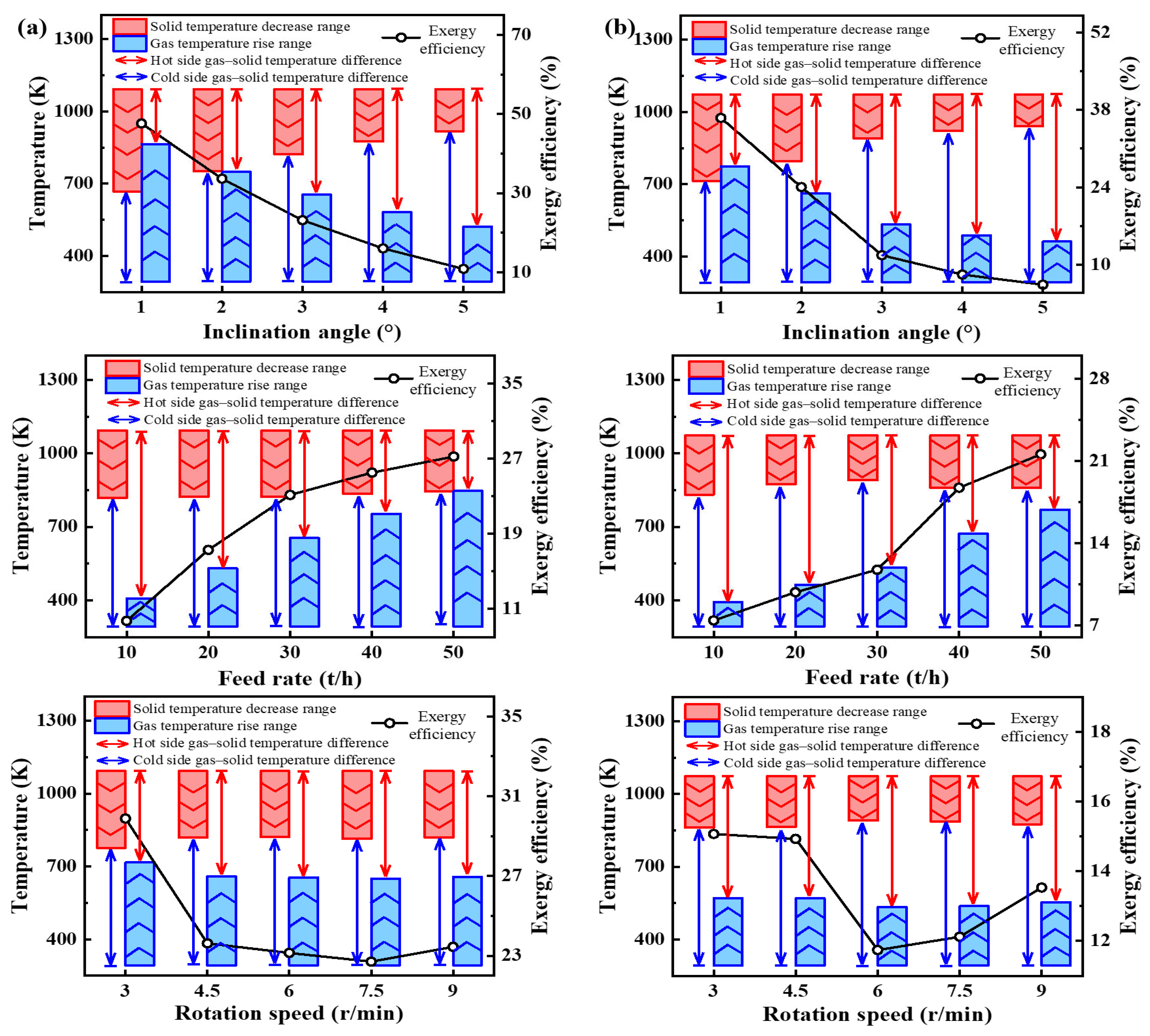
3.3. Capacity and Effectiveness of Heat Exchange
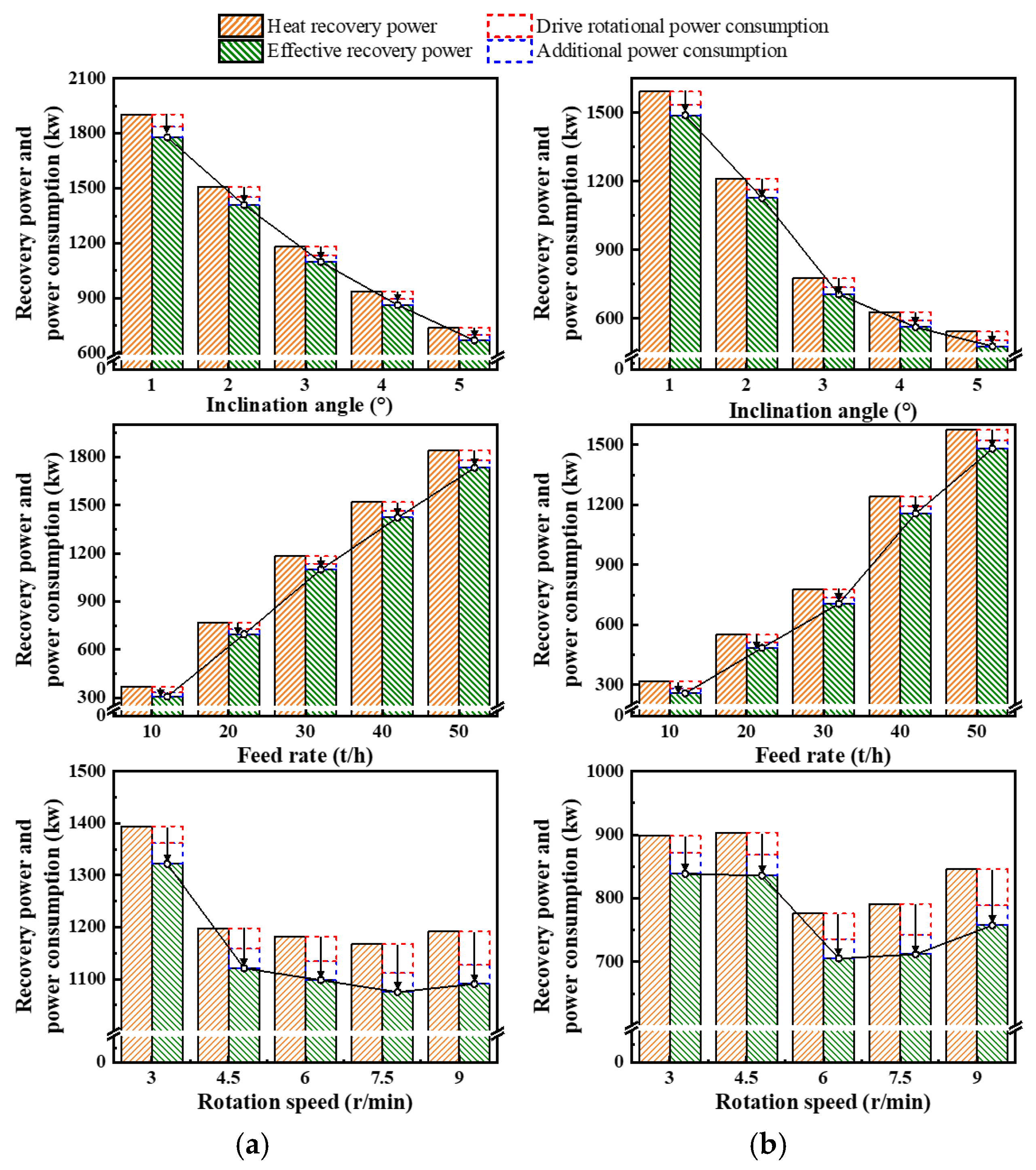
3.4. Power Recovery and Consumption
4. Conclusions
- (1)
- Particle motion in the axial direction of the drum exhibited greater randomness than in the radial direction. The use of a long-drum model enabled the identification of the true rheological characteristics of particle flow. Among all operating parameters, the inclination angle had the most pronounced effect on axial motion; as the inclination angle increased, the advancement speed of the particle bed increased approximately linearly, exhibiting a multiplicative growth trend. Compared with the aligned flight, the separated flight improved the overall flowability of the particle bed through a distinct discharge mechanism.
- (2)
- Reducing the inclination angle and increasing the feed rate significantly improved gas–solid contact, with the maximum enhancement of the heat exchange area exceeding a 2-fold increase, while also promoting a more uniform particle distribution. The rotation speed had a relatively minor influence on both heat exchange enhancement and distribution uniformity. The spiral particle curtain formed by the separated flight significantly improved distribution uniformity, reducing particle non-uniformity by nearly 4-fold compared with the aligned flight. However, the increased particle mobility also introduced a slight reduction in gas–solid contact efficiency. An appropriate filling degree played a decisive role in heat exchange enhancement.
- (3)
- Across all operating conditions, the combined ratio of additional power consumption and drive power to heat recovery power consistently remained below 20% for both flight shapes. In the case of the separated flight, when operated at a low inclination angle or high feed rate, further reductions in inclination or increases in feed rate contributed more significantly to the improvement in effective heat recovery performance. Achieving the same cooling performance with this shape required drum lengths over 30% longer than those of the aligned flight, thereby resulting in a considerable increase in equipment construction cost.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.H.; Zhang, Y.Q.; Liu, Z.; Zhang, P.B.; Liu, Y.Q. Flow properties of two-component metallized pellets in waste heat recovery drum cooler. Process Saf. Environ. Prot. 2023, 177, 1477–1484. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Zhang, P.B.; Yang, Z.Z.J.; Zhang, Y.Q.; Gao, H.B.; Gong, Z.X.; Liu, Y.Q.; Xiang, Z.Z.; Wang, Y.X. Optimizing waste heat recovery for hydrogen production: Modeling and simulation of ternary size metallic granule flow in a cooling cylinder. Int. J. Hydrogen Energy 2024, 91, 1306–1314. [Google Scholar] [CrossRef]
- Burgos-Florez, F.; Bula, A.; Marquez, J.; Ferrer, A.; Sanjuan, M. CFD-DEM Modeling and Simulation Coupled to a Global Thermodynamic Analysis Methodology for Evaluating Energy Performance: Biofertilizer Industry. Processes 2019, 7, 673. [Google Scholar] [CrossRef]
- Trojosky, M. Rotary drums for efficient drying and cooling. Dry. Technol. 2019, 37, 632–651. [Google Scholar] [CrossRef]
- Gao, H.B.; Liu, Y.Q.; Zheng, B.; Sun, P.; You, Y.Y.; Qi, X.N.; Mao, M.M.; Zhao, Q. Particles’ flow characteristics in a drum cooler with heat exchanger tubes: Simulation and comparison with traditional solution. J. Clean. Prod. 2020, 255, 120264. [Google Scholar] [CrossRef]
- Li, Y.H.; Liu, W.J.; Wang, W. Research on ash movement law of membrane bin drum slag cooler. Chem. Eng. Res. Des. 2023, 200, 202–210. [Google Scholar] [CrossRef]
- Witt, P.J.; Johnson, J.; Schwarz, M.P. An efficient method for computational flow-based simulation of heat transfer in a rotary kiln with pilot scale validation. Appl. Therm. Eng. 2022, 214, 118894. [Google Scholar] [CrossRef]
- Bisulandu, B.R.M.; Huchet, F. Rotary kiln process: An overview of physical mechanisms, models and applications. Appl. Therm. Eng. 2023, 221, 119637. [Google Scholar] [CrossRef]
- Portnikov, D.; Ziskind, G.; Kalman, H. Experimental and computational study of a flighted rotary drum cross-sectional characteristics. Powder Technol. 2022, 403, 117398. [Google Scholar] [CrossRef]
- Lomine, F.; Hellou, M.; Roques, Y. An analysis of optimal segmented flight design in a rotary dryer. Powder Technol. 2022, 407, 117594. [Google Scholar] [CrossRef]
- Zhou, Z.X.; Li, J.H.; Zhou, J.Z.; Li, S.Z.; Feng, J.X. Enhancing mixing of cohesive particles by baffles in a rotary drum. Particuology 2016, 25, 104–110. [Google Scholar] [CrossRef]
- Liao, H.B.; Lin, T.Q.; Gardoni, P.; Zhang, W.; Li, X.G.; Krolczyk, G.; Deng, L.; Li, Z.X. Molecular dynamics analysis of a flavoring drum combining numerical simulation and experimental evaluation. Eng. Anal. Bound. Elem. 2023, 146, 715–732. [Google Scholar] [CrossRef]
- Kozakovic, M.; Havlica, J.; Guen, L.L.; Parez, S.; Huchet, F. Recognition of the granular airborne portion in a flighted rotary drum. Powder Technol. 2023, 425, 118565. [Google Scholar] [CrossRef]
- Lange, A.; Meitzner, C.; Specht, E.; Kruggel-Emden, H. Exploring transverse particle motion in rotary drums: DEM analysis of the influence of cross-shaped internals on material transport. Powder Technol. 2024, 443, 119907. [Google Scholar] [CrossRef]
- Seidenbecher, J.; Herz, F.; Specht, E.; Dieguez-Alonso, A. Contact heat transfer analysis in flighted rotary drums. Therm. Sci. Eng. Prog. 2024, 47, 102265. [Google Scholar] [CrossRef]
- Xie, Q.; Chen, Z.B.; Hou, Q.F.; Yu, A.B.; Yang, R.Y. DEM investigation of heat transfer in a drum mixer with lifters. Powder Technol. 2017, 314, 175–181. [Google Scholar] [CrossRef]
- Silveira, J.C.; Brandao, R.J.; Lima, R.M.; Machado, M.V.C.; Barrozo, M.A.S.; Duarte, C.R. A fluid dynamic study of the active phase behavior in a rotary drum with flights of two and three segments. Powder Technol. 2020, 368, 297–307. [Google Scholar] [CrossRef]
- Karali, M.A.; Sunkara, K.R.; Herz, F.; Specht, E. Experimental analysis of a flighted rotary drum to assess the optimum loading. Chem. Eng. Sci. 2015, 138, 772–779. [Google Scholar] [CrossRef]
- Karali, M.A.; Herz, F.; Specht, E.; Mallmann, J. Comparison of image analysis methods to determine the optimum loading of flighted rotary drums. Powder Technol. 2016, 291, 147–153. [Google Scholar] [CrossRef]
- Karali, M.A.; Specht, E.; Herz, F.; Mallmann, J. Different camera and light positions to facilitate image analysis processing in rotary drums studies. Powder Technol. 2017, 306, 55–60. [Google Scholar] [CrossRef]
- Karali, M.A.; Specht, E.; Herz, F.; Mallmann, J.; Refaey, H.A. Unloading characteristics of flights in a flighted rotary drum operated at optimum loading. Powder Technol. 2018, 333, 347–352. [Google Scholar] [CrossRef]
- Ajayi, O.O.; Sheehan, M.E. Design loading of free flowing and cohesive solids in flighted rotary dryers. Chem. Eng. Sci. 2012, 73, 400–411. [Google Scholar] [CrossRef]
- Priessen, J.; Barths, F.; Behrens, M.; Schultz, H.J. The length of axially segmented lifters in flighted rotary drums: Influence on solid transport. Dry. Technol. 2021, 40, 3003–3020. [Google Scholar] [CrossRef]
- Silveira, J.C.; Lima, R.M.; Brandao, R.J.; Duarte, C.R.; Barrozo, M.A.S. A study of the design and arrangement of flights in a rotary drum. Powder Technol. 2022, 395, 195–206. [Google Scholar] [CrossRef]
- Lacombe, E.; Marchand, M.; Dupont, C.; Marechal, D.; Melkior, T. Residence time distribution of wood chips in a semi-industrial multiple hearth furnace using RFID tracers. Particuology 2024, 91, 268–279. [Google Scholar] [CrossRef]
- Miao, Q.H.; Zhu, W.C.; Wang, J.X.; Huang, P.; Hu, C.B.; Ge, Y. Application of the combination on data-driven and discrete element model: Particle segregation prediction and classification in rotary drums. Chem. Eng. Res. Des. 2023, 200, 456–468. [Google Scholar] [CrossRef]
- Brazhenko, V.; Mochalin, I. Terminal velocity and drag coefficient of a smooth steel sphere moving in the water-filled vertical and inclined glass pipe (Newton regime). Powder Technol. 2024, 446, 120120. [Google Scholar] [CrossRef]
- Bongo Njeng, A.S.; Vitu, S.; Clausse, M.; Dirion, J.L.; Debacq, M. Effect of lifter shape and operating parameters on the flow of materials in a pilot rotary kiln: Part III. Up-scaling considerations and segregation analysis. Powder Technol. 2016, 297, 415–428. [Google Scholar] [CrossRef]
- Zhang, L.; Weigler, F.; Idakiev, V.; Jiang, Z.; Mörl, L.; Mellmann, J.; Tsotsas, E. Experimental study of the particle motion in flighted rotating drums by means of Magnetic Particle Tracking. Powder Technol. 2018, 339, 817–826. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, Z.; Weigler, F.; Herz, F.; Mellmann, J.; Tsotsas, E. PTV measurement and DEM simulation of the particle motion in a flighted rotating drum. Powder Technol. 2020, 363, 23–37. [Google Scholar] [CrossRef]
- Zhu, X.; Xie, L.X.; Xu, S.C.; Zhang, W. DEM Simulation of a Rotary Drum with Inclined Flights Using the Response Surface Methodology. Processes 2023, 11, 1363. [Google Scholar] [CrossRef]
- Jian, Q.S.; Gu, H.L.; Wang, K.G.; Wang, S.; Zhan, M.X.; Wang, J.Q.; Ji, L.J.; Chi, Z.H.; Zhang, G.X. Numerical study of particle behaviours and heat transfer in a complex rotary kiln. Particuology 2024, 92, 81–94. [Google Scholar] [CrossRef]
- Xu, L.; Wu, X.K.; Wang, S.; Bao, S.Y. Multi-level coarse-grained discrete element method modeling of cylinder particle flow in a rotating drum. Particuology 2024, 88, 218–238. [Google Scholar] [CrossRef]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Renzo, A.D.; Di-Maio, F.P. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chem. Eng. Sci. 2004, 59, 525–541. [Google Scholar] [CrossRef]
- Feng, Y.H.; Zhang, Z.; Qiu, L.; Zhang, X.X. Heat recovery process modelling of semi-molten blast furnace slag in a moving bed using XDEM. Energy 2019, 186, 115876. [Google Scholar] [CrossRef]
- Delele, M.A.; Weigler, F.; Franke, G.; Mellmann, J. Studying the solids and fluid flow behavior in rotary drums based on a multiphase CFD model. Powder Technol. 2016, 292, 260–271. [Google Scholar] [CrossRef]
- Ma, J.; Lei, X.L.; Ma, R.C. Parameters Optimization of Rotary Drying by Uniform Design. Appl. Mech. Mater. 2014, 448–453, 3523–3531. [Google Scholar] [CrossRef]
- Mahdavy, S.; Norouzi, H.R.; Jordan, C.; Haddadi, B.; Harasek, M. Residence time distribution of non-spherical particles in a continuous rotary drum. Processes 2022, 10, 1069. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.R.; Lai, N.C.; Jiang, Z.Y.; Li, J.Z. A novel process for coke wastewater gasification quenching: Energy and exergy analysis. Appl. Therm. Eng. 2021, 191, 116863. [Google Scholar] [CrossRef]
- Lauredan, L.G.; Florian, H.; Jean, D. A wall heat transfer correlation for the baffled-rotary kilns with secondary air flow and recycled materials inlet. Exp. Therm. Fluid Sci. 2014, 54, 110–116. [Google Scholar] [CrossRef]
- Wu, W.N.; Liu, X.Y.; Zhang, R.; Hu, Z. DEM investigation of the power draw for material movement in rotary drums with axis offset. Chem. Eng. Res. Des. 2019, 144, 310–317. [Google Scholar] [CrossRef]





| Parameter (Unit) | Value |
|---|---|
| Particle diameter (mm) | 12 |
| Density (kg/m3) | 2800 |
| Shear modulus (Pa) | 5.3 × 109 |
| Poisson ratio (-) | 0.2 |
| Restitution for P-P (-) | 0.25 |
| Static friction for P-P (-) | 0.41 |
| Rolling friction for P-P (-) | 0.08 |
| Restitution for P-W (-) | 0.2 |
| Static friction for P-W (-) | 0.36 |
| Rolling friction for P-W (-) | 0.1 |
| Parameters | Base Value | Variation Value |
|---|---|---|
| Inclination angle (°) | 3 | 1, 2, 4, 5 |
| Feed rate (t/h) | 30 | 10, 20, 40, 50 |
| Rotation speed (r/min) | 6 | 3, 4.5, 7.5, 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; E, D.; Jiang, Z. Particle Motion and Gas–Solid Heat Exchange Enhancement in Rotary Drums with Aligned/Separated Flight. Processes 2025, 13, 1594. https://doi.org/10.3390/pr13051594
He Y, E D, Jiang Z. Particle Motion and Gas–Solid Heat Exchange Enhancement in Rotary Drums with Aligned/Separated Flight. Processes. 2025; 13(5):1594. https://doi.org/10.3390/pr13051594
Chicago/Turabian StyleHe, Yewei, Dianyu E, and Zeyi Jiang. 2025. "Particle Motion and Gas–Solid Heat Exchange Enhancement in Rotary Drums with Aligned/Separated Flight" Processes 13, no. 5: 1594. https://doi.org/10.3390/pr13051594
APA StyleHe, Y., E, D., & Jiang, Z. (2025). Particle Motion and Gas–Solid Heat Exchange Enhancement in Rotary Drums with Aligned/Separated Flight. Processes, 13(5), 1594. https://doi.org/10.3390/pr13051594







