In this section, the method presented above is applied on stable and unstable processes with time delay. In addition to investigating all cases of SBL, the method is also applied to a process with equal numerator and denominators, which is not commonly encountered in literature.
5.1. Example 1
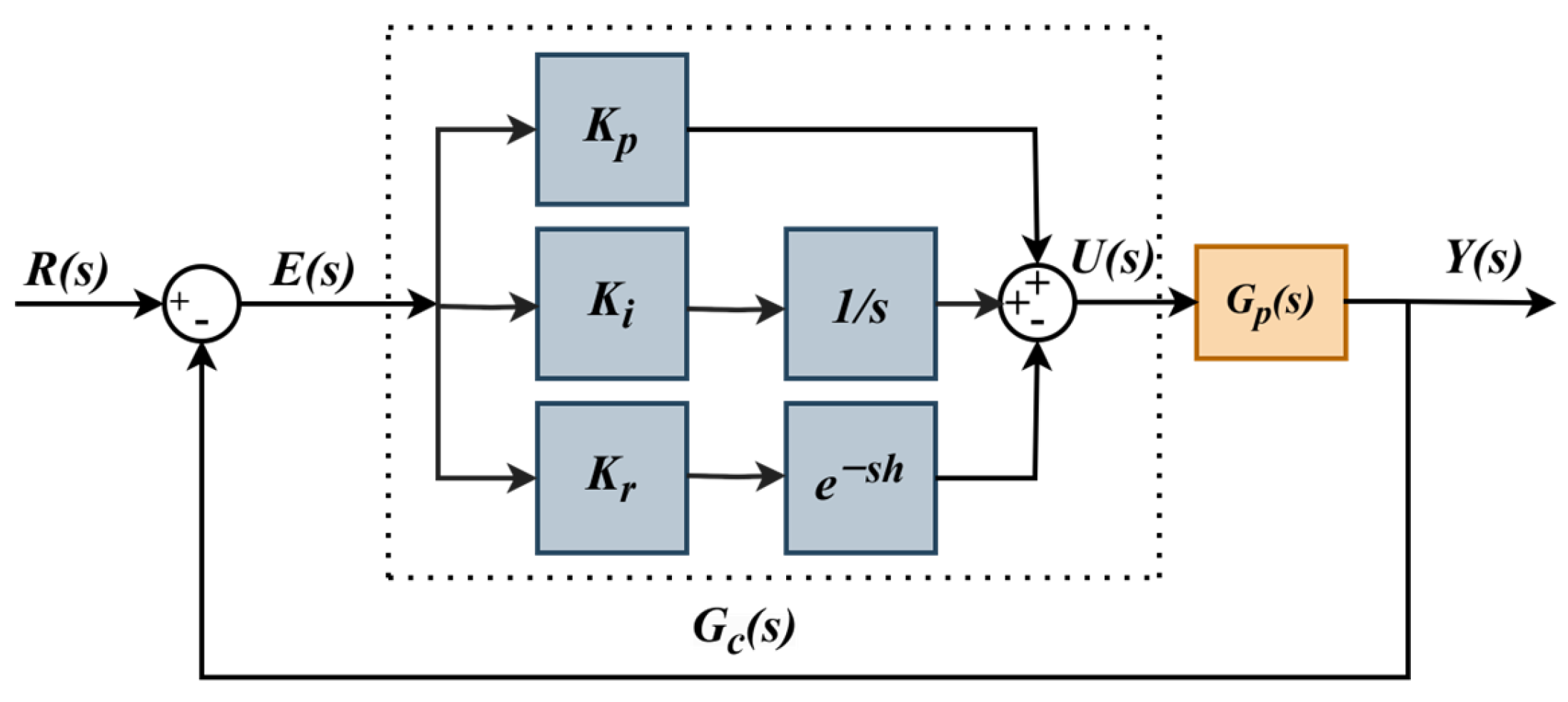
Let us examine the application of the methods described above on the 3rd-order stable time-delay process given in (26) in
Figure 1.
Before starting the analysis, the PIR controller time-delay value should be selected as a fixed value. For this example,
h = 1 was initially taken. Then, in order to draw
SBLs in the planes (
Ki,
Kr) for a fixed
Kp, (
Kr,
Kp) for a fixed
Ki value, and (
Kp,
Ki) for a fixed
Kr value, fixed
Kp, fixed
Ki, and fixed
Kr values should be selected. For this, the controller was initially selected as
, namely the PR controller (
Ki = 0). The
RRB line equation defined in Step 1 was updated for the system in (26) and obtained as
. As
n >
m, the
IRB line will not be formed. The
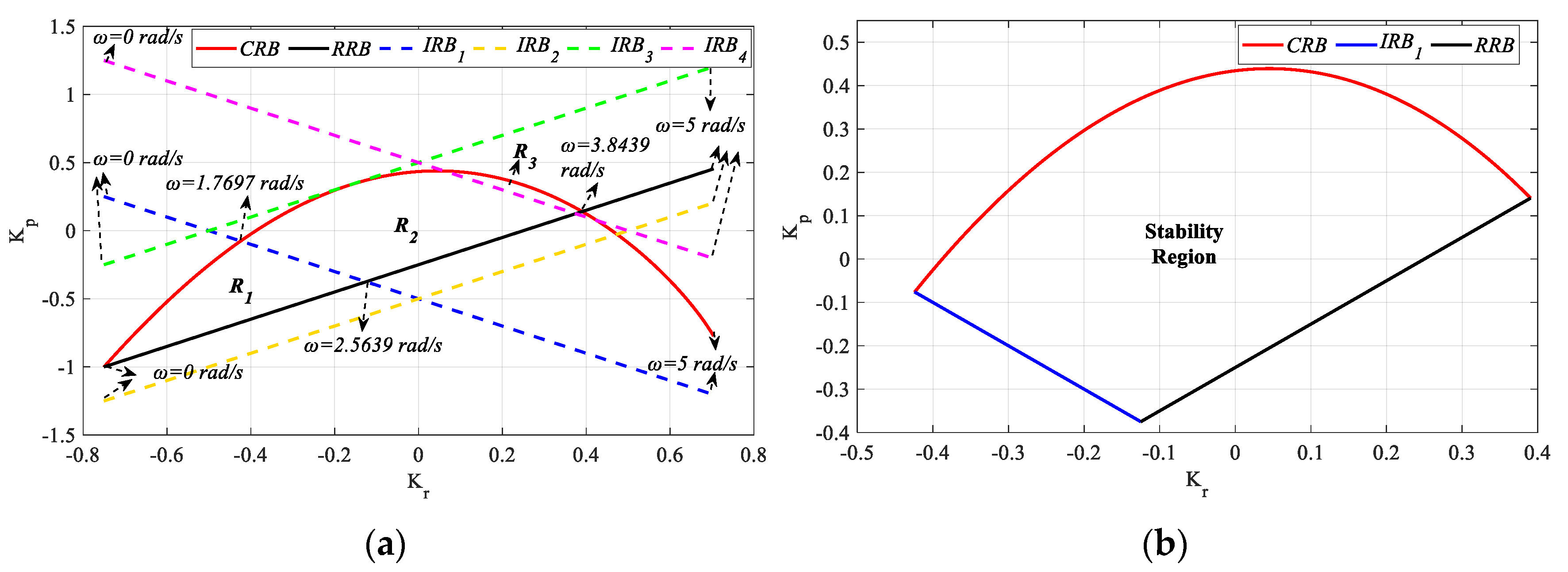
Kp(ω) and
Kr(ω)
CRB equations are obtained with the help of (24) and (25). Accordingly, the
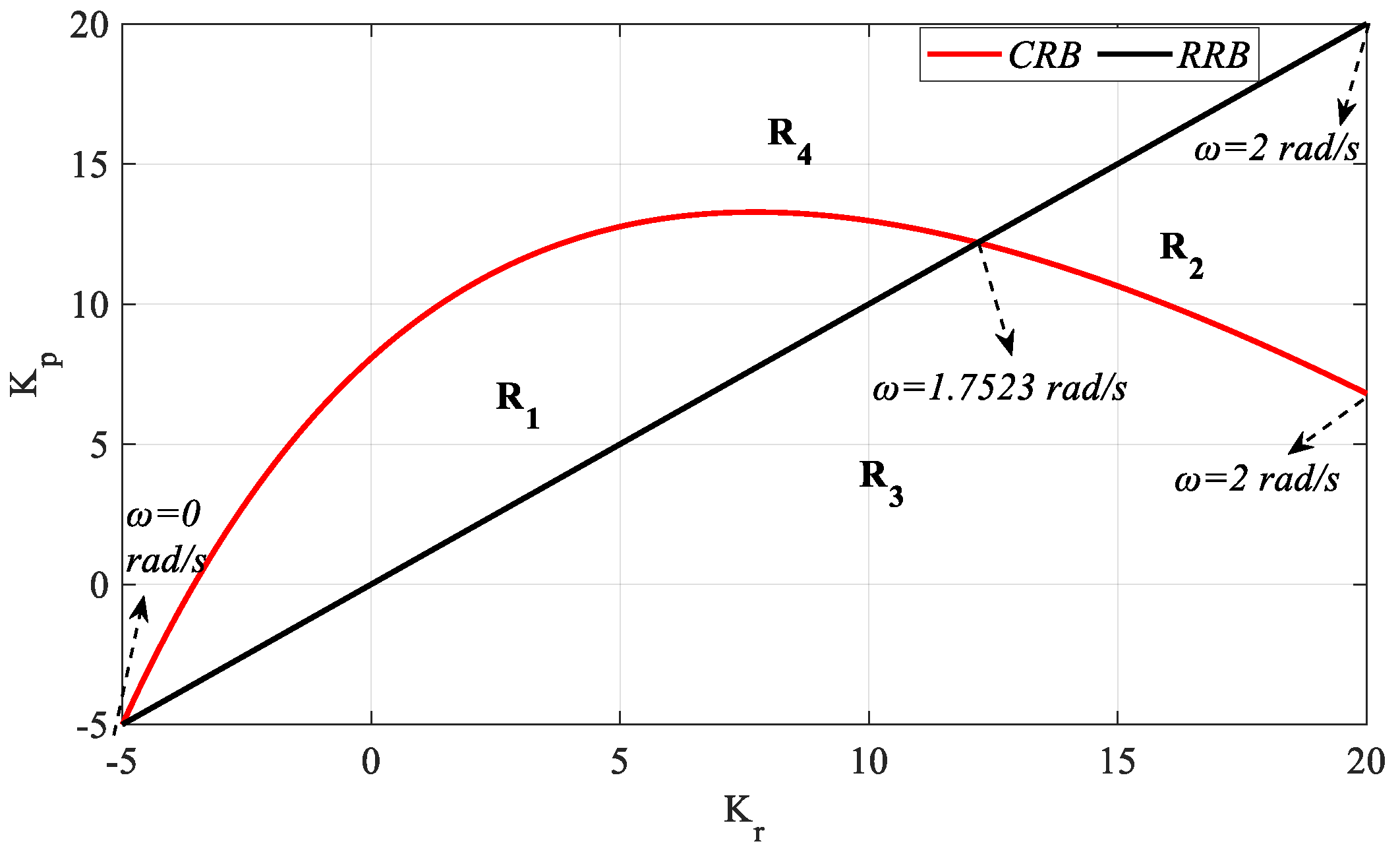
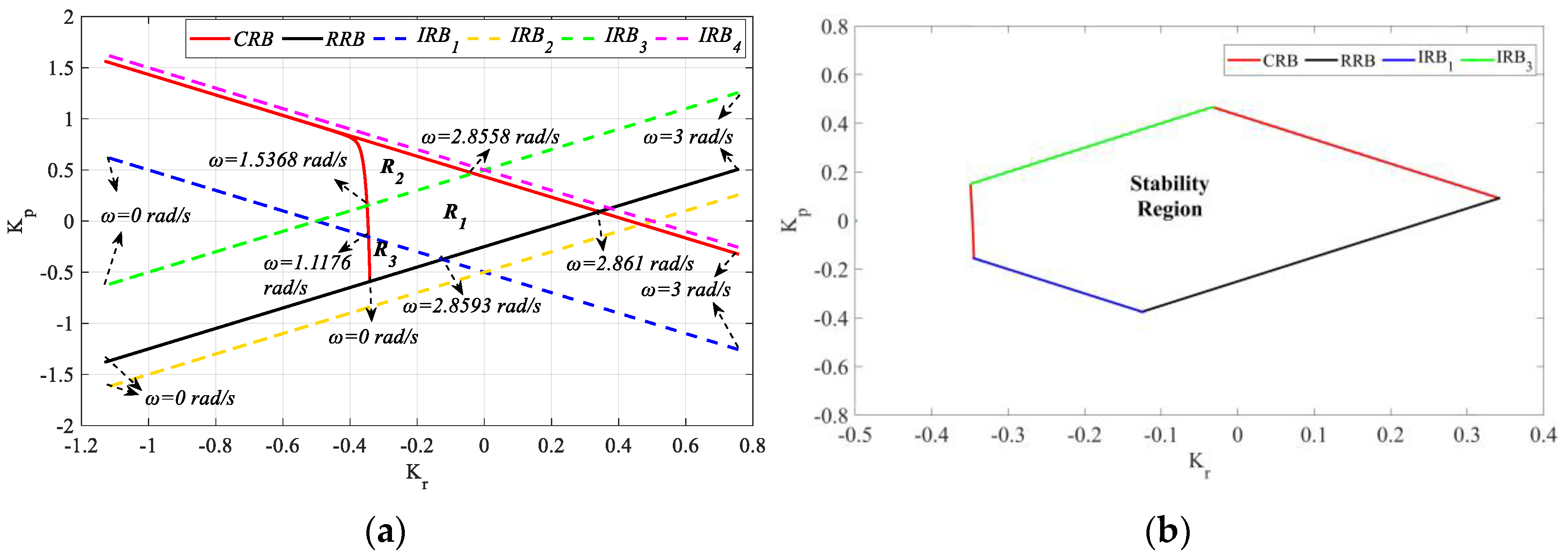
SBL curve was drawn as in
Figure 2 with the help of the
RRB and
CRB equations.
SBL is obtained for the frequency range
ω ∈ [0, 2] rad/s as in
Figure 2. Here, our aim was to find the entire (
Kr,
Kp) parameter region that makes the characteristic polynomial in (4) Hurwitz stable. For this purpose, the stability of (4) is examined by selecting the (
Kr,
Kp) parameter test points from the region bounded by the
CRB and
RRB lines and the regions outside this region. The test points (1.60, 3.16), (17.64, 13.22), (8.86, 4.3), and (6.5, 14.98) are selected from the determined
R1,
R2,
R3, and
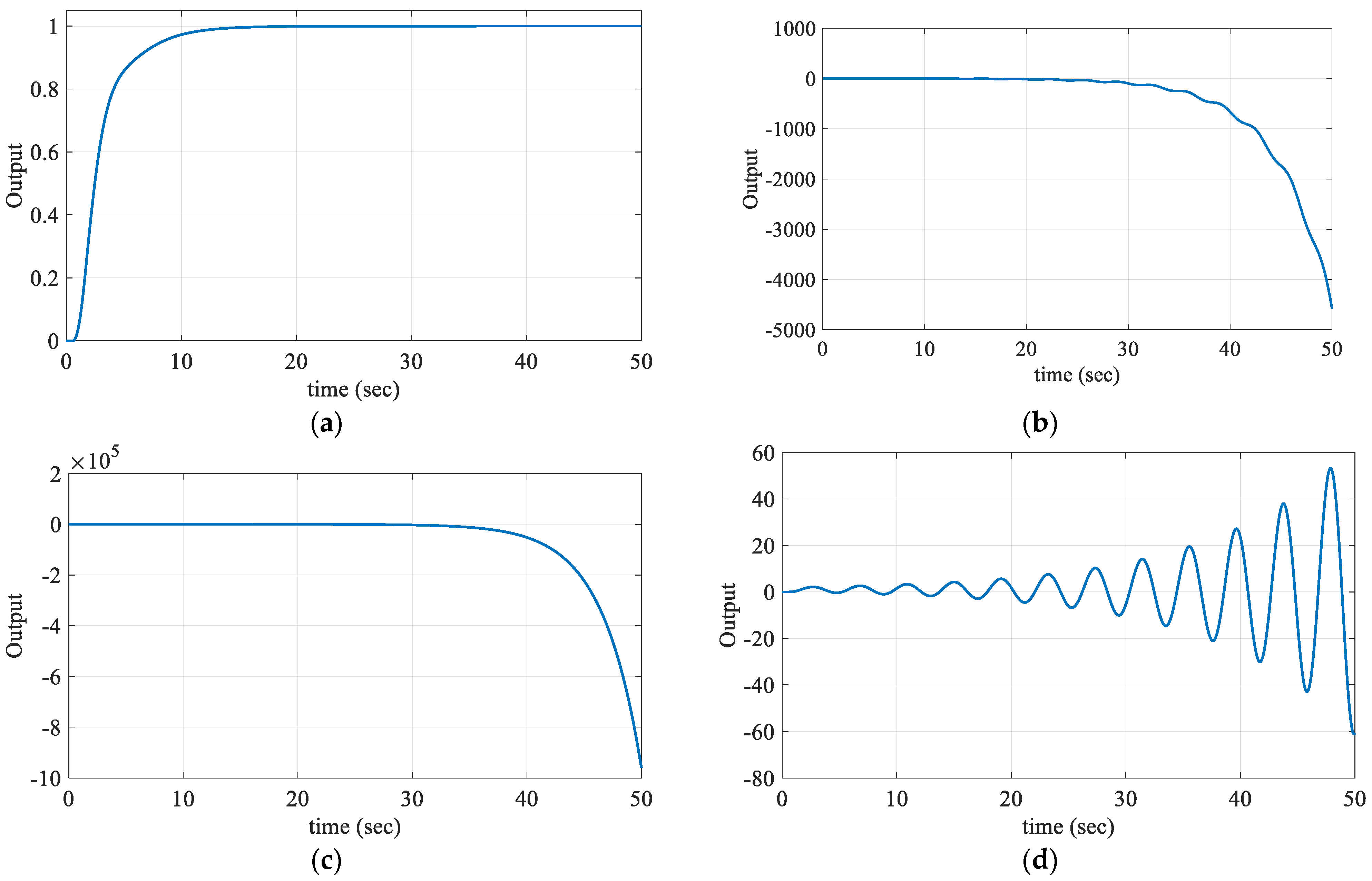
R4 regions, respectively. The unit step responses obtained according to these test points are given in
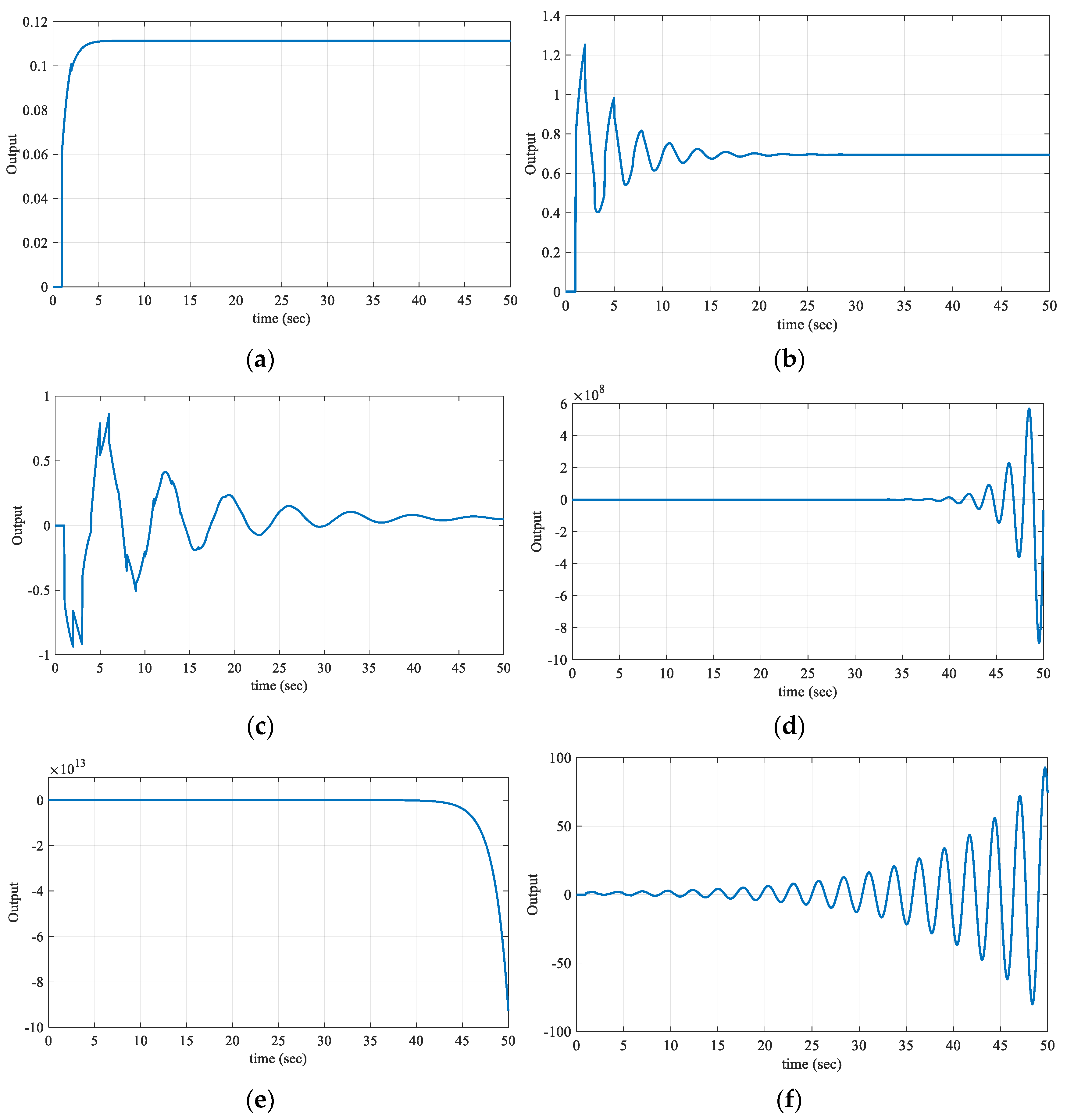
Figure 3.
As the characteristic equations written in (4) for the test points selected from the
R2,
R3, and
R4 regions have a right half-plane pole, these regions are unstable regions, as seen in
Figure 3b–d. The characteristic equation for the test point in the
R1 region has only a left half-plane pole. Therefore, the stable region is the
R1 region that covers the frequency range
ω ∈ [0, 1.7523] rad/s, that is, the region bounded by the
CRB and
RRB lines. Accordingly, the stability region drawn in the (
Kr,
Kp) plane for the PR controller is given in
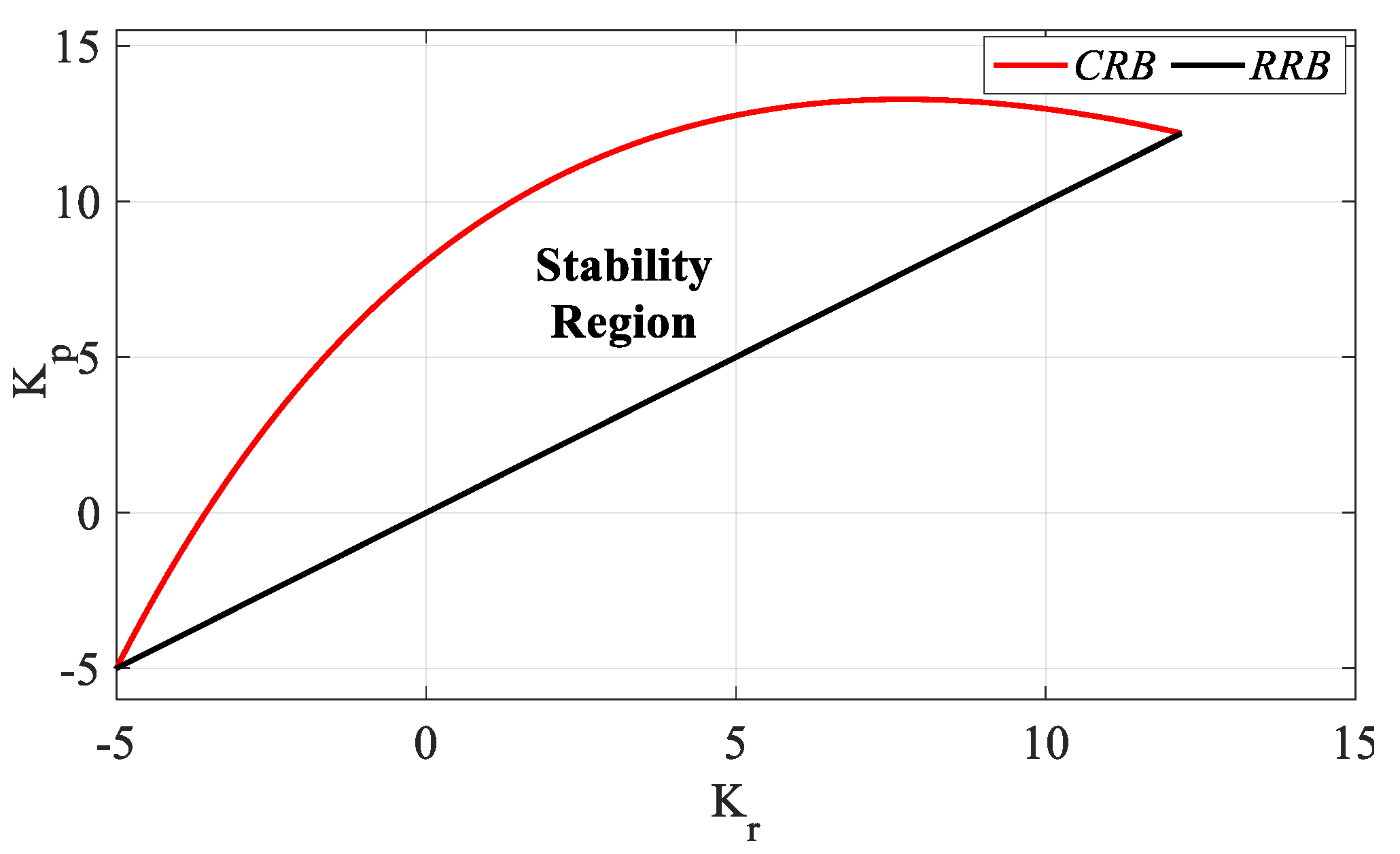
Figure 4.
When
Figure 4 is examined, the
Kp and
Kr controller parameter ranges that make the system stable are determined as [−5 13.28] and [−5 12.18], respectively. For the controller parameter range
Kr_fixed = [−2.5:2.5:10], the
Kp-Ki SBL graphs are drawn as in
Figure 5 with the help of the
RRB defined with the
Ki = 0 line equation and with the
CRB equations calculated with the help of (16) and (17).
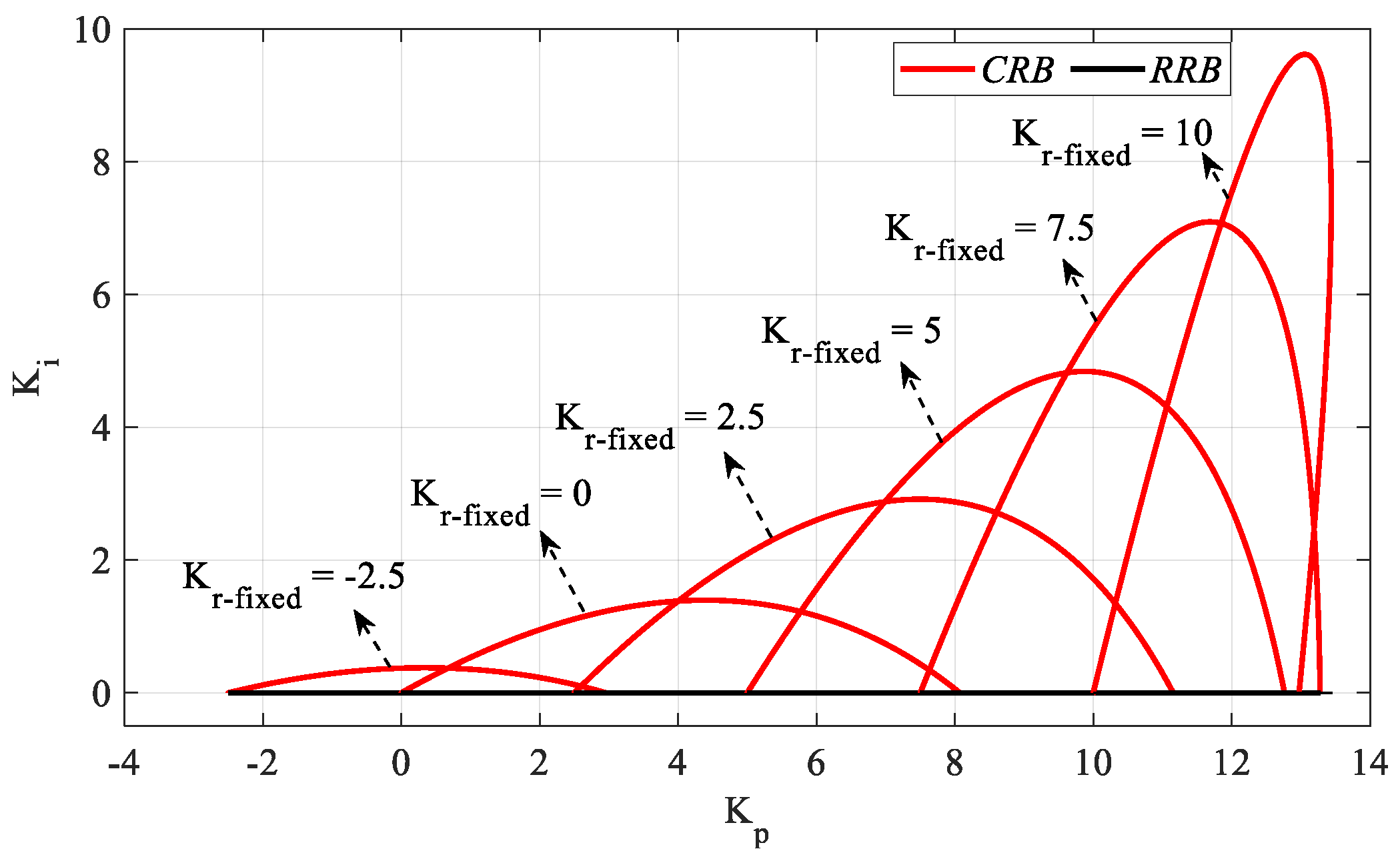
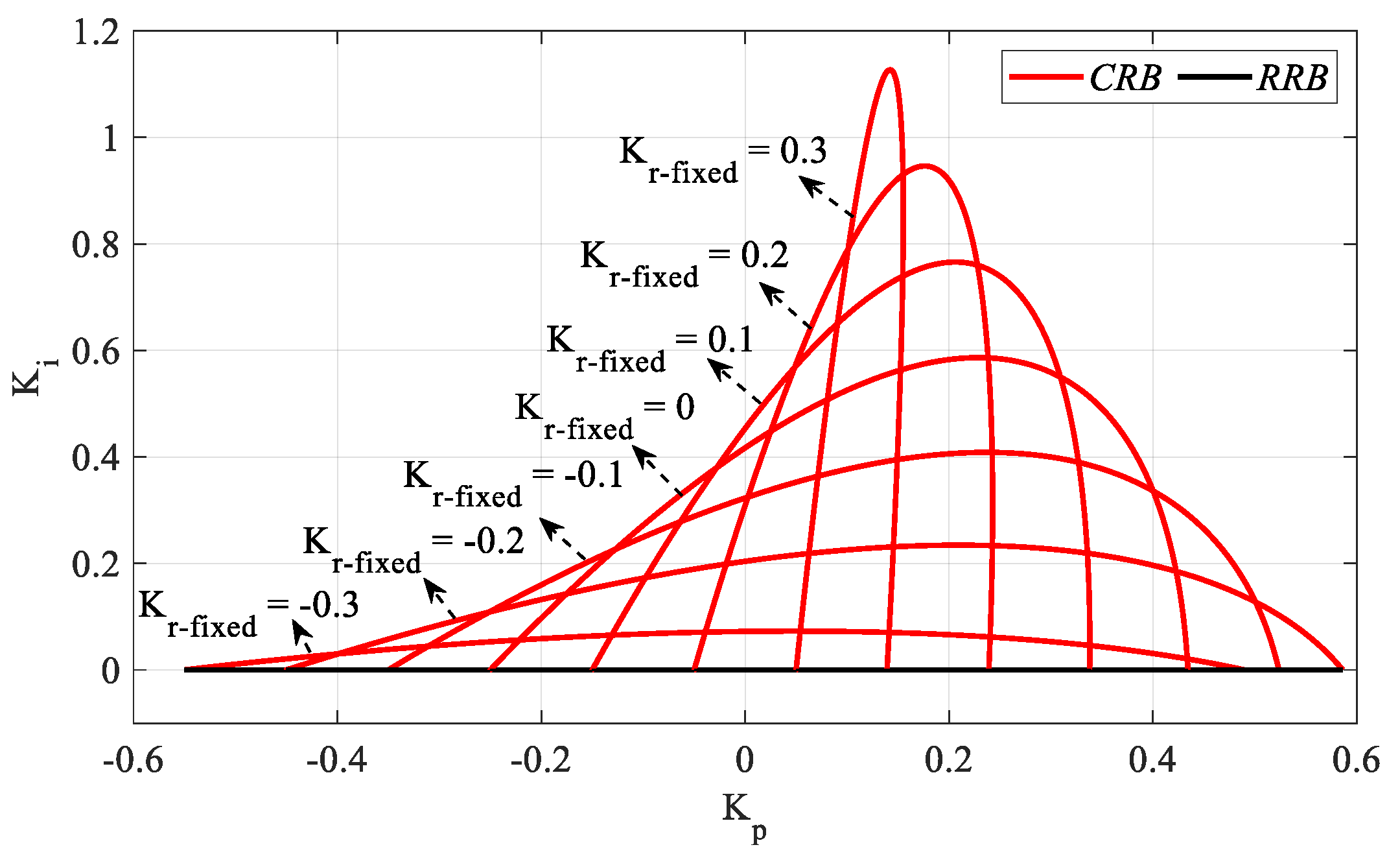
Figure 5 is obtained by plotting the
Kp-Ki SBLs in the frequency range
ω ∈ [0,
ωmax] rad/s for
Kr_fixed = −2.5, 0, 2.5, 5, 7.5, and 10 values. According to the stability analyses for these
Kr_fixed values,
ωmax values were found to be 0.7846, 1.0749, 1.2782, 1.4355, 1.5636, and 1.6710 rad/s, respectively. It should be noted that, for
Kr_fixed = 0, the controller will become a PI controller, and the controller time delay
h will have no effect on the
SBL. It is also concluded that the stability range
Kp corresponding to each
Kr value in the
SBL curve in
Figure 4 is the same as the
Kp range in the
SBL curve drawn for the corresponding
Kr value in
Figure 5. For example, it is seen in
Figure 4 that the
Kp range corresponding to
Kr = 5 is [5 12.76]. When the
Kp-Ki SBL graph in
Figure 5 drawn for
Kr_fixed = 5 is analyzed, it is seen that the stable
Kp range is [5 12.76] again. With the same reasoning, as there is no
Kp range that makes the system stable for
Kr = −5 and
Kr = 12 values in
Figure 4, these are not plotted in
Figure 5.
The
Ki controller parameter range will be determined for an
SBL selected from the
SBL graphs of the system with the PIR controller designed for different
Kr_fixed values in
Figure 5. According to the
Kp-Ki SBL graph of the PIR controller designed for
Kr_fixed = 7.5 selected from
Figure 5, it is seen that the
Ki controller parameter range that makes the system stable is [0 7.09]. For different
Ki_fixed values to be selected from the
Ki controller parameter range,
SBL graphs are obtained with the help of an
RRB defined by
and a
CRB line to be drawn with the help of (19) and (20).
SBL curves for the controller parameter range
Ki_fixed = [0:1:7] are drawn as shown in
Figure 6.
Figure 6 was obtained by plotting
Kr-
Kp SBLs in the frequency range
ω ∈ [
ωmin,
ωmax] rad/s for
Ki_fixed = 0, 1, 2, 3, 4, 5, 6 and 7. Accordingly, in the stability analyses performed for these
Ki_fixed values, the frequency ranges that make the system stable are ω ∈ [0, 1.7523], [0.244, 1.73], [0.35, 1.715], [0.432, 1.7], [0.505, 1.665], [0.575, 1.64], [0.641, 1.61] and [0.706, 1.58], respectively. For
Ki_fixed = 0, the controller will become a PR controller, and the
RRB line defined by
is the determining factor of the stability boundary only in this case, as can be seen from
Figure 6. For
Ki ≠ 0, the
RRB line is not a determining factor of the stability boundary.
When the
Kp-
Ki SBL graph for
Kr_fixed = 7.5 was analyzed in
Figure 5, it was seen that, as the value of
Ki_fixed increases, the
Kp controller parameter range that makes the system stable decreases. In
Figure 6 of this analysis, it is seen that
Kr-
Kp SBLs become smaller for increasing
Ki_fixed values, that is, the controller parameter space that makes the system stable becomes limited.
From the
SBL plot for the PR controller in
Figure 4, the
Kp controller parameter range that makes the system stable was determined as [−5 13.28]. Accordingly, for a
Kp_fixed selected from the
Kp controller parameter space,
SBL is generated by an
RRB line defined by the equation
Ki = 0 and a
CRB line to be drawn with the help of (22) and (23). Accordingly,
SBL plots for the controller parameters of
Kp_fixed = [−2.5:2.5:12.5] are drawn as shown in
Figure 7.
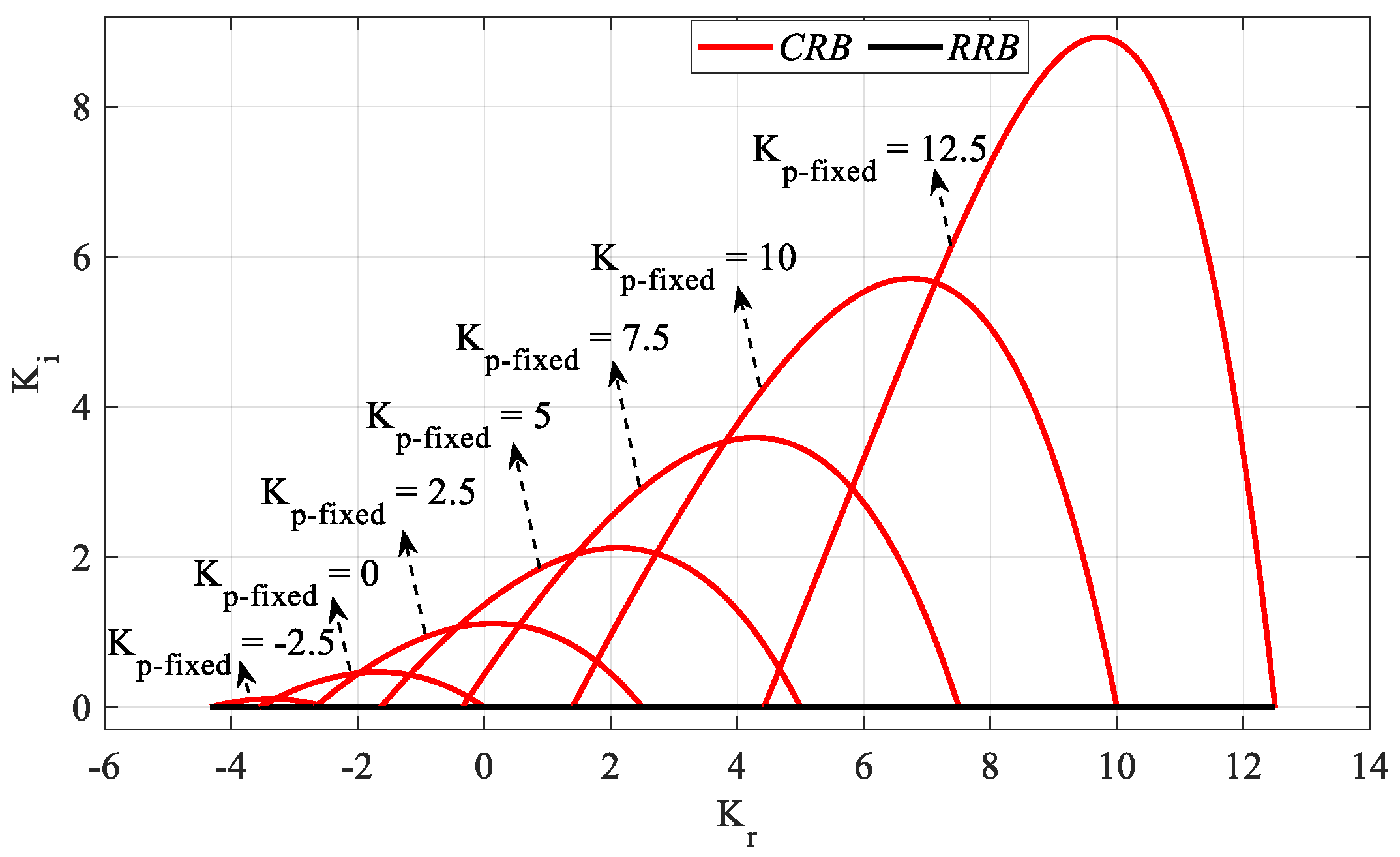
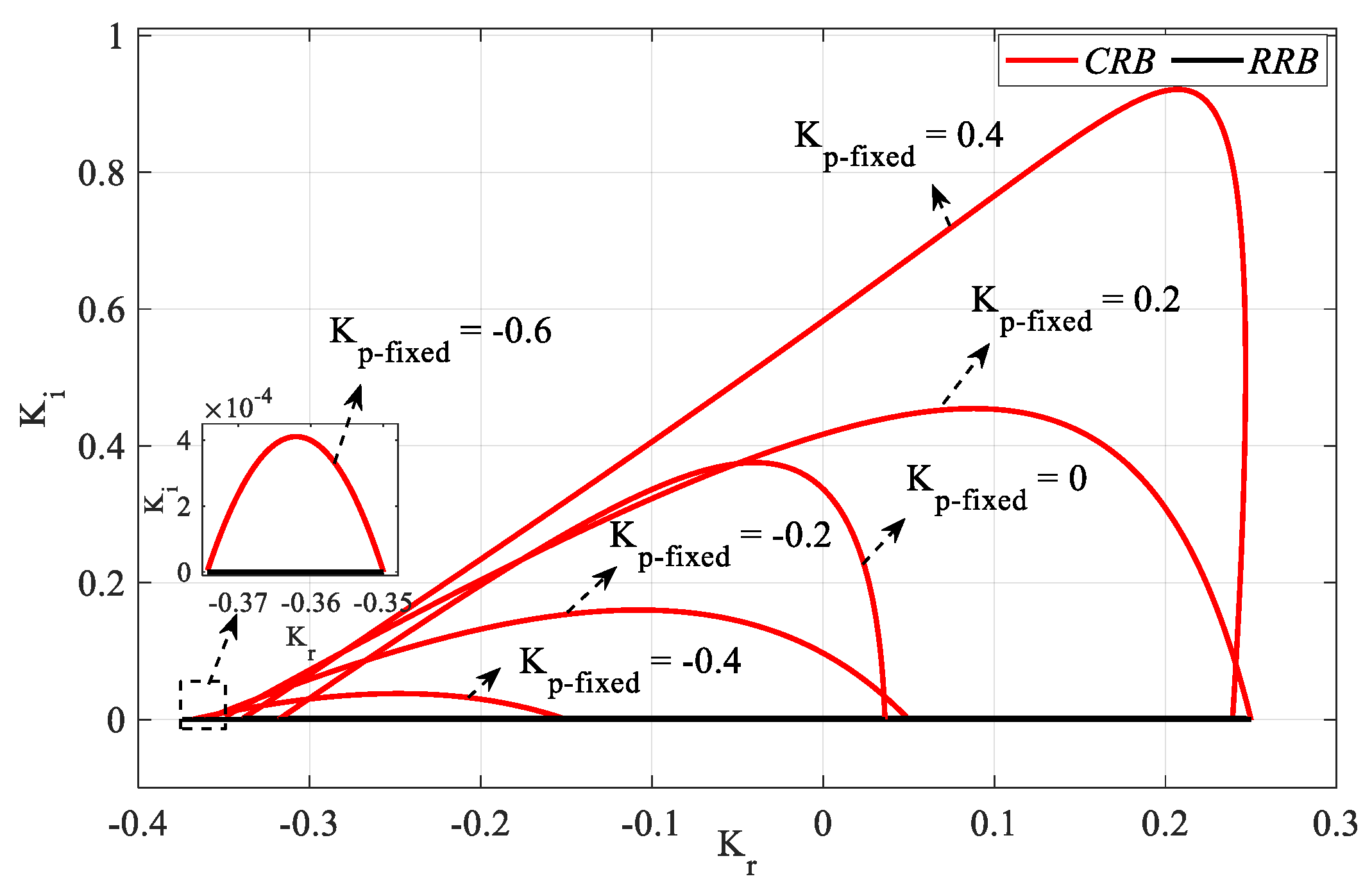
Figure 7 is obtained by plotting
Kr-Ki SBLs in the frequency range
ω ∈ [0,
ωmax] rad/s for
Kp_fixed = −2.5, 0, 2.5, 5, 7.5, 10, and 12.5 values. According to the stability analyses for these
Kp_fixed values,
ωmax values were found to be 0.4193, 0.6044, 0.7582, 0.901, 1.0415, 1.1953, and 1.4021 rad/s, respectively. It should be noted that, for
Kp_fixed = 0, the controller will become an IR controller. It is also concluded that the stability range
Kr corresponding to each
Kp value in the
SBL curve in
Figure 4 is the same as the
Kr range in the
SBL curve drawn for the corresponding
Kp_fixed value in
Figure 7. In
Figure 4, it is seen that the
Kr range corresponding to
Kp = 2.5 is [−2.67 2.5]. When the
Kr-Ki SBL graph in
Figure 7 drawn for
Kp_fixed = 2.5 is examined, it is seen that the stable
Kr range is the same. Therefore, there is no
Kr range that makes the system stable for
Kp = −5 and
Kp = 13.28 values in
Figure 4,
SBL plots for these values are not made in
Figure 7.
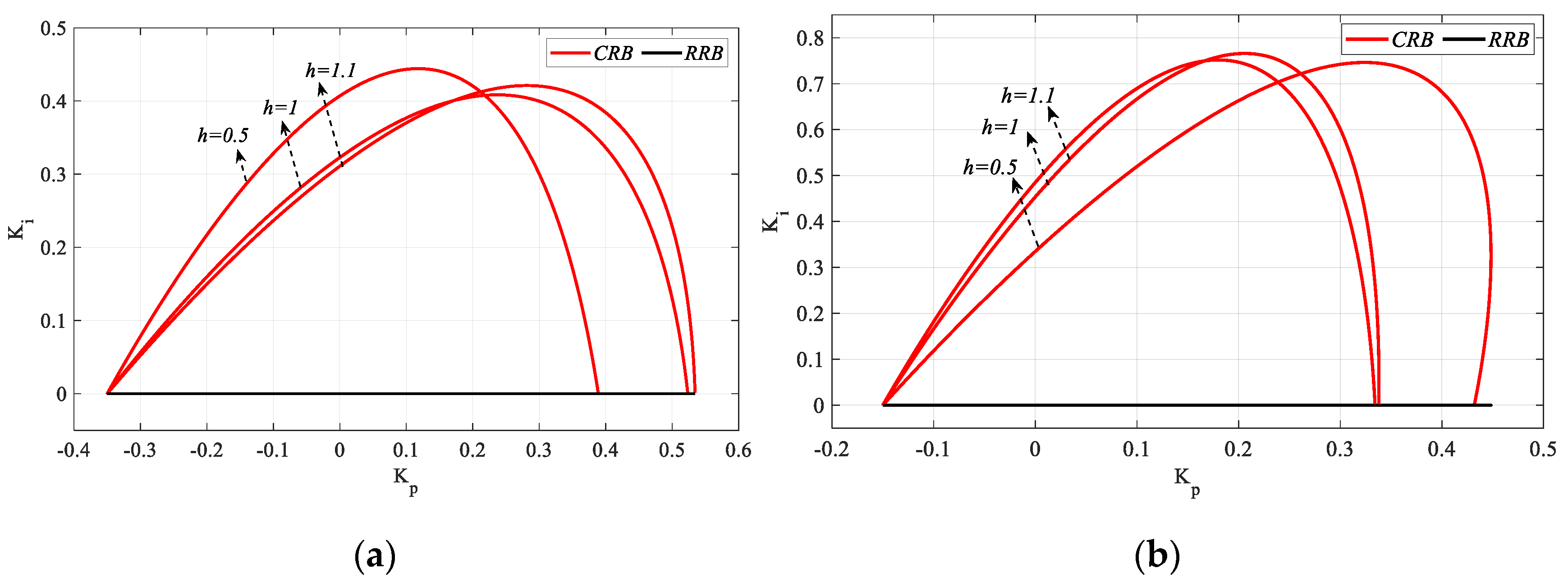
The above analyses were performed for the case where the controller time delay h is 1 s. SBL analyses should be repeated for different values of h to investigate the effect of the controller time delay on the stable controller parameter space. Therefore, three cases where the controller time delay is greater than, equal to, and less than the process time delay are analyzed in this study. The case where the controller time delay is greater than the process time delay is h = 1 as examined above, and the analyses are repeated for cases h = 0.5 (h = ) and h = 0.3 (h < ).
The analysis for
h = 1 in
Figure 2 is repeated for
h = 0.3 and
h = 0.5, and the frequency ranges that make the system stable are found as
ω ∈ [0, 2.3565] rad/s and
ω ∈ [0, 2.1386] rad/s, respectively. Accordingly, the
Kr and
Kp controller parameter ranges that make the system stable for
h = 0.3 are found to be [−16.67 47.913] and [−16.67 47.913], respectively, and [−10 26.68] and [−10 27.07] for
h = 0.5, respectively. It can be concluded that the stable controller parameter space will expand as the value of
h decreases. Then,
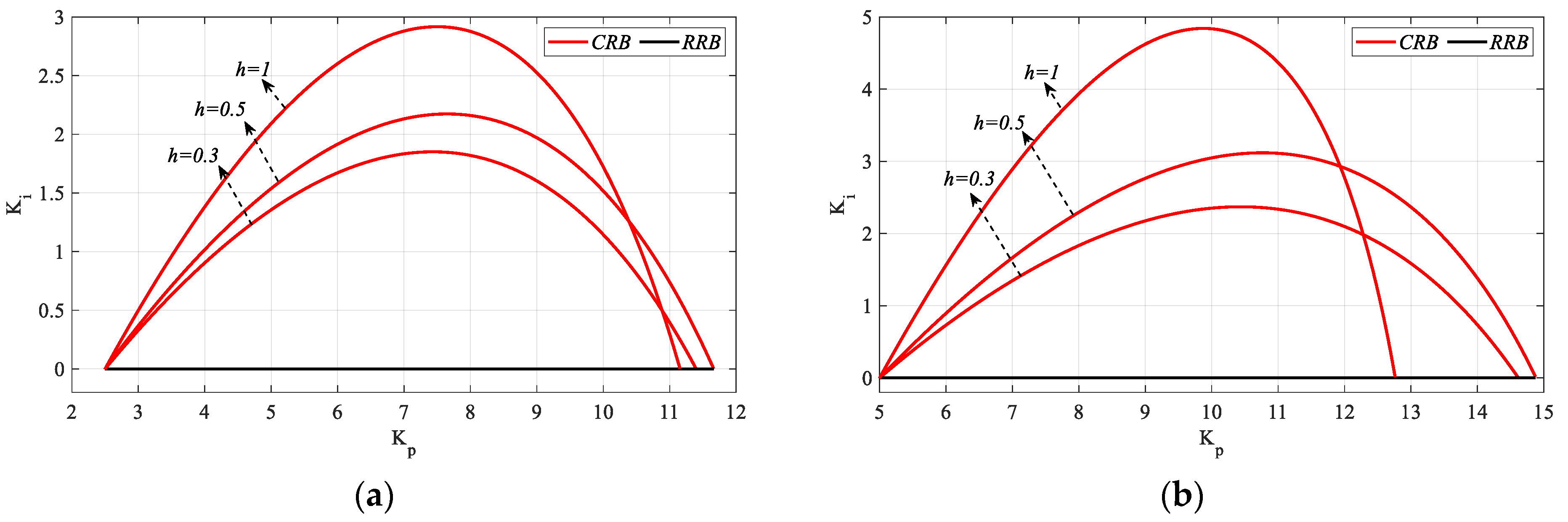
Kp-
Ki SBL plots for
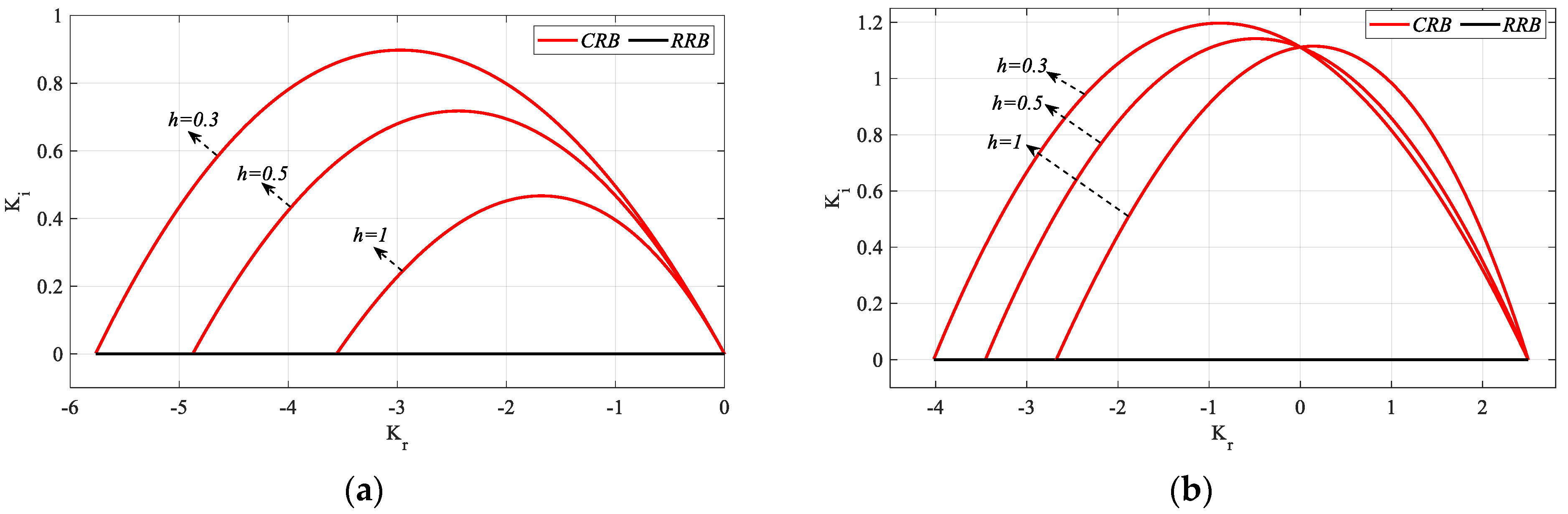
Kr_fixed = 2.5 and 5 values selected from the stable controller parameter range are obtained as shown in
Figure 8. In
Figure 8a,
ωmax values for
h = 0.3, 0.5 and 1 are 1.1575, 1.2051 and 1.2782 rad/s respectively, and in
Figure 8b,
ωmax values for
h = 0.3, 0.5, and 1 are 1.2359, 1.3239, and 1.4355 rad/s respectively. For
Kr_fixed = 0, as the controller will become a PI controller, the value of
h will have no effect on
SBL and the
SBL curve will be the same as in
Figure 5.
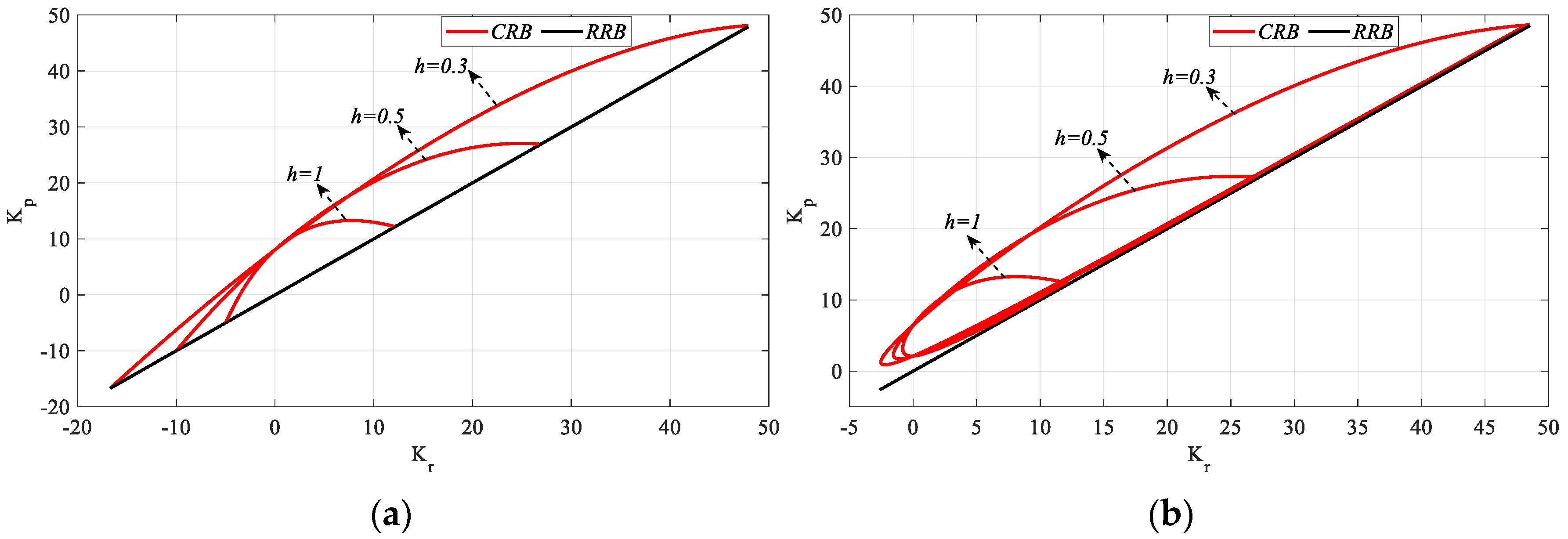
The
Kr-
Kp SBLs obtained for
Ki_fixed = 0 and 1 values selected from the range of common stable
Ki controller parameters for all
h values in
Figure 8 are shown in
Figure 9.
In
Figure 9a, the frequency ranges that make the system stable for
h = 0.3, 0.5 and 1 are
ω ∈ [0, 2.3565], [0, 2.1386] and [0, 2.1386] rad/s, respectively, while in
Figure 9b,
ω ∈ [0.2285, 2.35], [0.234, 2.13] and [0.244, 1.73] rad/s are found. Therefore, it can be said that the frequency range that stabilizes the system narrows as the value of
h increases. Accordingly, it is seen from
Figure 9 that the
SBL curves also narrow. Similarly,
Kr-
Ki SBL graphs were obtained for the
Kp_fixed = 0 and
Kp_fixed = 2.5 values selected from the stable
Kp controller parameter ranges shown in
Figure 8 and
Figure 10.
In
Figure 10a, the frequency ranges that make the system stable for
h = 0.3, 0.5, and 1 are
ω ∈ [0, 0.8614], [0, 0.7654] and [0, 0.6044] rad/s, respectively, while in
Figure 10b,
ω ∈ [0, 0.9303], [0, 0.8665] and [0, 0.7582] rad/s are found, respectively. Similar to the previous analyses, as the value of
h increases, the frequency range that makes the system stable narrows. Therefore, it is seen from
Figure 10 that the
SBL curves narrow as the
h value increases.
The unit step responses for different
Kp,
Ki, and
Kr values selected from the common regions of the
SBL curves obtained for
h = 0.3, 0.5, and 1 in respective
Figure 8a,
Figure 9b and
Figure 10b were analyzed. In this context, for
Kr_fixed = 2.5, PIR controllers were designed for the
Kp = 5.74 and
Ki = 0.76 values selected from the common region of the
Kp-
Ki SBL curves in
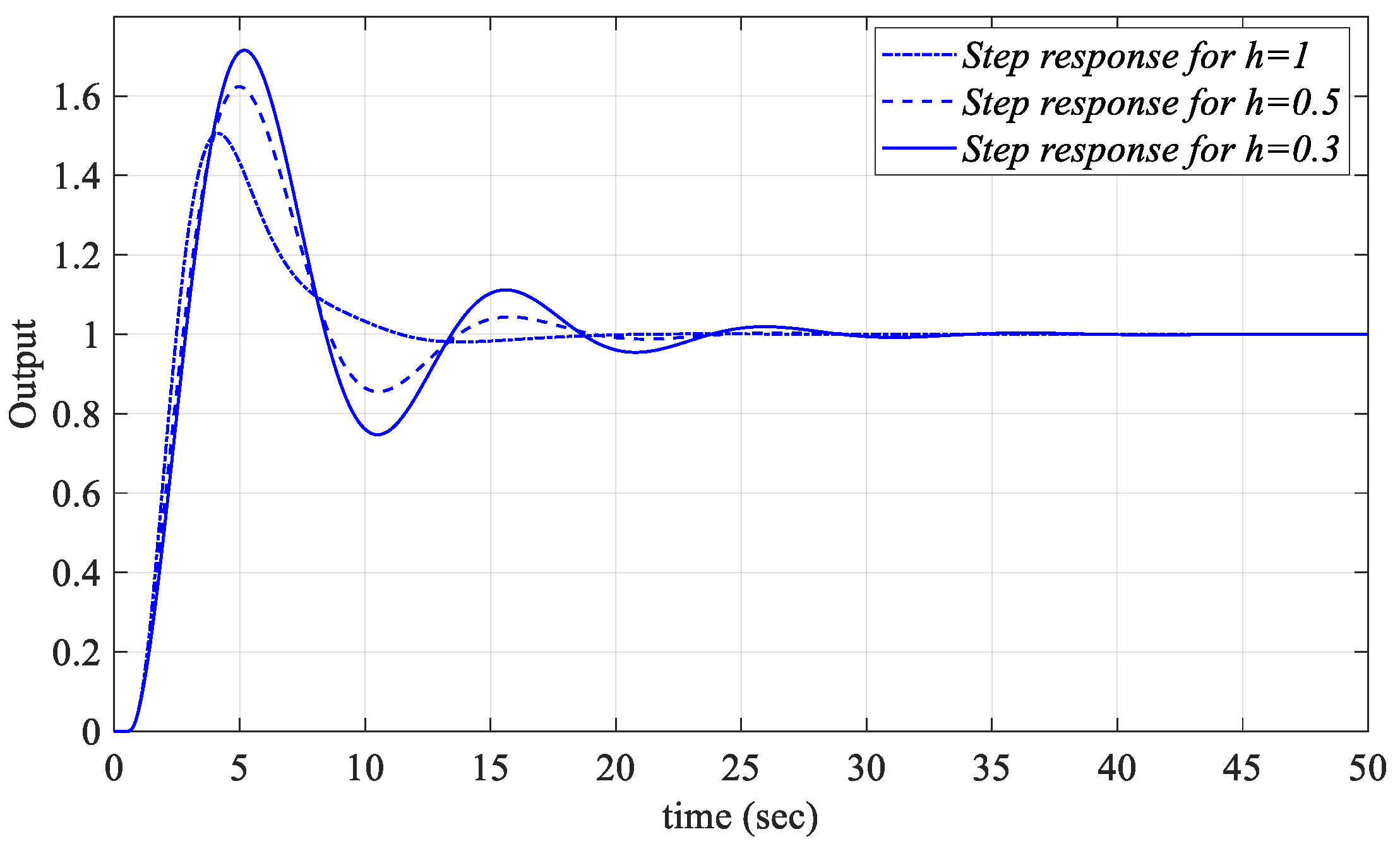
Figure 8a and the unit step responses obtained by implementing these PIR controllers to
Figure 1 are shown in
Figure 11. The unit step responses for the
Kr = 2.256 and
Kp = 5.9 controller parameter values selected from the
Kr-
Kp SBL plot in
Figure 9b for
Ki_fixed = 1 and for different
h values are shown in
Figure 12. Similarly, controller parameter values
of Kr = −0.13 and
Ki = 0.18 are selected from the
Kr-Ki SBL plot in
Figure 10b, which was obtained for
Kp_fixed = 2.5 and unit step responses for
h = 0.3, 0.5, and 1 are presented in
Figure 13.
When
Figure 11,
Figure 12 and
Figure 13 are analyzed, it can be said that the PIR controllers designed for different values of
h and different values of
Kp,
Ki, and
Kr selected from the stable controller parameter regions will control the closed-loop system in
Figure 1 successfully.
5.2. Example 2
The unstable first order plus time delay (UFOPTD) process given in (27) was selected from the literature [
36,
49,
50].
Initially, h = 1 was taken at the beginning. Then, to draw SBLs for a fixed Kp value in the (Ki, Kr) plane, for a fixed Ki value in the (Kr, Kp) plane and for a fixed Kr value in the (Kp, Ki) plane, fixed Kp, fixed Ki and fixed Kr values must be respectively selected in the planes. For this purpose, the controller was initially selected as a PR controller (Ki = 0).
The
RRB equation defined in Step 1 is updated for the system in (27) and obtained as
. As
n > m, there will be no
IRB line. The
CRB equations
Kp(ω) and
Kr(ω)are obtained from (24) and (25), respectively. Accordingly, with the help of the
RRB and
CRB equations, the
SBL curve is drawn as shown in
Figure 14.
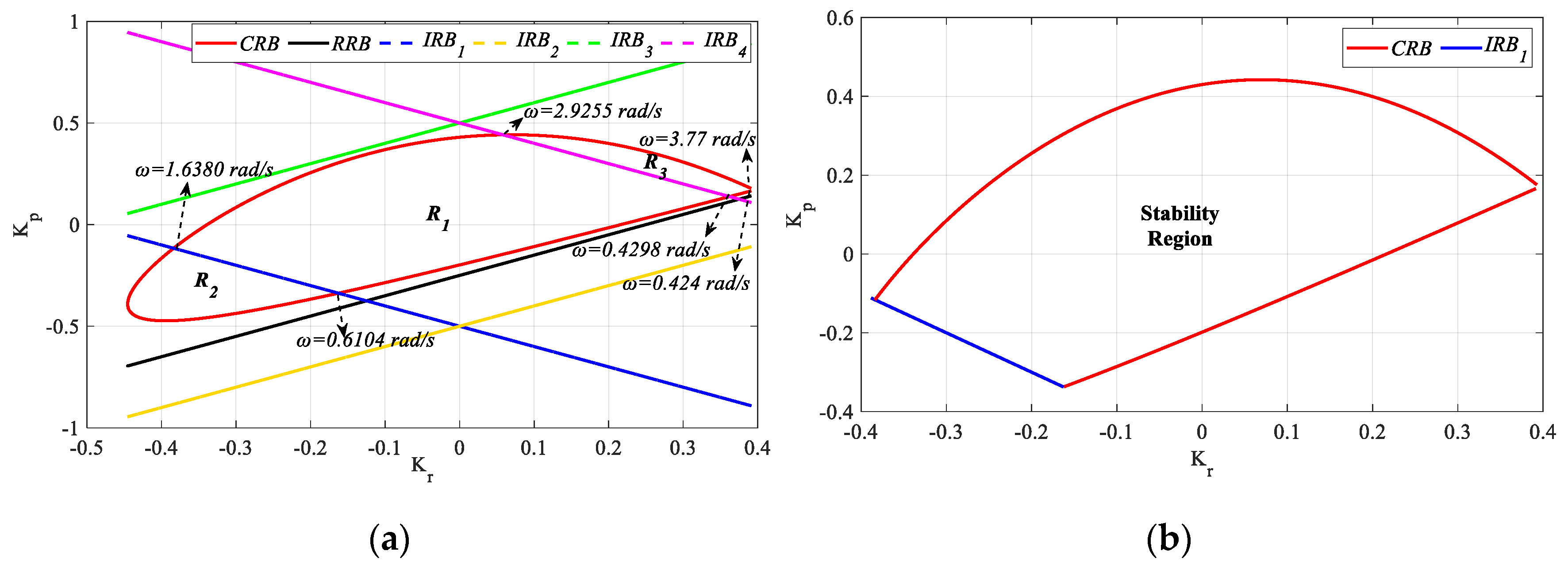
As can be seen from
Figure 14, the stability region for the PR controller is found as the intersection region of the
RRB and
CRB lines covering the frequency range
ω ∈ [0, 1.7523] rad/s. Accordingly, the
Kp and
Kr controller parameter ranges that make the system stable are determined as [−0.25 1.22] and [−0.5 0.93], respectively.
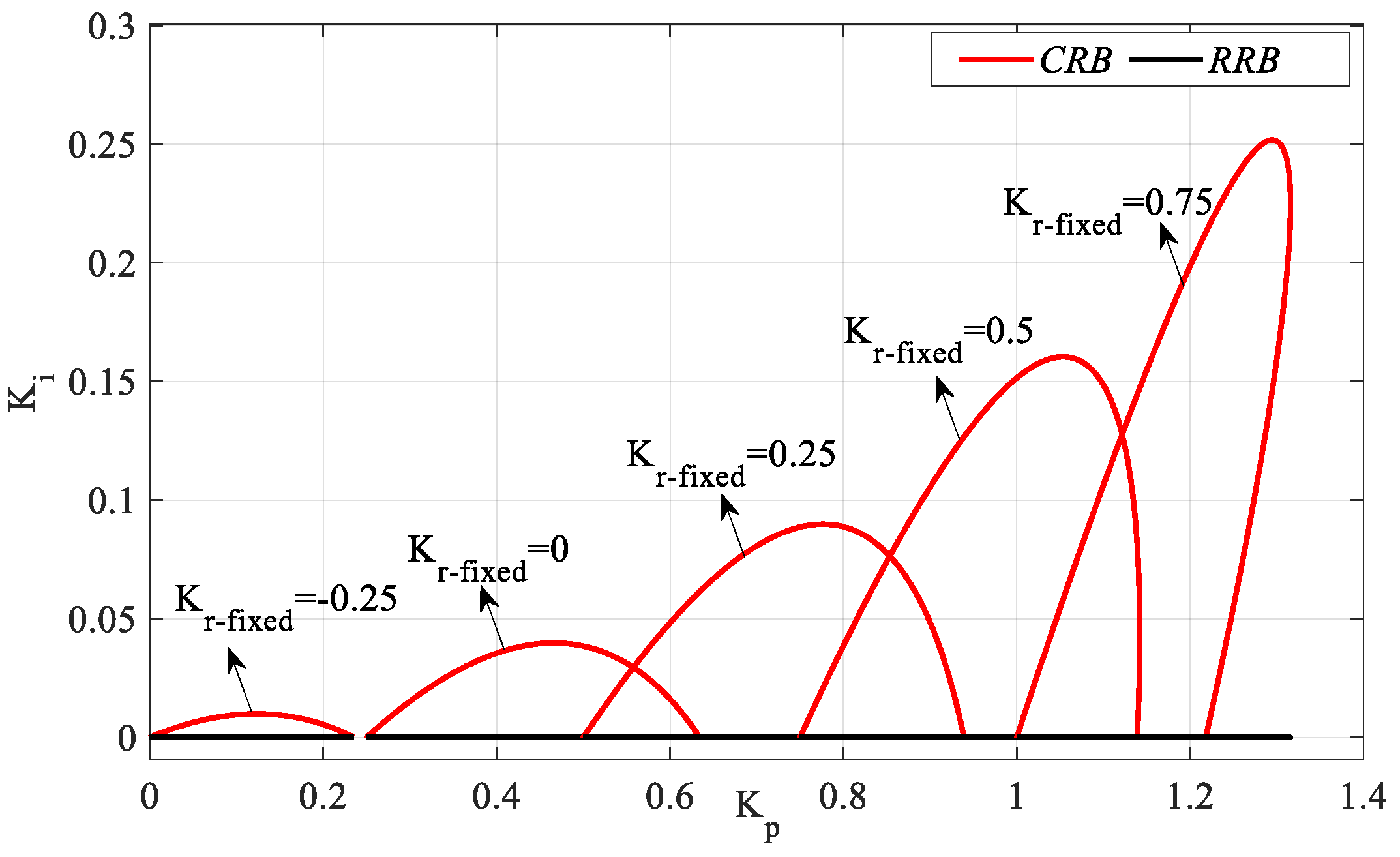
SBL graphs for the controller parameter range
Kr_fixed = [−0.25:0.25:0.75] are drawn as shown in
Figure 15 with the
RRB defined by the line equation
Ki = 0 and the
CRB equations calculated by (16) and (17).
Figure 15 was obtained by plotting the
Kp-Ki SBLs in the frequency range
ω ∈ [0,
ωmax] rad/s for
Kr_fixed = −0.25, 0, 0.25, 0.5, and 0.75. According to the stability analyses for these
Kr_fixed values,
ωmax values were found to be 0.4043, 0.5828, 0.7291, 0.8627, and 0.9923 rad/s, respectively. The
Ki controller parameter range will be determined for an
SBL selected from the
SBL curves of the system with a PIR controller designed for different
Kr_fixed values in
Figure 15. Accordingly, according to the
SBL graph of the PIR controller designed for
Kr_fixed = 0.75, the
Ki controller parameter range that makes the system stable is [0 0.25]. For different
Ki_fixed values to be selected from the
Ki controller parameter range,
SBL graphs are obtained with the help of an
RRB defined by
and a
CRB line to be drawn with the help of (19) and (20). Accordingly,
SBL plots for the controller parameter range
Ki_fixed = [0:0.05:0.25] are drawn as shown in
Figure 16.
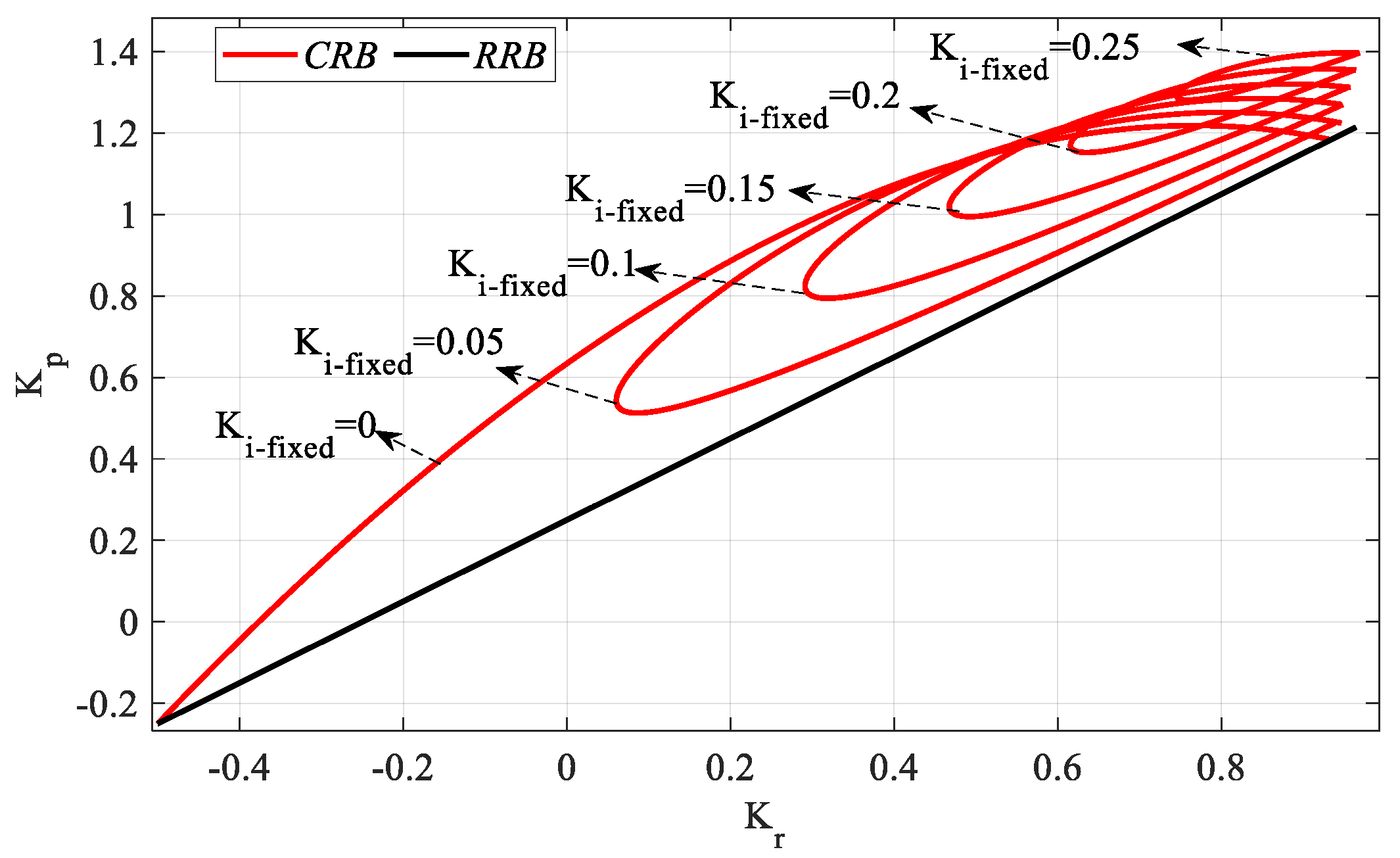
Figure 16 is obtained by plotting
Kr-Kp SBLs in the frequency range
ω ∈ [
ωmin,
ωmax] rad/s for
Ki_fixed = 0, 0.05, 0.1, 0.15, 0.2, and 0.25. For these
Ki_fixed values, the frequency ranges that make the system stable are ω ∈ [0, 1.0894], [0.1908, 1.068], [0.276, 1.036], [0.347, 1.009], [0.414, 0.975], and [0.482, 0.932], respectively. It is seen that the stable
Kr-Kp controller parameter region becomes smaller as the value of
Ki_fixed increases. In addition, the
RRB line defined by the equation of
is the determining factor of the stability boundary only in the case where
Ki_fixed = 0, as seen in
Figure 16.
From the
SBL curve for the PR controller in
Figure 14, the
Kp controller parameter range that makes the system stable was determined as [−0.25 1.22]. Accordingly, for a
Kp_fixed selected from the
Kp controller parameter space,
SBL is generated by an
RRB line defined by the equation
Ki = 0 and a
CRB line to be drawn with the help of (22) and (23). Accordingly,
SBL curves for the controller parameter range
Kp_fixed = [0:0.25:1.2] are drawn as shown in
Figure 17.
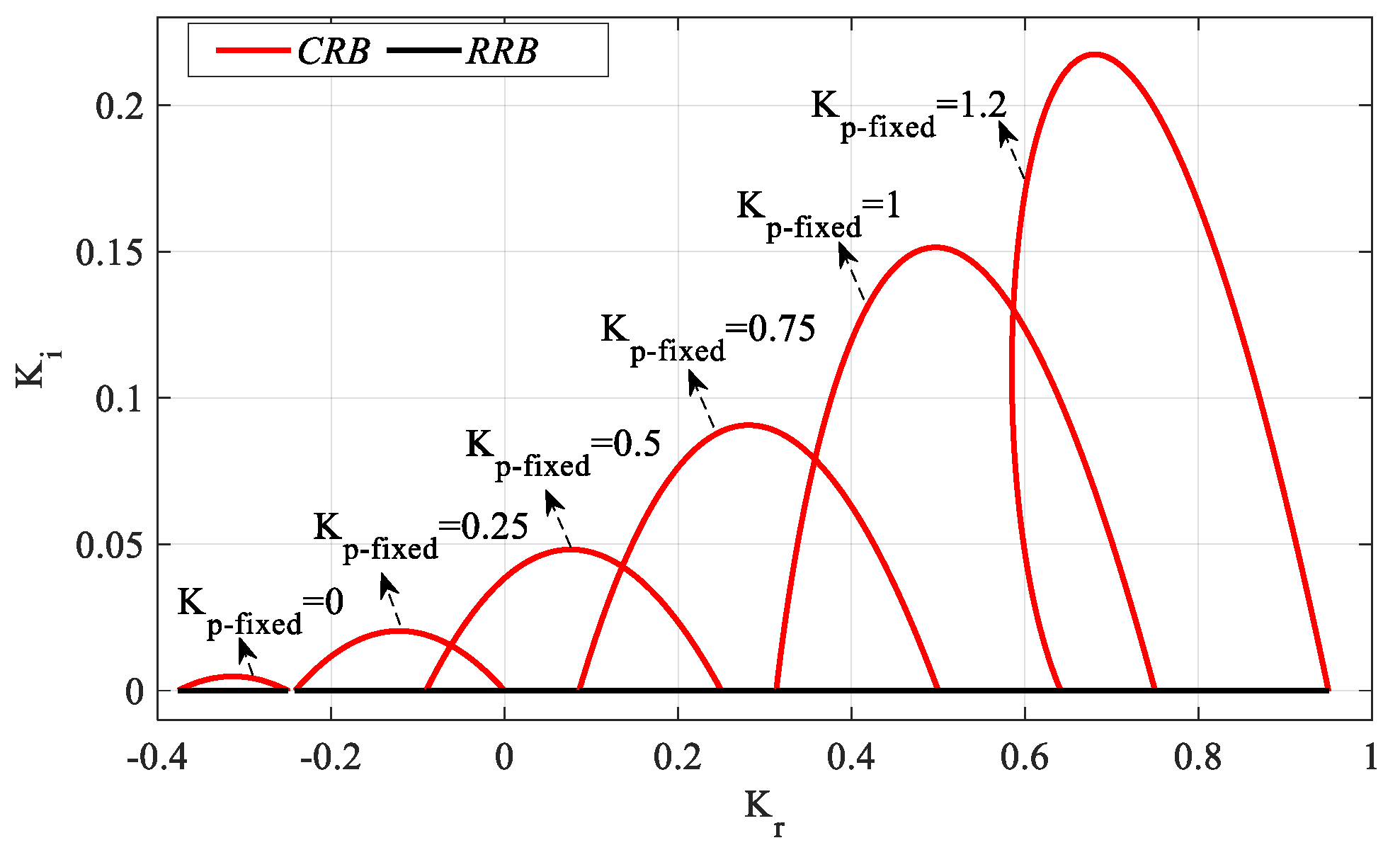
Figure 17 was obtained by plotting
Kr-Ki SBLs in the frequency range
ω ∈ [0,
ωmax] rad/s for
Kp_fixed = 0, 0.25, 0.5, 0.75, 1, and 1.2. In the stability analyses for these
Kp_fixed values,
ωmax values were found to be 0.2816, 0.4113, 0.5236, 0.6353, 0.7637, and 0.9359 rad/s, respectively. It is seen that the stable
Kr-Ki controller parameter region increases as the value of
Kp_fixed increases. The above analyses were performed for
h = 1, and the analyses were repeated to reflect the effect of different values of
h on
SBL. In this regard, the cases of
h >
,
h =
, and
h <
are examined. Although the case of
h <
is
h = 1 as examined above, the analyses are repeated for the cases of
h = 2 (
h =
) and
h = 2.2 (
h <
).
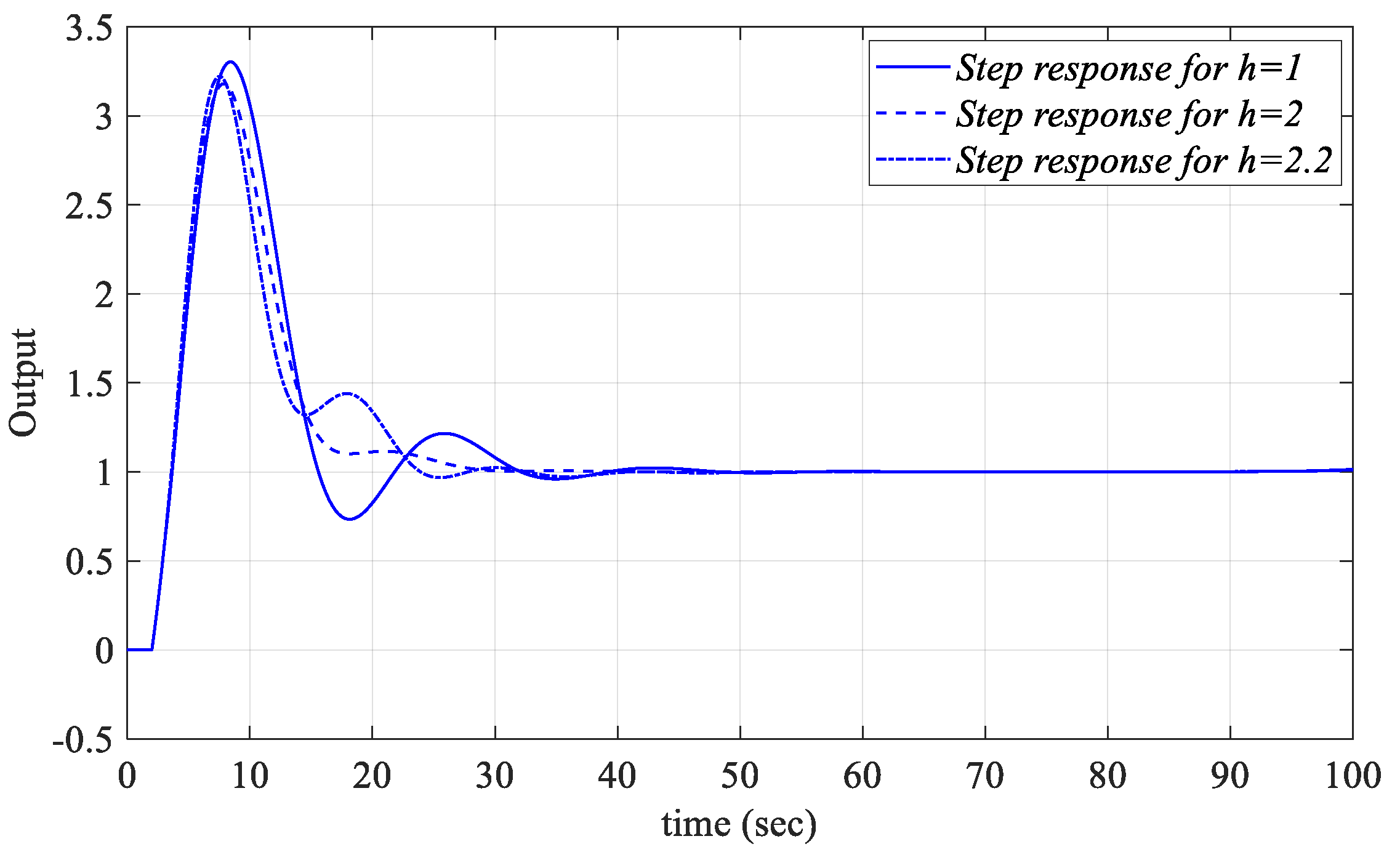
The analysis for
h = 1 in
Figure 14 was repeated for
h = 2 and
h = 2.2, and the frequency ranges that make the system stable were found to be
ω ∈ [0, 9015] rad/s and [0, 0.8721] rad/s, respectively. Accordingly, the
Kr and
Kp parameter ranges that stabilize the system for
h = 2 are [−0.25 0.46] and [0 0.785], respectively, and for
h = 2.2 are [−0.17 0.42] and [0.024 0.75], respectively. It can be concluded that, as the value of
h increases, the stable PR controller parameter region narrows. For
Kr_fixed = 2.5 selected from the stable
Kr controller parameter range,
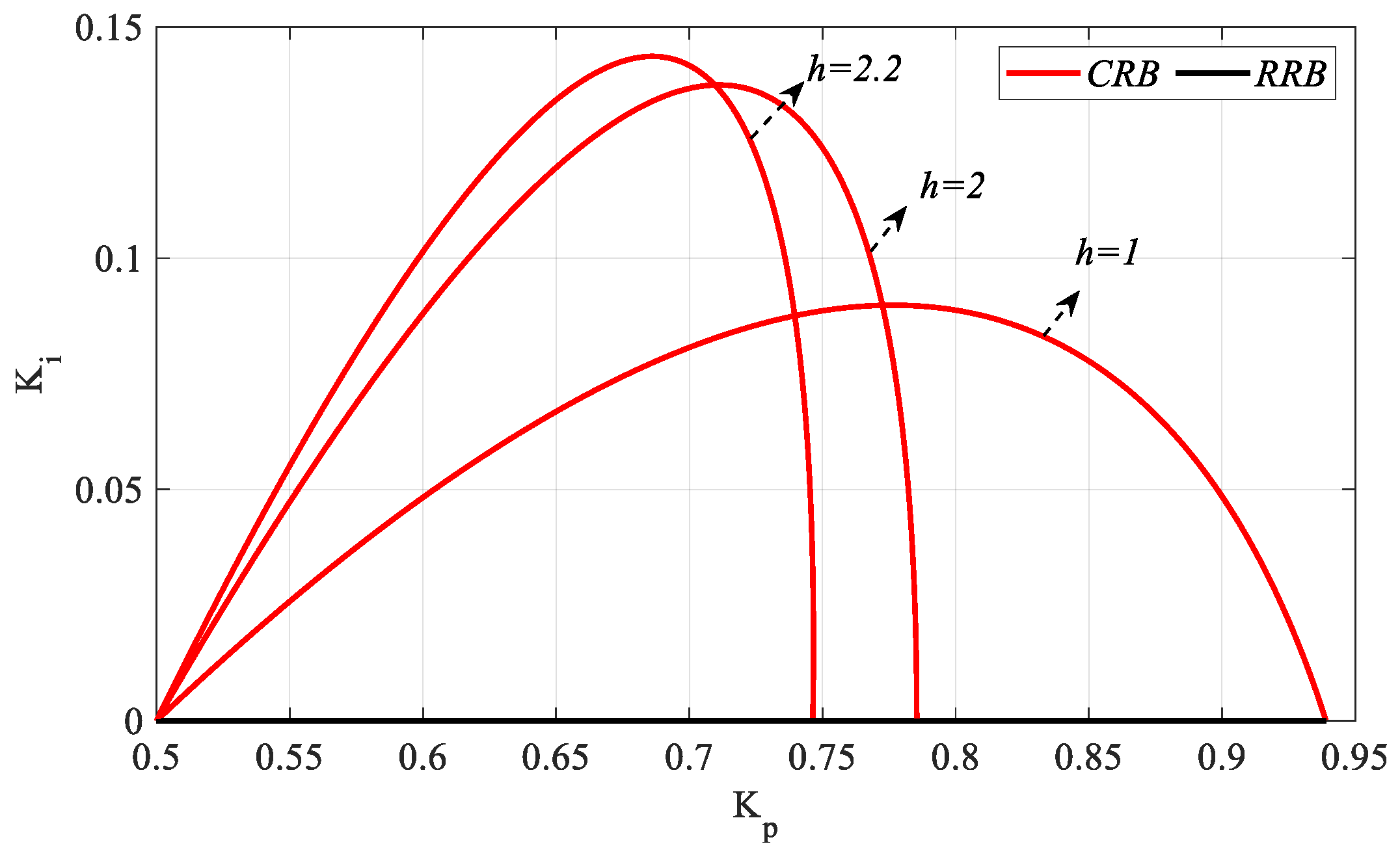
Kp-
Ki SBL curves are obtained as shown in
Figure 18. In
Figure 18,
ωmax values for
h = 1, 2, and 2.2 are found to be 0.7291, 0.7853, and 0.7835 rad/s, respectively. It is seen that, as
h increases, the stable
Kp controller parameter region narrows, and the stable
Ki controller parameter region expands. Moreover, as the controller will become a PI controller for
Kr = 0, the value of
h will have no effect on
SBL, and the
SBL curve will be the same as in
Figure 14.
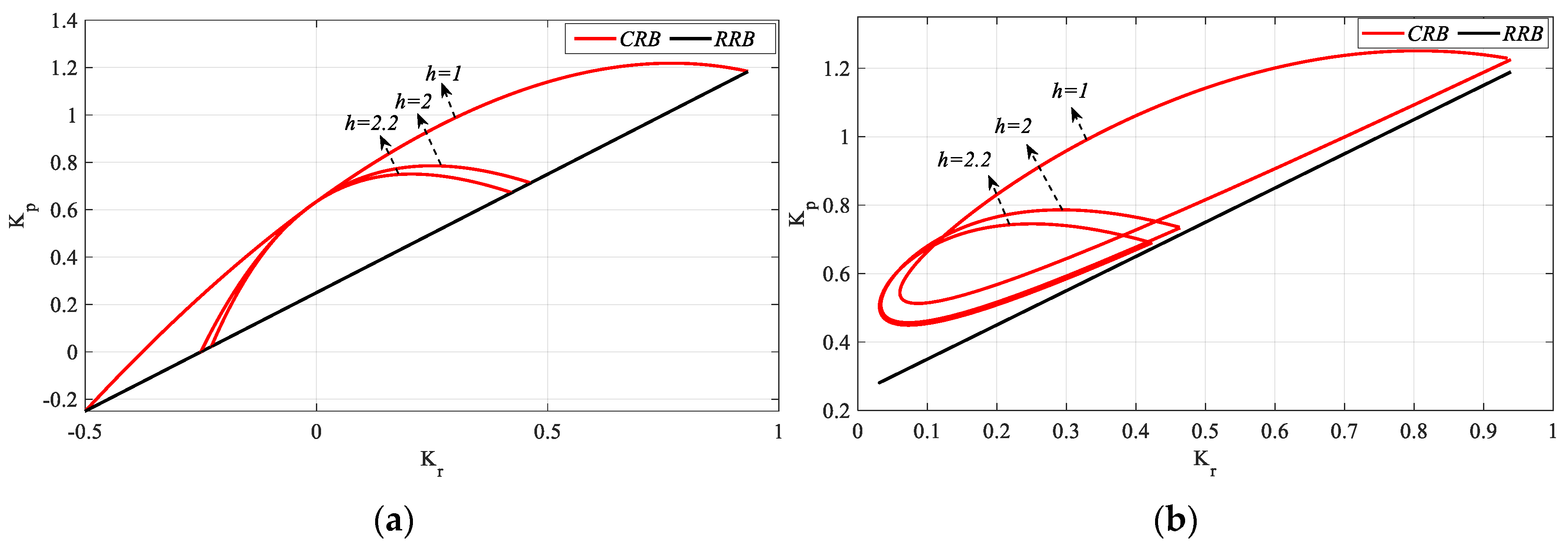
As demonstrated in
Figure 18, the
SBL curves obtained for
h = 1, 2, and 2.2 were analyzed, and
Ki_fixed = 0 and 0.05 values were selected considering the common stable
Ki controller parameter ranges and
Kr-
Kp SBL graphs for these
Ki_fixed values, as illustrated in
Figure 19.
As demonstrated in
Figure 19a, the frequency ranges that stabilize the system for
h = 1, 2, and 2.2 are
ω ∈ [0, 1.0894], [0, 0.9015], and [0, 0.8721] rad/s, respectively. Similarly,
Figure 19b illustrates the corresponding frequency ranges for
ω ∈ [0.1908, 1.068], [0.193, 0.879], and [0.193, 0.85] rad/s. Therefore, it can be said that the frequency range that stabilizes the system narrows as the value of
h increases. Accordingly, it is seen from
Figure 19 that the
SBL curves also narrow. In
Figure 19a, when
Ki_fixed = 0, the controller becomes a PR controller. The
RRB line, defined by the equation
, is thus a determining factor for the stability boundary. In
Figure 19b, however, the
RRB line is not a determining factor of the stability boundary; it is only shown as an approximate boundary line for the purpose of enhancing the comprehensibility of the
SBL representation. A similar representation is employed for
Kr-
Ki SBL plots for
Kp_fixed = 0.5, a parameter that is selected from the stable
Kp controller parameter range (see
Figure 20).
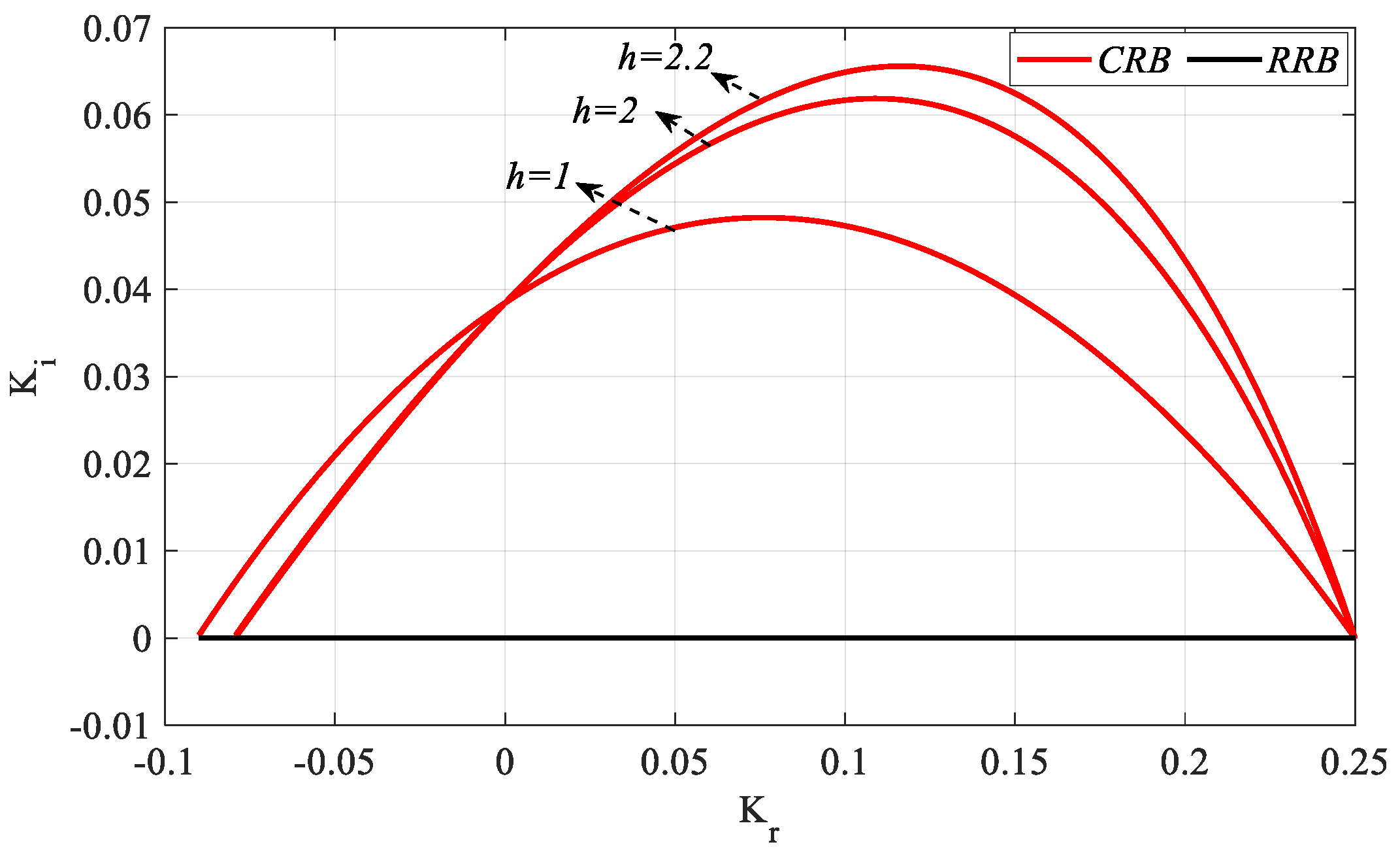
In
Figure 20, the frequency ranges
ω ∈ [0, 0.5236], [0, 0.4884], and [0, 0.4822] rad/s are found for
h = 1, 2, and 2.2, respectively. It is seen that, as the
h value increases, the
Kr range that makes the system stable remains almost the same, whereas the stable
Ki parameter space increases. For
Kp_fixed = 0, the controller becomes an IR controller. However, if the
SBLs obtained for
h = 2 and 2.2 in
Figure 19a are analyzed, it is seen that there is no stable
Kr controller parameter range corresponding to
Kp = 0. From this, it can be concluded that an IR controller that makes the system stable at
h = 2 and 2.2 cannot be designed for the
Gp2 process.
The unit step responses for
Kp,
Ki, and
Kr values selected from the common stability regions of the
SBL curves obtained for
h = 1, 2, and 2.2 in the respective
Figure 18,
Figure 19b and
Figure 20 are analyzed. The PIR controllers designed according to these parameters are expected to control the
Gp2 model in
Figure 1 stably for the cases
h = 1, 2, and 2.2. For
Kr_fixed = 0.25,
Kp = 0.6598, and
Ki = 0.0214, values were selected from the common region of the
Kp-
Ki SBL graphs drawn for
h = 1, 2 and 2.2 in
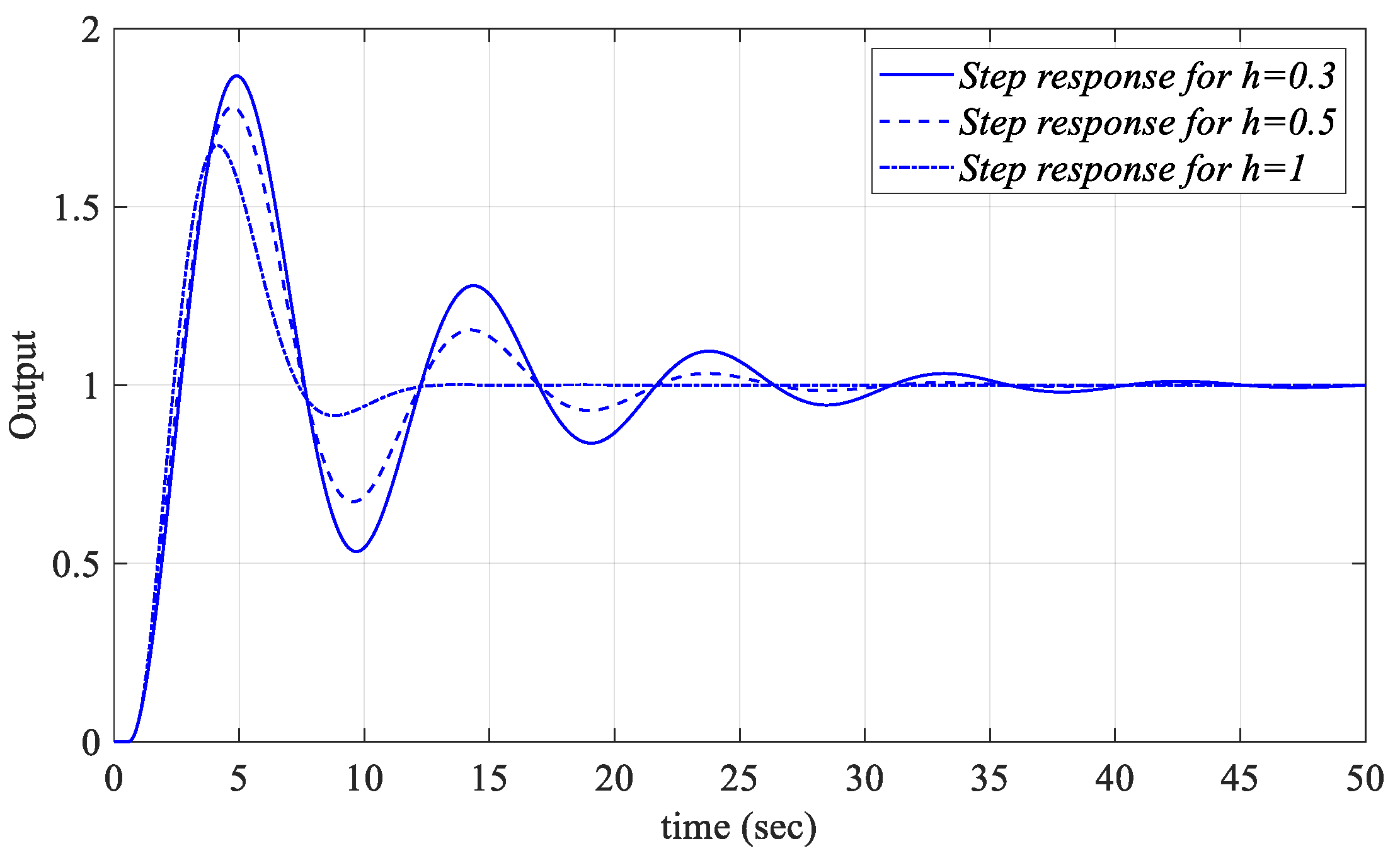
Figure 18, and the PIR controllers designed for these values were applied to
Figure 1. The unit step responses were obtained as shown in
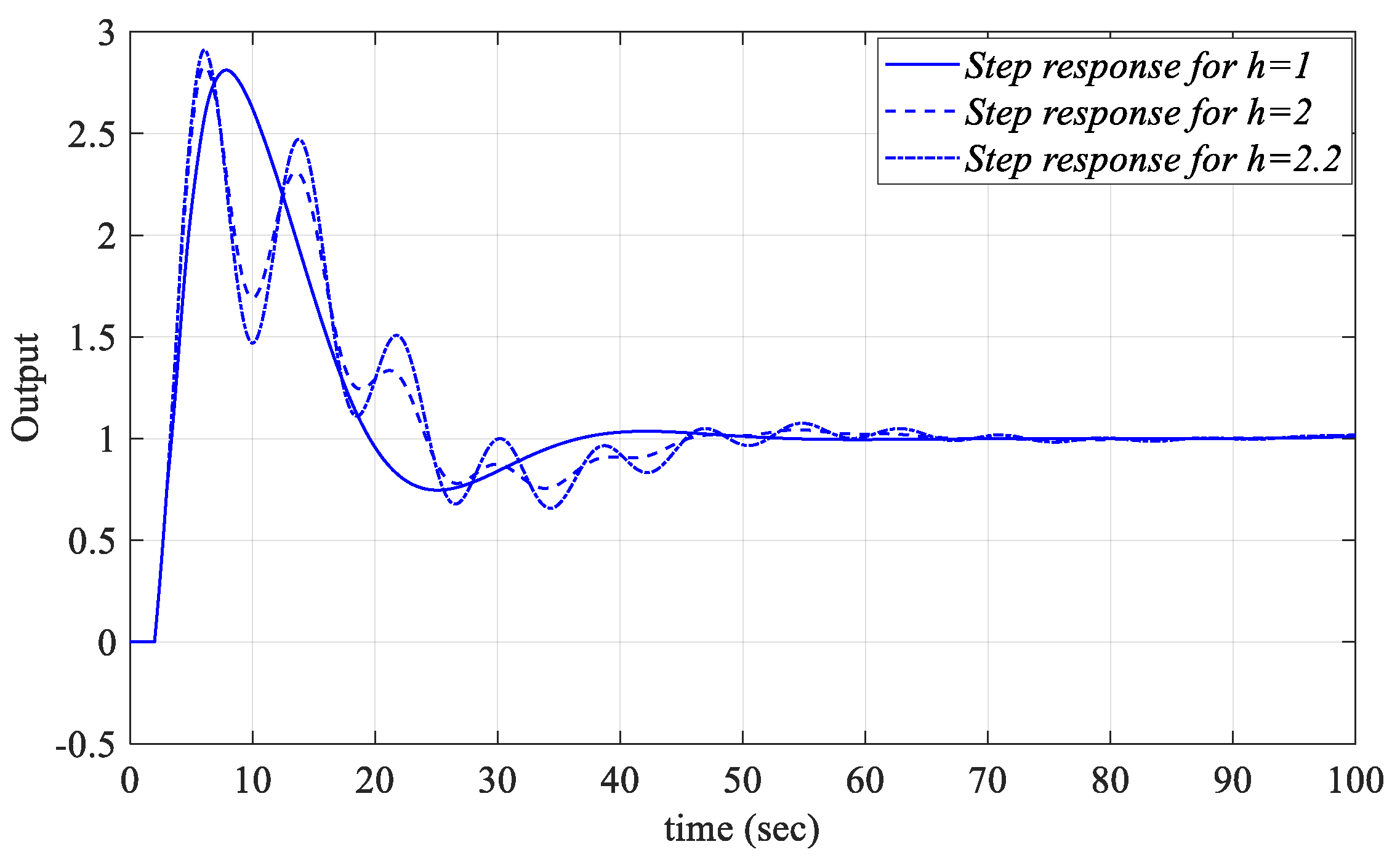
Figure 21. For
Ki_fixed = 0.05, PIR controllers were designed for the
Kp = 0.5984 and
Kr = 0.16 controller parameter values selected from the
Kr-
Kp SBL plot in
Figure 19b and unit step responses for different
h values are shown in
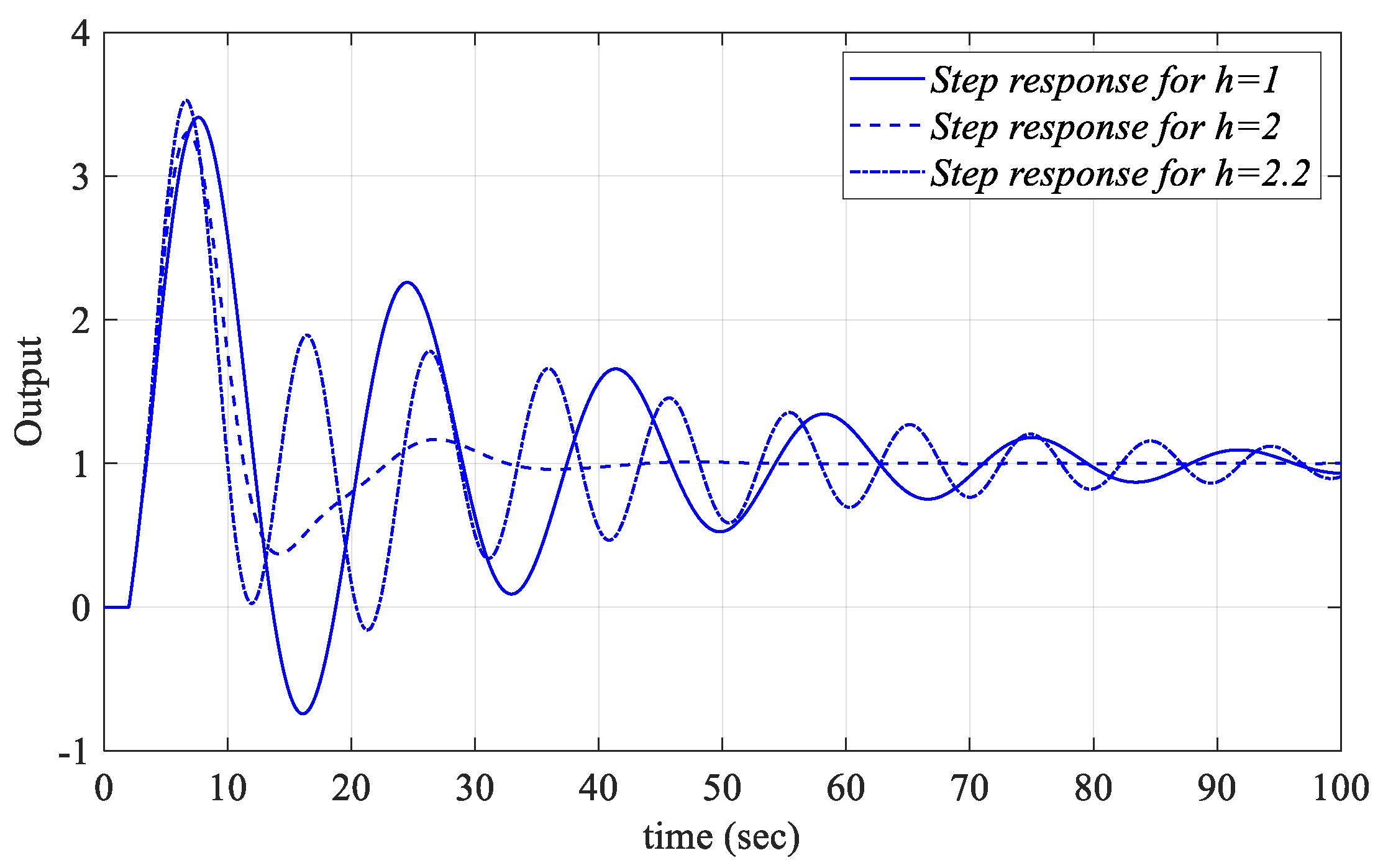
Figure 22. In a similar manner,
Kr = 0.0187 and
Ki = 0.073 controller parameter values are selected from the
Kr-
Ki SBL graph in
Figure 20, obtained for
Kp_fixed = 0.5. Unit step responses for
h = 1, 2, and 2.2 are presented as in
Figure 23.
When the unit step responses in
Figure 21,
Figure 22 and
Figure 23 are examined, it is seen that the PIR controllers, designed for the controller parameters selected from the common stability regions of the
SBL curves drawn for the cases
h = 1, 2 and 2.2, control the
Gp2 unstable time-delay process in
Figure 1 in a stable manner.
5.3. Example 3
As
IRB lines are only observed in processes with equal orders of numerator and denominator polynomials, (28) is chosen for analysis. The FOPTD
Gp3(
s) process is analyzed through
Figure 1.
Before starting the analysis, the PR controller time-delay value is taken as
h = 1. The defined
RRB equation is updated for the process in (28) and obtained as
. According to the
IRB rule defined in (11), as
n =
m,
IRB lines are expected to be formed, and one or some of these lines are expected to play a role in determining the stability region. Accordingly, this is achieved with the help of the
IRB1, IRB2, IRB3, and
IRB4 equations, which can be seen, respectively, as follows:
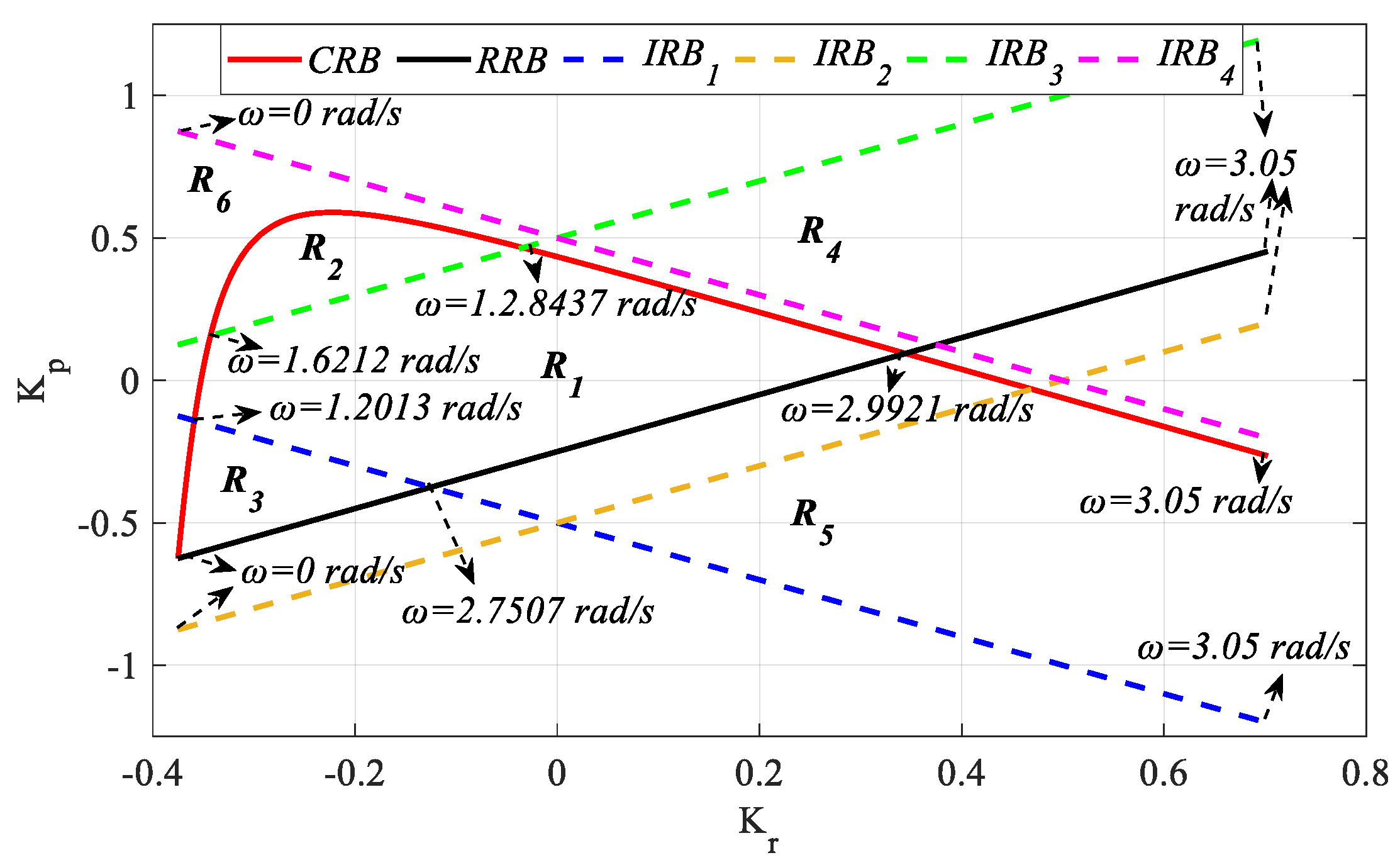
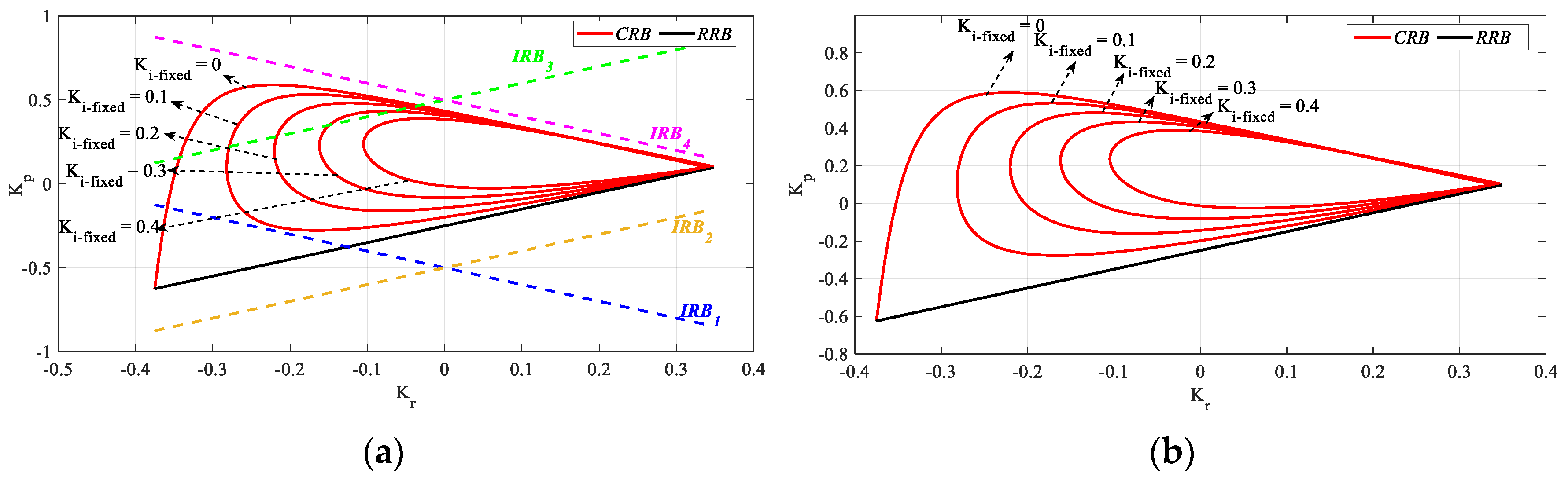
To determine the stable region, the
SBL curve for the frequency range
ω ∈ [0, 3.05] rad/s was plotted as shown in
Figure 24 with the help of
RRB,
IRB, and
CRB equations.
It has been explained in
Section 3.2 that, in processes with an equal order of numerators and denominators as in (28) (
n =
m),
IRB lines can affect stability, but not all
IRB lines always affect stability. Therefore, when determining the stable controller parameter region in such time-delay processes, all
IRB lines calculated by (11) are plotted. Then, regions are determined according to the intersection of
RRB,
IRB, and
CRB lines, and the stability test of these regions is performed. In
Figure 24, it is aimed to find the (
Kr,
Kp) parameter region that stabilizes, via Hurwitz stabilization, the characteristic polynomial in (4) from the
SBL obtained for the frequency range
ω ∈ [0, 3.05]. For this reason, the (
Kr,
Kp) parameter test points were selected from the region bounded by the
RRB,
IRB, and
CRB lines and the regions outside this region, and the stability of (4) was analyzed. Test points (−0.00046, 0.03), (−0.1857, 0.3838), (−0.3018, −0.2868), (0.2346, 0.5074), (0.2926, −0.4368), and (−0.3350, 0.6132) were selected from the determined
R1,
R2,
R3,
R4,
R5 and
R6 regions, respectively. The plotted unit step responses for these test points are presented in
Figure 25.
When the unit step responses in
Figure 25 obtained for the regions in
Figure 24 are analyzed, it is seen that the characteristic equations for the test point in regions
R1,
R2, and
R3 have only the left half-plane pole, thus, they are stable regions. As the characteristic equations written in (4) for the test points selected from the
R4,
R5, and
R6 regions have the right half-plane pole, these regions are unstable regions, as shown in
Figure 25. In other words, the PR controller to be designed for a (
Kr,
Kp) controller parameter pair selected from these regions (
R4,
R5, and
R6) will not provide the stability of the system in (28). Therefore, the stable region is the
R1,
R2, and
R3 regions covering the frequency range
ω ∈ [0, 2.9921] rad/s, i.e., the regions bounded by the
CRB and
RRB lines. Here, the boundary lines obtained by equations
IRB2 and
IRB4 do not intersect the
CRB and
RRB lines and therefore do not affect the stable region. Although the boundary lines obtained with the
IRB1 and
IRB3 equations intersect with
CRB and
RRB lines, they do not affect stability.
Accordingly, considering the frequencies of the boundary points where the
CRB and
RRB lines intersect, the stable controller parameter region of the system in (28) for
h = 1 is drawn as shown in
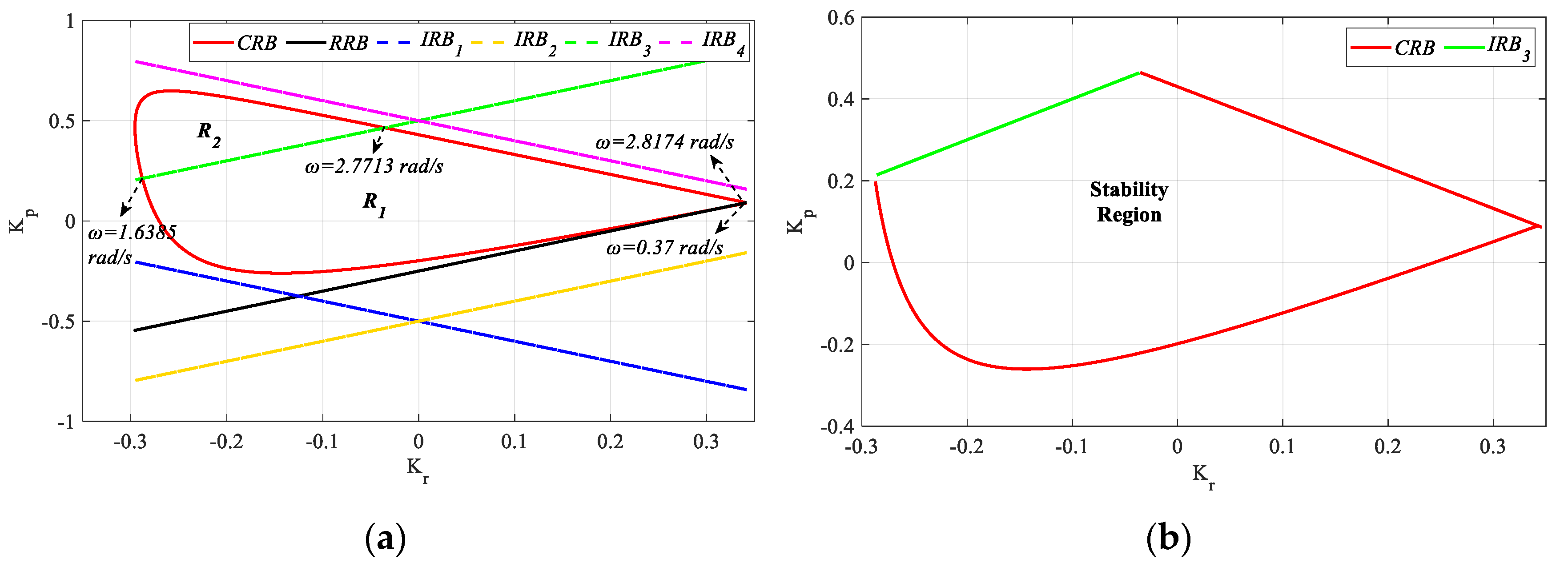
Figure 26.
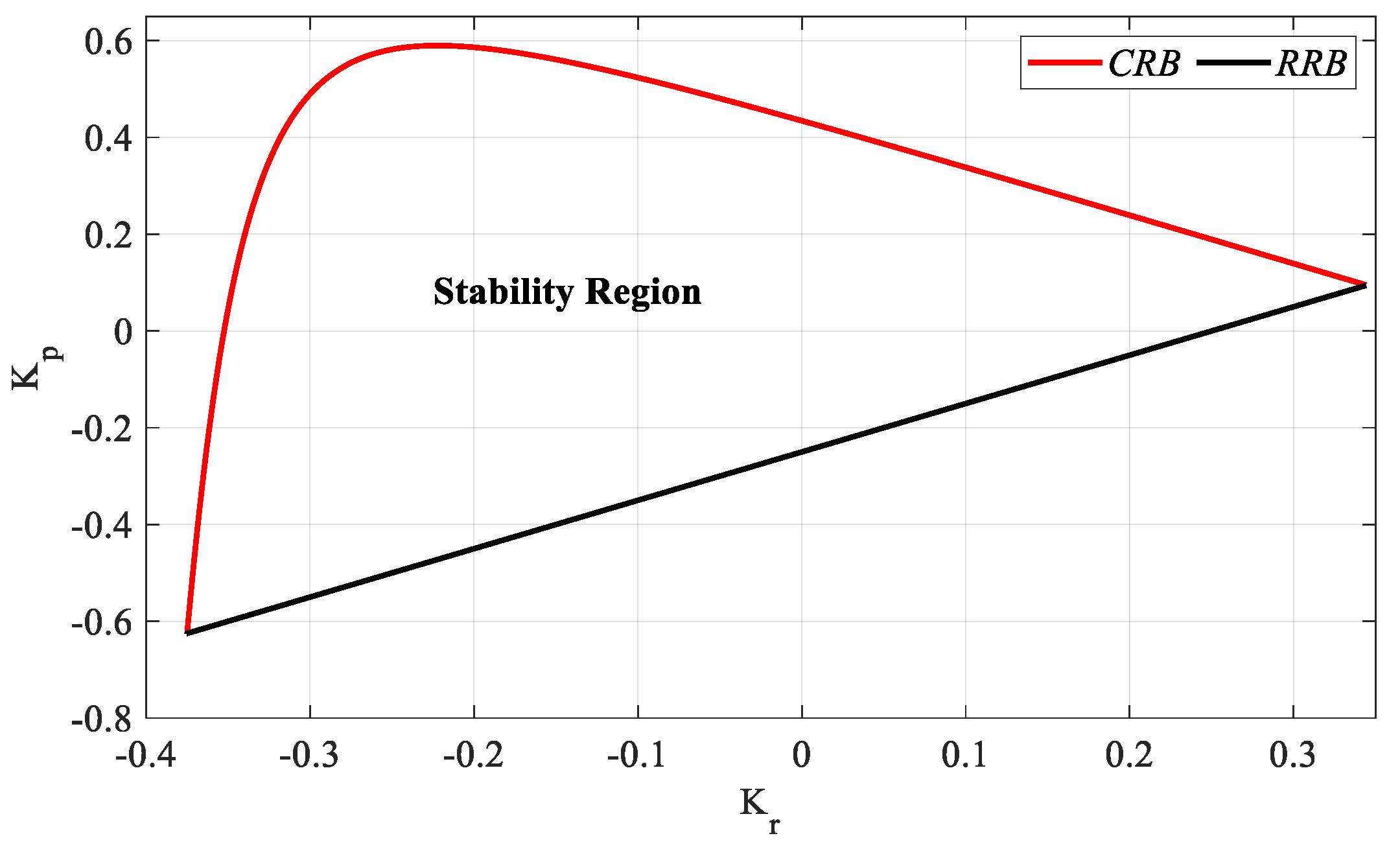
As can be seen from
Figure 26, the stability region for the PR controller is found as the intersection area of the
RRB and
CRB lines. Accordingly, the
Kp and
Kr controller parameter ranges that make the system stable are determined as [−0.625 0.59] and [−0.375 0.344], respectively. Accordingly,
SBL graphs for the controller parameter range
Kr_fixed = [−0.3:0.1:0.3] are drawn as shown in
Figure 27, with the
RRB defined by the line equation
Ki = 0 and the
CRB equations calculated by (16) and (17).
Figure 27 was obtained by plotting the
Kp-Ki SBLs in the frequency range
ω ∈ [0,
ωmax] rad/s for
Kr_fixed = −0.3, −0.2, −0.1, 0, 0.1, 0.2, and 0.3. Accordingly, the
ωmax values for these
Kr_fixed values are 2.1707, 2.6155, 2.7816, 2.868, 2.9212, 2.9570, and 2.9829 rad/s, respectively. The stable
Ki controller parameter range will be determined for an
SBL selected from the
SBL graphs of the system with a PIR controller designed for different
Kr_fixed values in
Figure 27. Therefore, according to the
SBL graph of the PIR controller designed for
Kr_fixed = −0.1, the
Ki controller parameter range that makes the system stable is [0 0.408].
SBL graphs for
Ki_fixed values to be selected from the
Ki controller parameter range are obtained with the help of the
RRB line defined by
, a
CRB line to be drawn with the help of (19) and (20), and
IRB lines to be obtained with the help of (11), if any. Accordingly,
SBL plots for the controller parameter range
Ki_fixed = [0:0.1:0.4] are drawn as shown in
Figure 28.
Figure 28 was obtained by plotting
Kr-Kp SBLs in the frequency range
ω ∈ [
ωmin,
ωmax] rad/s for
Ki_fixed = 0, 0.1, 0.2, 0.3, and 0.4. For these
Ki_fixed values, the frequency ranges that make the system stable are
ω ∈ [0, 2.9921], [0.378, 0.947], [0.54, 2.9], [0.672, 2.853], and [0.79, 2.803] rad/s, respectively. It is seen that the stable
Kr-Kp controller parameter region becomes smaller as the
Ki_fixed value increases.
It is seen from
Figure 28 that the
RRB line defined by the equation of
is the determinant of the stability boundary only in the case of
Ki_fixed = 0. Moreover, in the stability analysis in
Figure 24 for
Ki ≠ 0, it was shown that the
IRB2 and
IRB4 boundary lines do not intersect the
CRB and
RRB lines and do not affect the stable region. The
IRB1 and
IRB3 boundary lines intersect the
CRB and
RRB lines, but do not affect stability. The positions of these
IRB1,
IRB2,
IRB3, and
IRB4 boundary lines at
Ki ≠ 0 are shown in
Figure 28a. According to the stability analyses performed here, it is seen that these lines do not separate the system in (28) into unstable regions, and that the stability regions of the system with a PIR controller designed according to different
Ki_fixed values are shown in
Figure 28b.
From the
SBL graph for the PR controller in
Figure 26, the
Kp controller parameter range that makes the system stable was determined as [−0.625 0.59]. Accordingly, for a
Kp_fixed selected from the
Kp controller parameter space,
SBL is generated by an
RRB line defined by the equation
Ki = 0 and a
CRB line to be drawn with the help of (16) and (17). Accordingly,
SBL graphs for the controller parameter range
Kp_fixed = [−0.6:0.2:0.4] are drawn as shown in
Figure 29.
Figure 29 was obtained by plotting
Kr-Ki SBLs in the frequency range
ω ∈ [
ωmin,
ωmax] rad/s for
Kp_fixed = −0.6, −0.4, −0.2, 0, 0.2, and 0.4. In the stability analyses for these
Kp_fixed values, the frequency ranges
ω ∈ [0, 0.2555], [0, 0.7869], [0, 1.1146], [0, 1.4009], [1.6831, 2.9681] and [1.9666, 2.89] rad/s were found, respectively. It is seen that the stable
Kr-Ki controller parameter region increases as the value of
Kp_fixed increases.
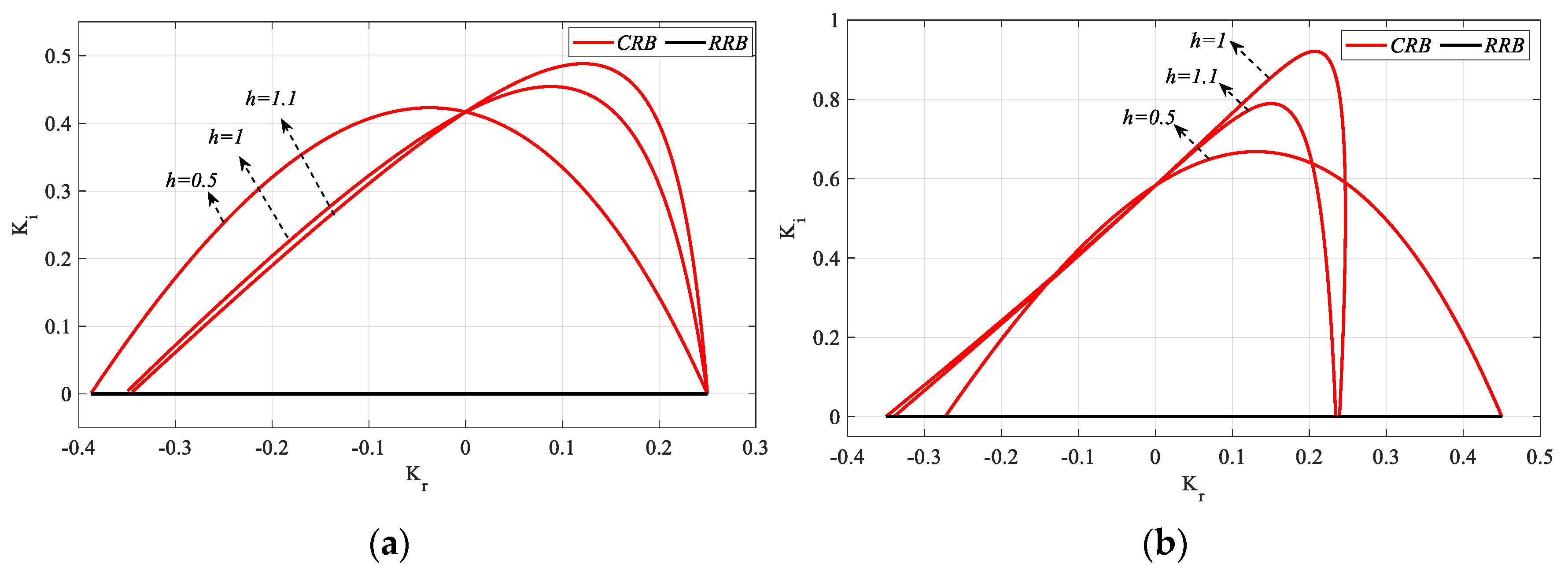
The above analyses were performed for h = 1, and the analyses were repeated to interpret the effect of different values of h on SBL. In this regard, the cases of h > , h = , and h < are examined. Although the case of h = is h = 1 as examined above, the analyses for the cases of h = 0.5 (h < ), and h = 1.1 (h > ) are repeated as follows.
In
Figure 30a, the
SBL graph for the PR controller is drawn for
h = 0.5 in the frequency range
ω ∈ [0, 5] rad/s. As can be seen from
Figure 30a, lines
CRB,
RRB,
IRB1, and
IRB4 intersect each other, while lines
IRB2 and
IRB3 are tangent to
CRB and
RRB. Stability analysis was performed for the three closed regions (
R1,
R2 and
R3) resulting from the intersection of the
CRB,
RRB,
IRB1, and
IRB4 lines. It was observed that the PR controllers designed for
Kr-
Kp selected from the closed
R2 and
R3 regions make the process in (28) stable, while the controller parameter pair selected from the
R1 region makes the system unstable. As a result of this analysis for
h <
, it was seen that the
CRB,
RRB, and
IRB1 lines affect stability, while the
IRB4 line does not. The
IRB2 and
IRB3 lines did not play a role in determining the stability as they passed tangentially to
CRB and
RRB. Accordingly, the stability region for
h = 0.5 is drawn in
Figure 30b by considering the frequencies of the boundary points where the
CRB,
RRB and
IRB1 lines intersect.
Figure 31a shows the
SBL curve for
h = 1.1 in the frequency range
ω ∈ [0, 3] rad/s. As can be seen from
Figure 31a, the lines
CRB,
RRB,
IRB1, and
IRB3 intersect each other, and the lines
IRB2 and
IRB4 are tangential to
CRB and
RRB. Stability analysis was performed for the three closed regions (
R1,
R2 and
R3) resulting from the intersection of the
CRB,
RRB,
IRB1 and
IRB3 lines and it was observed that the PR controllers designed for the controller parameter pair (
Kr,
Kp) selected only in the
R1 region make the process in (28) stable, while the controller parameter pair selected in the
R2 and
R3 regions make it unstable. As a result of this analysis for
h >
, it is seen that
CRB,
RRB,
IRB1, and
IRB3 lines affect stability.
IRB2 and
IRB4 lines did not play a role in determining stability as they passed tangentially to
CRB and
RRB. Accordingly, the stable region was found to be the closed
R1 region, and the stability region for
h = 1.1 was drawn in
Figure 31b by considering the frequencies of the boundary points where the
CRB, RRB, IRB1, and
IRB3 lines intersect.
From
Figure 30b and for
h = 0.5, the
Kp and
Kr controller parameter ranges that stabilize the system are [−0.37 0.44] and [−0.42 0.38], respectively. Similarly, from
Figure 31b, the
Kp and
Kr controller parameter range that makes the process stable for
h = 1.1 is determined as [−0.4 0.41] and [−0.35 0.34], respectively. For the
Kr_fixed = −0.1 and 0.1 values selected from the common stable controller parameter range,
RRB is defined by
Ki = 0 and
CRB equations are calculated with the help of (16) and (17).
Kp-Ki SBL plots are obtained as shown in
Figure 32.
In
Figure 32a, the
ωmax values for
Kr_fixed = −0.1 and
h = 0.5, 1, and 1.1 are 2.6255, 2.7816, and 2.8717 rad/s respectively, and in
Figure 32b, the
ωmax values for
Kr_fixed = 0.1 and
h = 0.5, 1 and 1.1 are 3.1093, 2.9212, and 2.8646 rad/s respectively. As the controller will turn into a PI controller for
Kr = 0, the value of
h will have no effect on
SBL, and it will be the same as
Kr_fixed = 0 in
Figure 27. The
Kr-
Kp SBL curves and stability regions for
Ki_fixed = 0.1 and
h = 0.5 and 1.1, which are selected from the common stable controller parameter ranges of the
SBL curves in
Figure 32, are presented in
Figure 33 and
Figure 34.
In
Figure 33a, the
CRB curve for
Ki_fixed = 0.1 and
h = 0.5 is plotted in the frequency range
ω ∈ [0.424, 3.77] rad/s. In the analysis for
Ki_fixed = 0 in
Figure 30a, it was found that the boundary lines determining the stability were the
CRB,
RRB, and
IRB1 lines. When the same analysis was performed for
Ki_fixed = 0.1, it was found that
CRB and
IRB1 lines affect stability, while
RRB does not affect stability as a result of it not intersecting with
CRB. Accordingly, considering the frequency points where the
CRB and
IRB1 lines intersect, the stable controller region for
Ki_fixed = 0.1 and
h = 0.5 is obtained as shown in
Figure 33b. Similarly, the
CRB curve for
Ki_fixed = 0.1 and
h = 1.1 in the frequency range
ω ∈ [0.37, 2.8174] rad/s is obtained as shown in
Figure 34a. In the analysis for
Ki_fixed = 0 in
Figure 31a, it was found that the boundary lines determining the stability were
CRB,
RRB,
IRB1, and
IRB3 lines. When the analysis was repeated for
Ki_fixed = 0.1, it was found that only
CRB and
IRB3 lines affected stability, and that
IRB1 and
RRB did not affect stability because of they do not intersect with
CRB. Accordingly, considering the frequency points where the
CRB and
IRB3 lines intersect, the stable controller region for
Ki_fixed = 0.1 and
h = 1.1 is obtained as shown in
Figure 34b.
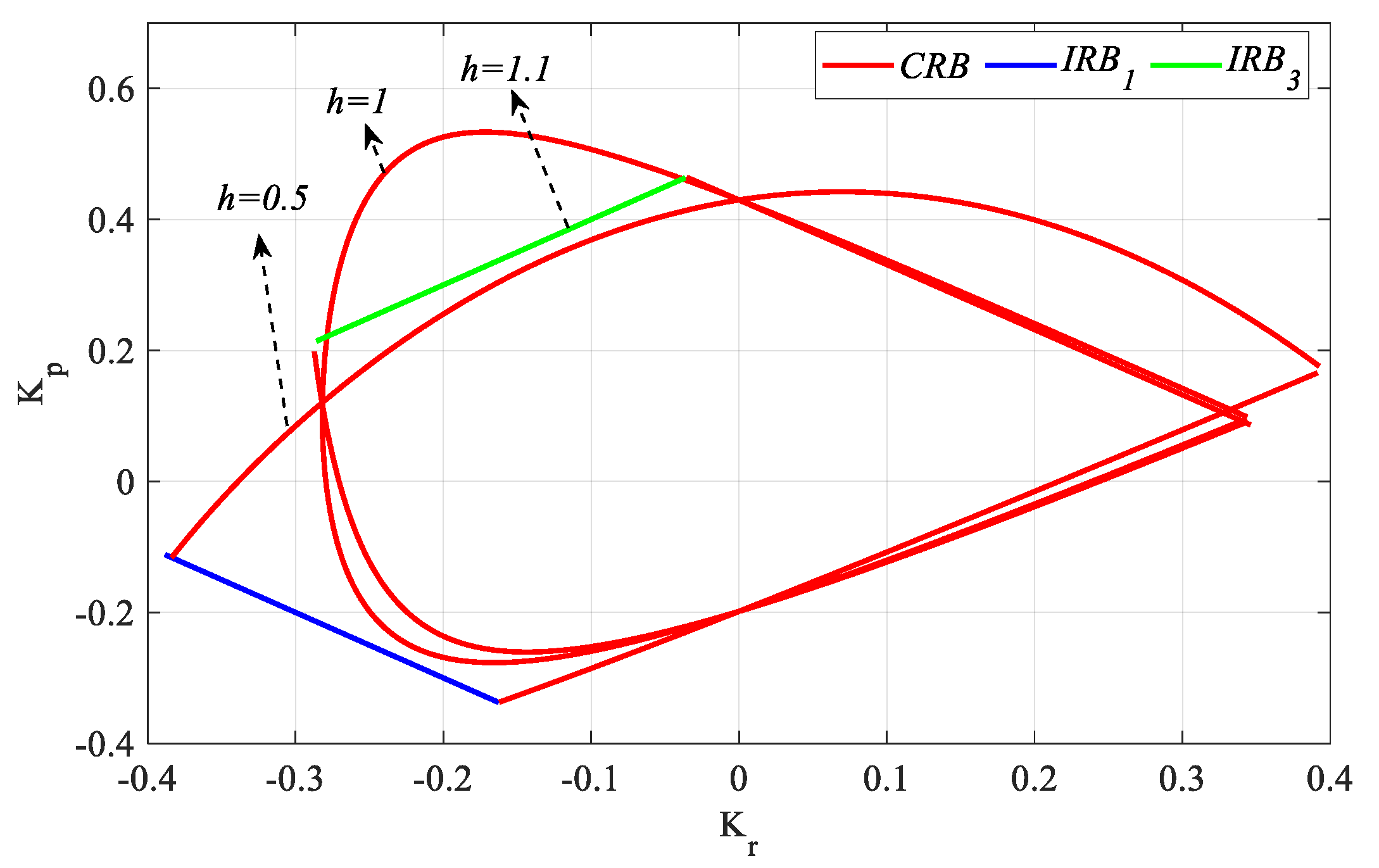
With the values obtained from
Figure 28b,
Figure 33b and
Figure 34b, the
SBL for the stable controller parameter regions for
Ki_fixed = 0.1 and
h = 0.5, 1, and 1.1 are drawn as in
Figure 35.
When
Figure 35 is examined, the stable
Kr-
Kp parameter region narrows as the
h value increases in the case of
Ki_fixed = 0.1. From
Figure 26,
Figure 30 and
Figure 31, the stable
Kp controller parameter ranges were found to be [−0.37 0.44], [−0.625 0.59], and [−0.4 0.41] for
h = 0.5, 1, and 1.1, respectively. Accordingly,
Kr-Ki SBL graphs for
Kp_fixed 0 and 0.2 selected from these stable regions were obtained and are shown in
Figure 36.
As illustrated in
Figure 36a, the frequency ranges that ensure system stability for
h = 0.5, 1, and 1.1 are presented as
ω ∈ [0, 1.8759], [0, 1.4009], and [0, 1.3341] rad/s, respectively. Similarly,
Figure 36b demonstrates the corresponding frequency ranges for
h = 0.5, 1, and 1.1, namely
ω ∈ [1.6831, 2.9681] and [1.6029, 2.8635] rad/s. When
Figure 36a is examined, as the
h value increases when
Kp_fixed = 0, the stable
Kr parameter range decreases relatively, while the stable
Ki parameter range increases. Similarly, in the analysis made for
Kp_fixed = 0.2 in
Figure 36b, it is seen that, as the
h value increases, the stable
Kr range decreases significantly, while the stable
Ki range increases. The unit step responses of the
SBL curves obtained for
h = 0.5, 1, and 1.1 in
Figure 32a,
Figure 35 and
Figure 36b were analyzed for
Kp,
Ki, and
Kr values selected from the common stability regions. It can thus be expected of the PIR controllers designed for the parameters selected from these regions that they will ensure the stabilizing of the
Gp3 process in
Figure 1 in the instances
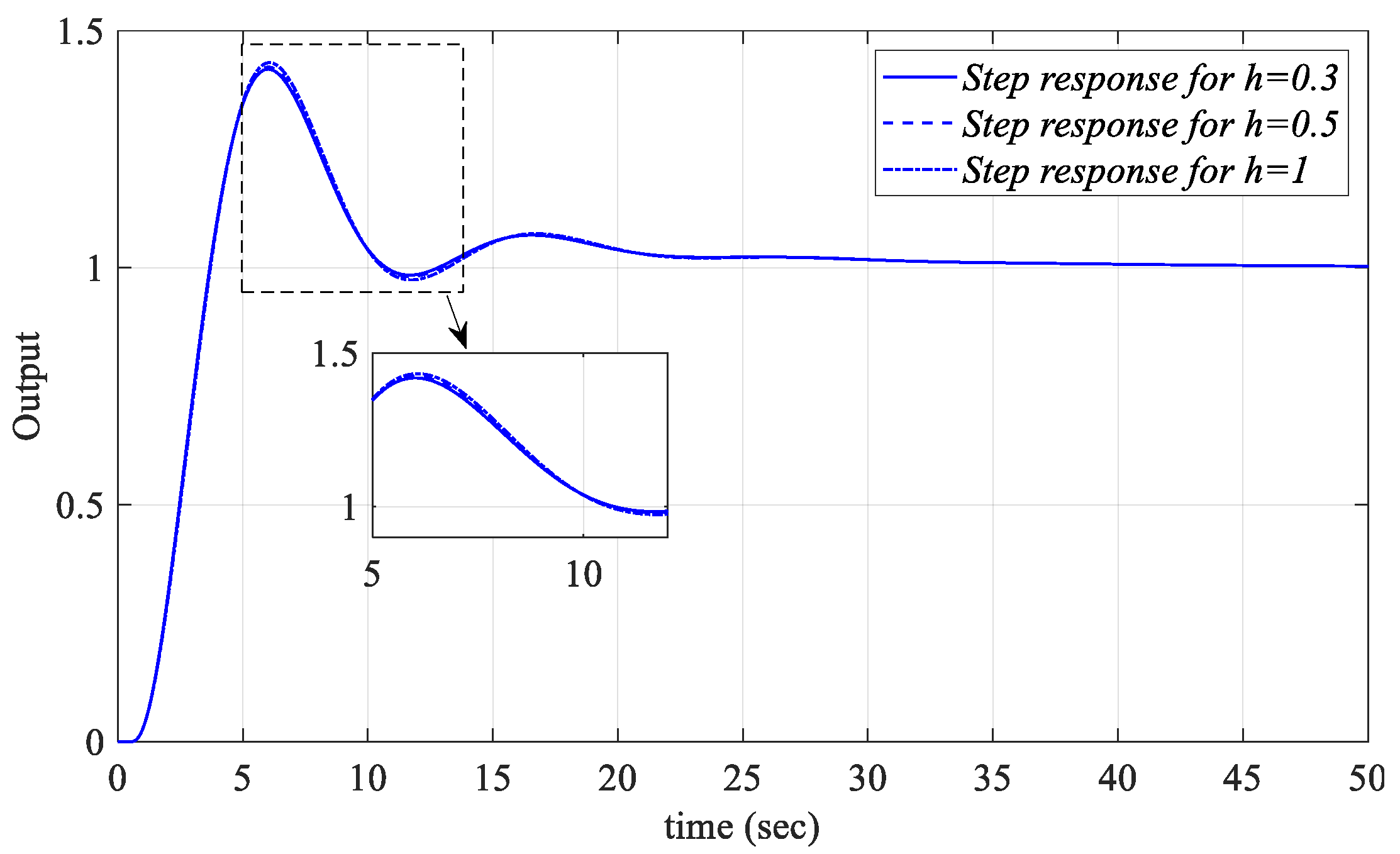
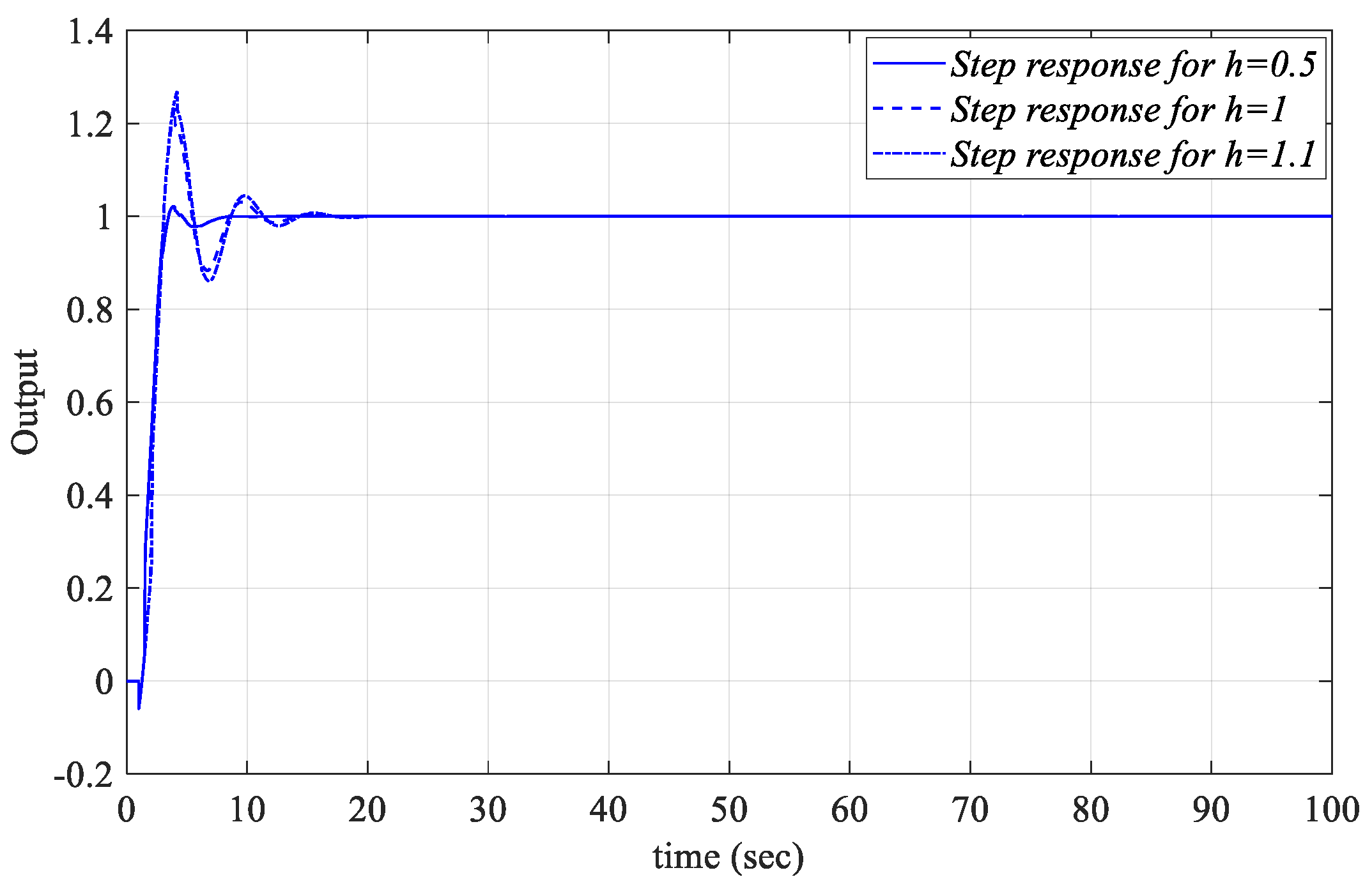
h = 0.5, 1, and 1.1. In this context, the unit step responses of the control system given in
Figure 1 obtained by applying the PIR controllers designed for
Kp =−0.0297 and
Ki =0.1183 values selected from the common region of the
Kp-Ki SBL curves drawn by taking
h=0.5, 1 and 1.1 values in
Figure 32.a when
Kr_fixed =−0.1 are shown in
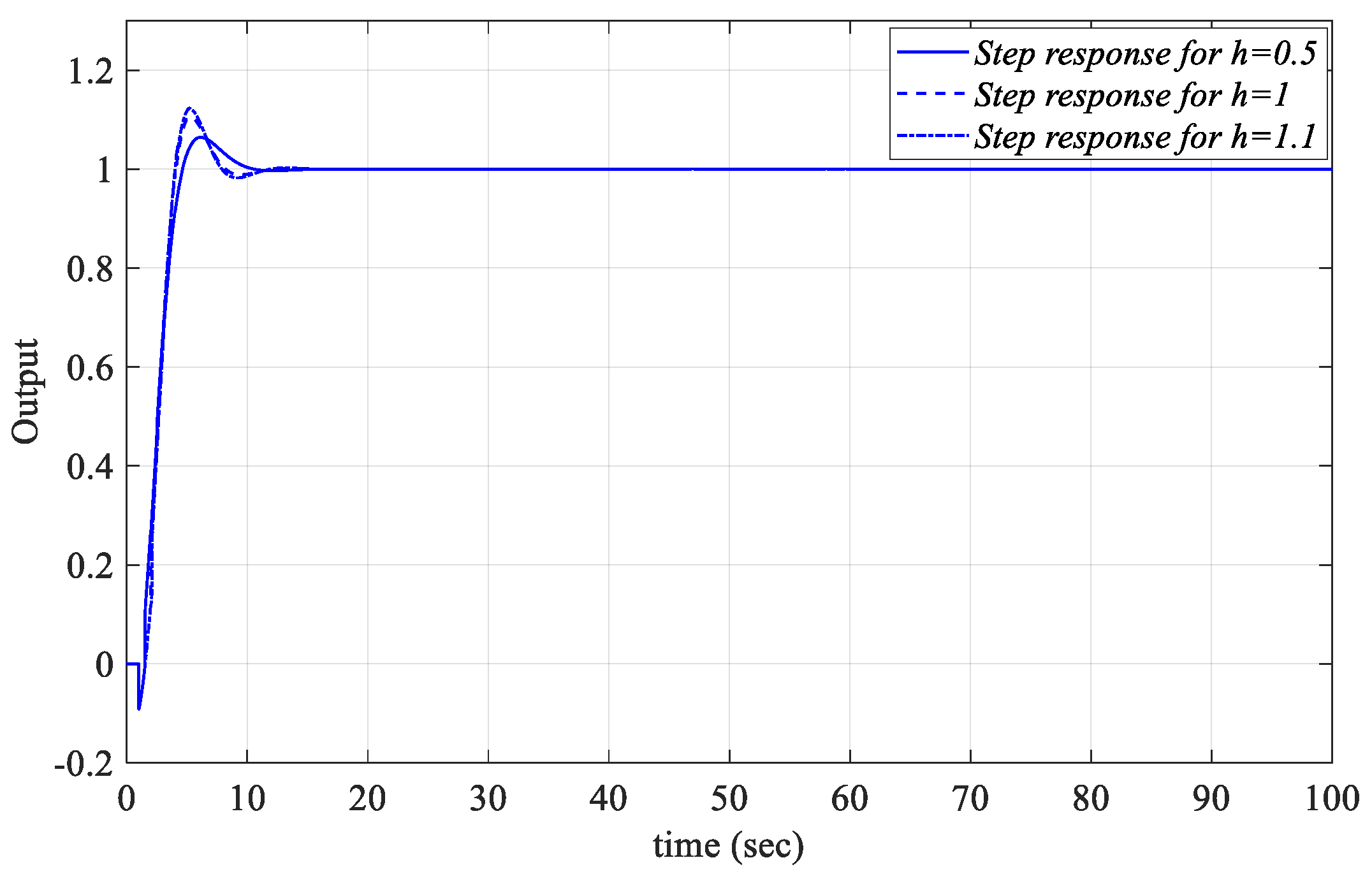
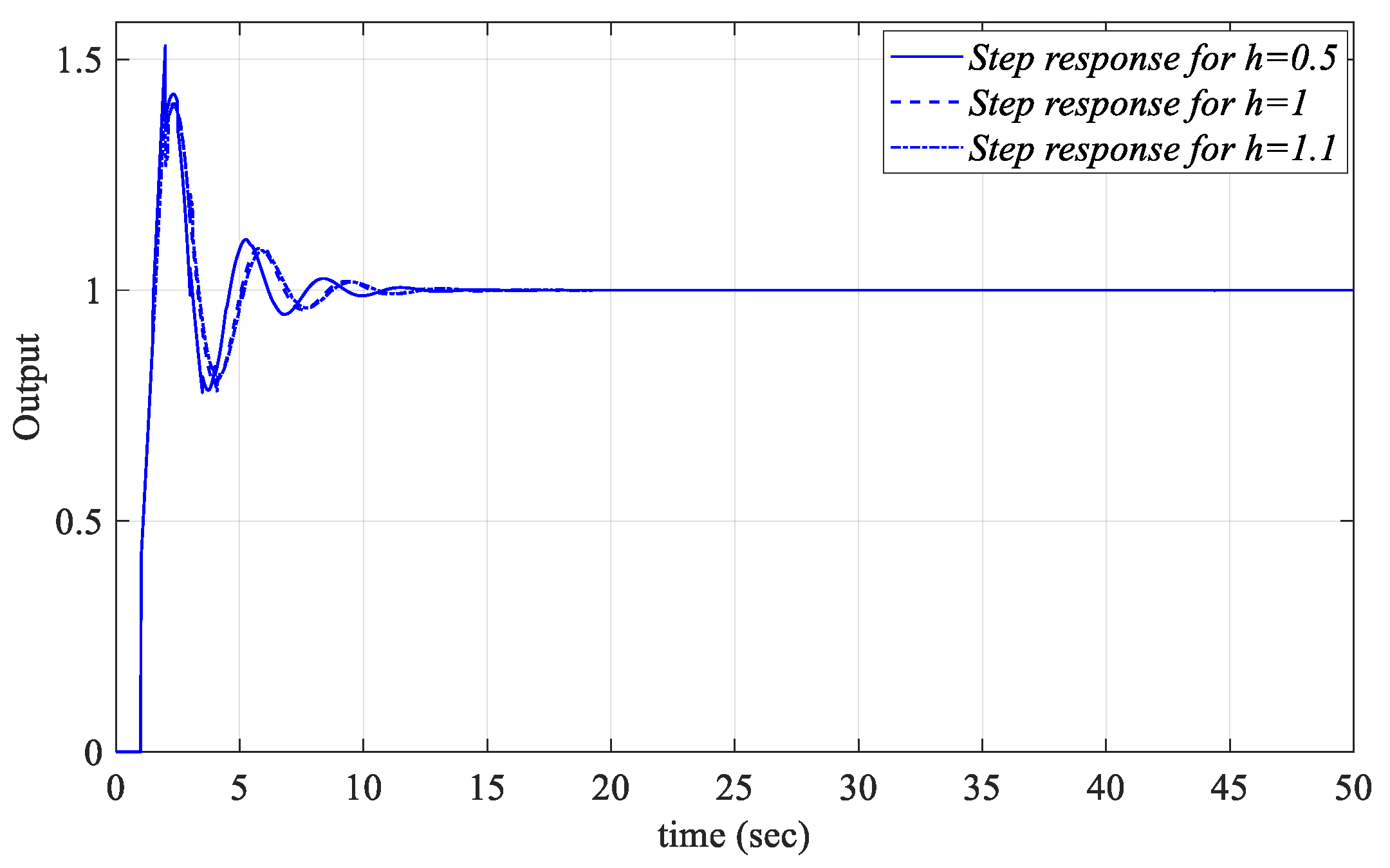
Figure 37. The PIR controllers are designed for the controller parameter values
Kp = −0.0544 and
Kr = −0.0460, which are selected from the
Kr-Kp SBL graph in
Figure 35, drawn for
Ki_fixed = 0.1. The unit step responses for different
h values are shown in
Figure 38. Similarly, the controller parameter values
Ki = 0.2833 and
Kr = −0.0460 are selected from the
Kr-
Ki SBL curve in
Figure 36b, obtained for
Kp_fixed = 0.2, and the unit step responses for
h = 0.5, 1, and 1.1 are presented as in
Figure 39.
When
Figure 37,
Figure 38 and
Figure 39 are examined, it is seen that the PIR controllers designed for the parameters selected from the common stability regions of the
SBL curves drawn for the cases
h = 0.5, 1 and 1.1 control the
Gp3 time-delay process with a first-order transfer function in the numerator and denominator in
Figure 1 in a stable manner.