1. Introduction
Green Ammonia, as an emerging zero-carbon energy carrier, is progressively emerging as a critical technological pathway for global energy transition and carbon neutrality attainment [
1]. Its core production process utilizes renewable energy sources (e.g., wind power, and photovoltaics) to drive hydrogen production through water electrolysis, which subsequently combines with atmospheric nitrogen via the low-carbon Haber–Bosch process for ammonia synthesis, thereby eliminating the dependence on fossil fuels inherent in traditional gray ammonia production. Compared with traditional ammonia production processes (emitting approximately 1.8 tons of CO
2 per ton of ammonia), green ammonia demonstrates an over 90% reduction in life-cycle carbon emissions, exhibiting significant decarbonization benefits [
2]. Regarding application scenarios, green ammonia serves not only as a clean fuel directly applicable to hard-to-decarbonize sectors like maritime shipping and power generation [
3] but also functions as an efficient hydrogen storage/transportation medium, addressing critical bottleneck challenges in hydrogen supply chains including high storage/transportation costs and safety concerns. Furthermore, as a raw material for green nitrogen fertilizers in agriculture, green ammonia can drive the transformation of conventional fertilizer industries toward sustainability. From a societal value perspective, the development of green ammonia value chains will facilitate large-scale renewable energy integration and promote deep decarbonization across industrial, transportation, and agricultural sectors, while creating new economic growth opportunities for regions abundant in renewable resources yet constrained by energy export limitations. According to International Energy Agency (IEA) projections, green ammonia is expected to account for 5% of global energy consumption by 2050, establishing it as a core technology portfolio supporting carbon neutrality goals. Consequently, the research, development, and industrialization of green ammonia technology extends beyond environmental benefits to encompass strategic imperatives for energy security, economic structural upgrading, and sustainable societal development.
The production of green ammonia—a cleaner alternative to conventional “gray ammonia”—relies on pairing renewable-powered water electrolysis (P2H) with an optimized Haber–Bosch process [
4]. At the heart of this system are two critical steps: hydrogen production and ammonia synthesis. For electrolysis, proton exchange membrane electrolyzers (PEMECs) are the preferred choice when dealing with erratic wind or solar input, thanks to their rapid response, though their high cost and limited lifespan remain sticking points. On the synthesis side, while traditional iron catalysts demand extreme heat and pressure, newer ruthenium-based alternatives operate efficiently at lower temperatures—but their expense keeps them from widespread use. The real challenge lies in the system’s layered dynamics: solar and wind fluctuations play out in seconds, electrolyzers respond over minutes, and the ammonia reaction unfolds across hours or even days. Bridging these mismatched timescales requires sophisticated modeling to untangle the knotted interactions between energy supply, hydrogen output, and chemical kinetics [
5].
Current modeling approaches for green ammonia production primarily employ mechanistic models and data-driven models. Mechanistic modeling constructs systems based on physicochemical principles (e.g., mass/energy conservation and reaction kinetics), whose strengths lie in theoretical rigor and strong interpretability that explicitly reveal causal relationships between reaction pathways and parameters, being particularly applicable to novel process development or systems with well-defined mechanisms; however, these models exhibit limited capability in detailed characterization of complex nonlinear processes (e.g., catalyst deactivation and multiphase flow coupling), while requiring precise physicochemical property parameters and boundary conditions that result in prolonged modeling cycles and elevated computational costs. In contrast, data-driven modeling (e.g., machine/deep learning) constructs surrogate models by extracting implicit patterns from historical data, demonstrating three core advantages: (1) efficient fitting of high-dimensional nonlinear relationships without requiring prior mechanistic knowledge, particularly suited for complex systems with ambiguous mechanisms or strong coupling; (2) rapid response and adaptive capabilities enabled by online data updating for real-time model optimization to meet dynamic operational demands; (3) significantly enhanced computational efficiency compared to mechanistic models, facilitating integration into real-time control or digital twin platforms. However, data-driven approaches necessitate substantial high-quality datasets and remain vulnerable to noise interference, requiring rigorous validation of model extrapolation capabilities and generalization performance. Collectively, data-driven modeling provides an efficient toolkit for the intelligent upgrading of green ammonia production, demonstrating particular strengths in multi-scale optimization and fault diagnosis scenarios. Nevertheless, their integration with mechanistic models through hybrid architectures like physics-informed neural networks (PINNs) is emerging as a cutting-edge direction to enhance modeling robustness [
6,
7].
Notably, recent advancements in Real-Time Monitoring Networks (RTMNs) have introduced a novel data collaboration paradigm for dynamic modeling. For instance, Lotrecchiano et al. [
8] achieved second-level online acquisition of air quality parameters through distributed sensor arrays, with their data streaming architecture being readily adaptable to real-time optimization requirements in chemical processes. Current research [
9] demonstrates that combining RTMNs’ high-frequency data streams with adaptive modeling approaches can significantly reduce the latency inherent in conventional offline analysis while enabling minute-level decision support for dynamic scheduling.
In deep learning methods, Long Short-Term Memory (LSTM) [
10] have proven to be highly effective for time-series data prediction, addressing the issues of gradient vanishing and explosion during long-sequence training. LSTM has been applied in chemical engineering fields including soft sensor modeling [
11,
12,
13], fault diagnosis [
14,
15], energy consumption prediction [
16,
17,
18], and control optimization [
19,
20,
21]. In characterizing the time-varying and dynamic characteristics of catalytic cracking processes [
22,
23], Zhang [
24] proposed a Recurrent Denoising Autoencoder (RDAE) based on LSTM to extract meaningful temporal features, while reducing input dimensions in the spatial domain. Subsequently, a Weighted Autoregressive LSTM (WAR-LSTM) structure was developed as a fundamental unit. By stacking multiple WAR-LSTM layers into a deep WAR-LSTM architecture, high-level representations were extracted from multivariate data, enabling full utilization of spatiotemporal information in both feature extraction and model construction. However, in practical industrial processes governed by physicochemical reaction mechanisms, process variables often exhibit differential influences on outputs. Input variables with stronger correlations to outputs should be assigned greater importance in prediction tasks. Appropriately adjusting input weights has been demonstrated to enhance model predictive performance. Consequently, weight optimization in LSTM models remains a critical research direction for advancing deep learning algorithms.
Given that the attention mechanism (AM) enhances neural multi-stage information processing capability through selective input sequence prioritization and semantic encoding in long-term memory, AM has become an essential component of neural network architectures [
25,
26,
27]. However, these methods predominantly rely on a single attention mechanism, which struggles to address the multidimensional challenges in green ammonia production. Specifically, existing single-layer attention models exhibit three key limitations: (1) Feature redundancy and noise sensitivity: green ammonia production data comprises multi-dimensional sensor parameters, yet conventional single-layer attention mechanisms fail to dynamically filter critical process variables, making them vulnerable to noise interference. (2) Multi-timescale dynamic coupling: the system’s behavior is governed by cross-scale interactions between renewable energy fluctuations and catalytic reaction dynamics. A monolithic attention mechanism cannot adaptively discern contribution differences across varying time windows. (3) Limited interpretability: current attention frameworks lack co-analysis of feature and temporal dimension weights, hindering quantitative identification of how key parameters drive output variations.
Consequently, in complex dynamic system modeling for green ammonia production, the implementation of an LSTM (Long Short-Term Memory) model integrated with a dual-layer attention mechanism effectively synthesizes temporal feature selection and critical state focusing capabilities, thereby significantly improving modeling accuracy and interpretability. The first-layer temporal attention mechanism adaptively allocates weights to capture influential temporal segments in production processes (e.g., power fluctuations during electrolytic hydrogen generation, catalyst activity variations in synthesis towers), effectively mitigating the historical information memory decay issue inherent in conventional LSTM architectures. The second-layer variable attention mechanism performs feature-dimensional weight screening to identify critical driving factors from multidimensional sensor data (temperature, pressure, H2/N2 ratio, reaction rates, etc.), thereby reducing interference from redundant/noisy variables. This dual-attention synergy endows the model with two core advantages: firstly, in highly nonlinear green ammonia production scenarios (e.g., input instability caused by renewable energy fluctuations), the model dynamically adjusts weights to precisely characterize time-varying coupling relationships among variables; secondly, the attention weight distributions quantitatively visualize the contribution degrees of different process parameters to outputs (e.g., ammonia yield), providing interpretable decision-making foundations for process optimization. Furthermore, the architecture significantly enhances training efficiency under industrial-scale data volumes through feature–time dual-dimensionality reduction, making it particularly suitable for real-time state prediction and closed-loop control in green ammonia digital twin systems.
The novelty of this study is reflected in three key aspects:
- (1)
Input-time dual attention mechanism: the input attention layer dynamically filters critical process variables to mitigate feature redundancy and noise interference; the temporal attention layer captures cross-step dependencies, effectively addressing multi-scale dynamic coupling;
- (2)
Adaptive weight visualization: through heatmap analysis of dual-attention weights, we quantitatively resolve the distinct contributions of feature and temporal dimensions to ammonia yield, providing interpretable guidance for process optimization;
- (3)
Industrial applicability: by performing feature–time dual-dimensionality reduction, the model significantly improves training efficiency on industrial-scale datasets while supporting real-time prediction and control requirements
2. Modeling of Green Ammonia Production Process Based on DA-LSTM
Time-varying characteristics are pivotal in process modeling, particularly for complex chemical production processes [
28,
29]. Chemical time-series production data modeling involves treating historical chemical production data as multivariate time series, utilizing extensive process condition parameters as feature inputs to predict values at future timesteps [
30]. The sliding window method is generally employed to process time-series datasets [
31].
Assuming the chemical production time-series dataset has N-dimensional process variables, with a batch size of T and a sliding window length (time steps) of L, the time-series data sliding window feature matrix is denoted as , where , and .
Given the historical value set of the target series
and the
t window at
and
t, the predicted value of the time series at
, where
2.1. Basic LSTM Structure
The Long-Short Term Memory (LSTM) neural network, a type of recurrent neural network (RNN), represents a short-term memory model capable of retaining information over extended time periods. LSTM demonstrates particular effectiveness in time-series classification, processing, and prediction, efficiently handling events with unknown time intervals and time lag issues. An RNN composed of LSTM units forms the basis of the temporal modeling network architecture for chemical production processes, as illustrated in
Figure 1.
A conventional LSTM unit consists of an input gate, output gate, and forget gate, as shown in the lower-right corner of
Figure 1. The LSTM unit functions as a cell, where the cell state is responsible for “remembering” values over arbitrary time intervals. Each of these three gates can be considered a “traditional” artificial neuron, with activation determined by sigmoid functions. Let the hidden state at the previous timestep be denoted as
and the cell state as
; then, the LSTM outputs are
and
, that is,
is generated through the input gate
and forget gate
, and subsequently processed via the output gate
to obtain
.
where
denotes the weight matrix,
represents the bias, and
indicates the number of hidden states in the LSTM.
2.2. AM-Based LSTM Structure
The attention mechanism (AM) fundamentally focuses attention on critical information within vast datasets by filtering key elements while disregarding non-essential components. By computing the alignment between current input sequences and output vectors, AM assigns higher attention scores to strongly correlated elements. In temporal prediction tasks for chemical production modeling, AM can be categorized into two types: spatial attention for process feature processing and temporal attention for time-dependent process variable characterization.
The incorporation of attention mechanisms (AMs) into neural network architectures is primarily motivated by three considerations: First, to achieve superior task performance. Second, to enhance the model’s interpretability, thereby improving reliability and transparency. Third, to mitigate inherent limitations of recurrent neural networks (RNNs), such as performance degradation with increasing input sequence length or computational inefficiency caused by sequential input processing [
32].
As an example, the LSTM for spatial attention is shown in
Figure 2.
Among them,
,
,
, and
are the weights and biases of the AM input layer, which are the learning parameters for training.
denotes the spatial attention weight of the
dimension input feature quantity at time step
indicating its feature importance. The SoftMax function is employed to compute this weight while ensuring the summation of all spatial attention weights equals 1.
Thus, by substituting the computed for in the LSTM architecture and incorporating Equations (3)~(8), we obtain .
2.3. Green Ammonia Model Based on DA-LSTM
Building upon the aforementioned preparatory work, the green ammonia production process model proposed in this study employs a Dual-Stage Attention-Based LSTM (DA-LSTM) architecture, as shown in
Figure 3.
By leveraging dual attention mechanisms, the DA-LSTM model adaptively selects the most relevant input features and captures long-term temporal dependencies in time series. The first layer employs an input attention mechanism to adaptively weight feature importance among green ammonia input variables at each timestep, as detailed in
Section 2.2; the second layer deploys a temporal attention mechanism to extract time-wise weights from all hidden states generated by the first layer across timesteps.
Among them, , , , and denote the learnable parameters of temporal attention weights and biases, and represents the number of hidden states in the temporal input layer. indicates the temporal attention weight at timestep when processing timestep .
By defining the temporal attention weight
, the weight-based input is derived.
Given a set of target sequence priors
, then
Among them, , and .
By incorporating
into the temporal LSTM unit and following Equations (16)–(21), we derive
.
Among them, denote the state of the implicit layer of the time input layer and all its deviations; denote the weighting matrix.
Therefore, the predicted value of time series
t at timestep
l is formulated as follows:
where
denotes the linear mapping function. Ultimately, the predicted output value
of time series
t is obtained.
3. Case Studies
3.1. Data Description and Pre-Processing
The green ammonia process modeling is based on operational data collected from a dynamic simulation model built in Honeywell UniSim R460.1@ software, with predicted process variables including ammonia production yield and first bed outlet temperature, utilizing data from load adjustment conditions spanning 90–50% of production capacity where the dataset contains 593 measurable process tags. Through field experience and domain knowledge, 56 process tags were systematically selected.
Select 56 key variables from 593 process tags, and the specific process is as follows: based on the green ammonia production process flowchart, prioritize retaining the core production process parameters for mechanism driven initial screening; furthermore, expert experience verification is utilized: the joint process engineer evaluates the operability of the initial screening variables to achieve expert experience verification, while excluding two types of variables: (1) uncontrollable parameters such as environmental temperature, which cannot be controlled in real time due to external climate influences; (2) high-redundancy parameters: such as pressure values repeatedly measured by parallel sensors. The final selection of 56 variables covers four aspects of green ammonia production, including reaction kinetics, energy efficiency, material balance, and equipment status.
The Honeywell UniSim simulation platform employed in this study strictly adheres to the design parameters and operational specifications of an actual green ammonia plant (referencing a 100,000-ton/year demonstration project in Sichuan), with comprehensive simulation model calibration and industrial consistency validation conducted as follows: (1) Mechanistic parameter calibration: laboratory kinetic data for iron-based catalysts (Fe3O4/γ-Al2O3) were used to calibrate activation energy parameters in the Arrhenius equation. (2) Dynamic response validation: step–response tests (e.g., ±10% fluctuations in renewable power input) comparing simulation data with historical plant data demonstrated 92% dynamic trajectory matching for key variables (e.g., synthesis reactor pressure and ammonia production rate). (3) Multi-condition coverage: the simulation dataset encompasses typical plant operating conditions (90–50% load) and incorporates actual failure modes (e.g., catalyst deactivation) to ensure model capability in capturing abnormal states.
3.2. Model Building and Training
Missing values were processed using linear interpolation, and the temporal dimensions of the data were aligned. The preprocessing procedures are detailed in the referenced literature. The dataset was chronologically partitioned into training, validation, and test sets at an 8:1:1 ratio. Multiple models were trained on the training data, with hyperparameters selected based on validation set performance and final evaluations conducted on the test set.
The baseline LSTM model parameters were determined via grid search [
33], with batch size
T = 32, time step
L = 18, and hidden state dimension
= 64. Further configurations included a learning rate of 0.002, decay exponent of 0.98, decay rate of 90, and 50 training epochs. To mitigate overfitting, dropout was applied to the LSTM hidden layer, with the model employing the Adam optimizer [
34] for parameter updating. Dropout (
p = 0.2) is applied to the LSTM hidden layer to randomly mask neurons, forcing the model to learn robust features. Weight decay (λ = 1 × 10
−4) in the Adam optimizer constrains the parameter space, preventing the dual-attention weights from overfitting to training-set-specific patterns.
The performance evaluation of the dual-layer attention LSTM for time-series prediction involved comparative experiments with baseline models, including Random Forest (RF), Support Vector Machine (SVM), Artificial Neural Network (ANN), and conventional LSTM models. To ensure fair comparison, all baseline models were optimized through either grid search or Bayesian Optimization, with their optimal parameter configurations presented in
Table 1.
The Python algorithm developed using the Torch framework was executed in the JetBrains PyCharm 2019.3.3 x64 environment on a computational platform equipped with an Intel(R) Core TM i7-7700K CPU @ 4.20 GHz, 8 GB RAM, and Windows 10 OS.
3.3. Model Evaluation Indicators
To evaluate model accuracy, this study employs the Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE) as evaluation metrics, defined as follows:
where
is the actual value,
denotes the predicted value, and
represents the number of test set samples.
4. Results and Discussion
4.1. Analysis of Model Performance Results
To evaluate the performance of the dual-layer attention LSTM in time-series prediction, comparative experiments were conducted with baseline models including Random Forest (RF), Support Vector Machine (SVM), Artificial Neural Network (ANN), and conventional LSTM models, with the final prediction results presented in
Table 2. The proposed model demonstrates reduced average random error across RMSE, MAE, and MAPE metrics, effectively enhancing predictive performance for time-series data in green ammonia production processes.
Specifically, as an ensemble learning method, Random Forest (RF) demonstrates relatively strong performance in handling nonlinear data, but its limited capability to capture temporal dependencies in time-series data results in lower prediction accuracy. Support Vector Machine (SVM), while advantageous in processing high-dimensional data and small-sample problems, suffers from poor adaptability to time-series data due to the sensitivity of kernel function selection and parameter tuning, making it difficult to capture complex temporal patterns. Traditional Artificial Neural Networks (ANNs), though theoretically capable of approximating any nonlinear relationship, lack inherent memory mechanisms for time-series data and thus fail to effectively utilize historical information for prediction. In contrast, the standard LSTM model can better capture long-term dependencies in time series through its gating mechanisms, yet it still exhibits insufficient utilization of critical temporal features when processing multivariate, high-dimensional green ammonia production data.
The proposed dual-layer attention mechanism LSTM model enhances its capability to capture critical temporal information by incorporating attention mechanisms. The first attention layer extracts the significance of different time steps in input sequences to dynamically adjust the weights of input information; the second attention layer optimizes the representation of LSTM hidden states, further enhancing the model’s ability to express temporal features. This integration of dual attention mechanisms enables the model to more accurately identify pivotal time points with the greatest impact on predictions in green ammonia production processes, thereby significantly improving predictive accuracy.
Furthermore, the proposed model demonstrates exceptional performance in reducing mean random error. Random errors typically arise from data noise, measurement inaccuracies, or model overfitting to non-critical information. The dual-layer attention mechanisms effectively mitigate such interference by focusing on critical temporal features, thereby suppressing irrelevant noise. This capability proves particularly crucial in green ammonia production scenarios, where conventional models often struggle to capture authentic process trends due to the inherent high noise levels and volatility in production data.
To further verify the model’s generalization capability and reduce overfitting risks, we conducted additional sensitivity analyses:
- (1)
Multi-ratio hold-out validation: while preserving time-series sequence integrity, we retrained the model using different data split ratios (e.g., 7:1.5:1.5; 8.5:0.75:0.75). Results demonstrate that the DA-LSTM model maintains remarkable robustness, with only a ±3.2% fluctuation in ammonia yield prediction RMSE across different splits (see
Table 3);
- (2)
Blocked k-fold cross-validation: to maintain temporal dependencies, we implemented a time-series blocked partitioning strategy (k = 5), reserving 10% of data as a buffer zone between training and test sets. The cross-validation shows that the DA-LSTM model achieves superior stability (mean RMSE = 0.089; σ = 0.006) compared to the baseline LSTM model (RMSE = 0.118; σ = 0.011), confirming its robust temporal dynamics capture capability.
These experiments collectively demonstrate the DA-LSTM model’s consistent performance across varying data distributions. Its dual-level attention mechanism—through dynamic feature selection and temporal weighting—effectively suppresses overfitting risks.
To evaluate the computational overhead of the dual-attention mechanism, we compared the training efficiency between DA-LSTM and the baseline LSTM model under identical hardware configurations. As shown in
Table 4, while DA-LSTM demonstrates significantly higher training time and memory requirements compared to conventional LSTM—representing a limitation of our approach—this cost is justified by its superior predictive accuracy.
4.2. Visual Analysis of Attentional Weights
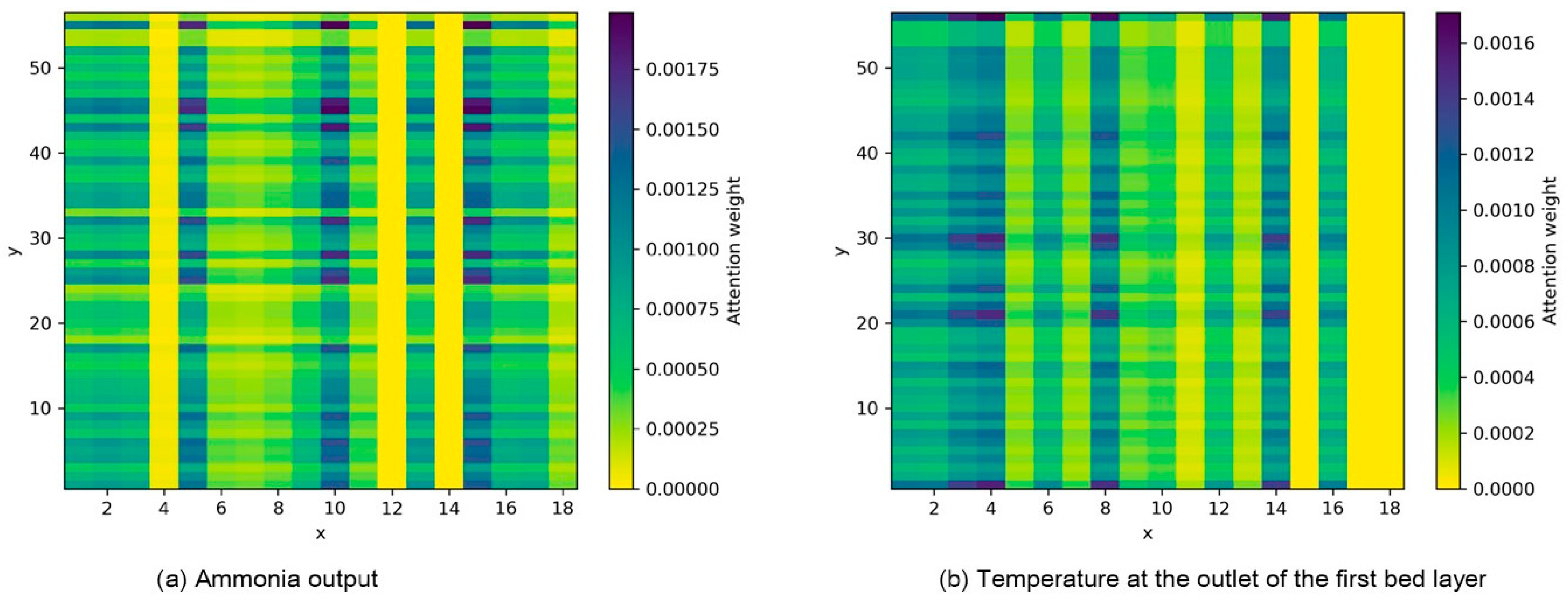
In dynamic modeling and optimization control, the attention mechanism effectively captures the influence of critical temporal points on output results by assigning distinct weights to each time step in input sequences. Specifically, the magnitude of attention weights directly reflects the significance level of corresponding temporal information, where input units with higher weights play a determinative role in shaping outputs. As illustrated in
Figure 4, heatmap visualization of ammonia yield and first bed outlet temperature predictions clearly demonstrates the varying degrees of impact from different time steps, thereby enabling precise identification of pivotal temporal points. This soft feature selection method based on attention weights not only fully utilizes localized information within sampling windows but also achieves efficient time-series importance sampling in large-scale complex chemical systems. The approach provides a powerful tool for dynamic modeling and optimization control, significantly enhancing predictive accuracy and control efficiency, particularly excelling in handling nonlinear, high-dimensional chemical processes.
Expanding further, the core principle of the attention mechanism lies in dynamically adjusting the contribution of input sequence information at different positions to the output by computing weights for each timestep. In chemical engineering systems, this mechanism holds particular significance, as the dynamic behaviors of such systems are often governed by states at a few critical timesteps. For instance, in ammonia synthesis processes, parameters such as reactor temperature, pressure, and gas flow rate at varying timesteps exert significant impacts on final production yield and quality. Through the attention mechanism, the model can automatically identify these critical timesteps and assign them higher weights, thereby capturing the system dynamics with enhanced precision.
Additionally, the attention mechanism exhibits strong interpretability. Through heatmap visualization, we can intuitively identify which timesteps exert the most significant influence on prediction outcomes. This visual analytical approach not only enhances the understanding of the model’s decision-making process but also provides valuable references for process optimization. For instance, if temperature variations at a specific timestep demonstrate substantial impacts on ammonia production yield, operational focus can be strategically directed toward temperature control at this critical temporal phase to achieve more efficient manufacturing.
When dealing with large-scale complex chemical systems, traditional modeling approaches often face the curse of dimensionality and high computational complexity. In contrast, attention mechanisms effectively reduce model complexity through soft feature selection while retaining critical information. This methodology not only enhances prediction accuracy but also significantly reduces computational resource consumption, enabling practical applications in real-time control and optimization.
In summary, the application of attention mechanisms in dynamic modeling and optimization control provides an efficient, flexible, and interpretable tool for addressing complex chemical engineering systems. Through rational allocation of attention weights, models can more accurately capture system dynamic behaviors, thereby enabling more precise predictions and more efficient control. This approach not only holds significant application value in ammonia synthesis processes but can also be extended to other intricate chemical processes, offering robust support for the intelligentization and automation of industrial production.
While this study primarily focuses on process prediction and optimization, the dual-layer attention mechanism of DA-LSTM naturally lends itself to fault detection tasks through two key capabilities: (1) The input attention layer suppresses non-critical sensor noise while amplifying fault-related features such as temperature spikes or pressure anomalies. This complements traditional LSTM autoencoder approaches that rely on reconstruction errors. (2) The temporal attention layer identifies the exact onset of abnormal events, such as early-stage catalyst deactivation, by detecting abrupt shifts in time-step weights. This is visually supported by the heatmap in
Figure 4. When integrated with Real-Time Monitoring Networks, the DA-LSTM model generates interpretable fault contribution heatmaps across both feature and temporal dimensions. For example, engineers can quickly pinpoint root causes like abnormal electrolyzer voltage patterns.