Numerical Simulation and Intelligent Prediction of Effects of Primary Air Proportion and Moisture Content on MSW Incineration

Abstract

As the core process of the thermal treatment of municipal solid waste (MSW), incineration process optimization has become a frontier topic in the field of environmental engineering. This study took a 500 t/d incinerator for engineering application as the research object. Based on a two-fluid model, a three-dimensional transient model of a proportional incinerator was established. The effects of primary air proportion and moisture content on the combustion state in the incinerator were verified and discussed using field test data, and the dynamic changes in flue gas temperature were predicted by a BPNN (Backpropagation Neural Network). The results show that the increase in air volume in the drying section promotes water evaporation but inhibits the devolatilization and combustion of fixed carbon. The position where complete devolatilization and fixed carbon combustion begins was delayed by 1.5 m~3 m. The moisture content (M) is negatively correlated with the devolatilization and combustion of fixed carbon. From M = 25% to M = 40%, the flue gas outlet temperature decreased by 140 K. In addition, a dynamic combustion BP neural network model with the movement of the grate under rated conditions was constructed, with the MSE (Mean Squared Error) being 1.629%. The model can learn data characteristics well and has a good prediction effect. This study provides a scientific basis for optimizing the operating parameters of municipal solid waste incinerators, helps to optimize the incineration process, and is of great significance to the thermal treatment of MSW.

1. Introduction

With the acceleration of urbanization and the expansion of the population, the annual generation of municipal solid waste (MSW) in China has exceeded 2.3 billion tons [1], and the demand for harmless treatment is becoming increasingly urgent [2]. Incineration technology accounts for more than 80% of China’s waste thermal treatment market share due to its significant reduction in volume (volume reduction of 80–90%), harmlessness (complete sterilization and decomposition of organic pollutants), and energy potential [3]. Incineration has become the primary method for converting MSW into energy because it has relatively low requirements for waste composition and quality and requires simple pretreatment. Additionally, the yield of fly ash is generally lower compared with other thermal treatment methods [4]. Since Shanghai took the lead in implementing waste sorting collection in 2019, it has had a significant impact on the physical and chemical properties of MSW [5]. The proportion of kitchen waste in MSW has decreased significantly; the proportion of rubber, plastic, and paper has increased [6]; and the proportion of combustibles per unit mass has increased, increasing in calorific value. This means that the thermal load capacity of the incinerator is under pressure because the increase in the calorific value of MSW is close to about one-third of the designed calorific value of the maximum waste treatment capacity of the incinerator [7].

The operating efficiency and pollutant emissions of incinerators are affected by multiple parameters, among which the primary air proportion and MSW moisture content are key variables. Studies have shown that the primary air distribution directly affects the combustion rate and temperature field uniformity of the MSW on the grate, while the moisture content changes the combustion dynamics through evaporation heat absorption and mass transfer resistance [8]. Existing studies have mostly focused on two-dimensional models or single-parameter optimization under fixed conditions, ignoring the coupling effects of three-dimensional dynamic combustion processes and MSW characteristics (such as moisture content fluctuations). For example, traditional models often simplify the grate movement and heat transfer mechanism, making it difficult to accurately predict periodic combustion fluctuations [9,10,11]. In addition, although some scholars have explored the effects of moisture content on CO and NOx generation [12,13], there are still deficiencies in the study of the mechanism of delayed volatile release and incomplete combustion of fixed carbon.

Due to the complex structure and diverse operating conditions of waste incineration devices, experimental research and computational simulation have become the core means to analyze their combustion mechanisms [14,15]. To achieve accurate modeling, it is necessary to systematically reveal the coupling mechanism between solid bed combustion and the gas-phase reaction process. For solid-phase combustion, the discrete element method (DEM) is widely used to simulate particle movement and pyrolysis behavior. Typical tools include EDEM (discrete element method), Rocky DEM, and FLIC (Fluid Dynamic Incinerator Code) [16,17,18,19]. Gas-phase combustion modeling is mostly based on finite element methods, such as the use of ANSYS Fluent and other software [20]. At present, in facing the increasing amount of MSW, limited by the high cost of transformation of incineration facilities, researchers are more inclined to improve the efficiency of existing devices through parameter optimization. Hu et al. [21] studied the effects of different secondary air ratios on nitrogen oxide emissions and combustion characteristics. Their study showed that the optimal NOX control method is using a 100% load combined with a secondary air ratio of 35%. Qi et al. [22] burned municipal solid waste in different O₂ concentration atmospheres (21%, 26%, 31%) to find the most effective oxygen-enriched atmosphere. The results showed that oxygen-enriched combustion reduced NOX emissions. As the O₂ concentration increased, the NO_X production could reach a minimum of 26.36% in an air atmosphere. Li et al. [23] used numerical simulation to optimize three denitrification technologies: air staging, flue gas recirculation (FGR), and selective non-catalytic reduction (SNCR). By optimizing the air distribution ratio of primary air to secondary air, the initial nitrogen oxide production was reduced by 8.39%. Their study proved that the air ratio has a significant impact on the efficiency and stability of the incinerator and NO_X emissions. Gu et al. [24] established a moving grate model of a 750 t/d waste incinerator to study the effects of heat capacity and excess air ratio on the velocity uniformity and mixing of MSW in the grate combustion zone. By optimizing the air supply volume, the fuel mixing efficiency can be increased by 51.39% to 81.04%. Li et al. [23] optimized the distribution ratio of primary air to secondary air through numerical simulation, reducing the nitrogen oxides of the MSW incinerator by 8.39%. In their experiment, Jia et al. [13] showed that the CO concentration showed a nonlinear variation rule with an increase in moisture content. Still, an increase in moisture content would inhibit the generation of NOx. Tang et al. [25] combined the simulation results and quantitatively analyzed the effects of different grate speeds and air volume ratios (primary air–secondary air) on incineration. Liu et al. [8] discussed the effects of the ratio of primary air to secondary air in a furnace on the combustion characteristics. It is worth noting that these models simplify solid-phase combustion into a two-dimensional static process and do not consider the effects of grate dynamic heat transfer on the combustion path. The precise control of primary air distribution can not only optimize the bed combustion rate but also improve the pollutant generation characteristics through temperature field reconstruction and oxygen concentration distribution adjustment, which is a key entry point for improving incineration efficiency.

Although existing research focuses on air ratio optimization, less attention is paid to the interference effects of MSW component fluctuations on the combustion process. Liang et al. [26] confirmed that an increase in the moisture content of MSW will significantly increase the amount of CO and NO in the solid-phase bed. Magnanelli et al. [27] found that moisture has a great influence on the dynamic response of the incinerator. Chen et al. [28] explored the effects of waste moisture content on gasification characteristics. The results showed that an increase in moisture content can promote the carbon conversion rate, and the lower calorific value decreases with an increase in moisture content. Wu et al. [29] analyzed the influence of MSW drying temperature and moisture content on process flow node parameters. When the moisture content is lower and the drying temperature is higher (less than 200 °C), it is more favorable to the pyrolysis gasification stage and requires less external energy input. The above results show that the moisture content of MSW not only determines the composition of combustion products but profoundly affects the incineration efficiency and emission characteristics. Therefore, it is urgent to construct a three-dimensional dynamic coupling model to simultaneously analyze the synergistic mechanism of primary air proportion and MSW characteristics (such as moisture content) to provide theoretical support for the full process optimization of incineration parameters.

Machine learning technology is widely employed in the field of intelligent prediction. It uses massive data to train models to reveal the inherent relationships between complex data. In the modeling process of waste incinerators, multivariate factors such as load, air ratio, and waste characteristics are coupled with each other and act together on the combustion process and component distribution. Neural network models have shown significant advantages in this field. For example, Hu et al. [30] innovatively constructed a time-span input neural network to accurately predict the main steam temperature change trend in a 750 t/d waste incineration boiler. By selecting 15 sensitive parameters with specific periods as network inputs, the prediction performance was significantly improved. Liu et al. [31] established a neural network model based on the gradient descent algorithm to predict the evaporation of a waste incinerator and achieved the advanced control of evaporation, thereby enhancing the operating stability of the equipment. To more accurately evaluate the utilization value of syngas, Li et al. [32] developed an artificial neural network (ANN) model that used process variables such as sludge type, catalyst type and dosage, pyrolysis temperature, and moisture content as inputs to effectively predict the high heating value (HHV) of syngas. Gu et al. [33] constructed a BP neural network model for the product distribution of different wastes under diversified pyrolysis conditions, and its prediction results were highly consistent with the experimental data. Xing et al. [34] combined three machine learning methods, an artificial neural network (ANN), support vector machine (SVM), and random forest (RF), to accurately estimate the HHV of biomass from industrial analysis and elemental analysis and verified the superiority of the machine learning method by comparing it with linear and nonlinear empirical correlations. Given the considerations of computing time and cost, future research will focus more on reducing computational complexity based on the neural network model to achieve the accurate prediction of the incinerator operation status. At the same time, considering the dynamic characteristics of the actual combustion process of the incinerator and the real-time influence of the periodic movement of the grate on the combustion condition of the furnace, constructing a model based on time domain input to achieve real-time online prediction will become an important research direction.

This study focuses on an engineering-scale incinerator as the research subject and develops a 3D transient numerical simulation model of the entire furnace based on the Euler–Euler two-fluid model. Combined with the verification data collected on-site in the incinerator, the synergistic mechanism of primary air proportion and MSW moisture content is deeply explored, providing theoretical support for the full process optimization of incineration parameters. At the same time, combined with machine learning technology, computational complexity is reduced based on the neural network model, and a time domain input model is constructed to realize the real-time online prediction of the incinerator operating status, providing scientific guidance for improving incinerator operation, improving efficiency, and reducing emissions.

2. Methods

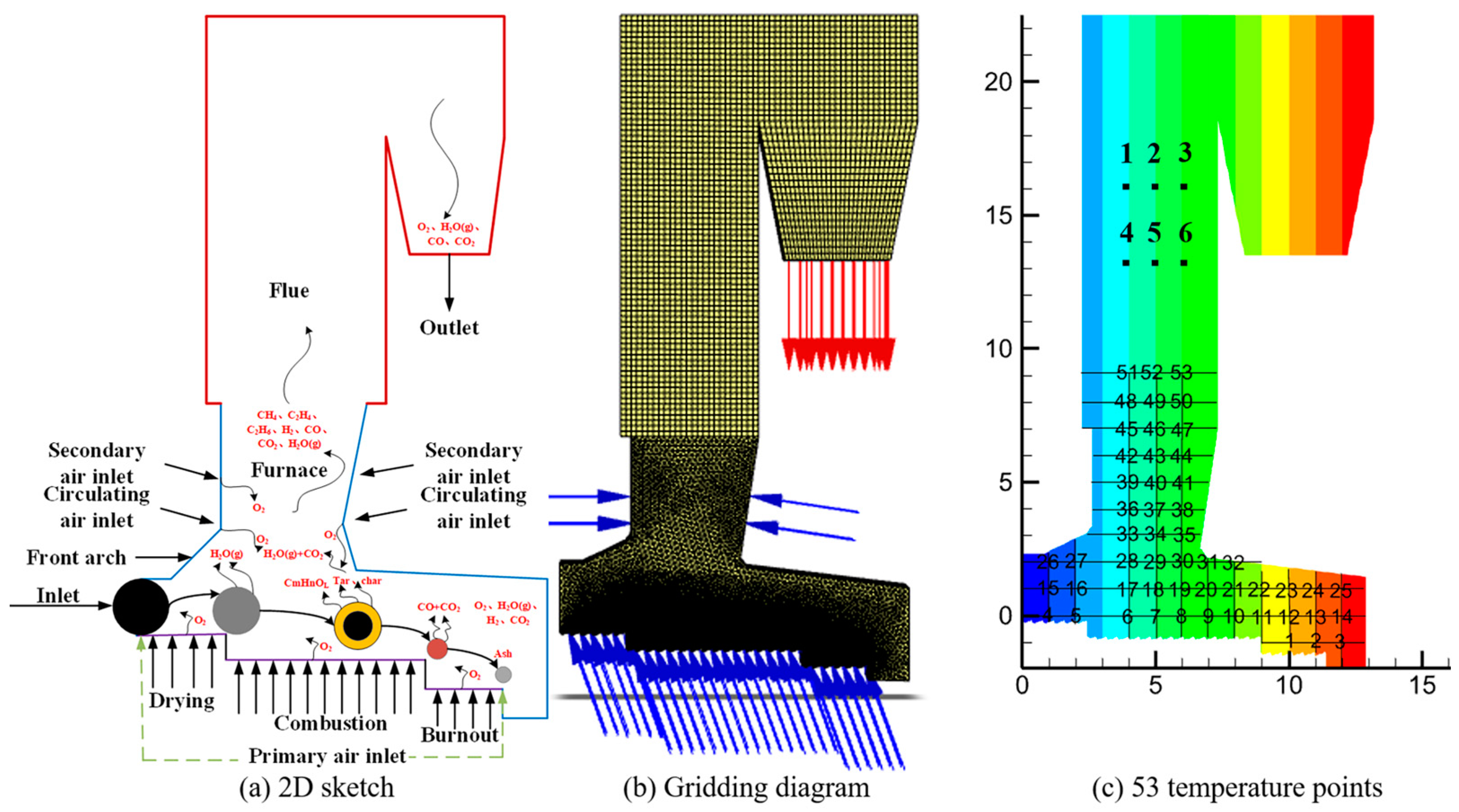
2.1. Physical Model

This study focuses on a 500 t/d grate-type waste incinerator, which features a total grate length of 12.88 m and a width of 9.1 m. The grate is segmented into three sections, measuring 2.45 m, 6.5 m, and 2.45 m in length, respectively. Drop walls with a height of 0.6 m are installed between adjacent grates. A 2D sketch is shown in Figure 1a and contains MSW heat exchange and gas generation in the incinerator. The geometric model is shown in Figure 1b. A hexahedral mesh was used for delineation, and the number of meshes was 950,000. The mesh’s Minimum Orthogonal Quality is 0.617860, the Maximum Aspect Ratio is 8.58404, and the Max skewness is 0.24848. To enhance the simulation accuracy, local mesh refinement was applied to the grate, primary air, secondary air, and circulating air regions. And Sugon supercomputer X86 64C 2.5 GHz 256 GB was used for high-performance computing (HPC) to improve the accessibility and reproducibility of the results. As shown in Figure 1b, 53 temperature measurement points were strategically placed along the centerline of the Z-plane, with 1 m intervals in both the X and Y directions. Data collected from these points were utilized to construct a furnace temperature BP neural network model based on time domain inputs, as detailed in Section 2.3.

Under rated conditions, the primary air volume is 70,000 Nm³/h, and the temperature is 493 K, and it is distributed in 6 air chambers. The secondary air volume is 13,300 Nm³/h; the temperature is 300 K; the secondary air nozzles are staggered, 10 on the front wall and 11 on the rear wall; and the air volume is the same. The nozzle diameter is about 80 mm. The circulating air temperature is 428 K; the wind nozzles are staggered, 15 on the front wall and 16 on the rear wall; and the diameter is about 80 mm. The air volume of each nozzle is the same, and the air volume is 15,600 Nm³/h. The higher heating value of MSW is 10 MJ/kg, where the heating value is determined by bomb calorimetry based on an as-received basis (ARB). The particle size is 15 mm, and the average density is 850 kg/m³.

The industrial analysis and elemental analysis results of MSW are shown in

Table 1. MSW industrial analysis and elemental analysis.

Type	Industrial Analysis (%)				Qnet,ar MJ·kg −1	Elemental Analysis (%)
	Mar	Aar	Var	FCar		Cd	Hd	Od	Nd	Sd
MSW	35.00	8.10	49.40	7.50	10.00	45.80	6.37	34.69	1.21	0.03

ar—as received; d—dry basis.

. The volatiles produced by pyrolysis were divided into pyrolysis liquid and non-condensable gas after condensation, and their composition and content were measured by GC-MS (SHIMADZU QP2010, ultra-gas chromatograph, quadrupole mass spectrometer with He as the carrier gas, a capillary column of 30 m RESTEK × 0.25 mm ID and a 0.25 μm film thickness) and GC (GC9160, Shanghai Ouhua analysis instrument factory), respectively. The calorific value of MSW is relatively low, which may be related to the high moisture content and low fixed carbon content in MSW. The volatile content is close to 50%, indicating that MSW is rich in organic matter and has a high combustion potential.

2.2. Governing Equation

Based on the two-fluid model, the mass conservation equation, momentum conservation equation, energy conservation equation, and component conservation equation for the solid material on the grate and the gas phase in the furnace are shown in

Table 2. Incineration process control equations.

Name	Equation	No.
Gas phase [35]	${\displaystyle \frac{\partial ({\alpha }_g{\rho }_g)}{\partial t}}+{\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_g{\rho }_g{u}_{gj})=S_g$	(1)
	${\displaystyle \frac{\partial }{\partial t}}({\alpha }_g{\rho }_g{u}_{gi})+{\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_g{\rho }_g{u}_{g_i}{u}_{gj})=-{\alpha }_g{\displaystyle \frac{\partial p}{\partial x_i}}+{\alpha }_g{\rho }_{g}g+{\displaystyle \frac{\partial }{\partial x_j}}[{\alpha }_g(\mu +{\mu }_t)({\displaystyle \frac{\partial u_{gj}}{\partial x_i}}+{\displaystyle \frac{\partial u_{gi}}{\partial x_j}})]+{\beta }_f(u_{sj}-u_{gj})$	(2)
	${\displaystyle \frac{\partial }{\partial t}}({\alpha }_g{\rho }_g{C}_{pg}{T}_g)+{\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_g{\rho }_g{u}_{gi}{C}_{pg}{T}_g)={\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_g{\lambda }_g{\displaystyle \frac{\partial T_g}{\partial x_j}})+h_{gs}(T_g-T_s)+S_g{H}_g$	(3)
	${\displaystyle \frac{\partial }{\partial t}}({\alpha }_g{\rho }_g{Y}_{gn})+{\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_g{\rho }_g{u}_{gj}{Y}_{gn})={\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_g{\rho }_g{D}_{gn}{\displaystyle \frac{\partial Y_{gn}}{\partial x_j}})+S_{gn}$	(4)
Solid phase [36]	${\displaystyle \frac{\partial ({\alpha }_s{\rho }_s)}{\partial t}}+{\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_s{\rho }_s{u}_{sj})=S_s$	(5)
	${\displaystyle \frac{\partial }{\partial t}}({\alpha }_s{\rho }_s{u}_{si})+{\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_s{\rho }_s{u}_{s_i}{u}_{sj})=-{\alpha }_s{\displaystyle \frac{\partial p}{\partial x_i}}+{\alpha }_s{\rho }_{s}g+{\displaystyle \frac{\partial }{\partial x_j}}[{\alpha }_s(\mu +{\mu }_t)({\displaystyle \frac{\partial u_{sj}}{\partial x_i}}+{\displaystyle \frac{\partial u_{si}}{\partial x_j}})]+{\beta }_f(u_{gj}-u_{sj})$	(6)
	${\displaystyle \frac{\partial }{\partial t}}({\alpha }_s{\rho }_s{C}_{ps}{T}_s)+{\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_s{\rho }_s{u}_{si}{C}_{ps}{T}_s)={\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_s{\lambda }_s{\displaystyle \frac{\partial T_s}{\partial x_j}})+h_{sg}(T_s-T_g)+S_s{H}_s$	(7)
	${\displaystyle \frac{\partial }{\partial t}}({\alpha }_s{\rho }_s{Y}_{sm})+{\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_s{\rho }_s{u}_{sj}{Y}_{sm})={\displaystyle \frac{\partial }{\partial x_j}}({\alpha }_s{\rho }_s{D}_{sm}{\displaystyle \frac{\partial Y_{sm}}{\partial x_j}})+S_{sm}$	(8)
Gas-phase turbulence [18]	${\displaystyle \frac{\partial (\rho k)}{\partial t}}+{\displaystyle \frac{\partial (\rho k{u}_i)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_i}}[(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}){\displaystyle \frac{\partial k}{\partial x_i}}]+G_K+G_b-\rho \epsilon -Y_M$	(9)
	${\displaystyle \frac{\partial (\rho \epsilon )}{\partial t}}+{\displaystyle \frac{\partial (\rho \epsilon u_i)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}[(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_s}}){\displaystyle \frac{\partial \epsilon }{\partial x_j}}]+{\displaystyle \frac{\epsilon }{k}}(G_{1\epsilon }{G}_k-G_{2\epsilon }\rho \epsilon )+S_{\epsilon }$	(10)

.

In the control equation, α is the volume fraction of the gas phase and the solid particle phase, satisfying the following:

$${\alpha }_g+{\alpha }_s=1$$

(11)

Due to the precipitation of volatiles and the combustion of fixed carbon, the mass of the solid phase decreases, and the mass of the gas phase increases. Sg and Ss in the mass conservation equation represent the mass source terms generated by heterogeneous chemical reactions:

$$S_g=-{\displaystyle \sum _i{S}_s}=-{\displaystyle \sum M_c{V}_c{R}_c}$$

(12)

The interphase force in the momentum conservation equation adopts the Ergun model [37]:

$${\beta }_f=150{\displaystyle \frac{{\alpha }_s^2{\mu }_g}{{\alpha }_g{d}_s^2}}+1.75{\displaystyle \frac{{\rho }_g{\alpha }_s\left|{\mathit{u}}_s-{\mathit{u}}_g\right|}{d_s}}$$

(13)

The interphase heat transfer model in the energy conservation equation adopts the Gunn model [38]:

$$Nu=\left(7-10{\alpha }_g+5{\alpha }_g^2\right)\left(1+0.7{\mathrm{Re}}_s^{0.2}{\mathrm{Pr}}^{1/3}\right)+\left(1.33-2.4{\alpha }_g+1.2{\alpha }_g^2\right){\mathrm{Re}}_s^{0.7}{\mathrm{Pr}}^{1/3}$$

(14)

$$h_{\mathrm{gs}}={\displaystyle \frac{6k_g\left(1-{\alpha }_{\mathrm{g}}\right)}{d_s{d}_s}}Nu$$

(15)

2.3. Boundary Conditions

The primary air, secondary air, circulating air nozzle, and municipal solid waste inlet below the grate are all set as velocity inlet boundary conditions. The furnace temperature is 573 K, and the municipal solid waste inlet temperature is set to 300 K. The part below the furnace throat adopts adiabatic boundary conditions, and the area above the furnace throat is set to water-cooled wall boundary conditions with a temperature of 700 K. The furnace wall is set to a boundary condition that does not allow for sliding, and the furnace outlet is defined as a pressure outlet boundary condition.

The incineration process of MSW covers the turbulence model, radiation model, and species transport model. Given the high-Reynolds-number turbulence generated during the combustion process, the standard turbulence model with standard wall treatment was adopted [39]. Considering the large volume of the incinerator, the radiation model selected the P-1 model combined with the weighted ash gas model (WSGGM). This model combination is based on the finite rate/eddy dissipation model and considers the influence of the gas mixture on the grate surface. This model can not only accurately describe the complex situation of radiation heat transfer in the furnace but also maintain the efficiency of calculation [40]. The pressure–velocity coupled momentum equation is solved by using the coupled SIMPLE algorithm. The turbulence equation, momentum equation, energy equation, and species conservation equation are all solved by the first-order upwind method. The chemical reaction process of the combustible gas in the gas phase is detailed in

Table 3. Gas-phase chemical reactions.

Reaction	A/s−1	E/J·kmol−1	Reference
CH4 + 1.5O2→CO + 2H2O	1.69 × 109	2.84 × 107	[11]
C2H4 + 2O2→2CO + 2H2O	1.6 × 1010	2 × 108	[41]
C2H6 + 2.5O2→2CO + 3H2O	1 × 1012	1.73 × 108	[42]
2H2 + O2→2H2O	7.97 × 1014	9.65 × 107	[43]
2CO + O2→2CO2	2.67 × 108	1.67 × 108	[44]
C5.71H9.25O0.51 + 4.9125O2→5.71CO + 4.625H2O	2.39 × 1013	1.7 × 108	Experimental

.

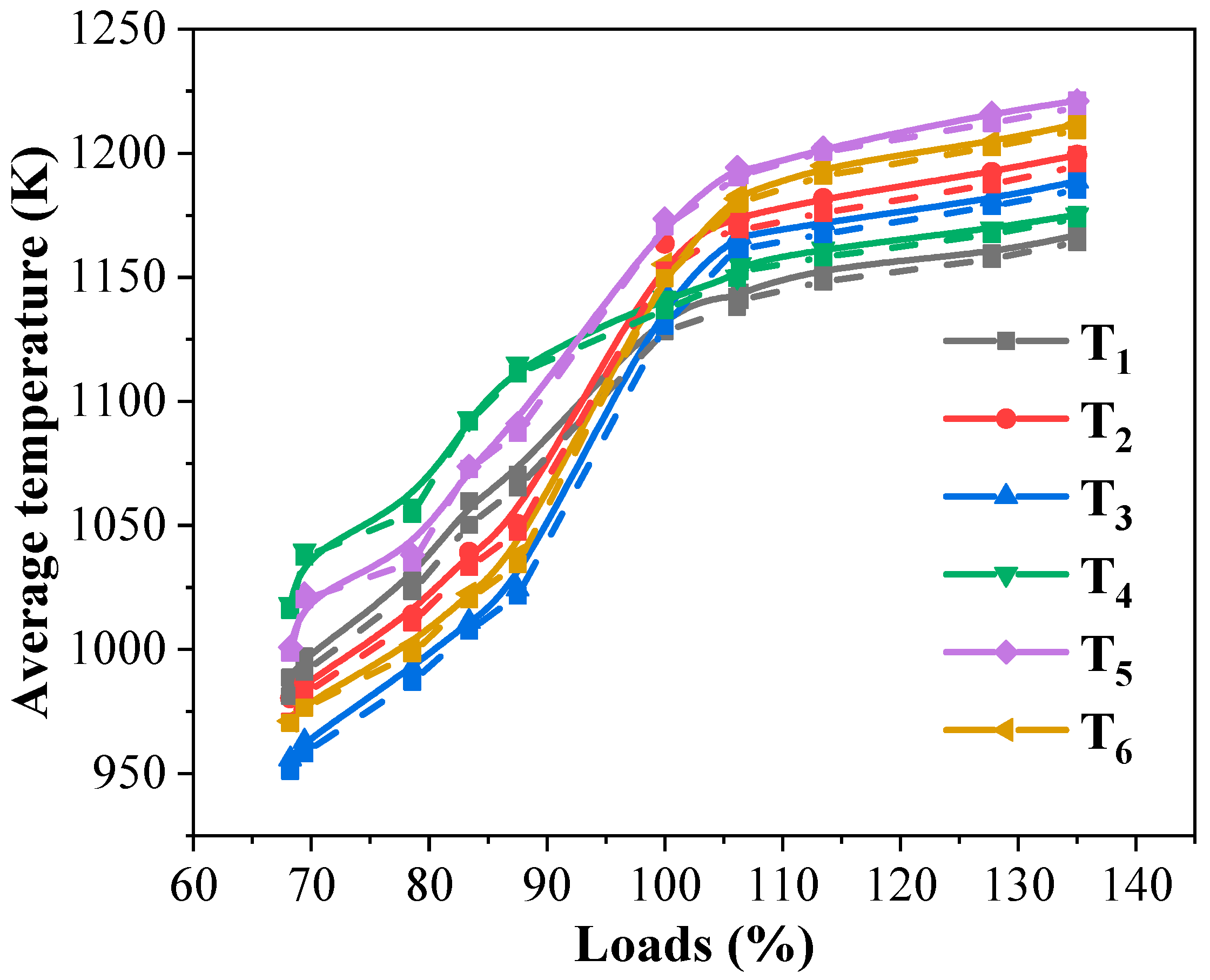
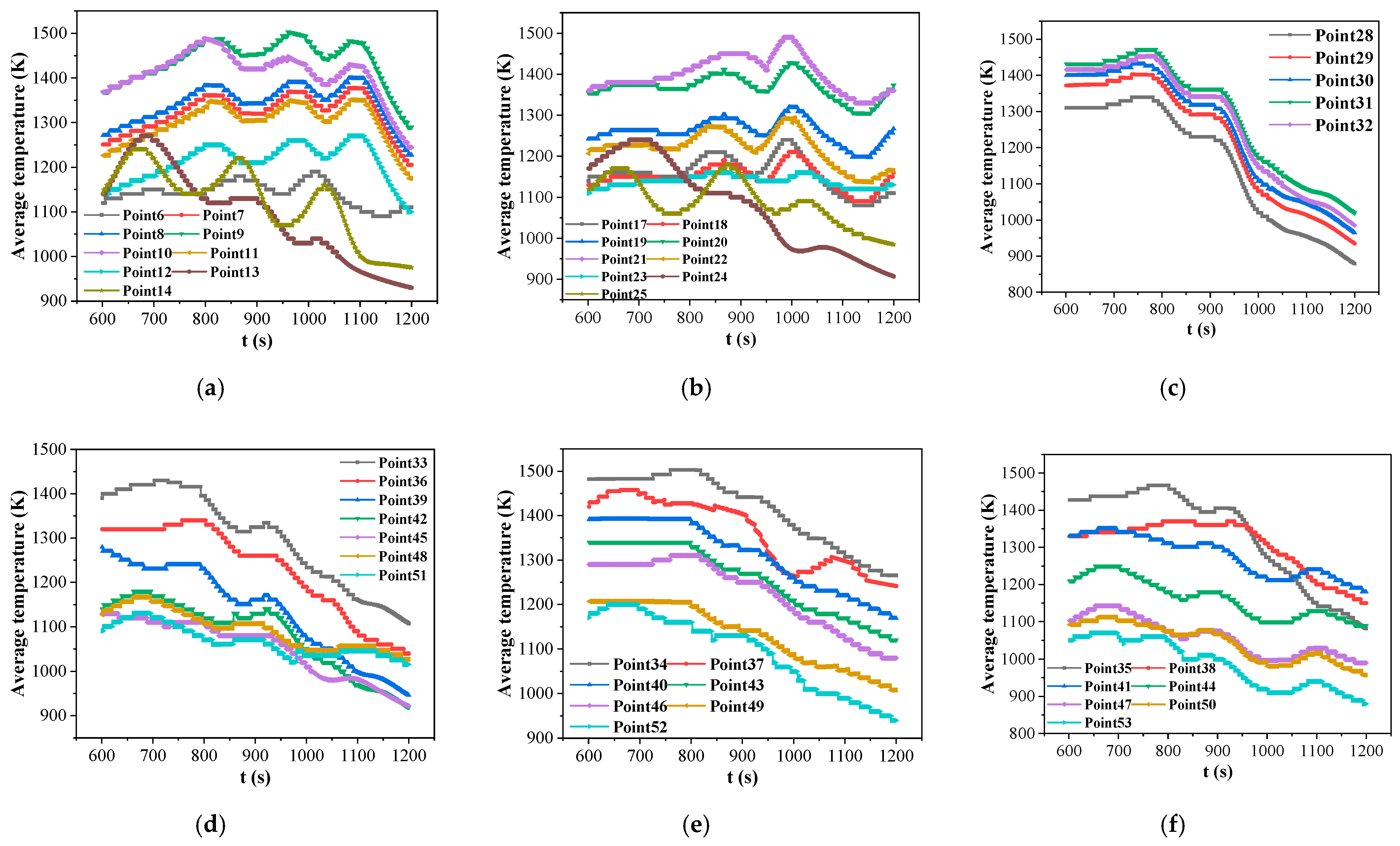
2.4. Validation

According to the data collected on-site on a 500 t/d mechanical grate incinerator in an incineration plant in Shanghai, China, the average temperature of six temperature measuring points under different loads within six months was recorded. The temperature measuring points T₁, T₂, T₃, T₄, T₅, and T₆ are shown in Figure 1b. The heights of the furnace center and the drying section grate are 16 m and 13 m, respectively, with an interval of 1.5 m.

To verify the accuracy of the simulation results, the field data collected at 6 temperature measuring points under the same load were selected for comparison with the simulation results. Figure 2 displays a curve chart comparing the simulated data and the measured data of the temperature measuring points under different loads. As can be seen from Figure 2, the error between the simulation results and the data on the six temperature measuring points of the furnace on-site is less than 0.6%, much smaller than the engineering tolerance of 20% [21]. It can be considered that the numerical simulation results are consistent with the trend results of the test data collected on-site, so the selected simulation model is credible.

3. Results and Discussion

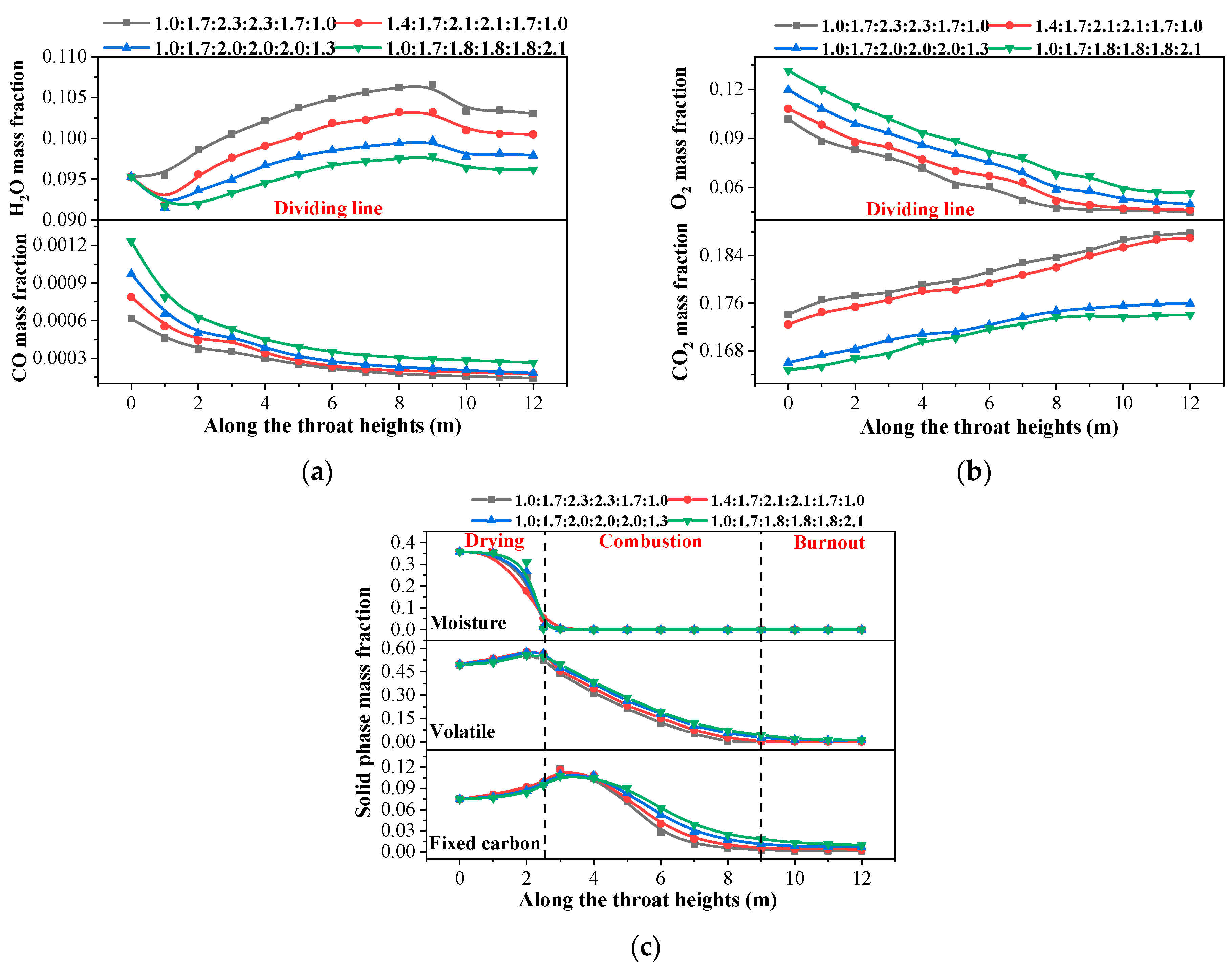
3.1. Effects of Primary Air Proportion on MSW Incineration Status

According to the rated operating condition calculation model, the combustion conditions of the incinerator under different primary air proportions of 1.0:1.7:2.3:2.3:1.7:1.0, 1.4:1.7:2.1:2.1:1.7:1.0, 1.0:1.7:2.0:2.0:2.0:1.3, and 1.0:1.7:1.8:1.8:1.8:2.1 are calculated to study the combustion differences in the incinerator under different operating conditions. The different air proportions refer to the primary air volume of 70,000 Nm³/h, the temperature of 493 K, and the air distribution in six air chambers. The other operating conditions are the same. Under Q = 100%, d = 15 mm, and M = 35%, the influence of the primary air proportion on the combustion state in the incinerator is studied.

Figure 3a shows the temperature distribution and velocity vector cloud diagram of the center section of the furnace under different primary air proportions. As illustrated in Figure 3a,b, increasing the air volume in the drying section leads to a gradual decrease in the overall gas-phase temperature in the furnace by 1.12% to 5.54%. This occurs because the higher air proportion in the drying section enhances turbulence intensity, increasing the mass transfer rate. Consequently, the moisture in MSW is more rapidly transferred to the gas phase. Since water evaporation is an endothermic process, it absorbs heat from the furnace, resulting in a lower gas-phase temperature. The range of the high-temperature combustion zone also decreases, primarily because the increased air proportion in the drying section reduces the air proportion in the combustion section, lowering combustion intensity.

Compare (iii) and (iv) in Figure 3a, an increase in the air proportion in the burnout section forms a small high-temperature zone in the grate burnout section. This is due to the enhanced O₂ supply in the burnout section, which allows incompletely burned combustibles to continue burning under sufficient O₂ conditions. Combining the observations from Figure 3a,b, it is evident that increasing only the air proportion in the drying or burnout section results in a lower overall furnace temperature. Therefore, the air proportion in the combustion section is crucial for maintaining flue gas temperature. To ensure the complete combustion of MSW in the incinerator, the air proportion in the combustion section must be optimized. This optimization should provide adequate oxygen supply while preventing excessively low furnace temperatures due to excessive air volume, thereby improving combustion efficiency and the burnout rate of combustibles.

Figure 3b shows the average temperature curve along the furnace height under different primary air proportions. As can be seen that when the primary air proportion is 1.0:1.7:2.3:2.3:1.7:1.0, 1.4:1.7:2.1:2.1:1.7:1.0, 1.0:1.7:2.0:2.0:2.0:1.3, and 1.0:1.7:1.8:1.8:1.8:2.1, the average temperature of the flue gas at the outlet is 1158 K, 1143 K, 1130 K, and 1126 K, respectively. A large amount of secondary air at the throat enters the flue at a speed of 38.4 m/s and the circulating air at a speed of 43.6 m/s. The temperature near the throat decreases in a short time. As the secondary combustion proceeds, the temperature rises again in a short time. As the air volume of the primary air-drying section increases and the air volume of the combustion section decreases, the flue outlet temperature gradually decreases. An increase in the air volume of the burnout section will also make the outlet temperature lower.

Figure 4 shows the distribution of the gas and solid phases at the height from the throat of the furnace under the primary air proportion. Figure 4a shows the distribution of water vapor and CO mass fractions, Figure 4b shows the distribution of O₂ and CO₂ mass fractions, and Figure 4c shows the distribution of moisture, volatile, and fixed carbon in MSW. Figure 4 shows that as the furnace height increases, the water vapor mass fraction generally decreases first, then gradually increases, and finally returns to a flat trend. The CO and O₂ mass fractions decrease as they are farther from the throat. On the contrary, the CO₂ mass fraction increases. The water vapor mass fraction decreases at a distance closer to the throat. This is because the combustibles in MSW begin to burn. Due to the need for combustion, water vapor may be partially reduced or consumed, resulting in a decrease in the water vapor mass fraction. The addition of secondary air at the throat further promotes combustion. At the same time, excess air also causes the dilution of water vapor [45]. Subsequently, the small molecular combustible gas analyzed by volatilization reacts with oxygen, and combustion gradually generates CO₂ and H₂O, causing the water vapor and CO₂ mass fractions to increase. Until the small molecule gas reacts completely, the mass fractions of water vapor and CO₂ gradually tend to be flat. An increase in the air volume in the drying section means that there is a decrease in the air volume in the combustion section, which in turn affects the temperature distribution in the furnace, thereby reducing the combustion efficiency and producing more CO. However, the addition of secondary air at the throat provides more oxygen, which helps to further oxidize the CO in the furnace into CO₂, and the mass fraction of O₂ also decreases.

As shown in Figure 4c, the mass fractions of moisture, volatile, and fixed carbon in MSW under different primary air proportions are constantly decreasing along the bed. After MSW enters the incinerator, heat is transferred from the high-temperature area in the furnace to MSW in the drying section by heat conduction and convection, so the moisture in MSW is converted into water vapor, the volatile is decomposed by heat, and the fixed carbon is burned. As the main area of incineration, the combustion section requires enough O₂ to participate in combustion. Due to the reduction in the air volume ratio in the combustion section, the overall temperature in the furnace drops, and the time for the complete evaporation of moisture and the distance required for complete evaporation are extended. Therefore, the distance for volatile analysis and the start of fixed carbon combustion is also relatively delayed.

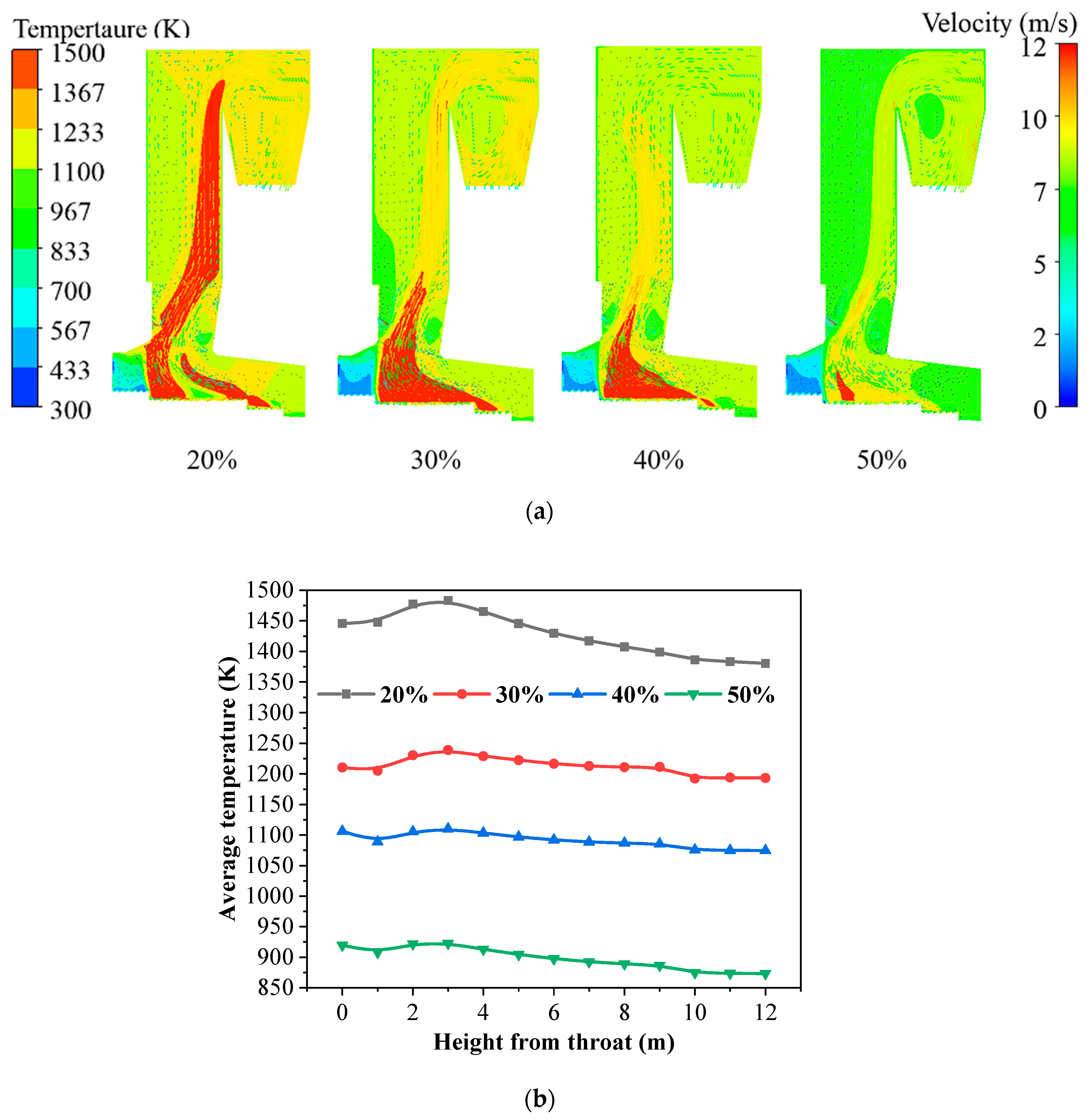
3.2. Effects of Moisture Content on MSW Incineration Status

To further illustrate the effects of moisture content on the combustion efficiency of the incinerator, the effects of different moisture contents (M) of MSW on the combustion in the incinerator were studied under the conditions of a primary air proportion of 1:1.7:2.3:2.3:1.7:1, Q = 100%, and d = 15 mm. Figure 5a shows the temperature distribution and velocity vector cloud diagram of the center section of the furnace at different moisture contents. Figure 5b shows the average temperature curve along the furnace height at different moisture contents.

As shown in Figure 5a,b, as the moisture content of MSW increases, the average temperature in the incinerator gradually decreases by 13.56%~37.79%. This is because water evaporation is an endothermic process that absorbs heat, reducing the heat available for combustion and thus lowering combustion efficiency. The high-temperature area also diminishes, and the increased moisture content reduces the calorific value of MSW. Since water itself does not burn and its evaporation requires energy, this further reduces the amount of heat available for the combustion of combustible materials. Additionally, due to the movement of the grate, the flames exhibit distinct S-shaped oscillations of varying sizes, leading to uneven temperature distribution in the furnace. This finding aligns with the conclusions of Ma et al. [46]. Higher moisture content in MSW worsens mass transfer and heat transfer effects, delays the area where water evaporates completely, and diverts part of the heat in the combustion section to evaporate water. This reduces the amount of air involved in combustion and significantly lowers the gas-phase temperature.

As shown in Figure 5b, at the flue outlet, the flue gas temperatures under the conditions of 20%, 30%, 40%, and 50% are 1480 K, 1300 K, 1082 K, and 873 K, respectively. An increase in the moisture content of MSW does reduce the temperature of the incinerator, but this does not mean that the lower the moisture content, the better. Too high a moisture content may lead to too low a temperature during the combustion process, which is not conducive to the complete combustion of MSW and increases the amount of harmful gasses.

Figure 6 shows the gas- and solid-phase distribution at different MSW moisture contents in the direction of the furnace throat height, Figure 6a shows the water vapor and CO mass fraction distribution, Figure 6b shows the O₂ and CO₂ mass fraction distribution, and Figure 6c shows the water, volatile, and fixed carbon distribution in MSW. Figure 6 shows that as the furnace height increases, the water vapor gradually increases and finally returns to a flat trend. The farther from the throat, the lower the CO and O₂ mass fractions, and the larger the CO₂ mass fraction. Since the addition of secondary air provides enough oxygen to promote the combustion process, making the combustion more complete, more water vapor and CO₂ are generated in the middle of the furnace, O₂ is gradually consumed, and CO is further oxidized to generate CO₂. Until the combustible small molecule gas reacts completely, the components gradually tend to be flat. As the MSW moisture content increases, the overall average temperature in the furnace gradually decreases, and the distance for the complete evaporation of water is prolonged, resulting in a relatively delayed volatile analysis and fixed carbon combustion distance, and the rate of water vapor generation gradually decreases. The release of volatiles and the combustion of fixed carbon are inhibited, and incomplete combustion is likely to produce CO. High moisture content may cause the surface of the material to become wet, hindering the release of volatiles, reducing the rate of precipitation and combustion of volatiles and fixed carbon, as well as the mass fraction of consumed O₂. For MSW with a lower moisture content, the evaporation of water consumes less heat, has a higher thermal efficiency, and produces more CO₂ during combustion. With an increase in the moisture content of MSW, the average temperature decreases, and the incomplete combustion of fuel in the combustion chamber increases. The distance delay for the complete evaporation of moisture causes a relatively delayed position for the precipitation of volatiles and the combustion of fixed carbon. The higher the moisture content, the higher the mass fraction of the volatiles and fixed carbon that are not completely burned in the burnout stage.

3.3. BP Neural Network Model of Flue Gas Temperature Based on Time Domain Input

Since the actual combustion process of the incinerator is dynamic combustion, the grate of the incinerator has a periodic motion of moving forward and backward, which causes the combustion situation in the furnace to change constantly with the movement of the grate. Consider building a dynamic combustion BP neural network model in which the furnace temperature changes with time under rated conditions to achieve the real-time online prediction of future changes in furnace combustion trends. Therefore, the input layer of the model consists of a single node, while the output layer comprises 53 nodes, representing the temperatures at 53 distinct temperature measurement points, as illustrated in Figure 1. In the furnace temperature BP neural network model based on time domain input, the number of hidden layer neurons ranges from 9 to 18. This study begins with 9 hidden layer neurons and progressively increases the number to 18 to evaluate the impact of different hidden layer neuron counts on model error. Ultimately, the number of hidden layer neurons that yields the smallest mean square error is selected as the final configuration. The mean square error is calculated using the following Formula (16):

$$MSE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{(f(x_i)-y_i)}^2}$$

(16)

In this equation, f(x_i) represents the output data in the original data set, n is the number of training samples, and y_i represents the output data after training.

The neural network model in this study is constructed using a data set derived from CFD simulations under different working conditions. Data are sampled at a frequency of one sample per second, resulting in a total of 660 data points. The data set is divided into training and testing sets, with 80% allocated for training and the remaining 20% reserved for testing. To prevent neurons from reaching an oversaturated state, normalization is applied to both the training and testing data sets using the Python 3.11 NumPy library. The normalization process scales the data to the range [0, 1], as shown in Equation (17).

During the training phase, the Sigmoid activation function is selected, and the training parameters are set as follows: the number of iterations is 10,000, the learning rate is 0.01, and the error threshold is 0.001. The performance of the BP neural network model is evaluated using the mean square error (MSE), mean absolute error (MAE), and determination coefficient (R²); see Formulas (18) and (19).

$$y={\displaystyle \frac{(y_{max}-y_{min})(x-x_{min})}{x_{max}-x_{min}}}+y_{min}$$

(17)

$$MSE={\displaystyle \sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}/n$$

(18)

$$MAE={\displaystyle \sum \left|Y_i-\widehat{Y}\right|}/n$$

(19)

In these equations, x represents the selected data; y is the output value; $x_{min}$ and $x_{max}$ are the minimum and maximum values in the data; $y_{min}$ and $y_{max}$ are 0 and 1. Y_i represents the output data in the original data set, $\overline{Y}$ represents the average output data in the original data set, $\widehat{Y}$ represents the output data after training, and n is the number of data.

All neural network algorithms in this study are implemented based on Pytorch 2.0. The optimizer setting uses the corrected adaptive moment estimation method (Adam) to dynamically adjust the adaptive learning rate. The training process of all networks is completed by NVIDIA GeForce RTX 4090 D GPU(NVIDIA Corporation, Santa Clara, CA, USA). The prediction calculation time for each sample is about 10 mi. The mean square error and standard deviation obtained for different numbers of hidden layer neurons are shown in Figure 7a. The lower the MSE, the more accurate the prediction of the model. When the number of hidden layer neurons is set to 18, the function approximation effect is the best, with MSE = 0.0160. Figure 7b shows the MSE and MAE of the training set and the test set. After multiple trainings, the MSE is as low as 1.629% and 1.635%, and the MAE is as low as 0.069% and 0.068%. The MSE and MAE of the training set and the test set are very close, which shows that the model performs similarly on the training set and the test set, without obvious overfitting or underfitting.

Using the trained neural network, the temperature of 53 temperature measuring points is predicted in the time domain, as shown in Figure 8. Since the temperature of temperature measuring points 1–6 does not change much, they are not predictions. The temperature of the other 47 temperature measuring points changes periodically with time, with a period of about 120 s. In the same period, as the grate continues to advance and retreat, the temperature of temperature measuring points 1–14, 15–25, and 26–32 shows a trend of first decreasing and then increasing due to their proximity to the grate. This is because, during the grate advancement process, MSW is pushed into the furnace. In the early stages, due to the moisture and low temperature of MSW, the temperature of the temperature measuring point decreases. As MSW combustion progresses, the furnace temperature gradually increases. The measured temperatures 33–53 show a trend of first increasing and then decreasing. This trend is due to their location: these points are far away from the material inlet and close to the secondary air inlet. As the grate moves, the furnace flame shows an S-shaped oscillation, causing the temperature to show the same change. Using a trained neural network to predict the temperature in the time domain can effectively capture the periodic changes and fluctuations in the temperature in the furnace. This prediction is of great significance for optimizing the incineration process, controlling pollutant emissions, and improving energy recovery efficiency.

4. Conclusions

This study aimed to enhance the incineration efficiency of MSW through a comprehensive simulation and experimental analysis of a 500 t/d mechanical grate incinerator. By integrating simulation results verified with on-site data, the impacts of moisture content and primary air proportion on both solid bed and gas-phase combustion were investigated. Additionally, a BP neural network model was developed to predict the relationship between furnace temperature and grate movement. The conclusions are as follows:

• Increasing the air proportion in the drying section accelerates the evaporation of moisture. In contrast, decreasing the air proportion in the combustion section lowers the average temperature by 59 K and extends the distance required for complete combustion by 0.5–2 m. Meanwhile, increasing the air proportion in the burnout section promotes the further combustion of unburned volatiles and fixed carbon.
• Higher moisture content in MSW reduces the average temperature and increases incomplete combustion, significantly raising CO emissions (by 79% at 50% moisture compared to 20%). The optimal combination parameters are as follows: the primary air proportion is 1:1.7:2.3:2.3:1.7:1, and M = 30%.
• A dynamic BP neural network model was successfully developed to predict the relationship between furnace temperature and grate movement. The model demonstrated high accuracy, with a minimum MSE of 1.629% and 1.635% during training and an MAE of approximately 0.069% and 0.068%. This model effectively captures nonlinear relationships and maintains high prediction accuracy under new operating conditions.
• The novelty of this study lies in the integrated approach combining computational simulation and on-site data to optimize incineration parameters and the application of artificial intelligence for the real-time prediction of combustion trends. Future work will focus on integrating advanced AI technologies with incinerator systems to dynamically adjust operational parameters based on actual conditions, further improving the efficiency and environmental performance of MSW incineration.