Extended State Observer Based Robust Nonlinear PID Attitude Tracking Control of Quadrotor with Lumped Disturbance
Abstract
1. Introduction
2. Quadrotor Attitude Dynamics
2.1. Attitude Dynamics
2.2. Useful Properties
3. Controller Design
3.1. Objective
3.2. Disturbance Estimation
3.3. Attitude Tracking Control
4. Simulation and Experimental Results
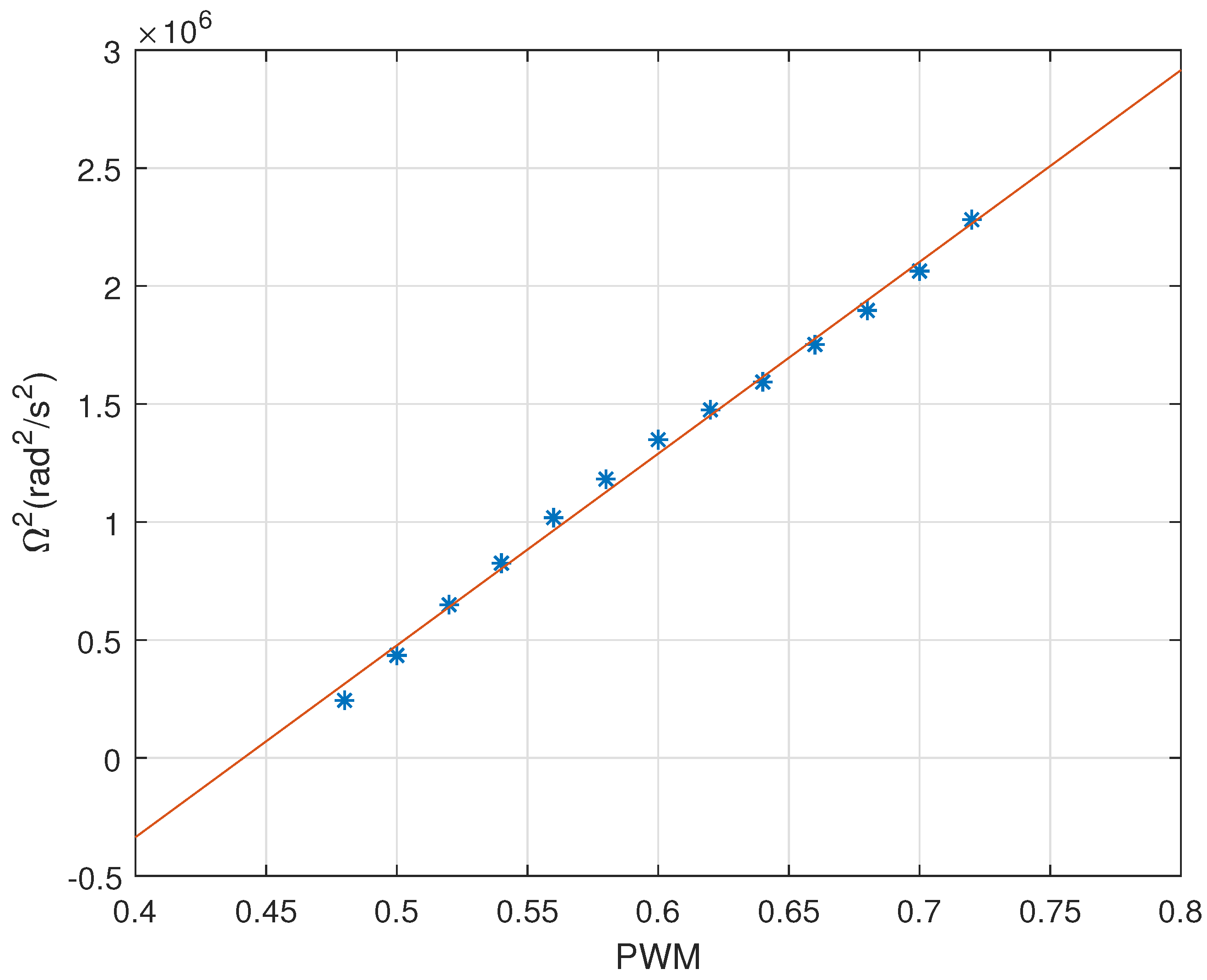
4.1. Parameters
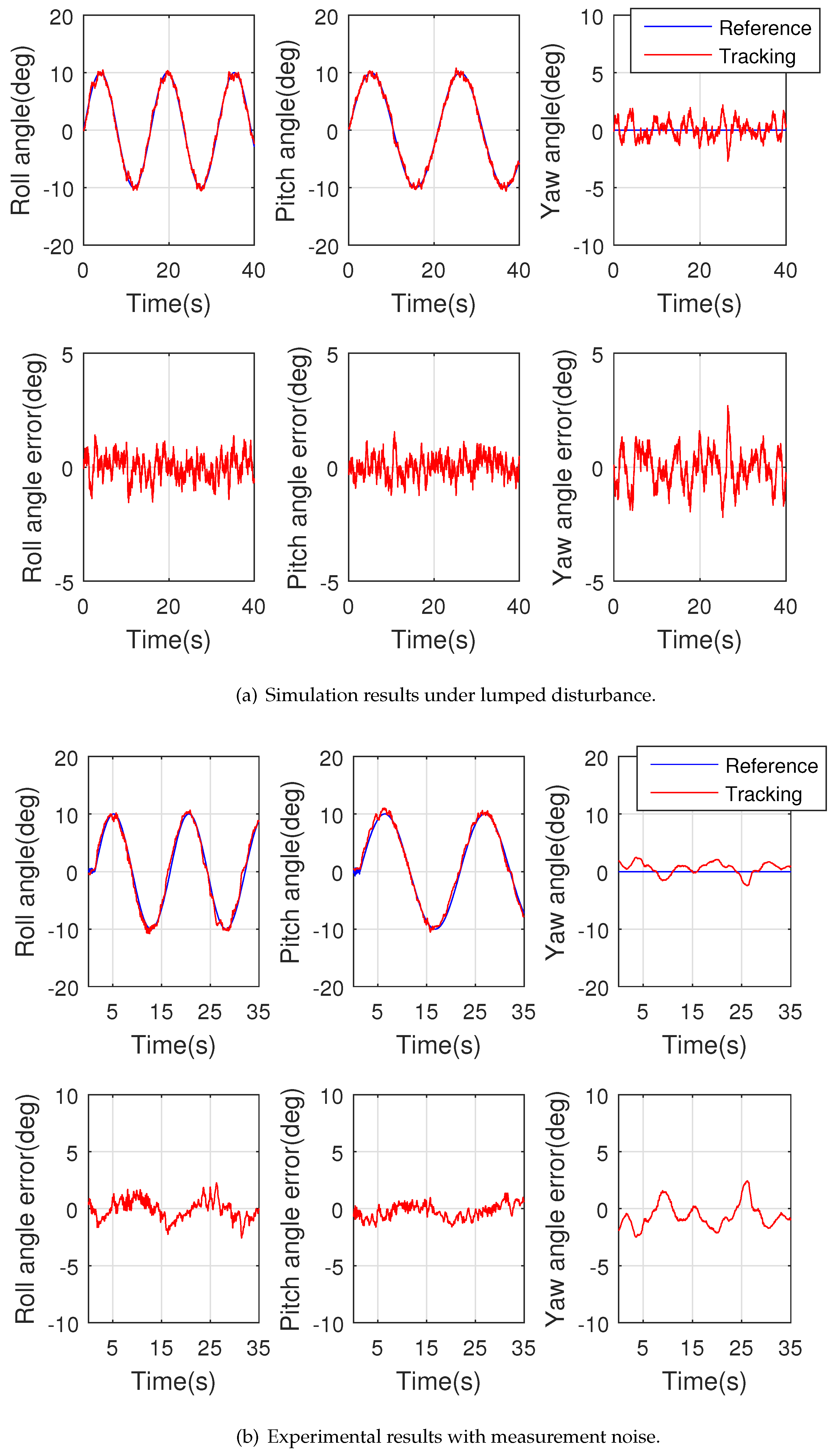
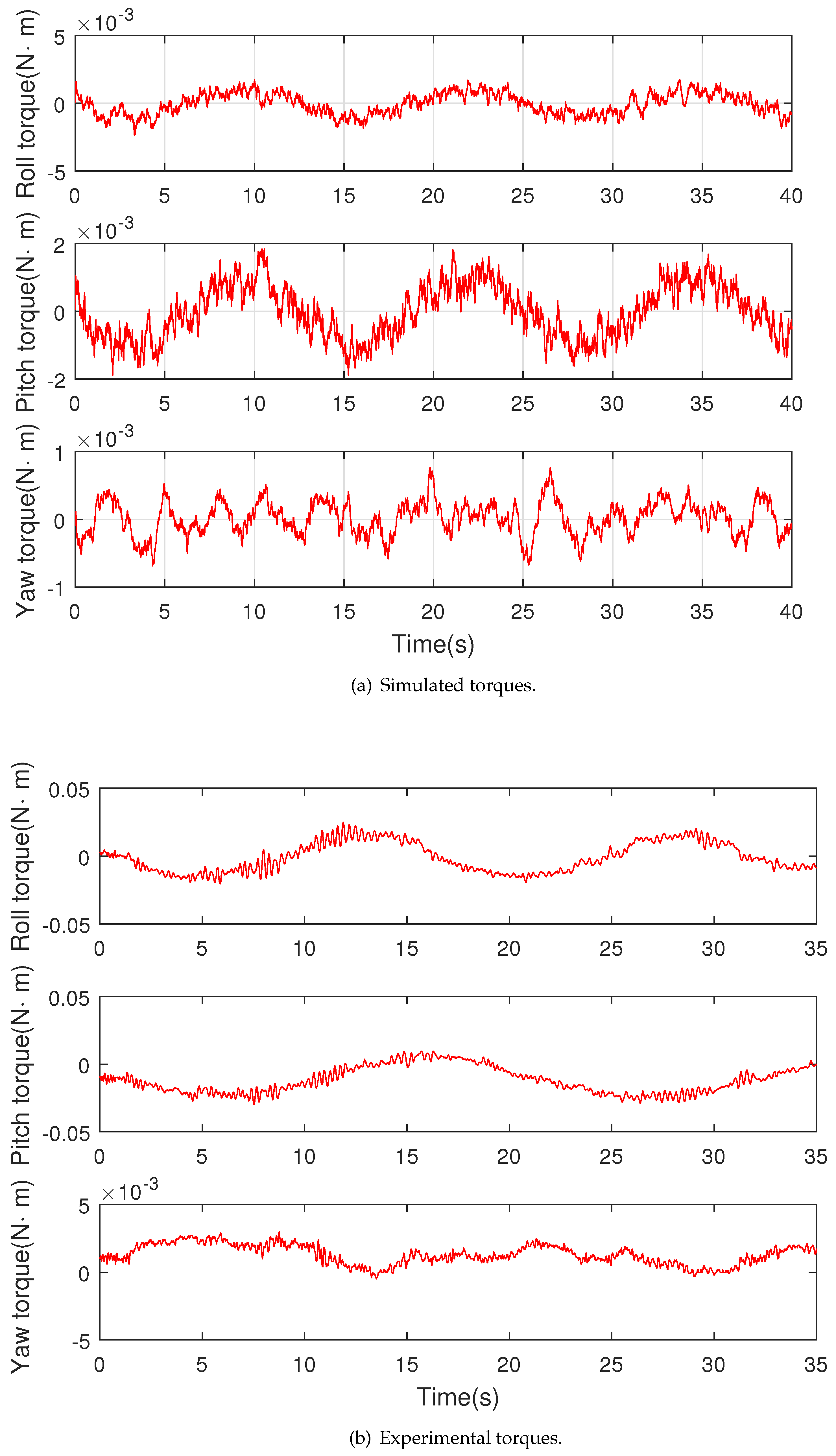
4.2. Simulation Results
4.3. Experimental Results
4.3.1. Attitude Tracking Control
4.3.2. Attitude Stabilization with Disturbance Torque
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bui, D.N.; Van Nguyen, T.T.; Phung, M.D. Lyapunov-based nonlinear model predictive control for attitude trajectory tracking of unmanned aerial vehicles. Int. J. Aeronaut. Space Sci. 2023, 24, 502–513. [Google Scholar] [CrossRef]
- Lopez-Sanchez, I.; Pérez-Alcocer, R.; Moreno-Valenzuela, J. Trajectory tracking double two-loop adaptive neural network control for a Quadrotor. J. Frankl. Inst. 2023, 360, 3770–3799. [Google Scholar] [CrossRef]
- Lopez-Sanchez, I.; Moyrón, J.; Moreno-Valenzuela, J. Adaptive neural network-based trajectory tracking outer loop control for a quadrotor. Aerosp. Sci. Technol. 2022, 129, 107847. [Google Scholar] [CrossRef]
- Lopez-Sanchez, I.; Moreno-Valenzuela, J. PID control of quadrotor UAVs: A survey. Annu. Rev. Control 2023, 56, 100900. [Google Scholar] [CrossRef]
- Hong, K. Simulation and analysis of stability of UAV control system based on PID control under different wind forces. J. Phys. Conf. Ser. 2023, 2649, 012011. [Google Scholar] [CrossRef]
- Ghanifar, M.; Kamzan, M.; Tayefi, M. Different Intelligent Methods for Coefficient Tuning of Quadrotor Feedback-linearization Controller. J. Aerosp. Sci. Technol. 2023, 16, 56–65. [Google Scholar]
- Najm, A.A.; Ibraheem, I.K. Nonlinear PID controller design for a 6-DOF UAV quadrotor system. Eng. Sci. Technol. Int. J. 2019, 22, 1087–1097. [Google Scholar] [CrossRef]
- Jin, G.G.; Pal, P.; Chung, Y.K.; Kang, H.K.; Yetayew, T.T.; Bhakta, S. Modelling, control and development of GUI-based simulator for a quadcopter using nonlinear PID control. Aust. J. Electr. Electron. Eng. 2023, 20, 387–399. [Google Scholar] [CrossRef]
- Wang, S.; Polyakov, A.; Zheng, G. Quadrotor stabilization under time and space constraints using implicit PID controller. J. Frankl. Inst. 2022, 359, 1505–1530. [Google Scholar] [CrossRef]
- Najm, A.A.; Azar, A.T.; Ibraheem, I.K.; Humaidi, A.J. A Nonlinear PID Controller Design for 6-DOF Unmanned Aerial Vehicles; Academic Press: Cambridge, MA, USA, 2021; pp. 315–343. [Google Scholar]
- Moreno-Valenzuela, J.; Pérez-Alcocer, R.; Guerrero-Medina, M.; Dzul, A. Nonlinear PID-type controller for quadrotor trajectory tracking. IEEE/ASME Trans. Mechatron. 2018, 23, 2436–2447. [Google Scholar] [CrossRef]
- Zhu, B.; Huo, W. Nonlinear control for a model-scaled helicopter with constraints on rotor thrust and fuselage attitude. Acta Autom. Sin. 2014, 40, 2654–2664. [Google Scholar] [CrossRef]
- Jeong, H.; Suk, J.; Kim, S. Control of quadrotor UAV using variable disturbance observer-based strategy. Control Eng. Pract. 2024, 150, 105990. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.; Yang, X. Adaptive fuzzy control of a quadrotor using disturbance observer. Aerosp. Sci. Technol. 2022, 128, 107784. [Google Scholar] [CrossRef]
- Gong, W.; Li, B.; Ahn, C.K.; Yang, Y. Prescribed-time extended state observer and prescribed performance control of quadrotor UAVs against actuator faults. Aerosp. Sci. Technol. 2023, 138, 108322. [Google Scholar] [CrossRef]
- Zhao, K.; Zhang, J.; Shu, P.; Dong, X. Composite Nonlinear Extended State Observer-Based Trajectory Tracking Control for Quadrotor Under Input Constraints. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 4126–4136. [Google Scholar] [CrossRef]
- Guo, B.; Zhao, Z. On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Wang, L.; Pei, H. Geometric prescribed-time control of quadrotors with adaptive extended state observers. Int. J. Robust Nonlinear Control 2024, 34, 7460–7479. [Google Scholar] [CrossRef]
- Li, J.; Cao, C.; Xu, J. An extended state observer-based active disturbance rejection control for quadrotor attitude stabilization. Mechatronics 2022, 85, 102853. [Google Scholar]
- Luo, Y.; Ma, J.; Hu, J. Fault-tolerant tracking control for quadrotor UAV with actuator saturation and multiple uncertainties. ISA Trans. 2023, 134, 373–385. [Google Scholar]
- Zhang, Y.; Ding, S.; Li, Y. Data-driven fault-tolerant tracking control for quadrotor UAV with actuator failure and external disturbance. IEEE Trans. Ind. Electron. 2023, 70, 5962–5972. [Google Scholar]
- Zhao, S.; Li, H.; Wang, L. Active disturbance rejection flight control for quadrotors based on nonlinear extended state observer. Aerospace 2023, 10, 327. [Google Scholar]
- Zhou, Y.; Liu, Z.; Zhang, C. Anti-saturation prescribed-time trajectory tracking control of quadrotors with nonlinear observers. IEEE Trans. Control Syst. Technol. 2024; early access. [Google Scholar]
- Ma, D.; Xia, Y.; Shen, G.; Jiang, H.; Hao, C. Practical fixed-time disturbance rejection control for quadrotor attitude tracking. IEEE Trans. Ind. Electron. 2020, 68, 7274–7283. [Google Scholar] [CrossRef]
- Chen, H.; Du, L.; Zhang, X. A robust disturbance observer-based control approach for quadrotors in uncertain environments. IEEE Access 2022, 10, 59338–59350. [Google Scholar]
- Tang, H.; Yu, M.; Zhang, J. Reduced-order disturbance observer-based trajectory tracking control for quadrotors under bounded uncertainties. Robot. Auton. Syst. 2023, 164, 104383. [Google Scholar]
- Yan, S.; Liu, Q.; Zhang, L. Robust trajectory tracking control of quadrotors under lumped disturbances: Simulation and experiments. Aerosp. Sci. Technol. 2022, 124, 107520. [Google Scholar]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. An integral predictive/nonlinear H∞ control structure for a quadrotor helicopter. Automatica 2010, 46, 29–39. [Google Scholar] [CrossRef]
- Shi, D.; Dai, X.; Zhang, X.; Quan, Q. A Practical Performance Evaluation Method for Electric Multicopters. IEEE/ASME Trans. Mechatron. 2017, 22, 1337–1348. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Luo, S.; Huang, Y.; Deng, X. Extended State Observer Based Robust Nonlinear PID Attitude Tracking Control of Quadrotor with Lumped Disturbance. Processes 2025, 13, 1470. https://doi.org/10.3390/pr13051470
Xu G, Luo S, Huang Y, Deng X. Extended State Observer Based Robust Nonlinear PID Attitude Tracking Control of Quadrotor with Lumped Disturbance. Processes. 2025; 13(5):1470. https://doi.org/10.3390/pr13051470
Chicago/Turabian StyleXu, Gang, Shengping Luo, Yiqing Huang, and Xiongfeng Deng. 2025. "Extended State Observer Based Robust Nonlinear PID Attitude Tracking Control of Quadrotor with Lumped Disturbance" Processes 13, no. 5: 1470. https://doi.org/10.3390/pr13051470
APA StyleXu, G., Luo, S., Huang, Y., & Deng, X. (2025). Extended State Observer Based Robust Nonlinear PID Attitude Tracking Control of Quadrotor with Lumped Disturbance. Processes, 13(5), 1470. https://doi.org/10.3390/pr13051470





