Three-Dimensional Numerical Simulation of Effective Thermal Conductivity and Fractal Dimension of Non-Aqueous Phase Liquid-Contaminated Soils at Mesoscopic Scale

Abstract

In situ thermal desorption is one of the most promising remediation techniques for soils contaminated with non-aqueous phase liquids (NAPLs), but its remediation efficiency is limited by the thermal conductivity (k) of NAPL-contaminated soils. The fractal dimension is an important factor affecting k. To systematically study the influence of the fractal dimension on k, firstly, this research establishes a three-dimensional numerical model of NAPL-contaminated soils and calculates its k. Subsequently, the reliability of the numerical simulation results is verified through experiments. Combining the numerical simulation method with Hausdorff fractal theory, we explored the relationship between the fractal dimension and k. This research shows that k decreases with increasing porosity and increases with increasing saturation. The liquid phase can form a “liquid bridge” between solid phases, greatly shortening the path of heat flux and increasing k. k is more affected by porosity. With the increase in porosity, the pore fractal dimension and liquid phase fractal dimension of NAPL-contaminated soils increase, while the solid phase fractal dimension and pore curvature fractal dimension decrease. The fractal dimension of the liquid phase increases with the increase in NAPL content. k increases with the increase in the solid phase fractal dimension, liquid phase fractal dimension, and pore curvature fractal dimension and decreases with the increase in the pore fractal dimension. This study provides a basis for the investigation of the thermal conductivity of NAPL-contaminated soils and the development of in situ thermal desorption technology.

1. Introduction

With the development of the economy, many petrochemical sites are polluted by NAPLs, which are volatile, difficult to degrade, and often toxic, damaging local ecosystems and endangering human health [1,2,3]. At present, in situ thermal desorption is considered a promising NAPL-contaminated soil remediation technology [4]. Its technical principle is to heat the contaminated soils in situ, separate the pollutants from the soil, and discharge them after centralized treatment [5]. The thermal conductivity of polluted soils is an important factor in the diffusion of heat in polluted soil, which restricts the remediation efficiency of in situ thermal desorption [6]. Soil has a large number of pore structures, which will directly affect the thermal conductivity of NAPL-contaminated soils [7]. This affects the repair efficiency of in situ thermal desorption. There are many studies on the distribution of pore parameters in geotechnical materials and their impact on thermal conductivity from the perspective of fractal geometry theory [8,9,10]. Hu et al. found through experiments that the curvature fractal dimension and fractal tree-like tortuosity characteristics of shale have a negative impact on thermal conductivity [8]. Shen et al. [11] compared the quality fractal dimension with the volume fractal dimension by comparative analysis. The volume fractal dimension formula was found to be more reasonable than the mass fractal dimension formula, and the most reasonable soil particle measurement method was the LD method. Xiao et al. analyzed the effect of the particle size distribution on the thermal conductivity of geotechnical materials through thermal needle experiments and found that the thermal conductivity of the sample increased with the increase in uniformity coefficient and fractal dimension [12]. Li et al. used ANSYS numerical simulation to simulate the thermal conductivity of rock and soil by changing material and element properties combined with the Fourier thermal transformation law [13]. They found that the effective thermal conductivity of rock and soil decreases exponentially with the increase in the volume fractal dimension. Cai et al. used thermal probe experiments and fractal model theory to elucidate the influence of soil structural parameters on thermal conductivity; that is, the influence of the soil fractal dimension and size ratio on thermal conductivity is relatively small, while the randomness of the soil pore structure has a significant impact on its thermal conductivity [14]. Shen et al. compared the effective thermal conductivity of soil media with indoor experiments and found that the pore structure has a significant impact on the thermal conductivity of unsaturated soil [15]. The effective thermal conductivity of soil gradually decreases with the increase in the pore fractal dimension, porosity, and tortuous fractal dimension. Qin et al. studied the theoretical model of soil’s effective thermal conductivity with different pore development characteristics, based on two-dimensional models and fractal geometry theory, and analyzed the influence of the geometric parameters of pores in soils on soils’ effective thermal conductivity [16]. Based on the development and distribution characteristics of root systems in soils, Huang et al. established using fractal theory a thermal resistance-based root–soil thermal conductivity theoretical model for alpine meadows. They studied the effects of the root area-to-total area ratio, area fractal dimension, and tortuosity fractal dimension on soil thermal conductivity in cold grasslands [17].

In summary, previous studies have mainly focused on uncontaminated soils; however, NAPL pollutants can affect the original thermal conductivity of the soils. In addition, the numerical models used in the fractal theory research of soil thermal conductivity are mostly two-dimensional models, and the existing models cannot reflect the real soil structure. This article uses the four-parameter random generation method (QSGS) to construct a three-dimensional soil structure model, and it uses the Lattice Boltzmann method to calculate its thermal conductivity. The reliability of the three-dimensional soil structure model constructed by QSGS was ultimately verified through series parallel models and indoor thermal conductivity testing experiments. The influence of saturation and porosity on k was studied. On this basis, the Hausdorff fractal theory was used to analyze the relationship between the fractal dimension and k, as well as the mechanism of the influence of the fractal dimension on k. This study provides a theoretical basis for the development and application of in situ thermal desorption remediation technology.

2. Materials and Methods

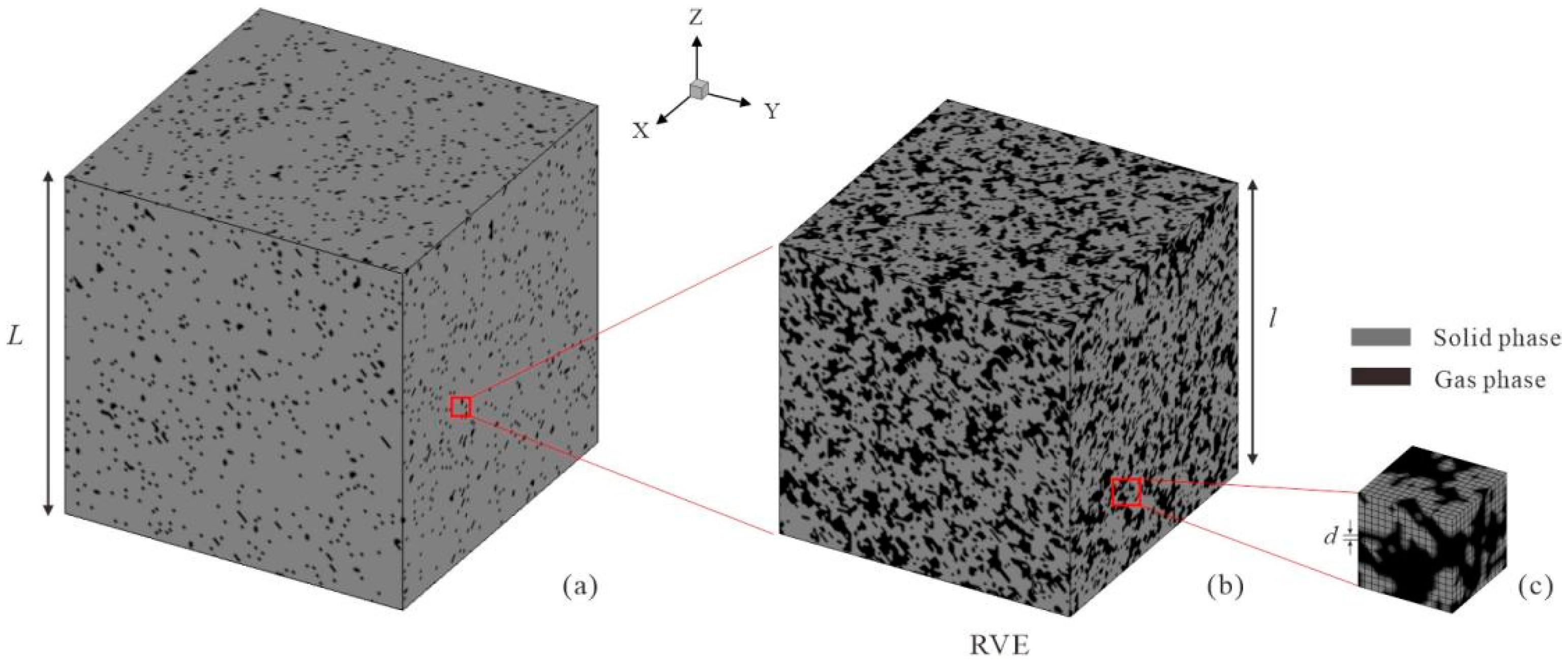
2.1. Materials

We remolded NAPL-contaminated soils by the compaction method [18]. Remolded silty clay samples with a porosity of 35% and diesel content of 8–20% wt.% (not exceeding the liquid limit) were prepared. Finally, we measured the thermal conductivity of the remolded soil samples using a thermal constant analyzer [19]. Figure 1 shows the experimental process.

2.2. Methodology

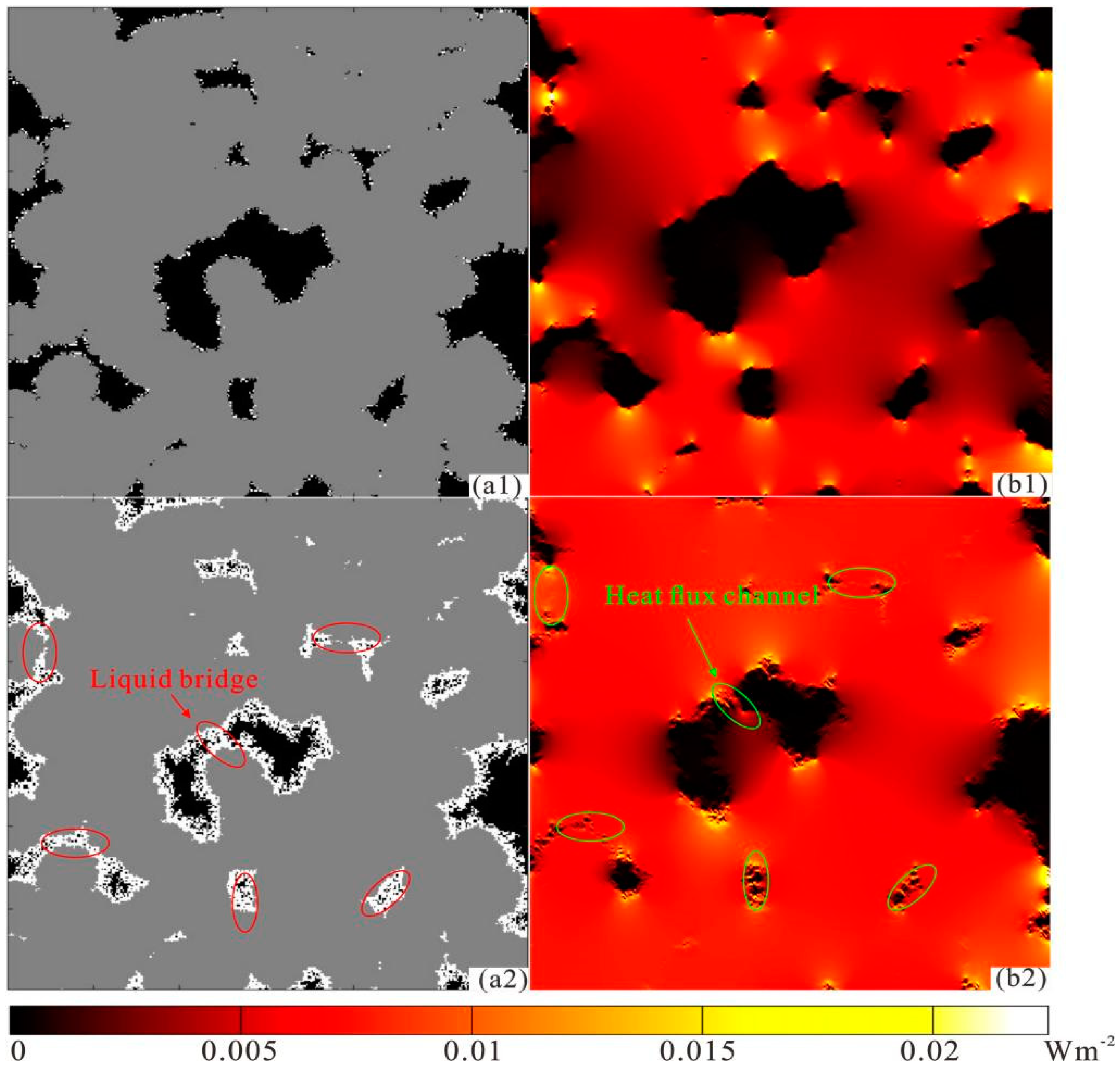
2.2.1. Establishment of NAPL-Contaminated Soil Model

LBM is a mesoscopic method that can be used for calculating heat transfer under multiphase complex boundary conditions [20]. According to the LBM theory, Qian et al. proposed the classical D_dQ_m model [21]. D₃Q₁₉ is the most commonly used 3D model, as shown in Figure 2 [22,23].

RVE is the basis for establishing NAPL-contaminated soil models [18,22,24,25]. As shown in Figure 3, l and L, respectively, represent RVE and the macroscopic dimension of the soil, and d represents the microscopic characteristic dimension of the soil. The porous media model established by QSGS and the real model have high similarity compared with other modeling methods [18]. QSGS controls the structure of soil models through four parameters (C_d, D_i, P_n, and I_i^1,2) [25,26,27]. NAPL-contaminated soil is a special porous medium. The specific parameters are D_i=1–6 = 4D_i=7–18, C_d = 0.02, I_o^o,o = 0.1, I_o^o,s = 0.9 [18,28,29,30].

The model grid established by QSGS is 100 × 100 × 100. The cell size is 1. Meanwhile, the saturation (S_o) is used to normalize the diesel content of different porosity models. The constructed polluted soil model is shown in Figure 4.

2.2.2. Calculation of k

The two planes perpendicular to the X direction are the heating interface and the testing interface, while the four planes parallel to the X direction are the adiabatic boundaries. The temperatures of the test interface and the heating interface are 20 °C and 22 °C, respectively. The heat flow balance method is used to solve the discrete equation of node temperature in the model grid, to determine k. k is obtained by Formula (1).

$$k={\displaystyle \frac{L\cdot {\displaystyle \int q\cdot \mathrm{d}\mathrm{A}}}{\Delta T{\displaystyle \int \mathrm{d}\mathrm{A}}}}$$

(1)

where q is thermal flux; k is the thermal conductivity; the temperature difference between the test interface and heating interface is ΔT; and the distance is L.

The model calculation parameters are k_s = 2.38 Wm⁻¹°C⁻¹ (the thermal conductivity of diesel oil), k_g = 0.024 Wm⁻¹°C⁻¹ (the thermal conductivity of air), and k_o = 0.127 Wm⁻¹°C⁻¹ (the thermal conductivity of soil particles) [18,31,32,33,34,35].

Figure 5 shows the heat flux distribution and temperature field of contaminated soil models with porosities of 25% and 45%.

Figure 6 shows the heat flux distribution and temperature field of contaminated soil models with saturation levels of 0.2 and 0.8.

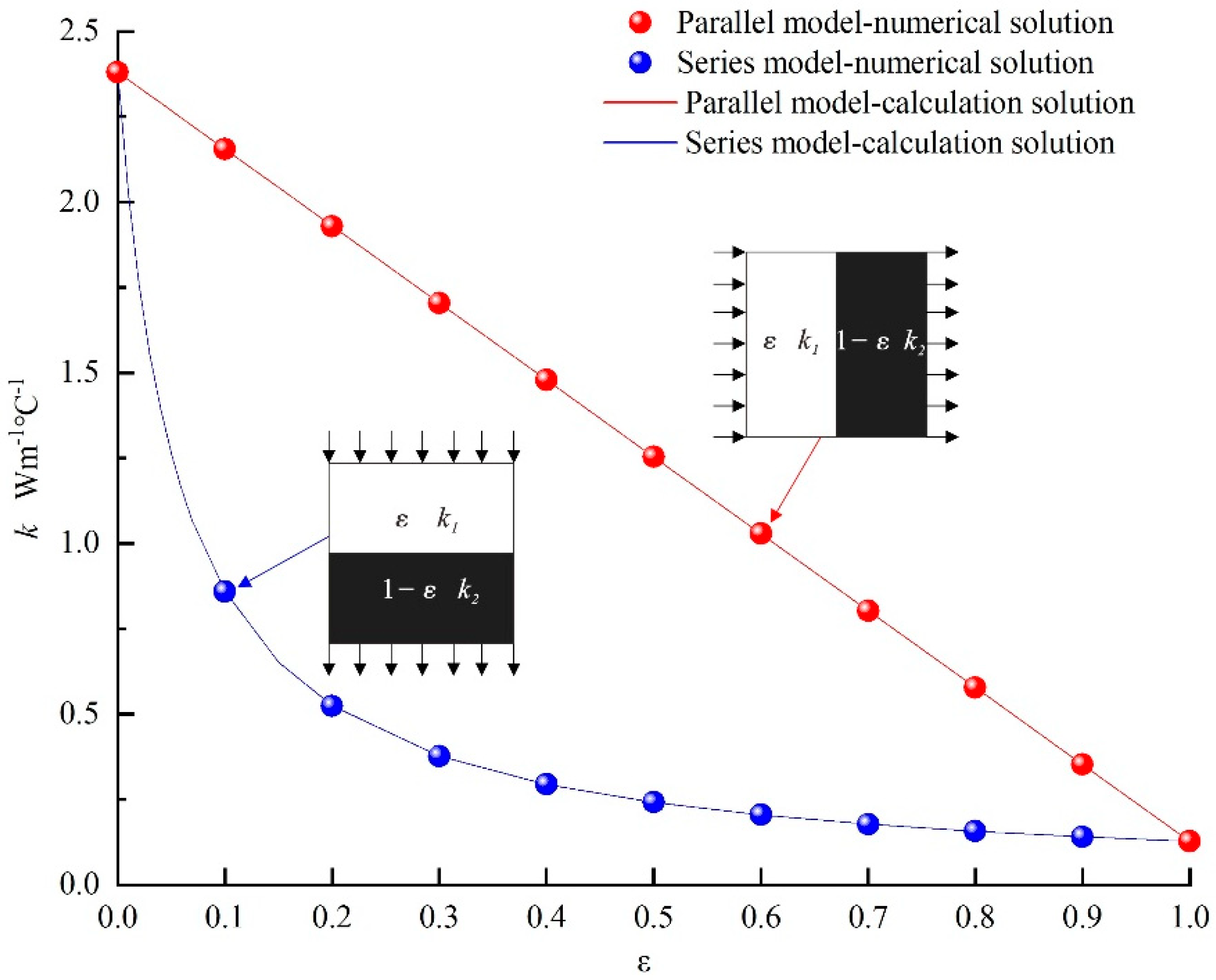
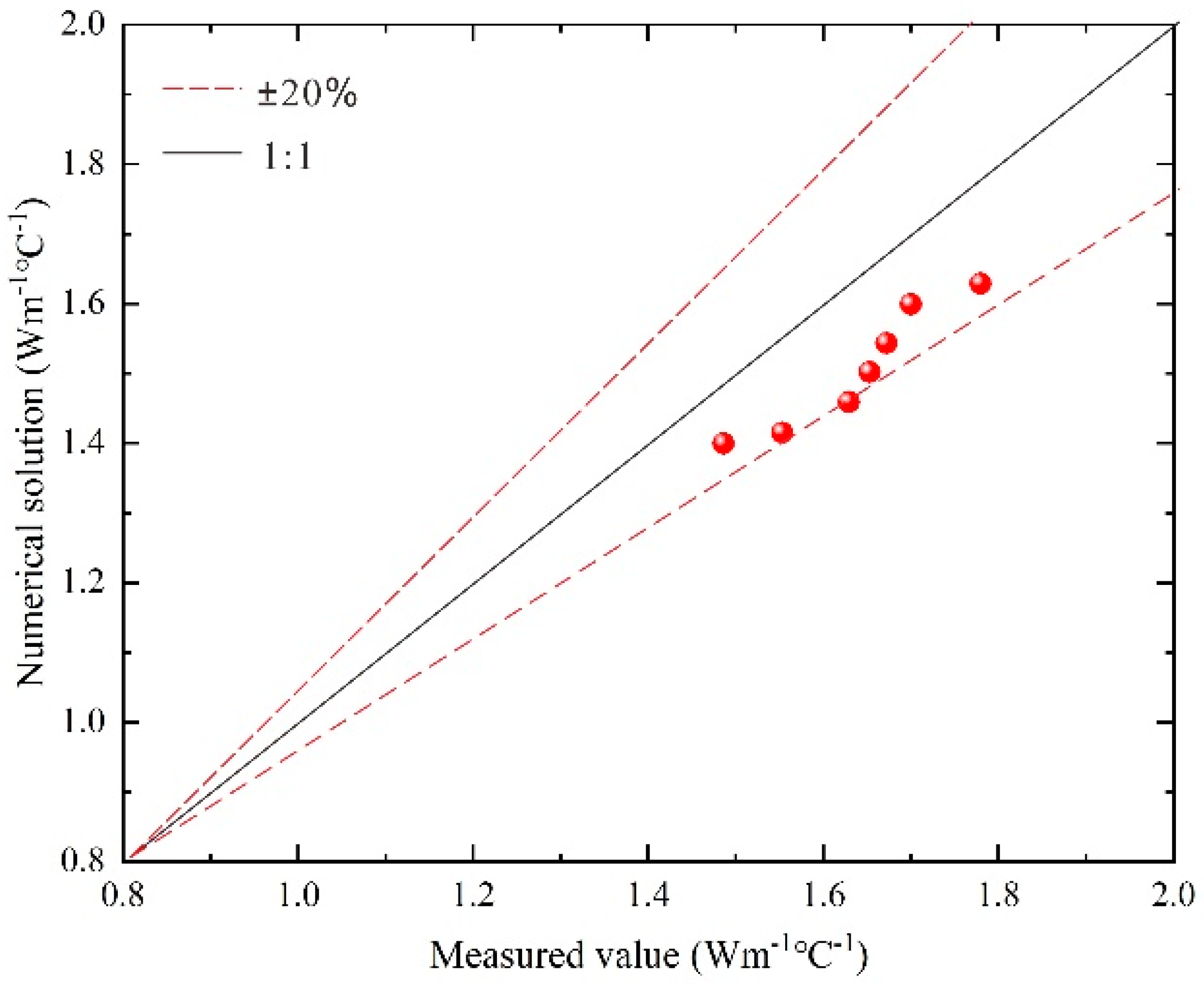
2.3. Verification of Numerical Models

The program is verified in the series mode and parallel mode before numerical simulation [36,37]. The theoretical calculation equation of k in the two basic modes is

$$\left\{\begin{array}{l}k={\displaystyle \frac{1}{\frac{\epsilon }{k_1}+\frac{1-\epsilon }{k_2}}} , \mathrm{Series} \mathrm{model} \hfill \\ k=\epsilon k_1+\left(1-\epsilon \right)k_2 , \mathrm{Parallel} \mathrm{model}\hfill \end{array}\right.$$

(2)

The comparison between the theoretical calculation values and numerical simulation results of the two models is shown in Figure 7. This indicates that the numerical calculation results have high reliability.

The internal structure of the model generated by QSGS is random, so a random seed algorithm is used to fix the structure of the model [20,38]. Finally, the LBM is used to calculate k. As shown in Figure 8, the numerical simulation values of the models fluctuate within ±20% of the measured values, indicating the reliability of the results obtained by the numerical calculation [39].

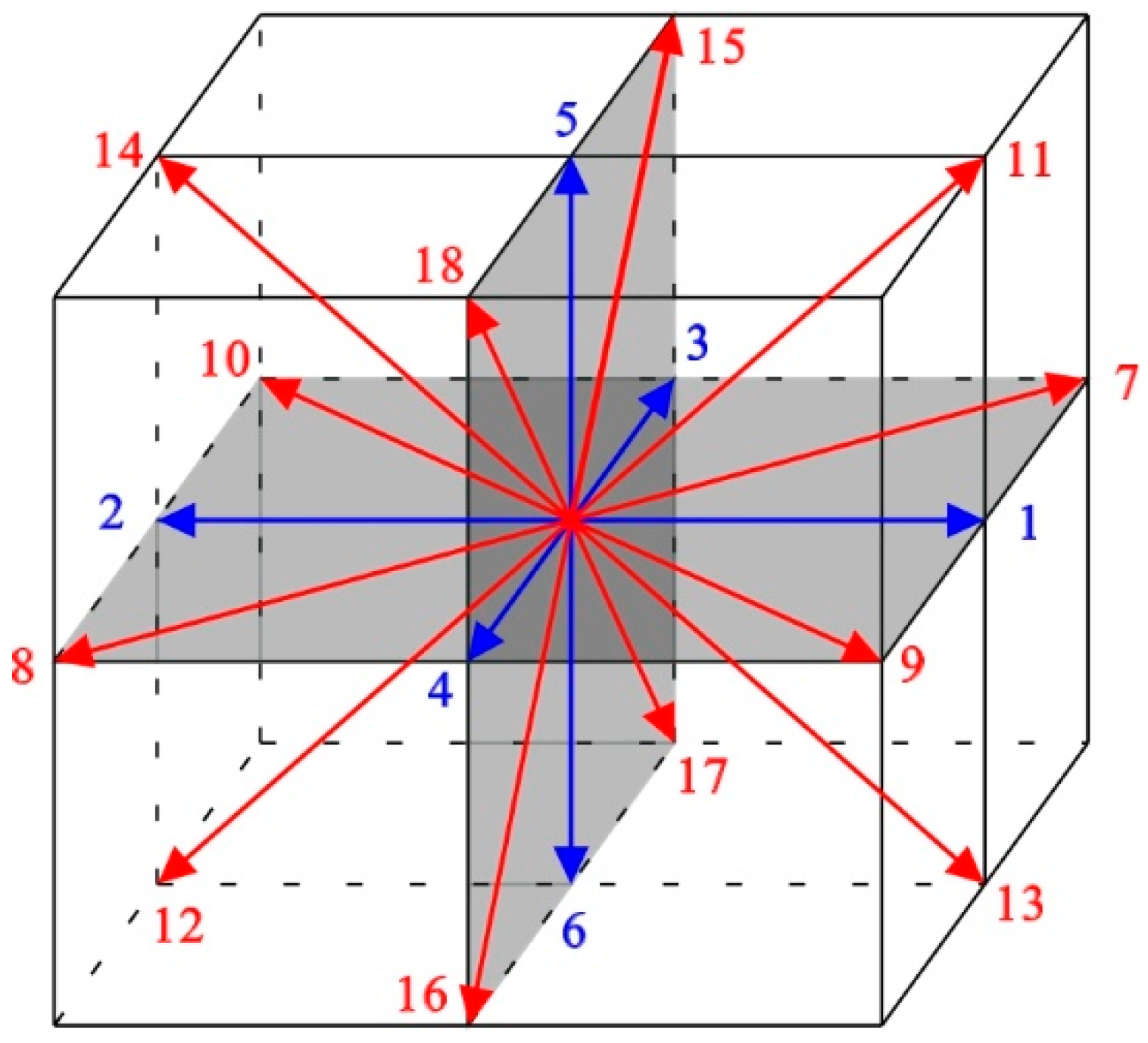
2.4. Hausdorff Fractal Dimension Method

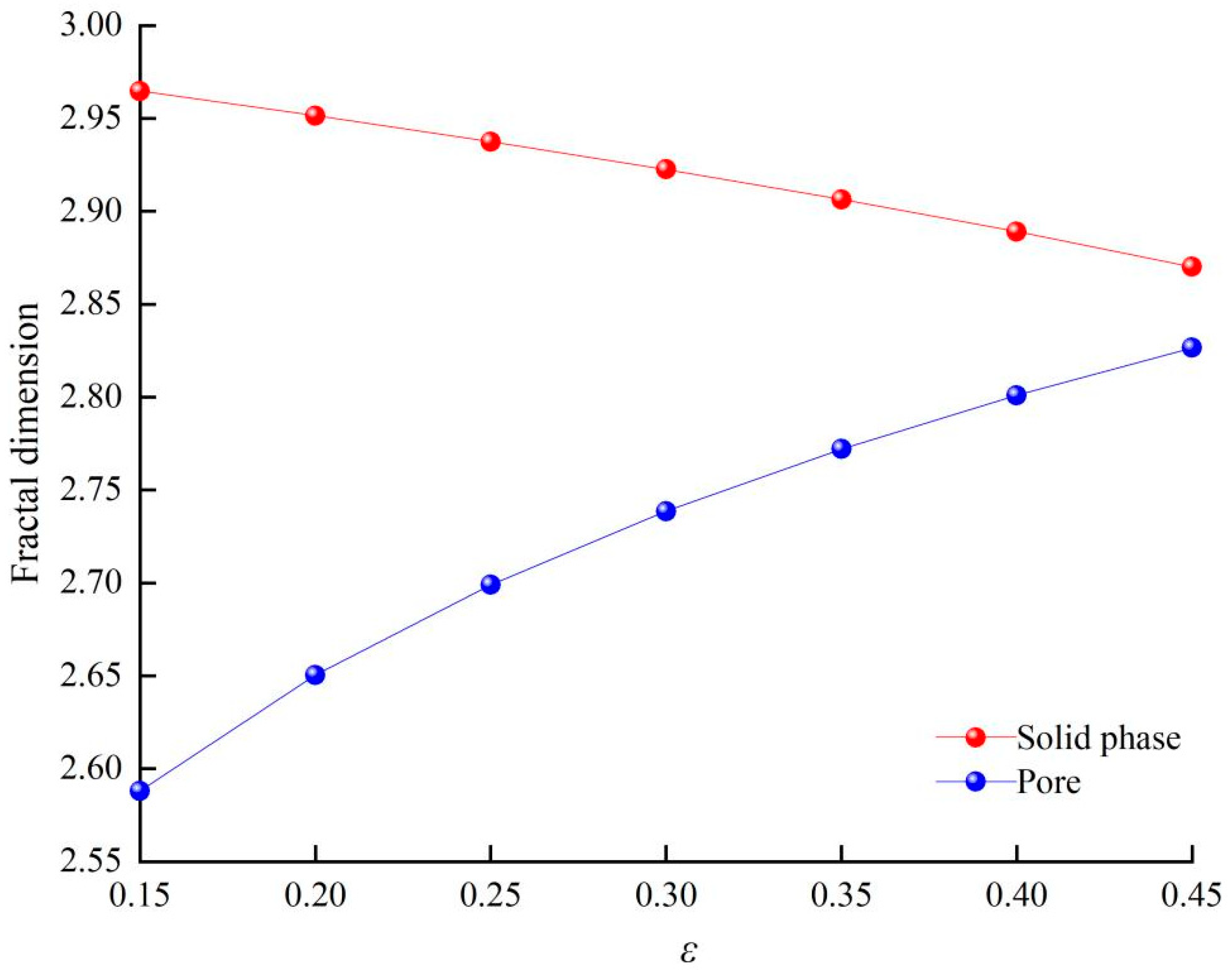
2.4.1. Fractal Dimensions of Solid Phase and Pore

According to the Hausdorff fractal dimension calculation method, the fractal dimensions of the solid phase and pores in polluted soil are

$$D_{\mathrm{fs}}={\displaystyle \frac{\ln \left(b^3-n\right)}{\ln b}}={\displaystyle \frac{\ln \left(b^3\left(1-\epsilon \right)\right)}{\ln b}}$$

(3)

$$D_{\mathrm{f}}={\displaystyle \frac{\ln \left(b^3-\left({\left(\frac{l}{d}\right)}^{D_E}-n\right)\right)}{\ln b}}={\displaystyle \frac{\ln \left(b^3\epsilon \right)}{\ln b}}$$

(4)

where D_fs is the fractal dimension of the solid phase; D_f is the fractal dimension of the pore; b is the scale factor (b = l/d); d is the size of the cell; ε is the porosity; and D_E is the Euclid fractal dimension (in three-dimensional space, D_E = 3). When ε = 0 and D_fs = 3, the solid phase is Euclid geometric fractal; when ε = 1 and D_f = 3, the pore is Euclid geometric fractal. In this paper, l = 100 and d = 1.

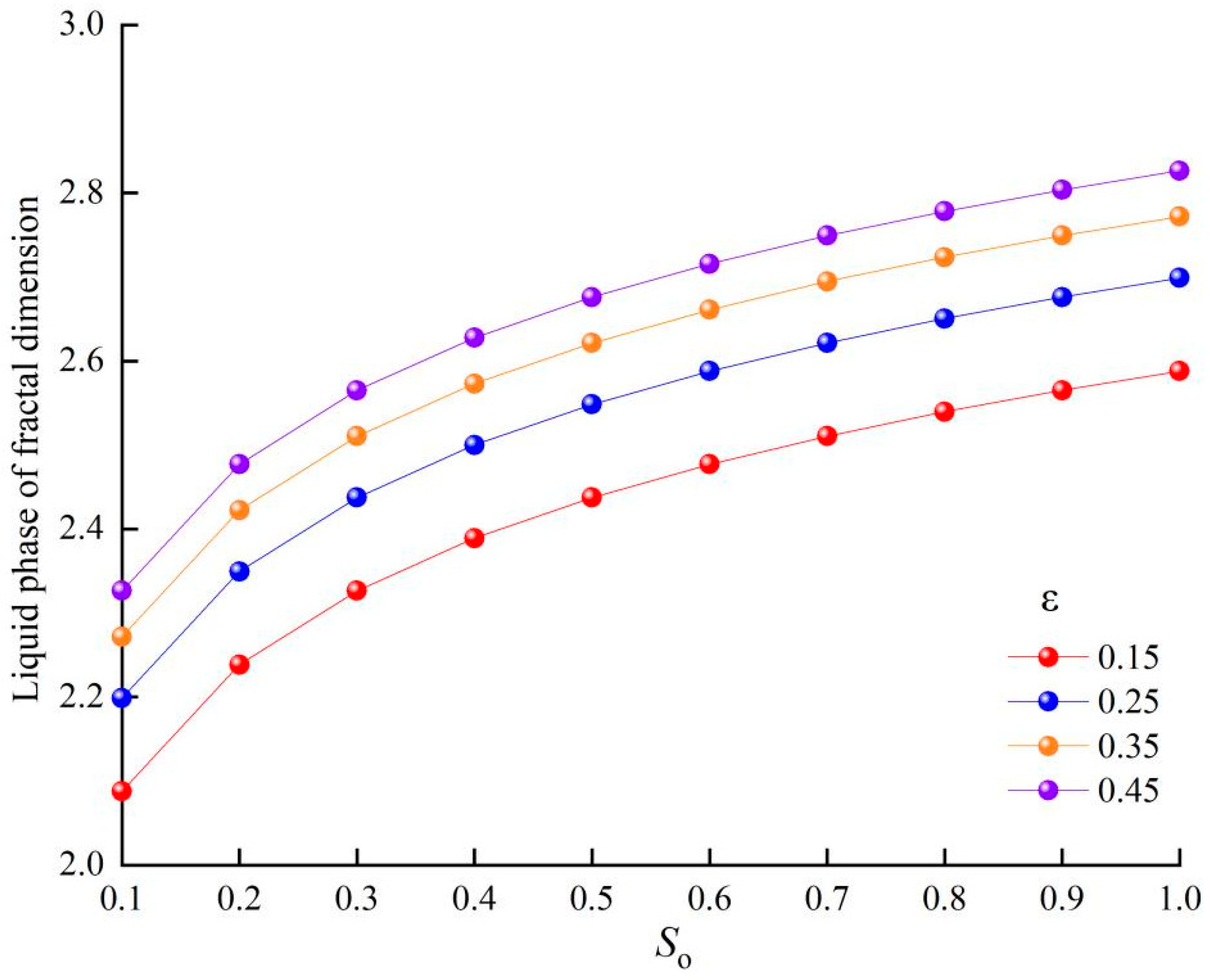
2.4.2. Fractal Dimension of Liquid Phase

NAPL pollutants in soils can affect the original thermal conductivity of the soils. The fractal dimension of NAPL pollutants in pores is the fractal dimension of the liquid phase (D_fo). Analogously, according to Formula (4), D_fo can be expressed as

$$D_{\mathrm{fo}}={\displaystyle \frac{\ln \left(b^3{S}_{\mathrm{o}}\epsilon \right)}{\ln b}}$$

(5)

The symbols in the formula are the same as above.

2.4.3. Fractal Dimension of Pore Curvature

In addition, the pore curvature of NAPL-contaminated soil will also affect its thermal conductivity. In the paper, the fractal dimension of pore curvature (D_T) is used to express the degree of pore curvature. The fractal dimension of pore curvature in a three-dimensional model is

$$D_{\mathrm{T}}=2+{\displaystyle \frac{\ln {\tau }_{\mathrm{av}}}{\ln \left(\frac{l}{{\lambda }_{\mathrm{av}}}\right)}}$$

(6)

where τ_av is the average curvature of the pore; λ_av is the average diameter of the pore; and l is the size RVE. τ_av and l/λ_av can be expressed by the following formula:

$${\tau }_{\mathrm{av}}=1+0.63\ln \left({\displaystyle \frac{1}{\epsilon }}\right)$$

(7)

$${\displaystyle \frac{l}{{\lambda }_{\mathrm{av}}}}={\displaystyle \frac{D_{\mathrm{fo}}-1}{{D_{\mathrm{fo}}}^{1/2}}}{\left({\displaystyle \frac{\pi \left(1-\epsilon \right)}{4\epsilon \left(3-D_{\mathrm{fs}}\right)}}\right)}^{1/2}{\displaystyle \frac{{\lambda }_{\min }}{{\lambda }_{\max }}}$$

(8)

where λ_min is the minimum solid particle diameter; and λ_max is the maximum solid particle diameter.

Generally, the value of λ_min/λ_max is between 10⁻² and 10⁻⁴, and its average value is 10⁻³. In this paper, λ_min/λ_max is taken as 10⁻³.

Formulas (6)–(8) are combined to obtain D_T.

$$D_{\mathrm{T}}=2+{\displaystyle \frac{\ln \left(1+0.63\ln \left(\frac{1}{\epsilon }\right)\right)}{\ln \left(\frac{D_{\mathrm{fo}}-1}{{D_{\mathrm{fo}}}^{1/2}}{\left(\frac{\pi \left(1-\epsilon \right)}{4\epsilon \left(3-D_{\mathrm{fs}}\right)}\right)}^{1/2}\frac{{\lambda }_{\min }}{{\lambda }_{\max }}\right)}}$$

(9)

3. Results and Discussion

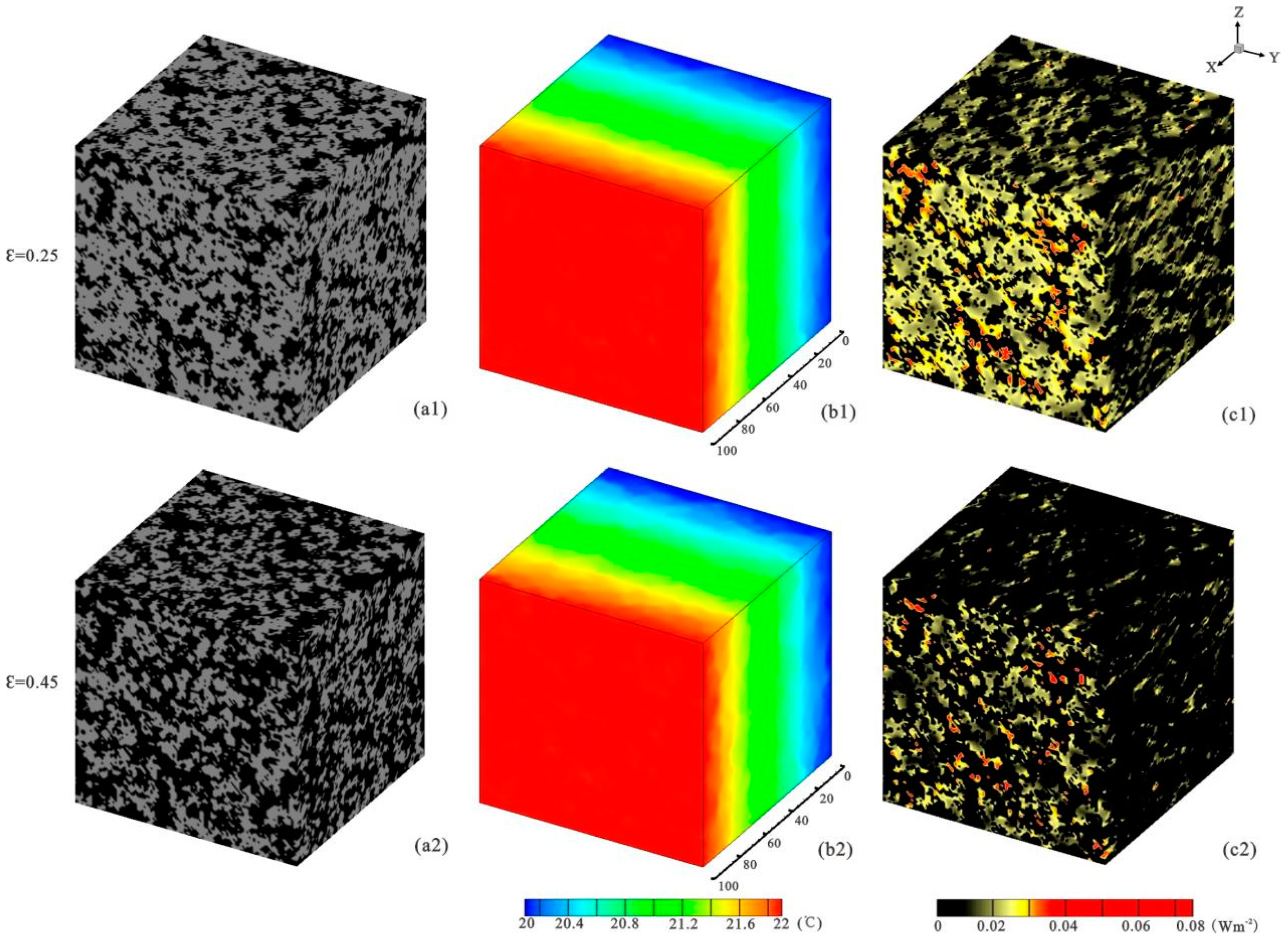
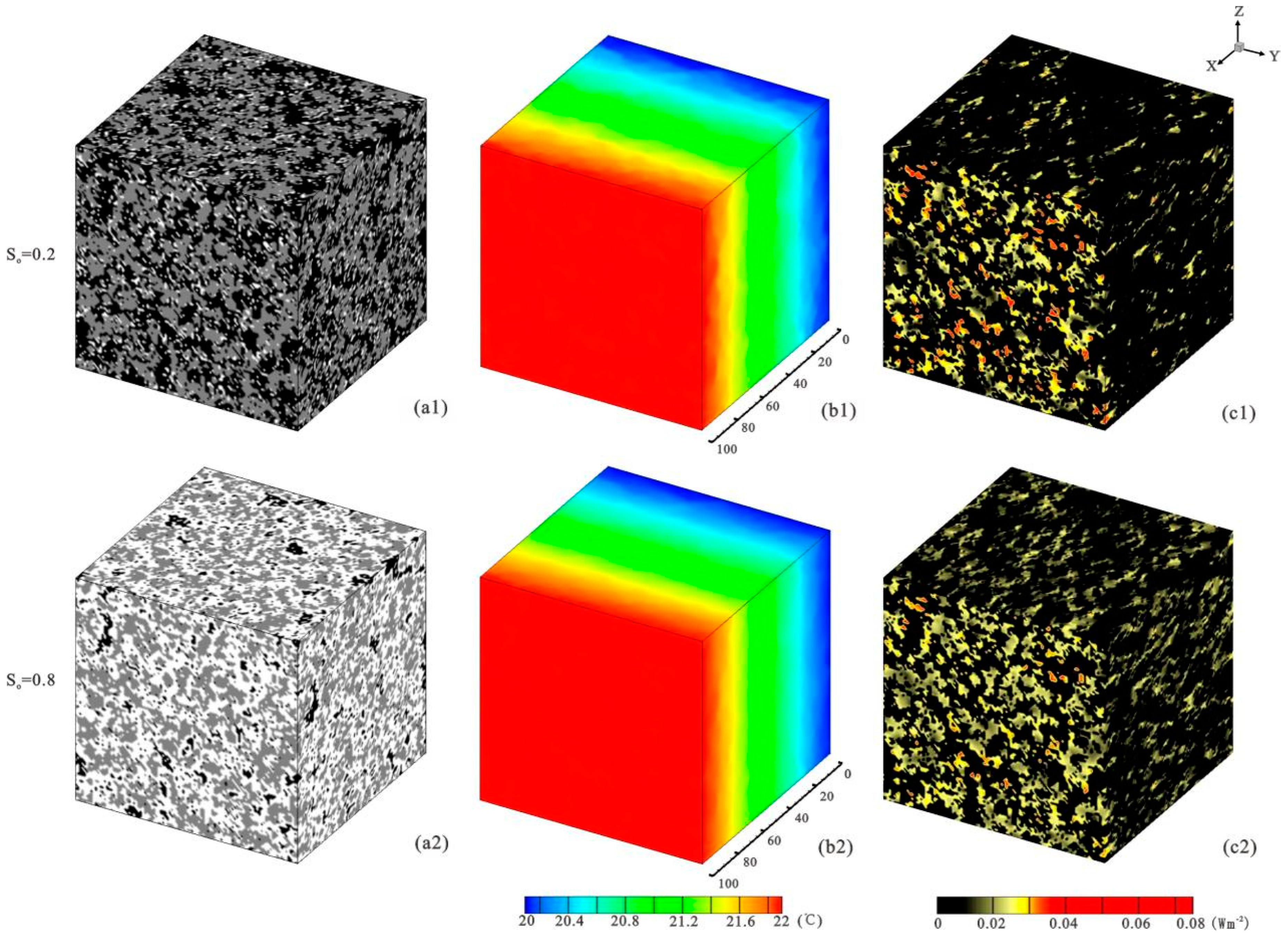
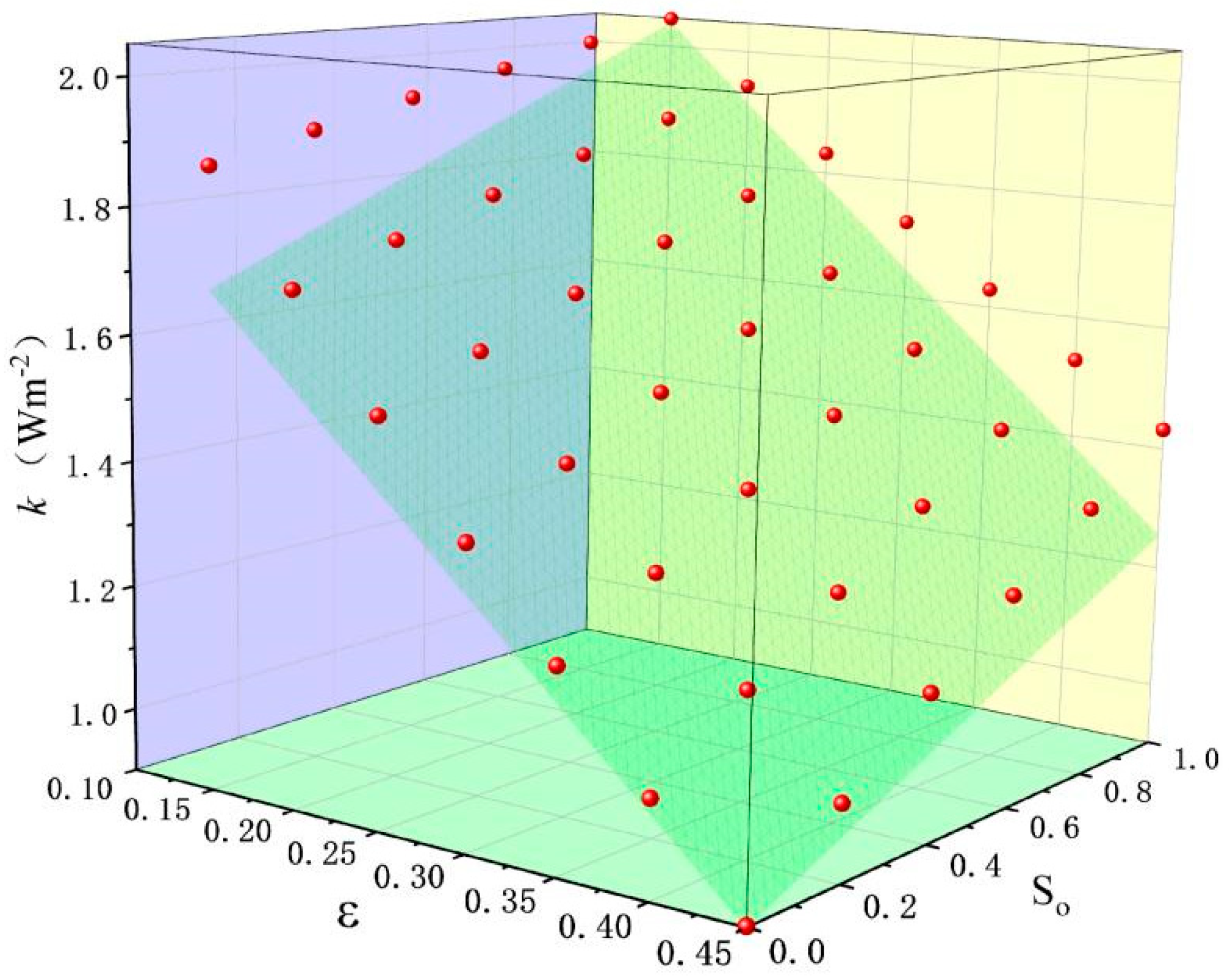
3.1. Effect of ε and S_o on k

In this paper, the content of NAPLs is normalized by saturation to explore the variation in k with different porosities and saturation levels. Taking a NAPL-contaminated soil model with a saturation of 0.1 as an example, Figure 9 shows the relationship between k and S_o, ε.

In the regression analysis of thermal conductivity and porosity, saturation is as follows:

$$k=-2.6235\epsilon +0.3541S_o+2.1743 R^2=0.97991$$

(10)

According to Figure 9 and Formula (10), k increases with the increase in S_o and the decrease in ε. ε and S_o have a linear relationship with k. k is more affected by ε.

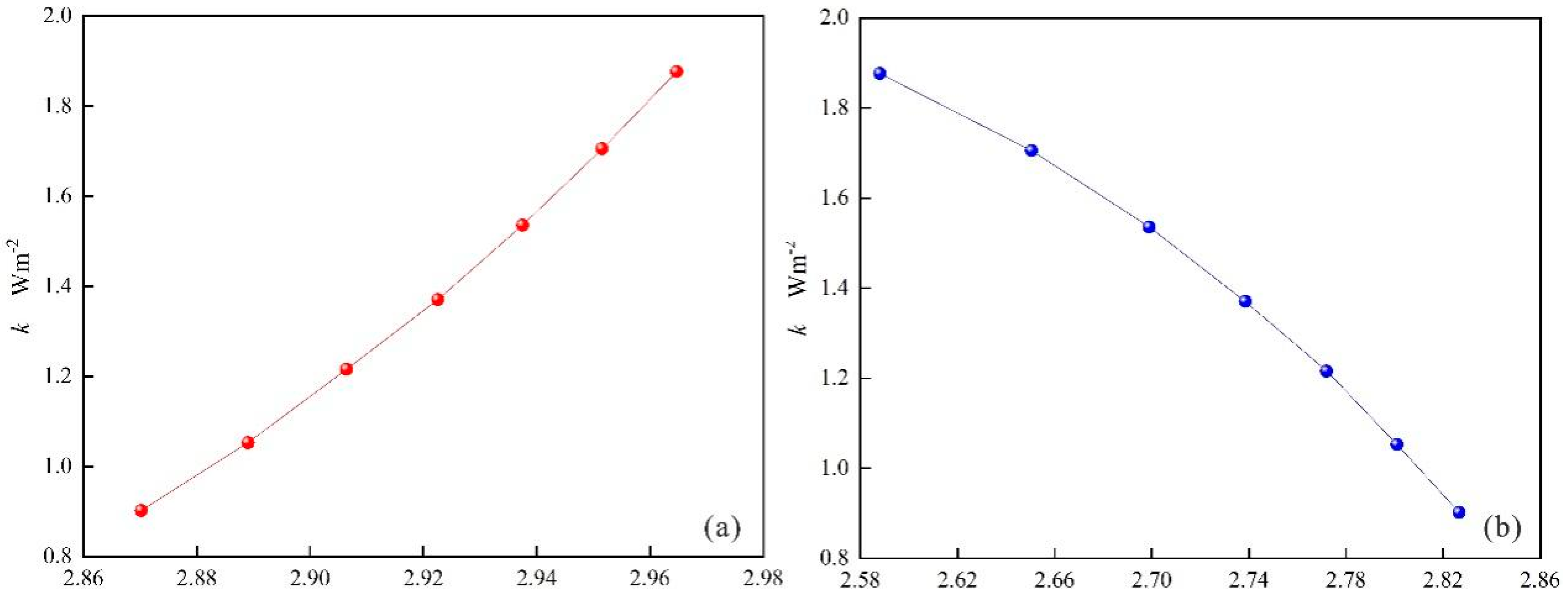
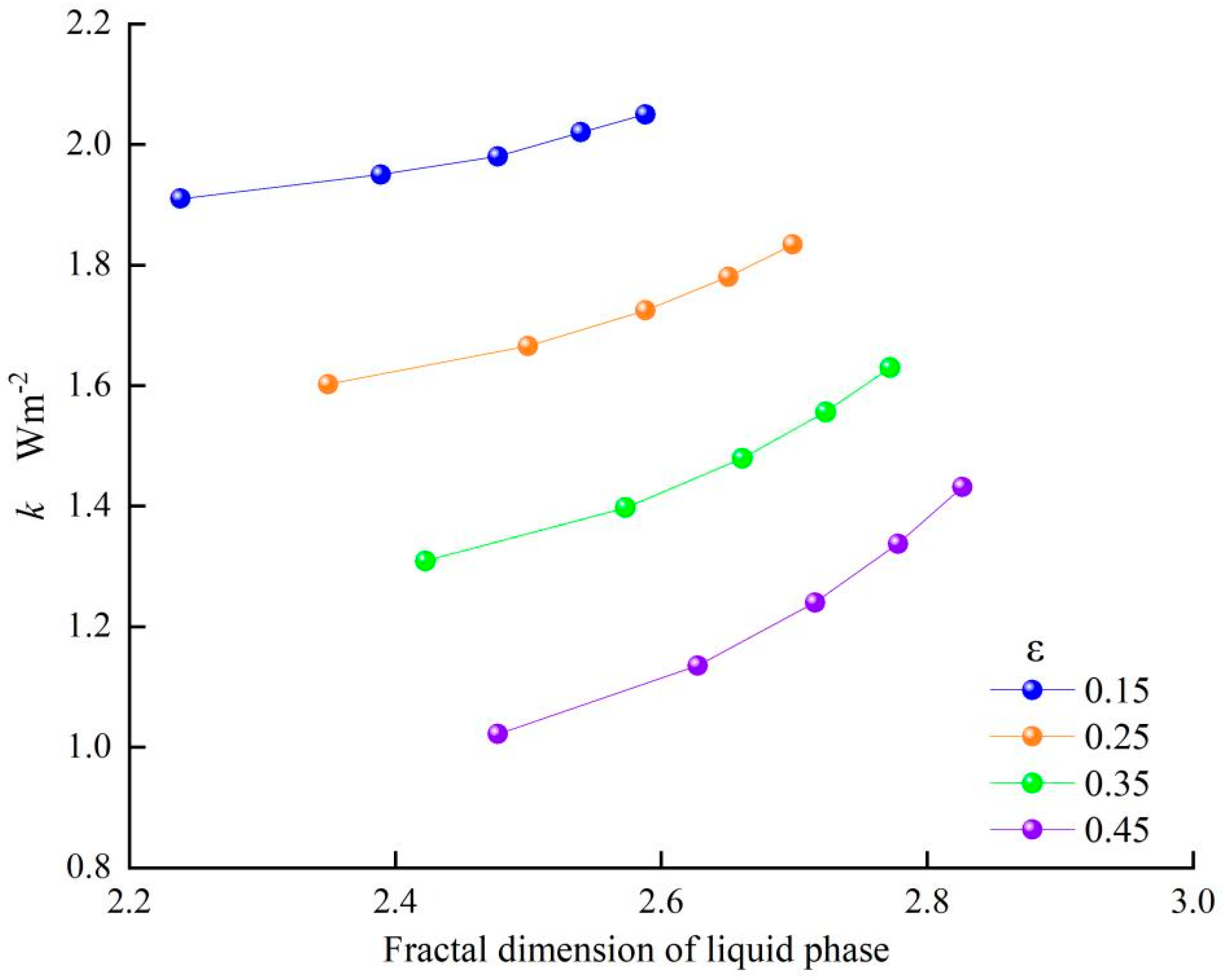
3.2. Relationship Between k and D_fs, D_f

It can be seen from Figure 10 that the D_fs and D_f of the three-dimensional NAPL-contaminated soil models are between 2 and 3, which conform to the fractal characteristics. The larger the porosity of the models, the larger the D_f, and the smaller the D_fs. For the same b, the larger the ε, the more uniform the pore distribution, the smaller the ε, and the more uneven the pore distribution. Meanwhile, the decreasing rate of D_fs is smaller than the increasing rate of D_f. When the pore volume is smaller than the solid volume (ε < 0.5), the change in pore uniformity caused by the increasing rate of porosity is larger.

Figure 11 shows the relationship between k and D_fs, D_f. k increases with the increase in D_fs and decreases with the increase in D_f. The thermal conductivity of soil particles is two orders of magnitude larger than that of air. The more the solid phase increases and the more its distribution is uniform, the greater the k.

3.3. Relationship Between D_fo and k

Figure 12 shows the relationship between the fractal dimension of the liquid phase (D_fo) and saturation (S_o). As S_o increases, D_fo increases, and the rate of increase in D_fo gradually decreases. In the case of a small S_o, the distribution of the liquid phase is more dispersed, and the increase in saturation will cause greater changes in the uniformity of the liquid phase and D_fo. Meanwhile, under the same S_o, the larger the ε, the larger the D_fo. In the case of a large ε, the larger the volume of the liquid phase, the more uniform the distribution and the larger the D_fo. In addition, with the increase in ε, the increasing rate of D_fo gradually decreases. In the case of a small ε, the liquid phase volume is smaller and the distribution is more dispersed. With the increase in ε, the uniformity and D_fo change more.

As shown in Figure 13, k increases with the increase in D_fo. In the case of a larger ε and larger D_fo, k increases more rapidly with the increase in D_fo. When ε and D_fo are large, the liquid phase is more uniform, and only more liquid phase can increase D_fo. That is consistent with the conclusion on the relationship between S_o and k.

3.4. Relationship Between D_T and k

Figure 14a shows that D_T decreases with the increase in ε, that is, the greater the ε, the greater the degree of pore curvature and the greater the degree of solid phase curvature. The smaller the D_T, the smaller the k (Figure 14b). The solid phase is a good heat flow channel. The smaller the D_T, the greater the curvature of the pores and the solid phase and the longer the heat flow path (Figure 15). In the case of the same D_T, the greater the S_o, the greater the k (Figure 14b). When D_T is small, the influence of saturation on k is greater. When D_T is smaller, the influence of S_o on k is greater. The existence of the liquid phase can form “liquid bridges” between the solid phase and form a good heat flow channel (Figure 16). In particular, for the model with great curvature of the pores and the solid phase, the length of the heat flow path can be greatly shortened. The thermal resistance is reduced to improve k.

4. Conclusions

In the paper, QSGS is used to establish a NAPL-contaminated soil model, and LBM is used to calculate k. The relationship between k and the fractal dimension of NAPL-contaminated soils is studied by combining the numerical simulation method with Hausdorff fractal dimension theory. The main conclusions of this study are as follows:

(1)

It is simple and feasible to calculate the thermal conductivity (k) of NAPL-contaminated soils using the four-parameter random generation method combined with LBM and Monte Carlo simulation.

(2)

k decreases with the increase in porosity and increases with the increase in saturation. The thermal conductivity varies linearly with porosity and saturation. Porosity has a greater influence on the thermal conductivity of NAPL-contaminated soils. A calculation formula of thermal conductivity related to saturation and porosity is proposed.

(3)

With the increase in porosity, the pore fractal dimension and liquid phase fractal dimension of NAPL-contaminated soils increased, while the solid phase fractal dimension and pore curvature fractal dimension decreased. The fractal dimension of the liquid phase increases with the increase in NAPL content. The thermal conductivity increases with the increase in the solid phase fractal dimension, liquid phase fractal dimension, and pore curvature fractal dimension and decreases with the increase in the pore fractal dimension.