Research on Electromagnetic Control Technology for the Roll Profile of Wide-Width Electrode Roll Press Rolls
Abstract
1. Introduction
2. Research Methods
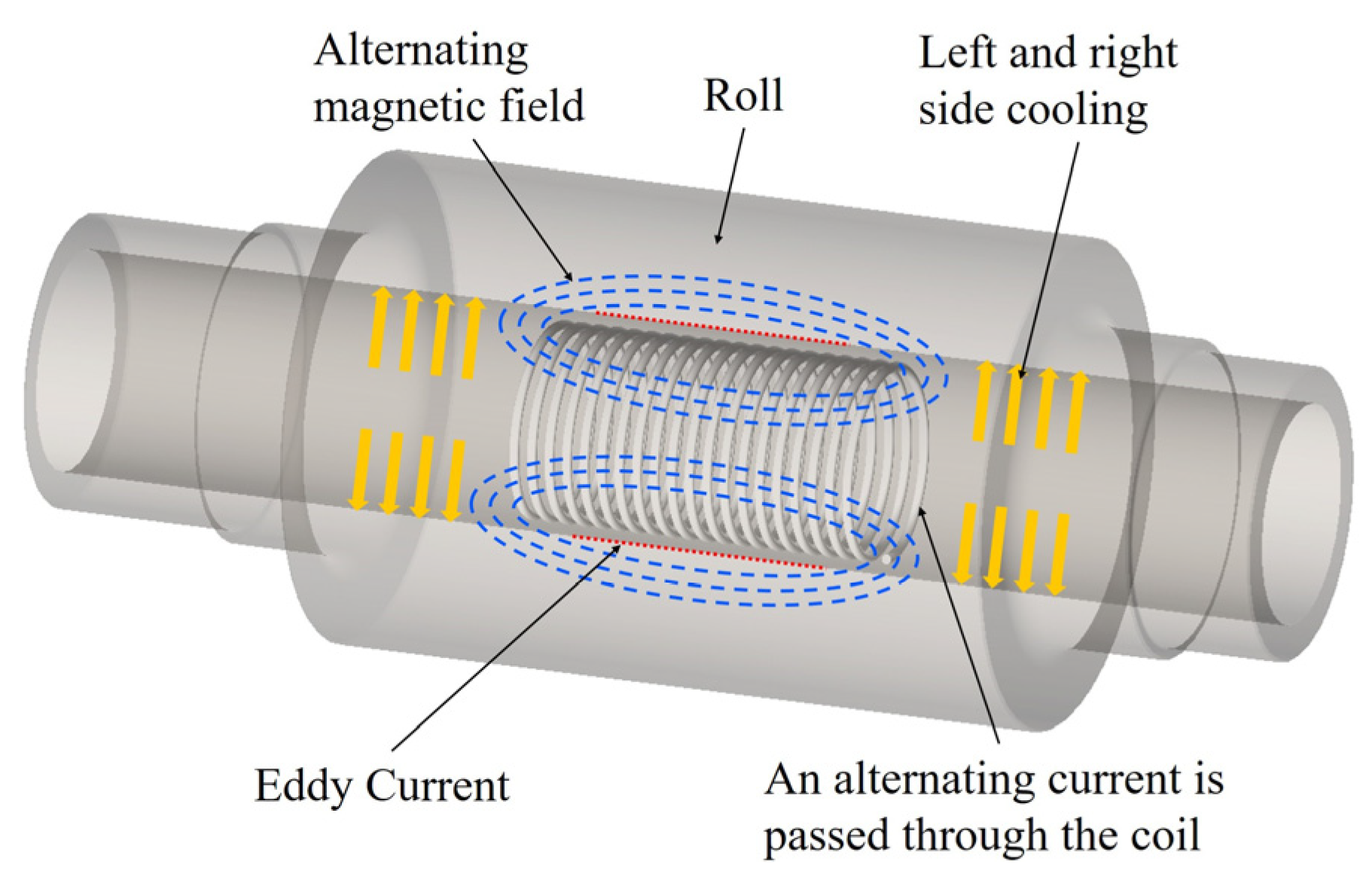
2.1. Basic Principle of Electromagnetic Control of Roll Profile
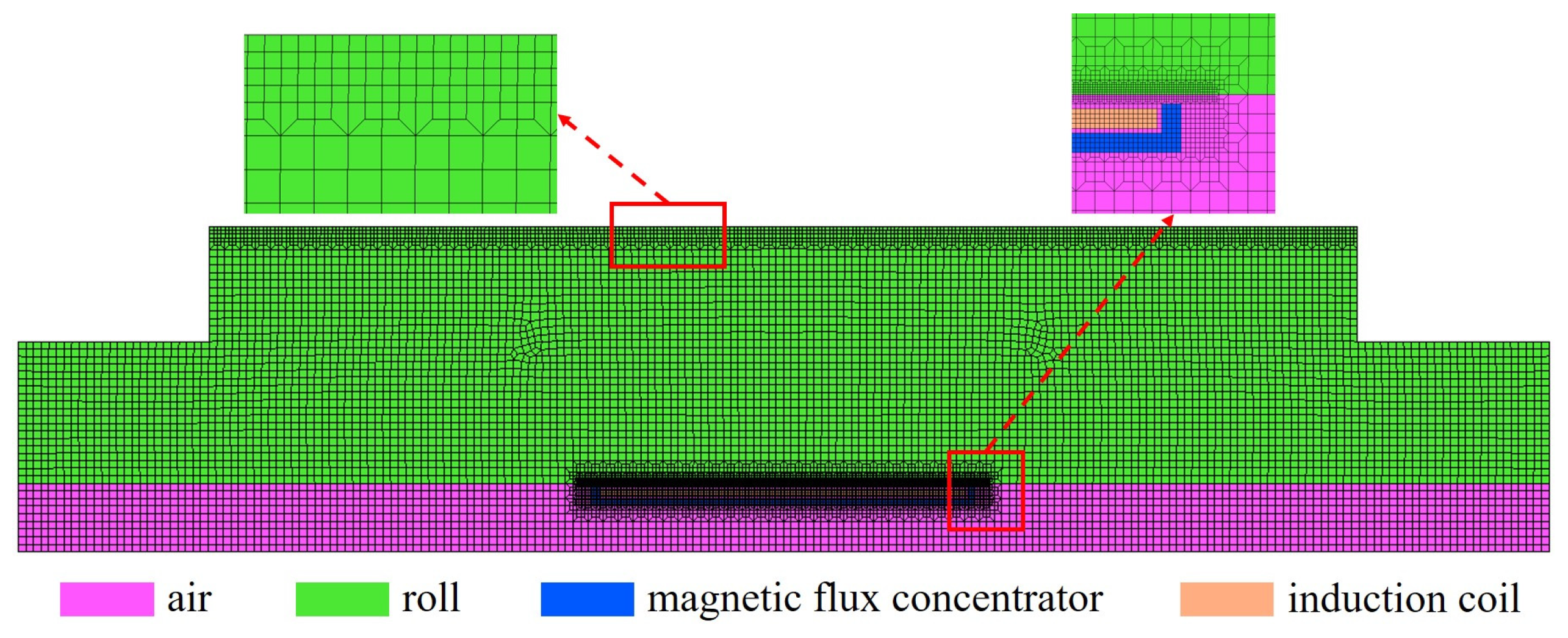
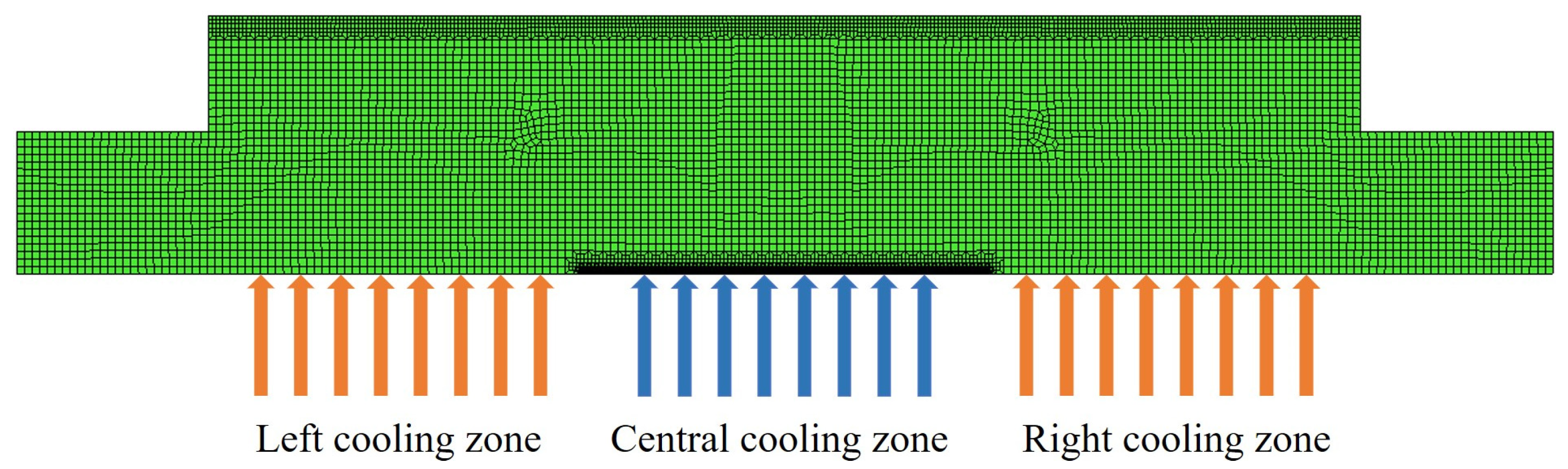
2.2. Finite Element Modeling
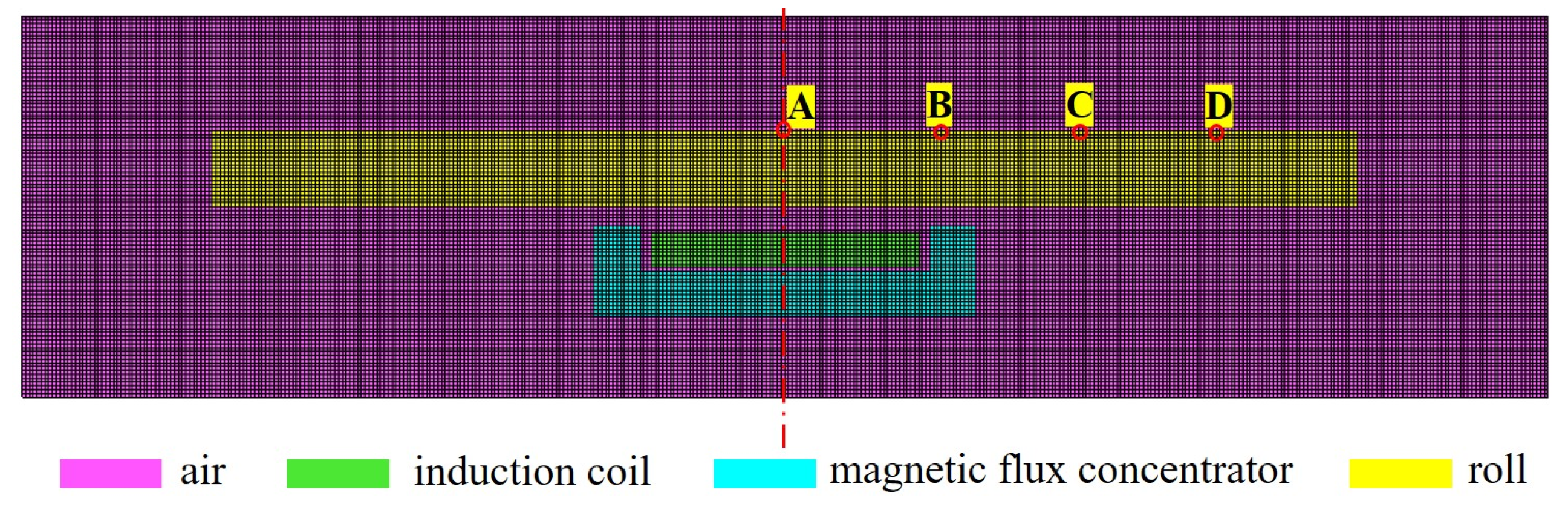
2.3. Validation Experiment
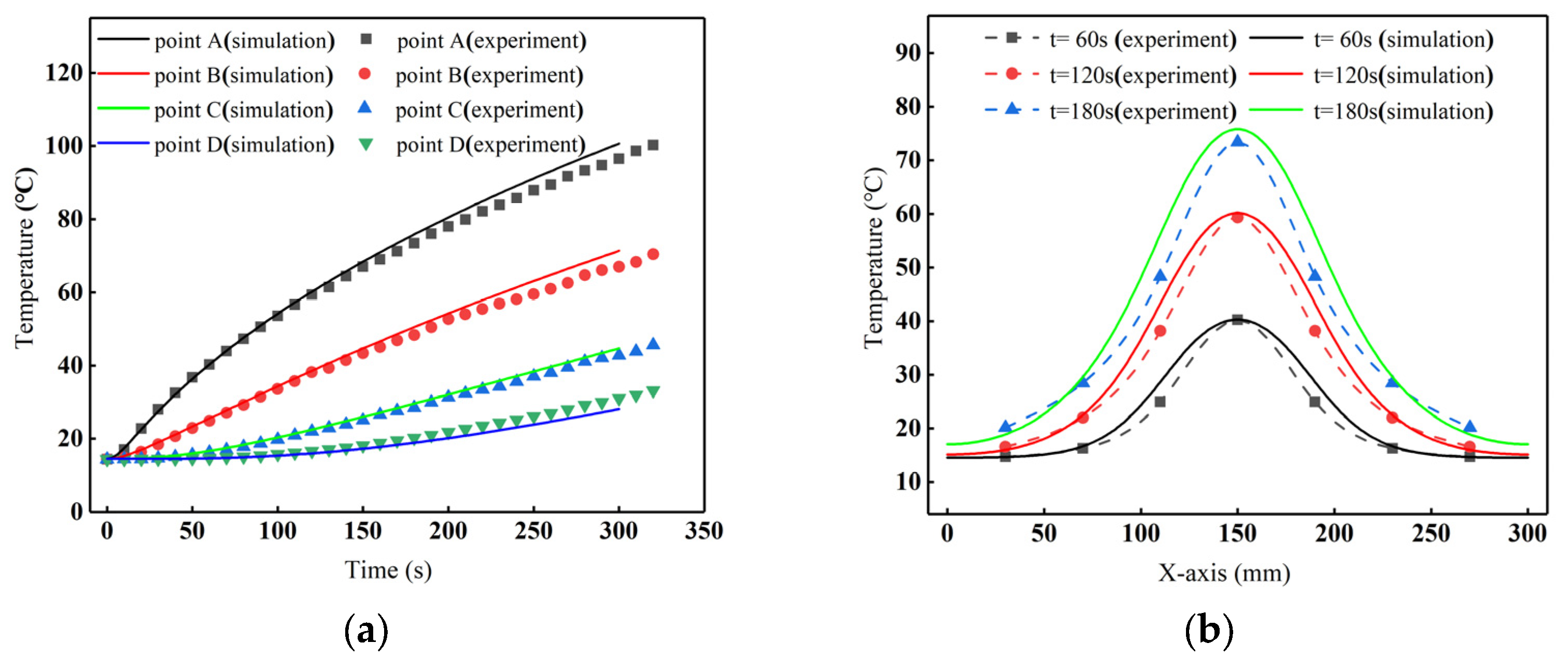
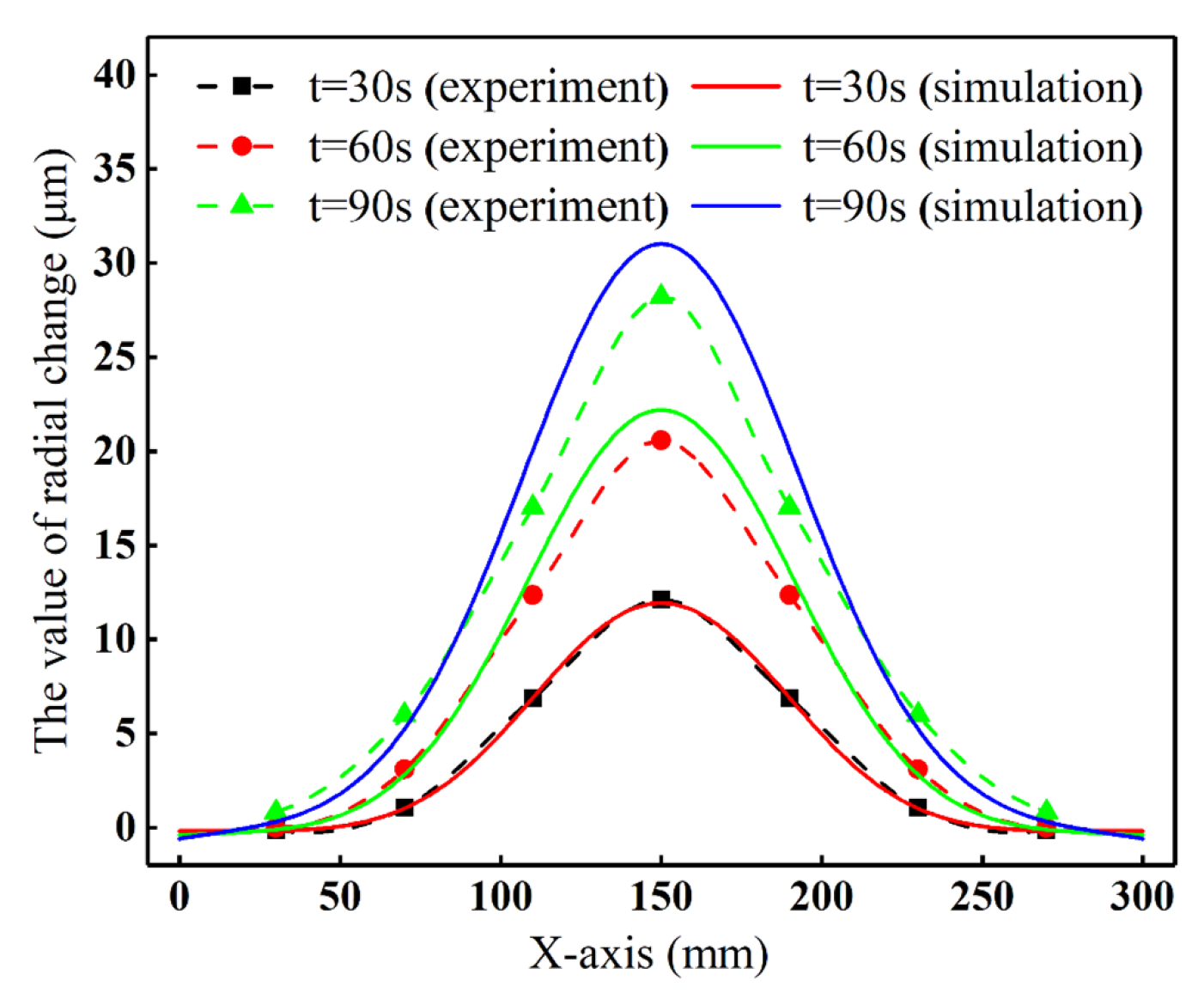
3. Validation of the Finite Element Model
4. Results
4.1. Effects of Electromagnetic Control Parameters on Roll Profile
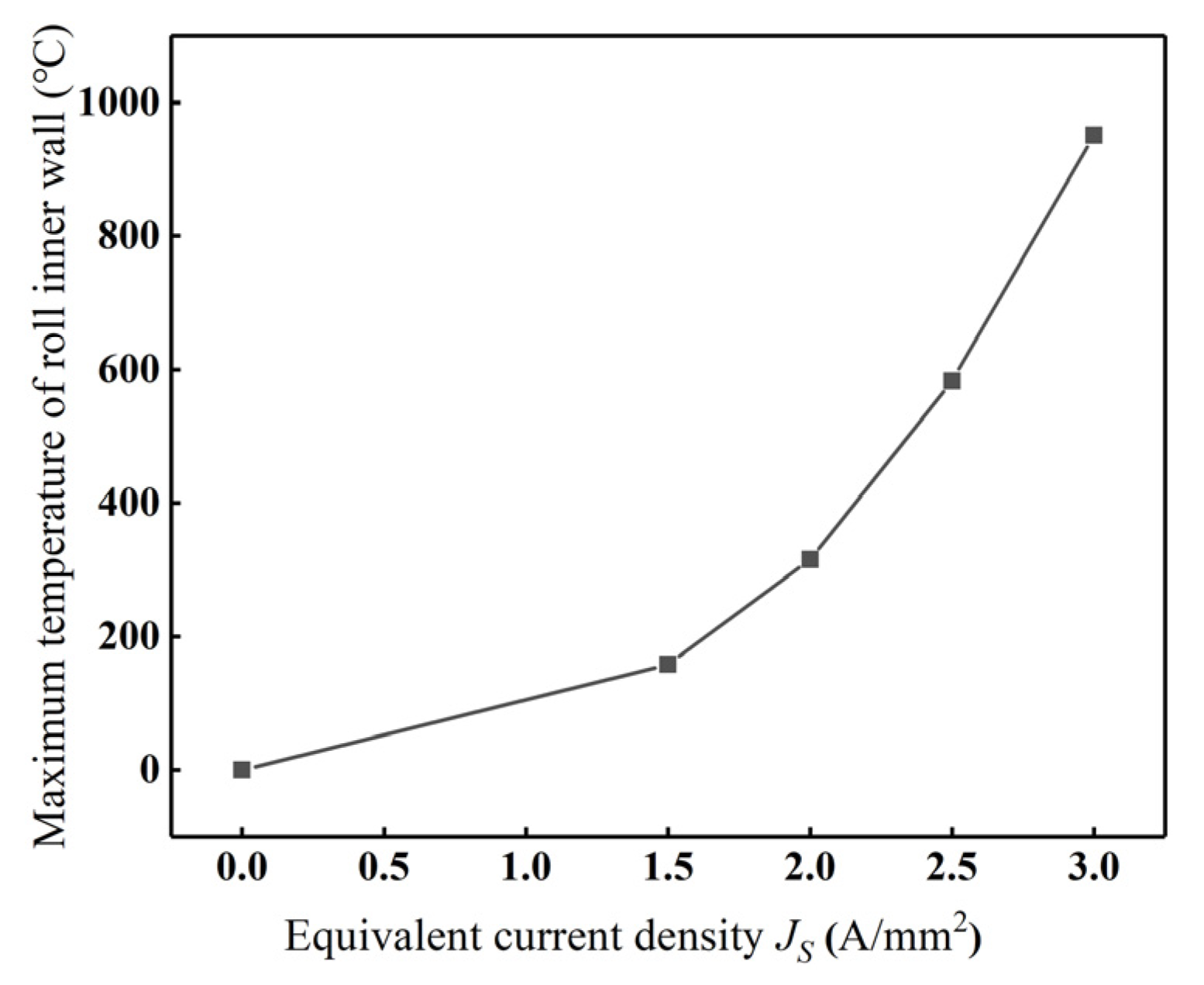
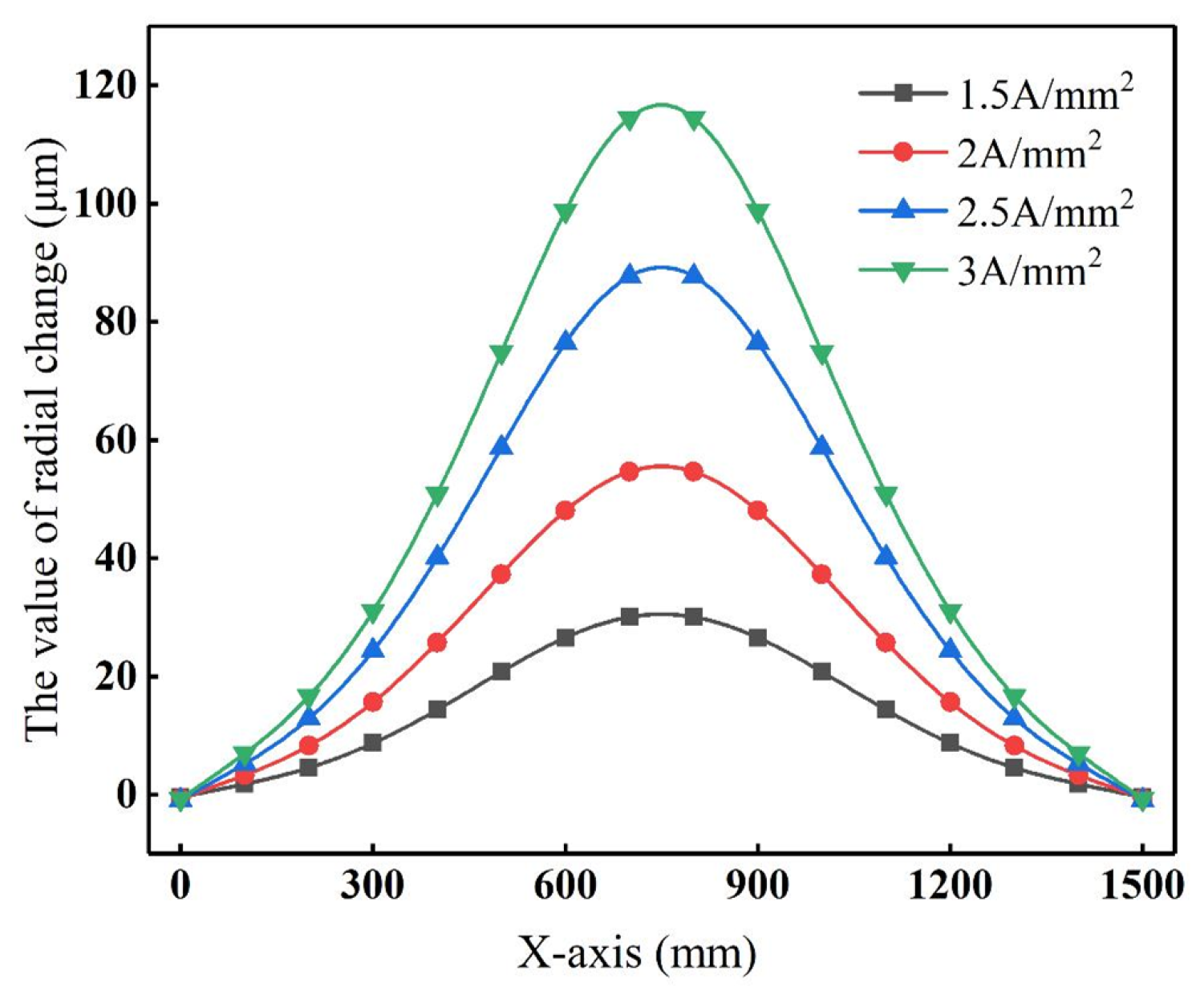
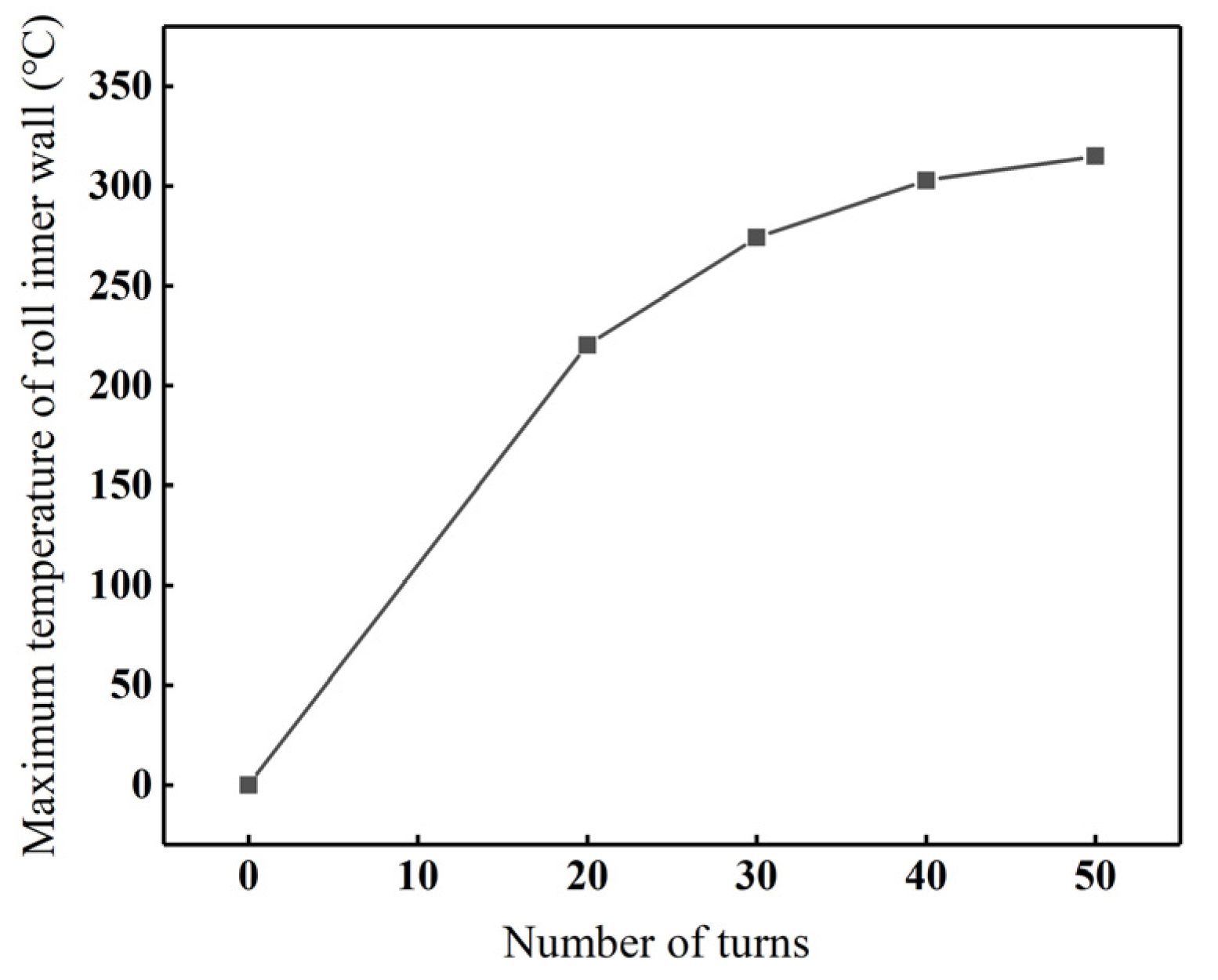
4.1.1. Equivalent Current Density
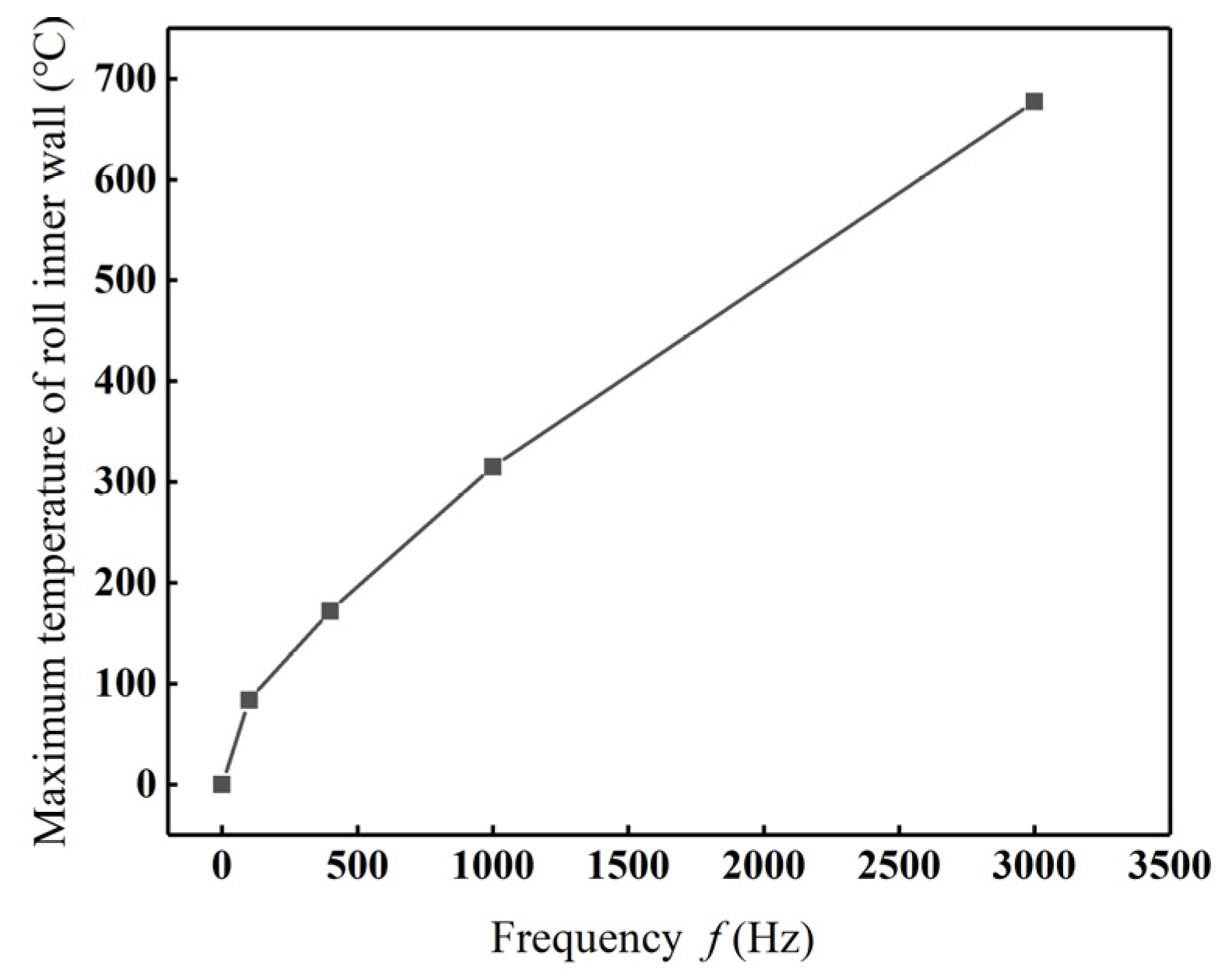
4.1.2. Current Frequency
4.2. Analysis of Roll Profile Control Strategy
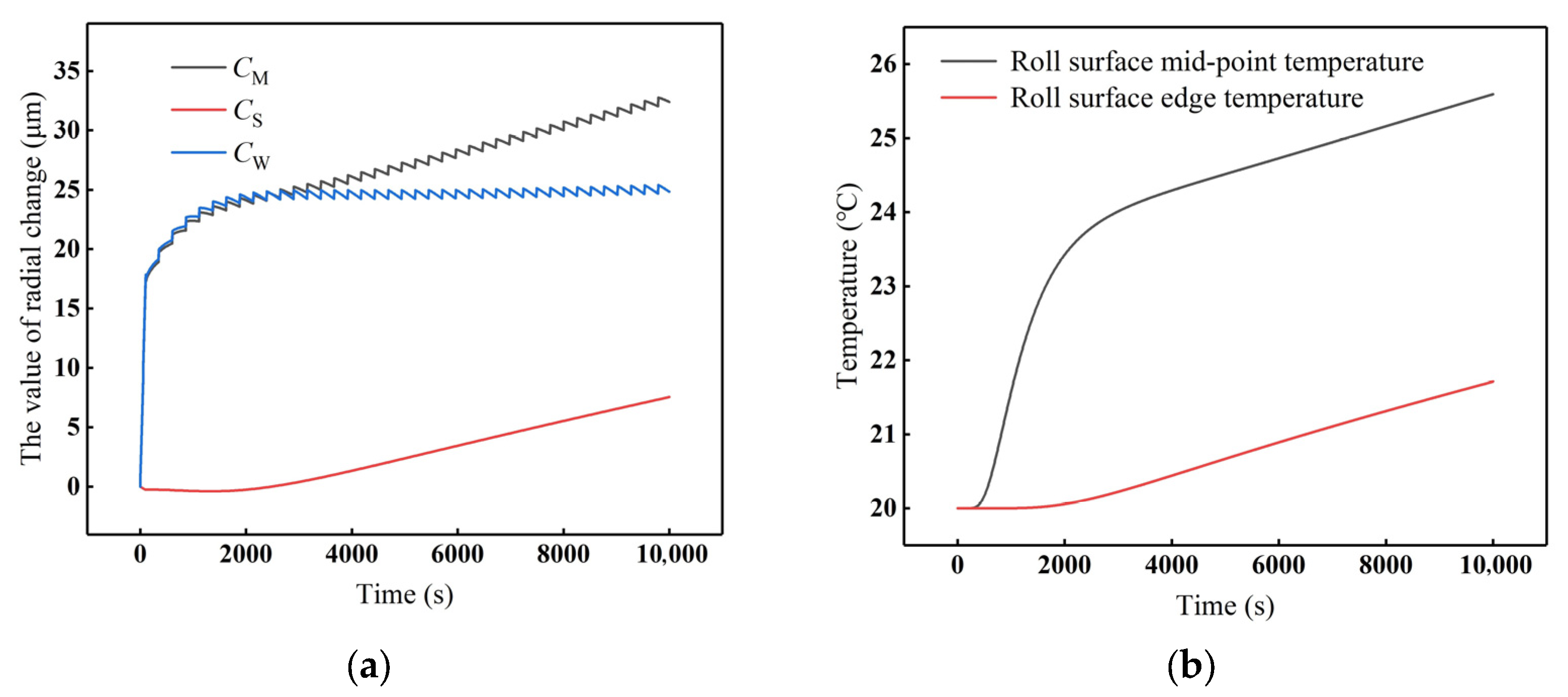
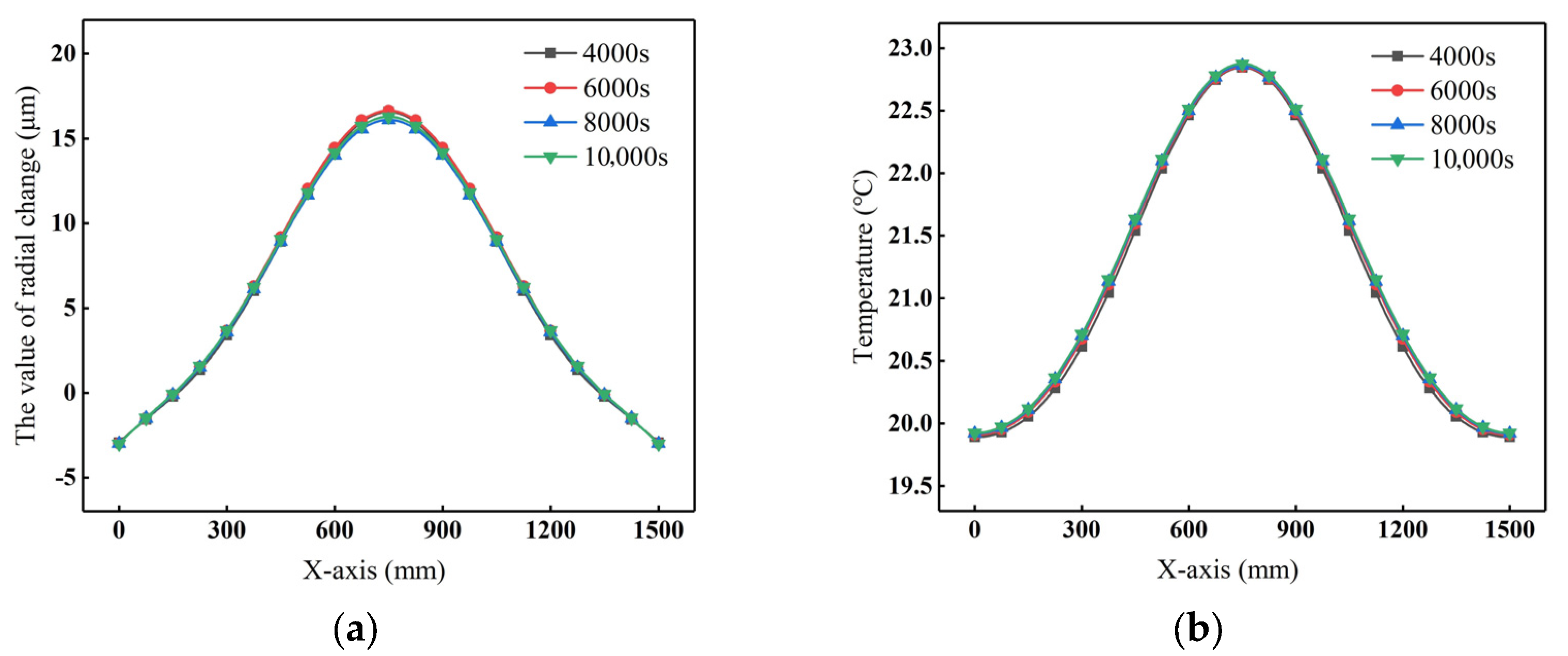
4.2.1. Effectiveness of the Segmented Periodic Heating Strategy
4.2.2. Effects of Critical Control Parameters Js and t1
5. Discussion and Conclusions
- (1)
- An axisymmetric electromagnetic–thermal–structural coupling finite element model was developed and experimental validation was performed using a self-built experimental platform, with measured temperature and deformation field data showing excellent agreement with FEM predictions.
- (2)
- The influence of key electromagnetic process parameters, including equivalent current density (Js), current frequency f, and coil turn n, on the roll temperature, roll profile, and roll crown was investigated. The maximum temperature of the roll’s inner bore and the roll crown exhibit an increasing trend as Js, f, and n increase. Moreover, the maximum temperature of the roll’s inner bore exhibits a quadratic relationship with Js. As Js continues to increase, the rate of temperature rise accelerates. However, the rate of temperature rise decreases with the increase in f and n.
- (3)
- A cyclic heating strategy was developed to control and stabilize the roll profile. The simulation results show that the roll profile can be effectively regulated by adjusting current density Js and heating durations t1. The stable crown CW shows linear correlation with t1, and a nonlinear trend with Js. Under fixed Js and t1, further optimization of duty cycle and cooling conditions enables long-term stabilization of the roll profile.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, G.D.; Sun, X.; Ai, C.S. Research on the on-line monitoring and control system of lithium battery pole piece surface density. Adv. Mater. Res. 2014, 889, 691–694. [Google Scholar] [CrossRef]
- Zheng, H.; Li, J.; Song, X.Y.; Liu, G.; Battaglia, V. A comprehensive understanding of electrode thickness effects on the electro-chemical performances of Li-ion battery cathodes. Nat. Energy 2012, 71, 258–265. [Google Scholar]
- Wang, D.C.; Wang, G.D.; Xu, C.J.; Liu, H.M. Mechanics and deformation behavior of lithium-ion battery electrode during calendering process. J. Energy Storage 2024, 87, 111521. [Google Scholar] [CrossRef]
- Haidar, A.; Kubra, U.; Yang, T.C. Low porosity NMC622 and NMC811 electrodes made by severe calendering. J. Energy Storage 2025, 105, 114559. [Google Scholar]
- Zu, C.X.; Li, H. Thermodynamic Analysis on Energy Densities of Batteries. Energy Environ. Sci. 2011, 4, 2614–2624. [Google Scholar] [CrossRef]
- Elzbieta, S.; Leszek, S. Comparative analysis of effectiveness of resistance and induction turnout heating. Energies 2020, 13, 5262. [Google Scholar] [CrossRef]
- Long, J.J.; Yu, H.; Liu, W.B. Structure engineering of cathode host materials for Li-S batteries. Rare Met. 2024, 43, 1370–1389. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z.D.; Kang, Z.R.; Liu, W.; Chen, Y.G. High-density crack-resistant Si-C microparticles for lithium ion batteries. Energy Storage Mater. 2023, 56, 40–49. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Gong, H. Partial conversion of current collectors into nickel copper oxide electrode materials for high-performance energy storage devices. ACS Appl. Mater. Amp Interfaces 2015, 7, 15277–15284. [Google Scholar] [CrossRef]
- Sun, J.N.; Xiang, W.J.; Huang, H.G.; Yuan, Z.G.; Li, J.R. Research progress on rolling technology of lithium-ion battery electrodes. China Metall. 2021, 31, 12–18. [Google Scholar]
- Zhang, J.P.; Sun, J.N.; Huang, H.G.; Ji, C.; Yan, M.; Yuan, Z.G. Deformation and fracture mechanisms in the calendering process of lithium-ion battery electrodes. Appl. Energy 2024, 373, 123900. [Google Scholar] [CrossRef]
- Duffner, F.; Kronemeyer, N.; Tübke, J.; Leker, J.; Winter, M.; Schmuch, R. Post-lithium-ion battery cell production and its compatibility with lithium-ion cell production infrastructure. Nat. Energy 2021, 6, 123–134. [Google Scholar] [CrossRef]
- Gavalas, E.; Papaefthymiou, S. Thermal Camber and Temperature Evolution on Work Roll during Aluminum Hot Rolling. Metals 2020, 10, 1434. [Google Scholar] [CrossRef]
- Gao, Y.J.; Zhao, J.Y.; Kong, X.D.; Wang, Y.Q. Dynamic simulation of a hydraulic AGC system for a strip mill. China Mech. Eng. 1998, 7, 23–26. [Google Scholar]
- Jia, C.Y.; Shan, X.Y.; Cui, Y.C.; Bai, T.; Cui, F.J. Modeling and simulation of hydraulic roll bending system based on CMAC neural network and PID coupling control strategy. J. Iron Steel Res. Int 2013, 20, 17–22. [Google Scholar] [CrossRef]
- Ding, J.G.; He, Y.H.C.; Song, M.X.; Jiao, Z.J.; Peng, W. Roll crown control capacity of sextic CVC work roll curves in plate rolling process. Int. J. Adv. Manuf. Technol. 2021, 113, 87–97. [Google Scholar] [CrossRef]
- Bai, Z.H.; Wang, K.; Wang, Y.J.; Chang, J.L.; Zhou, Q.T.; Ke, Y.L. Inner roll shape optimization design technology of VC mill. China Mech. Eng. 2013, 24, 3096–3100. [Google Scholar]
- Wang, Q.N.; Sun, J.Q.; Yang, J.X.; Wang, H.S.; Dong, L.J.; Jiao, Y.L.; Li, J.M.; Zhi, Z.Y.; Yang, L.P. Online Partition-Cooling System of Hot-Rolled Electrical Steel for Thermal Roll Profile and Its Industrial Application. Processes 2024, 12, 410. [Google Scholar] [CrossRef]
- Yang, T.S.; Hai, Y.; Fan, M.C.; Xu, Z.Q.; Du, F.S. Research on electronic temperature control capability of roll profile based on semiconductor thermoelectric effect. J. Plast. Eng. 2022, 29, 206–213. [Google Scholar]
- Du, F.S.; Liu, W.W.; Feng, Y.S.; Sun, J.N. Roll profile electromagnetic control process parameters in precision rolling mill. Chin. J. Eng. 2017, 39, 1874–1880. [Google Scholar]
- Yang, T.S.; Sun, W.Q.; Xu, Z.Q.; Du, F.S.; He, A.R. Analysis of the energy efficiency and control ability under different magnetic flux forms in RPECT. Int. J. Heat Mass Transf. 2023, 217, 124730. [Google Scholar] [CrossRef]
- Liu, W.W.; Feng, Y.F.; Yang, T.S.; Du, F.S.; Sun, J.N. Theoretical and experimental research on the law of flexible roll profile electromagnetic control. J. Mater. Process. Tech 2018, 262, 308–318. [Google Scholar] [CrossRef]
- Feng, Y.F.; Liu, W.W.; Yang, T.S.; Du, F.S.; Sun, J.N. A flexible electromagnetic control technique for interference adjustment in large-size sleeved backup rolls. Metall. Res. Technol 2019, 116, 405. [Google Scholar] [CrossRef]
- Liu, W.W.; Li, T.; Wang, T.; Fu, X.B.; Du, F.S. Analysis of the influence of roll size change on electromagnetic heat conversion capacity and roll profile control characteristics in the RPECT. Int. J. Heat Mass Transf. 2022, 189, 122686. [Google Scholar] [CrossRef]
- Li, W.G.; Liu, X.H.; Guo, Z.H. Numerical simulation of temperature field and thermal crown of work roll during hot strip rolling. Chin. J. Nonferrous Met. 2012, 11, 3176–3184. [Google Scholar]
- Zhiye, L.; Yuechao, M.; Anrui, H. Investigation and Application of Magnetic Properties of Ultra-Thin Grain-Oriented Silicon Steel Sheets under Multi-Physical Field Coupling. Materials 2022, 15, 8522. [Google Scholar] [CrossRef]
- Zhu, Y.; Yu, S.W.; Liang, R.; Luo, Y. Numerical simulation of induction heating process based on magnetic-thermal coupling. Hot Work. Technol. 2020, 49, 89–92. [Google Scholar]









| Temperature (°C) | Thermal Conductivity (W/(m·K)) | Relative Permeability | Specific Heat Capacity (J/(kg·K)) | Resistivity (10−6 Ω·m) |
|---|---|---|---|---|
| 20 | 47.68 | 200 | 472 | 0.198 |
| 100 | 43.53 | 195 | 480 | 0.254 |
| 200 | 40.44 | 186.6 | 498 | 0.339 |
| 400 | 36.02 | 167.1 | 560 | 0.541 |
| 500 | 34.16 | 154.9 | 615 | 0.656 |
| 600 | 31.98 | 137.8 | 700 | 0.790 |
| 700 | 28.66 | 92.5 | 854 | 0.949 |
| 742 | 26.20 | 1 | 986 | 1.019 |
| 760 | 25.14 | 1 | 1064 | 1.042 |
| 900 | 25.92 | 1 | 637 | 1.162 |
| 1000 | 24.02 | 1 | 602 | 1.20 |
| Electromagnetic Parameters | Variation Range |
|---|---|
| Current density (A/mm2) | 1.5, 2, 2.5, 3 |
| frequency (Hz) | 100, 400, 1000, 3000 |
| Number of turns | 20, 30, 40, 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, C.; Chen, H.; Sun, J.; Huang, H.; Fu, X.; Yang, Z. Research on Electromagnetic Control Technology for the Roll Profile of Wide-Width Electrode Roll Press Rolls. Processes 2025, 13, 1448. https://doi.org/10.3390/pr13051448
Guo C, Chen H, Sun J, Huang H, Fu X, Yang Z. Research on Electromagnetic Control Technology for the Roll Profile of Wide-Width Electrode Roll Press Rolls. Processes. 2025; 13(5):1448. https://doi.org/10.3390/pr13051448
Chicago/Turabian StyleGuo, Chaojian, Hao Chen, Jingna Sun, Huagui Huang, Xuening Fu, and Zhijie Yang. 2025. "Research on Electromagnetic Control Technology for the Roll Profile of Wide-Width Electrode Roll Press Rolls" Processes 13, no. 5: 1448. https://doi.org/10.3390/pr13051448
APA StyleGuo, C., Chen, H., Sun, J., Huang, H., Fu, X., & Yang, Z. (2025). Research on Electromagnetic Control Technology for the Roll Profile of Wide-Width Electrode Roll Press Rolls. Processes, 13(5), 1448. https://doi.org/10.3390/pr13051448





