Optimization of Active Disturbance Rejection Controller for Distillation Process Based on Quantitative Feedback Theory

Abstract

The continuously increasing requirements for product purity and heat exchange efficiency in distillation processes exacerbate the system’s nonlinearity, coupling effects, and uncertainties. To address these challenges, this research proposes an optimized design approach for multivariable active disturbance rejection control (ADRC) that integrates quantitative feedback theory (QFT). An extended state observer is first employed to estimate and compensate for coupling and uncertainties, thus enabling effective decoupling. Under a two-degree-of-freedom equivalent model, QFT performance boundaries are transformed into a fitness function, turning controller parameter tuning into a frequency-domain multi-objective optimization problem. An improved multi-objective grey wolf algorithm is then introduced to optimize the controller parameters. The proposed approach is verified in a toluene–methylcyclohexane (MCH) extractive distillation process and compared with proportional–integral (PI) control and model predictive control (MPC). The simulation results indicate that, under the same feed temperature disturbance, the ADRC–QFT strategy reduces the system settling time by over 67% and lowers the integral of absolute error (IAE) index by more than 53% compared with PI–QFT and MPC, while also exhibiting stronger robustness to model uncertainties. These findings suggest that the proposed method provides an effective solution for achieving high precision and robust control in complex coupled distillation processes.

1. Introduction

Distillation is a widely employed separation technique that efficiently separates multi-component mixtures. It is extensively used in industries such as petrochemicals, pharmaceuticals, and food processing. However, its high energy consumption has garnered significant attention [1]. Studies show that a substantial portion of the energy consumed in distillation is lost through cooling water or product streams, rather than being directly utilized for separation. Therefore, reducing energy consumption offers considerable potential for improvement. Striking a balance between energy efficiency and separation performance has become a central challenge in the industry. Current research focuses on innovative process designs, heat integration technologies, and the development of efficient control strategies [2,3].

Distillation processes are often affected by external disturbances, which may stem from changes in environmental conditions, fluctuations in raw material characteristics, or equipment malfunctions. Among these, variations in the physical and chemical properties of raw materials (such as boiling point, density, and viscosity) can influence the yield of various distillates during the process, especially when mixing different raw materials, where the actual distillate yield may deviate from the calculated value [4]. In practical operations, particular attention must be given to the normal functioning of the equipment to ensure process stability and product quality [5]. Meanwhile, the impact of disturbances can also increase energy consumption and even jeopardize the stability of the system. Therefore, maintaining system stability and reducing fluctuations under external disturbances has become one of the core challenges in the optimization and control of distillation processes. Although proportional–integral–derivative (PID) control is widely used in industrial process control due to its simple structure and ease of implementation [6], the increasing complexity of modern distillation processes and the system’s coupling make PID control less effective in achieving optimal results. In contrast, model predictive control (MPC) demonstrates superior performance in handling multivariable coupled dynamics through its receding horizon optimization framework that systematically incorporates process constraints [7]. However, the dependency of MPC on system models and its high implementation costs limit its widespread adoption in industrial applications.

As a disturbance rejection technique with inherent uncertainty estimation capability, active disturbance rejection control (ADRC) has demonstrated significant advantages in complex industrial processes, attracting growing research interest over the past decade [8,9,10]. The core concept of ADRC is to treat system uncertainty and external disturbances as a total disturbance, which is observed and compensated in real-time using an extended state observer (ESO), thereby simplifying the system into a cascaded integrator structure. Since ADRC does not rely on precise mathematical models and possesses strong disturbance rejection capabilities, it has been widely applied in industrial practice [11,12]. This includes application research on ADRC in power generation systems [13], highlighting its effectiveness in compensating for uncertainty, and research on an improved ADRC design for the main steam pressure process [14], demonstrating its ability to suppress input disturbances and measurement noise, further showcasing ADRC’s potential in complex industrial systems. However, the parameter tuning of ADRC remains a challenge in the complex distillation process [15]. Especially in multivariable uncertain systems, due to the numerous and coupled controller parameters, the selection of any single parameter can have a significant impact on the system’s stability and dynamic performance [16].

Quantitative feedback theory (QFT) is a robust control design methodology for uncertain systems [17,18]. QFT transforms system uncertainties and performance specifications into constraints on the Nichols chart, which aids in the design of robust controllers. Compared to conventional robust control methods (such as $H\infty$ and $\mu$-synthesis) [19], QFT enables the explicit consideration of phase information during the design phase and provides a quantitative assessment of feedback cost. Recently, QFT has been widely applied to multivariable systems [20,21], time-delay systems [22], non-minimum-phase systems [23], input saturation systems [24] and discrete sampling systems [25]. By employing a graphical approach in the frequency domain, QFT allows for an intuitive controller design process and often provides guidance in selecting controller parameters [26]. However, in complex chemical processes, such as distillation, the design workload associated with QFT increases significantly. Designers must adjust controller parameters for each uncertainty frequency point to satisfy performance specifications. Moreover, conflicting requirements can further complicate the design process.

Based on the above analysis, this work proposes the design of a disturbance rejection controller for complex distillation processes using an ADRC framework. Additionally, the system structure and parameters are optimized using QFT. Building upon Reference [24], the proposed approach transforms the complex loop shaping problem into a multi-objective optimization task via QFT. The main contributions of this work are as follows:

(1)

For the problem of disturbance rejection control in distillation processes, the coupling effects of the system are regarded as total disturbances, and a multivariable ADRC structure is designed to achieve decoupling control. Each loop controller is transformed into a two-degree-of-freedom equivalent structure, with controller parameter tuning achieved using QFT;

(2)

System performance involves multiple conflicting specifications, such as stability, settling time, and disturbance rejection, which increases the difficulty of QFT-based loop shaping process. To address this issue, this work proposes transforming the controller parameter tuning problem into a frequency-domain multi-objective optimization problem, achieving a balance among multiple performance specifications through optimization algorithms. For the multi-objective optimization problem, an improved multi-objective grey wolf optimization (MOGWO) is further proposed. By adopting Gaussian distribution-based population initialization, introducing a grid-based leader selection mechanism, and dynamically adjusting parameters, the algorithm can quickly and effectively find the optimal trade-off solution, thereby improving the overall performance of the controller;

(3)

The proposed method is applied to the toluene–methylcyclohexane extraction distillation process. Simulation experiments based on Aspen Dynamics and Matlab validate the proposed control method, demonstrating better tracking performance and disturbance rejection compared to traditional PI control and model predictive control.

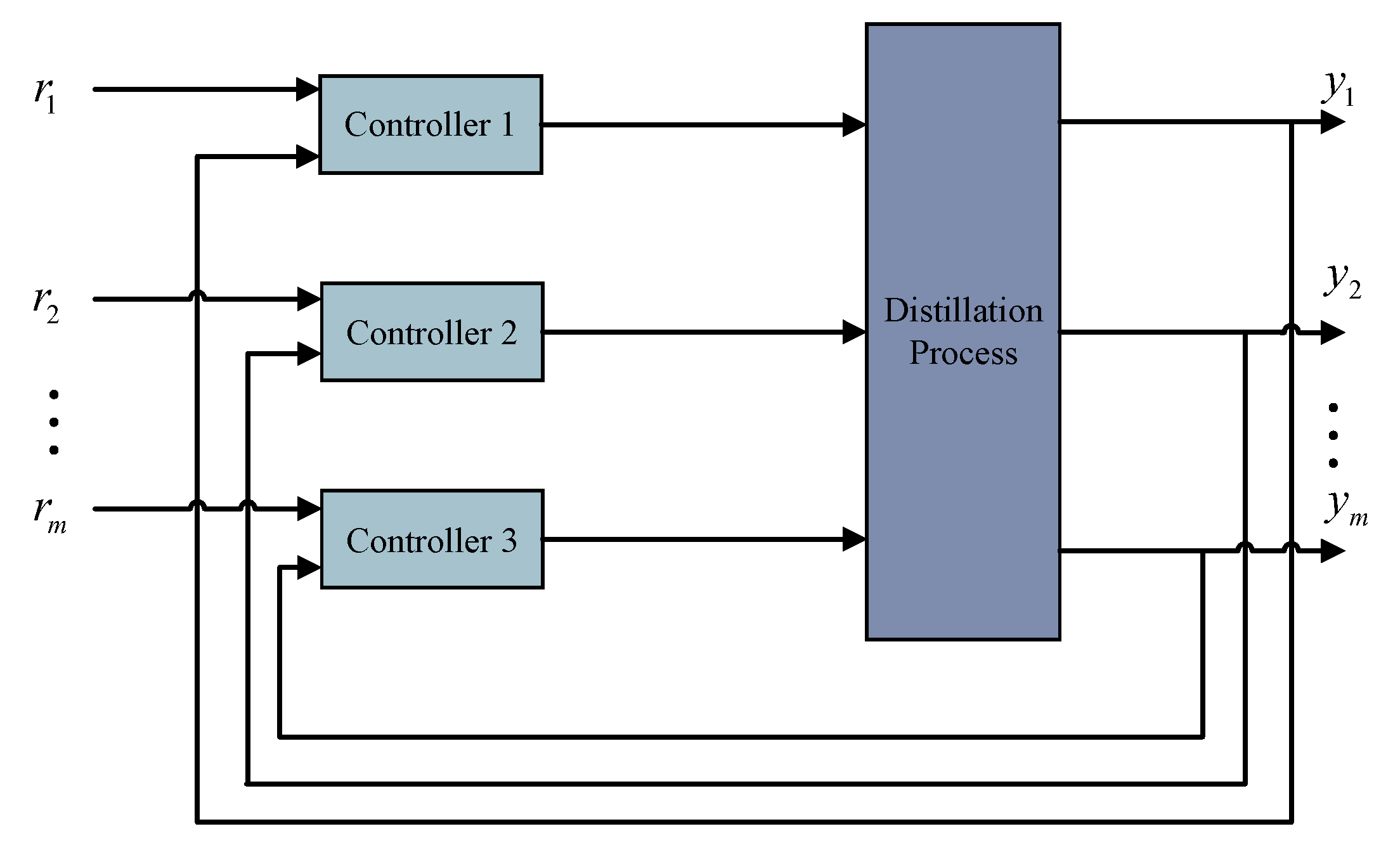
2. Problem Formulation

The distillation process is frequently modeled as a high-order, nonlinear, multiple-input multiple-output (MIMO) system due to the complex coupling between its input and output variables. To accurately represent the system’s dynamic behavior and facilitate the design of robust control strategies, linearization is performed while accounting for system uncertainties. We assume that the nonlinear dynamics of the distillation process can be represented as:

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=g(x,u,d,t)\hfill \\ y\left(t\right)=h(x,u,d,t)\hfill \end{array}\right.$$

(1)

where $x\left(t\right)\in R^n$ represents the system state vector, $u\left(t\right)\in R^m$ represents the control input vector, $y\left(t\right)\in R^m$ represents the system output vector, and $d\left(t\right)\in R^q$ represents the external disturbance vector. Expand $g\left(x,u,d,t\right)$ and $h\left(x,u,d,t\right)$ at the selected operating point $\left(x_0,u_0,d_0,t_0\right)$:

$$\left\{\begin{array}{c}g\left(x,u,d,t\right)=g\left(x_0,u_0,d_0,t_0\right)+\overline{A}\left(x-x_0\right)+\overline{B}\left(u-u_0\right)+E\left(d-d_0\right)\hfill \\ h\left(x,u,d,t\right)=h\left(x_0,u_0,d_0,t_0\right)+\overline{C}\left(x-x_0\right)+\overline{D}\left(u-u_0\right)+F\left(d-d_0\right)\hfill \end{array}\right.$$

(2)

where $x\left(t_0\right)=x_0$, $u\left(t_0\right)=u_0$, $d\left(t_0\right)=d_0$, $\overline{A}={{\displaystyle \frac{\partial g}{\partial x}|}}_{\left(x_0,u_0,d_0\right)}$, $\overline{B}={{\displaystyle \frac{\partial g}{\partial u}|}}_{\left(x_0,u_0,d_0\right)}$, $E={{\displaystyle \frac{\partial g}{\partial d}|}}_{\left(x_0,u_0,d_0\right)}$, $\overline{C}={{\displaystyle \frac{\partial h}{\partial x}|}}_{\left(x_0,u_0,d_0\right)}$, $\overline{D}={{\displaystyle \frac{\partial h}{\partial u}|}}_{\left(x_0,u_0,d_0\right)}$, and $F={{\displaystyle \frac{\partial h}{\partial d}|}}_{\left(x_0,u_0,d_0\right)}$.

According to Equation (2), the state-space model at the operating point is expressed as:

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=\left(\overline{A}+\Delta A\right)\left(x\left(t\right)-x_0\right)+\left(\overline{B}+\Delta B\right)\left(u\left(t\right)-u_0\right)+E\left(d\left(t\right)-d_0\right)\hfill \\ y\left(t\right)=\left(\overline{C}+\Delta C\right)\left(x\left(t\right)-x_0\right)+\left(\overline{D}+\Delta D\right)\left(u\left(t\right)-u_0\right)+F\left(d\left(t\right)-d_0\right)\hfill \end{array}\right.$$

(3)

where $\Delta A$, $\Delta B$, $\Delta C$, and $\Delta D$ represent dynamic perturbations introduced by model uncertainties.

The complexity of the distillation process results in a high-order linearized state-space model, making direct control design computationally intensive and challenging to implement. Consequently, model order reduction is commonly applied. The reduced-order linearized state-space model can be represented as:

$$\left\{\begin{array}{c}{\dot{x}}_r\left(t\right)=(\tilde{A}+\Delta \tilde{A})x_r\left(t\right)+(\tilde{B}+\Delta \tilde{B})u\left(t\right)+\tilde{E}\left(d\left(t\right)-d_0\right)\hfill \\ y\left(t\right)=({\tilde{C}}_r+\Delta \tilde{C})x_r\left(t\right)\hfill \end{array}\right.$$

(4)

where $\tilde{A}$, $\tilde{B}$, $\tilde{C}$, and $\tilde{E}$ represent the reduced-order system matrices; $\Delta \tilde{A}$, $\Delta \tilde{B}$, and $\Delta \tilde{C}$ represent the reduced-order uncertainty matrices; and $x_r\left(t\right)$ denotes the reduced-order state variables. The control objective is to design the control input $u\left(t\right)$ to ensure the system output $y\left(t\right)$ tracks the reference signal and suppresses disturbance signals, thereby maintaining system stability and meeting performance requirements.

3. Design of Disturbance Rejection Controller

3.1. Multivariable Active Disturbance Rejection Control Structure

The MIMO system described in Equation (4) can be expanded as follows:

$$\left\{\begin{array}{c}{y}_1^{\left(\tilde{n}\right)}\left(t\right)=f_1(x_r,d,t)+b_{11}{u}_1\left(t\right)+\cdots +b_{1m}{u}_m\left(t\right)\hfill \\ y_2^{\left(\tilde{n}\right)}\left(t\right)=f_2(x_r,d,t)+b_{21}{u}_1\left(t\right)+\cdots +b_{2m}{u}_m\left(t\right)\hfill \\ ⋮\hfill \\ y_m^{\left(\tilde{n}\right)}\left(t\right)=f_m(x_r,d,t)+b_{m1}{u}_1\left(t\right)+\cdots +b_{mm}{u}_m\left(t\right)\hfill \end{array}\right.$$

(5)

where $\tilde{n}$ represents the order of the reduced system, $y_i^{\left(\tilde{n}\right)}$ represents the $\tilde{n}$-th derivative of $y_i$, $b_{ii}$ is the input gain of $u_i\left(t\right)$, and $f_i$ represents the total disturbance in the i-th loop. This includes external disturbances, system uncertainties, and coupling effects between loops, which can be observed and compensated by designing an ESO, thereby achieving decoupling control. The original system is decoupled into multiple single-input single-output (SISO) systems for control. The control structure is shown in Figure 1.

3.2. SISO Active Disturbance Rejection Controller Design

The i-th loop in Equation (5) is expressed as:

$$y_i^{\left(\tilde{n}\right)}=f_i+b_{ii}{u}_i$$

(6)

where

$$f_i=f_i\left(x_r,d,u,t\right)$$

(7)

$y_i$ and $u_i$ represent the i-th output and input, respectively, while d denotes the external disturbance. By extending the total disturbance as the $(\tilde{n}+1)$-th state variable of the system, Equation (6) can be transformed into a continuous state-space equation of order $(\tilde{n}+1)$.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{x}}_i=A_i{x}_i+B_i{u}_i+E_i{\dot{f}}_i\hfill \\ y_i=C_i{x}_i\hfill \end{array}\right.\end{array}$$

(8)

where $A_i={\left[\begin{array}{ccccc}0& 1& 0& \cdots & 0\\ 0& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 1\\ 0& 0& 0& \cdots & 0\end{array}\right]}_{(\tilde{n}+1)\times (\tilde{n}+1)}$, $B_i={\left[\begin{array}{c}0\\ 0\\ ⋮\\ b_0\\ 0\end{array}\right]}_{(\tilde{n}+1)\times 1}$, $E_i={\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right]}_{(\tilde{n}+1)\times 1}$, $C_i={\left[\begin{array}{ccccc}1\hfill & 0& \cdots & 0& 0\end{array}\right]}_{1\times (\tilde{n}+1)}$, $b_0$ is the estimated value of $b_{ii}$.

The core concept of ADRC is to design an ESO to actively compensate for total disturbances, thereby reducing the system to an equivalent series of integrators for control. The structure of ADRC is illustrated in Figure 2. The ESO and control law are formulated as follows:

$$\left\{\begin{array}{c}\dot{z}\left(t\right)=A_i{z}_i\left(t\right)+B_i{u}_i\left(t\right)+L_i(y_i\left(t\right)-C_i{z}_i\left(t\right))\hfill \\ {\widehat{y}}_i\left(t\right)=C_i{z}_i\left(t\right)\hfill \end{array}\right.$$

(9)

$$u_i\left(t\right)=K_i({\overline{r}}_i\left(t\right)-z_i\left(t\right))$$

(10)

where $L_i={\left[\begin{array}{ccccc}{\beta }_1& {\beta }_2& \cdots & {\beta }_{\tilde{n}}& {\beta }_{\tilde{n}+1}\end{array}\right]}^{\mathrm{T}}$ is the observer’s error feedback gain, $z_i$ represents the estimated value of the system state $x_i$, $K_i\left[\begin{array}{ccccc}{l}_{\tilde{n}}& l_{\tilde{n}-1}& \cdots & l_1& 1\end{array}\right]/b_0$ is the controller’s error feedback gain, ${\overline{r}}_i\left(t\right)={\left[\begin{array}{ccccc}{r}_i\left(t\right)& {\dot{r}}_i\left(t\right)& \cdots & {r_i}^{\left(\tilde{n}-1\right)}\left(t\right)& 0\end{array}\right]}^{\mathrm{T}}$ is the extended form of the reference signal, and d is the external disturbance.

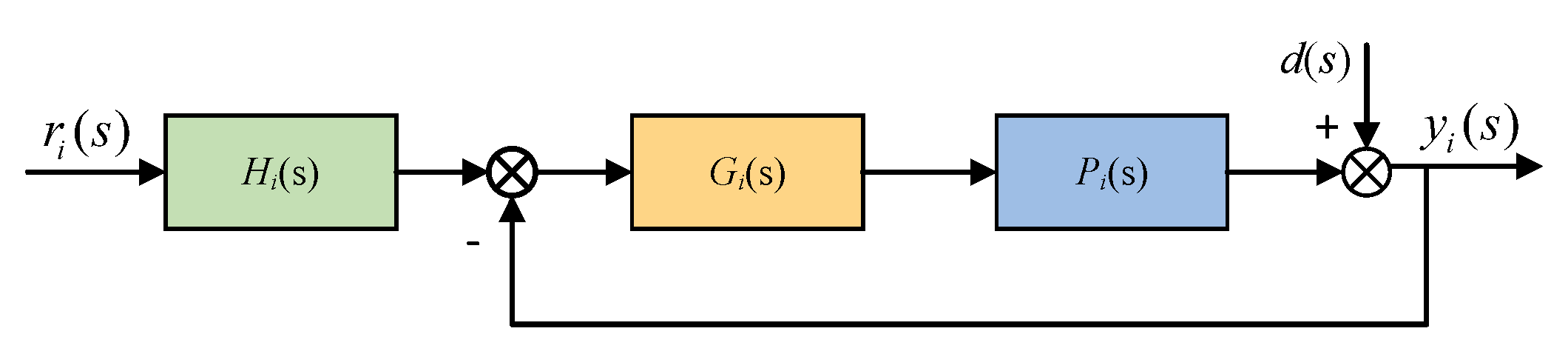
3.3. Equivalent Two-Degree-of-Freedom Control Structure

The structure shown in Figure 2 can be converted into an equivalent two-degree-of-freedom (2DOF) structure for analysis. Applying the Laplace transform to Equations (9) and (10) yields:

$$s{Z}_i\left(s\right)=(A_i-L_i{C}_i)Z_i\left(s\right)+B_i{U}_i\left(s\right)+L_i{Y}_i\left(s\right)$$

(11)

$$U_i\left(s\right)=K_i({\overline{R}}_i\left(s\right)-Z_i\left(s\right))$$

(12)

$${\overline{R}}_i\left(s\right)={\left[1s{s}^2\cdots s^{(\tilde{n}-1)}0\right]}^{\mathrm{T}}{R}_i\left(s\right)$$

(13)

where $Z_i\left(s\right)$, $U_i\left(s\right)$, $Y_i\left(s\right)$, and ${\overline{R}}_i\left(s\right)$ are the Laplace transforms of $z_i\left(t\right)$, $u_i\left(t\right)$, $y_i\left(t\right)$, and ${\overline{r}}_i\left(t\right)$, respectively. From Equation (11), it follows that:

$$Z_i\left(s\right)={(sI-A_i+L_i{C}_i)}^{-1}(B_i{U}_i\left(s\right)+L_i{Y}_i\left(s\right))$$

(14)

Substituting Equation (14) into Equation (12) results in

$$U_i\left(s\right)=G_i\left(s\right)(H_i\left(s\right)R_i\left(s\right)-Y_i\left(s\right))$$

(15)

where

$$G_i\left(s\right)={\displaystyle \frac{K_i{(sI-A_i+L_i{C}_i)}^{-1}{L}_i}{1+K_i{(sI-A_i+L_i{C}_i)}^{-1}{B}_i}}$$

(16)

$$H_i\left(s\right)={\displaystyle \frac{K_i{\left[1s\cdots s^{(\tilde{n}-1)}0\right]}^T}{K_i{(sI-A_i+L_i{C}_i)}^{-1}{L}_i}}$$

(17)

Based on Equations (16) and (17), the ADRC control structure can be transformed into the two-degree-of-freedom unit feedback structure shown in Figure 3. In this structure, the feedback controller $G_i\left(s\right)$ primarily ensures system stability and disturbance rejection performance, while the prefilter $H_i\left(s\right)$ filters the reference signal to maintain tracking performance.

4. Optimal Design of Controller Based on Quantitative Feedback Theory

4.1. Quantitative Feedback Theory

The basic procedure for designing controllers using QFT includes the following steps: template definition, performance specification design, loop shaping, and prefilter design [26].

4.1.1. Performance Specification in QFT

(1)

Robust stability performance specification

In minimum-phase systems, the relative stability of the closed-loop system can be represented by the closed-loop resonant peak:

$$\left|T_1\left(j\omega \right)\right|=\left|{\displaystyle \frac{P_i\left(j\omega \right)G_i\left(j\omega \right)}{1+P_i\left(j\omega \right)G_i\left(j\omega \right)}}\right|\le {\delta }_1=W_s$$

(18)

where $\omega \in \left[0,\infty \right)$, $P_i\left(j\omega \right)$ represents the plant model under all uncertainty conditions, $\left|T_1\left(j\omega \right)\right|$ is the magnitude–frequency response curve of the closed-loop transfer function, and $W_s$ is the closed-loop resonant peak. The relationship between the system’s gain margin ($GM$), phase margin ($PM$), and $W_s$ is:

$$\left\{\begin{array}{c}GM=20lg(1+{\displaystyle \frac{1}{W_s}})\hfill \\ PM=2arcsin{\displaystyle \frac{1}{2W_s}}\hfill \end{array}\right.$$

(19)

(2)

Disturbance rejection specification

The disturbance rejection specifications for the system output and input are defined as $T_2\left(j\omega \right)$ and $T_3\left(j\omega \right)$, respectively, as shown below:

$$\left|T_2\left(j\omega \right)\right|=\left|{\displaystyle \frac{1}{1+P_i\left(j\omega \right)G_i\left(j\omega \right)}}\right|\le {\delta }_2=\left|{\displaystyle \frac{a_o·j\omega }{a_o·j\omega +1}}\right|$$

(20)

$$\left|T_3\left(j\omega \right)\right|=\left|{\displaystyle \frac{P_i\left(j\omega \right)}{1+P_i\left(j\omega \right)G_i\left(j\omega \right)}}\right|\le {\delta }_3=\left|{\displaystyle \frac{a_i·j\omega }{a_i·j\omega +1}}\right|$$

(21)

where $a_o$ and $a_i$ are designable parameters.

(3)

Tracking performance specification

The system tracking performance specification is designed as follows:

$$\left\{\begin{array}{c}{\delta }_{4-lo}\left(\omega \right)\le \left|T_4\left(j\omega \right)\right|=\left|H_i\left(j\omega \right){\displaystyle \frac{G_i\left(j\omega \right)P_i\left(j\omega \right)}{1+G_i\left(j\omega \right)P_i\left(j\omega \right)}}\right|\le {\delta }_{4-up}\left(\omega \right)\hfill \\ {\delta }_{4-lo}\left(\omega \right)=\left|{\displaystyle \frac{a_l}{{\varsigma }_l·{\left(j\omega \right)}^2+{\xi }_l·j\omega +1}}\right|\hfill \\ {\delta }_{4-up}\left(\omega \right)=\left|{\displaystyle \frac{a_u·j\omega +{a_u}^{\prime }}{{\varsigma }_u·{\left(j\omega \right)}^2+{\xi }_u·j\omega +1}}\right|\hfill \end{array}\right.$$

(22)

where ${\delta }_{4_{l}o}\left(\omega \right)$ is the lower bound of the reference tracking performance specification, and ${\delta }_{4_{u}p}\left(\omega \right)$ is the upper bound. The parameters $a_l$, ${\varsigma }_l$, ${\xi }_l$, $a_u$, ${a_u}^{\prime }$, ${\varsigma }_u$, and ${\xi }_u$ are designable.

In performance specifications (18), (20), (21), and (22), the controlled plant can be represented in polar form as $P_i\left(j\omega \right)=p{e}^{j\theta }$. The controller of the i-th loop can be expressed as $G_i\left(j\omega \right)=g{e}^{j\phi }$. By substituting the polar form of the plant and controller into Equations (18), (20), (21), and (22), the performance specifications are transformed into a quadratic inequality system of the following form:

$$\left\{\begin{array}{c}{p}^2\left(1-{\displaystyle \frac{1}{{\delta }_1^2}}\right)g^2+2pcos(\theta +\phi )g+1\ge 0\hfill \\ p^2{g}^2+2pcos(\theta +\phi )g+\left(1-{\displaystyle \frac{1}{{\delta }_2^2}}\right)\ge 0\hfill \\ p^2{g}^2+2pcos(\theta +\phi )g+\left(1-{\displaystyle \frac{p}{{\delta }_3^2}}\right)\ge 0\hfill \\ p_e^2{p}_d^2\left(1-{\displaystyle \frac{1}{{\delta }_4^2}}\right)g^2+2p_e{p}_d\left(p_{e}cos({\theta }_d+\phi )-{\displaystyle \frac{p_d}{{\delta }_4^2}}cos(\theta +\phi )\right)g_r+\left(p_e^2-{\displaystyle \frac{p_d^2}{{\delta }_4^2}}\right)\ge 0\hfill \end{array}\right.$$

(23)

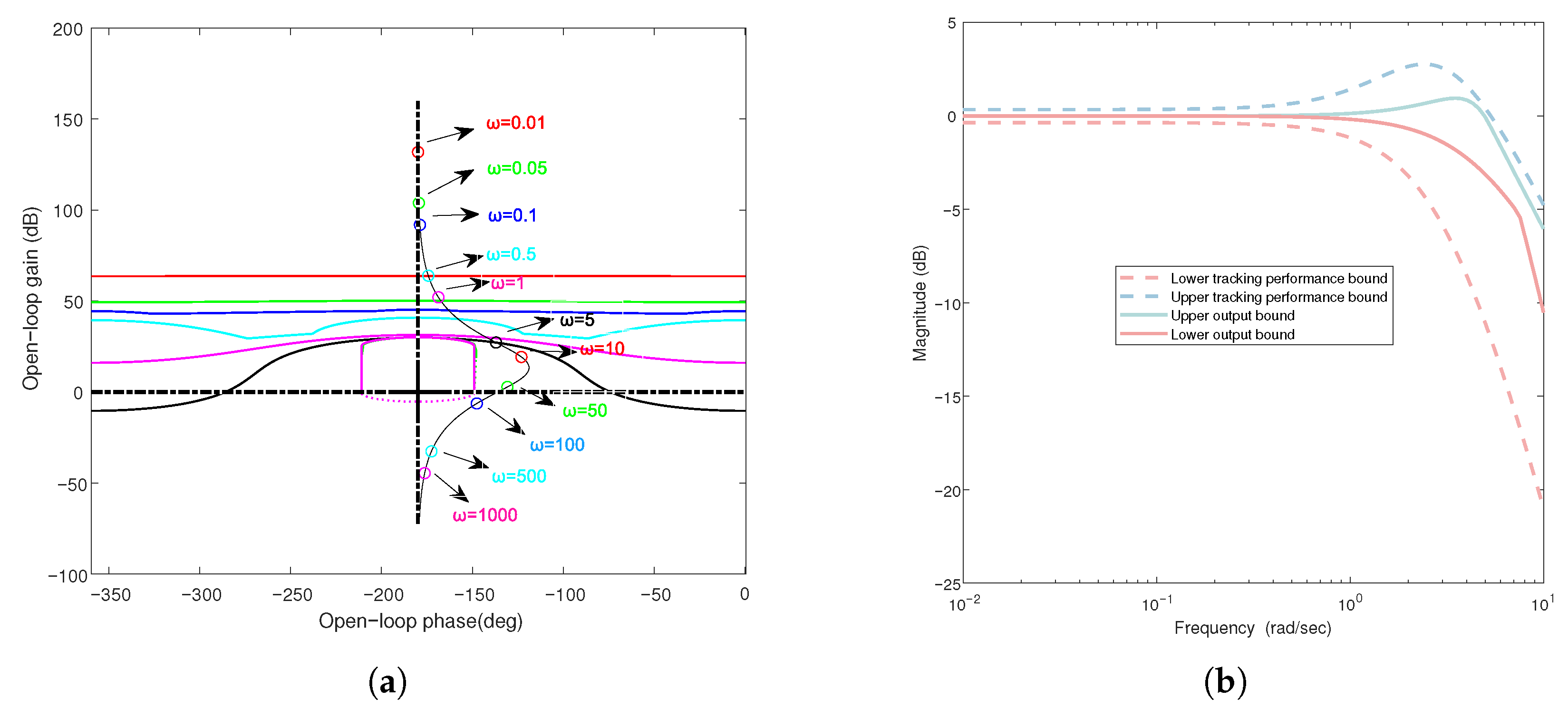
4.1.2. Loop Shaping

The structure of the controller $G\left(s\right)$ is presented as follows:

$$G_i\left(s\right)=k_G{\displaystyle \frac{{\prod }_{q=1}^{n_{rz}}((s/z_q)+1){\prod }_{q=1}^{n_{cz}}((s^2/{\omega }_{nq}^2)+(2{\zeta }_q/{\omega }_{nq})s+1)}{s^r{\prod }_{j=1}^{m_{rp}}((s/p_j)+1){\prod }_{j=1}^{m_{cp}}((s^2/{\omega }_{nj}^2)+(2{\zeta }_j/{\omega }_{nj})s+1)}}$$

(24)

where $k_G$ is the controller gain, $z_q$ is the real zero, ${\omega }_{nq}$ is the natural frequency, ${\zeta }_q$ is the damping of the complex zero, and $n_{rz}$ and $n_{cz}$ are the numbers of real and complex zeros, respectively. Additionally, $p_j$ is the real pole, ${\omega }_{nj}$ is the natural frequency, ${\zeta }_j$ is the damping of the complex pole, and $m_{rp}$ and $m_{cp}$ are the numbers of real and complex poles, respectively. The order, zeros, and poles of the controller are determined by the ADRC equivalent structure in Equation (16).

4.1.3. Prefilter Design and Validation

In the loop shaping process, only the ratio of the upper and lower bounds of the tracking performance is considered to meet the requirements, which does not guarantee full compliance. Therefore, the prefilter $H_i\left(s\right)$ is used to meet the tracking performance of the closed-loop system. The structure of the prefilter $H_i\left(s\right)$ is determined by Equation (17). Once the parameters of the controller $G_i\left(s\right)$ are determined in the loop shaping process, the parameters of the prefilter $H_i\left(s\right)$ are also fixed. It is necessary to verify whether the obtained prefilter meets the tracking performance requirements. If it does, the design is complete; otherwise, additional tracking differentiators $T_d$ are considered to meet the tracking performance. The prefilter is then designed as follows:

$${H_i}^{\prime }\left(s\right)=H_i\left(s\right)·T_d$$

(25)

where the linear tracking differentiator can be designed as $T_d={\displaystyle \frac{1}{(s/r_1+1)(s/r_2+1)}}$, where $r_1$ and $r_2$ are the parameters to be designed.

4.2. Parameter Optimization Based on QFT

Performance specifications are defined using QFT, generating boundary curves on the Nichols chart. These boundary curves are used to construct objective functions and constraints, reformulating controller parameter tuning as a frequency-domain multi-objective optimization problem. Optimization algorithms are then applied to balance conflicting performance specifications, seeking an optimal trade-off solution to improve overall controller performance.

For the loop shaping process, the first objective function regarding the open-loop gain of the system is defined as:

$$J_1=K_g^2$$

(26)

where $K_g={\displaystyle \frac{K_i{(L_i{C}_i-A_i)}^{-1}{L}_i}{1+K_i{(L_i{C}_i-A_i)}^{-1}{B}_i}}$.

The second objective function, $J_2$, focuses on low-frequency performance, ensuring the system meets tracking and disturbance rejection specifications. The system should demonstrate effective tracking and disturbance rejection in the low-frequency range. The objective minimizes the distance between the system response and its predefined low-frequency performance boundaries (typically non-closed curves) to ensure satisfactory performance.

$$J_2={\sum }_{\lambda =1}^N\left|R_d\left({\omega }_{\lambda }\right)-R_a\left({\omega }_{\lambda }\right)\right|$$

(27)

where $\lambda =1,2,\cdots ,\eta$, with $\eta$ being the number of selected frequency points; ${\omega }_{\lambda }$ represents the $\lambda$-th selected frequency point; $R_d\left({\omega }_{\lambda }\right)$ represents the boundary curve in the low-frequency range; $R_a\left({\omega }_{\lambda }\right)$ is the open-loop frequency response of the system; and N is the number of frequency points in the low-frequency range.

The third objective function, $J_3$, focuses on optimizing high-frequency stability. The high-frequency stability boundaries of the system are typically represented as closed curves. Stability is quantitatively analyzed by evaluating the gain and phase deviations between the system’s frequency response and these boundaries, as well as the geometric distance between the system response and the boundary curve. The goal is to minimize these deviations and distances while ensuring the system remains stable at high frequencies.

$$J_3={\sum }_{\lambda =1}^M\sqrt{\Delta G{\left({\omega }_{\lambda }\right)}^2+\Delta \varphi {\left({\omega }_{\lambda }\right)}^2+d{\left({\omega }_{\lambda }\right)}^2}$$

(28)

where $\Delta G\left({\omega }_{\lambda }\right)$ and $\Delta \varphi \left({\omega }_{\lambda }\right)$ represent the gain and phase deviations at frequency ${\omega }_{\lambda }$, respectively, $d\left({\omega }_{\lambda }\right)$ denotes the distance between the system’s open-loop frequency response and the stability boundary at frequency ${\omega }_{\lambda }$, and M is the number of frequency points in the high-frequency range.

To ensure that the solutions obtained during the optimization process always meet the system design requirements, three constraint functions are selected based on the different QFT boundary conditions, as follows:

(1)

In a reasonable loop shaping result, the system’s magnitude–frequency characteristic curve should change monotonically. This is verified by calculating the difference in magnitude characteristics across the frequency range and checking whether it changes monotonically.

$${\varphi }_1\left(x\right)=max\left(0,V\left({\omega }_{\lambda +1}\right)-V\left({\omega }_{\lambda }\right)\right)$$

(29)

where $V\left({\omega }_{\lambda }\right)$ denotes the magnitude of the system’s frequency response at that frequency point.

(2)

For the low-frequency range, the system’s open-loop frequency characteristics should correspond to points above the boundary curve for tracking and disturbance rejection synthesis, ensuring the system can accurately track the input signal and effectively reject disturbances.

$${\varphi }_2\left(x\right)=max\left(0,\left|B_0\left({\omega }_{\lambda }\right)\right|-\left|T_{2,3,4}\left({\omega }_{\lambda }\right)\right|\right)$$

(30)

where $T_{2,3,4}\left({\omega }_{\lambda }\right)$ represents the disturbance and tracking performance specifications of the system at frequency ${\omega }_{\lambda }$, and $B_0\left({\omega }_{\lambda }\right)$ is the synthesized boundary for tracking and disturbance rejection performance.

(3)

For the high-frequency range, the system’s open-loop frequency characteristics should correspond to points outside the stability boundary curve, ensuring the system’s stability.

$${\varphi }_3\left(x\right)=\left\{\begin{array}{c}1,T_1\left(j{\omega }_{\lambda }\right)\in B_s\left(j{\omega }_{\lambda }\right)\hfill \\ 0,T_1\left(j{\omega }_{\lambda }\right)\notin B_s\left(j{\omega }_{\lambda }\right)\hfill \end{array}\right.$$

(31)

where $T_1\left(j{\omega }_{\lambda }\right)$ represents the robust stability index of the system at frequency ${\omega }_{\lambda }$ (in the high-frequency range), and $B_s\left(j{\omega }_{\lambda }\right)$ is the robust stability boundary.

Finally, the multi-objective optimization problem is formulated as:

$$W=min\left(J_1,J_2,J_3\right),\begin{array}{c}\end{array}s.t.{\varphi }_1\left(x\right)+{\varphi }_2\left(x\right)+{\varphi }_3\left(x\right)=0$$

(32)

4.3. Optimization Based on Improved Multi-Objective Grey Wolf Optimizer

To extend the grey wolf optimizer (GWO) [27] for multi-objective optimization, researchers developed MOGWO [28], enabling it to handle multiple conflicting objectives simultaneously. However, the original MOGWO suffers from uneven solution distribution and a tendency to converge to local optima in complex multi-objective problems. To address these issues, this research proposes improvements to the MOGWO.

Optimization Process of Improved MOGWO

Figure 4 shows the detailed steps of the improved multi-objective grey wolf optimization algorithm. The process is as follows:

• Initialize population and parameters:
  The initial positions of the grey wolf population vectors $X_I$ are generated through a Gaussian distribution-based initialization mechanism.

  $$X_I=normrnd\left(\mu ,\sigma \right)$$

  (33)

  where $I=1,2,\cdots ,p$, with p being the population size; $\mu$ represents the midpoint of the lower and upper bounds of the search space; and $\sigma$ denotes the standard deviation.
• Non-dominated sorting:
  Non-dominated sorting is performed on the initial solution set to generate different levels of non-dominated solution sets $Y_1,Y_2,\cdots ,Y_k$. Based on the sorting results, an archive population is established to store all non-dominated solutions.

  $$Y_k=\left\{X_I\mid X_I\mathrm{not}\mathrm{dominated}\mathrm{by}\mathrm{any}\mathrm{solution}\right\}$$

  (34)

  where k is the number of non-dominated solution sets.
• Dynamically adjust parameters based on the iteration count:
  As the number of iterations increases, the parameters a, A, and C are dynamically adjusted.

  $$\left\{\begin{array}{c}a=2-2t/t_{max}\hfill \\ A=2a·rand\left(\right)-a\hfill \\ C=2·rand\left(\right)\hfill \end{array}\right.$$

  (35)

  where t is the current iteration number, $t_{max}$ is the maximum number of iterations, and $rand\left(\right)$ represents a random number uniformly distributed in the range [0, 1].
• Grid-based leader selection mechanism:
  Based on fitness values and grid density, the alpha, beta, and delta wolves are selected, representing the best solution, the second-best solution, and the third-best solution, respectively.
• Update the positions of wolves in the population:
  The positions of the wolves in the population are updated based on the positions of the $\alpha$, $\beta$, and $\delta$ wolves. The position update equations are as follows:

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{D}_{\alpha }=\left|C_1·X_{\alpha }-X\right|\hfill \\ D_{\beta }=\left|C_2·X_{\beta }-X\right|\hfill \\ D_{\delta }=\left|C_3·X_{\delta }-X\right|\hfill \end{array}\right.\end{array}$$

  (36)

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{X}_1=X_{\alpha }-A_1·D_{\alpha }\hfill \\ X_2=X_{\beta }-A_2·D_{\beta }\hfill \\ X_3=X_{\delta }-A_3·D_{\delta }\hfill \end{array}\right.\end{array}$$

  (37)

  $$\begin{array}{c}\hfill X\left(t+1\right)=\left(X_1+X_2+X_3\right)/3\end{array}$$

  (38)

  where $X\left(t\right)$ represents the position of the wolves at the t-th generation; $X_{\alpha }$, $X_{\beta }$, and $X_{\delta }$ represent the positions of the $\alpha$, $\beta$, and $\delta$ wolves, respectively; $A_i$ and $C_i$ are update parameters; and $D_i$ is the distance vector.
• Update the archive population:
  The fitness value of each individual is calculated, and the archive population is updated based on the fitness values.

  $$\begin{array}{c}\hfill w_{\tau }=\left[w_1\left(X_I\right),w_2\left(X_I\right),\dots ,w_{\vartheta }\left(X_I\right)\right]\end{array}$$

  (39)

  where $w_{\tau }$ is the fitness value vector of the $\tau$-th individual, $w_{\vartheta }$ is the value of the $\vartheta$-th objective function, and $\vartheta$ is the number of objective functions.
• Check the archive population:
  If the number of individuals in the archive population reaches the upper limit, the crowding distance is calculated and the individuals with higher crowding distances are removed to maintain the diversity of the solution set. The crowding distance calculation is:

  $$\begin{array}{c}\hfill {\phi }_{\gamma }=\sum _{\psi =1}^{\vartheta }\left(w_{\psi }^{\gamma +1}-w_{\psi }^{\gamma -1}\right)\end{array}$$

  (40)

  where ${\phi }_{\gamma }$ is the crowding distance of the $\gamma$-th solution, and $w_{\psi }^{\gamma +1}$ and $w_{\psi }^{\gamma -1}$ are the values of the objective function $w_{\vartheta }$ of the adjacent individuals after sorting.
• Iteration:
  Check whether the maximum iteration number $t_{max}$ has been reached. If so, terminate the algorithm; otherwise, dynamically adjust parameters a, A, and C and continue iterating.

4.4. Optimization Result Selection

The results of multi-objective optimization are not directly applicable. To derive practical solutions, the weighted sum method based on multi-objective optimization is employed in this research. The objective function $J_{sum}$ is defined as:

$$\begin{array}{c}\hfill J_{sum}={\theta }_1{J}_1+{\theta }_2{J}_2+{\theta }_3{J}_3\end{array}$$

(41)

where the weight coefficients ${\theta }_1$, ${\theta }_2$, and ${\theta }_3$ satisfy ${\theta }_1+{\theta }_2+{\theta }_3=1$. The weights are determined based on the Pareto front results and the practical requirements of the distillation process. In this research, ${\theta }_1=0.3$, ${\theta }_2=0.3$, and ${\theta }_3=0.4$.

5. Simulation and Discussion

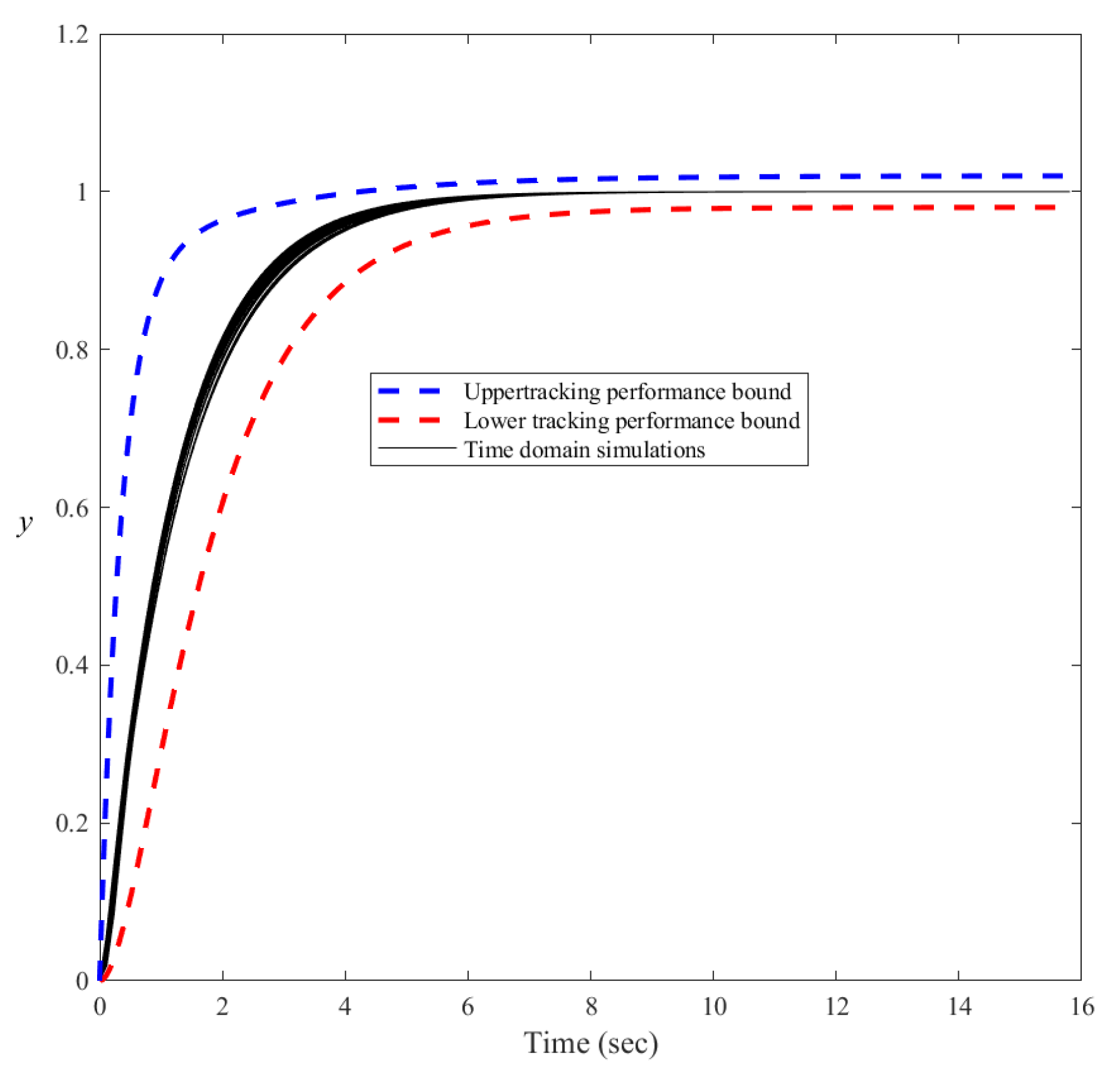
5.1. Numerical Simulation

To systematically validate the design procedure and overall effectiveness of the proposed control strategy, this work utilizes a second-order ADRC controller for numerical simulations on a second-order system with uncertainties. The choice of a second-order model is primarily driven by its capability to accurately represent the dominant dynamic behavior of the system, while also allowing for a direct assessment of the proposed method’s robustness to model uncertainties through controller parameter optimization.

$$\begin{array}{c}\hfill P\left(s\right)={\displaystyle \frac{k}{1+2\zeta s/{\omega }_n+s^2/{\omega }_n^2}}\end{array}$$

(42)

where $k\in \left[2,5\right]$, $\zeta \in \left[0.3,0.6\right]$, ${\omega }_n=\left[4,8\right]$, and the specific selection criteria for the model and parameter ranges were determined based on the methodology outlined in Reference [26].

The performance specifications are selected as follows [26]:

(1)

Robust stability specification:

$$\begin{array}{c}\hfill \left|\left.{\displaystyle \frac{P\left(j\omega \right)G\left(j\omega \right)}{1+P\left(j\omega \right)G\left(j\omega \right)}}\right|\right.\le W_s=1.46\end{array}$$

(43)

where $\omega =\left[\begin{array}{cccccccccc}0.01& 0.05& 0.1& 0.5& 1& 5& 10& 50& 100& 500\end{array}\right]$ rad/s.

(2)

Output disturbance performance specification:

$$\begin{array}{c}\hfill \left|\left.{\displaystyle \frac{1}{1+P\left(j\omega \right)G\left(j\omega \right)}}\right|\right.\le \left|\left.{\displaystyle \frac{0.32\left(j\omega \right)}{0.32\left(j\omega \right)+1}}\right|\right.\end{array}$$

(44)

where $\omega =\left[\begin{array}{ccccc}0.01& 0.05& 0.1& 0.5& 1\end{array}\right]$ rad/s.

(3)

Input disturbance performance specification:

$$\begin{array}{c}\hfill \left|\left.{\displaystyle \frac{P\left(j\omega \right)}{1+P\left(j\omega \right)G\left(j\omega \right)}}\right|\right.\le \left|\left.{\displaystyle \frac{1.5\left(j\omega \right)}{1.5\left(j\omega \right)+1}}\right|\right.\end{array}$$

(45)

where $\omega =\left[\begin{array}{ccccc}0.01& 0.05& 0.1& 0.5& 1\end{array}\right]$ rad/s.

(4)

Reference tracking specification:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\delta }_{lo}\left(\omega \right)=\left|{\displaystyle \frac{0.98}{8.16{\left(j\omega \right)}^2+5.714\left(j\omega \right)+1}}\right|\hfill \\ {\delta }_{up}\left(\omega \right)=\left|{\displaystyle \frac{2.1\left(j\omega \right)+1.02}{0.6384{\left(j\omega \right)}^2+2.048\left(j\omega \right)+1}}\right|\hfill \end{array}\right.\end{array}$$

(46)

where $\omega =\left[\begin{array}{ccccc}0.01& 0.05& 0.1& 0.5& 1\end{array}\right]$ rad/s.

Figure 5a presents the results of the initial optimization iteration, where black points represent the solutions obtained through the search process, and red points denote the non-dominated solution set. The initial iteration produced numerous candidate solutions. To enhance the quality and accuracy of the solution set, a second optimization iteration was conducted, as shown in Figure 5b. After the second iteration, the algorithm more effectively concentrated on the high-quality solution space, reducing the risk of local optima. Figure 6 illustrates the final solution obtained using the weighted sum method, where red circles indicate the final weighted solutions.

After weighting and selection, the optimal solution is determined as follows: $l_1=4.97$; $l_2=25.78$; ${\beta }_1=453.11$; ${\beta }_2=18486.14$; ${\beta }_3=567104.88$; $b_0=151.92$. Figure 7a presents the feedback controller design results during the loop shaping. The responses at specific frequency points closely match the designed curves. Furthermore, in the high-frequency range (e.g., $\omega =50$ and $\omega =500$), the system response meets the robust stability boundaries. Figure 7b presents the prefilter design results. The filter $H\left(s\right)$ fully meets the tracking performance constraints. Figure 8 presents the time-domain simulation results for the controlled system under all uncertainties. The system response meets the upper and lower bounds, achieving fast and accurate set-point tracking performance.

To evaluate the system’s disturbance rejection performance, input and output disturbances are introduced at $t=2\mathrm{s}$. The simulation results, considering all uncertainties, are shown in Figure 9. The controller effectively rejects the effects of both input and output disturbances, ensuring stable system operation.

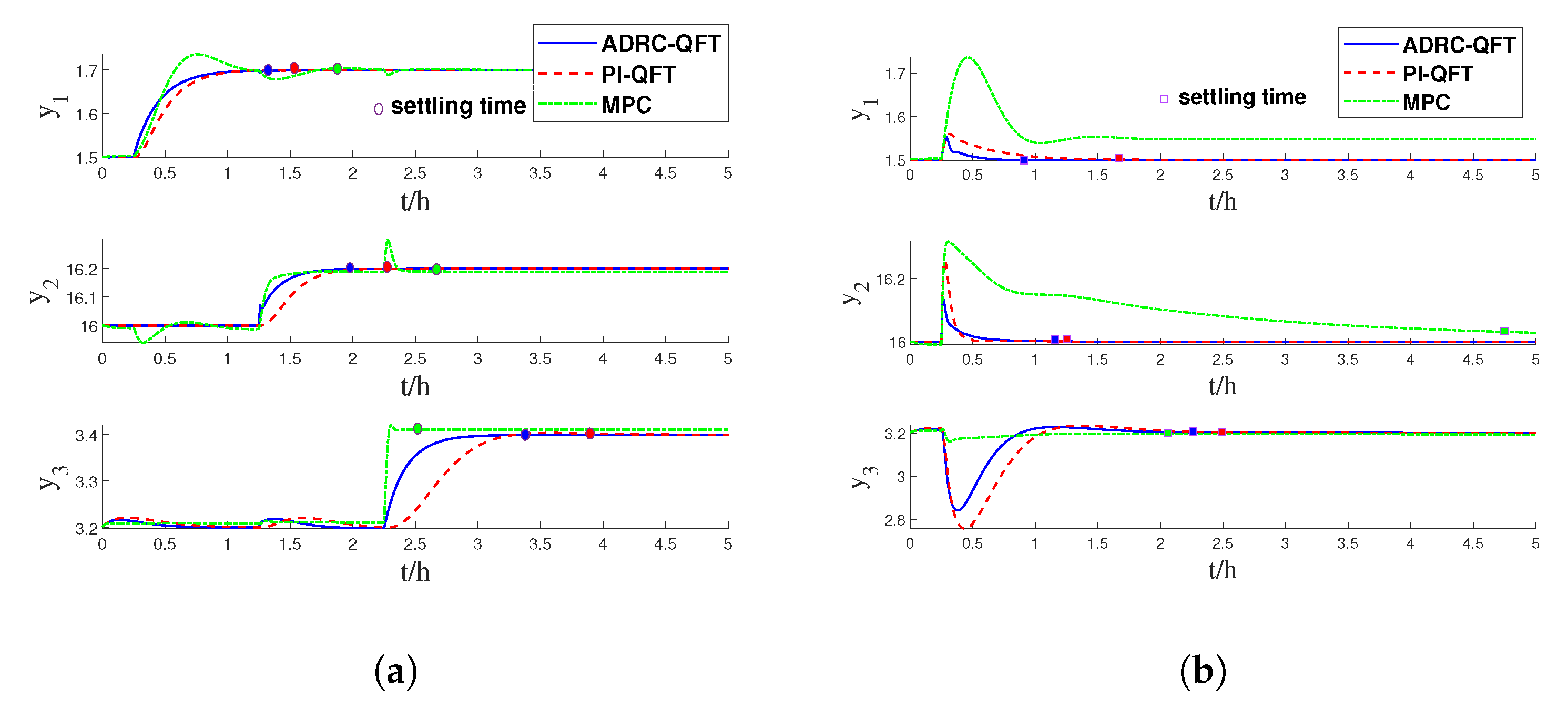
5.2. Application in Extraction Distillation Process

In this section, an extractive distillation process for separating toluene and MCH [29] was developed in Aspen Plus, and a controller was implemented in Matlab Simulink. By performing integrated simulations, the effectiveness of the proposed method was further verified. The control structure of the extractive distillation process is shown in Figure 10. Phenol was chosen as the entrainer, with a total condenser and a kettle reboiler. The feed flow rate was set to 1600 lbmol/h, and the feed temperature was 200 °F. The mixture contained 12.5% MCH. The MCH recovery in the distillate was required to be no lower than 97%, while the phenol recovery in the bottoms was no lower than 85%. The thermodynamic model employed was UNIFAC.

The process variables and operating conditions are summarized in

Table 1. Description of the variables and operation conditions.

Symbol	Description	Operating Point
$n_t$	Number of trays	22
$n_f$	Feed tray	14
$P_d$	Distillate top pressure	6 kPa
$P_{dr}$	Tray pressure drop	0.68 kPa
F	Feed flow rate	1600 lbmol/hr
D	Distillate flow rate	200 lbmol/hr
B	Bottom flow rate	1400 lbmol/hr
R	Reflux ratio	8
$u_1$	MCH mass flow rate	19,605 lb/hr
$u_2$	Condenser medium flow rate	180,250 lb/hr
$u_3$	Bottom mass flow rate	131,296 lb/hr
$y_1$	Liquid level of tray 1	1.5 Ft
$y_2$	Pressure of tray 1	16 psi
$y_3$	Liquid level of tray 22	3.2 Ft
$d_1$	Phenol feed temperature	220 F

, where $u_1$, $u_2$, and $u_3$ are the manipulated variables; $y_1$, $y_2$, and $y_3$ are the controlled variables; and $d_1$ is an external disturbance. The steady-state results were then imported into Aspen Dynamics, and following the procedure described in Section 2, the system was linearized and reduced-order state-space models were obtained. Subsequently, the proposed method was utilized to design the controller.

In Figure 10, the control structure consists of three loops, where the level $y_1$ is regulated by $u_1$ in loop 1, the pressure $y_2$ is regulated by $u_2$ in loop 2, and the level $y_3$ is regulated by $u_3$ in loop 3. The allowable ranges for the manipulated variables $u_1$, $u_2$, and $u_3$ are defined as $u_1\in [16105,23105]$, $u_2\in [176350,184150]$, and $u_3\in [128796,133796]$. The performance indices are chosen as $W_s=1.93$, $a_o=1$, $a_l=3.5$, $a_l=0.96$, ${\varsigma }_l=0.0977$, ${\xi }_l=0.0625$, $a_u=0.06667$, $a_u^{\prime }=1.04$, ${\varsigma }_u=0.1124$, and ${\xi }_u=0.5589$. The frequency points are chosen as $\omega =[0.01,0.05,0.1,0.5,1,5,10,50,100,500,1000]\mathrm{rad}/\mathrm{s}$.

Based on the performance specifications outlined above, the parameters of the ADRC controller are first selected using the proposed method. The results of the ADRC loop shaping and prefilter design are illustrated in Figure 11 (using loop 1 as an example). The parameters of the PI controller are tuned using the same method, and the resulting ADRC and PI controller parameters are presented in

Table 2. The set of ADRC-QFT and PI-QFT parameters.

ADRC-QFT Parameters
Loop 1	$l_1=65.24;l_2=3410.11;k_1=5.11;b_0=2.94$
Loop 2	$l_1=79.12;l_2=1918.61;k_1=11.04;b_0=7.74$
Loop 3	$l_1=77.24;l_2=549.74;k_1=5.94;b_0=8.49$
PI-QFT Parameters
Loop 1	$k_p=11.37;k_i=19.80;r_1=4.80;r_2=15.40$
Loop 2	$k_p=0.52;k_i=21.70;r_1=6.57;r_2=12.83$
Loop 3	$k_p=0.44;k_i=1.50;r_1=4.13;r_2=4.93$

. The MPC control strategy employs a sampling period of 0.01 h, a prediction horizon of 20, and a control horizon of 2.

Figure 12a shows the tracking simulation results for three different control strategies (ADRC-QFT, PI-QFT, and MPC). Step signals with an amplitude of 0.2 are introduced at $t=0.25$ h, $t=1.25$ h, and $t=2.25$ h for the three loops. For loop 1 ($y_1$), the ADRC-QFT control strategy reaches steady state within 1 h after the setpoint change, with an overshoot of less than 2%. Although there are slight fluctuations in the initial stage, the overall response speed is fast, and the stability is good. In comparison, the response speed of PI-QFT is slower, reaching steady state after approximately 1.5 h. The MPC control strategy responds relatively quickly, but due to the differences between the linearized model and the actual model, significant coupling effects between the loops lead to a large overshoot.

Figure 12b shows the dynamic response characteristics of different control strategies in disturbance rejection simulations. When the feed temperature rises from 220 °F to 230 °F at $t=0.25$ h, ADRC-QFT exhibits good disturbance rejection performance in the first two loops, with a settling time of about 0.6 h. Although PI-QFT eventually recovers to steady state, the settling time in all three loops is longer, especially in loops 1 and 2, where the settling time is between 1.3 h and 1.6 h. Its disturbance rejection capability is inferior to that of ADRC-QFT. The settling time for MPC is noticeably longer than both ADRC-QFT and PI-QFT, indicating that MPC has a longer adjustment and settling time after disturbances, making it difficult to stabilize the system quickly, and its disturbance rejection performance is weaker.

Table 3. Comparison of IAE index specification for ADRC-QFT, MPC, and PI-QFT control strategies in tracking and disturbance rejection simulations. (* indicates the best-performing strategy).

Control Strategy	Simulation Type	Loop 1	Loop 2	Loop 3
ADRC-QFT	Tracking	0.0406 *	0.0274 *	0.0487 *
	Disturbance rejection	0.0069 *	0.0159 *	0.1309
PI-QFT	Tracking	0.0570	0.0581	0.1181
	Disturbance rejection	0.0217	0.0222	0.2089
MPC	Tracking	0.0562	0.0766	0.1489
	Disturbance rejection	0.2956	0.4598	0.0376 *

further quantifies the performance of each control strategy in tracking and disturbance rejection tasks using the IAE index as the performance evaluation metric. ADRC-QFT generally performs well in both tracking and disturbance rejection tasks, especially in the disturbance rejection task of loop 1, where the IAE index value is only 0.0069, which is significantly lower than MPC’s 0.2956 and PI-ADRC’s 0.0217, highlighting its advantage in disturbance suppression. In contrast, although MPC performs decently in certain loops, its IAE index value in disturbance rejection tasks is higher, indicating limitations in disturbance suppression when there are prediction errors in the model. Overall, ADRC-QFT demonstrates stable dynamic performance in all tasks.

6. Conclusions

A novel ADRC methodology integrating QFT and an enhanced multi-objective grey wolf optimizer is proposed for robust control of extractive distillation processes. The key contributions can be summarized as follows. First, a multivariable ADRC framework based on an ESO is developed to decouple system dynamics through the real-time estimation and compensation of coupling effects and model uncertainties. Second, a two-degree-of-freedom equivalent model is utilized to map QFT performance boundaries into objective functions and constraints, thereby reformulating the ADRC parameter tuning process as a multi-objective optimization problem. Third, the conventional multi-objective grey wolf algorithm is augmented with a Gaussian distribution-based initialization mechanism, grid-based leader selection, and dynamic parameter adjustment, enabling more effective solution-space exploration and ensuring a balance among stability, rapid response, and robustness.

Simulation studies in Aspen Dynamics on a toluene–methylcyclohexane extractive distillation process demonstrate the superiority of the proposed approach. Under setpoint changes, ADRC-QFT achieves a 60 min settling time with only 2.5% overshoot, outperforming PI-QFT and MPC in both settling time and disturbance rejection. Specifically, it reduces settling time by 67% and the integral of absolute error by 53% when faced with temperature disturbances, while maintaining robustness under ±15% model parameter variations. These results validate the method’s effectiveness in complex distillation control and offer actionable guidance for industrial implementation.

The primary limitation of this work arises from the potential inadequacy of controllers designed under the assumption of system linearity when applied to strongly nonlinear systems. Such controllers may fail to meet the prescribed performance specifications in practical scenarios. To address this issue, future research will focus on explicitly modeling the nonlinear characteristics of the system, incorporating their impact into the controller design process, and validating the proposed approach through experimental implementation on physical platforms.