Optimal Strategy for Grid Loss Reduction Under Electricity Transmission and Distribution Reform Considering Low-Carbon Benefits
Abstract
1. Introduction
- (1)
- The model accounts for indirect costs associated with carbon emissions, providing a more comprehensive evaluation of the economic and environmental impacts of different loss reduction strategies.
- (2)
- This study employs an adaptive genetic algorithm to solve the optimization problem, which is more efficient and effective than traditional enumeration methods, especially when dealing with a large number of possible strategy combinations.
- (3)
- The model is validated using data from a provincial power grid company in China, demonstrating its practical applicability and effectiveness in reducing grid losses and carbon emissions.
2. Literature Review
3. Methods and Analysis
3.1. Objective Function
- (1)
- Comprehensive investment for loss-reduction measures :
- (2)
- Direct cost due to loss of electricity :
- (3)
- Indirect cost due to loss of electricity :
3.2. Constraint
- (1)
- The voltage deviation is [30]:
- (2)
- Branch constraints. The actual transmission capacity of the branch shall not exceed its maximum transmission capacity, expressed by the transmission current [30]:
- (3)
- The quantitative restriction of loss reduction measures is:
- (4)
- The total investment limit is:
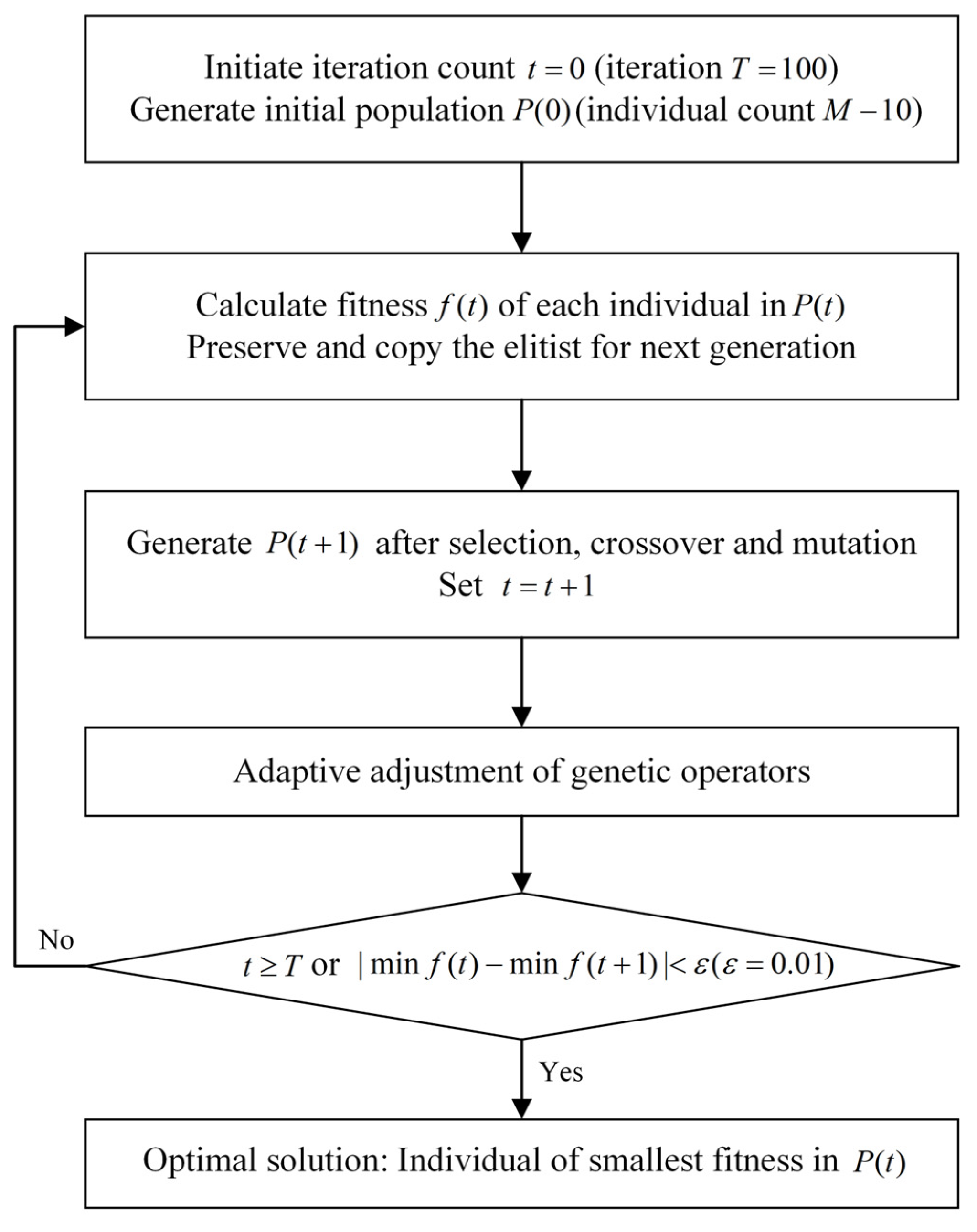
3.3. Optimization
- (1)
- Encoding
- (2)
- Fitness function
- (3)
- Genetic manipulation
- (1)
- Adaptive cross operation
- (2)
- Mutation operation
- (4)
- Iterative termination condition
- (1)
- The number of iterations has reached the maximum number of iterations M;
- (2)
- The difference in the fitness of the mutated individual between iteration and satisfies:
4. Results and Discussion
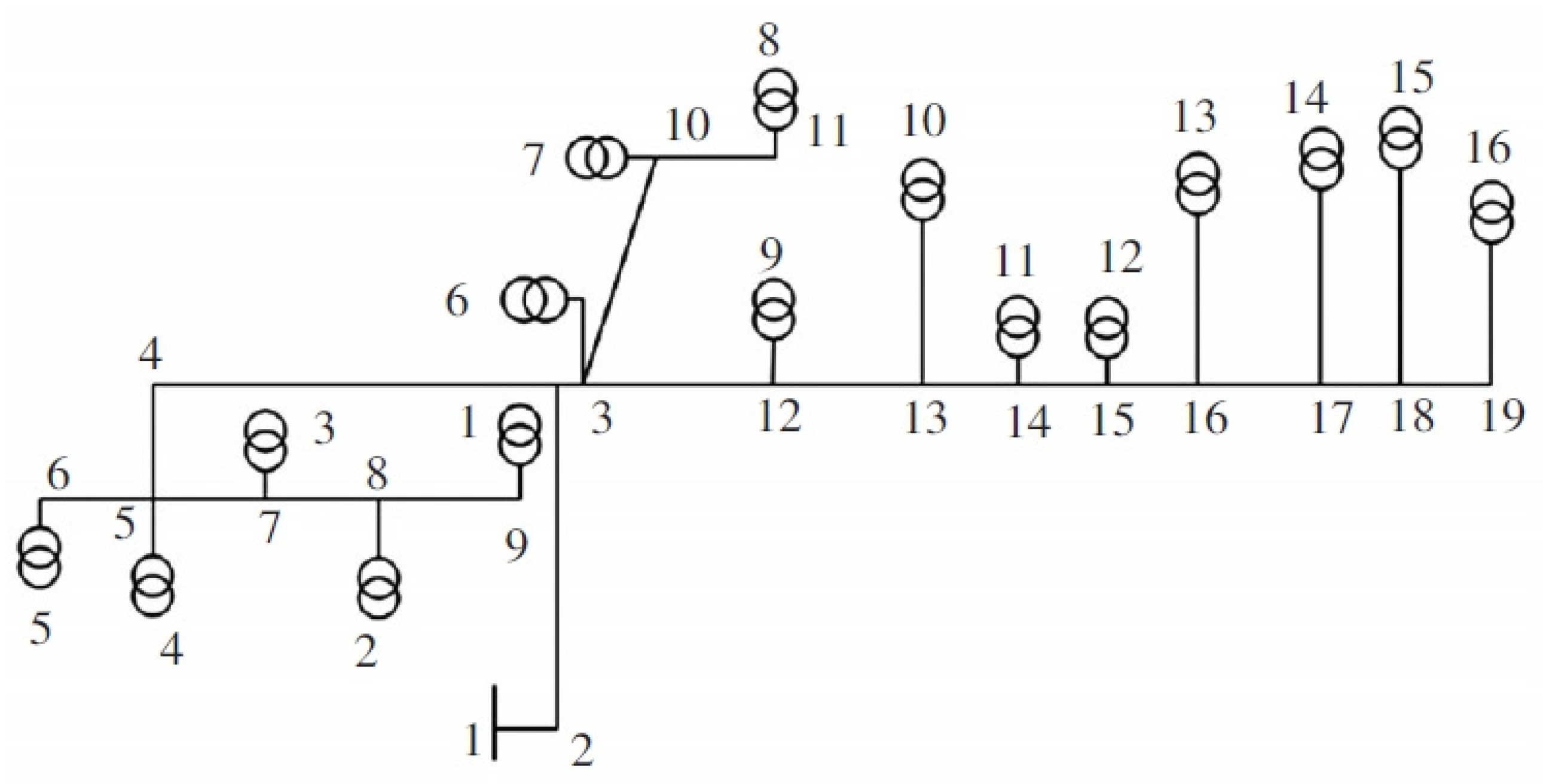
4.1. Case Description
4.2. Application in One Small Sample
4.2.1. Data
4.2.2. Solutions
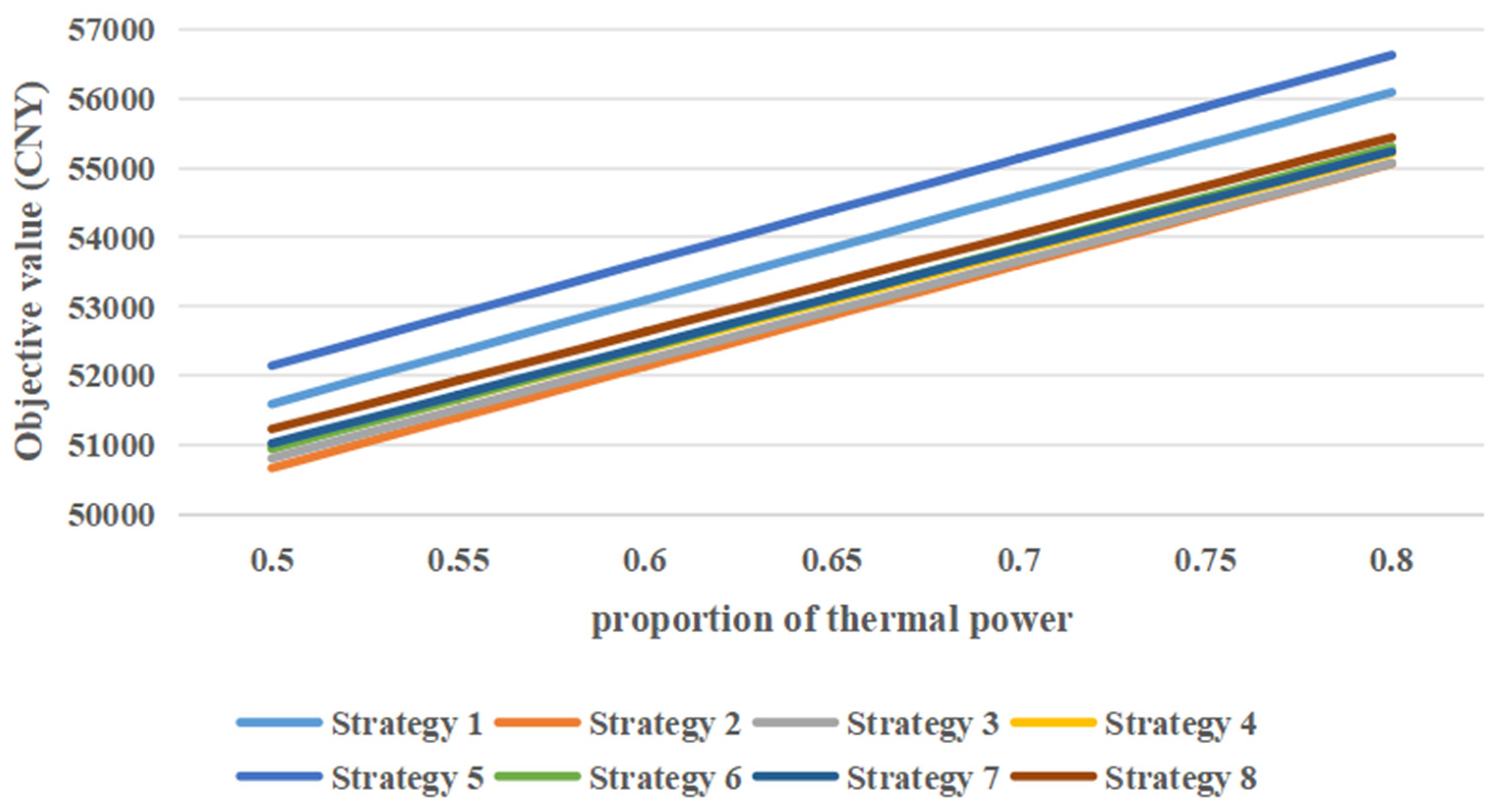
4.2.3. Sensitivity Analysis
4.3. Application in the Provincial Power Gird Company
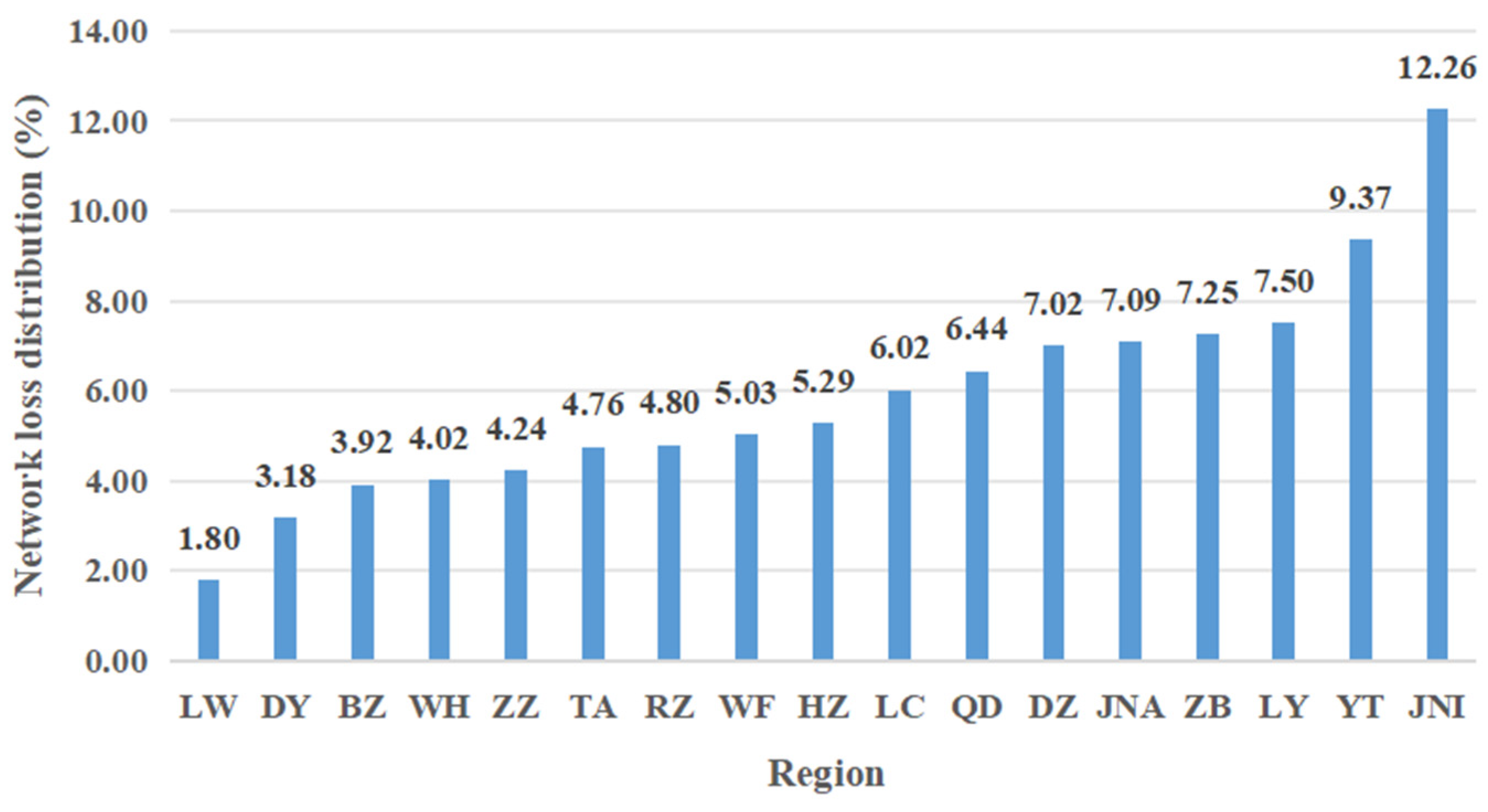
4.3.1. Power Grid Loss Distribution
4.3.2. Analysis of Loss Reduction Potential
4.4. Discussion
- (1)
- Potential synergies with renewable energy sources and technologies
- (2)
- Economic concerns
- (3)
- Scalability of the model and optimization method
- (4)
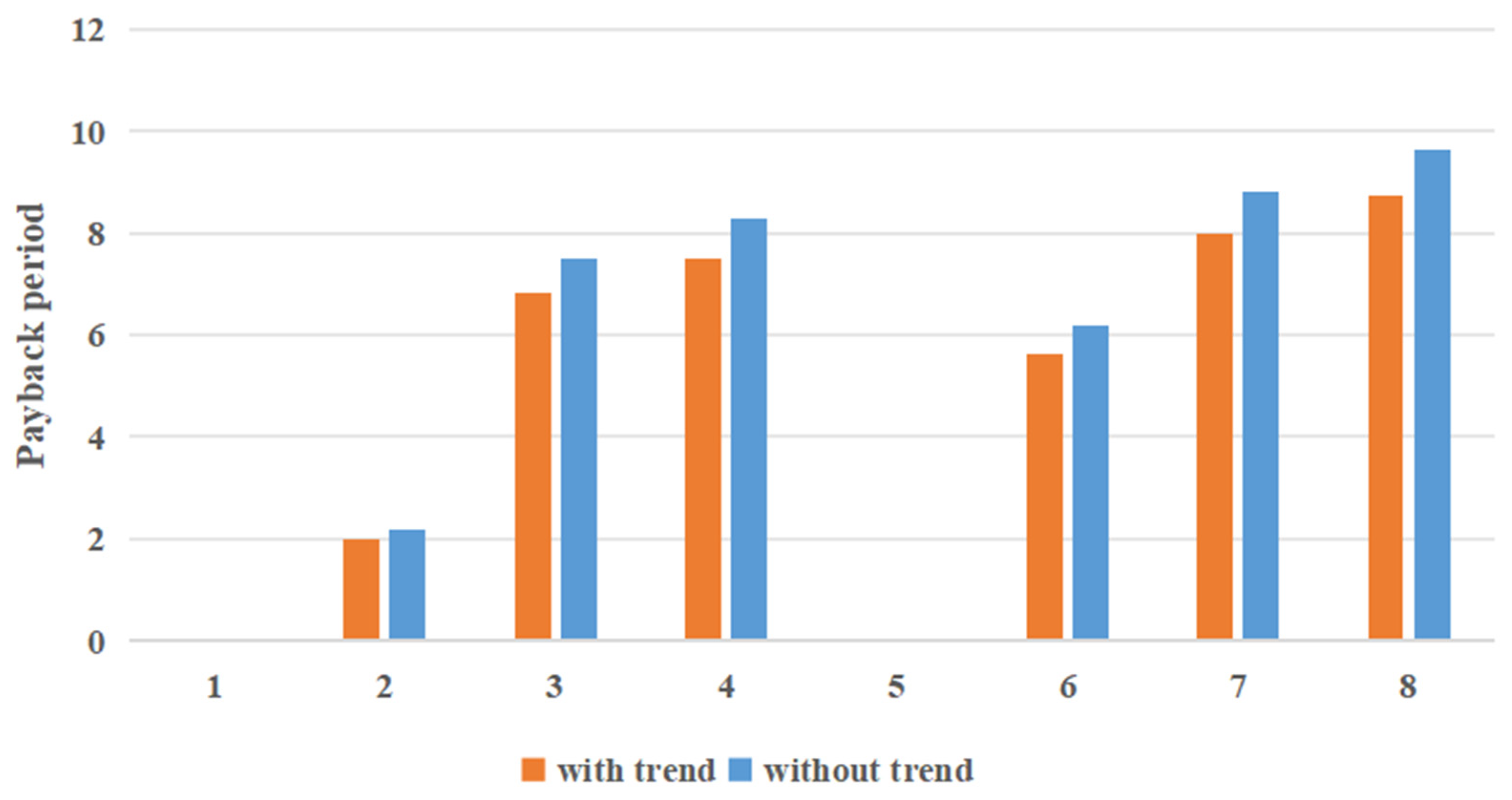
- Effect of the trend
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pang, B.; Zhang, L.H.; Ten, Y.F.; Chang, Z.W.; Tang, C.; Hu, C.Q.; Liu, Z.W.; Wang, B.L. An incentive scheme of peak-valley price based on differential privacy. J. Chongqing Univ. 2023, 46, 56–68. [Google Scholar]
- Yu, X.; Dong, Z.; Zheng, D.; Deng, S. Analysis of critical peak electricity price optimization model considering coal consumption rate of power generation side. Environ. Sci. Pollut. Res. 2024, 31, 41514–41528. [Google Scholar] [CrossRef]
- Tian, X.; Niu, X.; Zhu, X.; Zhao, G. Optimal strategy and assessment method for minimizing power loss of Shandong power network under lowcarbon background. Autom. Electr. Power Syst. 2014, 38, 67–72. [Google Scholar]
- Bouakkaz, A.; Gil Mena, A.J.; Haddad, S.; Ferrari, M.L. Efficient energy scheduling considering cost reduction and energy saving in hybrid energy system with energy storage. J. Energy Storage 2021, 33, 101887. [Google Scholar] [CrossRef]
- Eid, A. Cost-based analysis and optimization of distributed generations and shunt capacitors incorporated into distribution systems with nonlinear demand modeling. Expert Syst. Appl. 2022, 198, 116844. [Google Scholar] [CrossRef]
- Li, C.; Xu, D. Family of enhanced ZCS single-stage single-phase isolated AC–DC converter for high-power high-voltage DC supply. IEEE Trans. Ind. Electron. 2017, 64, 3629–3639. [Google Scholar] [CrossRef]
- Long, Y.; Wang, X.Y.; Zhou, Q.; An, H.Y.; Chen, Z. Distribution network reconfiguration for loss reduction considering maximum power supply capability index. Proc. CSU-EPSA 2017, 29, 131–134. [Google Scholar]
- Sadeghian, O.; Moradzadeh, A.; Mohammadi-Ivatloo, B.; Abapour, M.; Anvari-Moghaddam, A.; Lim, J.S.; Marquez, F.P.G. A comprehensive review on energy saving options and saving potential in low voltage electricity distribution networks: Building and public lighting. Sustain. Cities Soc. 2021, 72, 103064. [Google Scholar] [CrossRef]
- Sambaiah, K.S.; Jayabarathi, T. Loss minimization techniques for optimal operation and planning of distribution systems: A review of different methodologies. Int. Trans. Electr. Energy Syst. 2020, 30, e12230. [Google Scholar] [CrossRef]
- Sun, K.; Xiao, H.; Liu, S.; You, S.; Yang, F.; Dong, Y.; Wang, W.; Liu, Y. A Review of Clean Electricity Policies—From Countries to Utilities. Sustainability 2020, 12, 7946. [Google Scholar] [CrossRef]
- Kyriakopoulos, G.L. Energy Communities Overview: Managerial Policies, Economic Aspects, Technologies, and Models. J. Risk Financ. Manag. 2022, 15, 521. [Google Scholar] [CrossRef]
- Lazzeroni, P.; Repetto, M. Optimal planning of battery systems for power losses reduction in distribution grids. Electr. Power Syst. Res. 2019, 167, 94–112. [Google Scholar] [CrossRef]
- Xie, J.; Chen, C.; Long, H. A loss reduction optimization method for distribution network based on combined power loss reduction strategy. Complexity 2021, 2021, 9475754. [Google Scholar] [CrossRef]
- Wang, W.; Cai, D.; Liu, H.; Zhou, C.; Cao, K.; Zhou, K.; Liu, C. Theoretical Analysis of Power Loss Reduction for Typical Power Grid. In Proceedings of the ICASIT 2020: 2020 International Conference on Aviation Safety and Information Technology, Weihai, China, 14–16 October 2020; pp. 383–387. [Google Scholar]
- Suresh, M.; Edward, J.B. A hybrid algorithm based optimal placement of DG units for loss reduction in the distribution system. Appl. Soft Comput. 2020, 91, 106191. [Google Scholar] [CrossRef]
- Pokhrel, B.R.; Karthikeyan, N.; Bak-Jensen, B.; Pillai, J.R. Loss optimization in distribution networks with distributed generation. In Proceedings of the 2017 52nd International Universities Power Engineering Conference (UPEC 2017), Heraklion, Greece, 28–31 August 2017; pp. 1–6. [Google Scholar]
- Ahmadi, I.; Ahmadigorji, M.; Tohidifar, E. A novel approach for power loss reduction in distribution networks considering budget constraint. Int. Trans. Electr. Energy Syst. 2018, 28, e2635. [Google Scholar] [CrossRef]
- Iweh, C.D.; Gyamfi, S.; Tanyi, E.; Effah-Donyina, E. Distributed Generation and Renewable Energy Integration into the Grid: Prerequisites, Push Factors, Practical Options, Issues and Merits. Energies 2021, 14, 5375. [Google Scholar] [CrossRef]
- Kataray, T.; Nitesh, B.; Yarram, B.; Sinha, S.; Cuce, E.; Shaik, S.; Vigneshwaran, P.; Roy, A. Integration of smart grid with renewable energy sources: Opportunities and challenges–A comprehensive review. Sustain. Energy Technol. Assess. 2023, 58, 103363. [Google Scholar] [CrossRef]
- Alotaibi, I.; Abido, M.A.; Khalid, M.; Savkin, A.V. A comprehensive review of recent advances in smart grids: A sustainable future with renewable energy resources. Energies 2020, 13, 6269. [Google Scholar] [CrossRef]
- Mu, H.; Pei, Z.; Wang, H.; Li, N.; Duan, Y. Optimal Strategy for Low-Carbon Development of Power Industry in Northeast China Considering the ‘Dual Carbon’ Goal. Energies 2022, 15, 6455. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Wang, J.; Zhang, Y. Deep Reinforcement Learning Based Volt-VAR Optimization in Smart Distribution Systems. IEEE Trans. Smart Grid 2020, 12, 361–371. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, K.; Zhang, G. Power distribution system reconfiguration based on genetic algorithm. In Proceedings of the 2016 IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 3–5 October 2016; pp. 80–84. [Google Scholar]
- Sehgal, S.; Swarnkar, A.; Gupta, N.; Niazi, K.R. Reconfiguration of distribution network for loss reduction at different load schemes. In Proceedings of the 2012 IEEE Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 1–2 March 2012; pp. 1–4. [Google Scholar]
- Gautam, M.; Bhusal, N.; Benidris, M.; Louis, S. A Spanning Tree-based Genetic Algorithm for Distribution Network Reconfiguration. In Proceedings of the 2020 IEEE Industry Applications Society Annual Meeting, Detroit, MI, USA, 10–16 October 2020; pp. 1–6. [Google Scholar]
- Kamel, S.; Hamour, H.; Nasrat, L.; Yu, J.; Xie, K.; Khasanov, M. Radial distribution system reconfiguration for real power losses reduction by using salp swarm optimization algorithm. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 720–725. [Google Scholar]
- Wu, H.; Li, T.; Chen, H.; Li, B.; Liu, T. Distribution network line loss optimization method based on war strategy algorithm. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 395–402. [Google Scholar]
- Zhang, L.; Yan, Y.; Xu, W.; Sun, J.; Zhang, Y. Carbon emission calculation and influencing factor analysis based on industrial big data in the “double carbon” era. Comput. Intell. Neurosci. 2022, 2022, 2815940. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Hou, H.; Ge, X.D.; Wang, X.H.; Lu, Y.C.; Wang, Y.X. Two-stage mixed-game win-win strategy for integrated energy system considering multi-stage utilization of carbon emission. Autom. Electr. Power Syst. 2025, 49, 69–79. [Google Scholar]
- Zheng, W.; Wu, W.; Zhang, B.; Sun, H.; Liu, Y. A fully distributed reactive power optimization and control method for active distribution networks. IEEE Trans. Smart Grid 2015, 7, 1021–1033. [Google Scholar] [CrossRef]
- Srinivas, M.; Patnaik, L. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Trans. Syst. Man. Cybern. 1994, 24, 656–667. [Google Scholar] [CrossRef]
- Zhai, L.; Feng, S. A novel evacuation path planning method based on improved genetic algorithm. J. Intell. Fuzzy Syst. 2022, 42, 1813–1823. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Zhan, Z.H.; Zhang, J.; Li, Y.; Chung, H.S.H. Adaptive Particle Swarm Optimization. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2009, 39, 1362–1381. [Google Scholar] [CrossRef]



| Name | Physical Meaning | Values Range | Units Measured |
|---|---|---|---|
| comprehensive investment | (0, ∞) | CNY | |
| direct cost due to loss of electricity | (0, ∞) | CNY | |
| indirect cost due to loss of electricity | (0, ∞) | CNY | |
| power loss | (0, ∞) | kW·h | |
| electricity price | (0, ∞) | CNY/(kW·h) | |
| carbon penalty | (0, ∞) | CNY/kg | |
| f | carbon emission penalty per unit of electricity generation | (0, ∞) | CNY |
| Q | carbon emissions per unit of electricity generation | (0, ∞) | kg/(kW·h) |
| ∆U% | voltage deviation | (0, 100) | % |
| Ij | actual transmission capacity of the branch | (0, ∞) | A |
| Regional Name | Active Loss/(MW) | Active Power Generation/(MW·h) | Active Load/(MW) | Received Power/(MW) |
|---|---|---|---|---|
| LW | 0.102 | 18.600 | 12.585 | −6.015 |
| DY | 0.180 | 8.000 | 26.257 | 18.257 |
| BZ | 0.222 | 8.250 | 7.407 | −0.843 |
| WH | 0.228 | 19.600 | 13.027 | −6.573 |
| ZZ | 0.240 | 17.700 | 16.899 | −0.802 |
| TA | 0.270 | 26.799 | 21.454 | −5.345 |
| RZ | 0.272 | 20.600 | 19.115 | −1.485 |
| WF | 0.285 | 19.800 | 52.417 | 32.617 |
| HZ | 0.300 | 30.100 | 25.656 | −4.444 |
| LC | 0.341 | 44.650 | 20.471 | −24.179 |
| QD | 0.365 | 25.400 | 13.596 | −11.804 |
| DZ | 0.398 | 26.700 | 27.306 | 0.606 |
| JNA | 0.402 | 23.100 | 45.757 | 22.657 |
| ZB | 0.411 | 32.480 | 40.712 | 8.232 |
| LY | 0.425 | 29.950 | 53.534 | 23.584 |
| YT | 0.531 | 53.900 | 48.279 | −5.622 |
| JNI | 0.695 | 79.746 | 35.237 | −44.509 |
| ID | MMR/(kW·h) | AAP/kW | ARP/kvar | ALF/% |
|---|---|---|---|---|
| 1 | 31,630 | 43.93 | 27.22 | 55 |
| 2 | 40,769 | 56.62 | 30.09 | 18 |
| 3 | 5340 | 7.42 | 3.6 | 14.8 |
| 4 | 22,880 | 31.78 | 19.7 | 10 |
| 5 | 0 | 0 | 0 | 0 |
| 6 | 48,960 | 68 | 46.16 | 34 |
| 7 | 8927 | 12.4 | 5.69 | 41.3 |
| 8 | 41,640 | 57.83 | 30.86 | 72.3 |
| 9 | 0 | 0 | 0 | 0 |
| 10 | 45,120 | 62.67 | 34.85 | 12.5 |
| 11 | 52,000 | 72.22 | 40.78 | 14.4 |
| 12 | 21,000 | 29.17 | 18.09 | 29.2 |
| 13 | 28,600 | 39.72 | 22.63 | 39.7 |
| 14 | 33,540 | 46.58 | 26.88 | 23.3 |
| 15 | 135,360 | 188 | 116.56 | 29.8 |
| 16 | 97,200 | 135 | 83.7 | 42.8 |
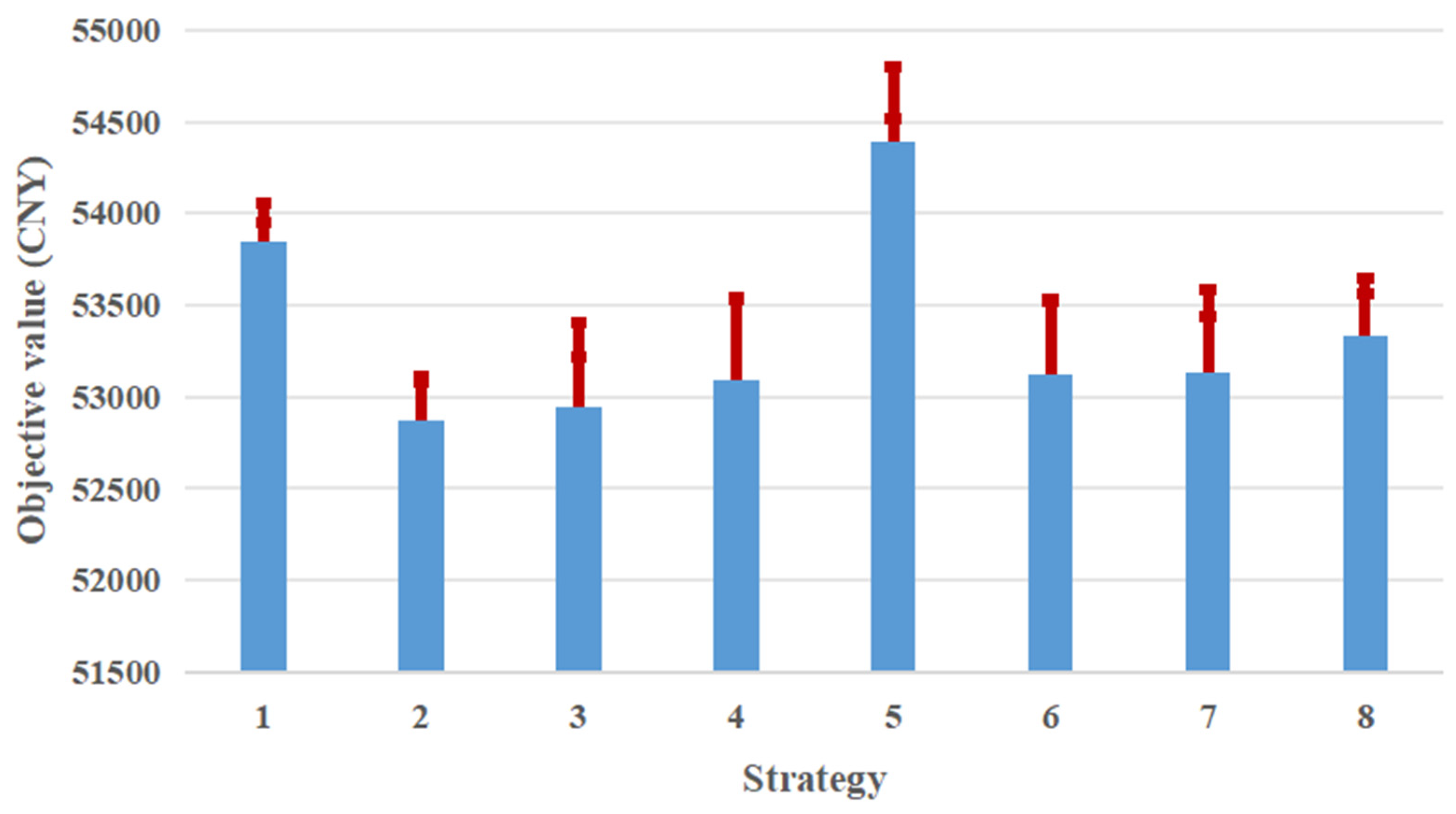
| Strategy | RC | UT | EC | PLB | PLA |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 88,192 | 88,192 |
| 2 | 0 | 0 | 1 | 88,192 | 86,160 |
| 3 | 0 | 1 | 0 | 88,192 | 83,520 |
| 4 | 0 | 1 | 1 | 88,192 | 83,326 |
| 5 | 1 | 0 | 0 | 88,192 | 87,938 |
| 6 | 1 | 0 | 1 | 88,192 | 85,436 |
| 7 | 1 | 1 | 0 | 88,192 | 82,684 |
| 8 | 1 | 1 | 1 | 88,192 | 82,587 |
| Strategy | Optimal Solution | Suboptimal Solution |
|---|---|---|
| RC | 0 | 0 |
| UT | 0 | 1 |
| EC | 1 | 0 |
| direct loss | 43,080 | 41,760 |
| indirect loss | 9520.37 | 9228.66 |
| annual investment | 264.4 | 1950 |
| objective function | 52,864.77 | 52,938.66 |
| Optimal Strategy | Objective Function | ||
|---|---|---|---|
| 0.25 | 0.2 | 2 | 31,324.77 |
| 0.75 | 0.2 | 7 | 73,799.28 |
| 0.5 | 0.1 | 2 | 48,104.58 |
| 0.5 | 0.3 | 3 | 57,552.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Xu, Q.; Wang, X.; Liu, Z.; Li, T.; Zhang, D. Optimal Strategy for Grid Loss Reduction Under Electricity Transmission and Distribution Reform Considering Low-Carbon Benefits. Processes 2025, 13, 1406. https://doi.org/10.3390/pr13051406
Li W, Xu Q, Wang X, Liu Z, Li T, Zhang D. Optimal Strategy for Grid Loss Reduction Under Electricity Transmission and Distribution Reform Considering Low-Carbon Benefits. Processes. 2025; 13(5):1406. https://doi.org/10.3390/pr13051406
Chicago/Turabian StyleLi, Weiwu, Qing Xu, Xinying Wang, Zhengying Liu, Tianshou Li, and Dandan Zhang. 2025. "Optimal Strategy for Grid Loss Reduction Under Electricity Transmission and Distribution Reform Considering Low-Carbon Benefits" Processes 13, no. 5: 1406. https://doi.org/10.3390/pr13051406
APA StyleLi, W., Xu, Q., Wang, X., Liu, Z., Li, T., & Zhang, D. (2025). Optimal Strategy for Grid Loss Reduction Under Electricity Transmission and Distribution Reform Considering Low-Carbon Benefits. Processes, 13(5), 1406. https://doi.org/10.3390/pr13051406





