Abstract
With the widespread adoption of highways in the mountainous regions of southwestern China, the electricity load of numerous tunnels and service areas has increased rapidly. Constructing photovoltaic (PV) microgrids in service areas has become an important means of energy conservation, consumption reduction, and carbon emission mitigation. However, constrained by mountainous terrain, the PV power generation conditions in highway service areas exhibit significant micro-terrain variations, making it difficult to effectively evaluate PV utilization efficiency. This paper proposes a dynamic block optimization model for PV microgrids that considers regional layout constraints. The model utilizes an intelligent adjustment mechanism to plan PV panel layouts in highway service areas, optimizing energy utilization efficiency and economic benefits. Additionally, long short-term memory (LSTM) networks are employed for short-term PV output prediction to address the challenges posed by varying weather and seasonal changes. This approach comprehensively considers the intermittency and instability of PV power generation, enabling dynamic block optimization to autonomously adjust the PV power output in response to load fluctuations. Through simulation case studies, the model is validated to effectively improve the utilization rate and economic performance of PV microgrids under various environmental conditions and demonstrates superior performance compared with traditional static block methods.
1. Introduction
With the transformation of the global energy structure and the intensification of climate change, the development and utilization of renewable energy have become a critical focus of global energy policies. Since the implementation of the 13th Five-Year Plan, China has prioritized green energy and sustainable development, enacting a series of policies to promote the growth of photovoltaic (PV) renewable energy. As PV power generation increasingly shifts toward small-scale distributed systems, users such as highway service areas, toll stations, and tunnels—located far from primary load centers—have begun establishing PV microgrids to reduce reliance on centralized power grids.
However, the inherent intermittency (stochastic generation outages) and dynamic instability (frequency excursions > 0.5 Hz) of PV systems challenge grid stability, especially under composite weather stressors and seasonal irradiation variations. While existing studies have made progress in hybrid microgrid control strategies [1,2,3,4,5,6,7,8], recent Industrial Internet of Things (IIoT) implementations reveal that 78% of the proposed architecture remains conceptual, with limited experimental validation under real-world operating conditions [9]—especially for spatially distributed PV deployments like highway service areas where equipment heterogeneity and communication latency are prevalent. Similarly, though advanced optimization methods like genetic algorithm and model predictive control (GA-MPC) hybrids demonstrate cost-effectiveness in campus-scale microgrids (achieving $0.19/kWh energy costs [10]), their centralized control paradigms inherently fail to address the topological constraints of linearly distributed highway PV systems, where panels are fragmented across parking lots, rooftops, and sloping terrains with varying shading patterns.
The effective management and optimization of PV output remain critical challenges [1,2,3,4]. While existing studies have developed various control strategies for hybrid microgrids—including grid-connected/islanded operation modes [1], PV-battery energy management [5,6], and parallel inverter control [7]—these approaches typically assume uniform PV array behavior. In reality, spatially distributed installations experience 12–18% efficiency losses due to mismatched conditions [9]. Although coordinated control strategies [8] and auxiliary voltage regulation methods [11] have been proposed, they face computational limitations when applied to the large-scale dispersed PV systems (>50 blocks) common in highway infrastructures [10,12,13]. Emerging digital twin technologies show potential [14] but currently lack the dynamic reconfiguration capabilities for clustered PV arrays.
Traditional optimization methods exhibit several limitations:
- MPPT techniques suffer up to 22% efficiency loss in fragmented layouts due to delayed shadow response [14];
- Configuration optimization often ignores microclimate variations across service areas [15,16];
- Environmental adaptation models [17,18,19] assume homogeneous conditions, unlike the GA-MPC approach [10], which reduces losses by 31% but requires uniform irradiation data;
- Dynamic adjustment systems [20,21,22] lack the distributed MPPT capabilities for PV clusters [9];
- Storage coordination methods [23] cannot simultaneously optimize multiple distant units [10].
Three fundamental limitations emerge from prior work:
- Spatial–Temporal Decoupling: Current models treat PV blocks as static entities [24] or assume uniform environmental impacts [10], ignoring the dynamic coupling effects where shadow migration across service area subzones creates time-varying power mismatches (e.g., morning roof shading vs. afternoon canopy shading).
- Scalability–Accuracy Tradeoff: GA-based sizing [10] and IIoT monitoring [9] either sacrifice resolution for scalability (coarse-grained cluster control) or become computationally prohibitive (per-panel optimization).
- Digital–Physical Disconnect: DT platforms [14] prioritize virtual prototyping over real-time reconfiguration, lacking embedded algorithms to translate weather forecasts into optimal block topology adjustments for highway PV arrays.
Given the distributed placement of PV panels in highway service areas (e.g., parking lots, rooftops), this study proposes a dynamic block optimization model that employs an intelligent adjustment mechanism to optimize PV block configurations under varying environmental and grid demands. The model integrates advanced optimization algorithms with operational data, utilizing long short-term memory (LSTM) networks for short-term PV output prediction to achieve optimal power matching and cost control. Furthermore, it dynamically adjusts the PV generation in response to load fluctuations, enhancing system utilization efficiency and economic performance. Against the backdrop of China’s vigorous promotion of green energy transition and carbon neutrality goals, this research not only holds practical significance but also provides theoretical and methodological support for deploying efficient PV microgrids in complex terrains, aligning with global strategies for sustainable development and clean energy utilization.
2. Planning Strategy for Highway Photovoltaic Microgrids
2.1. Photovoltaic Microgrid
The load characteristics of highway service areas exhibit notable time-varying and uncertain behavior. Influenced by traffic flow, weather conditions, and traffic incidents, load demand fluctuates significantly across different time periods, particularly during peak morning/evening hours and nighttime troughs. Additionally, sudden changes in traffic volume and vehicle parking demands further amplify load uncertainty. Consequently, service area systems require high flexibility and real-time responsiveness to ensure stable and reliable operation.
A photovoltaic microgrid is a compact integrated power system comprising PV generation, intelligent control units, electrical loads, and energy storage devices. A typical configuration is illustrated in Figure 1. Through grid-connected PV systems, it provides an effective power supply for highway service areas distant from the main grid. Operating under a “self-consumption with surplus electricity fed back to the grid” mode, it not only meets local power demands but also enables bidirectional interaction with the traditional grid, facilitating energy sharing and optimized utilization [22]. As illustrated in Figure 2, the photovoltaic (PV) installation areas within the expressway service area microgrid are geographically dispersed and exhibit distinct zoning characteristics, including but not limited to the following: office and dormitory building rooftops, highway-side slopes, and parking lot canopies.
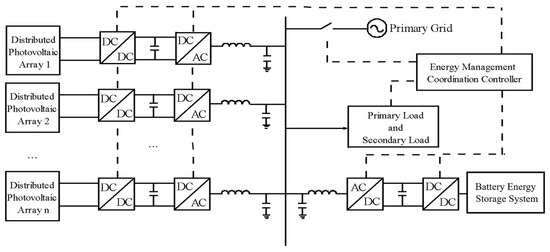
Figure 1.
Structure of a photovoltaic microgrid.
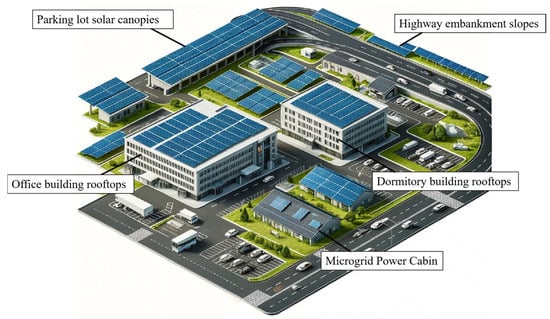
Figure 2.
Conceptual diagram of a highway service area photovoltaic microgrid.
Integrating PV generation units into microgrids is a common approach for renewable energy utilization. Traditional microgrids typically employ centralized PV panel configurations to uniformly distribute power within designated areas [23,24]. However, in high-penetration distributed PV microgrid environments, system uncertainties—such as voltage violations and imbalances—may significantly impact node voltages and power flow distribution [25]. To address these issues, conventional strategies include deploying energy storage systems and regulating reactive power output. Nevertheless, energy storage deployment faces constraints such as energy density limitations, cycle life degradation, safety and environmental concerns, and resource dependencies, resulting in relatively high costs [26].
As shown in Figure 3, the photovoltaic (PV) systems installed along mountainous expressway service areas face significant micro-terrain variations, including different degrees of roadside slopes and rooftop installations. These variations cause fluctuations in solar irradiance and power generation efficiency among different PV blocks, ultimately affecting the overall PV utilization efficiency and system stability. To address this challenge, this study proposes a dynamic block optimization model for PV microgrids that considers regional layout constraints.

Figure 3.
Geospatial distribution map of PV installations along mountainous expressway service areas.
2.2. Photovoltaic Matrix Block Partitioning
As shown in Figure 4, photovoltaic matrix block partitioning involves distributing PV panels across distinct zones (e.g., office buildings ‘block #1’, dormitories ‘block #2’, parking lots ‘block #3’ etc.) based on installation environments to optimize energy utilization and management efficiency. In service area microgrids, the spatial distribution of PV panels is particularly critical. Each block is configured according to local irradiance conditions, available area, and load demands, enabling flexible layouts. Through block partitioning, PV systems achieve independent and centralized dispatchability, improving energy utilization rates and power supply reliability. This approach replaces traditional centralized energy distribution, better aligning with the self-sufficient microgrid requirements of off-grid loads.
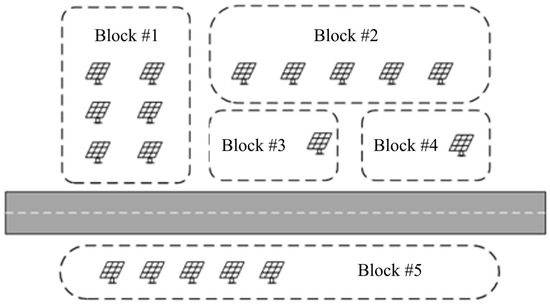
Figure 4.
Block partition structure diagram of microgrid.
2.3. Dynamic Block Optimization Model for Construction Phase
2.3.1. Objective Function
The power generation capacity of different microgrids is constrained by geographical, climatic, and solar irradiance conditions. To simultaneously reduce node voltage deviations and network losses in distributed PV microgrids, enhance the system’s economic efficiency, and minimize the gap between the PV power output and the grid’s absorption capacity, this scheme requires predefined block partitioning and power allocation for PV panels during the grid construction phase. Notably, ref. [27] proved that optimal microgrid partitioning can reduce voltage deviations by 12–18% compared with traditional radial networks.
Based on these operational requirements, we propose the following original optimization framework extending the work in [27]: Assuming that the objective is to minimize the total discrepancy between PV generation and load demand while maximizing the potential output of each block, the problem can be formulated as follows:
where is the PV power generation at time t, is the load demand at time t, is the weighting factor balancing cost and power matching, and denotes the total cost of PV blocks.
2.3.2. Block-Based Layout Optimization Model for Construction Phase
To determine the optimal number of blocks and load allocation for each block during the construction phase, a constrained optimization model is defined. The objective is to minimize the discrepancy between the total power generation and total load demand while satisfying the capacity, cost, and block configuration requirements. The optimization model can be formulated as follows:
where is a represents the maximum number of blocks, is the PV generation of the i-th block, is the load demand of the i-th block, and is the construction cost of the i-th block.
The total PV capacity constraint is as follows:
where is the total allowable PV capacity of the system.
The PV block capacity constraints can be formulated as:
where is the maximum installable capacity of the i-th block (determined by the on-site available area) and is the minimum capacity requirement per block.
The output constraint (actual output of each block shall not exceed its maximum installable capacity) is as shown:
The cost constraint (the total construction cost must remain within budget) can be written as follows:
The cost function (the cost of each block is determined by its capacity via an exponential relationship) is as follows:
where a and b are the parameters of the exponential function defining the cost-capacity relationship. Note: preliminary estimates indicate that the capital cost of PV modules decreases by approximately 20% for every doubling of capacity, reflecting economies of scale.
3. Energy Supply Strategy for Highway Photovoltaic Microgrids
3.1. Dynamic Block Optimization Model for Operation and Maintenance Phase
3.1.1. Short-Term Load and PV Generation Prediction Model Based on LSTM
To achieve high-precision load forecasting and optimize the dispatch strategy for off-grid PV microgrids, this study employs a long short-term memory (LSTM) network for load demand prediction. LSTM is an improved variant of recurrent neural networks (RNNs) that utilizes a unique gating mechanism to effectively capture both long-term and short-term dependencies in time-series data, addressing the vanishing and exploding gradient problems inherent in traditional RNNs. The LSTM model is particularly well-suited for handling complex load demand data and has demonstrated excellent performance in load forecasting tasks.
The structure of an LSTM unit consists of three core gating mechanisms: the Forget Gate, the Input Gate, and the Output Gate. These gates determine which information is retained, updated, or output. Following the established framework in [28], the specific computational processes are described as follows:
Forget Gate: determines how much of the previous memory state is retained. The calculation formula is:
where is the output of the Forget Gate, is the weight matrix, is the bias term, and is the Sigmoid activation function.
Input Gate: controls the degree to which the current input updates the memory state, determined jointly by the Input Gate and the candidate memory :
where is the candidate memory state, and are the corresponding weight matrices, and and are the bias terms.
Memory Update: combines the results of the Forget Gate and Input Gate to update the current memory state :
Output Gate: determines the output value of the current memory state and updates the hidden state :
where is the control signal of the Output Gate, is the weight matrix, and is the bias term.
Short-Term Load Forecasting: Short-term load forecasting aims to predict future electricity demand over a short time horizon, providing a basis for real-time dispatch decisions. The LSTM model excels at capturing temporal dependencies in load demand data, enabling it to model both short-term fluctuations and long-term trends. This study develops an original forecasting framework based on the following author-derived formulations.
Input Data:
where represents the load demand at the i-th time step. Output: the predicted load for the next time step .
Loss Function: The mean squared error (MSE) is used as the loss function, defined as follows:
Short-Term PV Generation Forecasting Model: The input data for the PV generation forecasting model includes historical irradiance, weather features (e.g., temperature, humidity, cloud cover), and PV generation data sequences, expressed as follows:
where is the irradiance at the i-th time step, is the temperature at the i-th time step, and is the PV generation at the -th time step. Output: the predicted PV generation for the next time step .
Loss Function: Similarly, the mean squared error (MSE) is used as the loss function, defined as follows:
3.1.2. Dynamic Block Adjustment Optimization for Operation and Maintenance
During the operation and maintenance phase, the operating states of each block are dynamically adjusted based on real-time load forecasts and changes in PV generation (similar to the model’s predictive framework in [29]). At a given time t, the relationship between the total power generation and total load demand can be expressed as follows:
The block operating states are adjusted according to the following logic:
If , some blocks may be shut down (reducing generation or switching to energy storage mode) to maintain balance.
If , additional energy storage systems or inactive blocks may be activated to provide supplementary power.
This dynamic adjustment mechanism can be formulated as:
where is a control variable indicating whether the i-th block is active ( or inactive ).
3.2. Algorithm Flow of the Dynamic Block Optimization Model
The proposed PV microgrid optimization algorithm in this study consists of two phases: the construction phase and the operation and maintenance phase. Each phase has distinct input parameters and optimization objectives, as illustrated in Figure 5. The model inputs and outputs are summarized in Table 1.
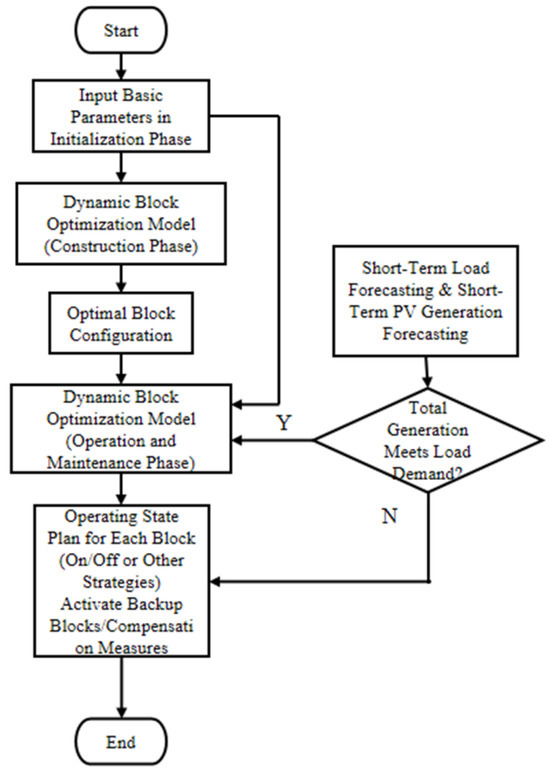
Figure 5.
Flowchart of the dynamic block optimization model for PV microgrids.

Table 1.
Model inputs and outputs.
The algorithm initializes by inputting the basic parameters of the PV system, including the PV generation capacity, load demand, maximum number of blocks, minimum capacity per block, cost limit, and total PV capacity. The objective function is defined to minimize the discrepancy between the PV generation curve and the load demand curve.
Construction Phase: During the construction phase, the algorithm evaluates each potential block configuration based on input parameters such as generation capacity, load conditions, and cost, ensuring that the total cost does not exceed the predefined limit. An optimization algorithm (e.g., linear programming, genetic algorithm, or particle swarm optimization) is then employed to solve the objective function, determining the optimal block configuration and load allocation. The best block configuration is output as the final solution.
Operation and Maintenance Phase: In the operation and maintenance phase, the algorithm periodically acquires real-time data, including short-term load forecasts and PV generation conditions, to dynamically adjust the operating states of each block and maintain the power balance. If the total generation exceeds the load demand, the algorithm selectively deactivates certain blocks. Conversely, if generation is insufficient, backup blocks are activated, or other compensatory measures are implemented.
4. Case Study and Analysis
4.1. Microgrid in a Service Area in Yunnan
This study analyzes a real-world case of a highway service area located in the southwestern region of Yunnan Province. The service area is situated in the low-heat river valley area of southwestern Yunnan, south of the Tropic of Cancer, within the tropical zone, characterized by a typical subtropical monsoon climate. The surrounding region includes three counties: A, B, and C. According to the Yunnan Annual Climate Bulletin (2024), the area enjoys an annual average sunshine duration of 1900 to 2200 h, making it a Class-II solar resource region with abundant solar energy potential. Based on these conditions and the referencing literature [28,29,30], the simulated comprehensive PV output for the region is shown in Figure 6.
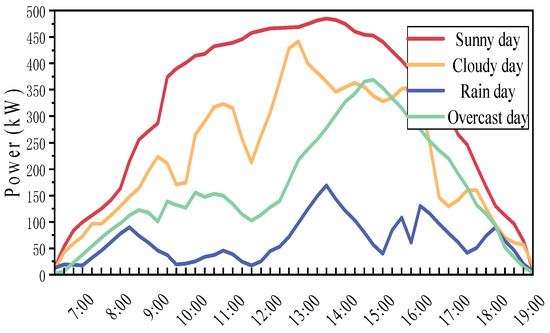
Figure 6.
Typical daily PV generation output.
The service area has approximately 300 m2 of rooftop space (including office buildings, staff dormitories, power distribution rooms, and canteens) and 200 m2 of parking area. Additionally, 1300 m2 of space is available per kilometer along the roadside slopes for PV module installation, with a capacity of 0.15 kWp per square meter. The load demand peaks during the morning and evening rush hours, correlating with commuting and travel patterns, while the midday load is relatively low. Seasonal factors also significantly influence electricity demand, with higher midday loads in summer and higher morning/evening loads in winter. These load variations are critical for the design and operation strategies of PV microgrids, particularly during peak hours and across different seasons. Based on field-measured conditions, we estimated the typical daily load profile of the service area, as shown in Figure 7.
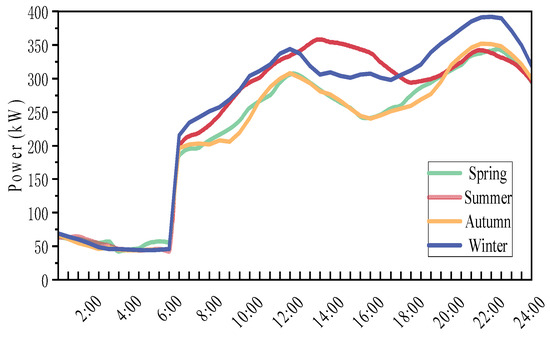
Figure 7.
Typical daily load of the service area.
4.2. Analysis of Block-Based Layout Optimization in the Construction Phase
This section validates the effectiveness of the proposed PV microgrid operation and maintenance optimization model in dynamically adjusting the operating states through a real-world case study. A highway service area was selected as the research object to analyze how the model optimizes the matching between PV generation and load demand under varying weather conditions and load changes, thereby improving the overall performance and economic efficiency of the system. The case study calculations were performed in a Python 3.9 environment. Based on the mathematical model proposed in this study and referencing the actual case, the analysis focuses on power balance and cost efficiency under different scenarios (e.g., weather, seasons). Key parameters for the case study are listed in Table 2.

Table 2.
Key parameters.
This study analyzes the microgrid of a service area in southern Yunnan, optimizing the load and PV output data through the dynamic block model to derive the optimal block configuration. The capacities of the blocks are 10 kW, 20 kW, 40 kW, 60 kW, 60 kW, 60 kW, 60 kW, 60 kW, 60 kW, and 70 kW, corresponding to blocks 1 through 10. This configuration, tailored to the specific conditions of the case, maximizes power dispatch flexibility while ensuring economic efficiency.
4.3. Analysis of Dynamic Block Adjustment Optimization in Operation and Maintenance
Considering the uncertainty of PV output, especially under complex weather conditions, this study analyzes PV power output under different weather scenarios. Based on the annual weather frequency of the region (clear days: 35%, cloudy days: 30%, rainy days: 25%, other weather: 10%), the optimal block configuration was determined through weighted calculations. The daily power adjustment characteristics under different weather conditions in autumn are illustrated in Figure 8. The optimization model effectively reduces the discrepancy between generation and load demand, particularly during midday and evening periods with significant load fluctuations, by rapidly adjusting generation to match demand.

Figure 8.
The autumn power dispatch curve for the service area (shaded periods indicate intervals without PV output due to special circumstances).
As shown in Figure 8, during autumn rainy weather, the PV system in the highway service area may fail to generate sufficient power due to significantly reduced solar radiation and prolonged cloud cover. Consequently, there may be periods with no PV output, which can be compensated by deploying energy storage systems or other power dispatch methods.
Figure 9 illustrates the on/off states of each block during different time periods on a clear autumn day. Through dynamic adjustment, the system deactivates some blocks when generation exceeds demand to avoid power surplus and activates backup blocks when generation is insufficient to ensure that the load demand is met.
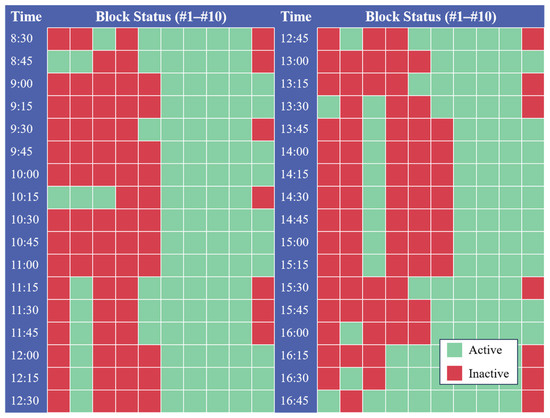
Figure 9.
Typical power dispatch state diagram for a clear autumn day in the service area.
To address the power mismatch between the photovoltaic generation and actual load demand in highway service area microgrids, the proposed case study derives an optimal block disconnection scheme for a typical autumn day through numerical optimization, achieving superior power balance performance. Theoretically, the model’s accuracy improves with increased block partitioning, though the maximum number of blocks is ultimately constrained by the physically allocable PV panels on site. Extensive experiments under diverse climatic conditions demonstrate that the optimal block configuration achieves 23.91% average power adjustment and 98.94% dispatch accuracy, confirming the method’s reliability under complex weather conditions.
5. Conclusions
This study addresses the energy management and optimization challenges of photovoltaic microgrids in highway service areas within the mountainous regions of southwestern China by proposing a dynamic block optimization model. The model integrates an intelligent adjustment mechanism and long short-term memory (LSTM) networks for short-term PV output prediction. By determining the optimal block configuration during the construction phase and dynamically adjusting the operating states of the blocks during the operation and maintenance phases, the model significantly improves the utilization efficiency of PV generation and the economic performance of the system. The key findings are summarized as follows:
(1) Dynamic Block Optimization Mechanism: The proposed dynamic block optimization model intelligently adjusts the partitioning of PV systems based on real-time load demand and generation conditions. By flexibly activating or deactivating blocks, the model achieves optimal matching between power supply and demand.
(2) LSTM-Based Prediction for Enhanced Stability: The LSTM network effectively predicts short-term PV output and load demand, addressing challenges posed by weather and seasonal variations. Accurate prediction results enhance the efficacy of dynamic adjustment strategies, mitigating the impact of power fluctuations on system stability.
(3) Superior Performance Over Static Methods: The simulation results demonstrate that the dynamic block optimization model outperforms traditional static partitioning methods under diverse environmental conditions. Reduced operational costs and enhanced system stability highlight the advantages of the dynamic strategy in complex terrains and dynamic environments.
(4) Dual Benefits of Economic and Environmental Efficiency: By optimizing the PV layout and dynamically adjusting operational states, the model reduces reliance on the main grid, lowers operational costs, and significantly reduces carbon emissions. This aligns with the goals of green energy adoption and sustainable development.
Author Contributions
This work was collaboratively developed with the following individual contributions: Z.S. and H.W.: conceptualization and methodology development; Z.M.: software implementation and writing (review and editing); T.X.: formal analysis, investigation, and resources; X.H.: investigation, data curation, and resources; L.S.: investigation, resources, and project administration; P.C.: supervision and writing (review and editing); Z.S.: original draft preparation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the following grants: National Natural Science Foundation of China (Grant No. 52167012); Yunnan Provincial Department of Transportation Science & Technology Demonstration Project (Key Technologies for Photovoltaic Integration and Energy Efficiency Enhancement in Yunnan Expressways, Yun-Jiao-Ke-Jiao-Bian [2022] No. 124); Yunnan Communications Investment & Construction Group Science & Technology Innovation Project (Key Technologies for Photovoltaic Integration and Comprehensive Energy Efficiency Improvement along Border Expressways, YCIC-YF-2022-19); Yunnan Provincial Department of Transportation Science & Technology Project (Research on Green Low-Carbon Construction Management Technologies, 4530000HT202209089); Yunnan Provincial Key Laboratory of Digital Transportation (Grant No. 202205AG070008); The Article Processing Charge (APC) was funded by [Yunnan Provincial Institute of Transportation Planning and Design].
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Ze Shi, Tianxiang Xiao, Xiliu Huang, and Long Shao are employed by the Yunnan Demeng Expressway Investment and Development Co., Ltd.; Author Hao Wu is employed by the Yunnan Provincial Institute of Transportation Planning and Design; The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Sun, W.; He, G.; Liu, C.; Feng, S. A review of voltage violation solutions in distribution networks with high-penetration distributed photovoltaics. Mod. Electr. Power 2024, 41, 302. [Google Scholar] [CrossRef]
- Alhawsawi, E.Y.; Salhein, K.; Zohdy, M.A. A Comprehensive Review of Existing and Pending University Campus Microgrids. Energies 2024, 17, 2425. [Google Scholar] [CrossRef]
- Zhong, H.; Fang, C.; Li, S.; Chen, Z. Consideration of photovoltaic output volatility and microgrid coordination for distribution network black start strategy. Electr. Meas. Instrum. 2024. Advance online publication. Available online: http://kns.cnki.net/kcms/detail/23.1202.th.20220916.1600.004.html (accessed on 24 April 2025).
- Gao, S.; Wang, Y.; Zhou, Y.; Yu, H. An improved scheduling approach for multi-energy microgrids considering scenario insufficiency and computational complexity. Processes 2025, 13, 576. [Google Scholar] [CrossRef]
- Kumar, M. Control techniques for operation of roof-top solar photovoltaics based microgrid in islanded mode. Int. J. Electr. Power Energy Syst. 2024, 155 Pt A, 109511. [Google Scholar] [CrossRef]
- Su, H.; Dong, Z.; Wang, X. Improved droop control strategy for microgrids based on auto disturbance rejection control and LSTM. Processes 2024, 12, 2535. [Google Scholar] [CrossRef]
- Cao, X.; Yang, X.; Li, L.; Shen, L.; Ma, W.; Yang, R.; Zou, H. Prediction model-assisted optimization scheduling strategy for renewable energy in the microgrid. Processes 2024, 12, 1786. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Y.; Zhao, H.; Luo, Y.; Xu, X. Two-stage optimal scheduling of an islanded microgrid considering uncertainties of renewable energy. Int. J. Electr. Power Energy Syst. 2024, 162, 110324. [Google Scholar] [CrossRef]
- Calderón, D.; Folgado, F.J.; González, I.; Calderón, A.J. Implementation and Experimental Application of Industrial IoT Architecture Using Automation and IoT Hardware/Software. Sensors 2024, 24, 8074. [Google Scholar] [CrossRef]
- Agoundedemba, M.; Kim, C.K.; Kim, H.-G.; Nyenge, R.; Musila, N. Modelling and optimization of microgrid with combined genetic algorithm and model predictive control of PV/Wind/FC/battery energy systems. Energy Rep. 2025, 13, 238–255. [Google Scholar] [CrossRef]
- Hui, H.; Li, R.; Zhu, Y.; Zhang, Y.; Li, T.; Lu, W.; Xiao, Q. Multi-objective probabilistic programming method for distribution networks with high penetration of distributed photovoltaics. Electr. Meas. Instrum. 2023, 60, 2–10. [Google Scholar] [CrossRef]
- Kumar, M.; Panda, K.P.; Rosas-Caro, J.C.; Gonzalez, A.V.; Panda, G. Comprehensive review of conventional and emerging maximum power point tracking algorithms for uniformly and partially shaded solar photovoltaic systems. IEEE Access 2023, 11, 31778–31812. [Google Scholar] [CrossRef]
- Ren, X.; Li, T.; Ma, J.; Huang, Y.; Zhang, D.; Wu, Y. Optimization of photovoltaic microgrid hybrid energy storage capacity considering state of charge. Electr. Meas. Instrum. 2024, 61, 150–156. [Google Scholar] [CrossRef]
- Olayiwola, O.; Cali, U.; Elsden, M.; Yadav, P. Enhanced Solar Photovoltaic System Management and Integration: The Digital Twin Concept. Solar 2025, 5, 7. [Google Scholar] [CrossRef]
- Hoffart, F.M.; D’Orazio, P.; Holz, F.; Kemfert, C. Exploring the interdependence of climate, finance, energy, and geopolitics: A conceptual framework for systemic risks amidst multiple crises. Appl. Energy 2024, 361, 122885. [Google Scholar] [CrossRef]
- Zheng, X.; Guan, Q.; Xu, J.; Xiong, W.; Lin, J.; Guo, T.; Zhang, W. Reactive power optimization method for AC-DC hybrid networks considering transient overvoltage suppression by distributed energy clusters. Renew. Energy 2023, 41, 1089–1094. [Google Scholar] [CrossRef]
- Liu, R.; Wu, K.; Feng, L.; Liang, R.; Wang, X.; Yang, S. Coordinated optimization and control of voltage zones in active distribution networks with high-penetration distributed photovoltaics. J. Sol. Energy 2022, 43, 189–197. [Google Scholar] [CrossRef]
- Chai, Y.; Guo, L.; Wang, C.; Liu, J.; Lu, C.; Jin, W.; Pan, J. Distributed voltage control in distribution networks with high-penetration photovoltaics. Power Grid Technol. 2018, 42, 738–746. [Google Scholar] [CrossRef]
- Wu, H.; Li, H.; Gu, X. Optimal energy management for microgrids considering uncertainties in renewable energy generation and load demand. Processes 2020, 8, 1086. [Google Scholar] [CrossRef]
- Wen, S.; Wang, S.; Tian, G. Energy management and coordinated control strategy of photovoltaic-storage AC microgrids in island mode. Renew. Energy 2018, 36, 862–868. [Google Scholar] [CrossRef]
- Xu, W.; Liu, Z.; Wang, H.; Liu, S. Socio-economic benefit evaluation of rural photovoltaic systems based on the LCOE model: A case study of a rooftop distributed photovoltaic project in suburban Beijing. J. China Agric. Univ. 2023, 28, 208–217. [Google Scholar]
- Xu, W.; Luo, J.; Fan, W. Capacity planning of grid-connected photovoltaic-storage microgrids under uncertain environments. Syst. Eng. Theory Pract. 2022, 42, 981–1000. [Google Scholar]
- Meng, Y.; Bi, M.; Shi, Z.; Yuan, G.; Huang, S. Maximum capacity analysis of distributed photovoltaic poverty alleviation with multiple access points in distribution networks. J. Electr. Power Syst. Autom. 2019, 31, 110–116. [Google Scholar] [CrossRef]
- Xu, X.; Huang, Y.; Liu, C.; Wang, W. Impact of distributed photovoltaic generation on voltage in distribution networks and solutions for voltage violation. Power Grid Technol. 2010, 34, 140–146. [Google Scholar] [CrossRef]
- Chen, J.; Mo, R.; Dang, H.; Li, S.; Zhou, G. Optimization of battery capacity and economic analysis for energy storage photovoltaic systems. Sci. Technol. Eng. 2019, 19, 165–171. [Google Scholar]
- Jia, H.; Peng, J.; Li, N.; Zou, C.; Yin, R.; Tai, Y. Optimization and economic analysis of distributed photovoltaic-storage systems under dynamic electricity pricing. J. Sol. Energy 2021, 42, 187–193. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, C.; Zhao, J.; Li, Y. Quantification of flexibility in PV-rich distribution systems using cluster-based modeling. IEEE Trans. Sustain. Energy 2021, 12, 356–366. [Google Scholar]
- Dong, C.; Wang, Z.; Bai, J.; Jiang, J.; Wang, B.; Liu, G. A review of ultra-short-term forecasting methods for photovoltaic power generation. High Volt. Technol. 2023, 49, 2938–2951. [Google Scholar] [CrossRef]
- Parisio, A.; Rikos, E.; Glielmo, L. A Model Predictive Control Approach to Microgrid Operation Optimization. IEEE Trans. Control Syst. Technol. 2014, 22, 1813–1827. [Google Scholar]
- Polimeni, S.; Nespoli, A.; Leva, S.; Valenti, G.; Manzolini, G. Implementation of different PV forecast approaches in a multi-good microgrid: Modeling and experimental results. Processes 2021, 9, 323. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).