A Fast Simulation Method for Predicting the Production Behavior of Artificial Fractures Based on Diffusive Time of Flight

Abstract

Multi-stage hydraulic fracturing is a widely used technology in the development of shale oil and gas reservoirs that creates artificial fractures and forms fracture networks that enhance fluid flow within reservoirs. A well-designed fracture network can significantly enhance the production performance of oil and gas wells, thereby improving the recovery of shale oil and gas reservoirs. To achieve this, understanding the gas production performance of individual artificial fractures is crucial, as it provides valuable insights for refining subsequent fracturing designs, ultimately leading to an optimized fracture network design. At present, numerical simulations are commonly used to study the production performance of individual artificial fractures by modeling the production process of the entire shale oil and gas reservoir. However, due to the heterogeneity of reservoirs and the presence of numerous natural fractures, traditional numerical simulations require high-resolution grids to model the production process, making them computationally expensive and time-consuming. To address this issue, in this work, based on the concept of diffusive time of flight (DTOF), the authors propose a fast simulation method to efficiently simulate the production behavior of individual artificial fractures throughout the shale oil and gas reservoir production process. The DTOF can be obtained by solving the Eikonal equation using the fast marching method (FMM), which is then used to calculate the drainage volume of individual artificial fractures. Subsequently, a geometric approximation of the drainage volume is used to efficiently compute the production rates of individual artificial fractures. Unlike traditional numerical simulations, this method uses a single non-iterative calculation to determine the drainage volume of individual artificial fractures, followed by a geometric approximation to compute the production rates. This eliminates the need for high-resolution grids, significantly reducing computational cost and time, which allows the proposed method to provide faster simulations compared to traditional numerical methods while maintaining sufficient accuracy.

1. Introduction

Shale gas resources have attracted growing attention in recent years due to the depletion of conventional oil and gas reserves [1,2]. With low carbon dioxide emissions and zero sulfur dioxide content, shale gas represents an environmentally preferable energy source, particularly when compared to conventional fuels such as oil and coal [3,4,5]. Due to the low porosity and permeability of shale gas reservoirs, multi-stage hydraulic fracturing is commonly used to enhance their development by creating artificial fractures and forming complex fracture networks. These networks provide high-permeability pathways, significantly facilitating fluid flow within the reservoirs [6,7,8]. The development of shale gas reservoirs is highly influenced by the design of multi-stage hydraulic fracturing, as it determines the capacity of fracture networks to enhance fluid flow and increase production. To optimize multi-stage hydraulic fracturing design, it is crucial to simulate the production behavior of individual artificial fractures under varying fracture parameters [9,10]. At present, this is usually achieved by simulating the production process of the entire reservoir. However, shale gas reservoirs are highly heterogeneous and contain complex fracture networks, requiring high-resolution grids in each simulation to accurately represent the reservoir properties and fracture interactions [11]. This significantly increases the computational cost. Moreover, determining optimal fracture parameters requires running numerous simulations, which further increases the computational costs and time. Therefore, improving the efficiency of simulating the production behavior of individual artificial fractures is essential for optimizing multi-stage hydraulic fracturing design in shale gas reservoirs.

To address the challenge of high computational cost, recent advancements have focused on improving the efficiency of numerical simulations. One such approach is the concept of diffusive time of flight (DTOF), which represents the travel time of the peak pressure disturbance from an impulse source or sink to a certain point in the reservoir [12,13]. The DTOF can be rapidly obtained by solving the Eikonal equation using the fast marching method (FMM) [13,14] and can then be used to improve the computational efficiency of numerical simulations. Zhang [15] proposed a fast simulation method that involves transforming fluid-transport coordinates from the physical 3D space to the 1D DTOF space. The results show that by transforming high-dimensional equations into low-dimensional equations, the proposed method can significantly reduce computational time while maintaining accuracy. Teng [16] proposed a fast simulation method by using DTOF to reduce the model size. Their results indicate that focusing exclusively on simulating the regions affected by production can significantly reduce the number of grids used in simulation, thereby decreasing computational time. Lu [17] proposed a new approach for determining the control volumes of production wells using DTOF. The results indicate that fracture length, well distribution, and the number of wells substantially affect control volumes, whereas fracture conductivity has a negligible impact. Chen [18] developed a rapid simulation method using a multidomain, multiresolution discretization scheme based on the DTOF. The results show that by partitioning the reservoir into local and shared domains using DTOF contours, this method can provide fast and sufficiently accurate simulation results regardless of the production regime of the wells. More applications of DTOF can be found in Zhang [19], Fujita [20], and Iino [21]. However, DTOF has not yet been used to evaluate the production performance of individual artificial fractures in hydraulically fractured reservoirs.

According to the aforementioned arguments, one can find that improving the efficiency of simulating fracture production behavior is crucial for optimizing multi-stage hydraulic fracturing design, while the concept of DTOF can be used to enhance the simulation efficiency. Therefore, in this work, based on the concept of DTOF, the authors propose a fast simulation method to efficiently simulate the production behavior of individual artificial fractures. Furthermore, the proposed method is used to investigate the effects of various geological and fracture parameters on the production behavior of individual artificial fractures, as well as on well productivity.

2. Methodology

In this section, the authors first introduce the Eikonal equation and the fast marching method (FMM) for calculating the diffusive time of flight (DTOF), followed by an introduction to the calculation of the drainage volume of individual artificial fractures using the obtained DTOF. Then, the production calculation based on a geometric approximation of the drainage volume is presented in detail.

2.1. Drainage Volume Calculation Using DTOF

The conservation of mass for isothermal gas flow within the gas reservoirs is described by the well-known continuity equation, which is given by Al-Hussainy [22]:

$$\nabla \cdot \left[{\rho }_g\overrightarrow{v}\right]=-{\displaystyle \frac{\partial \left({\rho }_g\varphi \right)}{\partial t}}$$

(1)

where ρ_g is gas density, v is gas flow rate, ϕ is porosity, and t is time. The gas flow rate can be calculated by Darcy’s law [23]:

$$v={\displaystyle \frac{k}{{\mu }_g}}\nabla p$$

(2)

where k is permeability, μ_g is gas viscosity, p is pressure. The gas properties such as density, compressibility, and viscosity are highly pressure-dependent, which makes the gas flow equations nonlinear. This pressure-dependent nonlinearity complicates the solution process of Equation (1). The normalized pseudo-pressure and normalized pseudo-time are often used to linearize the gas flow equations, facilitating their solution. The normalized pseudo-pressure is defined as [22]

$$p_{pn}={\left({\displaystyle \frac{{\mu }_{g}Z}{p}}\right)}_i{\displaystyle {\int }_0^p\frac{p}{{\mu }_{g}Z}}\mathrm{d}p$$

(3)

where Z is compressibility factor, p is pressure, and i is the initial state. Similarly, the normalized pseudo-time is defined as [24]

$$t_{pn}={\left({\mu }_g{c}_t\right)}_i{\displaystyle {\int }_0^t\frac{1}{{\mu }_g{c}_t}}\mathrm{d}t$$

(4)

where c_t is total compressibility. Incorporating Equations (3) and (4) with Equation (1) yields

$${\displaystyle \frac{\partial p_{pn}}{\partial t_{pn}}}={\displaystyle \frac{k}{\varphi {\left({\mu }_g{c}_t\right)}_i}}{\nabla }^2{p}_{pn}$$

(5)

The form of Equation (5) (i.e., gas diffusion equation) is consistent with the oil diffusion equation. Similar to the derivation of the Eikonal equation for describing the propagation of pressure disturbances within an oil reservoir [25], the equation for describing the propagation of the pseudo-pressure front within a gas reservoir can be derived from the gas diffusion equation (Equation (5)), which can be expressed as

$$\sqrt{{\displaystyle \frac{k}{\varphi {\left({\mu }_g{c}_t\right)}_i}}}\left|\nabla \tau \right|=1$$

(6)

where τ is the propagation time of the pseudo-pressure front (i.e., diffusive time of flight). It is worth noting that the gas viscosity and total compressibility used in Equation (8) are taken at the initial reservoir conditions.

The Eikonal equation (i.e., Equation (6)) can be efficiently solved by the fast marching method (FMM). The detailed solution procedure can be found in Teng [16] and Zhang [19]. By solving the Eikonal equation using the FMM, the distribution of τ values in the entire reservoir can be obtained. However, the τ cannot be directly used to determine the drainage volume. Since τ is a parameter used in the simulation to represent pseudo-pressure disturbance, it is not directly related to pseudo-time. Therefore, the τ values distribution needs to be converted into the pseudo-front-time distribution [16,26]:

$$t_{f,pn}={\displaystyle \frac{{\tau }^2}{\beta }}$$

(7)

where t_f,pn is the pseudo-front time, which refers to the shortest pseudo-time that the pseudo-pressure disturbance reaches in a certain position, and β is the time conversion factor. For homogeneous reservoirs, the factor β depends on the flow geometry: β = 2, 4, and 6 for linear, radial, and spherical flows, respectively [25]. For heterogeneous reservoirs, β should be determined based on specific reservoir conditions. In this work, despite considering reservoir heterogeneity, the conversion factor for radial flow (β = 4) is used for the two-dimensional calculations. Subsequently, the drainage volumes at a given pseudo-time can be calculated by contouring the corresponding pseudo-front time and by summing up the pore volumes inside the contour.

2.2. Production Rate Calculation with Geometric Approximation

For radial flow in shale gas reservoirs, the gas mass flow rate under normalized pseudo-time can be described using Darcy’s law [23]:

$$q_m\left(r,t_{pn}\right)={\displaystyle \frac{{\rho }_{g}kA\left(r\right)}{{\mu }_g}}{\displaystyle \frac{\partial p\left(r,t_{pn}\right)}{\partial r}}$$

(8)

where ρ_g is gas density, q_m is gas mass flow rate, r is the distance from the wellbore, t_pn is normalized pseudo-time, k is permeability, A is flow area, μ_g is gas viscosity, and p is pressure.

To derive the gas production rate, the Darcy flow equation (i.e., Equation (8)) is integrated over the drainage volume. The geometric approximation of the drainage volume is obtained using the fast marching method (FMM), and the pseudo-steady-state flow assumption is applied to facilitate the calculation, which is widely adopted in shale gas production prediction, as demonstrated in previous studies [27,28]. Consequently, the gas production rate can be expressed as

$$q_r\left(t_{pn}\right)={\displaystyle \frac{T_{sc}}{T{p}_{sc}}}{\left({\displaystyle \frac{p}{{\mu }_{g}Z}}\right)}_i{\displaystyle \frac{{\overline{p}}_{pn}-p_{pn,wf}}{{\displaystyle {\int }_0^{V_p\left(t_{pn}\right)}\frac{1}{k\varphi A^2}}\cdot \left(1-\frac{V}{V_p(t_{pn})}\right)\mathrm{d}V}}$$

(9)

where p_sc and T_sc are pressure and temperature under standard conditions, respectively, T is reservoir temperature, Z is compressibility factor, $\overline{p_n}$ is the average pseudo-pressure of the drainage volume, P_pn,wf is pseudo-pressure of wellbore, V_p is drainage volume, V is specific volume within the drainage volume, k is average permeability of the drainage volume, ϕ is average porosity of the drainage volume, A is the flow area. The detailed derivation of this equation is provided in Appendix A.

2.3. Framework of the Proposed Method

The key aspect of our proposed method is to use the pseudo-front time to divide the hydraulically fractured reservoir model into independent subdomains associated with each artificial fracture. The gas production rate for each artificial fracture is then calculated using the volume of its corresponding subdomain. Figure 1 schematically shows the simulation framework of the proposed method. As one can see in this figure, the simulation steps are as follows:

Firstly, calculate the pseudo-front time distribution of pressure disturbance propagation in the reservoir with each artificial fracture respectively by using FMM to solve Equation (6) (as described in Section 2.1) (see Figure 1a).

Secondly, divide the reservoir into independent subdomains by comparing the pseudo-front times at each location with each artificial fracture. If the pseudo-front time corresponding to artificial fracture 1 is the smallest, it can be inferred that the reservoir volume contributes to the production of artificial fracture 1 earlier than that of other artificial fractures. Therefore, this volume can be considered as part of the control volume for artificial fracture 1 (see Figure 1b).

Finally, calculate the gas production rate for each artificial fracture using Equation (9) based on the volume of the independent subdomains (as described in Section 2.2) (see Figure 1c).

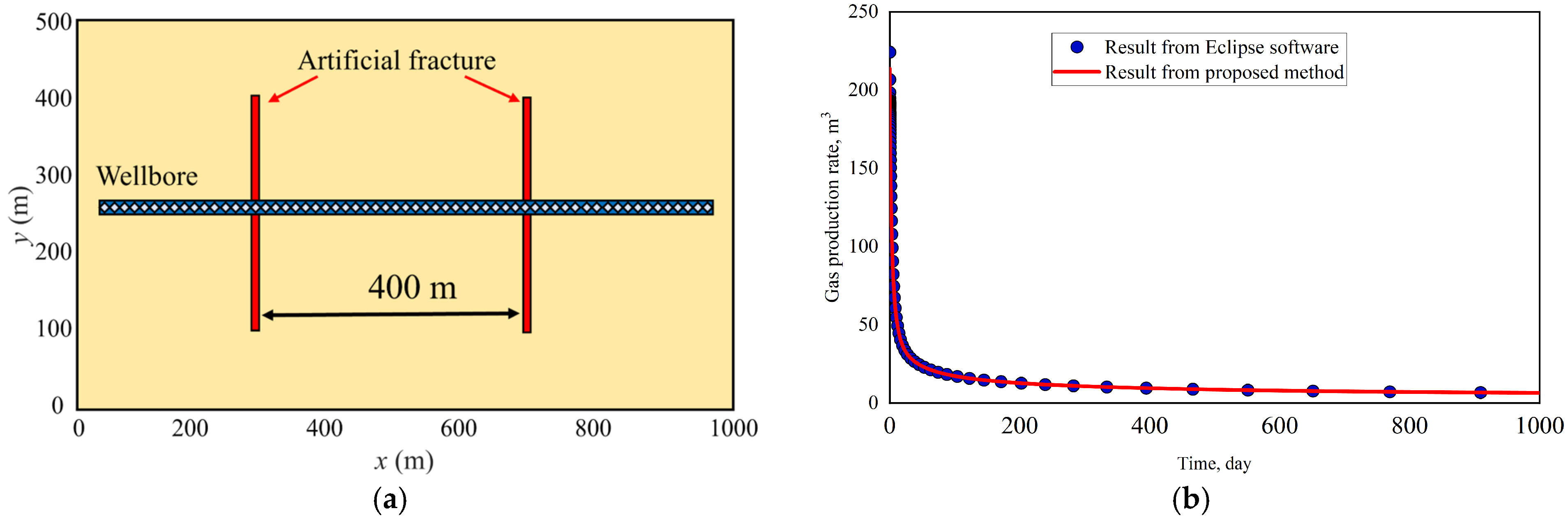
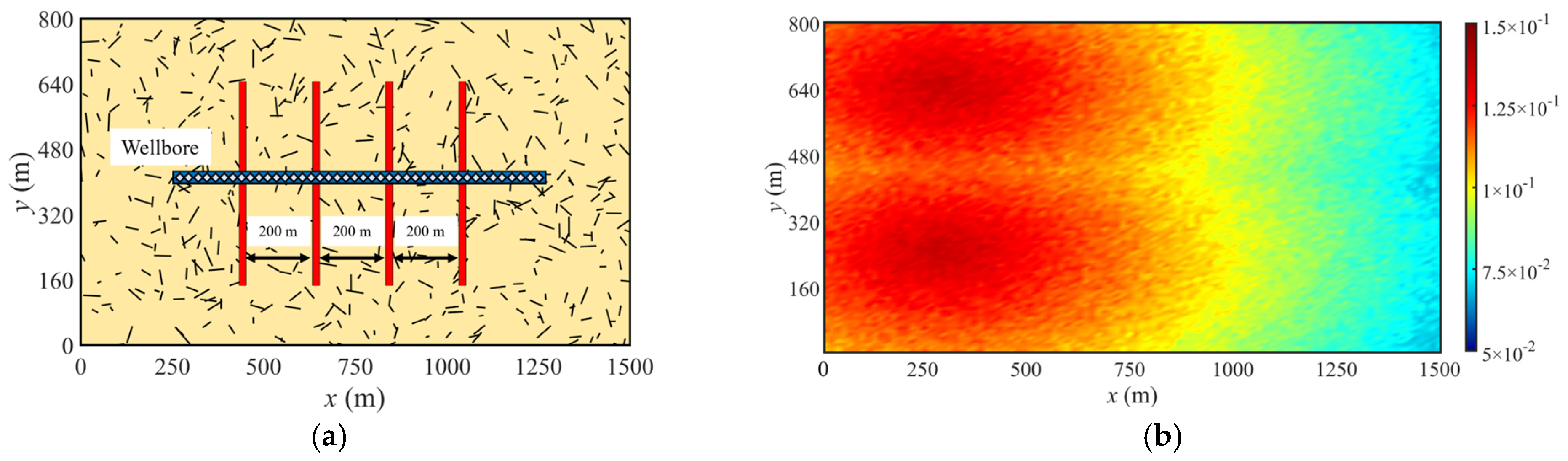
3. Validation

To examine the validity and reliability of the proposed method for gas production calculation, the simulated results are compared to the results of the commercial software Eclipse 2006.1. The validation is conducted on a 2D shale gas reservoir model with two artificial fractures, which is shown in Figure 2a. As shown in Figure 2a, the artificial fracture spacing is 400 m. The reservoir dimensions are 1000 × 500 × 20 m, with a porosity of 0.2 and a permeability of 0.01 mD. The artificial fracture (red lines) length is 300 m, with a width of 0.01 m, a porosity of 0.5, and a permeability of 1 × 10⁶ mD. The reservoir temperature is 125 °C, the initial reservoir pressure is 25 Mpa, and the wellbore pressure is maintained at a constant value of 5 MPa. The extraction time t is 1000 days. Figure 2b compares the gas production rates obtained from Eclipse and the proposed method. It can be seen from this figure that the gas production rate from the proposed method shows a good agreement with the Eclipse software, indicating that the proposed DTIV-EDFM method can effectively calculate the gas production of shale gas reservoirs.

4. Result and Discussion

In this section, heterogeneous shale gas reservoir models with different conditions are established to investigate the effects of various geological and fracture parameters on the production behavior of individual artificial fractures, as well as on the well productivity. It is important to clarify that our study employs a two-dimensional (2D) model. While we describe the reservoir dimensions as 2000 × 1200 × 10 m to provide realistic lateral extent and thickness, the vertical dimension (10 m) is not explicitly incorporated into the simulation framework, as our method is specifically designed for 2D analysis. This choice is made to reduce computational complexity while capturing the lateral distribution and production behavior of fractures, which are typically the primary focus in shale gas reservoir optimization. The benchmark shale gas reservoir model is shown in Figure 3a. The artificial fracture (red lines) length is 300 m, with a width of 0.01 m and a compressibility of 1.2 × 10⁻³ MPa⁻¹. The randomly generated natural fractures (black lines) within the reservoir range in length from 10 to 100 m, with a width of 1 × 10⁻² m and a compressibility of 1.2 × 10⁻³ MPa⁻¹. Figure 3b shows the porosity distribution of the shale gas reservoir. As shown in this figure, the matrix porosity is non-uniformly distributed, with higher values on the left and gradually decreasing values towards the right. The average porosity of the shale gas reservoir is 0.15. Figure 4a,b illustrate the permeability distribution along the x and y directions, respectively. Similar to the porosity distribution, the matrix permeability decreases from left to right in both the x and y directions. The average permeability of the shale gas reservoir in both the x direction and y direction is 0.01 mD. The values of other parameters applied in the benchmark shale gas reservoir models are shown in

Table 1. Values of the other parameters applied in the benchmark shale gas reservoir model.

Property	Value	Property	Value
Initial reservoir pressure pini (MPa)	25	Wellbore pressure pw (MPa)	5
Temperature of the reservoir T (°C)	125	Gas molar mass Mmg (g/mol)	16
Permeability of artificial fracture kaf (mD)	1 × 106	Permeability of natural fracture knf (mD)	1 × 104
Porosity of artificial fracture ϕaf	0.5	Porosity of natural fracture ϕnf	0.8

.

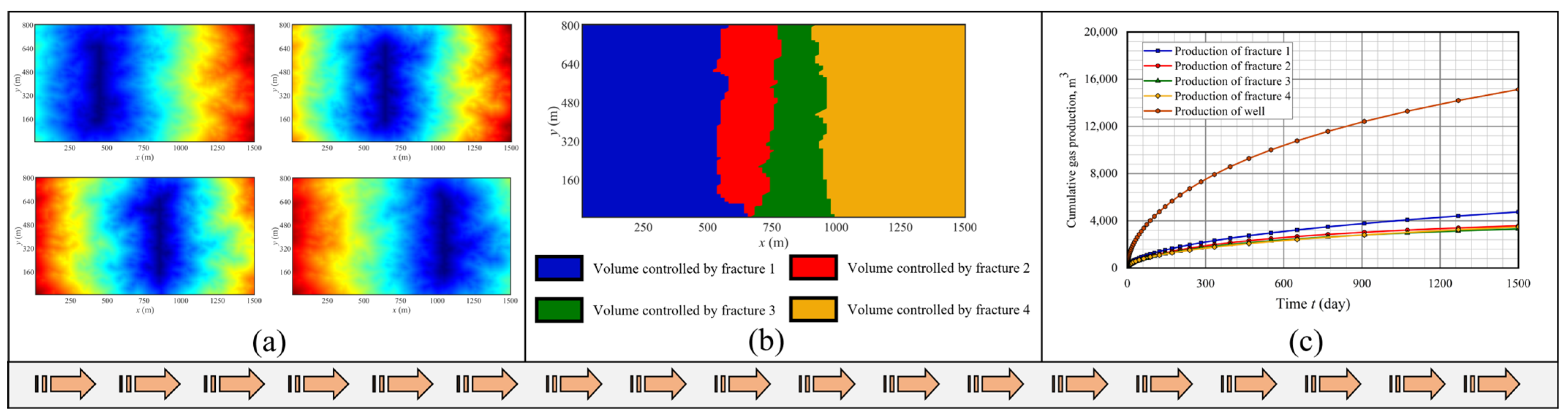
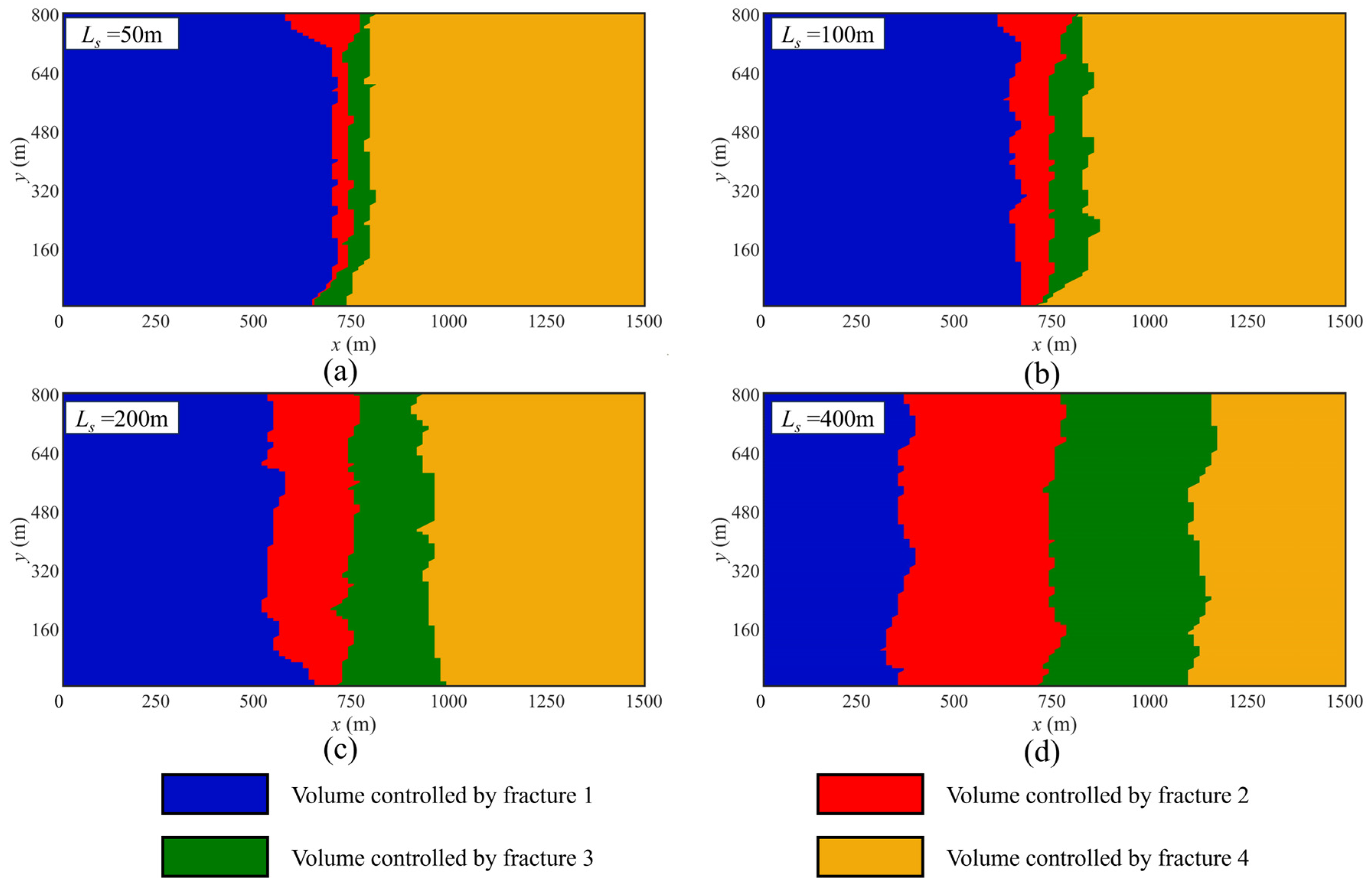
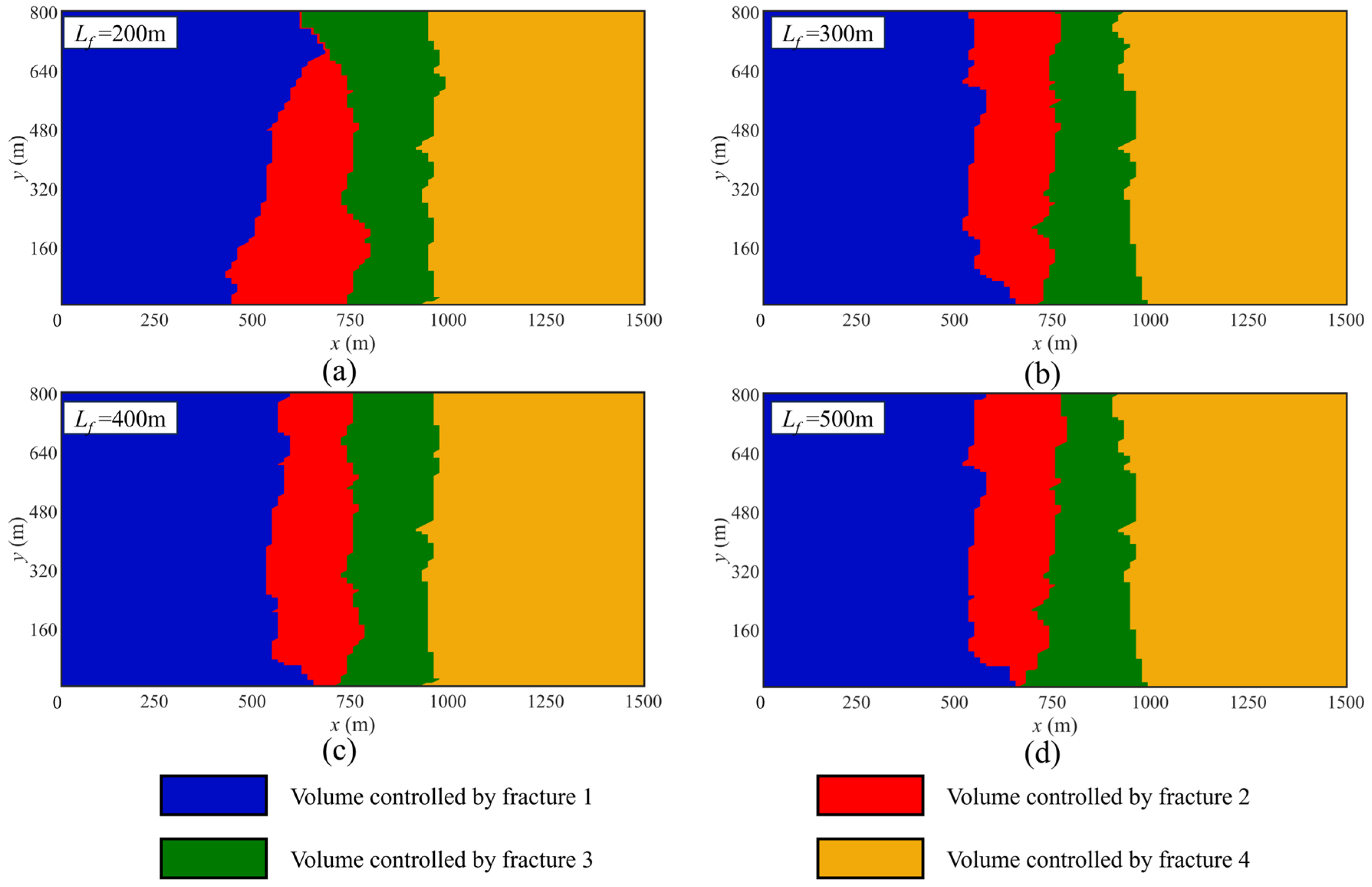
4.1. Artificial Fracture Spacing

The artificial fracture spacing is varied from 50 m to 200 m to examine its impact on both the control volumes and production performance of each artificial fracture, as well as on the well productivity. Figure 5 illustrates the distribution of the controlled volume of each artificial fracture with different artificial fracture spacing. As observed in the figure, when the artificial fracture spacing is small, the controlled volume of fracture 2 (red region) and fracture 3 (green region) only corresponds to a small portion of the surrounding volume. This occurs because the close spacing between fractures restricts their influence on the surrounding reservoir. As the artificial fracture spacing increases, the controlled volumes of fractures 2 and 3 gradually expand, reflecting their increased influence on a larger portion of the surrounding reservoir. This trend is further evidenced in Figure 6a, where the variation in controlled volume with artificial fracture spacing is shown quantitatively. Figure 6b compares the cumulative gas production of each artificial fracture and the well with varying artificial fracture spacing (calculated by Equation (9)). As the artificial fracture spacing increases, the cumulative production of the well increases. Specifically, as the fracture spacing increases from 50 m to 400 m, the cumulative gas production from the well rises significantly from approximately 8.05 × 10³ m³ to 1.71 × 10⁴ m³, representing an increase of about 112%. This is primarily because, with larger fracture spacing, the cumulative production from fracture 1 (blue dotted line) and fracture 4 (yellow dotted line) shows little change, while the cumulative production from fracture 2 (red dotted line) and fracture 3 (green dotted line) increases significantly. This is because the controlled volumes of fractures 2 and 3 expand as the artificial fracture spacing increases, leading to a greater contribution to the well’s cumulative production. This trend is consistent with the results shown in Figure 4, where the total controlled volumes of fractures 2 and 3 increase with larger fracture spacing.

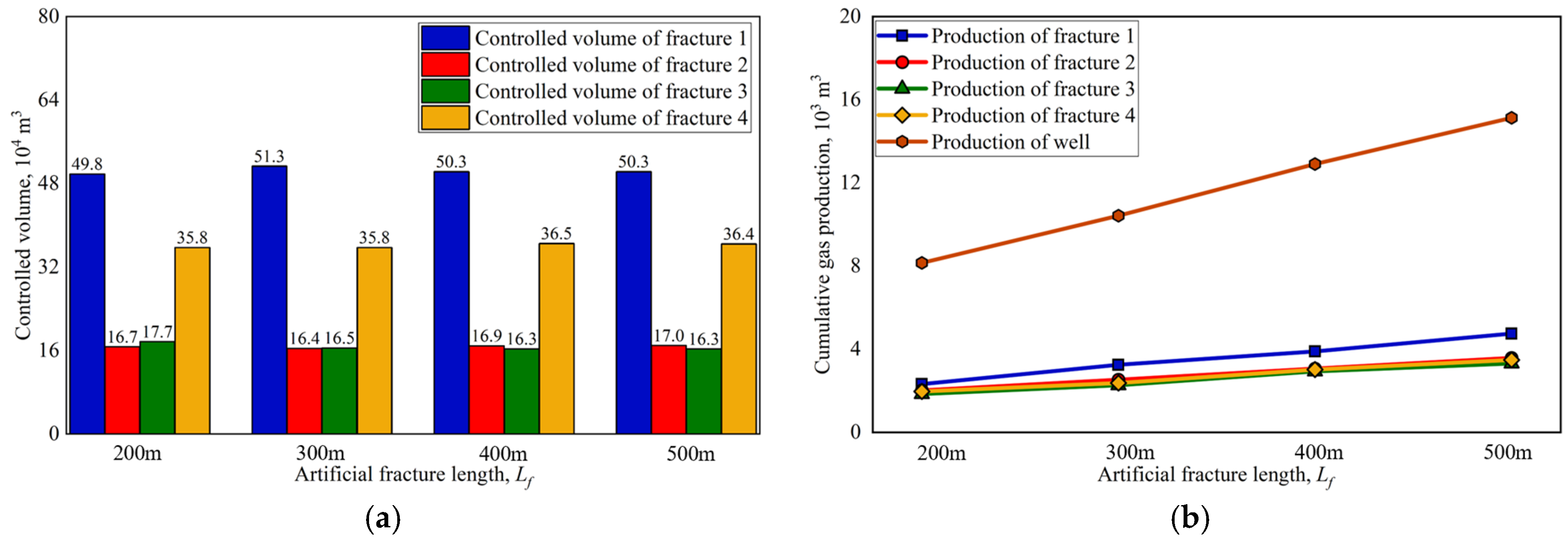
4.2. Artificial Fracture Length

A series of artificial fracture lengths, ranging from 200 m to 500 m, is used to study its impact on both the control volumes and production performance of each artificial fracture, as well as on the well productivity. Figure 7 illustrates the distribution of the controlled volume of each artificial fracture with varying artificial fracture lengths. As depicted in the figure, when the artificial fracture length is small, the distribution of controlled volumes shows noticeable changes as the fracture length increases. However, as the fracture length continues to increase, the distribution of controlled volumes stabilizes and becomes less sensitive to further increases in fracture length. Despite these initial changes in distribution, the total controlled volume for each fracture remains nearly constant across different fracture lengths, as shown in Figure 8a. This suggests that while the fracture length influences the spatial distribution of controlled volumes, it does not significantly alter the overall controlled volume for each fracture. Figure 8b compares the cumulative gas production of each fracture and the well, with different artificial fracture lengths (calculated by Equation (9)). As the fracture length increases, the cumulative production of the well increases significantly. This is primarily driven by the increase in fracture length, which enhances connection with a larger portion of the reservoir, allowing more reservoir area to contribute to production. Although the controlled volumes for each fracture remain almost unchanged, as shown in Figure 8a, longer fractures effectively connect more regions of the reservoir, leading to higher cumulative gas production. Specifically, the cumulative gas production from the well increases from approximately 8.15 × 10³ m³ at L_f = 200 m to 1.51 × 10⁴ m³ at L_f = 500 m, corresponding to an approximate 85.27% increase.

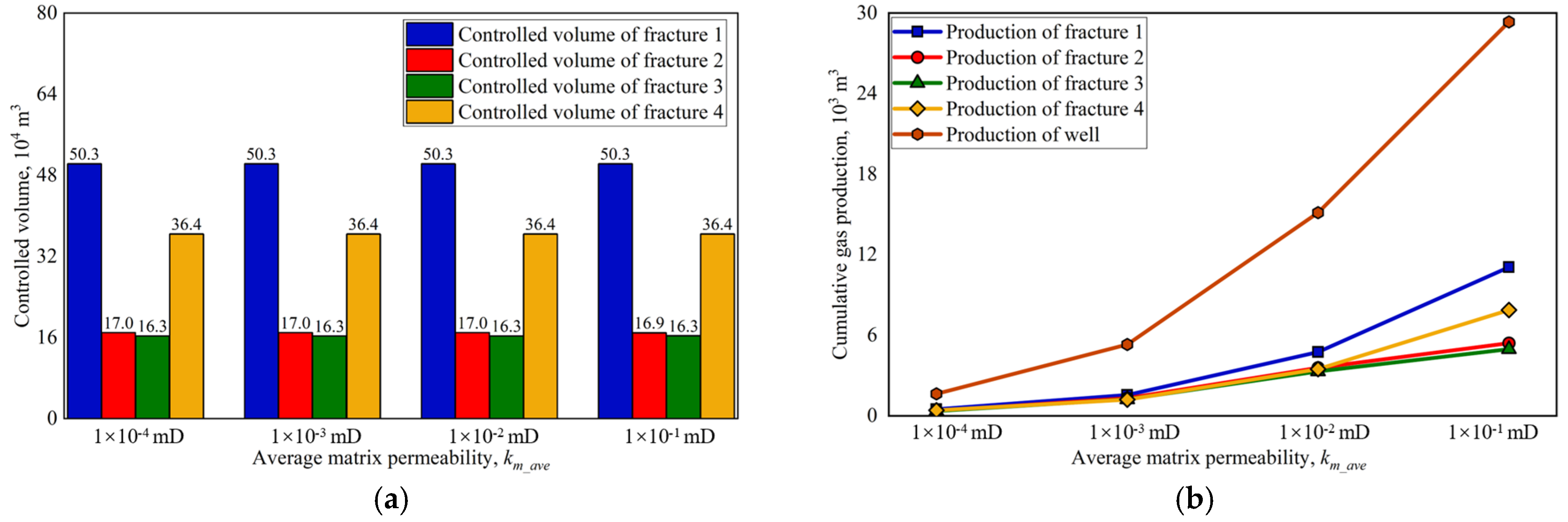
4.3. Average Matrix Permeability

The average matrix permeability is varied from 1 × 10⁻⁴ mD to 1 × 10⁻¹ mD (i.e., the average matrix permeability in the x and y directions) to investigate its impact on both the control volumes and production performance of each artificial fracture, as well as on the well productivity. These values are based on previously generated random values of the benchmark shale gas reservoir model, scaled by a multiplier. Figure 9 illustrates the distribution of the controlled volume of each artificial fracture with different average matrix permeabilities. It can be observed that the distribution of volumes controlled by each fracture remains consistent across these varying permeability conditions. This is attributed to the fact that changes in the average matrix permeability predominantly affect the fluid flow capacity within the entire reservoir. However, this alteration does not significantly impact the volume controlled by each artificial fracture, which is primarily determined by the fracture geometry and connectivity. This trend is confirmed by Figure 10a, which compares the controlled volume of each artificial fracture across different average matrix permeabilities. As seen in the figure, the total controlled volume for each fracture remains nearly constant, regardless of the changes in matrix permeability. Figure 10b further investigates the cumulative gas production from each artificial fracture and the well with different average matrix permeabilities (calculated by Equation (9)). The results show that, as the average matrix permeability increases, the cumulative gas production from fracture 1 (blue dotted line) and fracture 4 (yellow dotted line) increases significantly, while the production from fractures 2 (red dotted line) and 3 (green dotted line) rises at a slower rate. This aligns with the previous observation that the volumes controlled by fractures 1 and 4 are more substantial, leading to higher production. In contrast, fractures 2 and 3, which have smaller controlled volumes, show a less-pronounced increase in production. These findings indicate that although the controlled volumes are stable across different permeability conditions, the matrix permeability does impact the flow rate and ultimately the cumulative production from fractures, especially for fractures with larger volumes. Notably, as the average matrix permeability increases from 1 × 10⁻⁴ mD to 1 × 10⁻¹ mD, the cumulative gas production from the well increases from approximately 1.64 × 10³ m³ to 2.9 × 10⁴ m³, representing an increase of about 16.7 times.

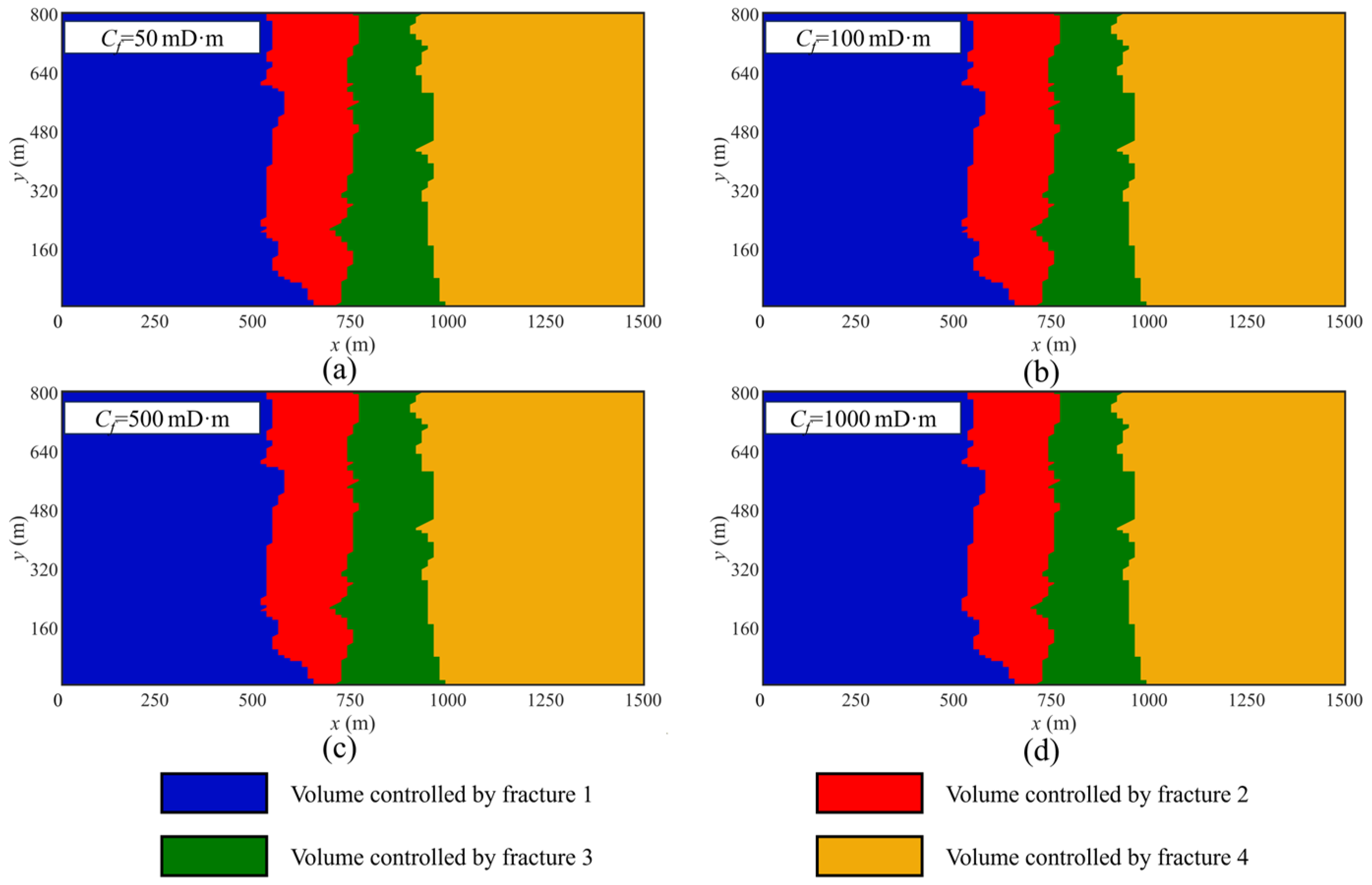
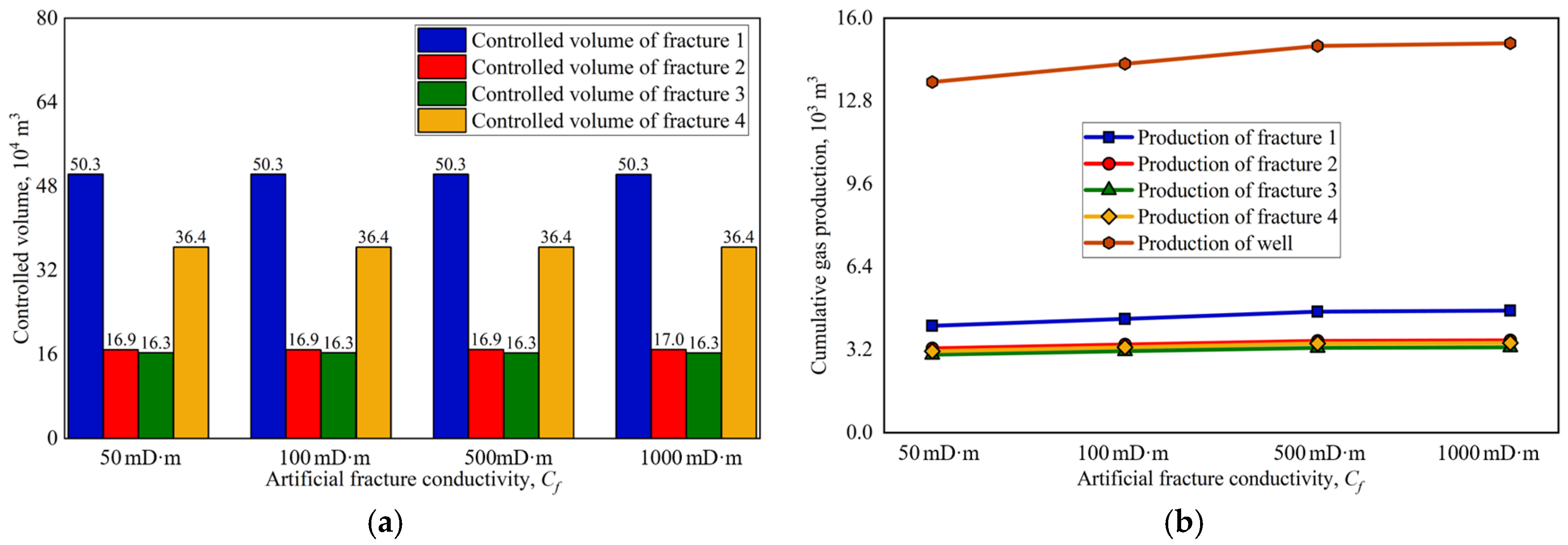
4.4. Artificial Fracture Conductivity

A series of artificial fracture conductivities, ranging from 50 mD·m to 1000 mD·m, is used to study its impact on both the control volumes and production performance of each artificial fracture, as well as on the well productivity. Figure 11 shows the distribution of the controlled volume of each artificial fracture with varying artificial fracture conductivities. It can be observed that the controlled volume distribution remains consistent despite variations in fracture conductivity. This consistency is mainly because the fracture conductivity primarily affects the fluid transport efficiency along the fractures, while fluid flow in regions far from the fractures is mainly influenced by the properties of the matrix and natural fractures. This observation is further supported by Figure 12a, which compares the controlled volume of each fracture under different fracture conductivities. This figure indicates that the controlled volume of each fracture remains nearly unchanged as the fracture conductivity increases. Figure 12b presents the cumulative gas production from each fracture and the well under varying fracture conductivity. It can be observed that the cumulative production from the well significantly increases with higher fracture conductivity, indicating enhanced fluid transport and reduced flow resistance within the fracture network. Specifically, the cumulative gas production from the well increases from approximately 1.35 × 10⁴ m³ at C_f = 50 mD·m to 1.5 × 10⁴ m³ at C_f = 1000 mD·m, corresponding to an approximate 11.11% increase.

5. Conclusions

In this work, based on the concept of DTOF, the authors propose a fast simulation method to efficiently simulate the production behavior of each artificial fracture throughout the shale gas reservoir production process. The method utilizes the fast marching method (FMM) to solve the Eikonal equation, enabling efficient calculation of controlled volumes and production of individual fractures. According to the obtained results in this work, the authors provide the following conclusions:

• The proposed method provides a computationally efficient approach to simulate the production behavior of each artificial fracture in shale gas reservoirs without simulating the production process of the entire reservoir.
• The controlled volume directly determines the production of each artificial fracture, with a greater controlled volume leading to higher gas production.
• Fracture parameters, including the length and spacing of artificial fractures, significantly influence the distribution and volume of the controlled area for each fracture within the reservoir, thereby affecting the production performance of artificial fractures. In contrast, the conductivity of artificial fractures has little impact on the distribution and volume of the controlled area but plays a crucial role in enhancing production performance. Specifically, longer artificial fractures, wider fracture spacing, and higher fracture conductivity result in increased gas production from the gas well.
• The matrix permeability has a minimal impact on the distribution of the controlled volume of artificial fractures, but it significantly influences the gas production from these fractures. Specifically, a higher matrix permeability leads to increased production from artificial fractures, especially those with large, controlled volumes.