Reservoir Surrogate Modeling Using U-Net with Vision Transformer and Time Embedding

Abstract

Accurate and efficient modeling of subsurface flow in reservoir simulations is essential for optimizing hydrocarbon recovery, enhancing water management strategies, and informing critical decision-making processes. However, traditional numerical simulation methods face significant challenges due to their high computational cost and limited scalability in handling large-scale models with uncertain geological parameters, such as permeability distributions. To address these limitations, we propose a novel deep learning-based framework leveraging a conditional U-Net architecture with time embedding to improve the efficiency and accuracy of reservoir data assimilation. The U-Net is designed to train on permeability maps, which encode the uncertainty in geological properties, and is trained to predict high-resolution saturation and pressure maps at each time step. By utilizing the saturation and pressure maps from the previous time step as inputs, the model dynamically captures the spatiotemporal dependencies governing multiphase flow processes in reservoirs. The incorporation of time embeddings enables the model to maintain temporal consistency and adapt to the sequential nature of reservoir evolution over simulation periods. The proposed framework can be integrated into a data assimilation loop, enabling efficient generation of reservoir forecasts with reduced computational overhead while maintaining high accuracy. By bridging the gap between computational efficiency and physical accuracy, this study contributes to advancing the state of the art in reservoir simulation. The model’s ability to generalize across diverse geological scenarios and its potential for real-time reservoir management applications, such as optimizing production strategies and history matching, underscores its practical relevance in the oil and gas industry.

1. Introduction

Simulating underground flow in reservoir studies with accuracy and effectiveness is critical in enhancing hydrocarbon recovery, improving water management, and supporting key decision-making processes. Nevertheless, traditional numerical simulation methods are computationally expensive and struggle with large-scale models containing geological uncertainties such as permeability distributions [1]. To address such concerns, surrogate models have proven useful tools in reducing computational costs while maintaining high accuracy in reservoir simulations [2]. Surrogate models, particularly deep learning (DL)-based ones, have proven to have a lot of potential in optimizing reservoirs and combining data, offering efficient and real-life results [3].

In the field of reservoir optimization, surrogate models have been utilized intensively for deciding well placement locations and for controlling parameters, critical for the maximization of hydrocarbon production and minimizing operational expenses [4]. Well placement-related optimization problems often exhibit numerous local optima, and therefore, gradient-based approaches become less effective in such cases. In such scenarios, metaheuristic global stochastic search algorithms, such as differential evolution (DE), have become a common practice; nevertheless, such algorithms require a significant number of function evaluations and therefore involve high computational costs [5]. To counteract such a challenge, machine learning (ML) and deep learning (DL)-based surrogate models have been developed for predicting key performance factors, such as net present value (NPV) and overall oil production, in terms of well configuration and management options [6]. For example, Kim et al. [7] used convolutional neural networks (CNNs) to predict the NPVs for two-phase oil–water problems, while Tang and Durlofsky [8] applied tree-based ML models to correct errors in NPV predictions due to the use of low-fidelity geomodels. Unlike traditional machine learning methods such as random forests or Gaussian processes, which rely on manually engineered features and struggle with high-dimensional data, deep learning models automatically learn hierarchical representations from raw inputs. This ability enables DL models, particularly convolutional neural networks (CNNs) and U-Net architectures, to capture complex spatial and temporal dependencies in reservoir simulations more effectively than traditional ML approaches, which may require extensive preprocessing and feature selection.

On the other hand, surrogate models for reservoir data assimilation focus on reducing uncertainty in model parameters, such as permeability and porosity, by integrating observed data into the simulation process [9]. Data assimilation, also known as history matching, is crucial for improving the accuracy of reservoir forecasts and optimizing production strategies [10]. Traditional data assimilation techniques, represented in the form of the Ensemble Kalman Filter (EnKF), rely on many high-fidelity simulations, whose computational requirements can become excessive in high-dimensional modeling scenarios [11]. To counter such requirements, deep learning (DL) surrogate models have been developed to represent flow variables, such as pressure and saturation, with a considerable reduction in computational cost compared to that of traditional simulation approaches [12]. As an example, a deep-learning-inspired surrogate model proposed in [13] utilizes residual U-Nets in a recurrent neural network model for predicting flow and surface displacement in simulation scenarios for carbon storage.

Using DL-based surrogate models in reservoir data assimilation is increasingly prevalent in recent times. These models utilize the power of neural networks in describing complex, nonlinear relationships between input factors (e.g., distributions of permeability) and output values (e.g., pressure and saturation fields) [14]. For example, Mo et al. [9] developed a deep encoder–decoder network with a convolutional neural network for predicting 2D Gaussian permeability field pressure and saturation, and Wen et al. [15] proposed a single-well axisymmetric injection case with a temporal convolutional neural network. In a recent work, Yan et al. [11] developed a Fourier neural operator (FNO)-based surrogate model for predicting saturation and pressure in 3D cases with variable permeability and porosity fields.

Recent advancements in deep learning have further expanded the capabilities of surrogate models. Surrogate models have also been applied in history-matching workflows, as demonstrated by [16], who evaluated the performance of Fourier neural operators and transformer U-Net in reducing uncertainty in permeability fields for geological carbon storage. Similarly, ref. [17] extended the recurrent surrogate model to handle CO₂ storage problems with multiple geological scenarios, demonstrating the model’s ability to generalize across diverse geological conditions. Additionally, ref. [18] explored the use of graph neural networks (GNNs) for subsurface flow modeling, highlighting the potential of GNNs in capturing complex spatial relationships in reservoir simulations. Furthermore, ref. [19] proposed a reduced-order model (ROM) for history matching of fractured simulation models, showcasing the effectiveness of ROMs in accelerating history-matching processes. Finally, ref. [20] introduced Fourier neural operators (FNOs) for subsurface flow modeling, demonstrating their ability to handle large-scale, high-dimensional problems with improved computational efficiency.

Even with such improvements, it is challenging to apply surrogate models to complex real-life geologic scenarios. One such challenge is uncertainty in quantities characterizing such geologic scenarios, referred to as metaparameters. Examples include the mean and standard deviation of porosity and log-permeability, spatial correlation lengths, and anisotropy factors of permeability [8]. These metaparameters which should be included in the training data to increase the ability of surrogate models to generalize are uncertain and have a significant impact on the accuracy of reservoir simulations. To be more clear, in history matching, traditional numerical simulations require running high-fidelity models multiple times to estimate these uncertain parameters, which is computationally expensive. Surrogate models aim to replace these simulations with faster approximations, but their accuracy depends on the quality of the training data and their ability to generalize to unseen geological scenarios. To address such a problem, Tang et al. [3] enhanced their recurrent R-U-Net surrogate model to apply to geomodel realizations of various geologic scenarios. They utilized a hierarchical Markov chain Monte Carlo (MCMC) history-matching algorithm to mitigate uncertainty in metaparameters.

The U-Net architecture was initially developed for biomedical image segmentation [21]. It is a critical part of deep learning nowadays, capable of both big-picture and small-detail information capture. Its encoder–decoder configuration, with skip connections, enables the model to effectively tackle complex spatial relations [3]. It is particularly well-suited for operations that require correct location, such as reservoir simulation [3]. U-Net’s architecture is particularly well suited for geologic applications, as it effectively captures both spatial continuity and heterogeneity, key factors influencing fluid flow behavior in reservoirs. Its encoder–decoder structure, enhanced by skip connections, allows it to simultaneously preserve large-scale geological patterns and fine-grained details in pressure and saturation distributions. Unlike standard convolutional neural networks (CNNs), which primarily extract features for classification tasks, U-Net maintains spatial resolution throughout the network. The skip connections mitigate information loss during downsampling, ensuring that critical geological structures, such as permeability variations and multiphase flow dynamics, are accurately represented. This capability makes U-Net a powerful tool for reservoir modeling, where capturing intricate spatial dependencies is essential for reliable flow predictions. In subsurface flow simulation, U-Net has been modified to forecast pressure and saturation fields through the use of permeability maps, representing uncertainty in geologic properties [9]. The encoder extracts significant features from the input, and the decoder constructs high-fidelity output, ensuring that the model retains small details important for the correct prediction of fluid flow [2]. It has performed effectively in numerous reservoir simulation operations, and it can effectively tackle uneven and disparate permeability fields [11].

To make U-Net function effectively, residual blocks are incorporated in its structure. Residual blocks, developed by He et al. [22], correct vanishing gradient and deep network issues through allowing the model to learn through residual differences rather than direct transformations. Convolutional layers, normalization, and nonlinear activation functions, together with skip connections bypassing the convolutional operations [23], make up a residual block. In reservoir simulations, residual blocks enable networks to comprehend complex relations between input information (e.g., permeability maps and previous states) and output forecasts (e.g., pressure and saturation fields) in a better manner [8]. Including residual blocks in the U-Net structure stabilizes training and enables the model to comprehend both spatial and temporal patterns, critical for effective reservoir forecasting [14].

Time embedding is a significant feature in the proposed model, allowing the U-Net to monitor time and adapt to changing reservoirs over a period of time. Time embedding transforms simple values of time into a complex form, allowing the model to make its prediction based on information about time [24]. It is particularly significant in reservoir simulations, in which the state of a reservoir keeps changing due to fluid injection, production, and other operations [12]. Sinusoidal embedding functions, utilized in many transformer models [25], are utilized for discovering recurring trends and smoothing trends over a period of time. By including time embeddings in the residual blocks, the model can comprehend changing saturation and pressure levels in a better manner, ensuring that prediction adheres to a natural sequence of reservoir change [13]. Not only does it enhance the model’s predictive capabilities for future conditions, but it also enables it to work effectively at any simulation time [10].

Using an attention mechanism, particularly the vision transformer (ViT), enables the model to perceive long-range relations and overall relations in the input information. The mechanism of attention was initially developed for natural language processing [24] but is extended to computer vision through the consideration of an image as a sequence of patches and employing self-attention in describing how they interact [25]. In reservoir simulations, the mechanism of attention enables the model to pay attention to significant regions of the permeability map and saturation/pressure field, and therefore, it is capable of dealing with complex, heterogeneous geologic scenarios [11]. Since it can perceive long-range relations, the vision transformer is particularly effective in predicting fluid flow in big reservoirs, in which nearby relations cannot necessarily capture overall behavior [2]. By combining U-Net’s capability in maintaining spatial information with the vision transformer’s capability in perceiving the big picture, the proposed model finds a balance between extracting overall and local information and therefore generates more real and accurate predictions [3].

This work introduces a novel deep learning model that enhances reservoir data assimilation by integrating a specialized U-Net architecture, time embedding, and an attention mechanism. The model is designed to process permeability maps that capture geological uncertainties and predict high-resolution saturation and pressure distributions over time. By incorporating time embeddings, the model effectively learns temporal variations in multiphase flow processes, while the attention mechanism improves its ability to capture both local and global dependencies in reservoir dynamics. This enables more accurate and computationally efficient predictions compared to traditional methods. The purpose of this report is to present a detailed analysis of the proposed model, including its architecture, implementation, and performance in reservoir simulations. By leveraging deep learning techniques, this work aims to bridge the gap between computational efficiency and physical accuracy in reservoir modeling. It contributes to the field by demonstrating how integrating time-aware embeddings and attention mechanisms can improve the predictive capabilities of surrogate models. The insights gained from this study can aid in the development of more robust and scalable reservoir simulation tools, ultimately supporting more effective decision-making in hydrocarbon recovery and reservoir management.

2. Materials and Methods

2.1. Overview of Reservoir Simulation

Reservoir simulation provides a mathematical framework for modeling subsurface multiphase fluid flow in porous media. This involves conservation laws, constitutive relations, and Darcy’s law to predict the spatial and temporal evolution of pressure and saturation distributions. These simulations are crucial for optimizing hydrocarbon recovery and reservoir management. Beyond hydrocarbon recovery, reservoir simulation plays a vital role in several other subsurface applications, such as geothermal energy extraction and CO₂ sequestration. In geothermal energy systems, accurate reservoir modeling is essential for optimizing heat extraction while ensuring long-term sustainability and preventing thermal depletion. Similarly, in CO₂ sequestration, understanding multiphase flow dynamics and caprock integrity is critical for ensuring secure long-term storage and minimizing leakage risks. By providing detailed insights into fluid behavior in porous media, reservoir simulations support decision-making in these diverse applications, contributing to sustainable energy solutions and climate change mitigation efforts.

The mathematical description begins with the mass conservation equation, which accounts for fluid flow and storage in porous media. For each phase (i), the mass conservation equation can be expressed as:

$$\nabla \cdot \left({\mathsf{\rho }}_i{v}_i\right)+{\displaystyle \frac{\partial }{\partial t}}\left({\mathsf{\rho }}_i\phi S_i\right)-{\mathsf{\rho }}_i{q}_i=0$$

(1)

Here, ${\rho }_i$ represents the fluid density, $v_i$ is the velocity of phase i, $\phi$ is the porosity, $S_i$ is the saturation of phase i, and $q_i$ is the volumetric source or sink term (e.g., injection or production rates). The source/sink term $q_i$ in the mass conservation equation represents external fluid additions or extractions within the reservoir, playing a crucial role in modeling injection and production wells. In the context of reservoir simulation, positive values of $q_i$ correspond to injection wells, where fluids such as water, gas, or CO₂ are introduced to enhance recovery or storage. Conversely, negative values represent production wells, where hydrocarbons or other fluids are extracted.

The velocity of each phase is governed by Darcy’s law, which relates the fluid flow to pressure gradients, gravitational forces, and fluid properties. Darcy’s law is expressed as:

$$v_i=-{\displaystyle \frac{{\mathsf{\mu }}_i}{k_{ri}}}K\left(\nabla p_i-{\mathsf{\rho }}_{i}g\nabla D\right)$$

(2)

where $k_{ri}$ is the relative permeability, $K$ is the absolute permeability tensor, ${\mu }_i$ is the fluid viscosity,$p_i$ is the pressure, $g$ is the gravitational acceleration vector which accounts for vertical or inclined reservoirs, and $D$ is the depth. The permeability tensor in Darcy’s law characterizes the ability of a porous medium to transmit fluids and can be either isotropic or anisotropic. In isotropic formations, permeability is uniform in all directions, leading to relatively straightforward flow predictions. However, in many real-world reservoirs, $K$ is anisotropic, meaning permeability varies with direction due to geological heterogeneity, layering, or fractures. This anisotropy significantly affects fluid flow by creating preferential flow paths or flow barriers, influencing pressure distributions and recovery efficiency.

To ensure a well-defined system, additional closure relations are incorporated. The saturation constraint ensures that the sum of fluid saturations equals one, $S_w+S_o=1$, where $S_w$ and $S_o$ are the water and oil saturations, respectively. Additionally, the relationship between the pressures of different phases is defined by the capillary pressure, $p_c=p_w-p_o$, where $p_c$ is a nonlinear function of water saturation.

The governing equations are discretized in space and time using finite difference or finite volume methods. In this study, we employed the finite volume method (FVM) due to its inherent conservation properties and ability to handle complex geometries and heterogeneous media more effectively than finite difference methods. The spatial discretization was applied implicitly to ensure numerical stability, particularly for the nonlinear and stiff nature of the multiphase flow equations. For time discretization, a fixed time-stepping scheme was used, with a constant time step size determined based on the Courant–Friedrichs–Lewy (CFL) condition to ensure stability. While adaptive time-stepping schemes can offer computational efficiency by adjusting the time step size dynamically based on the solution’s behavior, a fixed time step was chosen for simplicity and to maintain consistency across all simulations. The resulting system of nonlinear algebraic equations is expressed as:

$$r\left(x^n,x^{n+1},u^{n+1}\right)=0$$

(3)

Here, $r$ represents the residuals, $x^n$ and $x^{n+1}$ are the state variables (e.g., pressure and saturation) at time steps $n$ and $n+1$, and $u^{n+1}$ represents control variables such as well injection or production rates.

Newton’s method is often employed to solve this nonlinear system iteratively. The solution involves linearizing the equations using the Jacobian matrix $J$, resulting in:

$$J\delta =-r$$

(4)

where $\delta$ is the correction vector. This iterative process continues until the residuals converge to a predefined tolerance, ensuring an accurate numerical solution. However, the convergence rate of Newton’s method can be sensitive to the initial guess and the nature of the system, especially in complex, heterogeneous reservoirs where large variations in material properties or fluid flow behavior may lead to slow convergence or divergence in reservoir simulations. To improve convergence speed, specific preconditioning techniques are often employed. One common approach is the use of diagonal scaling, where the Jacobian matrix is preconditioned by scaling each row or column, which can enhance stability and accelerate convergence. Another technique involves incomplete factorization methods, such as the ILU (Incomplete LU) factorization, which provides a sparse approximation of the Jacobian matrix. Additionally, multigrid methods are sometimes applied, which accelerate the solution process by solving the system on multiple scales. These preconditioning strategies help mitigate issues related to slow convergence in heterogeneous systems and can significantly improve the efficiency and accuracy of Newton’s method in practical applications. In this study, ILU has been applied.

2.2. Residual Attention U-Net with Time Embedding

In this section, we detail the architecture of U-Net, augmented with time embedding, for improving predictions in reservoir simulations over time. U-Net is augmented with time embedding in an attempt to comprehend how state in a reservoir varies with time, and in a manner that enables it to make forecasts regarding saturation and pressure distribution with time. In the following, we discuss the general U-Net structure, role-played by residual blocks, and in what manner including time embedding aids in enhancing model performance in terms of both space and time in reservoir simulations.

2.2.1. U-Net

The U-Net model was initially developed for use in image segmentation processes. It is renowned for its capability to comprehend general information and minor details simultaneously. That feature renders it particularly effective for operations that require correct location and prediction, such as reservoir simulations. In our work, we modify U-Net to serve as a proxy model for permeability maps for predicting saturation and pressure at any time step. It consists of two principal parts: an encoder (the contracting path) and a decoder (the expanding path). Skip connections join these two and allow them to pass information regarding minor details to one another.

• Encoder Path: The encoder extracts significant features of the input information. The kernel size is 3, a common choice in U-Net. It consists of several layers that utilize convolution, with each successive layer processing a larger region than its predecessor and then pool layers that successively make the input smaller. In this manner, both big and small flow patterns in the reservoir can be detected, and both contribute to describing multiphase fluid flow accurately. How the encoder perceives space is significant in terms of handling complex relations between flow and distributions of permeability. This is addressed by using conditioning the input with permeability map as well as using the skip connections.
• Bottleneck: The bottleneck, located between encoder and decoder, is narrowest part of U-Net structure. In it, most abstraction feature representations of the input information are acquired, and complex relations between the permeability map, saturation, and pressure map at the current time step and the predicted output are represented. In most scenarios, a sequence of a few convolutional layers with nonlinear activations constitutes a bottleneck, enabling the model to represent high-level abstraction of the input information. The convolutional layers in the bottleneck are designed to capture deeper, more abstract relationships in the data. By reducing the dimensionality of the input, the bottleneck forces the network to learn compressed representations that highlight essential features, effectively capturing complex patterns and dependencies within the data. Nonlinear activation functions, here ReLU, are applied after convolution operations to introduce nonlinearity into the model. This nonlinearity allows the neural network to learn complex mappings and interactions within the data, which are essential for modeling intricate relationships in reservoir simulations.
• Decoder Path: The decoder generates high-resolution saturation and pressure maps out of high-level, abstracted features of the encoder. It employs transposed convolutions (upsampling) iteratively to increase feature map resolution in a spatial manner. Transposed convolutions, also known as deconvolutions or fractionally strided convolutions, work by applying learned filters to expand the spatial dimensions of the feature maps. Unlike standard convolutions that reduce spatial size, transposed convolutions perform the opposite operation, allowing the decoder to reconstruct finer details lost during encoding. In each upsampling stage, the decoder adds feature maps with similar ones in the encoder via skip connections. Skip connections play a key role in providing high resolution and spatial accuracy in output maps, with high-granularity information retained in them. It is through blending high, coarse feature with low, high-granularity detail that the decoder can accurately make state predictions in reservoirs. While transposed convolutions offer the advantage of learning optimal upsampling filters during training, they can sometimes produce artifacts such as checkerboard patterns. These methods are computationally efficient and can produce smooth outputs, but they lack the adaptability of learned filters. The choice between transposed convolutions and interpolation methods depends on the specific requirements of the application, such as the need for learned upsampling filters versus computational efficiency.
• Skip Connections: One of the key new features of U-Net architecture is its incorporation of skip connections between encoder and decoder. A skip connection is a direct link between corresponding layers of the encoder and decoder, allowing feature maps from earlier layers to be concatenated or added to later layers. By doing so, skip connections help mitigate information loss caused by pooling operations and deep network architectures. They enable the model to retain fine-grained details that are essential for precise predictions, particularly in tasks requiring spatial accuracy, such as segmentation and reconstruction. Skip connections preserve finer details that help the model avoid losing resolution during downsampling and upsampling. Skip connections allow the model to bypass a bottleneck and transmit low-level information directly between encoder and decoder. Skip connections allow the network to maintain high-granularity spatial information that can otherwise be lost in encoder pool operations. In reservoir simulations, skip connections become critical for holding small-scale information in predicted saturation and pressure maps, critical for proper modeling of fluid flow at the pore level.
  Skip connections, a key feature in architectures like U-Net, play a significant role in reducing overfitting in deep learning models. By providing direct pathways for gradient flow during backpropagation, skip connections mitigate the vanishing gradient problem, enabling more stable and efficient training of deeper networks. They also promote feature reuse, allowing the model to retain and leverage low-level information from earlier layers, which reduces the need to relearn these features and prevents overfitting to noise in the training data. Additionally, skip connections act as an implicit regularization mechanism by encouraging the model to learn more robust and generalizable representations, rather than memorizing specific patterns.
• Conditioning on Permeability Maps: To adapt the U-Net for reservoir data assimilation, we extend the traditional model to train on external information, such as permeability maps. In practice, the permeability map is concatenated with the input feature maps (e.g., saturation and pressure from the previous time step) at the initial layer, treating it as an additional channel in the input tensor. This allows the model to learn spatial relationships between permeability distributions and flow behavior from the start. The time-embedding mechanism integrates temporal information by projecting time embeddings into the feature space of residual blocks, where they are combined with feature maps derived from the permeability map. This enables the model to capture both spatial heterogeneity and temporal dynamics, ensuring predictions account for the evolving reservoir state. Permeability uncertainty significantly impacts reservoir flow predictions, as variations in permeability can lead to vastly different flow patterns and pressure distributions. By conditioning on permeability maps, the model generalizes across geological realizations, improving accuracy under uncertain geological conditions.

Figure 1 illustrates the overall architecture of the U-Net, highlighting the encoder and decoder paths and skip connections.

2.2.2. U-Net with Time Embedding

Residual blocks make an integral part of our U-Net model, and they are responsible for resolving vanishing gradient and training stability concerns. In reservoir simulations, such blocks enable efficient learning of complex mappings between output and input information. A residual block is composed of a convolutional layer, a nonlinear activation function, and a normalization layer, with a skip connection bypassing the operations of a convolution. With a skip connection, the model can learn about mappings of residuals, and training is eased and gradient flow is facilitated.

Our model involves a group normalization layer at the beginning of each residual block, a 3 × 3 convolutional layer, and then a nonlinear activation function (SiLU) following a pass through a normalization layer and a pass through a convolution, with a mix of output and input through a skip connection at output stage. With such a structure, both spatio-temporal and temporal dependencies can effectively be captured, and such dependencies make an integral part of successful reservoir simulations. Crucially, time embedding is integrated into the residual blocks, enabling the model to track the evolution of the reservoir state over time. The time embedding, represented as a high-dimensional feature vector, is added to convolutional layer output before the group normalization. This allows the model to condition its predictions on the current time step, capturing temporal dependencies that are critical for accurate reservoir simulations.

Mathematically, the residual block operation for input $x$ at time $t$ is:

$$\begin{array}{c}Output=Conv\left(SiLU\right(GroupNorm\left(Conv\right(GroupNorm\left(x\right)\\ +LinearEmbed\left(t\right)\left)\right)\left)\right)+x\end{array}$$

(5)

To better understand the role of time embedding in our residual blocks, it is essential to consider how LinearEmbed(t) influences the computation. The time embedding t is first mapped to a high-dimensional space through a learned transformation, allowing it to be effectively incorporated into the feature representations. By adding LinearEmbed(t) to the output of the first GroupNorm operation, the model ensures that temporal information is seamlessly fused with spatial features before applying nonlinear activation and convolution. This design allows the network to modulate its feature extraction process based on the current time step, thereby improving its ability to capture long-range temporal dependencies. The integration of time embedding is particularly useful in reservoir simulations, where the evolution of subsurface conditions over time plays a critical role in accurate predictions. By conditioning the residual block on time, the model can better generalize across different time steps and improve the stability of training in time-dependent learning tasks.

Figure 2 provides a representation of the residual block architecture, highlighting the integration of time embedding and the role of skip connections.

2.2.3. Time Embedding

Time embedding is a critical component of our surrogate model, enabling the U-Net to maintain temporal continuity and react to the sequential nature of reservoir development. By embedding temporality in the network, the model can learn about changing saturation and pressure distributions over time (these distributions change because of sink and source terms in Equation (1)). For reservoir simulations, specifically, this is significant, since the state of the reservoir is in constant flux through fluid injection, production, and other operations. Time embedding takes a scalar value t (the current time step) and embeds it in a high-dimensional feature and enables conditioning of model prediction with temporality information. In our case, a sinusoidal embedding function, a prevalent one in deep learning for its efficacy in representing periodical structures and continuous transition over time, is adopted. The function for time embedding $e\left(t\right)$ can be computed:

$$e\left(t\right)=\left[\sin \left(2\mathsf{\pi }\cdot f_1\cdot t\right),\cos \left(2\mathsf{\pi }\cdot f_1\cdot t\right),\sin \left(2\mathsf{\pi }\cdot f_2\cdot t\right),\cos \left(2\mathsf{\pi }\cdot f_2\cdot t\right),\dots ,\sin \left(2\mathsf{\pi }\cdot f_d\cdot t\right),\cos \left(2\mathsf{\pi }\cdot f_d\cdot t\right)\right]$$

(6)

where $t$ is the scalar time value, $\left(f_1,f_2,\dots ,f_d\right)$ are frequency components that determine the scale of the embedding, and $d$ is the dimensionality of the embedding space. The frequencies $f_i$ are typically chosen to form a geometric progression, ensuring that the embedding captures both fine-grained and coarse-grained temporal patterns. For example, $f_i={\mathrm{base}}^{i-1}$, where base is a hyperparameter controlling the progression of frequencies.

Once computed, the time embedding $\mathrm{e}\left(\mathrm{t}\right)$ is projected into the feature space of the residual blocks using a learnable linear transformation:

$$\mathit{z}\left(t\right)=\mathit{W}\cdot \mathit{e}\left(t\right)+\mathit{b}$$

(7)

where $\mathit{b}$ is a learnable vector, $\mathit{W}$ is a learnable matrix, and $\mathit{z}$ is a result of the last time-conditioned embedding in a network. It is added to feature maps in a sequence of residual blocks, allowing a model to condition its output at any current time step. Integration of a time embedding allows a network to effectively model temporal relations in governing multiphase flow processes in a reservoir. With integration of such a mechanism, not only its prediction of future state is enhanced, but its generalizability over simulation times is boosted, too. For example, in a real-world reservoir scenario, time embedding enables the model to accurately predict future fluid levels (e.g., water or oil saturation) and pressure distributions as the reservoir evolves over time.

2.2.4. Vision Transformer

The vision transformer (ViT) adapts the transformer architecture, originally designed for natural language processing, to computer vision tasks. By treating images as sequences of patches and leveraging self-attention mechanisms, ViT excels at capturing global dependencies and spatial relationships. The input image $X\in R^{H\times W\times C}$ is divided into $N$ non-overlapping patches of size $P\times P$. Each patch $x_p\in R^{P^{\mathbb{2}}\times C}$ is flattened and projected into a D-dimensional embedding space:

$${\mathit{z}}_{\mathit{p}}=\mathit{E}\cdot {\mathit{x}}_{\mathit{p}}+\mathit{b}$$

(8)

where $E\in R^{D\times \left(P^{\mathbb{2}}\cdot C\right)}$ is a learnable projection matrix, and $b\in R^D$ is a bias vector. The resulting sequence of patch embeddings (the feature vectors of individual image patches) $Z=\left[z_1,z_2,\dots ,z_N\right]$ is passed to the transformer encoder. For a 224 × 224 grayscale image with 16 × 16 patches, there would be (224/16)² = 196 patches, each with 768 features if D = 768.

To retain spatial information, positional encodings $P\in R^{N\times D}$ are added to the patch embeddings:

$${\mathit{Z}}^{\prime }=\mathit{Z}+\mathit{P}$$

(9)

These encodings can be learned or predefined using sinusoidal functions. The input sequence ${\mathit{Z}}^{\prime }$ is fed into the transformer encoder consisting of alternating layers of multi-head self-attention (MSA) and feedforward neural networks (FFNs) to capture global dependencies.

The self-attention mechanism computes attention scores between all patches:

$$\mathrm{Attention}\left(\mathit{Q},\mathit{K},\mathit{V}\right)=\mathrm{softmax}\left({\displaystyle \frac{\mathit{Q}{\mathit{K}}^{\mathit{T}}}{\sqrt{D}}}\right)\mathit{V}$$

(10)

where $Q=Z^{\prime }{W}_Q$, $K=Z^{\prime }{W}_K$, and $V=Z^{\prime }{W}_V$ are the query, key, and value matrices, respectively. $W_Q,W_K,W_V\in R^{D\times D}$ are learnable matrices and D is a scaling factor to stabilize gradients during training. Multi-head self-attention splits the input into $h$ heads, processes them independently, and concatenates the results. Moreover, the FFN consists of two linear transformations with a ReLU activation:

$$FFN\left(\mathit{x}\right)=\mathrm{ReLU}\left(\mathit{x}{\mathit{W}}_1+{\mathit{b}}_1\right){\mathit{W}}_2+{\mathit{b}}_2$$

(11)

In addition, each sub-layer (MSA and FFN) is followed by layer normalization and residual connections. Figure 3 shows the architecture of the vision transformer.

While the vision transformer (ViT) represents a significant shift in processing visual data by treating images as sequences of patches and employing self-attention mechanisms, it is insightful to contrast this approach with traditional Convolutional Neural Networks (CNNs), which have been the cornerstone of computer vision tasks. CNNs operate by applying convolutional filters across an image, effectively capturing local features such as edges, textures, and simple shapes. This localized processing allows CNNs to build hierarchical representations, gradually combining simple patterns into more complex features as data progress through deeper layers. The inherent design of CNNs enables them to efficiently learn spatial hierarchies, making them particularly adept at tasks where local information is paramount. In contrast, ViTs lack this inherent inductive bias toward local features, instead relying on self-attention mechanisms to capture both local and global dependencies across an image. This design allows ViTs to model relationships between distant parts of an image more effectively, potentially leading to better performance on tasks requiring an understanding of global context. However, this flexibility comes at the cost of requiring larger datasets for effective training, as ViTs must learn spatial relationships from scratch without the built-in assumptions that guide CNNs.

2.3. Surrogate Model

The U-Net surrogate is designed for integration into ensemble-based data assimilation workflows (e.g., Ensemble Kalman Filter). By predicting states $x^{n+1}=\{S^{n+1},p^{n+1}\}$ from $x^n$ and permeability $K$, the model accelerates forecast generation while preserving physical fidelity. Temporal embeddings ensure that predictions respect the causal structure of reservoir evolution, avoiding unphysical “time-aliasing” artifacts common in static surrogate models. This architecture bridges computational efficiency and geological realism, making it a robust tool for uncertainty quantification in reservoir management. This study does not intend to perform reservoir data assimilation, but it intends to show the potential of a new proxy model for it.

3. Results

To evaluate the performance of the proposed residual-attention U-Net model for reservoir simulation, we generated a dataset by running 1500 numerical simulations, each with different permeability realizations while keeping other input parameters constant. Other parameters, including fluid viscosity, reservoir temperature, and injection/production rates, were kept constant across simulations to isolate the impact of permeability variations. Each simulation spanned 61 timesteps, during which saturation and pressure maps were recorded. The reservoir setup consisted of a five-spot well pattern with four production wells and one injection well. The grid resolution for each model was set at 100 × 100.

The dataset was divided into training (80%) and validation (20%) subsets. The proposed U-Net model was designed with an encoder–decoder architecture, where the encoder consisted of five downsampling layers, each containing two blocks. The first four layers featured residual blocks, while the last layer included attention blocks. Similarly, the decoder had five upsampling layers, following the same configuration as the encoder, with the first four layers using residual blocks and the final layer incorporating attention mechanisms. The number of feature channels for the encoder layers were 64, 64, 128, 128, and 256, while the decoder layers followed the reverse order: 256, 128, 128, 64, and 64.

Since the U-Net model requires input sizes that are multiples of 2, the original 100 × 100 pressure and saturation maps were padded to 128 × 128. The input consisted of three channels: saturation, pressure, and permeability maps. Model training employed the Mean Squared Error (MSE) loss function, with the AdamW optimizer used to mitigate overfitting. The learning rate was set to 1 × 10⁻⁴, and a batch size of 32 was used.

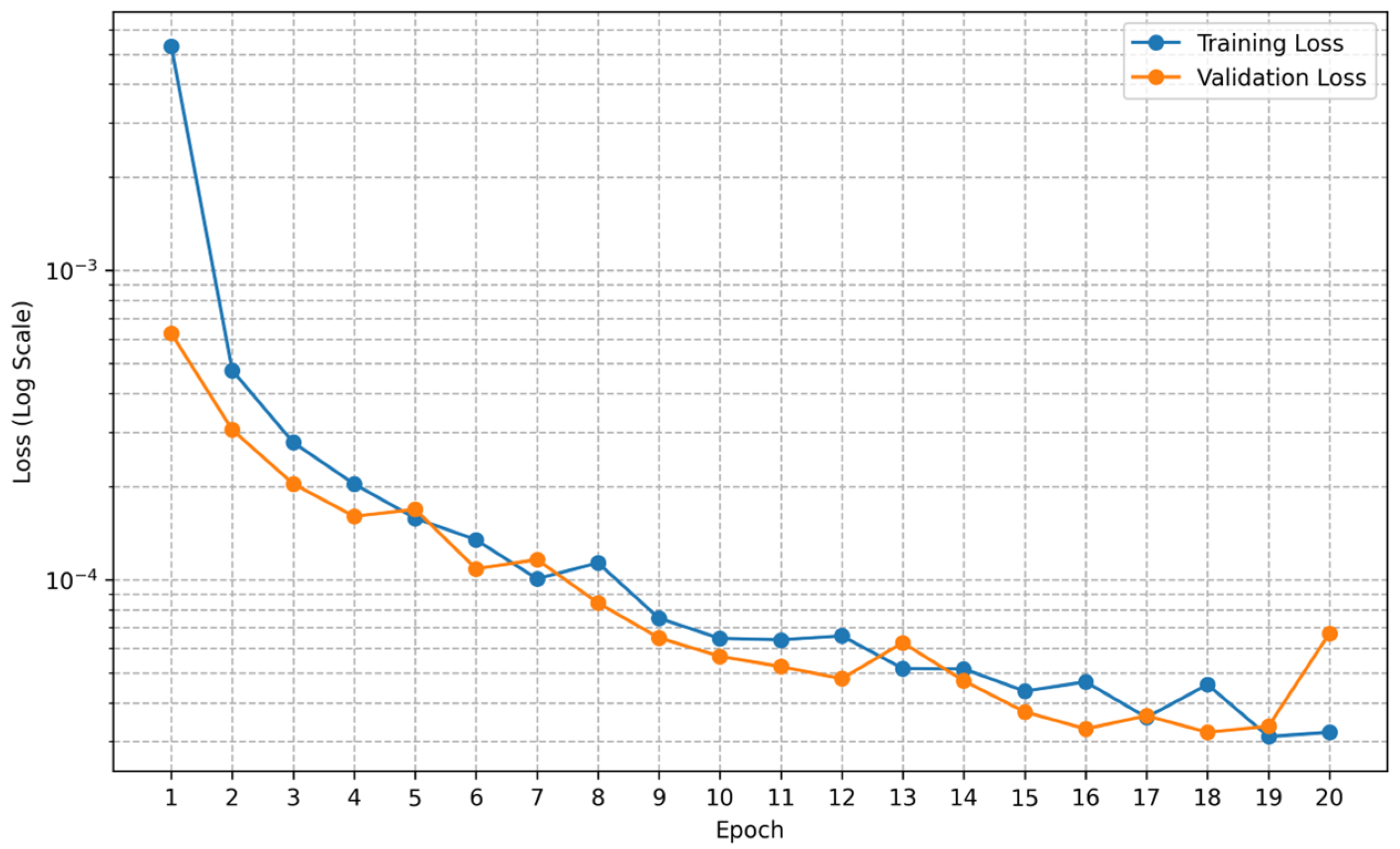
Figure 4 illustrates the training and validation loss curves across different epochs, indicating stable convergence. The best model was selected at epoch 18, as determined by the lowest validation loss. Figure 5 and Figure 6 compare the predicted mean saturation and pressure maps with the ground truth. The results demonstrate that the model achieved high predictive accuracy, with R-squared values of 1.000 for mean saturation and 0.997 for mean pressure. The MAE and RMSE for normalized pressure maps are 0.0023 and 0.0026, respectively; while for normalized saturation maps, they are 0.0007 and 0.0009, respectively. Figure 7 show the predicted pressure maps for some samples.

4. Discussion

The results indicate that the proposed residual attention U-Net effectively captures the complex spatial relationships governing multiphase flow in reservoir simulations. The high R-squared values suggest that the model generalizes well to unseen data, making it a reliable surrogate for numerical simulations. The use of residual blocks in the encoder and decoder allowed for efficient feature extraction while mitigating vanishing gradient issues. The integration of attention mechanisms in the deepest layers further enhanced the model’s ability to focus on critical regions of the permeability map, leading to improved accuracy in pressure and saturation predictions.

Compared to traditional numerical simulation approaches, the proposed method significantly reduces computational overhead while maintaining high accuracy. The ability to train on predictions on permeability maps ensures adaptability across various geological scenarios, making this approach potentially valuable for real-time reservoir management and data assimilation tasks. Although the current model significantly accelerates simulations, further optimization of the inference time and hardware efficiency is required for fully real-time applications.

The model can support history matching by assimilating observed data (e.g., well production rates or pressure measurements) to update reservoir models and reduce uncertainty in geological parameters. This is particularly valuable for fields with complex geology or limited historical data. Furthermore, the model’s ability to generate high-resolution predictions at reduced computational costs makes it suitable for scenario analysis, where multiple realizations of reservoir behavior are evaluated to assess risks and optimize development plans. By integrating the proposed model into existing workflows, reservoir engineers can enhance decision-making processes, improve operational efficiency, and reduce costs.

Despite the strong performance, limitations should be acknowledged. The model’s training and validation were conducted on synthetic datasets generated from numerical simulations. While this approach ensures controlled conditions for evaluating the model, it may not fully capture the complexities and uncertainties present in real-world reservoir data. For example, real reservoirs often exhibit additional sources of uncertainty, such as measurement errors, incomplete geological data, or unmodeled physical processes, which could affect the model’s performance in practical applications. Moreover, the computational efficiency of the proposed model depends on the availability of high-quality training data and computational resources for training deep learning models. The model’s reliance on permeability maps as input also assumes that these maps are accurately characterized, which may not always be the case in practice.

To address these limitations, future work could focus on validating the model using real-world reservoir data and exploring its performance under more diverse and challenging geological conditions. Incorporating additional sources of uncertainty, such as measurement noise or incomplete data, could further enhance the model’s robustness. Additionally, integrating other geological parameters (e.g., porosity, fracture networks) could broaden its applicability and predictive capabilities. Moreover, using other types of time embedding, residual blocks, or vision transformers might improve the results.

Overall, this study demonstrates the potential of deep learning-based surrogate modeling for accelerating reservoir simulations while maintaining physical fidelity. The proposed U-Net model with residual and attention mechanisms provides a promising framework for reservoir simulations applicable to data assimilation.

5. Conclusions

In this study, we introduced a novel deep learning-based framework applicable to reservoir data assimilation, leveraging a conditional U-Net architecture enhanced with time embedding and attention mechanisms. The proposed model addresses the limitations of traditional numerical simulation methods by significantly reducing computational costs while maintaining high accuracy in predicting saturation and pressure distributions over time. By training on permeability maps and incorporating time embeddings, the model effectively captures the spatio-temporal dependencies governing multiphase flow processes in reservoirs. The integration of residual blocks and attention mechanisms further enhances the model’s ability to handle complex, heterogeneous geological scenarios, ensuring robust and reliable predictions. The results demonstrate that the proposed residual attention U-Net model achieves high predictive accuracy, with R-squared values of 1.000 for mean saturation and 0.997 for mean pressure, outperforming those of traditional simulation approaches. The model’s ability to generalize across different geological realizations and adapt to the sequential nature of reservoir evolution makes it a powerful tool for data assimilation tasks. This work bridges the gap between computational efficiency and physical accuracy, advancing the state of the art in reservoir simulation and data assimilation. Future research could incorporate additional geological parameters to further enhance its predictive capabilities. Overall, the proposed framework offers a promising approach for accelerating reservoir simulations while maintaining the fidelity required for critical decision-making in hydrocarbon recovery and reservoir management.