Data-Driven Model for Cyclic Tasks of Robotic Systems: Study of the Repeatability Conditions
Abstract
1. Introduction
2. Conditions for Repeatability in Robotics
2.1. Differential Form Condition
2.2. Lie-Bracket Condition
- The fact that (13) holds under ideal circumstances is to be expected for a system like (the linear velocity partition of ) since its structure meets the criteria for holonomic systems. Then, should perfectly represent the relationship between and ; thus, the Jacobian must fulfill to be well defined and non-singular. In addition, must reflect the actual changes in p with respect to q, which is not guaranteed in hybrid task-space control approaches (when the end-effector pose is measured and the Jacobian is derived from the forward kinematics).
- The angular velocity partition is a generalization of any rotational system that can be written in such a form. Regardless of its angular expression, parameters, or rotation order, (13) is valid under the same assumptions as . However, for systems in where , the non-integrability inherently arises from the basis that generates the directions of rotation, typically path- and configuration-dependent. This effect is captured by the Lie-bracket condition (17).
- Fulfilling both (13) and (17) is a necessary and sufficient condition for integrability. Note that (11) and (19) have a closely related formulation, although not identical. In fact, the condition is considered stronger than (13) and (17) as it naturally implies them both but also requires either perfect symmetry:or a trivial solution: , which requires a constant J. Although this constraint is a stronger indicator of integrability than (17), it is more restrictive as Lie brackets do not strictly require generating vectors of zeroes as long as these point are in the same directions of the original basis.
3. Non-Integrable Systems
3.1. Rotational Systems
3.1.1. Euler-Angle Sequences in 3D Rotation
3.1.2. Rotation Group SO(3) and Axis-Angle Representation
3.1.3. Unit Quaternion Parameterization
3.2. Coupled Translation and Rotation
3.2.1. Mapping Velocities Across Flat Surfaces
3.2.2. Mapping Velocities Across Flat and Curved Surfaces
3.3. Serial-Link Mechanisms
3.3.1. Forward Kinematics
3.3.2. Velocity Kinematics
3.3.3. Minimal Representation of the Task-Space
4. Dealing with Non-Integrable Systems for Repeatability
4.1. Hybrid Control System
4.2. Data-Driven Forward and Inverse Kinematics
4.3. Optimal Estimated Basis Vectors
4.4. Subspaces for Learned Tasks
- 1.
- The distribution defined by the converged Jacobian:is integrable and involutive, satisfying the conditions of Frobenius’ theorem and the Lie-bracket condition.
- 2.
- Consequently, there exists an integral manifold described by a globally continuously differentiable function :ensuring global repeatability and path independence for trajectories generated by integrating within . Note that is the observed pose implicitly affected by q, unlike the forward kinematics function built explicitly as a function of q.
- 3.
- For cyclic or repetitive tasks defined by distinct references , integrability and repeatability are maintained in the union of optimal subspaces:
- 1.
- Consider the converged Jacobian estimate for which . Thus, the exterior derivative Condition (21) holds trivially since . Therefore, Frobenius’ integrability condition is satisfied automatically as follows:Similarly, the Lie-bracket condition is trivially satisfied as follows:due to constant basis vectors such that . Thus, the distribution is involutive.
- 2.
- By Frobenius’ theorem, since is involutive, there exists a continuously differentiable function , generating an integral manifold . Thus, the task-space coordinates depend uniquely on the configuration q, making any integrated trajectory path-independent and uniquely defined by the endpoints of .
- 3.
- Consider repetitive tasks defined by sequences of reference points . For each distinct , the iterative estimation converges to a corresponding subspace , ensuring local integrability. When the reference is changed incrementally , the integrability persists if transitions occur within or smoothly across the subspace intersection:remaining integrable provided that changes in reference configurations are accommodated through stable transitions. Consequently, all feasible repetitive task trajectories lie on a global integral manifold .
- 4.
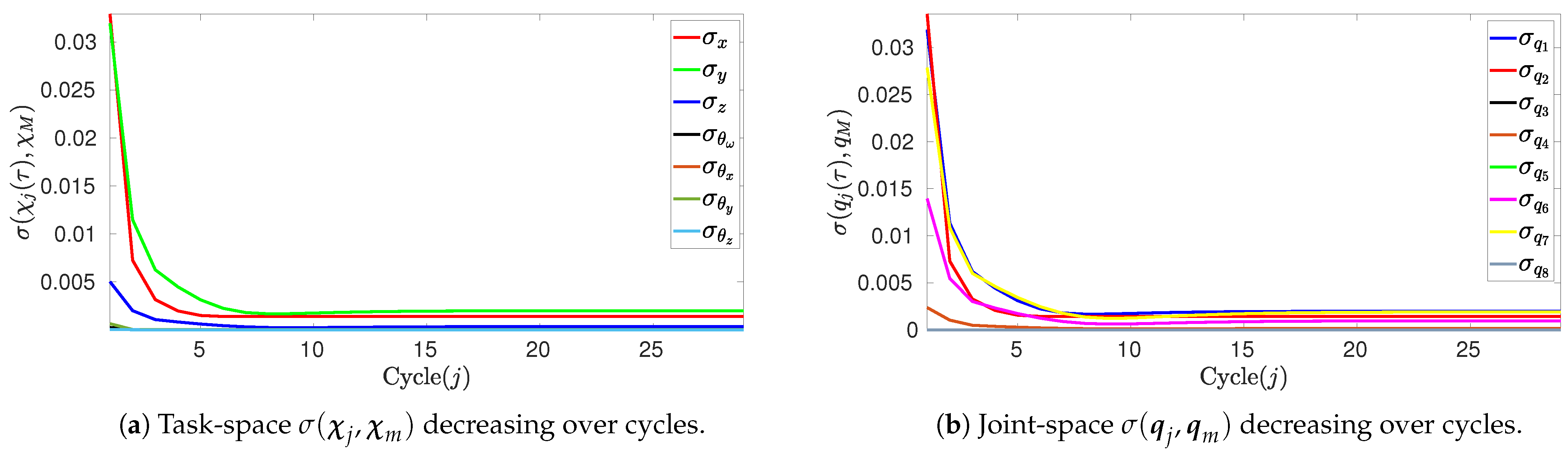
- This theoretical conclusion is compatible with empirical methods to support its validity, such as the standard deviations of sampled trajectories of , defined as and , for N samples and their sample-mean , , such that, ifit indicates repeatable and unique trajectories independent of integration path, as defined by the constructed integral manifold .
5. Simulations of an Omnidirectional Mobile Manipulator
5.1. Simulated Robot and Virtual Environment
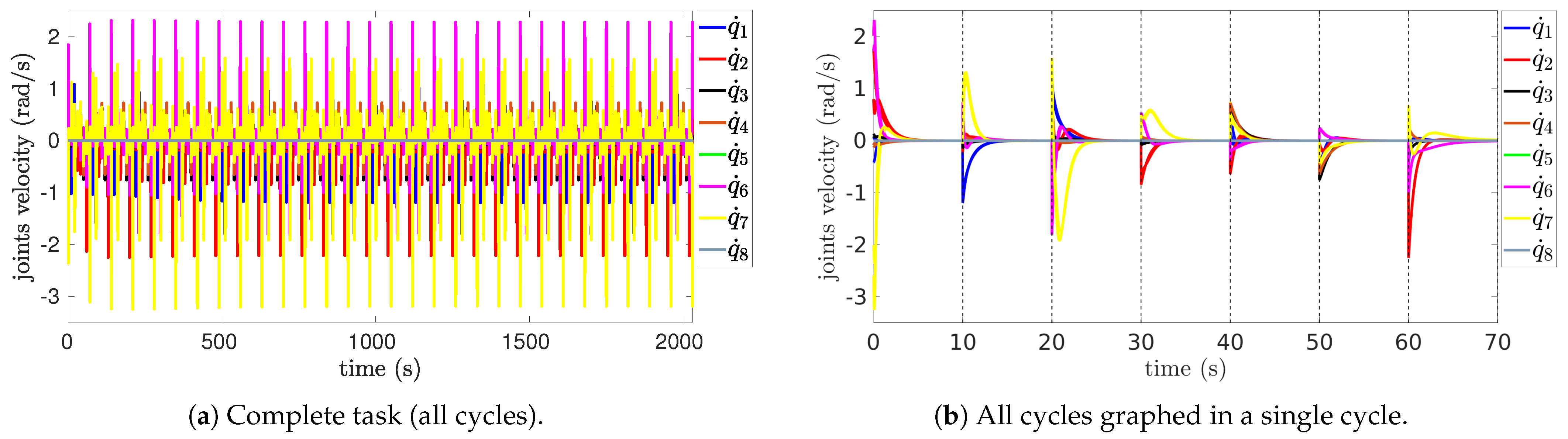
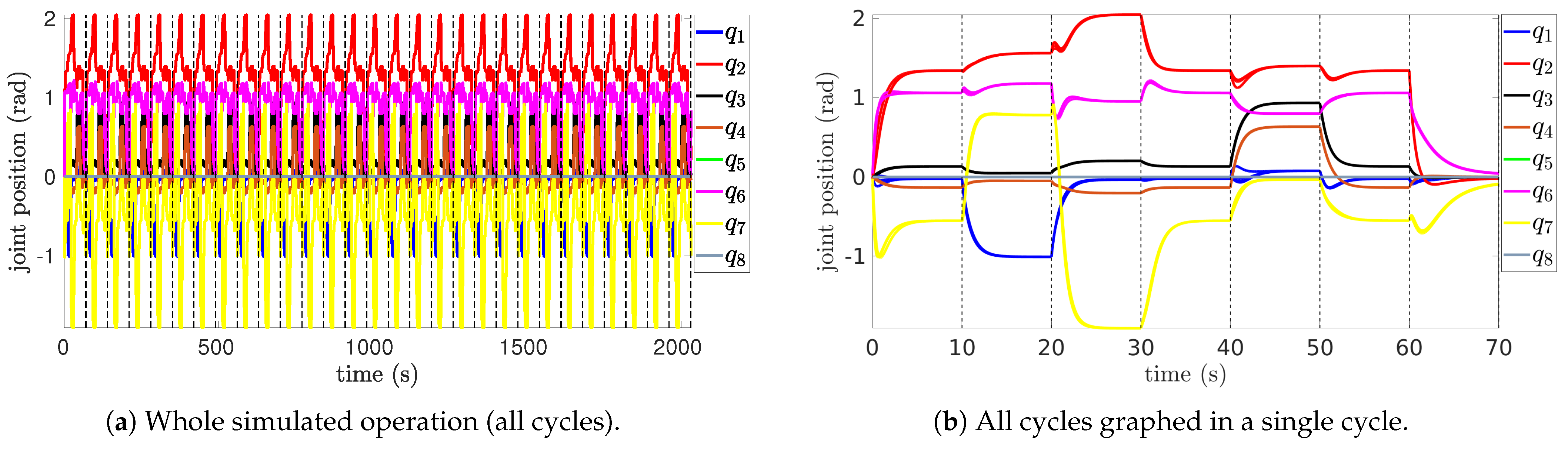
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cañas, H.; Mula, J.; Díaz-Madroñero, M.; Campuzano-Bolarín, F. Implementing industry 4.0 principles. Comput. Ind. Eng. 2021, 158, 107379. [Google Scholar] [CrossRef]
- Ribeiro, J.; Lima, R.; Eckhardt, T.; Paiva, S. Robotic process automation and artificial intelligence in industry 4.0—A literature review. Procedia Comput. Sci. 2021, 181, 51–58. [Google Scholar]
- Axmann, B.; Harmoko, H. Robotic process automation: An overview and comparison to other technology in industry 4.0. In Proceedings of the 2020 10th International Conference on Advanced Computer Information Technologies (ACIT), Deggendorf, Germany, 16–18 September 2020; pp. 559–562. [Google Scholar]
- Urrutia, P.; Guamán-Molina, J.; Peñaloza, A.; Salazar, F.; Madroñero, D.G.; Jácome, J.A. Control System for the Teleoperation of Kuka Youbot Robot via Wireless Communication and the Use of Embedded Cards. In Proceedings of the International Conference on Computer Science, Electronics and Industrial Engineering (CSEI), Ambato, Ecuador, 6–10 November 2023; Springer: Cham, Switzerland, 2023; pp. 615–628. [Google Scholar]
- Pająk, G.; Pająk, I. Trajectory Planning for Mobile Manipulators with Control Constraints. Pomiary Autom. Robot. 2023, 27, 21–30. [Google Scholar]
- Hernandez-Barragan, J.; Villaseñor, C.; Lopez-Franco, C.; Arana-Daniel, N.; Gomez-Avila, J. Image based visual servoing with kinematic singularity avoidance for mobile manipulator. PeerJ Comput. Sci. 2024, 10, e2559. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, Y. Motion planning of redundant dual-arm robots with multicriterion optimization. IEEE Syst. J. 2023, 17, 4189–4199. [Google Scholar]
- Zheng, L.; Zhang, Z. Time-varying quadratic-programming-based error redefinition neural network control and its application to mobile redundant manipulators. IEEE Trans. Autom. Control 2021, 67, 6151–6158. [Google Scholar]
- Hou, Z.; Chi, R.; Gao, H. An overview of dynamic-linearization-based data-driven control and applications. IEEE Trans. Ind. Electron. 2016, 64, 4076–4090. [Google Scholar]
- Treesatayapun, C. Data-driven fault-tolerant control with fuzzy-rules equivalent model for a class of unknown discrete-time MIMO systems and complex coupling. J. Comput. Sci. 2022, 63, 101827. [Google Scholar]
- Treesatayapun, C. Fuzzy rules emulated discrete-time controller based on plant’s input–output association. J. Control Autom. Electr. Syst. 2019, 30, 902–910. [Google Scholar]
- Campos-Torres, I.; Gómez, J.; Baltazar, A. Data-Driven Adaptive Force Control for a Novel Soft-Robot Based on Ultrasonic Atomization. In Proceedings of the Advances in Computational Intelligence: 21st Mexican International Conference on Artificial Intelligence, MICAI 2022, Monterrey, Mexico, 24–29 October 2022; Proceedings, Part II. Springer: Berlin/Heidelberg, Germany, 2022; pp. 279–290. [Google Scholar]
- Gao, S.; Zhao, D.; Yan, X.; Spurgeon, S.K. Model-Free Adaptive State Feedback Control for a Class of Nonlinear Systems. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1824–1836. [Google Scholar]
- Liu, T.; Hou, Z. Model-Free Adaptive Containment Control for Unknown Multi-Input Multi-Output Nonlinear MASs with Output Saturation. IEEE Trans. Circuits Syst. Regul. Pap. 2023, 70, 2156–2166. [Google Scholar] [CrossRef]
- Hou, Z.; Jin, S. Model Free Adaptive Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Esmaeili, B.; Baradarannia, M.; Salim, M.; Farzamnia, A. Data-driven MIMO discrete-time predictive model-free adaptive integral terminal sliding mode controller design for robotic manipulators driven by pneumatic artificial muscles. In Proceedings of the 2019 6th International Conference on Control, Instrumentation and Automation (ICCIA), Sanandaj, Kurdistan, 30–31 October 2019; pp. 1–8. [Google Scholar]
- Tutsoy, O.; Barkana, D.E.; Tugal, H. Design of a completely model free adaptive control in the presence of parametric, non-parametric uncertainties and random control signal delay. ISA Trans. 2018, 76, 67–77. [Google Scholar] [CrossRef]
- Gómez, J.; Treesatayapun, C.; Morales, A. Multi-Inputs and Multi-Outputs equivalent model based on data driven controller for a robotic system. IFAC-PapersOnLine 2020, 53, 9784–9789. [Google Scholar] [CrossRef]
- Gómez, J.; Treesatayapun, C.; Morales, A. Data-driven identification and control based on optic tracking feedback for robotic systems. Int. J. Adv. Manuf. Technol. 2021, 113, 1485–1503. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, Y.; Na, J.; Li, Z.; Cheng, L.; Su, C.Y. Finite-Time Convergence Adaptive Fuzzy Control for Dual-Arm Robot with Unknown Kinematics and Dynamics. IEEE Trans. Fuzzy Syst. 2019, 27, 574–588. [Google Scholar] [CrossRef]
- Li, M.; Kang, R.; Branson, D.T.; Dai, J.S. Model-free control for continuum robots based on an adaptive Kalman filter. IEEE/ASME Trans. Mechatron. 2017, 23, 286–297. [Google Scholar] [CrossRef]
- Goméz-Casas, J.; Toro-Arcila, C.A.; Rodríguez-Rosales, N.A.; Obregón-Flores, J.; Ortíz-Ramos, D.E.; Martínez-Villafañe, J.F.; Gómez-Casas, O. Data-Driven Kinematic Model for the End-Effector Pose Control of a Manipulator Robot. Processes 2024, 12, 2831. [Google Scholar] [CrossRef]
- Brake, M.; Schwingshackl, C.; Reuß, P. Observations of variability and repeatability in jointed structures. Mech. Syst. Signal Process. 2019, 129, 282–307. [Google Scholar] [CrossRef]
- Yang, C.; Liang, M.; Xingbao, L.; Yangqiu, X.; Teng, Q.; Han, L. Uncertainty evaluation of measurement of orientation repeatability for industrial robots. Ind. Robot Int. J. Robot. Res. Appl. 2020. ahead-of-print. [Google Scholar]
- Yang, C.; Liu, X.; Xiaobin, Y.; Mi, L.; Wang, J.; Xia, Y.; Yu, H.; Heng, C. Uncertainty analysis and evaluation of measurement of the positioning repeatability for industrial robots. Ind. Robot 2018, 45, 492–504. [Google Scholar]
- Slotine, J.J. Robustness issues in robot control. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 19–23 May 1985; Volume 2, pp. 656–661. [Google Scholar]
- Zhang, F.; Zhang, X.; Li, Q.; Zhang, H. Universal nonlinear disturbance observer for robotic manipulators. Int. J. Adv. Robot. Syst. 2023, 20, 17298806231167669. [Google Scholar]
- Yoo, B.K.; Ham, W.C. Adaptive control of robot manipulator using fuzzy compensator. IEEE Trans. Fuzzy Syst. 2000, 8, 186–199. [Google Scholar]
- Neila, M.B.R.; Tarak, D. Adaptive terminal sliding mode control for rigid robotic manipulators. Int. J. Autom. Comput. 2011, 8, 215–220. [Google Scholar]
- Kolhe, J.P.; Shaheed, M.; Chandar, T.; Talole, S. Robust control of robot manipulators based on uncertainty and disturbance estimation. Int. J. Robust Nonlinear Control 2013, 23, 104–122. [Google Scholar]
- Yin, X.; Pan, L. Enhancing trajectory tracking accuracy for industrial robot with robust adaptive control. Robot. Comput.-Integr. Manuf. 2018, 51, 97–102. [Google Scholar]
- Obregón-Flores, J.; Arechavaleta, G.; Becerra, H.M.; Morales-Díaz, A. Predefined-time robust hierarchical inverse dynamics on torque-controlled redundant manipulators. IEEE Trans. Robot. 2021, 37, 962–978. [Google Scholar]
- Klein, C.A.; Huang, C.H. Review of pseudoinverse control for use with kinematically redundant manipulators. IEEE Trans. Syst. Man Cybern. 1983, SMC-13, 245–250. [Google Scholar]
- Shamir, T.; Yomdin, Y. Repeatability of redundant manipulators: Mathematical solution of the problem. IEEE Trans. Autom. Control 1988, 33, 1004–1009. [Google Scholar]
- Roberts, R.; Maciejewski, A. Repeatable generalized inverse control strategies for kinematically redundant manipulators. IEEE Trans. Autom. Control 1993, 38, 689–699. [Google Scholar]
- De Luca, A.; Lanari, L.; Oriolo, G. Control of redundant robots on cyclic trajectories. In Proceedings of the 1992 IEEE International Conference on Robotics and Automation, Nice, France, 12–14 May 1992; Volume 1, pp. 500–506. [Google Scholar]
- Michellod, Y.; Mullhaupt, P.; Gillet, D. On Achieving Periodic Joint Motion for Redundant Robots. IFAC Proc. Vol. 2008, 41, 4355–4360. [Google Scholar]
- Schaufler, R.; Fedrowitz, C.; Kammuller, R. A simplified criterion for repeatability and its application in constraint path planning problems. In Proceedings of the 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2000) (Cat. No.00CH37113), Takamatsu, Japan, 31 October–5 November 2000; Volume 3, pp. 2345–2350. [Google Scholar]
- Mukherjee, R. Design of holonomic loops for repeatability in redundant manipulators. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Piscataway, NJ, USA, 21–27 May 1995; Volume 3, pp. 2785–2790. [Google Scholar]
- Zhang, Y.; Zhang, Z. Repetitive Motion Planning and Control of Redundant Robot Manipulators; Springer Publishing Company: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cefalo, M.; Oriolo, G.; Vendittelli, M. Planning safe cyclic motions under repetitive task constraints. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3807–3812. [Google Scholar]
- Oriolo, G.; Cefalo, M.; Vendittelli, M. Repeatable Motion Planning for Redundant Robots over Cyclic Tasks. IEEE Trans. Robot. 2017, 33, 1170–1183. [Google Scholar]
- Cang, N.; Guo, D.; Zhang, W.; Shen, L.; Li, W. A new discrete-time repetitive motion planning scheme based on pseudoinverse formulation for redundant robot manipulators with joint constrains. Robot. Auton. Syst. 2024, 176, 104689. [Google Scholar]
- Islam, R.U.; Iqbal, J.; Manzoor, S.; Khalid, A.; Khan, S. An autonomous image-guided robotic system simulating industrial applications. In Proceedings of the 2012 7th International Conference on System of Systems Engineering (SoSE), Genoa, Italy, 16–19 July 2012; pp. 344–349. [Google Scholar]
- Yu, Q.; Wang, G.; Hua, X.; Zhang, S.; Song, L.; Zhang, J.; Chen, K. Base position optimization for mobile painting robot manipulators with multiple constraints. Robot. Comput.-Integr. Manuf. 2018, 54, 56–64. [Google Scholar]
- Gracia, L.; Solanes, J.E.; Munoz-Benavent, P.; Miro, J.V.; Perez-Vidal, C.; Tornero, J. Adaptive sliding mode control for robotic surface treatment using force feedback. Mechatronics 2018, 52, 102–118. [Google Scholar]
- Saxena, A.; Kumar, J.; Sharma, K.; Roy, D. Controlling of Manipulator for Performing Advance Metal Welding. In Recent Innovations in Mechanical Engineering: Select Proceedings of ICRITDME 2020; Springer: Berlin/Heidelberg, Germany, 2022; pp. 41–48. [Google Scholar]
- Lynch, K.M.; Park, F.C. Modern Robotics: Mechanics, Planning, and Control, 1st ed.; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Spong, M.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; Wiley select coursepack; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Hou, Z.; Jin, S. Data-driven model-free adaptive control for a class of MIMO nonlinear discrete-time systems. IEEE Trans. Neural Netw. 2011, 22, 2173–2188. [Google Scholar]
- Gómez, J.; Morales, A.; Treesatayapun, C.; Muñiz, R. Data-driven-modelling and Control for a Class of Discrete-Time Robotic System Using an Adaptive Tuning for Pseudo Jacobian Matrix Algorithm. In Proceedings of the Advances in Computational Intelligence: 21st Mexican International Conference on Artificial Intelligence, MICAI 2022, Monterrey, Mexico, 24–29 October 2022; Proceedings, Part II. Springer: Berlin/Heidelberg, Germany, 2022; pp. 291–302. [Google Scholar]
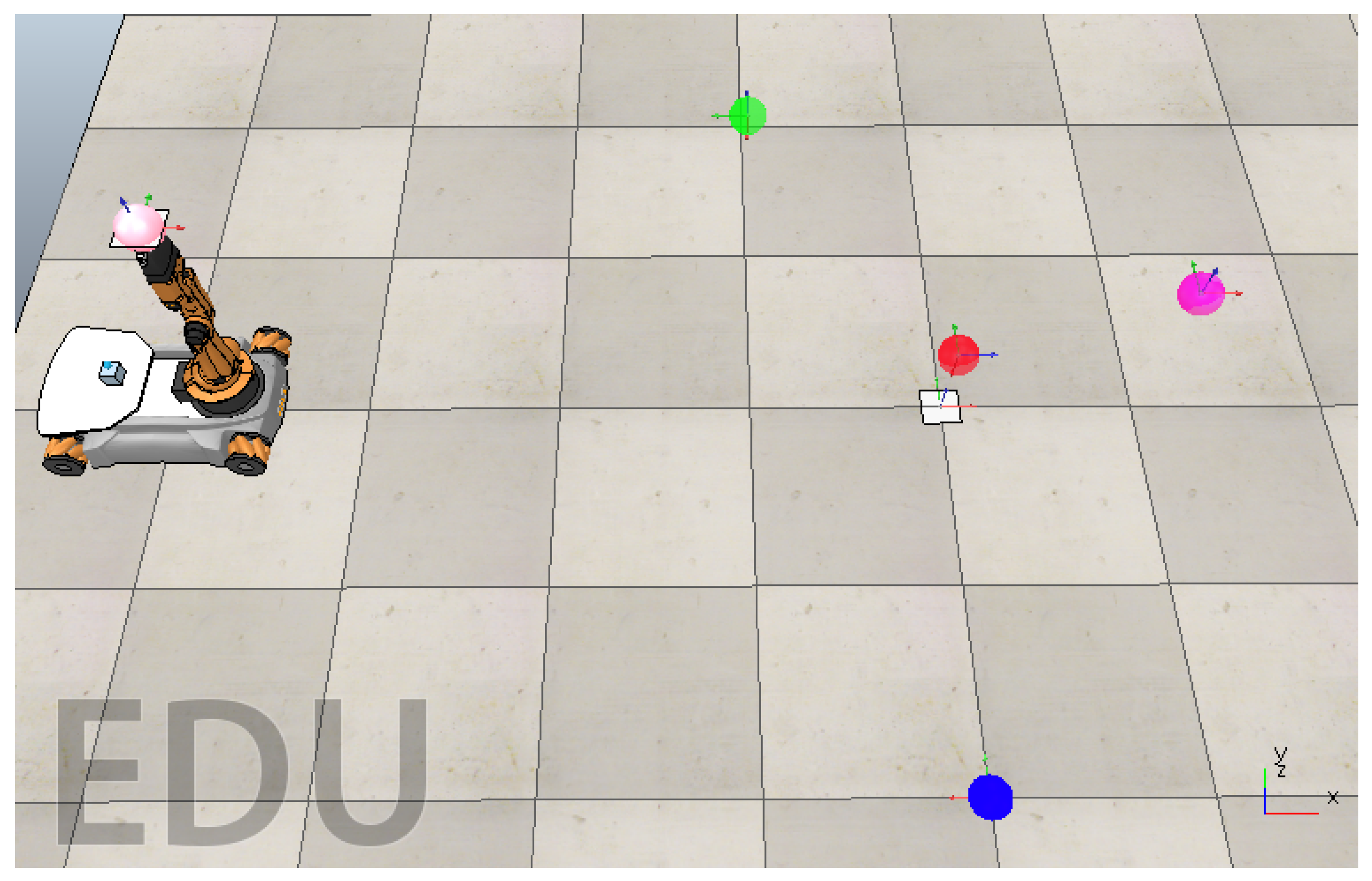
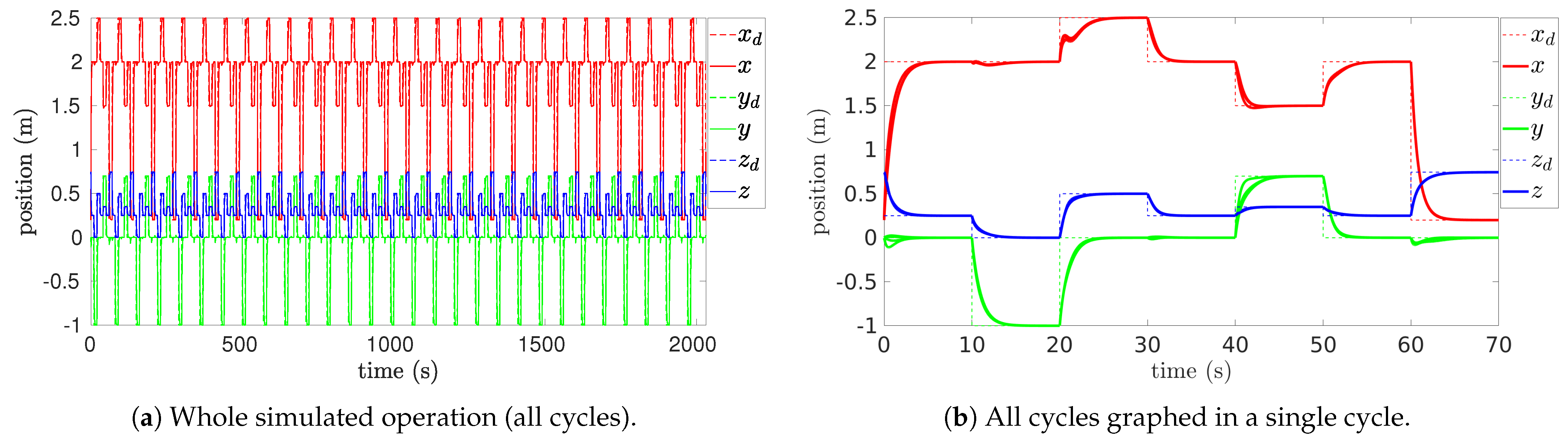

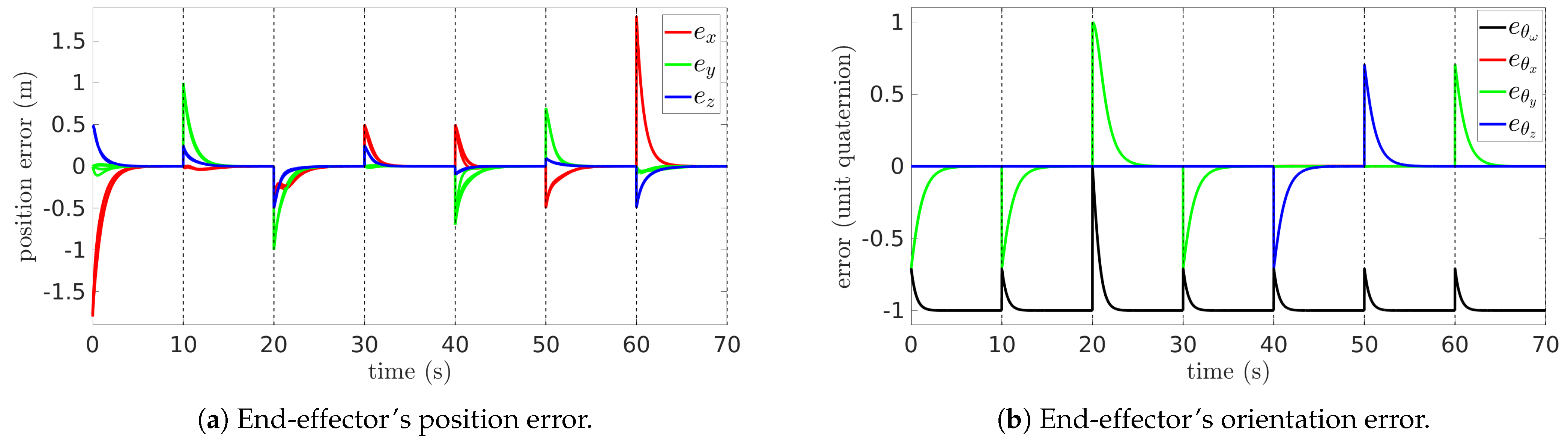
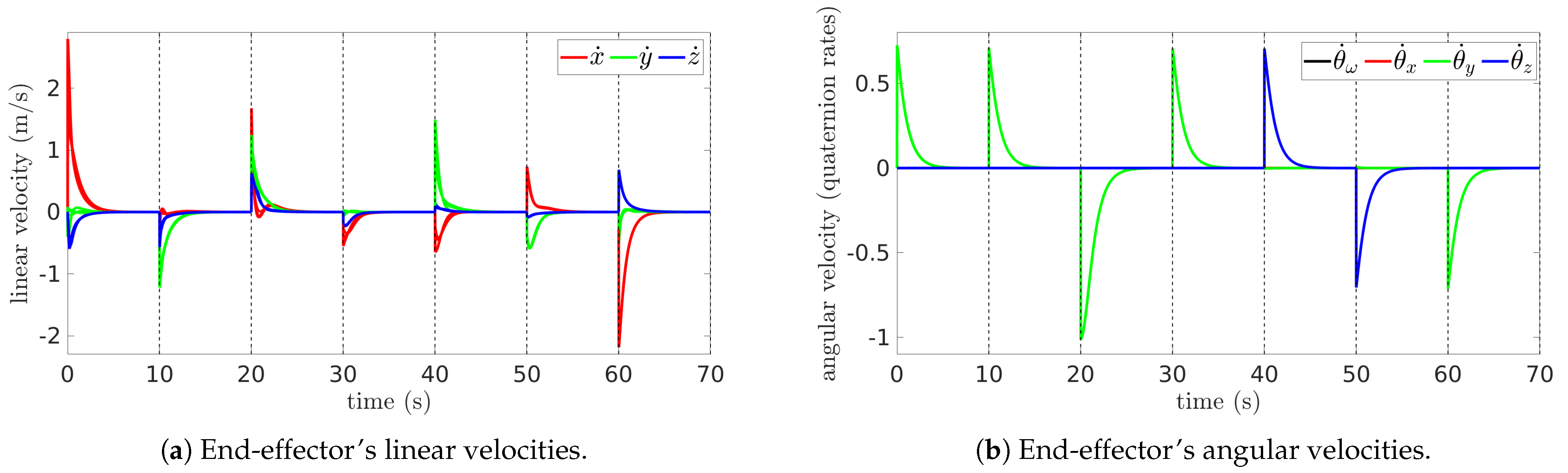




| Reference | Target | Position [m] | Orientation | Schedule [s] |
|---|---|---|---|---|
| red | ||||
| blue | ||||
| purple | ||||
| red | ||||
| green | ||||
| red | ||||
| beige (home) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obregón-Flores, J.; Toro-Arcila, C.A.; Gómez-Casas, J.; Galindo-Valdes, J.S.; Muñiz-Valdez, C.R.; Rodriguez-Rosales, N.A.; Martínez-Villafañe, J.F.; Ortiz-Ramos, D.E. Data-Driven Model for Cyclic Tasks of Robotic Systems: Study of the Repeatability Conditions. Processes 2025, 13, 953. https://doi.org/10.3390/pr13040953
Obregón-Flores J, Toro-Arcila CA, Gómez-Casas J, Galindo-Valdes JS, Muñiz-Valdez CR, Rodriguez-Rosales NA, Martínez-Villafañe JF, Ortiz-Ramos DE. Data-Driven Model for Cyclic Tasks of Robotic Systems: Study of the Repeatability Conditions. Processes. 2025; 13(4):953. https://doi.org/10.3390/pr13040953
Chicago/Turabian StyleObregón-Flores, Jonathan, Carlos A. Toro-Arcila, Josué Gómez-Casas, Jesús Salvador Galindo-Valdes, Carlos Rodrigo Muñiz-Valdez, Nelly Abigaíl Rodriguez-Rosales, Jesús Fernando Martínez-Villafañe, and Daniela Estefania Ortiz-Ramos. 2025. "Data-Driven Model for Cyclic Tasks of Robotic Systems: Study of the Repeatability Conditions" Processes 13, no. 4: 953. https://doi.org/10.3390/pr13040953
APA StyleObregón-Flores, J., Toro-Arcila, C. A., Gómez-Casas, J., Galindo-Valdes, J. S., Muñiz-Valdez, C. R., Rodriguez-Rosales, N. A., Martínez-Villafañe, J. F., & Ortiz-Ramos, D. E. (2025). Data-Driven Model for Cyclic Tasks of Robotic Systems: Study of the Repeatability Conditions. Processes, 13(4), 953. https://doi.org/10.3390/pr13040953










