Comparative Analysis of Kalman-Based Approaches for Fault Detection in a Clean-In-Place System Model

Abstract

The most appropriate operating conditions are necessary in industrial manufacturing to maintain product quality and consistency. In this respect, Clean-In-Place (CIP) is a widely adopted method in the food, beverage, pharmaceutical, and chemical industries, which ensures equipment cleanliness without dismantling. A detailed analysis and simulation for the assessment of accuracy, computational efficiency, and adaptability in fault detection, such as valve malfunction, pump failure, and sensor error, are necessary for the CIP system. Advanced fault detection methods within a five-tank CIP model are investigated in this paper, comparing the extended Kalman filter (EKF) with the unscented Kalman filter (UKF). Both techniques have their merits for fault detection in complex systems. The results indicate that the UKF mostly performs better than the EKF in treating the nonlinearities of the given CIP system with the chosen system characteristics and fault type. This approach helps improve the reliability and efficiency of the CIP process, thus providing insights into enhancing fault detection strategies in industrial applications.

1. Introduction

In industrial manufacturing processes, to ensure product quality and consistency, all the systems must be run under ideal operating conditions. The Clean-In-Place (CIP) process plays an important role in achieving these goals, as it is an easy, direct, and proven technique for cleaning and sanitizing different types of equipment and systems without the need for their dismantling. In the food and beverage, pharmaceutical, and chemical production industries, where strict hygiene standards are maintained and production downtime is minimized, this automated process has been widely used [1,2]. The functionality of the CIP process is a critical factor in its overall success, as it is the core of the process; therefore, the ratio of the solution remaining constant. Additionally, any unsuited point solution can be detrimental to the quality and safety of the end product, in addition to factory inefficiency. Therefore, the security and reliability of CIPs are focal issues for process engineers [3].

Fault detection is a key measure to ensure the smooth performance and functionality of the CIP process. Fault detection alone is a smart method that guarantees the highest product quality. By promptly identifying situations such as system overload or malfunctioning parts, human operators can take appropriate action to prevent deterioration, reduce downtime, and minimize product contamination. The fault detection facility not only generates process stability but also leads to resource optimization and waste reduction; thus, in the long run, it also contributes to sustainable manufacturing practices [4].

Existing fault detection strategies in Clean-In-Place (CIP) systems use rules-based methods, controlled manual inspections, and preset alarm thresholds. These methods are fairly ineffective in more sophisticated environments with complex conditions and are often hampered by human error. There is little to no consideration for sensor noise, nonlinear system activity, and adaptability, so, as a result, the diagnosis process becomes extremely inefficient. To improve the CIP system’s reliability and efficiency, advanced fault detection approaches based on state estimation are needed [5,6].

This research primarily aims to explore and compare advanced fault detection methods within a complex five-tank CIP model. The methods studied are the extended Kalman filter (EKF) and the unscented Kalman filter (UKF). Notably, both of these methods have certain features that distinguish them from the others, and such features make them attractive for fault detection in complex and dynamic systems. Through an in-depth analysis and comparison, this study proposes identifying the strengths and weaknesses of the EKF and UKF to work in the different scenarios to define a technique that not only meets the criteria of fault detection accuracy, computational efficiency, and adaptability to real-world industrial scenarios, but also enhances it.

In the following sections, we explain the theoretical basis of the CIP process and the fault detection techniques that are under investigation. Next, we detail the EKF and UKF methodology and experimental settings. Finally, the conclusions driven from the experiments contribute to the theoretical understanding of this process.

2. Literature Review

The industrial sector is characterized by a ceaseless quest for operational excellence. In such situations, the need to maintain high product quality, process efficiency, and overall reliability is the driving force behind the pursuit of operational excellence. Throughout industrial plants, the Clean-In-Place (CIP) process is a critical unit operation that guarantees the cleanliness and integrity of equipment, particularly in food and beverages, pharmaceuticals, and chemicals. As the industrial sector evolves, fault detection methods have become important tools that help prevent stoppages, optimize resource utilization, and adhere to safety standards. This study is an exhaustive review of fault detection strategies both in the general area of industrial systems and in the CIP process. First, this study aims to survey the existing research on the subject of fault detection via Kalman filter techniques such as the extended Kalman filter (EKF) and unscented Kalman filter (UKF). Additionally, we examine the literature on fault detection strategies in hydraulic systems, highlighting the importance of this knowledge and providing a comprehensive understanding of fault detection methodologies within the context of the five-tank CIP model. Through this study, we attempt to combine the collective insights of previous researchers, which include the most significant advances, trends, and gaps that make the current study stand out.

2.1. Related Work on Industrial Systems and CIP Processes

The Clean-In-Place (CIP) technique was discovered in the 1950s, primarily present in the dairy industry. Over time, newly developed technologies that use CIPs have been introduced in the food, beverage, pharmaceutical, and biotechnology industries. The technology referred to as CIPs in this case removes the equipment and systems from the process soil in an efficient manner. The CIP system is highly complex and can have several applications, such as ensuring cleanliness, preventing cross-contamination, generating reproducible results, self-automation, and reducing downtime. The most frequent steps are water purification, caustic washing, rinsing, and acid washing. Proper design is performed so that the product can easily pass through suitable temperatures and pressures without any risk of contamination. To do this, the proper implementation of control and monitoring measures is highly important [7].

This study focused on the influence of various cleaning methods on the removal of milk contaminants from a plate heat exchanger in a Clean-In-Place (CIP) system. The research project took place in a laboratory equipped with a cleaning station for sterilization purposes. These new elements included, among others, water temperature, flow rate, and cleaning duration. On the basis of this research, we can conclude that the cleaning process depends on the rate and temperature of the cleaning agent. Moreover, the results show that there is a temperature zone for the initial rinse stage [8].

This research examined the effects of concentration and storage duration on the equilibrium surface tension of chemical solutions within a Clean-In-Place (CIP) system. This research contrasted conventional cleaning agents with industrial solutions utilized in a brewery CIP system. The findings indicated that an increase in the concentration of the chemical in the cleaning solution led to a reduction in wetting qualities. A similar effect has been noted with prolonged storage duration, with the most significant alteration transpiring within the first eight weeks. The research indicated that the incorporation of chemicals to stabilize cleaning solutions inhibited the degradation of their wetting qualities, irrespective of the concentration of the active ingredient or duration of storage. The study determined that prolonged use of these cleaning solutions for CIP significantly jeopardizes food production hygiene, potentially resulting in inadequate cleaning of production equipment surfaces and secondary contamination from solid deposits. This study advocates for a broader pursuit of solutions designed to prolong their useful life [9].

2.2. Related Work on Fault Detection for the Kalman Filter

This thesis presents a novel method for analyzing real-time sensor data from a hydraulic test rig to automatically generate problem symptoms. The major goals are to increase hydraulic system safety, lower maintenance costs, and increase productivity. The suggested approach entails building a precise state space model and a cutting-edge model-based fault detection method that uses the unscented Kalman filter (UKF) to gauge system states and spot flaws. The key hydraulic components make up the experimental setup, which was constructed at UBC’s Process Automation and Robotics Laboratory, and the generated model is tested against it. Five fault types—loss of load, dynamic friction load, and internal and exterior leakages in the actuator—are the focus of this research. The UKF-based method produces accurate results by detecting and diagnosing system issues in real time. This work is essential for avoiding catastrophic failures, increasing productivity, and ensuring that hydraulic systems are operated effectively in industrial applications [10].

One of these studies provides an unscented Kalman filter (UKF)-centered fault diagnostic system for hydraulic methods. A real hydraulic test rig is a tool that is used to carry out UKF-based processes, such as fault recognition and diagnosing different fault types. In particular, the novel method is focused mostly on the detection of conditions such as inner and outer leakages, dynamic friction loads, sudden loss of load, and load enlargements, and it is expected to create system states in advance and generate residual errors in real time. The experiments were carried out on test rigs subjected to various levels of leakage. The UKF algorithm is capable of effectively diagnosing the developed faults and hence demonstrates its effectiveness. In addition, the UKF is the best choice for online real-time applications in hydraulic systems that are necessary for reliable and effective fault monitoring in this work. The selling point of the UKF method is that it can contribute to enhancing the security, dependability, and efficiency of hydraulics by means of the rapid detection and elimination of defective parts in business [11].

In this paper, because highly nonlinear network equations are introduced into dynamic state estimation in power systems, a new approach is presented—the unscented Kalman filter (UKF). The UKF uses unscented transformation instead of more traditional approaches that linearize such equations to be able to handle nonlinearities. After the UKF was applied to three test power systems under typical network and measurement conditions, performance comparisons with the extended Kalman filter were made. The proposed UKF is tested on power systems in various scenarios, and the benefits of the UKF over the EKF in handling nonlinearities and offering better estimation accuracy are highlighted. The inclusion of a flawed data processor helps in the detection of anomalies, and the performance of the UKF stands out in situations where dynamic changes are slow. Although it faces difficulties with abrupt state changes, it bounces back quickly and performs better than the EKF when tracking new operating points. The UKF is effective and simple, especially for nonlinear models with complicated dynamics. Thus, the UKF can be a very promising solution for dynamic state estimation in power systems [12].

In this work, the UKF algorithm, which is based on unscented transformation, is applied to nonlinear semiexplicit index 1 differential algebraic Equation (DAE) systems. The UKF algorithm is applied to a hydraulic system for state estimation and fault detection. This paper proposes a simple, reliable residual definition for fault detection and introduces an adapted formulation of the UKF for the considered application. Its efficiency is shown with simulation results obtained in the case of a hydraulic system. Starting with the stochastic model of the system and initial condition noise, one can perform an analysis related to fault detection in nonlinear DAE systems. This paper describes the capabilities of the UKF algorithm, discusses its use in fault detection, and emphasizes the importance of model improvement for enhanced operational mode identification. The development of observers for nonlinear dynamic systems, unscented filtering, and topics related to nonlinear state estimation are also covered in the text. Additionally, the topic of filtering nonlinear systems is covered in relation to the scaled unscented transformation [13].

The three filters presented in this paper—the adaptive fading unscented Kalman filter (AFUKF), augmented unscented Kalman filter (AUKF), and adaptive hybrid unscented Kalman filter (AHUKF)—introduce a novel approach to fault detection, isolation, and reconstruction (FDIR) via robust adaptive Kalman filters. While the AUKF attempts to identify and reconstruct input faults, the AFUKF addresses the unbiased reconstruction of output faults. To address input and output faults simultaneously, both filters have been integrated into an adaptive strategy. An application to aircraft sensor FDIR is performed through the implementation of the method via kinematic equations so that it is resilient against model uncertainties. In this paper, the approach proposed herein is applied in simulations to the Cessna Citation II CE-550 model to show its efficacy with respect to proving the potential of the developed approach for input and output FDIR in fault scenarios of complex systems. The AFUKF, AUKF, and AHUKF detect, isolate, and estimate faults precisely after model uncertainties and sensor noise are considered. The method has the potential to improve FDIR for nonlinear systems [14].

This paper presents a study on unscented Kalman filter (UKF)-based intelligent fault detection for wind turbines. The UKF is used to forecast generator temperature and make fault detection easier. It is well known for its advantages in handling nonlinear and nonstationary systems. To represent the temperature variation of the generator stator winding under operational conditions, a model based on the thermal dynamics and principles of heat generation is developed. The UKF incorporates this model for temperature forecasting and fault finding. The UKF’s predictions and the model’s results are contrasted to show how well the UKF detects faults in wind turbines. This is accomplished by including two failure modes in the model. This paper emphasizes the importance of precise system modeling and crucial parameter selection for fault identification via the UKF approach in complex wind turbine systems [15].

This paper presents a novel method for fault isolation and detection in wind turbines via the unscented Kalman filter (UKF). The model is assessed for three distinct failure modes as follows: gearbox damage, lubrication oil leakage, and pitch failure. It is based on a thorough analysis of the operating principles of wind turbines. The UKF model is a powerful tool for fault identification because of its distinctive response to various fault conditions. The UKF framework’s precise definition of the state space and control vectors is emphasized as essential for improving sensitivity to various fault types. Using data from supervisory control and data acquisition (SCADA), the model’s capabilities for online fault detection are verified. For applications in real-time online fault detection and diagnosis in wind energy systems, this technique has promising potential [16].

This study uses a nonlinear vehicle dynamics model to present a novel method for diagnosing motor torque faults in a four-wheel independent motor-drive vehicle. To represent discrepancies between actual motor torques and those ordered by the vehicle control unit, the authors introduce fault parameters. The model includes nonlinear tire, wheel, and vehicle body characteristics, with fault parameters acting as motor torque command coefficients. To identify these fault parameters in real time, the unscented Kalman filter (UKF) is used. The method’s efficacy is shown in both common and unusual handling scenarios. The suggested algorithm has the potential to provide accurate and immediate motor torque fault diagnosis under various driving conditions [17].

For parameter estimation in dynamic systems, the unscented Kalman filter (UKF) is a sigma-point Kalman filter that makes use of unscented transformation. It is suitable for Gaussian approximate nonlinear estimation because it does not require Jacobian matrices during linearization. To simplify the computation, this paper introduces a modified method for parameter estimation known as modified joint unscented Kalman filtering (MJUKF). During the measurement update step, MJUKF converts measurement errors into parameter errors, effectively decoupling parameters from the state vector. Compared with conventional Joint Unscented Kalman Filtering (JUKF), creating separate sigma points for states and parameters reduces the computational complexity. When measurements and parameters are subject to a linear transformation, the suggested modification performs especially well. The method is tested on nonlinear dynamic systems and shows superior performance to the JUKF, especially under conditions with considerable noise. This study recommends adaptive rules for determining noise covariance, as well as heuristic techniques for choosing scaling and transformation matrices. The MJUKF is suitable for systems with many parameters because it provides a promising method for lowering computational complexity while maintaining precise parameter estimation [18].

This study introduces a novel method for unscented Kalman filter (UKF)-based real-time input-parameter-state estimation. This approach uses two stages per time step to estimate the unknown input as follows: first, it predicts dynamic states and system parameters; second, it refines the estimation via measurements. Through the use of perturbation analysis, how distinct it is to recognize systems with known zero or nonzero inputs is shown. Compared with conventional output-only approaches, this method improves system understanding by jointly estimating dynamic states, parameters, and inputs. This method helps engineers extract information from the available data and is particularly useful for systems with unknown parameters. The mathematical formulations of the UKF, the suggested methodology, identifiability traits, real-world applications for linear and nonlinear systems, sensitivity analysis, and concluding remarks are all covered in the study’s sections. The study suggests that a data fusion technique could make it unnecessary to use displacement, velocity, and acceleration signals for full estimation. The study, which was funded by the U.S. National Science Foundation, demonstrates the potential of the suggested method for locating systems with known inputs and emphasizes its practical utility [19].

2.3. Related Work in Fault Detection for Hydraulic Systems

An extended Kalman filter (EKF) is used in this paper to introduce a novel method for locating leakage faults in hydraulically powered actuators. Internal leakage at the piston seal and external leakage at the shaft seal or connecting pipes are the two types of leakage that are discussed in this study. The EKF-based estimator takes into account the stick-slip friction present in the actuator and incorporates nonlinear models of hydraulic functions. The effectiveness of the proposed EKF-based fault detection scheme is shown in experiments on a hydraulic actuator circuit designed for a lab environment. These experiments show that both internal and external leakage faults can be quickly and accurately identified. The residual errors are examined to find fault patterns, and the EKF model monitors changes in the chamber pressures and displacement measurements. This study makes a significant contribution to the field of fault detection and isolation in fluid power systems, particularly in hydraulic actuators, and offers insightful information for improving system performance and reliability by promptly identifying faults. Future applications of this technique for monitoring conditions in real time and its robustness in a variety of environments are still promising areas for further study and development [20].

This article discussed a step-by-step methodology for the detection of internal leakage and worn piston seals in hydraulic cylinders. The present study focuses on a double-acting seal used in the support oil cylinder of a QY110 mobile crane model, in which the wavelet transform is used for feature extraction from raw oil pressure data for fault pattern recognition via the WNN classifier. The proposed FDI scheme provides very clear classification of wear patterns on the piston seal. The performance of the proposed BPNN is much better than that of the conventional BPNN. The authors would like to acknowledge the financial support for the project by a number of programs, expanding the repository on fault simulation and diagnosis studies in hydraulic systems. This paper addresses physical simulations and experimental setups of the internal leakage rates caused by the wear of piston seals, which provide useful information for hydraulic system fault diagnosis. In this work, an attempt was made to develop online monitoring systems for the real-time health assessment in hydraulic systems, which will provide a theoretical basis for further research on seal wear [21].

The presented paper addresses the detailed study of the UIO and EKF for fault diagnosis in a three-tank hydraulic system. In this system, modeling is performed by using the LMI for the computation of residuals from measured and estimated outputs, and the state estimation is carried out by the EKF. However, under noise-free conditions, the UIO performs better. The present work focuses on how well different fault estimation and isolation methods perform under various scenarios to show the importance of fault detection and isolation in hydraulic systems. Among them, the multiplicative and additive errors due to aging instruments, system deterioration, and improper operation of instruments are discussed, and special emphasis has been given to the importance of fault detection for the reliability of the system. In particular, this paper has focused on the detection of faults in sensors, components, and actuators concerning fault detection and isolation and fault tolerance control systems with linear and nonlinear multivariable feedback control strategies. This paper describes the experimental results of the performance analysis of the UIO and EKF, which were applied for fault diagnosis in a three-tank hydraulics benchmark system. This shows how to apply the UIO and EKF effectively in such a system. The work uses MATLAB R2018b for simulations and analyses, which shows the relative merits and demerits of these methods for solving fault diagnosis problems in hydraulic systems [22].

The extended Kalman filter (EKF) represents an important tool for fault detection applications in systems with moderate nonlinearity. Its ability to linearize nonlinear system dynamics around the current estimate enables it to handle problems with this type of signal. The EKF, in contrast with conventional filters, competently fuses both measured and system dynamics information, causing the primary state to be estimated well. Nevertheless, the EKF is not flawless. The linearization process introduces errors, thereby reducing accuracy, particularly in highly nonlinear systems. Furthermore, the performance is the most crucial initial estimate quality, which can be the cause of divergence or slow convergence if the initial estimate is far from the true state. In addition, the EKF is built on Gaussian distributions that may not hold in hard real-world situations; therefore, it limits its effectiveness in situations with non-Gaussian distributions or multiple modes [23].

The unscented Kalman filter (UKF) uses a deterministic sampling technique that helps overcome some of the limitations of the EKF. It is an exact nonlinear method for nonlinearities. The UKF technique provides a better materialization of the estimation; hence, this method, the UKF, is suitable for fault detection in systems with nonlinearity. The nonlinear transformation applied by the UKF uses UOT to better reproduce the distribution shape, hence lessening the linearization errors encountered by the EKF. Nevertheless, the merits of the UKF are related to several costs. The computational requirements for a UKF are higher than those for an EKF; therefore, they require more computations. This makes the UKF slightly hard to deploy in real-time applications. This is in addition to other parameters involved in the UKF, such as the scaling factors for sigma points; hence, tuning needs to be properly performed to obtain the maximum performance. The UKF, similar to the EKF, may have limitations in modeling distributions that are Gaussian in scenarios of non-Gaussian distributions [24].

Based on the available literature

Table 1. Literature summary.

Author and Year	Methodology	Application	Key Fdings
Sepasi, 2007 [10]	Unscented Kalman Filter (UKF)	Hydraulic Systems	Demonstrated UKF’s effectiveness in monitoring and diagnosing faults in hydraulic actuators.
Sepasi and Sassani, 2010 [11]	Online Fault Diagnosis using UKF	Hydraulic Systems	Achieved real-time fault detection with high accuracy, emphasizing UKF’s robustness in nonlinear systems.
Valverde and Terzija, 2011 [12]	UKF for Dynamic State Estimation	Power Systems	Enhanced state estimation accuracy, crucial for reliable fault detection in power grids.
Alkov and Weidemann, 2013 [13]	UKF in Nonlinear Differential-Algebraic Systems	General Nonlinear Systems	Applied UKF to complex systems, improving fault detection capabilities in nonlinear environments.
Lu et al., 2014 [14]	Adaptive Hybrid UKF	Aircraft Sensor Systems	Developed a hybrid UKF for sensor fault detection, isolation, and reconstruction, enhancing flight safety.
Cao et al., 2016 [16]	UKF with SCADA Data	Wind Turbines	Improved fault diagnosis accuracy in wind turbines by integrating UKF with supervisory control and data acquisition systems.
Zhou et al., 2017 [17]	UKF for Motor Torque Fault Diagnosis.	Electric Vehicles.	Applied UKF to detect and diagnose motor torque faults, contributing to the reliability of electric vehicles.
Onat, 2019 [18]	Joint UKF for Parameter Estimation.	Nonlinear Systems.	Proposed a computationally efficient UKF variant for parameter estimation in nonlinear systems.
Hassan, 2021 [22]	Unknown Input Observer and Extended Kalman Filter	Hydraulic Nonlinear Systems.	Applied UIO and the EKF to detect and diagnose three-tank system faults.
Impraimakis and Smyth, 2022 [19]	UKF for Real-Time Estimation.	Structural Systems.	Utilized UKF for real-time input-parameter-state estimation, aiding in structural health monitoring.
G. Anitha and J. Murugan, 2024 [25]	Robust Unscented Kalman Filter (UKF).	Air Data Sensor Fault Detection and Diagnosis.	The study presents a robust UKF approach for fault detection and diagnosis in air data sensors, effectively handling nonlinearities and sensor uncertainties.

, the EKF and UKF have not been specifically applied for fault detection in Clean-In-Place (CIP) systems before. Most studies focus on their applications in hydraulic systems, power grids, wind turbines, electric vehicles, and general industrial processes, but there is no direct study comparing the EKF and UKF for CIP fault detection:

Kalman filters, particularly the Extended Kalman Filter (EKF) and the Unscented Kalman Filter (UKF), have demonstrated effectiveness in fault detection across various industrial applications, including hydraulic systems, power grids, and robotics. However, their direct application and comparative performance in CIP systems remain unexplored. The EKF, a commonly used approach, linearizes nonlinear system dynamics, making it computationally efficient but less accurate for highly nonlinear systems. In contrast, the UKF employs a sigma-point approach, offering higher accuracy and better handling of nonlinearities, albeit at an increased computational cost

Table 2. Advantages and limitations of the extended Kalman filter and unscented Kalman filter.

Algorithm	Advantages	Limitations
Extended Kalman Filter (EKF)	- Handles moderate nonlinearities through linearization. - Fuses measurement and system dynamics information. - Well-established and widely used technique.	- Linearization errors impact accuracy in highly nonlinear systems. - Sensitive to initial estimate quality, leading to divergence or slow convergence. - Assumes Gaussian distributions, limiting applicability in non-Gaussian scenarios.
Unscented Kalman Filter (UKF)	- Accurately handles nonlinear systems through deterministic sampling. - Preserves distribution shape, reducing linearization errors. - Provides more accurate state estimates compared to EKF.	- Higher computational complexity compared to the EKF, demanding more computations. - Requires parameter tuning, like scaling factors for sigma points. - Assumes Gaussian distributions, limiting applicability in non-Gaussian scenarios.

.

Given the inherent nonlinearities, sensor uncertainties, and time-sensitive nature of CIP processes, it is essential to determine which Kalman-based approach—EKF or UKF—offers superior performance for fault detection in industrial cleaning systems. This research aims to bridge this gap by comparing the EKF and UKF in detecting faults within a five-tank CIP model, assessing their accuracy, computational efficiency, and adaptability to real-world industrial scenarios.

3. Methodology

This section develops the dynamics of the five-tank CIP model, determines possible faults, and develops a mathematical model using the Bernoulli and Continuity Equations. In addition, some advanced Kalman-based strategies, i.e., the Extended Kalman Filter (EKF) and the Unscented Kalman Filter (UKF), are studied for the improvement of the monitoring and control of the system to achieve optimal performance and reliability in industrial environments.

3.1. Five-Tank Clean-In-Place (CIP) Model

The five-tank CIP model is simply a depiction of the industrial process that is deployed in the cleaning and sensitization of equipment. The system comprises five tanks, that are interconnected with each other and depict the consecutive stages of the CIP process. In turn, each of the tanks participates in a specific phase of the cleaning cycle as follows: prerinsing, detergent washing, intermediate rinsing, acid washing, and final rinsing. These tanks are linked by pumps and pipes, and cleaning solutions can be moved through them. Liquid valves control the movement of chemicals, whereas sensors monitor parameters such as fluid levels, temperatures, and pressures.

The CIP five-tank model is composed of the further elaboration of the flows that occur between tanks and how they interact. Initially, the tanks are charged with cleaning solution and water if needed. With the aid of the pumps, the liquid is transported, and the valves help to regulate the flow rate and direction. The temperature of the cleaning solutions is normal and constant when the heating and cooling elements are controlled. The operation set is dependent upon the specific CIP politics, which might include paddling, rinsing, draining, and refilling.

3.2. Potential Faults in the Five-Tank CIP Model

The five-tank CIP model has the potential for mechanical errors, which may affect its efficiency. As a result, the model should be monitored at all times to identify problems as they occur. Such faults may include the following:

• Pump failures: Pumps that start to malfunction have a direct effect on the desired flow rate and the specific volume that needs to be handled in between the tanks. Failure to do this will lead to a possibility of cleaning the required volume not being completed or even overflowing.
• Valve malfunctions: Damaged valves are responsible for improper flow during the distribution and availability of cleaning solutions in different tanks, thereby affecting the sequence of operations.
• Sensor errors: Lack of functioning, or even the poor performance of these sensors, can result in disastrous outcomes, as there is a risk of every transfer or even operation failure due to drastic temperature or pressure control.
• Leakages: Pipes, valves, or even tanks have the potential to leak. Process disruption fluid containment will not only lead to such cleaning solutions being contained for too long, resulting in lowered efficiency but also lead to safety hazards in the long run.
• Temperature fluctuations: Inaccurate temperature control can impact the effectiveness of cleaning solutions. Deviations from optimal temperature ranges can lead to inadequate cleaning or even equipment damage.
• Overflow or drainage issues: Failure to fill or empty tanks and improper flooding can also result in waste, resulting in mixture disorder and contamination with regard to the distribution of cleaning products.
• Process delays: The cycle of cleaning may not only be prolonged, but the objectives and processes of the sequence of cleaning may also not be attained as a result of lagging behind the performance of various stages of the cleaning process.
• Clogging: Damaging clogs or blockages in pipes or valves leads to disturbances in the flow of fluid and the resulting disturbances during the entire cycle of cleaning.

3.3. Five-Tank CIP System Mathematical Model

The system shown in Figure 1 consists of five cylindrical tanks with equal cross-sectional areas as follows: S1, S2, S3, S4, and S5. Each of the tanks receives input through a pump, but the output from each is controlled by an output valve at the outlet of each tank. In our research, we control the liquid level in each tank while ensuring the state of the input actuators and output valves. We can apply the Bernoulli and Continuity Equation to model this, as it was referred to in the sources [26,27]:

Figure 1. Five-tank CIP model [28].

Figure 1. Five-tank CIP model [28].

$$\begin{array}{c}\mathrm{\Delta }hg={\displaystyle \frac{1}{2}}{v}^2\\ q=s_{v}v\end{array}$$

(1)

$$q=s_v\sqrt{2g\mathrm{\Delta }h}$$

(2)

where

• Δh = difference between liquid levels.
• v = Liquid velocity.
• q = Liquid flow rate.
• s_v = Flow space of the pipe (cross-section).
• g = Gravity.

The flow space $S_v$ is controlled by the valve position P.

$$S_v=P{S}_{vmax};0\le P\le 1$$

(3)

where $S_{vmax}$= Maximum flow rate.

$$q=P{S}_{vmax}\sqrt{2g}\sqrt{\mathrm{\Delta }}h$$

(4)

Since the rate of change of the liquid volume in a tank is equal to the amount entering the tank minus the amount leaving it, as follows:

$$\begin{array}{c}{\displaystyle \frac{dV}{dt}}=Q_{\mathrm{in}}-Q_{\mathrm{out}},\mathrm{where}V=h\times s_T\\ {\displaystyle \frac{dh}{dt}}={\displaystyle \frac{Q_{in}}{s_T}}-{\displaystyle \frac{P{s}_{vmax}\sqrt{2g}}{s_T}}\end{array}$$

(5)

Now, we generalize the above equation for all five tanks, as follows:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d{h}_1}{dt}}={\displaystyle \frac{Q_{in1}}{s_T}}-{\displaystyle \frac{P_1{s}_{vmax}\sqrt{2g}}{s_T}}\hfill \\ \hfill & {\displaystyle \frac{d{h}_2}{dt}}={\displaystyle \frac{Q_{in2}}{s_T}}-{\displaystyle \frac{P_2{s}_{vmax}\sqrt{2g}}{s_T}}\hfill \\ \hfill & {\displaystyle \frac{d{h}_3}{dt}}={\displaystyle \frac{Q_{in3}}{s_T}}-{\displaystyle \frac{P_3{s}_{vmax}\sqrt{2g}}{s_T}}\hfill \\ \hfill & {\displaystyle \frac{d{h}_4}{dt}}={\displaystyle \frac{Q_{in4}}{s_T}}-{\displaystyle \frac{P_4{s}_{vmax}\sqrt{2g}}{s_T}}\hfill \\ \hfill & {\displaystyle \frac{d{h}_5}{dt}}={\displaystyle \frac{Q_{in5}}{s_T}}-{\displaystyle \frac{P_5{s}_{vmax}\sqrt{2g}}{s_T}}\hfill \end{array}$$

(6)

where

• h_i = The liquid level in tank i.
• Q_in = The tank input.
• s_T = Tank cross-sectional area.

Therefore, the system state space can be represented as follows:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{\dot{h}}_1\hfill \\ {\dot{h}}_2\hfill \\ {\dot{h}}_3\hfill \\ {\dot{h}}_4\hfill \\ {\dot{h}}_5\hfill \end{array}\right]& ={\displaystyle \frac{-1}{S_T}}\left[\begin{array}{ccccc}{P}_1{s}_{vmax}\sqrt{2g}& 0& 0& 0& 0\\ 0& P_2{s}_{vmax}\sqrt{2g}& 0& 0& 0\\ 0& 0& P_3{s}_{vmax}\sqrt{2g}& 0& 0\\ 0& 0& 0& P_4{s}_{vmax}\sqrt{2g}& 0\\ 0& 0& 0& 0& P_5{s}_{vmax}\sqrt{2g}\end{array}\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{S_T}}\left[\begin{array}{c}{Q}_{in1}\hfill \\ Q_{in2}\hfill \\ Q_{in3}\hfill \\ Q_{in4}\hfill \\ Q_{in5}\hfill \end{array}\right]\hfill \end{array}$$

(7)

The first four tank volumes are 0.547964 m³ (cubic meters), and the fifth tank volume is 1.636874 m³ (cubic meters). Consider a nonlinear stochastic system described as follows:

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=h(x\left(t\right),u\left(t\right))+E{F}_p\left(t\right),\\ y\left(t\right)=g\left(x\left(t\right)\right)+L{F}_v\left(t\right)\end{array}\right.$$

(8)

where $x\left(t\right)\in {\mathbb{R}}^n$ is the state vector, $y\left(t\right))\in {\mathbb{R}}^m$ is the output vector, $u\left(t\right))\in {\mathbb{R}}^r$ is the input vector, $F_p\left(t\right))\in {\mathbb{R}}^s$ is the input fault distribution matrix, $F_v\left(t\right))\in {\mathbb{R}}^q$ is the output fault distribution matrix, $h(.)$ and $g(.)$ are nonlinear functions, and the fault state matrix is the identity matrix E = I and L = I.

The fault state space matrix is represented as follows:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{\dot{h}}_1\hfill \\ {\dot{h}}_2\hfill \\ {\dot{h}}_3\hfill \\ {\dot{h}}_4\hfill \\ {\dot{h}}_5\hfill \end{array}\right]& ={\displaystyle \frac{-1}{S_T}}\left[\begin{array}{ccccc}{P}_1{s}_{vmax}\sqrt{2g}& 0& 0& 0& 0\\ 0& P_2{s}_{vmax}\sqrt{2g}& 0& 0& 0\\ 0& 0& P_3{s}_{vmax}\sqrt{2g}& 0& 0\\ 0& 0& 0& P_4{s}_{vmax}\sqrt{2g}& 0\\ 0& 0& 0& 0& P_5{s}_{vmax}\sqrt{2g}\end{array}\right]\hfill \\ \hfill & +{\displaystyle \frac{1}{S_T}}\left[\begin{array}{c}{Q}_{in1}\hfill \\ Q_{in2}\hfill \\ Q_{in3}\hfill \\ Q_{in4}\hfill \\ Q_{in5}\hfill \end{array}\right]+\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]F_p\left(t\right)\hfill \end{array}$$

(9)

$$y\left(t\right)=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{h}_1\hfill \\ h_2\hfill \\ h_3\hfill \\ h_4\hfill \\ h_5\hfill \end{array}\right]+\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]F_v\left(t\right)$$

(10)

3.4. Kalman-Based Approaches

3.4.1. Extended Kalman Filter (EKF)

The extended Kalman filter is an extension of the Kalman filter for nonlinear systems. It approximates the nonlinear system dynamics via linearization around the current estimated state. The equations for the prediction and update steps are as follows:

• Prediction step:
  • Predicted state estimate:

    $${\widehat{x}}_{(k\mid k-1)}=f\left({\widehat{x}}_{(k-1\mid k-1)},u_k\right)$$
  • Predicted error covariance:

    $$P_{k\mid k-1}=A_k{P}_{k-1\mid k-1}{A}_k^T+Q_k$$
• Update step:
  • Kalman Gain:

    $$K_k=P_{k\mid k-1}{H}_k^T{(H_k{P}_{k\mid k-1}{H}_k^T+R_k)}^{-1}$$
  • Corrected state estimate:

    $${\widehat{x}}_{k\mid k}={\widehat{x}}_{k\mid k-1}+K_k(z_k-h\left({\widehat{x}}_{k\mid k-1}\right))$$
  • Corrected error covariance:

    $$P_{k\mid k}=(I-K_k{H}_k)P_{k\mid k-1}$$

where

• ${\widehat{x}}_{(k\mid k-1)}$ is the predicted state estimate at time k given observations up to time $k-1$.
• $P_{k|k-1}$ is the predicted error covariance at time k.
• f represents the nonlinear system dynamics.
• $A_k$ is the Jacobian matrix of k.
• $u_k$ is the control input at time k.
• $Q_k$ is the process noise covariance.
• $H_k$ represents the Jacobian matrix of the measurement function.
• $z_k$ is the actual measurement at time k.
• k is the measurement function.
• $R_k$ is the measurement noise covariance.

3.4.2. Unscented Kalman Filter (UKF)

The unscented Kalman filter avoids linearization by approximating the distribution of the state through a set of carefully chosen sigma points. The equations for the prediction and update steps are as follows:

• Prediction step:
  • Generate sigma points:

    $$X_k^{\left[i\right]}={\widehat{x}}_{(k\mid k-1)}+{\left(\sqrt{(n+\lambda )P_{k\mid k-1}}\right)}_i$$
  • Predicted state estimate:

    $${\widehat{x}}_{(k\mid k-1)}=\sum _{i=0}^{2n}{w}_i^m{X}_k^{\left[i\right]}$$
  • Predicted error covariance:

    $$P_{k\mid k-1}=\sum _{i=0}^{2n}{w}_i^{\left[c\right]}{X}_k^{\left[i\right]}\left(X_k^{\left[i\right]}-{\widehat{x}}_{(k\mid k-1)}\right){\left(X_k^{\left[i\right]}-{\widehat{x}}_{(k\mid k-1)}\right)}^{\mathrm{T}}+Q_k$$
• Update step:
  • Generate sigma points via ${\widehat{x}}_{(k\mid k-1)}$ and $P_{(k\mid k-1)}$.
  • Propagate sigma points through measurement function h to obtain $Z_k^{\left[i\right]}$.
  • The predicted measurement mean and covariance are calculated as follows:

    $$\begin{array}{c}{\widehat{z}}_{k\mid k-1}={\displaystyle \sum _{i=0}^{2n}}{w}_i^m{Z}_k^{\left[i\right]}\\ P_{z,k\mid k-1}={\displaystyle \sum _{i=0}^{2n}}{w}_i^{\left[c\right]}\left(Z_k^{\left[i\right]}-{\widehat{z}}_{(k\mid k-1)}\right){\left(Z_k^{\left[i\right]}-{\widehat{z}}_{(k\mid k-1)}\right)}^{\mathrm{T}}+R_k\end{array}$$
  • Calculate the cross-covariance matrix $P_{(xz,k|k-1)}$ as follows:

    $$P_{xz,k\mid k-1}=\sum _{i=0}^{2n}{w}_i^{\left[c\right]}\left(X_k^{\left[i\right]}-{\widehat{x}}_{(k\mid k-1)}\right){\left(Z_k^{\left[i\right]}-{\widehat{z}}_{(k\mid k-1)}\right)}^{\mathrm{T}}$$
  • Calculate the Kalman gain $K_k$ as follows:

    $$K_k=P_{xz,k\mid k-1}{P}_{z,k\mid k-1}^{-1}$$
  • Update the state estimate and error covariance as follows:

    $$\begin{array}{c}{\widehat{x}}_{k\mid k}={\widehat{x}}_{k\mid k-1}+K_k\left(z_k-{\widehat{z}}_{k\mid k-1}\right)\\ P_{k\mid k}=P_{k\mid k-1}-K_k{P}_{z,k\mid k-1}{K}_k^T\end{array}$$

where

• n is the dimension of the state vector.
• $\lambda$ is a scaling parameter.
• $w_i^m$ and $w_i^{\left[c\right]}$ are the weight coefficients for the mean and covariance calculations.
• $X_k^{\left[i\right]}$ are the sigma points.
• $Z_k^{\left[i\right]}$ are the propagated measurement sigma points.

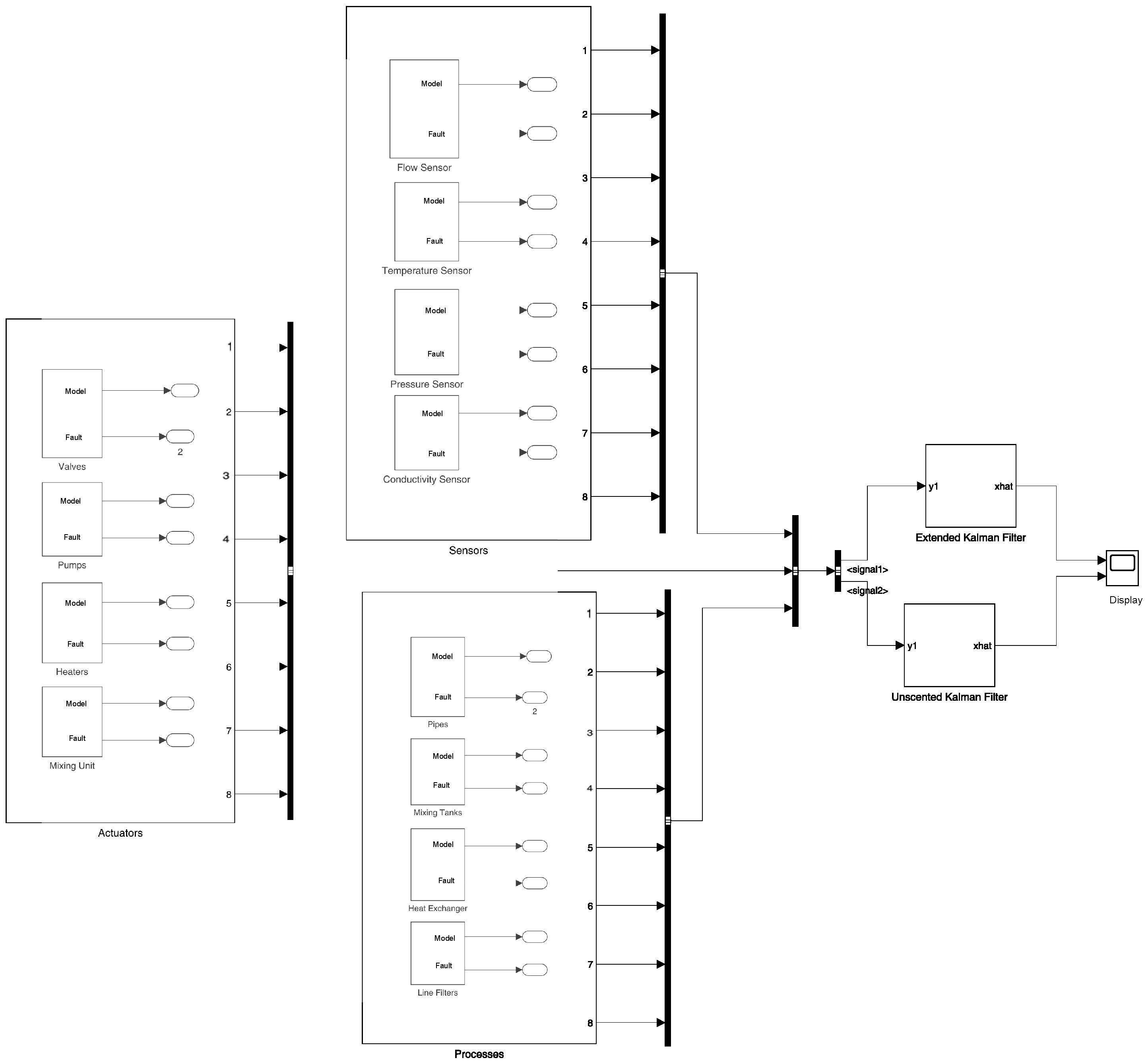
Figure 2 represent the fault detection scheme (Actuators, sensors, and process faults).

4. Experiments

We conducted trials on the Clean-In-Place (CIP) system model by simulating five tanks to test the effectiveness of the fault detection technique. The simulation, which was developed in MATLAB R2023b, incorporated many factors, including the input pump, output valves, and tank dynamics. To reflect the noise usually manifested in real-world sensor readings, noise was added to the synthetic sensor data acquired. The following two faults were selected for analysis: one involving output valve leakage, and the other involving input pump failure. Device malfunction or damage does not appear to be deliberate sabotage and fits pump scenarios.

In the case of input pump failure, a set time was established where the pump pumping rate was reduced. In the case of an output valve leakage, the system was subjected to a low drainage rate for a fixed period of time. The devices just described are examples of typical faults that people in an industrial setting might encounter when running a CIP system.

The extended Kalman filter (EKF) and unscented Kalman filter (UKF) are two different fault detection techniques that we separately implement. The simulated sensor measurements were processed by integrating the EKF and UKF algorithms to estimate the tank levels and find faults.

We simulate the five-tank CIP system in a variety of scenarios, including normal operation and two predefined fault scenarios, to assess the effectiveness of the fault detection methods. The application of the EKF and UKF algorithms to the synthetic sensor measurements in each simulation run allowed us to estimate the system state and identify faults. This allowed us to evaluate the accuracy with which each method could detect the existence and traits of the introduced faults.

Following the simulations, we used a variety of performance metrics to evaluate the capabilities of the fault detection techniques in a quantitative manner. For each method, metrics such as detection delay, False-Positive Rate (FPR) and False-Positive Rate (FPR), and Root Mean Square Errors (RMSEs) between the estimated and actual states were calculated. These metrics provide a thorough picture of how each technique fared in a variety of fault and noise scenarios.

We used data visualization techniques to help people understand the results clearly. For each method under both normal operation and fault scenarios, we plotted the estimated tank levels against the actual tank levels. To compare the effectiveness of the methods in identifying the introduced faults visually, we also created plots that showed the detected fault states against the real injected faults.

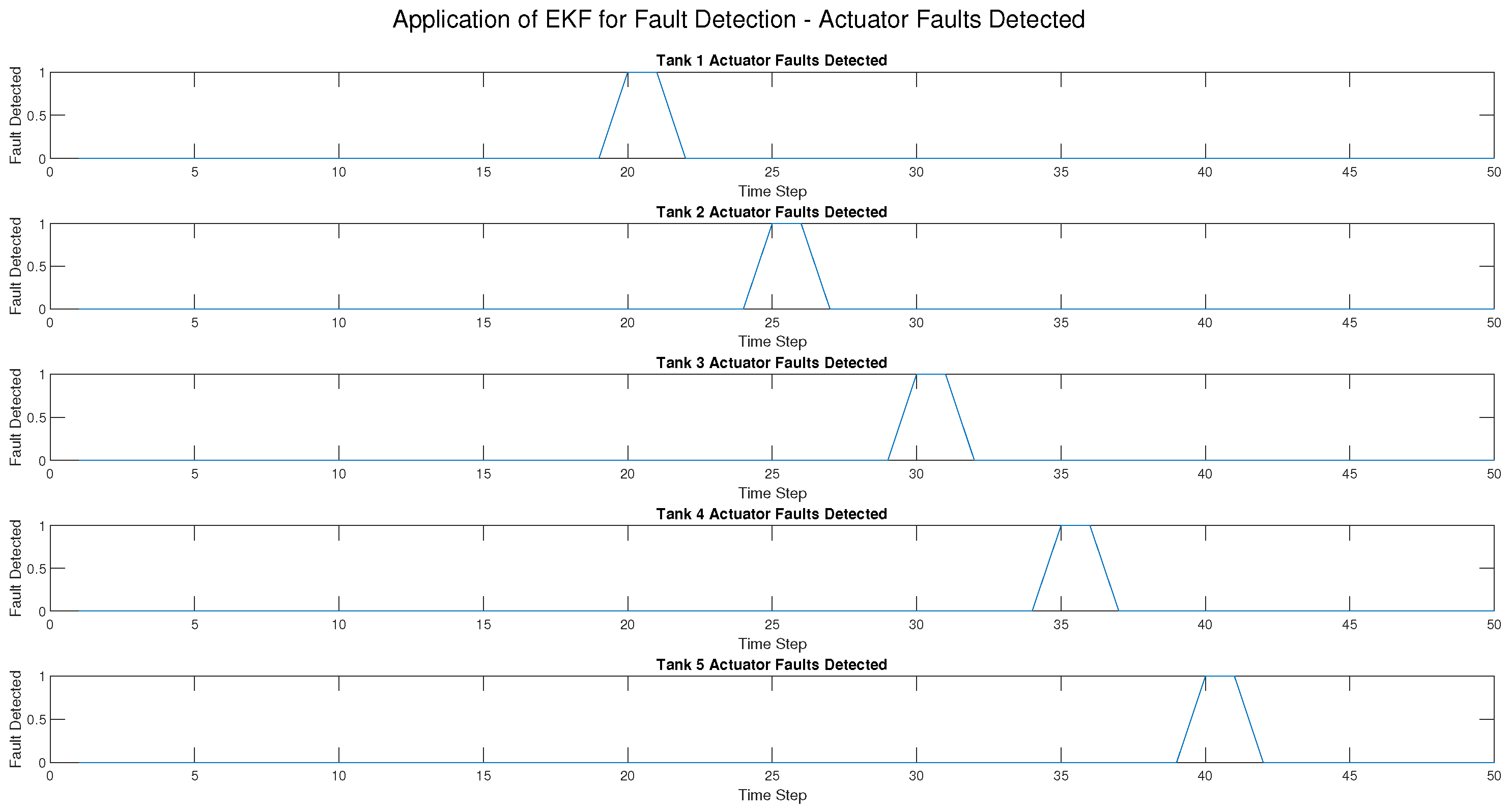
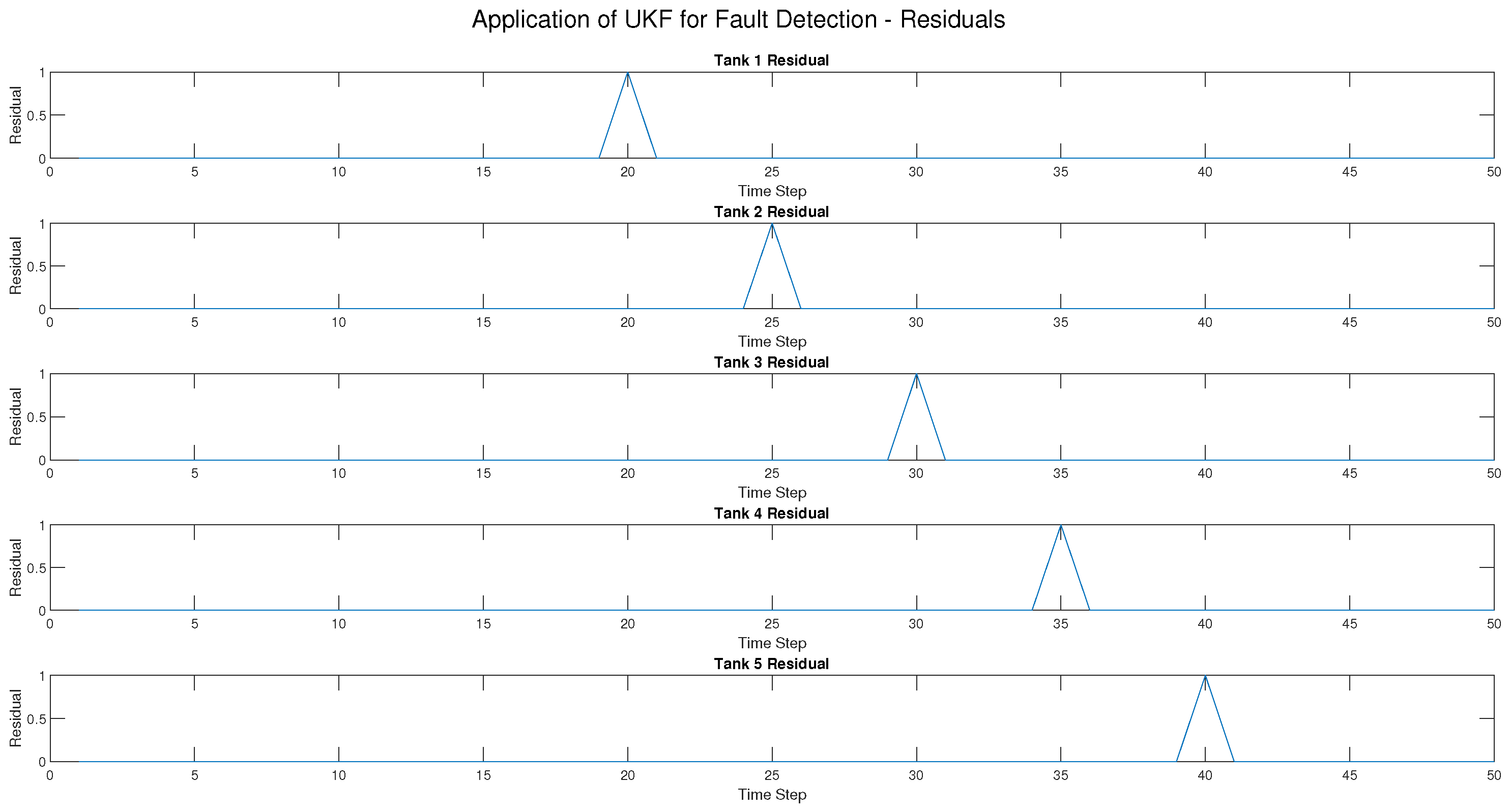
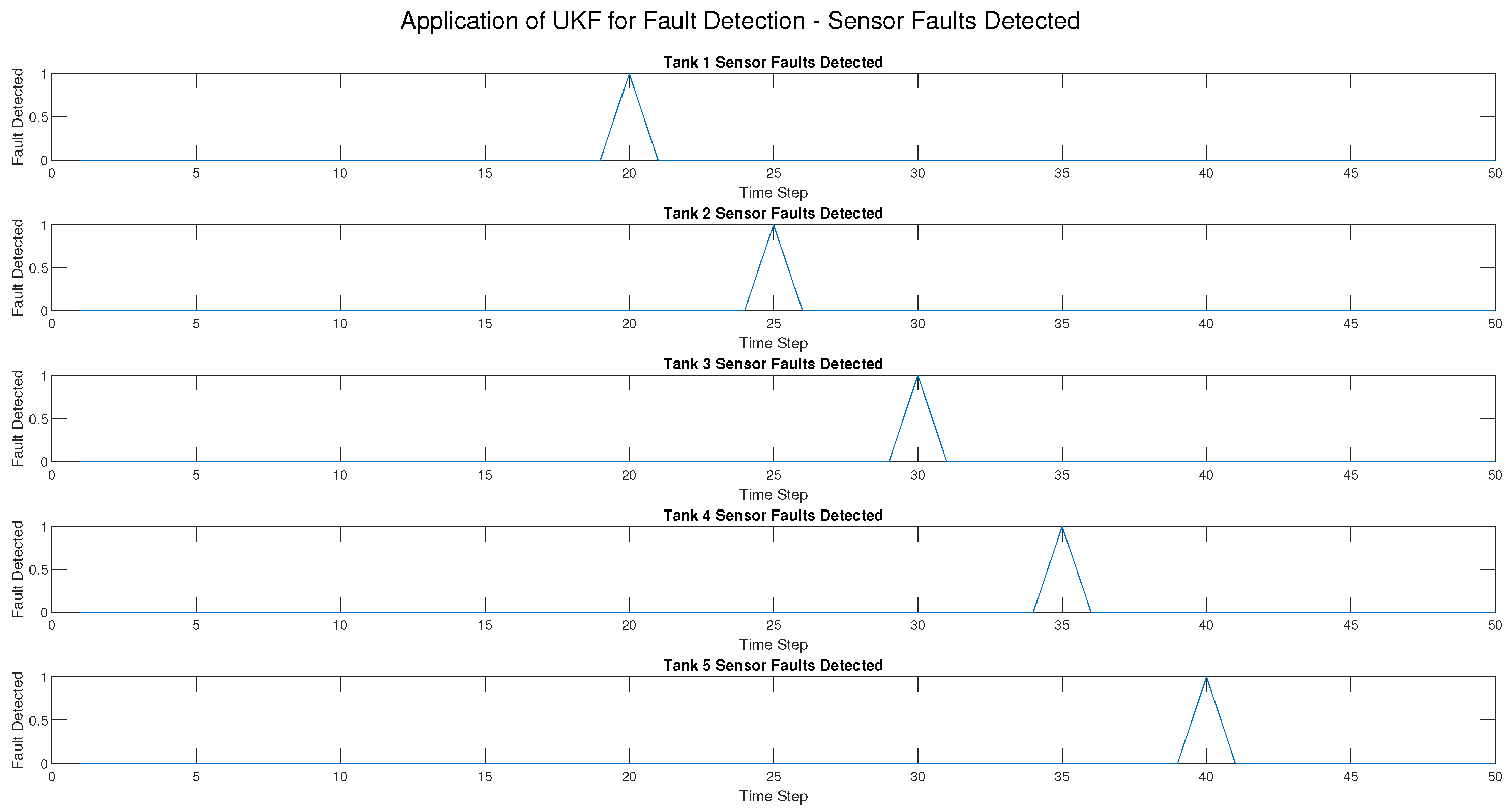
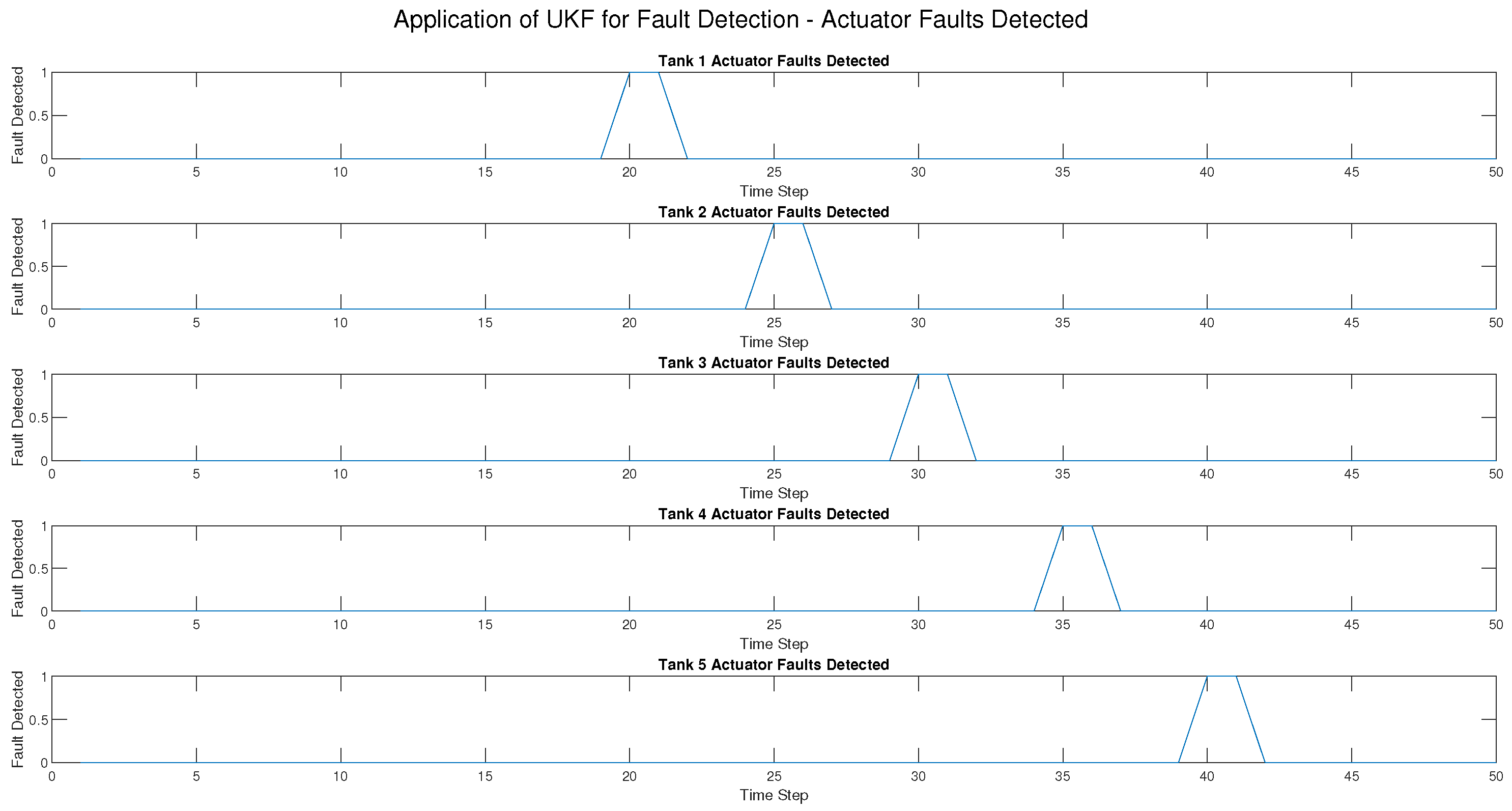
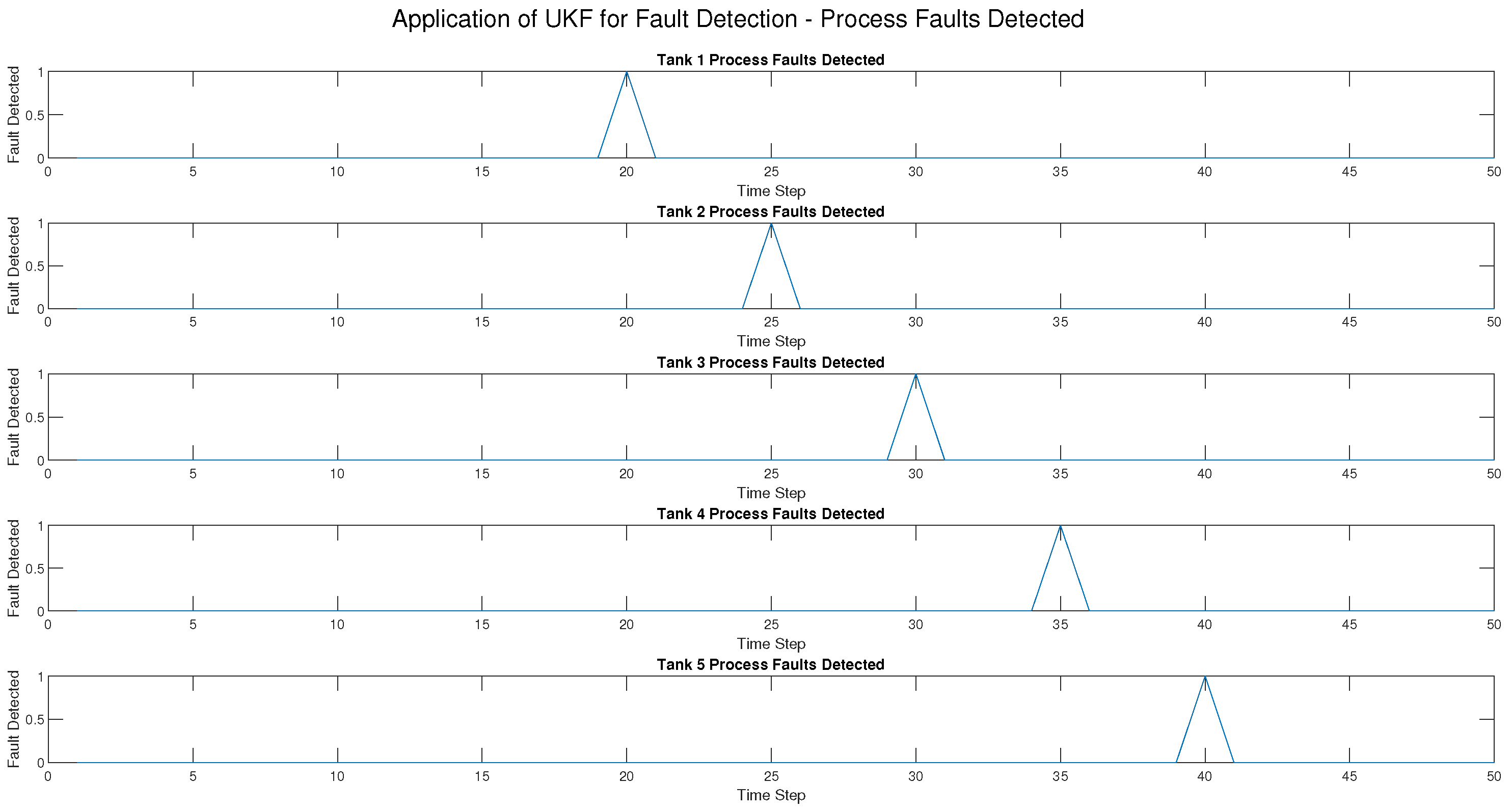
Sensor, actuator, and process faults have been injected at different time steps for each tank as follows:

• Tank 1 at $t=20$.
• Tank 2 at $t=25$.
• Tank 3 at $t=30$.
• Tank 4 at $t=35$.
• Tank 5 at $t=40$.

To quantify the performance differences between the EKF and UKF, we computed the RMSE, detection delay, True Positive Rates, and False Positive Rates for fault detection accuracy, as shown in

Table 3. Extended Kalman filter performance analysis.

Fault Type—EKF
	Sensor Fault	Acuator Fault	Process fault
RMSE	0	0	0
Detection Delay	NaN	0	NaN
TPR	0	1	0
FPR	0	0.020408	0

and

Table 4. Unscented Kalman filter performance analysis.

Fault Type—UKF
	Sensor Fault	Acuator Fault	Process fault
RMSE	0.1414	0.1414	0.1414
Detection Delay	0	0	0
TPR	1	1	1
FPR	0	0.020408	0

, where:

• True Positive Rate (TPR): TPR is the proportion of actual faults that are correctly identified by the fault detection system.
  TPR = $\left(NumberofTruePositives\right)/\left(NumberofActualPositives\right)$
• False Positive Rate (FPR): FPR is the proportion of non-fault cases that are incorrectly identified as faults by the fault detection system.
  FPR = $\left(NumberofFalsePositives\right)/\left(NumberofActualNegatives\right)$
• Detection delay: Detection delay is the time difference between the actual occurrence of a fault and its detection by the fault detection system.
  Detection Delay = $\left(TimeofFaultDetection\right)-\left(TimeofFaultOccurrence\right)$
• Root Mean Square Error (RMSE): The RMSE measures the average magnitude of the errors between the actual and estimated states of the system.
  $\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}\sum {(\mathrm{estimated}\mathrm{state}-\mathrm{actual}\mathrm{state})}^2}$

5. Results and Discussion

Three types of faults—sensor faults, actuator faults, and process faults—were introduced into the five-tank CIP system at various times in this research to evaluate how well the Extended Kalman Filter (EKF) as shown in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 and the Unscented Kalman Filter (UKF) in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 can detect them. The results indicated a distinct difference between the two approaches in accuracy, detection speed, and robustness.

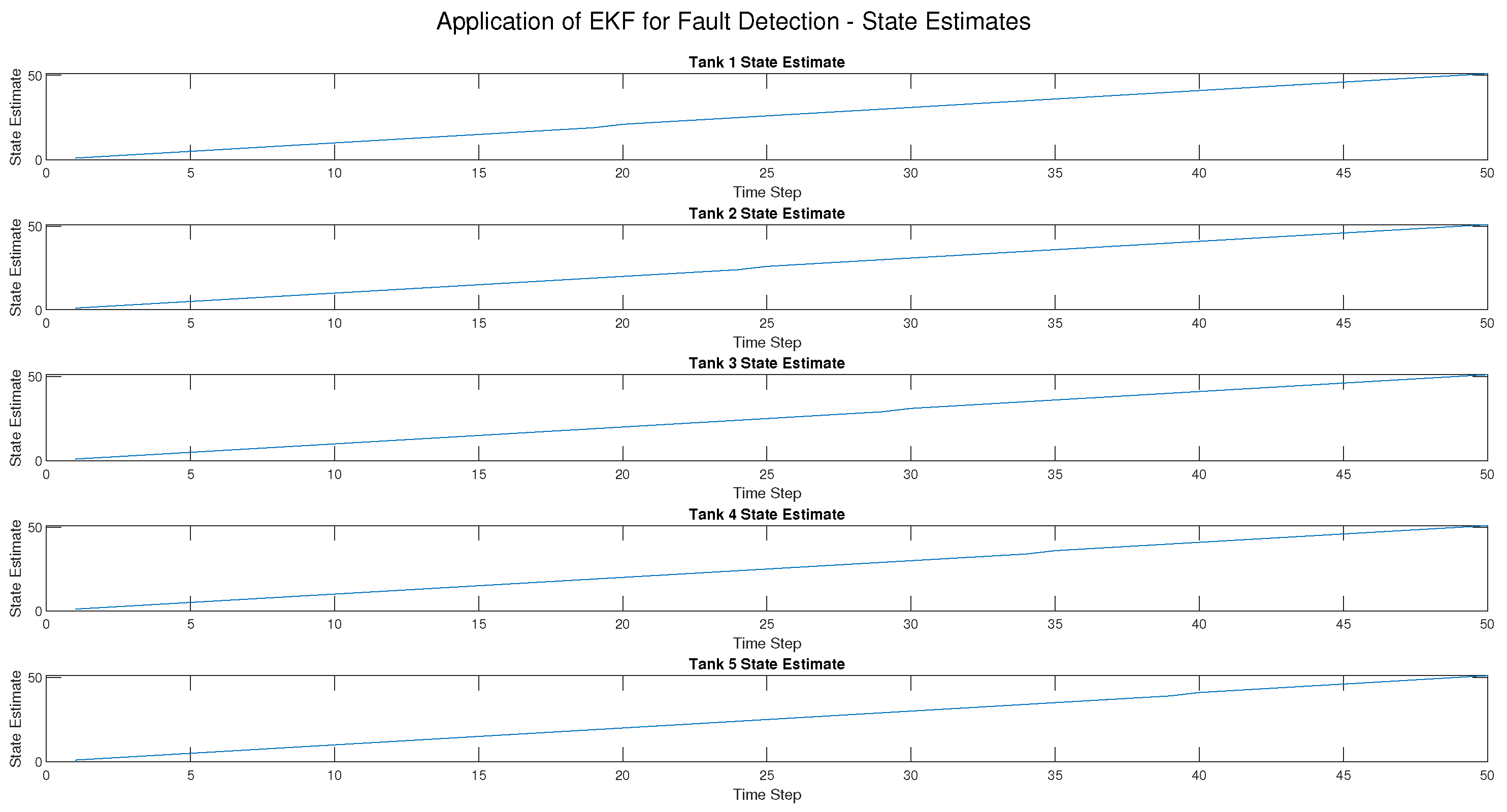
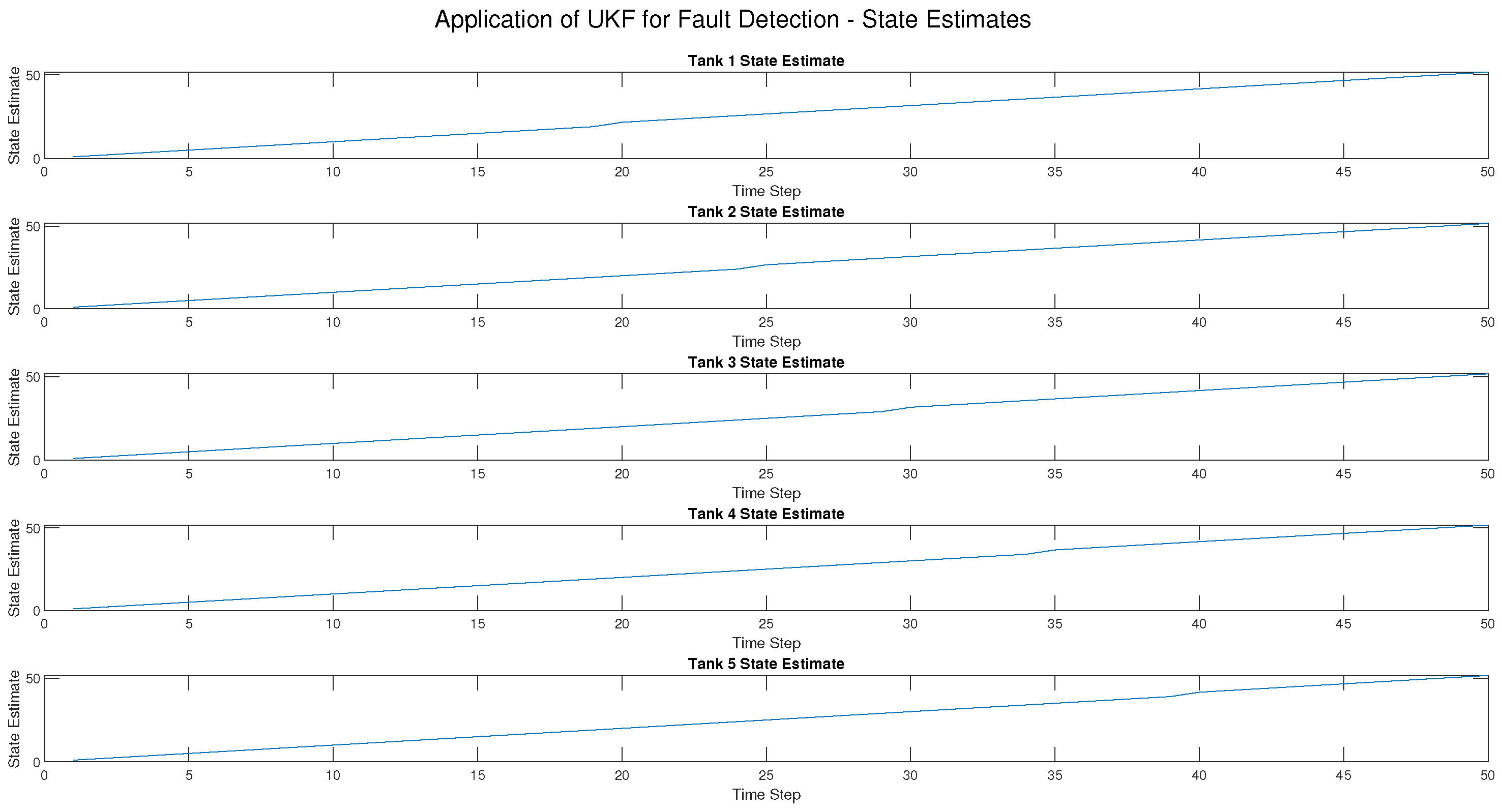
For the UKF, the result was a 100% True Positive Rate (TPR) across all fault types, i.e., all injected faults were detected. Moreover, the False Positive Rate (FPR) was very low (2.04%) and only occurred in actuator fault detection, which means there were very few classification errors. Most importantly, the UKF suffered no detection delay, i.e., faults were detected at the exact time of occurrence. In addition, the RMSE for all tanks was kept at 0.1414, showing that the UKF gave very precise state estimations despite the presence of faults.

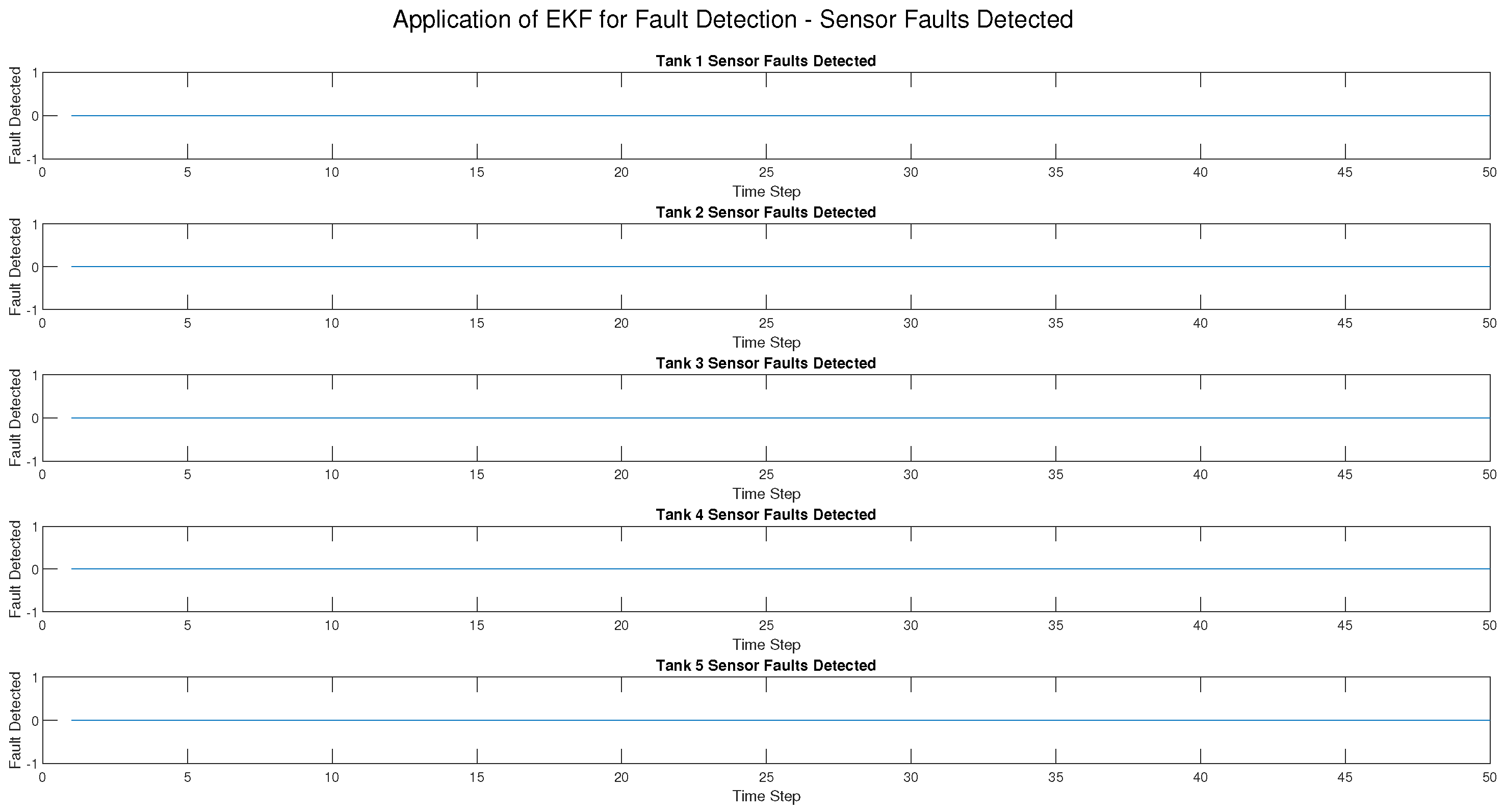
On the other hand, the EKF performed much worse in detecting sensor and process faults. The True Positive Rate (TPR) was 0% for such fault types, i.e., the EKF failed to detect them altogether. While the EKF could detect actuator faults with a TPR of 100%, it performed worse than the UKF. The False Positive Rate (FPR) was the same as the UKF (2.04%), but the detection delay was varied, with sensor and process fault detection failures recorded as NaN (not detected at all). Additionally, the RMSE for the EKF was zero, indicating that it did not produce useful estimates under sensor and process fault conditions.

The evaluation metrics further reinforced these findings. The True Positive Rate (TPR) highlighted the ability of the UKF to detect all fault types, whereas the EKF was limited to actuator faults. The False Positive Rate (FPR) was low in both methods, showing that neither method frequently misclassified normal conditions as faults. Detection delay was zero for the UKF but varied for the EKF, particularly in process and sensor faults. Finally, the RMSE values confirmed that the UKF produced accurate state estimation, while the EKF was not good under fault conditions.

Overall, the UKF performed better than the EKF consistently, having higher fault detection accuracy, faster response times, and better robustness in dealing with nonlinearities and sensor noise, while the EKF was still effective in actuator fault detection, it could not detect process and sensor faults and therefore is not a good choice for comprehensive fault detection in CIP systems.

The results of this study highlight the superior performance of the UKF in handling nonlinearities and sensor noise, making it a more robust choice for fault detection in CIP systems. This is consistent with previous research which also found the UKF to be effective in hydraulic rig [10] and for PMSG Stator Inter-Turn [29].

The differences in capabilities between fault detection techniques are based on many factors, such as the nonlinearity of system dynamics, the magnitude and nature of faults, the presence of measurement noise, system complexity, and model accuracy. Different strategies can be more successful in instances where they inherently have edges over others.

However, the EKF remains a viable option for systems with mild nonlinearities or limited computational resources. In practical terms, the UKF’s ability to accurately detect faults such as valve malfunctions and pump failures can significantly reduce downtime and improve product quality in industries that rely on CIP systems. Future research could explore hybrid approaches that combine the strengths of the EKF and UKF, as well as validate these methods using data from real-world CIP systems.

6. Conclusions

This research effort presents a novel application of Kalman filtering (EKF and UKF) for fault detection in CIP systems, which fills a significant research gap in industrial automation research. While Kalman filters have been extensively used in hydraulic systems, power networks, and other industrial processes, their use in CIP fault detection has not been explicitly addressed prior to this research effort.

The outcome of our study emphasizes the performance characteristics of each technique, which inherently result from their ability to handle the nonlinear dynamics, fault magnitude, measurement noise, complexity of the system, and accuracy of the model. In particular, the UKF outperforms the extended Kalman filter because of its ability to handle moderate five tanks CIP system nonlinearities well, without the need for explicit linearization. This is due to its clear probabilistic framework, which includes uncertainties in an appropriate form. The technique was chosen in view of the specific features of the given system and types of searched faults. This research highlights the importance of choosing an appropriate methodology to achieve the best results in fault detection in industrial systems.