RLANet: A Kepler Optimization Algorithm-Optimized Framework for Fluorescence Spectra Analysis with Applications in Oil Spill Detection
Abstract
1. Introduction
- (1)
- The integration of ResNet with LSTM and multihead attention mechanisms enhances the extraction of both local and global spectral features, while the attention mechanism captures relationships between these features.
- (2)
- By incorporating global average pooling (GAP) and eliminating the traditional fully connected layer, the model reduces the parameter count at the output of the convolutional block while maintaining classification performance. This makes the model suitable for deployment on resource-constrained hardware for real-time detection and analysis.
- (3)
- The dataset is constructed using fluorescence spectra obtained under multiple laser power settings, enhancing the richness of the data and improving the model’s robustness.
2. Materials and Methods
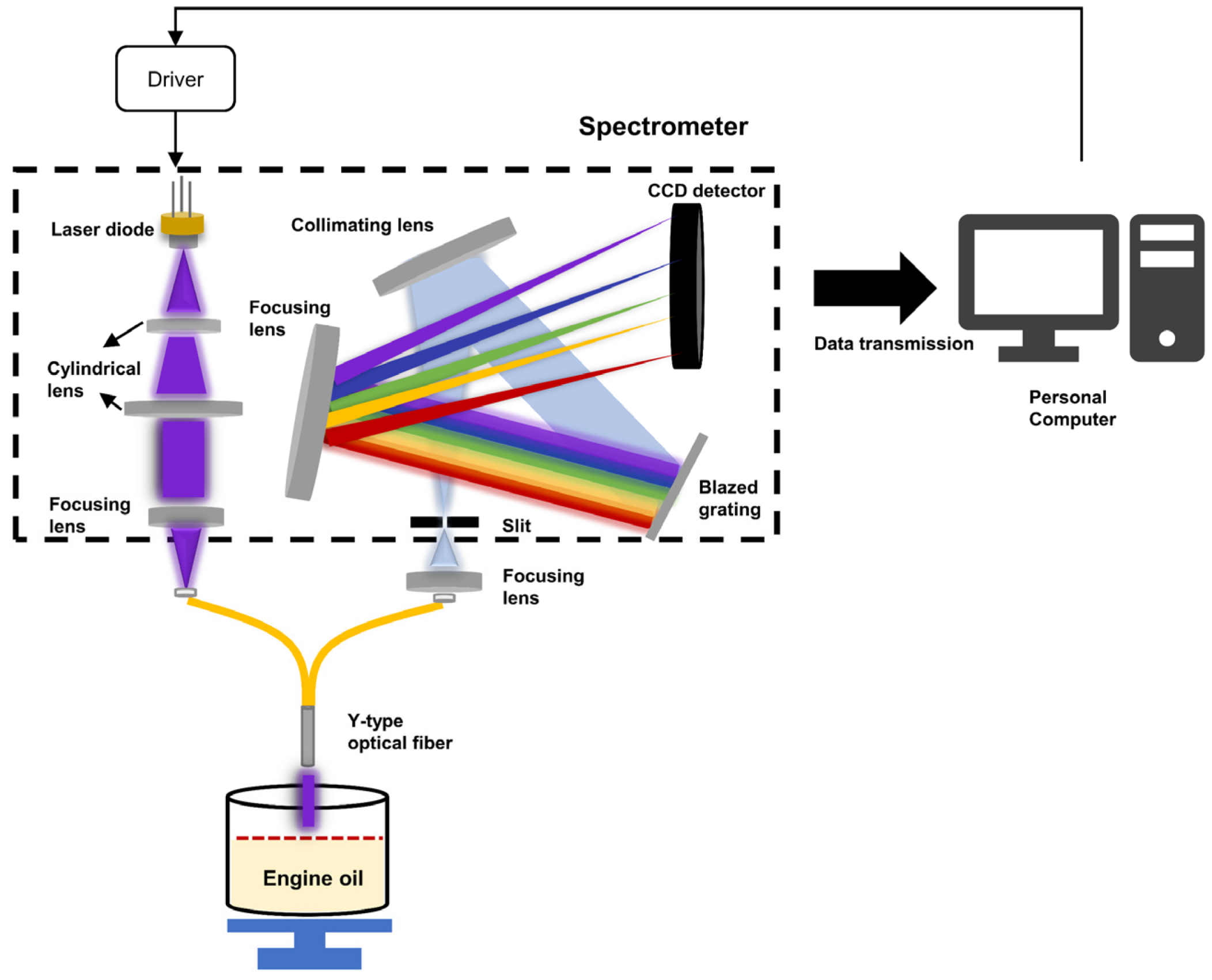
2.1. Data Acquisition
2.2. Data Preprocessing and Augmentation
2.3. ResNet-LSTM-Attention Network Model
- (1)
- Comprehensive feature extraction: ResNet captures local spectral features, LSTM handles long-term dependencies, and Multihead Attention flexibly focuses on different feature regions. This combination enables the model to extract both global and local features, surpassing CNNs and other models limited to local patterns.
- (2)
- Efficient parameter utilization: GAP reduces model parameters and improves training speed by replacing fully connected layers, making the model computationally efficient and suitable for resource-constrained applications.
- (3)
- Handling long sequences: LSTM excels in processing temporal information in spectra, capturing complex dependencies. This makes it particularly suitable for sequential data like spectra, outperforming traditional deep learning models such as CNN and MLP in processing long sequences.
- (4)
- Stronger generalization and robustness: The Attention mechanism enhances model robustness in noisy or diverse data by focusing on different features using multiple heads. GAP also reduces model parameters, minimizing overfitting risk and improving performance in both test and real-world environments.
2.4. Model Implementation
- (1)
- Gravitational Attraction: Each candidate solution (planet) is attracted to the best solution (the Sun), helping it explore the solution space and find areas with potential global optima.
- (2)
- Orbital Motion: Similarly to how the planets orbit the Sun, the candidate solutions undergo random movements that allow for the simultaneous exploration of multiple regions of the solution space.
- (1)
- Initialization: The algorithm initializes a population of candidate solutions (hyperparameter configurations). For instance, the learning rate might be initialized within the range [1 × 10−5, 1 × 10−2], batch size within [16, 32, 64, 128, 256, 512], and the kernel size varied between [3, 21]. These initial solutions are evaluated based on the model’s performance using a validation set.
- (2)
- Gravitational Update: Each candidate solution (planet) is updated by being attracted to the best solution (the Sun). The quality of each candidate solution is evaluated based on the model’s performance (average loss rate of the training and validation sets) and its distance from the best solution. The gravitational force draws the candidate solutions toward regions of the solution space with the highest-quality configurations (e.g., optimal learning rates, batch sizes, etc.). This process ensures that the algorithm focuses on areas of the search space with the most promising hyperparameter configurations.
- (3)
- Orbital Adjustment: To explore the solution space more broadly and avoid getting trapped in local optima, the candidate solutions undergo orbital adjustments. This allows the algorithm to explore multiple regions of the solution space simultaneously. For example, the kernel size may need to vary more widely to capture features at different scales, and the batch size may need to be fine-tuned to balance computational cost with model performance. The orbital motion ensures that the solutions do not become overly focused on a small region of the search space, promoting a more thorough exploration.
- (4)
- Parallelization: Unlike BO’s sequential approach, KOA supports parallel computation, allowing multiple candidate solutions to be evaluated at once. This is particularly useful when dealing with a large number of hyperparameter configurations. For example, KOA can evaluate various combinations of learning rate, batch size, and kernel size simultaneously, significantly speeding up the optimization process. In deep learning tasks like RLANet, with high-dimensional hyperparameter spaces, this parallelism is especially beneficial for efficiently exploring the search space and finding optimal solutions faster.
- (1)
- Global and Local Search: KOA combines gravitational attraction with orbital motion, allowing it to search the solution space more broadly and effectively than BO. This reduces the risk of getting stuck in local optima and enhances the algorithm’s robustness in high-dimensional spaces.
- (2)
- Parallelization: Unlike BO’s sequential approach, KOA supports parallel computation by evaluating multiple candidate solutions simultaneously. This makes KOA particularly well-suited for deep learning tasks, where large hyperparameter search spaces need to be explored efficiently and at scale.
- (3)
- Scalability: KOA’s parallelism and efficient global search make it scalable to larger models and datasets, which is a key advantage over BO when optimizing hyperparameters in complex deep learning models, like RLANet.
3. Results and Discussion
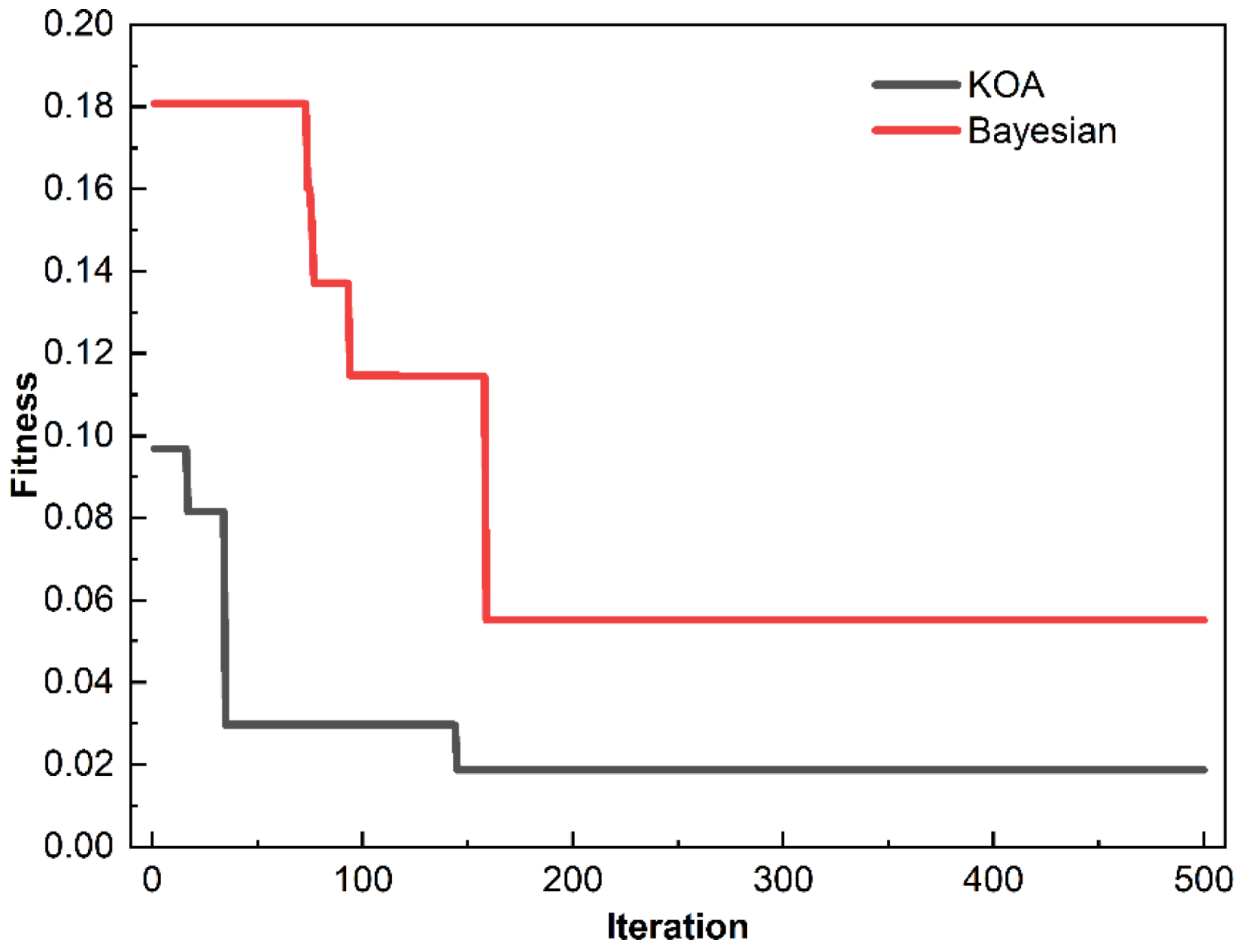
3.1. Neural Network Training Process
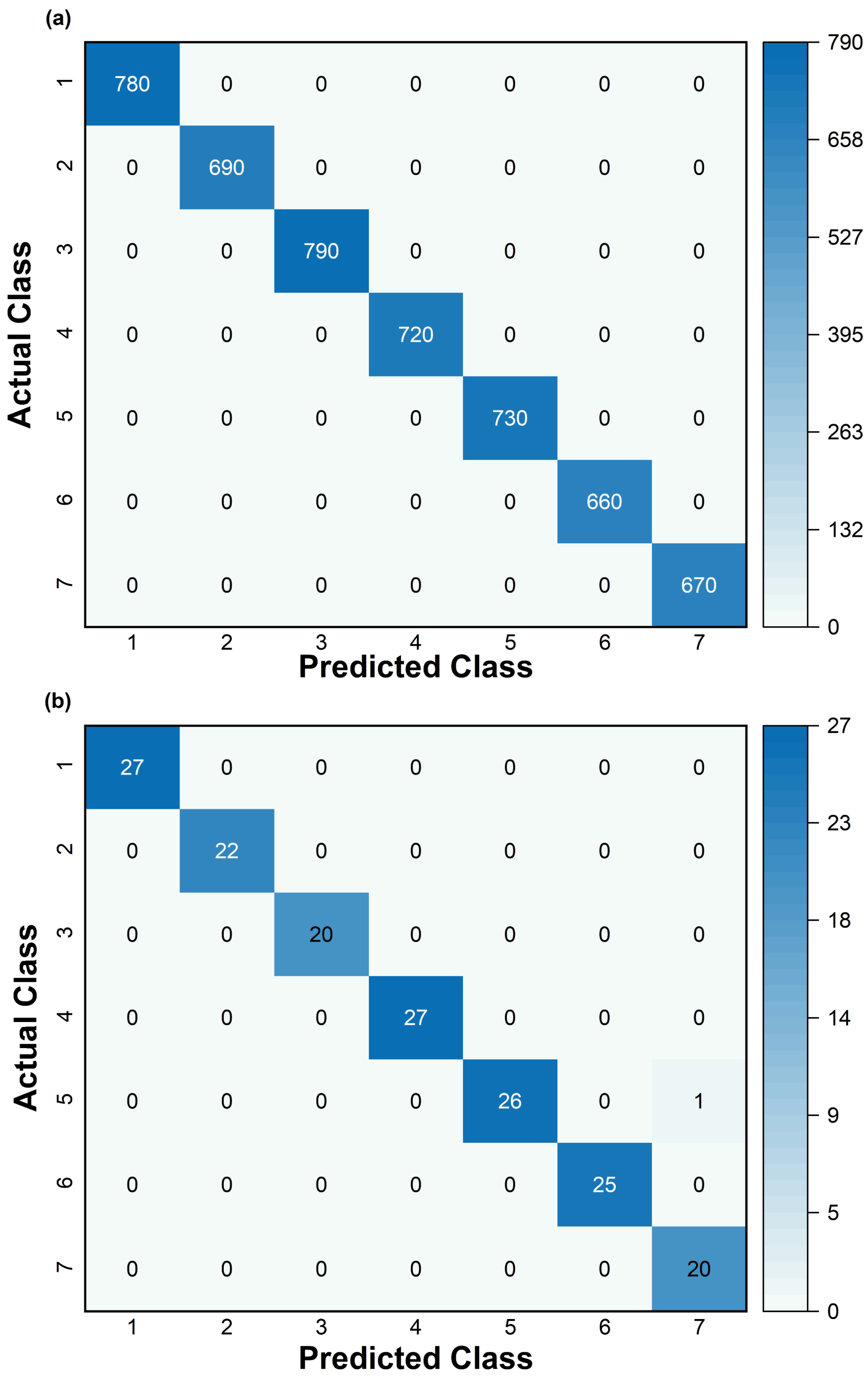
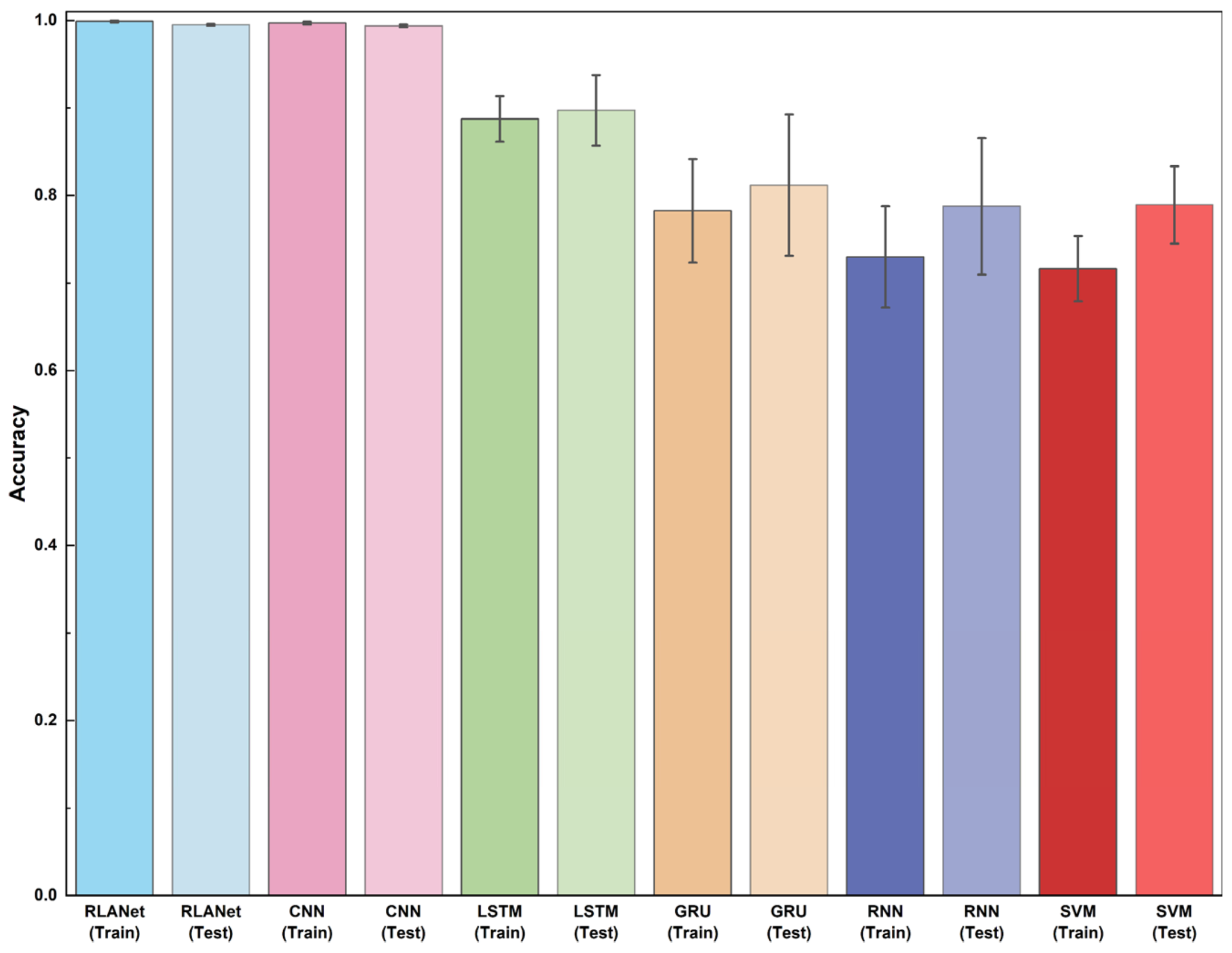
3.2. Classification Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lourenco, R.A.; Combi, T.; Alexandre, M.D.R.; Sasaki, S.T.; Zanardi-Lamardo, E.; Yogui, G.T. Mysterious oil spill along Brazil’s northeast and southeast seaboard (2019–2020): Trying to find answers and filling data gaps. Mar. Pollut. Bull. 2020, 156, 111219. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, L.G.; Araújo, K.C.; Barreto, M.C.; Bastos, M.E.P.A.; Lemos, S.G.; Fragoso, W.D. Applications of chemometrics in oil spill studies. Microchem. J. 2021, 166, 106216. [Google Scholar] [CrossRef]
- Spaulding, M.L. State of the art review and future directions in oil spill modeling. Mar. Pollut. Bull. 2017, 115, 7–19. [Google Scholar] [CrossRef]
- Laffon, B.; Pasaro, E.; Valdiglesias, V. Effects of exposure to oil spills on human health: Updated review. J. Toxicol. Environ. Health B Crit. Rev. 2016, 19, 105–128. [Google Scholar] [CrossRef] [PubMed]
- Campelo, R.P.S.; Lima, C.D.M.; de Santana, C.S.; Jonathan da Silva, A.; Neumann-Leitao, S.; Ferreira, B.P.; Soares, M.O.; Melo Junior, M.; Melo, P. Oil spills: The invisible impact on the base of tropical marine food webs. Mar. Pollut. Bull. 2021, 167, 112281. [Google Scholar] [CrossRef] [PubMed]
- Qayum, S.; Zhu, W.D. An overview of International and Regional laws for the prevention of Marine oil pollution and “International obligation of Pakistan”. Indian J. Geo-Mar. Sci. 2018, 47, 529–539. [Google Scholar]
- Fingas, M.; Brown, C. Review of oil spill remote sensing. Mar. Pollut. Bull. 2014, 83, 9–23. [Google Scholar] [CrossRef]
- Patra, D. Applications and New Developments in Fluorescence Spectroscopic Techniques for the Analysis of Polycyclic Aromatic Hydrocarbons. Appl. Spectrosc. Rev. 2003, 38, 155–185. [Google Scholar] [CrossRef]
- Okparanma, R.N.; Mouazen, A.M. Determination of Total Petroleum Hydrocarbon (TPH) and Polycyclic Aromatic Hydrocarbon (PAH) in Soils: A Review of Spectroscopic and Nonspectroscopic Techniques. Appl. Spectrosc. Rev. 2013, 48, 458–486. [Google Scholar] [CrossRef]
- Chua, C.C.; Brunswick, P.; Kwok, H.; Yan, J.; Cuthbertson, D.; van Aggelen, G.; Helbing, C.C.; Shang, D. Enhanced analysis of weathered crude oils by gas chromatography-flame ionization detection, gas chromatography-mass spectrometry diagnostic ratios, and multivariate statistics. J. Chromatogr. A 2020, 1634, 461689. [Google Scholar] [CrossRef]
- Lemkau, K.L.; Peacock, E.E.; Nelson, R.K.; Ventura, G.T.; Kovecses, J.L.; Reddy, C.M. The M/V Cosco Busan spill: Source identification and short-term fate. Mar. Pollut. Bull. 2010, 60, 2123–2129. [Google Scholar] [CrossRef] [PubMed]
- Leifer, I.; Lehr, W.J.; Simecek-Beatty, D.; Bradley, E.; Clark, R.; Dennison, P.; Hu, Y.; Matheson, S.; Jones, C.E.; Holt, B.; et al. State of the art satellite and airborne marine oil spill remote sensing: Application to the BP Deepwater Horizon oil spill. Remote Sens. Environ. 2012, 124, 185–209. [Google Scholar] [CrossRef]
- Li, Y.; Yu, Q.; Xie, M.; Zhang, Z.; Ma, Z.; Cao, K. Identifying Oil Spill Types Based on Remotely Sensed Reflectance Spectra and Multiple Machine Learning Algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9071–9078. [Google Scholar] [CrossRef]
- Fedotov, Y.V.; Belov, M.L.; Kravtsov, D.A.; Gorodnichev, V.A. Laser fluorescence method for detecting oil pipeline leaks at a wavelength of 355 nm. J. Opt. Technol. 2019, 86, 81–85. [Google Scholar] [CrossRef]
- Xie, M.; Xu, Q.; Xie, L.; Li, Y.; Han, B. Establishment and optimization of the three-band fluorometric indices for oil species identification: Implications on the optimal excitation wavelengths and the detection band combinations. Anal. Chim. Acta 2023, 1280, 341871. [Google Scholar] [CrossRef]
- Brown, C.E.; Fingas, M.F. Review of the development of laser fluorosensors for oil spill application. Mar. Pollut. Bull. 2003, 47, 477–484. [Google Scholar] [CrossRef]
- Raimondi, V.; Palombi, L.; Lognoli, D.; Masini, A.; Simeone, E. Experimental tests and radiometric calculations for the feasibility of fluorescence LIDAR-based discrimination of oil spills from UAV. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 46–54. [Google Scholar] [CrossRef]
- Hou, Y.; Li, Y.; Liu, Y.; Li, G.; Zhang, Z. Effects of polycyclic aromatic hydrocarbons on the UV-induced fluorescence spectra of crude oil films on the sea surface. Mar. Pollut. Bull. 2019, 146, 977–984. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Y.; Ouyang, C.; Yin, S.; Ren, X.; Fu, S. A portable UAV-based laser-induced fluorescence lidar system for oil pollution and aquatic environment monitoring. Opt. Commun. 2023, 527, 128914. [Google Scholar] [CrossRef]
- Yin, S.; Cui, Z.; Bi, Z.; Li, H.; Liu, W.; Tian, Z. Wide-Range Thickness Determination of Oil Films on Water Based on the Ratio of Laser-Induced Fluorescence to Raman. IEEE Trans. Instrum. Meas. 2022, 71, 3134320. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, Y.; Wang, Z.; Li, J. The application of laser-induced fluorescence in oil spill detection. Environ. Sci. Pollut. Res. 2024, 31, 23462–23481. [Google Scholar] [CrossRef] [PubMed]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Zhao, W.-L.; Wang, H.; Ngo, C.-W. Approximate k-NN Graph Construction: A Generic Online Approach. IEEE Trans. Multimed. 2022, 24, 1909–1921. [Google Scholar] [CrossRef]
- Speiser, J.L.; Miller, M.E.; Tooze, J.; Ip, E. A comparison of random forest variable selection methods for classification prediction modeling. Expert Syst. Appl. 2019, 134, 93–101. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, S.; Yan, X.; Yang, C.; Feng, M.; Xiao, L.; Song, X.; Zhang, M.; Shafiq, F.; Sun, H.; et al. Evaluation of data pre-processing and regression models for precise estimation of soil organic carbon using Vis–NIR spectroscopy. J. Soils Sediments 2023, 23, 634–645. [Google Scholar] [CrossRef]
- Engel, J.; Gerretzen, J.; Szymańska, E.; Jansen, J.J.; Downey, G.; Blanchet, L.; Buydens, L.M.C. Breaking with trends in pre-processing? TrAC Trends Anal. Chem. 2013, 50, 96–106. [Google Scholar] [CrossRef]
- Temitope Yekeen, S.; Balogun, A.-L. Advances in Remote Sensing Technology, Machine Learning and Deep Learning for Marine Oil Spill Detection, Prediction and Vulnerability Assessment. Remote Sens. 2020, 12, 3416. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, H.; Eom, K.B. Active Deep Learning for Classification of Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 712–724. [Google Scholar] [CrossRef]
- Gu, J.X.; Wang, Z.H.; Kuen, J.; Ma, L.Y.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.X.; Wang, G.; Cai, J.F.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Zhang, H.G.; Wang, Z.S.; Liu, D.R. A Comprehensive Review of Stability Analysis of Continuous-Time Recurrent Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1229–1262. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, W.H.; Wu, X.M.; Chen, P.C.Y.; Liu, J.M. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef]
- Shao, H.D.; Cheng, J.S.; Jiang, H.K.; Yang, Y.; Wu, Z.T. Enhanced deep gated recurrent unit and complex wavelet packet energy moment entropy for early fault prognosis of bearing. Knowl. Based Syst. 2020, 188, 105022. [Google Scholar] [CrossRef]
- Li, Y.; Jia, Y.; Cai, X.; Xie, M.; Zhang, Z. Oil pollutant identification based on excitation-emission matrix of UV-induced fluorescence and deep convolutional neural network. Environ. Sci. Pollut. Res. Int. 2022, 29, 68152–68160. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Du, X.; Zhao, W.; Guo, P.; Chen, H.; Jiang, Y.; Wu, H. Olive oil classification with Laser-induced fluorescence (LIF) spectra using 1-dimensional convolutional neural network and dual convolution structure model. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2022, 279, 121418. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Li, J.; Yao, X.; Forsberg, E.; He, S. Fluorescence Hyperspectral Imaging of Oil Samples and Its Quantitative Applications in Component Analysis and Thickness Estimation. Sensors 2018, 18, 4415. [Google Scholar] [CrossRef]
- Zhang, X.; Kong, D.; Cui, Y.; Zhong, M.; Kong, D.; Kong, L. An Evaluation Algorithm for Thick Oil Film on Sea Surface Based on Fluorescence Signal. IEEE Sens. J. 2023, 23, 9727–9738. [Google Scholar] [CrossRef]
- Liu, X.N.; Qiao, S.D.; Ma, Y.F. Highly sensitive methane detection based on light-induced thermoelastic spectroscopy with a 2.33 μm diode laser and adaptive Savitzky-Golay filtering. Opt. Express 2022, 30, 1304–1313. [Google Scholar] [CrossRef]
- Bi, Y.M.; Yuan, K.L.; Xiao, W.Q.; Wu, J.Z.; Shi, C.Y.; Xia, J.; Chu, G.H.; Zhang, G.X.; Zhou, G.J. A local pre-processing method for near-infrared spectra, combined with spectral segmentation and standard normal variate transformation. Anal. Chim. Acta 2016, 909, 30–40. [Google Scholar] [CrossRef]
- Bjerrum, E.J.; Glahder, M.; Skov, T. Data augmentation of spectral data for convolutional neural network (CNN) based deep chemometrics. arXiv 2017, arXiv:1710.01927. [Google Scholar]
- Zhang, X.; Xu, J.; Yang, J.; Chen, L.; Zhou, H.; Liu, X.; Li, H.; Lin, T.; Ying, Y. Understanding the learning mechanism of convolutional neural networks in spectral analysis. Anal. Chim. Acta 2020, 1119, 41–51. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, Y.; Wang, Z.; Wei, S.; Zhang, X.; Zhang, T.; Song, X.; Zou, Y.; Wang, J.; Chen, F.; et al. A novel deep learning model for spectral analysis: Lightweight ResNet-CNN with adaptive feature compression for oil spill type identification. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2025, 329, 125626. [Google Scholar] [CrossRef]
- Passos, D.; Mishra, P. A tutorial on automatic hyperparameter tuning of deep spectral modelling for regression and classification tasks. Chemom. Intell. Lab. Syst. 2022, 223, 104520. [Google Scholar] [CrossRef]
- Mishra, P.; Passos, D.; Marini, F.; Xu, J.; Amigo, J.M.; Gowen, A.A.; Jansen, J.J.; Biancolillo, A.; Roger, J.M.; Rutledge, D.N.; et al. Deep learning for near-infrared spectral data modelling: Hypes and benefits. TrAC Trends Anal. Chem. 2022, 157, 116804. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; Freitas, N.d. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Dirks, M.; Poole, D. Automatic neural network hyperparameter optimization for extrapolation: Lessons learned from visible and near-infrared spectroscopy of mango fruit. Chemom. Intell. Lab. Syst. 2022, 231, 104685. [Google Scholar] [CrossRef]
- Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.-L.; et al. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. WIREs Data Min. Knowl. Discov. 2023, 13, e1484. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler?s laws of planetary motion. Knowl. Based Syst. 2023, 268, 110454. [Google Scholar] [CrossRef]
- Li, X.X.; Chang, D.L.; Tian, T.; Cao, J. Large-Margin Regularized Softmax Cross-Entropy Loss. IEEE Access 2019, 7, 19572–19578. [Google Scholar] [CrossRef]
- Zhang, Y.; Dai, L. On the Optimal Placement of Base Station Antennas for Distributed Antenna Systems. IEEE Commun. Lett. 2020, 24, 2878–2882. [Google Scholar] [CrossRef]
- Pekel, E. Deep Learning Approach to Technician Routing and Scheduling Problem. Adcaij-Adv. Distrib. Comput. Artif. Intell. J. 2022, 11, 191–206. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Zhang, X.; Lin, T.; Xu, J.; Luo, X.; Ying, Y. DeepSpectra: An end-to-end deep learning approach for quantitative spectral analysis. Anal. Chim. Acta 2019, 1058, 48–57. [Google Scholar] [CrossRef] [PubMed]




| Hyperparameter | Range/Values | Optimal Solution (KOA) | Optimal Solution (BO) |
|---|---|---|---|
| Learning rate | [1 × 10−5, 1 × 10−2] | 3.363 × 10−5 | 6.725 × 10−5 |
| Number of Layers (CNN Block) | [2, 5] | 3 | 3 |
| Batch size | [16, 32, 64, 128, 256, 512] | 128 | 512 |
| Kernel sizes | [3, 21] | [21, 11, 11] | [21, 3, 15] |
| Strides | [1, 5] | [4, 3, 3] | [4, 5, 2] |
| LSTM hidden units | [8, 16, 32, 64, 128, 256, 512] | 32 | 32 |
| Number of layers (LSTM) | [1, 5] | 2 | 2 |
| Number of attention heads | [2, 16] | 6 | 10 |
| Epochs | [50, 100, 200, 300, 400, 500, 600, 700] | 500 | 500 |
| Method | Epochs | Accuracy (Train) | Std (Train) | Loss Rate (Train) | Accuracy (Valid) | Std (Valid) | Loss Rate (Valid) |
|---|---|---|---|---|---|---|---|
| KOA-RLANet | 300 | 0.9985 | 0.0009 | 0.0098 | 0.9772 | 0.0059 | 0.083 |
| 400 | 0.9987 | 0.0009 | 0.0058 | 0.9760 | 0.0082 | 0.0902 | |
| 500 | 0.9988 | 0.0012 | 0.0037 | 0.9793 | 0.0052 | 0.0785 | |
| 600 | 0.9988 | 0.0008 | 0.0026 | 0.9743 | 0.0167 | 0.0973 | |
| 700 | 0.9987 | 0.0009 | 0.0019 | 0.9771 | 0.0083 | 0.0837 | |
| BO-RLANet | 300 | 0.9843 | 0.0076 | 0.0830 | 0.9647 | 0.0081 | 0.1522 |
| 400 | 0.9884 | 0.0048 | 0.05 | 0.9631 | 0.0216 | 0.1558 | |
| 500 | 0.9899 | 0.0043 | 0.0367 | 0.9694 | 0.0101 | 0.1274 | |
| 600 | 0.9904 | 0.0058 | 0.029 | 0.9641 | 0.0327 | 0.1496 | |
| 700 | 0.9912 | 0.0034 | 0.0235 | 0.9690 | 0.0113 | 0.1322 |
| Method | Accuracy | Steady Iteration | Time | Parameter |
|---|---|---|---|---|
| RLANet | 99.51% | 500 | 1 min 12 s | 0.09 M |
| CNN | 99.40% | 1000 | 3 min | 11.35 M |
| LSTM | 89.73% | 5000 | 12 min 40 s | 4.57 M |
| GRU | 81.18% | 3000 | 7 min 8 s | 1.52 M |
| RNN | 78.76% | 3000 | 5 min 15 s | 0.64 M |
| Methods | Raw | SG | SG+SNV | SG+SNV+NORM | ||||
|---|---|---|---|---|---|---|---|---|
| RLANet | Best | 100% | Best | 100% | Best | 100% | Best | 100% |
| Worst | 98.81% | Worst | 99.40% | Worst | 99.40% | Worst | 99.35% | |
| Mean | 99.51% | Mean | 99.68% | Mean | 99.81% | Mean | 99.73% | |
| Std | 0.0008 | Std | 0.0012 | Std | 0.0008 | Std | 0.0010 | |
| CNN | Best | 100% | Best | 99.98% | Best | 99.98% | Best | 99.98% |
| Worst | 98.81% | Worst | 98.79% | Worst | 99.09% | Worst | 98.81% | |
| Mean | 99.40% | Mean | 99.43% | Mean | 99.52% | Mean | 99.55% | |
| Std | 0.0012 | Std | 0.0023 | Std | 0.0024 | Std | 0.0028 | |
| LSTM | Best | 97.62% | Best | 98.81% | Best | 99.40% | Best | 88.69% |
| Worst | 79.76% | Worst | 80.95% | Worst | 96.43% | Worst | 85.71% | |
| Mean | 89.73% | Mean | 90.10% | Mean | 97.96% | Mean | 87.42% | |
| Std | 0.0405 | Std | 0.0497 | Std | 0.0075 | Std | 0.0058 | |
| GRU | Best | 93.45% | Best | 95.83% | Best | 80.95% | Best | 77.38% |
| Worst | 60.71% | Worst | 64.88% | Worst | 72.62% | Worst | 73.81% | |
| Mean | 81.18% | Mean | 82.89% | Mean | 77.32% | Mean | 74.61% | |
| Std | 0.0807 | Std | 0.0730 | Std | 0.0193 | Std | 0.0068 | |
| RNN | Best | 94.05% | Best | 86.90% | Best | 82.14% | Best | 80.95% |
| Worst | 61.90% | Worst | 39.29% | Worst | 73.81% | Worst | 74.40% | |
| Mean | 78.76% | Mean | 67.32% | Mean | 78.63% | Mean | 77.74% | |
| Std | 0.0781 | Std | 0.0929 | Std | 0.0218 | Std | 0.0141 | |
| SVM | Best | 87.5% | Best | 89.29% | Best | 94.04% | Best | 89.88% |
| Worst | 69.04% | Worst | 69.64% | Worst | 75% | Worst | 68.45% | |
| Mean | 78.93% | Mean | 78.46% | Mean | 85.55% | Mean | 81.30% | |
| Std | 0.044 | Std | 0.0431 | Std | 0.0483 | Std | 0.0439 | |
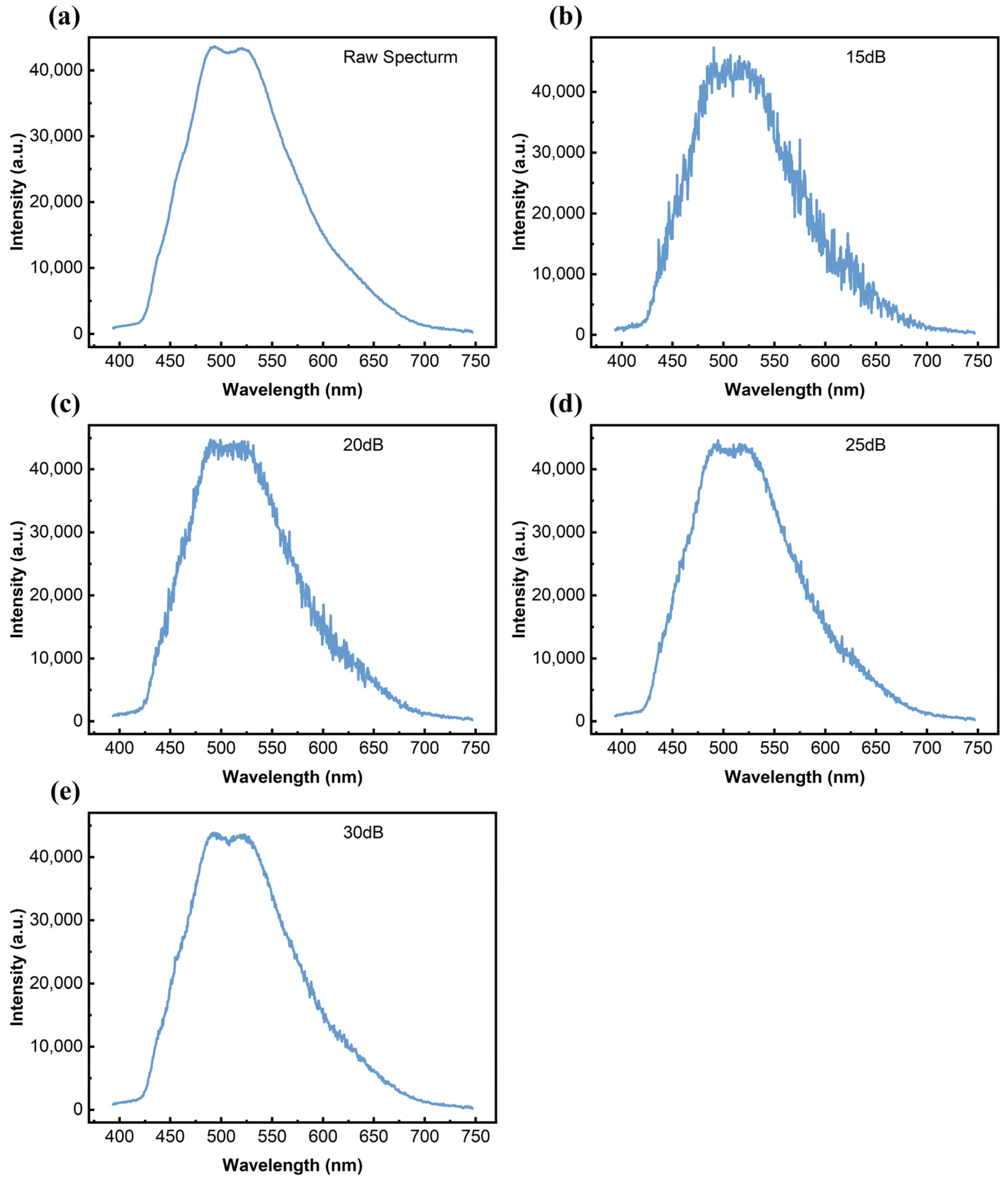
| Model | SNR (dB) | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|---|
| RLANet | GT | 0.994 | 0.9932 | 0.9947 | 0.9938 |
| 15 | 0.8036 | 0.8043 | 0.8058 | 0.8041 | |
| 20 | 0.8988 | 0.9006 | 0.9026 | 0.9004 | |
| 25 | 0.9583 | 0.9576 | 0.9574 | 0.9574 | |
| 30 | 0.994 | 0.9949 | 0.9947 | 0.9947 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Yuan, Y.; Li, J. RLANet: A Kepler Optimization Algorithm-Optimized Framework for Fluorescence Spectra Analysis with Applications in Oil Spill Detection. Processes 2025, 13, 934. https://doi.org/10.3390/pr13040934
Zhang S, Yuan Y, Li J. RLANet: A Kepler Optimization Algorithm-Optimized Framework for Fluorescence Spectra Analysis with Applications in Oil Spill Detection. Processes. 2025; 13(4):934. https://doi.org/10.3390/pr13040934
Chicago/Turabian StyleZhang, Shubo, Yafei Yuan, and Jing Li. 2025. "RLANet: A Kepler Optimization Algorithm-Optimized Framework for Fluorescence Spectra Analysis with Applications in Oil Spill Detection" Processes 13, no. 4: 934. https://doi.org/10.3390/pr13040934
APA StyleZhang, S., Yuan, Y., & Li, J. (2025). RLANet: A Kepler Optimization Algorithm-Optimized Framework for Fluorescence Spectra Analysis with Applications in Oil Spill Detection. Processes, 13(4), 934. https://doi.org/10.3390/pr13040934






