Evaluation of the Impact of Multi-Scale Flow Mechanisms and Natural Fractures on the Pressure Transient Response in Fractured Tight Gas Reservoirs
Abstract
1. Introduction
2. Methodology
2.1. Governing Equation
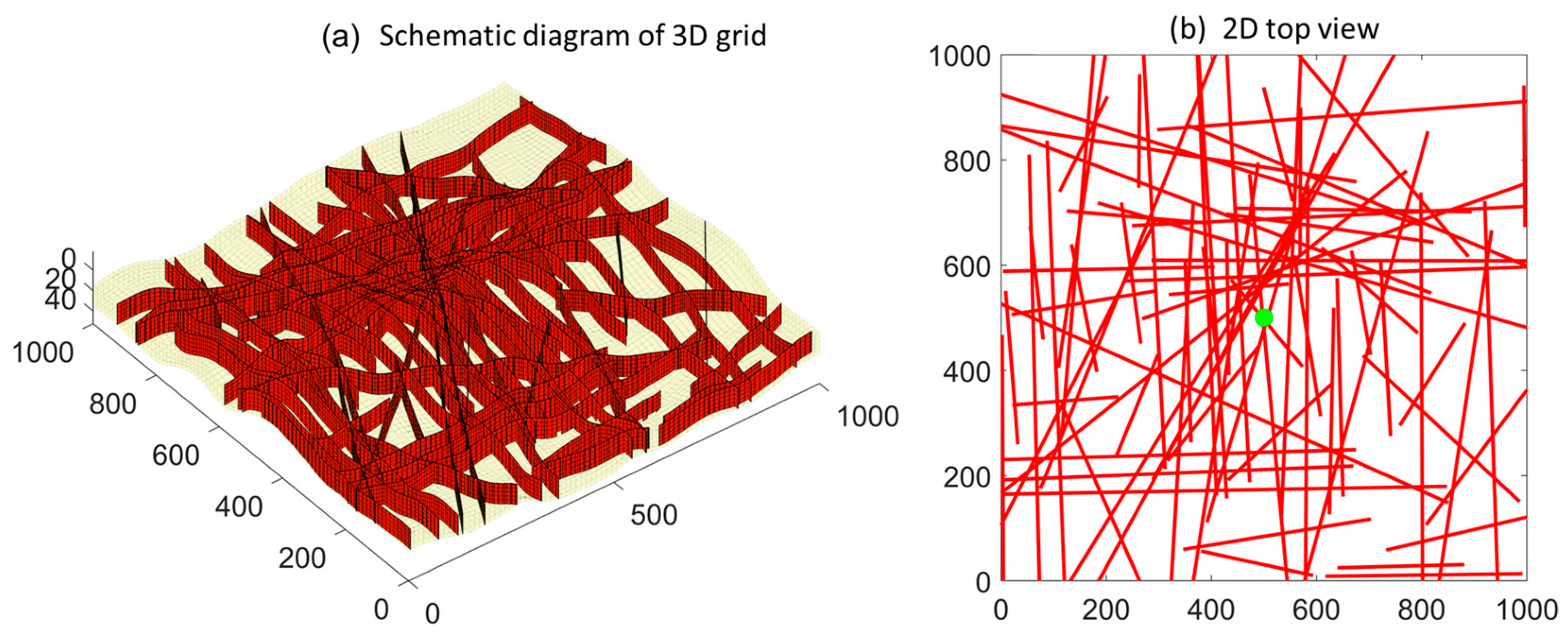
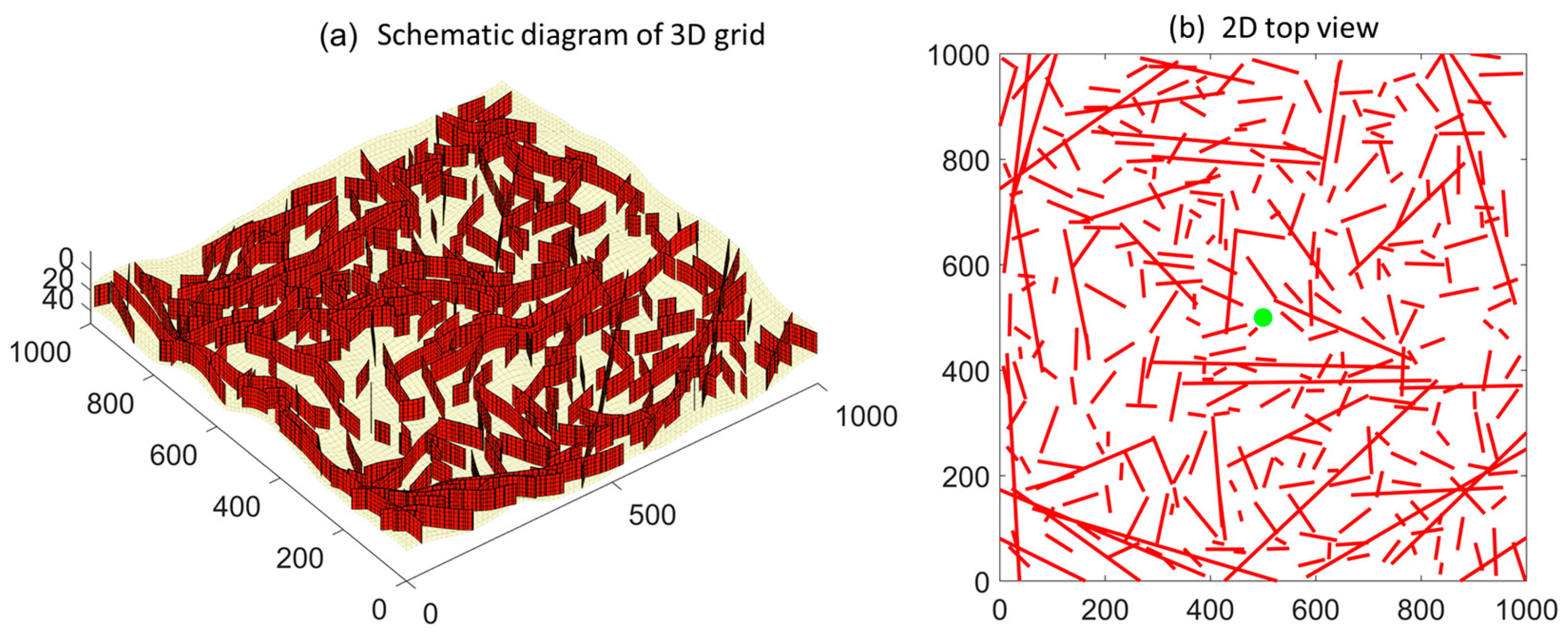
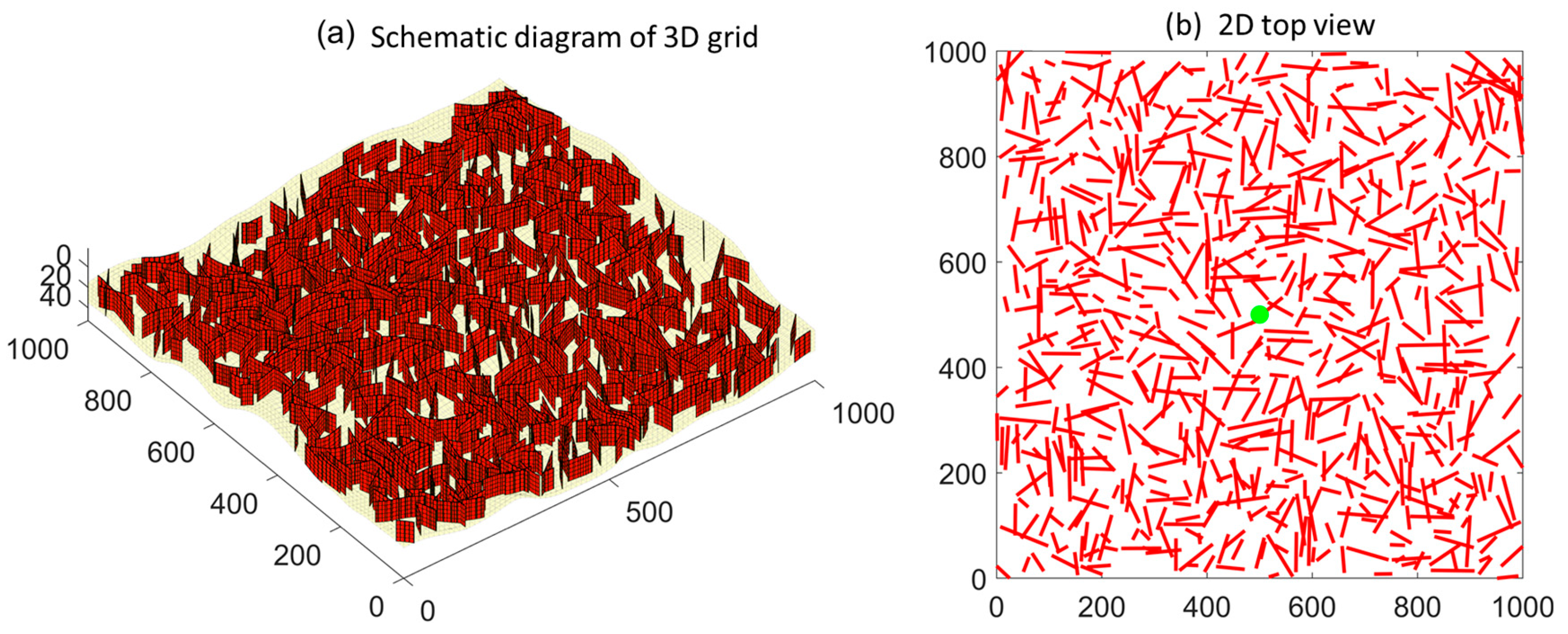
2.2. Numerical Model and Solutions
2.3. Evaluation of Pressure and PD Evaluation
3. Model Validation
4. Results
4.1. Typical Curves of Pressure Response in Fractured Gas Reservoirs
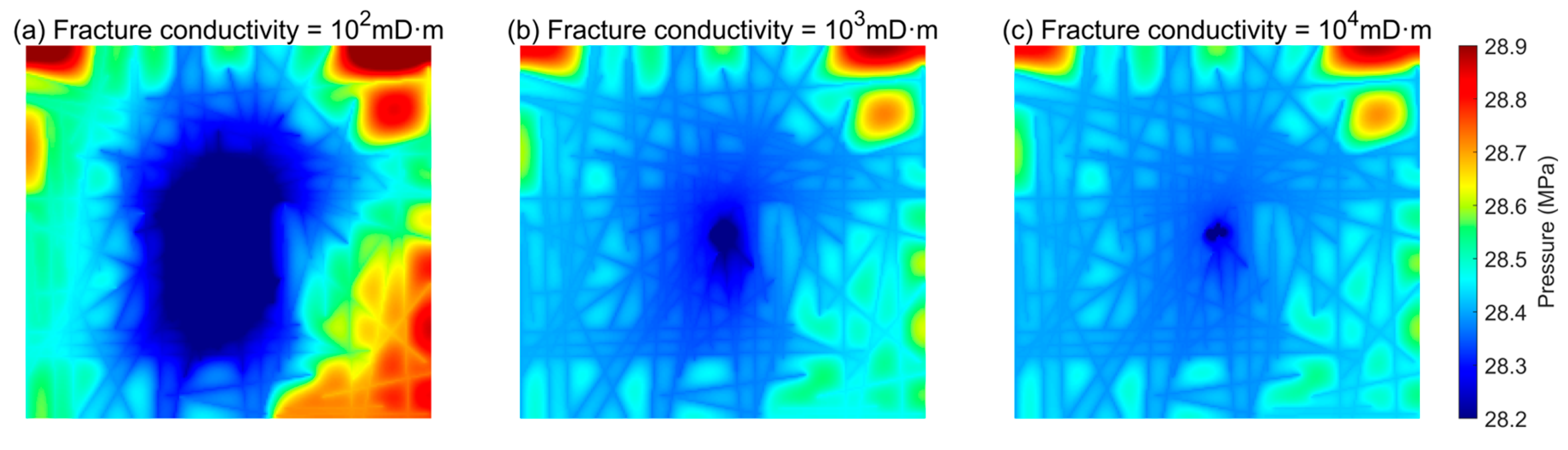
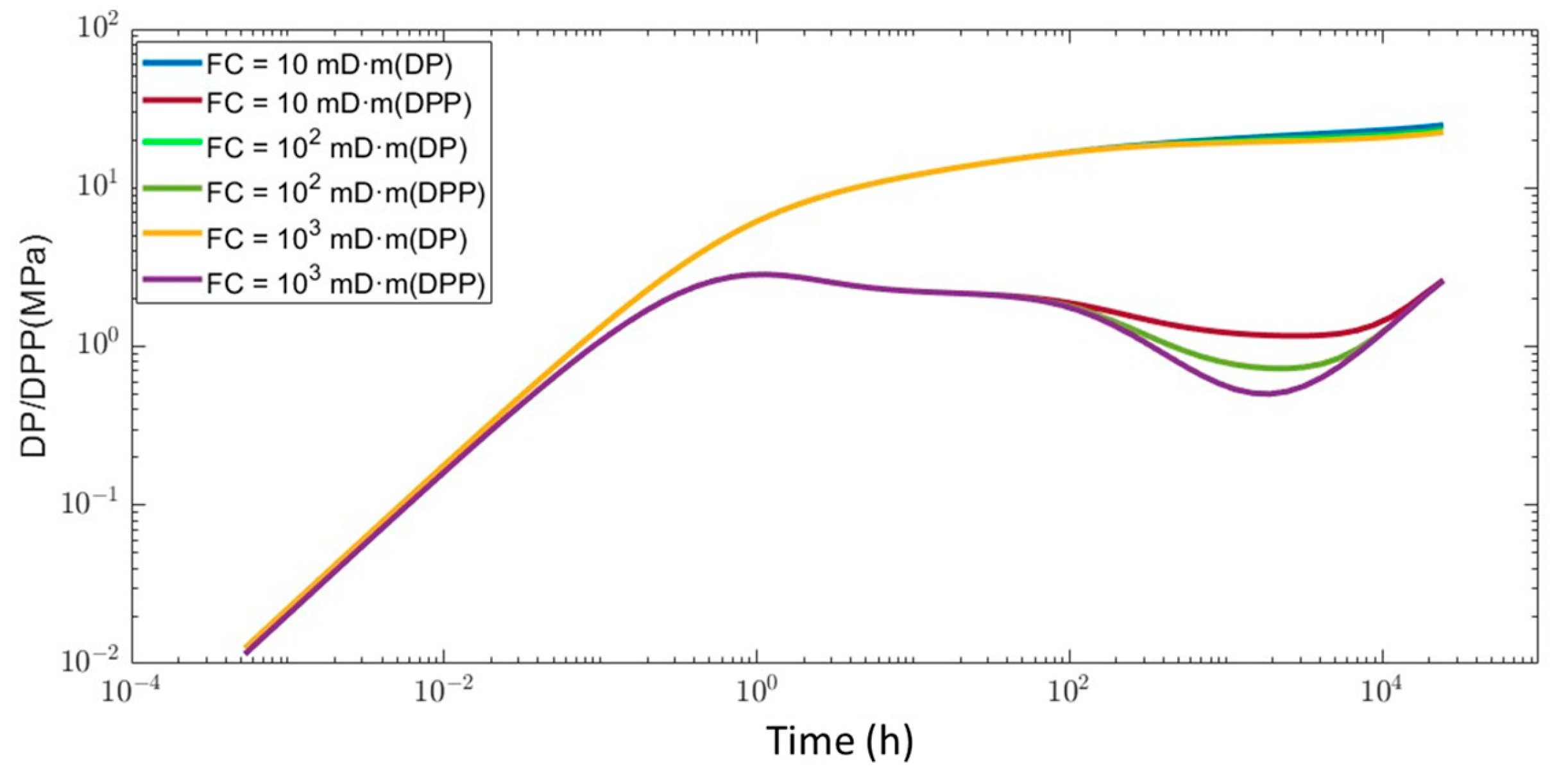
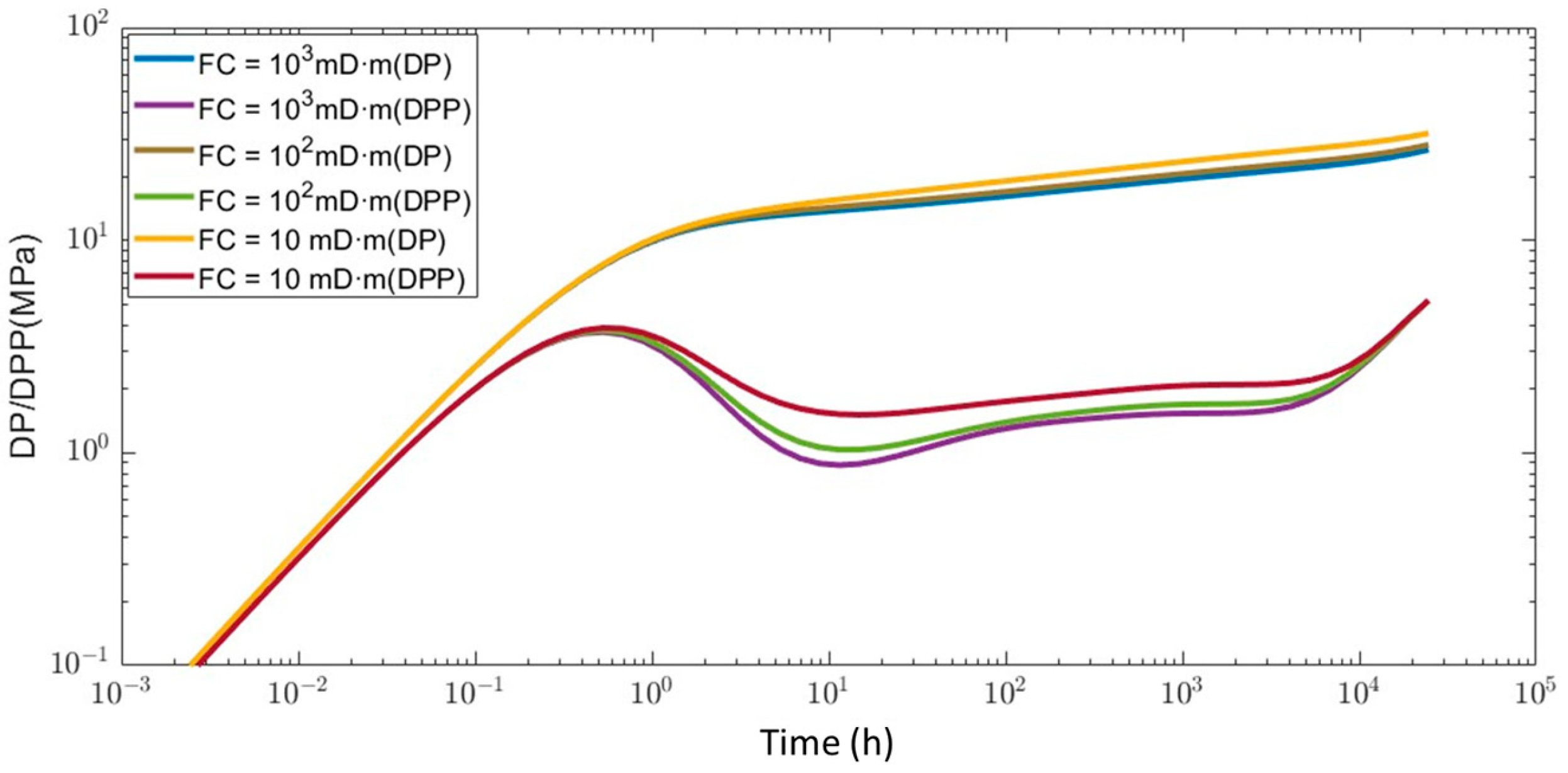
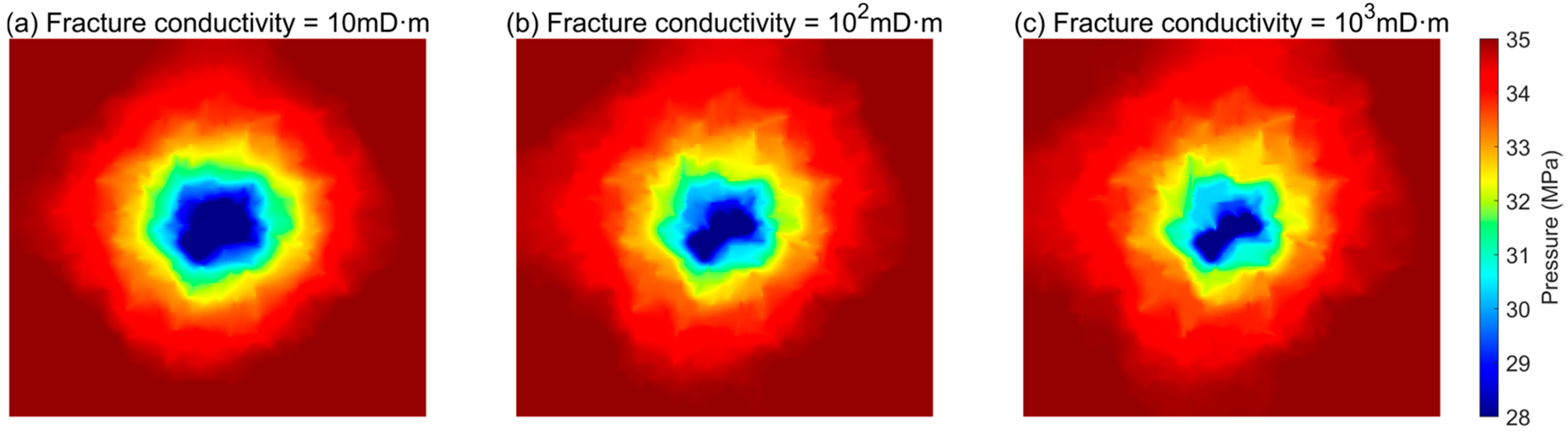
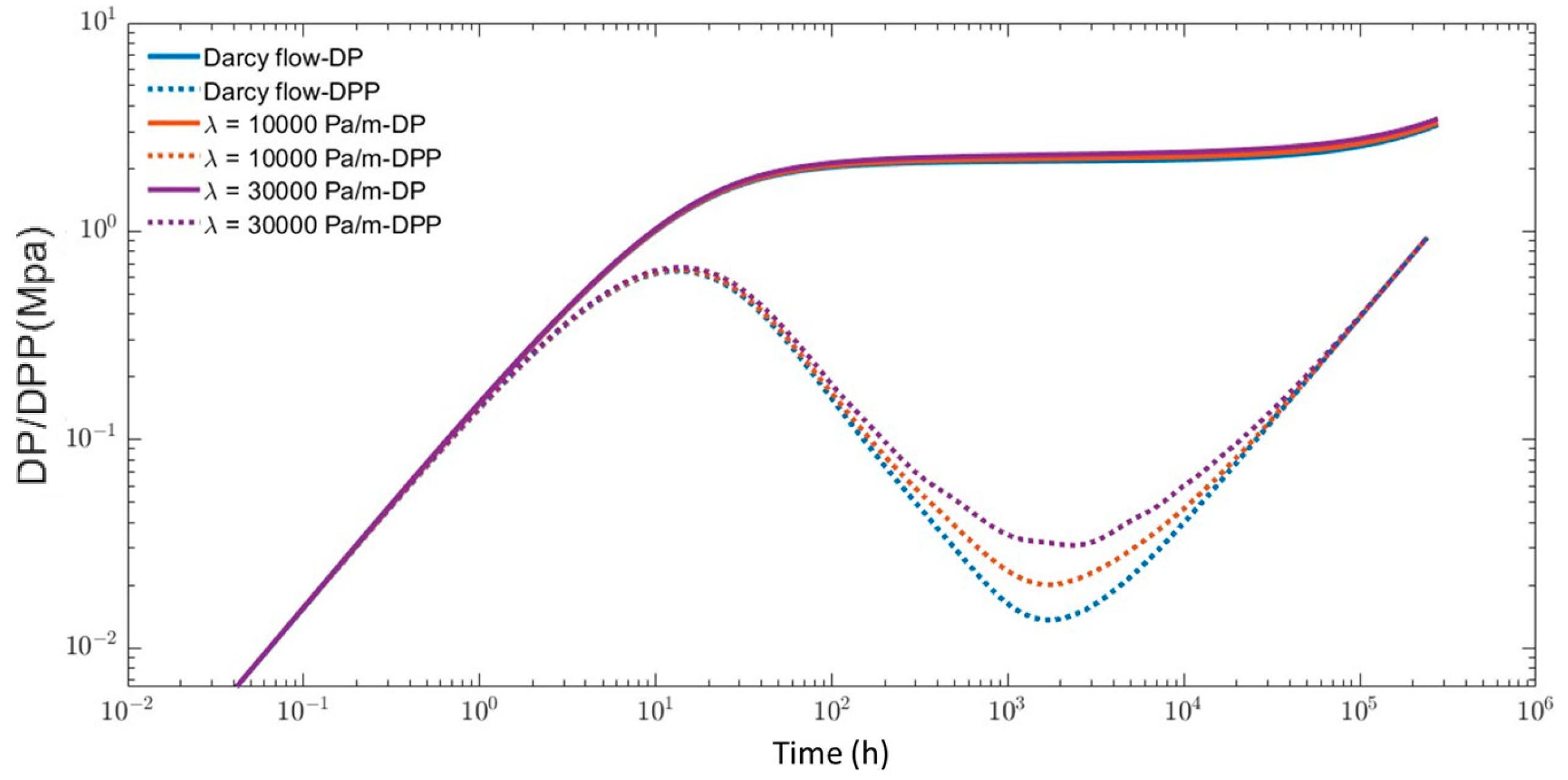
4.2. Effect of Natural Fractures on Pressure Transient Response
4.3. Influence of Nonlinear Flow Mechanisms on Pressure Transient
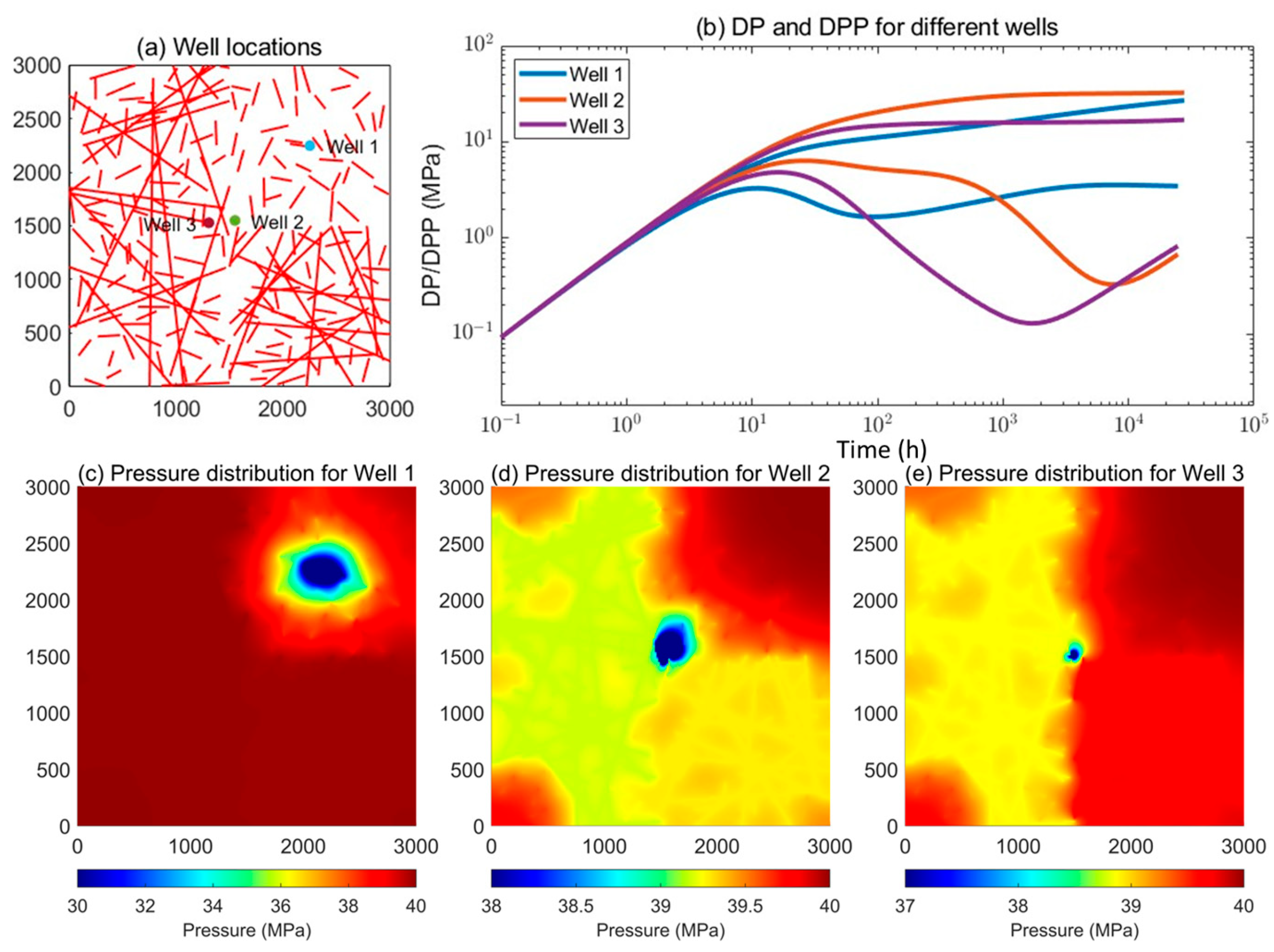
5. Field Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DF | Darcy flow |
| Non-DF | Non-Darcy flow |
| PD | Pressure derivative |
| DP | Pressure difference |
| DPP | Pressure difference derivative |
| FC | Fracture conductivity |
References
- Jia, A.; Wei, Y.; Guo, Z.; Wang, G.; Meng, D.; Huang, S. Development status and prospect of tight sandstone gas in China. Nat. Gas Ind. B 2022, 9, 467–476. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, J.; Yong, Z. Characteristics of Tight Gas Reservoirs in the Xujiahe Formation in the Western Sichuan Depression: A Systematic Review. Energies 2024, 17, 587. [Google Scholar] [CrossRef]
- Wu, Z.; Cui, C.; Wang, Z.; Sui, Y.; Jia, P.; Tang, W. Well Testing Model of Multiple Fractured Horizontal Well with Consideration of Stress-Sensitivity and Variable Conductivity in Tight Gas Reservoirs. Math. Probl. Eng. 2018, 2018, 1693184. [Google Scholar] [CrossRef]
- Zhang, Y.; Zeng, L.; Lyu, W.; Sun, D.; Chen, S.; Guan, C.; Tang, L.; Shi, J.; Zhang, J. Natural fractures in tight gas sandstones: A case study of the Upper Triassic Xujiahe Formation in Xinchang gas field, Western Sichuan Basin, China. Geol. Mag. 2021, 158, 1543–1560. [Google Scholar] [CrossRef]
- Mohammed, I.; Olayiwola, T.O.; Alkathim, M.; Awotunde, A.A.; Alafnan, S.F. A review of pressure transient analysis in reservoirs with natural fractures, vugs and/or caves. Pet. Sci. 2021, 18, 154–172. [Google Scholar] [CrossRef]
- Berre, I.; Doster, F.; Keilegavlen, E. Flow in Fractured Porous Media: A Review of Conceptual Models and Discretization Approaches. Transp. Porous Media 2019, 130, 215–236. [Google Scholar] [CrossRef]
- Kharrat, R.; Ott, H. A Comprehensive Review of Fracture Characterization and Its Impact on Oil Production in Naturally Fractured Reservoirs. Energies 2023, 16, 3437. [Google Scholar] [CrossRef]
- Tarhuni, M.-N.; Sulaiman, W.-R.; Jaafar, M.-Z.; Milad, M.; Alghol, A.-M. A Review of the Dynamic Modeling Approaches for Characterizing Fluid Flow in Naturally Fractured Reservoirs. Energy Eng. 2021, 118, 761–795. [Google Scholar] [CrossRef]
- Jiang, T.; Sun, H.; Xiao, X.; Zhu, S.; Ouyang, W.; Tang, Y. Multi-scale flow mechanism and water control strategy of ultra-deep multi-porosity fractured tight sandstone gas reservoirs. Front. Energy Res. 2022, 10, 977439. [Google Scholar] [CrossRef]
- Sun, H.; Ouyang, W.; Zhu, S.; Wan, Y.; Tang, Y.; Cao, W. A new numerical well test method of multi-scale discrete fractured tight sandstone gas reservoirs and its application in the Kelasu Gas Field of the Tarim Basin. Nat. Gas Ind. B 2023, 10, 103–113. [Google Scholar] [CrossRef]
- Hui, G.; Chen, Z.; Schultz, R.; Chen, S.; Song, Z.; Zhang, Z.; Song, Y.; Wang, H.; Wang, M.; Gu, F. Intricate Unconventional Fracture Networks Provide Fluid Diffusion Pathways to Reactivate Pre-Existing Faults in Unconventional Reservoirs. Energy 2023, 282, 128803. [Google Scholar] [CrossRef]
- Geng, S.; Li, C.; Zhai, S.; Gong, Y.; Jing, M. Modeling the Mechanism of Water Flux in Fractured Gas Reservoirs with Edge Water Aquifers Using an Embedded Discrete Fracture Model. J. Energy Resour. Technol. 2022, 145, 033002. [Google Scholar] [CrossRef]
- Yao, J.; Ding, Y.; Sun, H.; Fan, D.; Wang, M.; Jia, C. Productivity Analysis of Fractured Horizontal Wells in Tight Gas Reservoirs Using a Gas–Water Two-Phase Flow Model with Consideration of a Threshold Pressure Gradient. Energy Fuels 2023, 37, 8190–8198. [Google Scholar] [CrossRef]
- Nie, R.-S.; Fan, X.; Li, M.; Chen, Z.; Deng, Q.; Lu, C.; Zhou, Z.-L.; Jiang, D.-W.; Zhan, J. Modeling transient flow behavior with the high velocity non-Darcy effect in composite naturally fractured-homogeneous gas reservoirs. J. Nat. Gas Sci. Eng. 2021, 96, 104269. [Google Scholar] [CrossRef]
- Zhu, W.; Liu, Y.; Shi, Y.; Zou, G.; Zhang, Q.; Kong, D. Effect of dynamic threshold pressure gradient on production performance in water-bearing tight gas reservoir. Adv. Geo-Energy Res. 2022, 6, 286–295. [Google Scholar] [CrossRef]
- Fu, J.; Su, Y.; Li, L.; Wang, W.; Wang, C.; Li, D. Productivity model with mechanisms of multiple seepage in tight gas reservoir. J. Pet. Sci. Eng. 2022, 209, 109825. [Google Scholar] [CrossRef]
- Geng, S.; Li, C.; Li, Y.; Zhai, S.; Xu, T.; Gong, Y.; Jing, M. Pressure transient analysis for multi-stage fractured horizontal wells considering threshold pressure gradient and stress sensitivity in tight sandstone gas reservoirs. Gas Sci. Eng. 2023, 116, 205030. [Google Scholar] [CrossRef]
- Zhao, L.; Jiang, H.; Wang, H.; Yang, H.; Sun, F.; Li, J. Representation of a new physics-based non-Darcy equation for low-velocity flow in tight reservoirs. J. Pet. Sci. Eng. 2020, 184, 106518. [Google Scholar] [CrossRef]
- Yin, P.; Zhao, C.; Ma, J.; Huang, L. A Unified Equation to Predict the Permeability of Rough Fractures via Lattice Boltzmann Simulation. Water 2019, 11, 1081. [Google Scholar] [CrossRef]
- Geng, S.; Wang, Q.; Zhu, R.; Li, C. Experimental and numerical investigation of Non-Darcy flow in propped hydraulic fractures: Identification and characterization. Gas Sci. Eng. 2024, 121, 205171. [Google Scholar] [CrossRef]
- Geng, S.; He, X.; Zhu, R.; Li, C. A new permeability model for smooth fractures filled with spherical proppants. J. Hydrol. 2023, 626, 130220. [Google Scholar] [CrossRef]
- Liu, X.; Geng, S.; Sun, J.; Li, Y.; Guo, Q.; Zhan, Q. Novel coupled hydromechanical model considering multiple flow mechanisms for simulating underground hydrogen storage in depleted low-permeability gas reservoir. Int. J. Hydrog. Energy 2024, 85, 526–538. [Google Scholar] [CrossRef]
- Najafian Jazi, F.; Ghasemi-Fare, O.; Rockaway, T.D. Natural convection effect on heat transfer in saturated soils under the influence of confined and unconfined subsurface flow. Appl. Therm. Eng. 2024, 237, 121805. [Google Scholar] [CrossRef]
- Lie, K.-A. An Introduction to Reservoir Simulation Using MATLAB/GNU Octave: User Guide for the MATLAB Reservoir Simulation Toolbox (MRST); Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Liu, X.; Geng, S.; Hu, P.; Li, Y.; Zhu, R.; Liu, S.; Ma, Q.; Li, C. Blasingame production decline curve analysis for fractured tight sand gas wells based on embedded discrete fracture model. Gas Sci. Eng. 2024, 121, 205195. [Google Scholar] [CrossRef]
- Luo, H.; Deng, H.; Xiao, H.; Geng, S.; Hou, F.; Luo, G.; Li, Y. A Transient-Pressure-Based Numerical Approach for Interlayer Identification in Sand Reservoirs. Fluid Dyn. Mater. Process. 2024, 20, 641–659. [Google Scholar] [CrossRef]






| Parameter | Value | Unit | |
|---|---|---|---|
| Reservoir | Matrix porosity | 0.1 | decimal |
| Matrix permeability | 0.01 × 10−3 | μm2 | |
| Original formation pressure | 30 | MPa | |
| Water saturation | 0.2 | decimal | |
| Gas saturation | 0.8 | decimal | |
| Fluid | Gas specific gravity | 0.67 | dimensionless |
| Viscosity of water phase | 1 | mPa·s | |
| Gas viscosity | 0.2 | mPa·s | |
| Water phase density | 1000 | kg/m3 | |
| Gas phase density | 200 | kg/m3 | |
| Fracture | Fracture roughness | 15 | dimensionless |
| Fracture opening | 0.002 | m | |
| Well | Bottomhole pressure | 4 | MPa |
| Wellbore radius | 0.1 | m |
| Parameter | Value | Unit |
|---|---|---|
| Wellbore storage factor | 0.31 | m3/MPa |
| Skin factor | 0.18 | dimensionless |
| Number of large-scale fractures | 12 | item |
| Average length of large-scale fractures | 510 | m |
| Large-scale FC | 1.2 × 104 | mD·m |
| Number of small- and medium-sized fractures | 180 | item |
| Average length of small- and medium-sized fractures | 45 | m |
| Conductivity of small- and medium-scale fractures | 2.3 × 102 | mD·m |
| Hydraulic fracture half length | 74 | m |
| Hydraulic FC | 1.4 × 103 | mD·m |
| Darcy FlowF | Non-Darcy Flow | |||
|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | |
| DP | −5.0958 | 0.3932 | 0.8778 | 0.0588 |
| DDP | 0.6126 | 0.0193 | 0.717 | 0.0167 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, X.; Li, F.; Bai, F.; Bai, Y.; Zhou, Y.; Zhu, Z. Evaluation of the Impact of Multi-Scale Flow Mechanisms and Natural Fractures on the Pressure Transient Response in Fractured Tight Gas Reservoirs. Processes 2025, 13, 1163. https://doi.org/10.3390/pr13041163
Hou X, Li F, Bai F, Bai Y, Zhou Y, Zhu Z. Evaluation of the Impact of Multi-Scale Flow Mechanisms and Natural Fractures on the Pressure Transient Response in Fractured Tight Gas Reservoirs. Processes. 2025; 13(4):1163. https://doi.org/10.3390/pr13041163
Chicago/Turabian StyleHou, Xiaoben, Feng Li, Fangfang Bai, Yuanyuan Bai, Yuhui Zhou, and Zhuyi Zhu. 2025. "Evaluation of the Impact of Multi-Scale Flow Mechanisms and Natural Fractures on the Pressure Transient Response in Fractured Tight Gas Reservoirs" Processes 13, no. 4: 1163. https://doi.org/10.3390/pr13041163
APA StyleHou, X., Li, F., Bai, F., Bai, Y., Zhou, Y., & Zhu, Z. (2025). Evaluation of the Impact of Multi-Scale Flow Mechanisms and Natural Fractures on the Pressure Transient Response in Fractured Tight Gas Reservoirs. Processes, 13(4), 1163. https://doi.org/10.3390/pr13041163






