Ultra-Short-Term Load Forecasting for Extreme Scenarios Based on DBSCAN-RSBO-BiGRU-KNN-Attention with Fine-Tuning Strategy
Abstract
1. Introduction
- (1)
- A novel use of DBSCAN for identifying extreme load scenarios is presented, addressing the challenge of insufficient validation data in rare and critical events.
- (2)
- An integrated forecasting framework is introduced, which captures key features and long-term dependencies in the data. The use of RSBO enhances model accuracy and robustness, particularly under extreme conditions.
- (3)
- A fine-tuning approach based on transfer learning is developed to improve the model’s adaptability and generalization performance in extreme scenarios.
2. Methodology
2.1. Data Reconstruction
2.2. Extreme Scenario Extraction
2.3. Load Forecasting Model
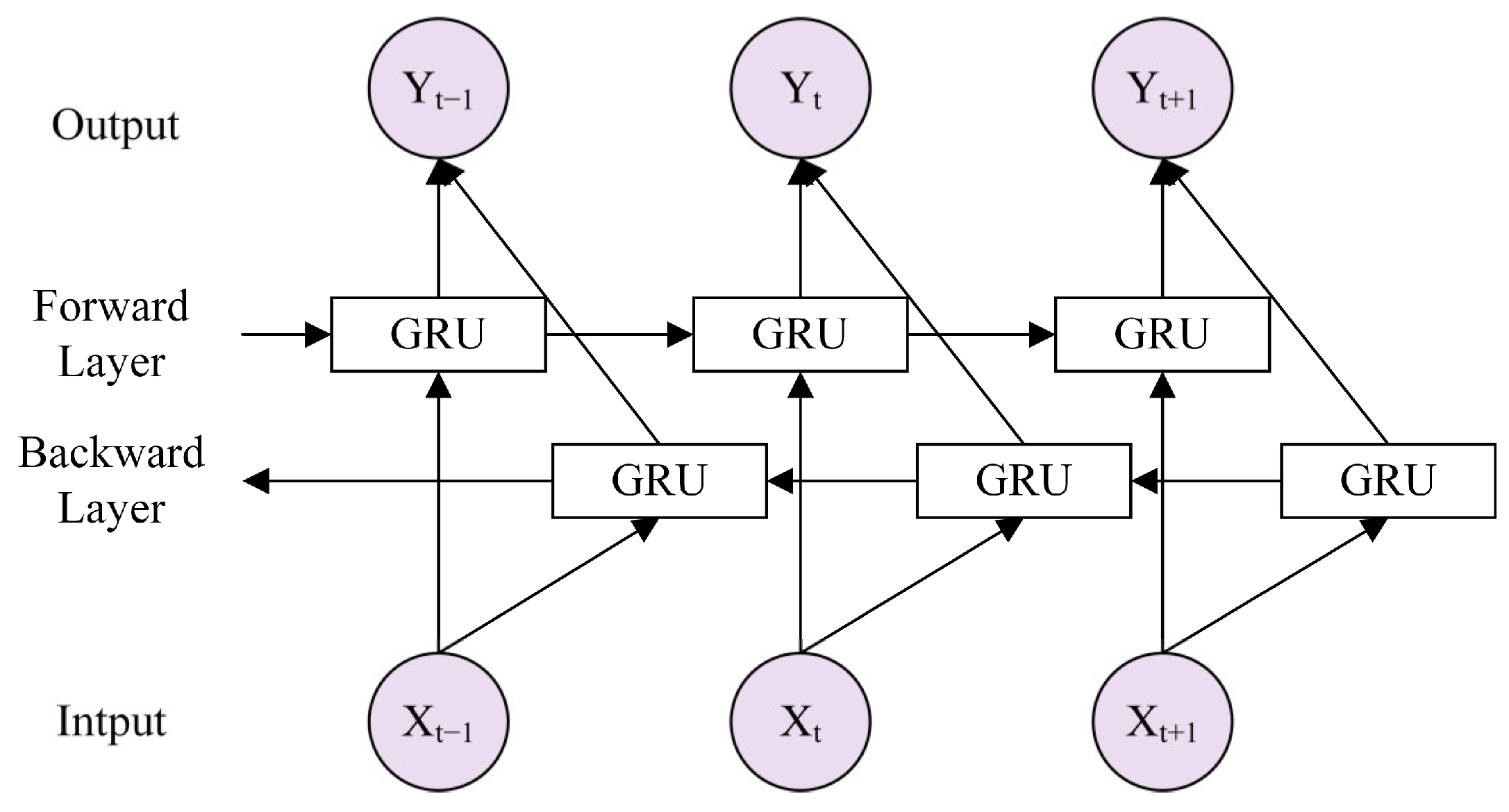
2.3.1. BiGRU-KNN-Attention
2.3.2. RSBO
2.3.3. Fine-Tuning
2.4. Data Acquisition and Models’ Parameters
2.5. Evaluation Metrics
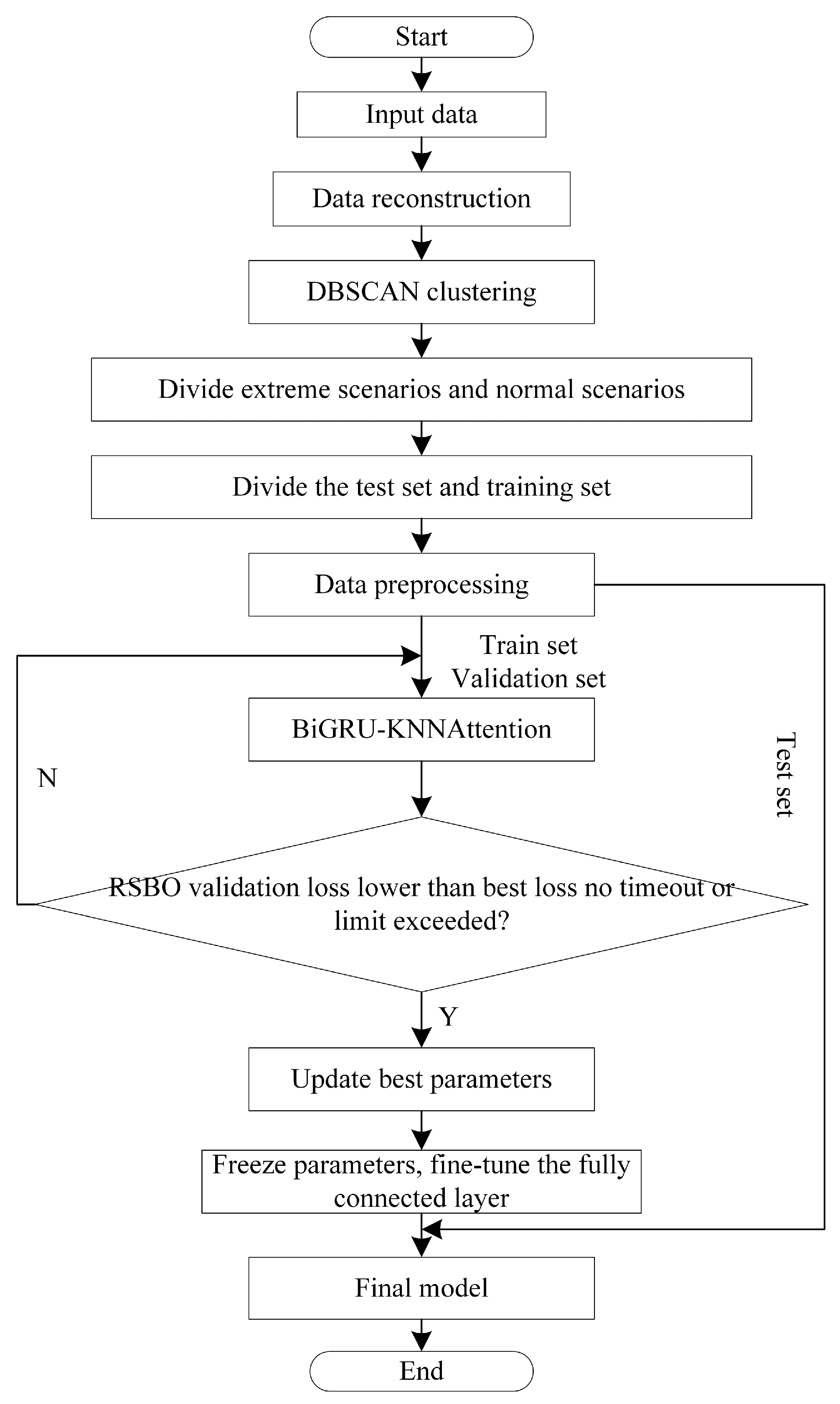
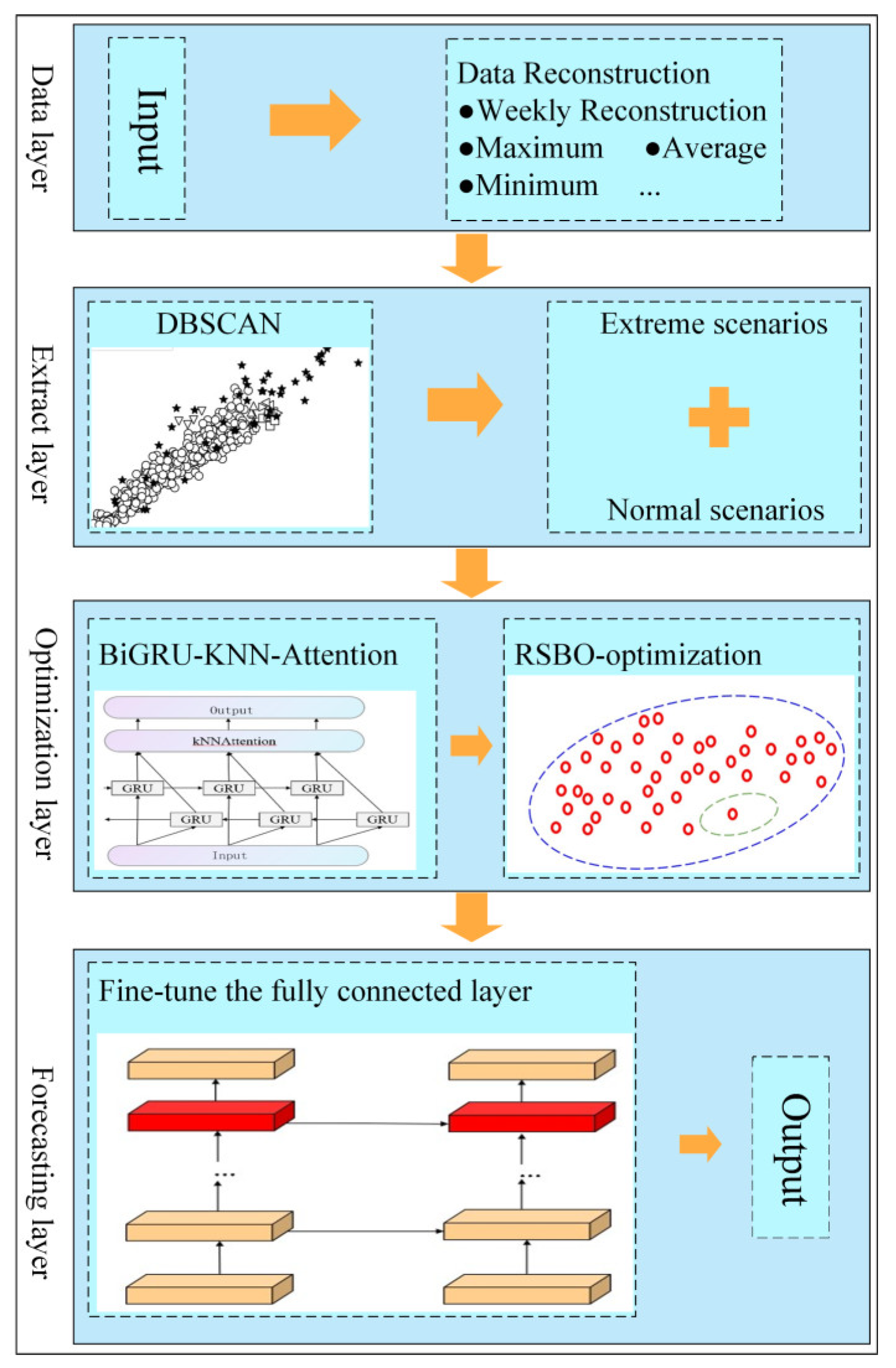
2.6. The Load Forecasting Framework for Extreme Scenarios
- (1)
- The data are reconstructed on a weekly basis, with key features extracted. DBSCAN is then used to identify extreme scenarios from the dataset.
- (2)
- The time series data are processed through the BiGRU layer, which captures temporal dependencies. The features extracted by BiGRU are then sent to the KNN-Attention mechanism, which highlights the most important parts of the sequence.
- (3)
- After the initial training of the BiGRU-KNN-Attention model, RSBO is applied to explore the hyperparameter space and determine the optimal set of initial hyperparameters.
- (4)
- Once the hyperparameters are optimized, the model enters the fine-tuning stage. During this phase, most of the model’s parameters are frozen, and only the final fully connected layer is fine-tuned. The final forecasting results are generated, and the accuracy of the forecasts for extreme scenarios is evaluated using various metrics.
3. Case Study
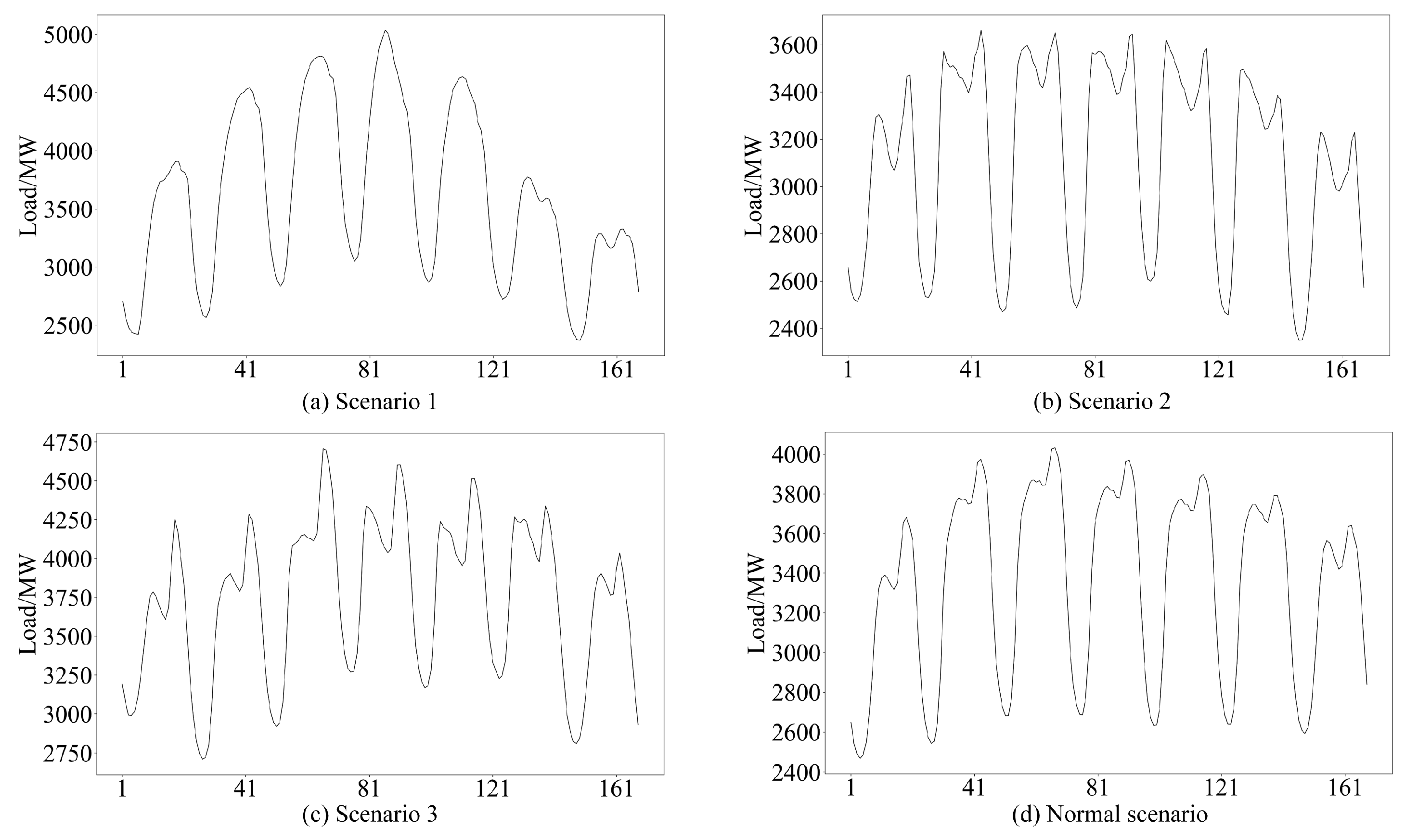
3.1. Scenario Extraction
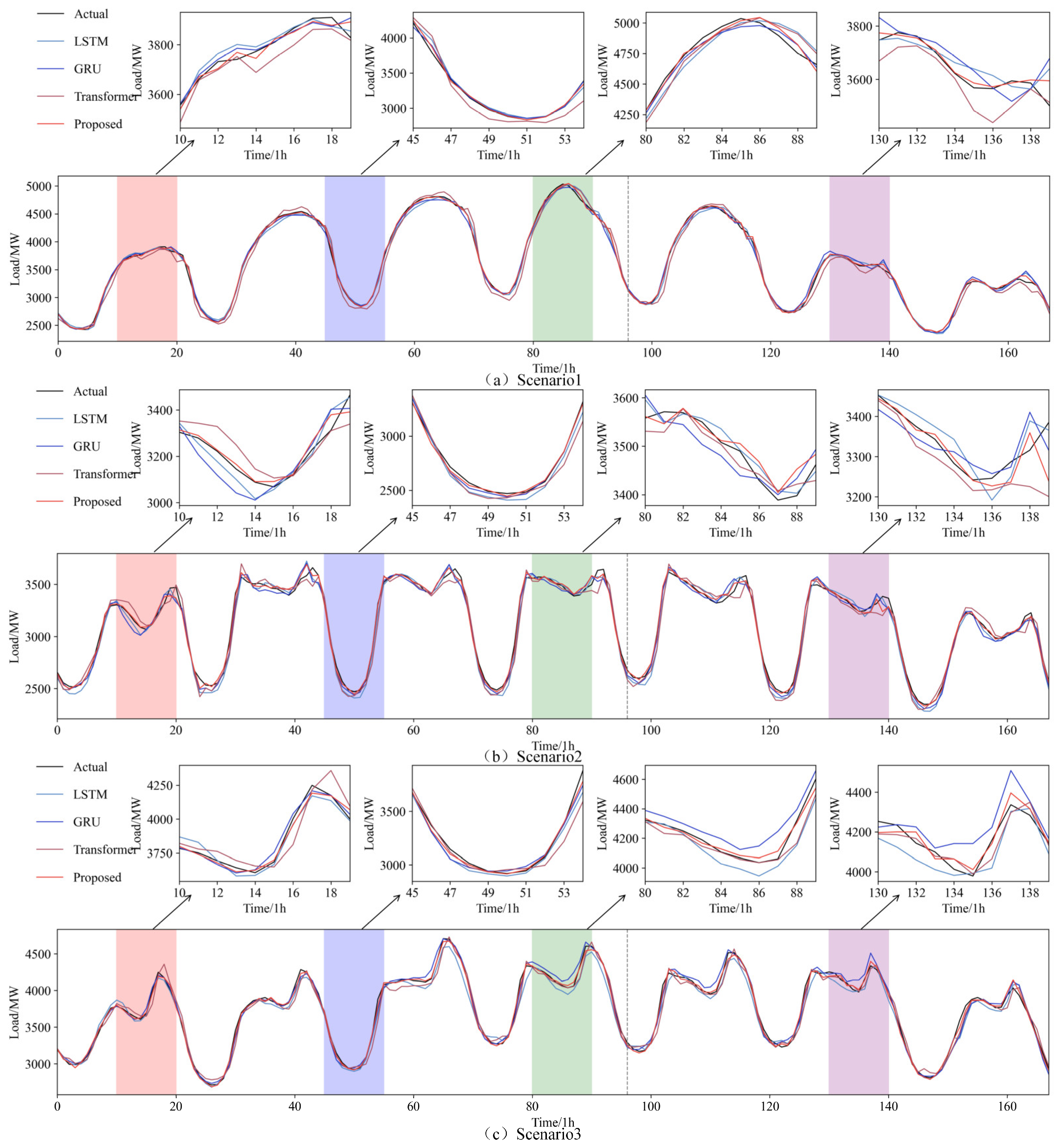
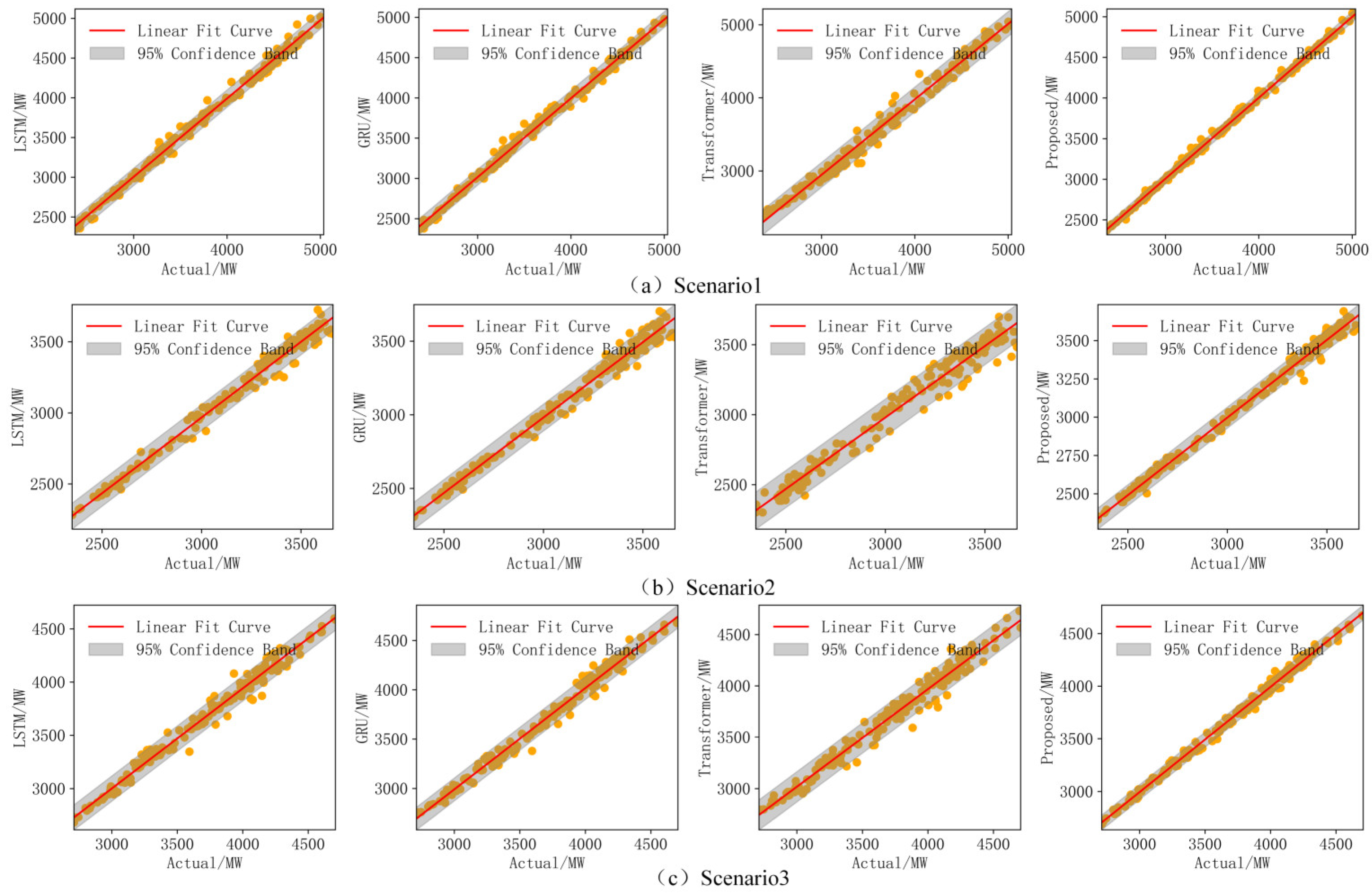
3.2. Comparison Simulation
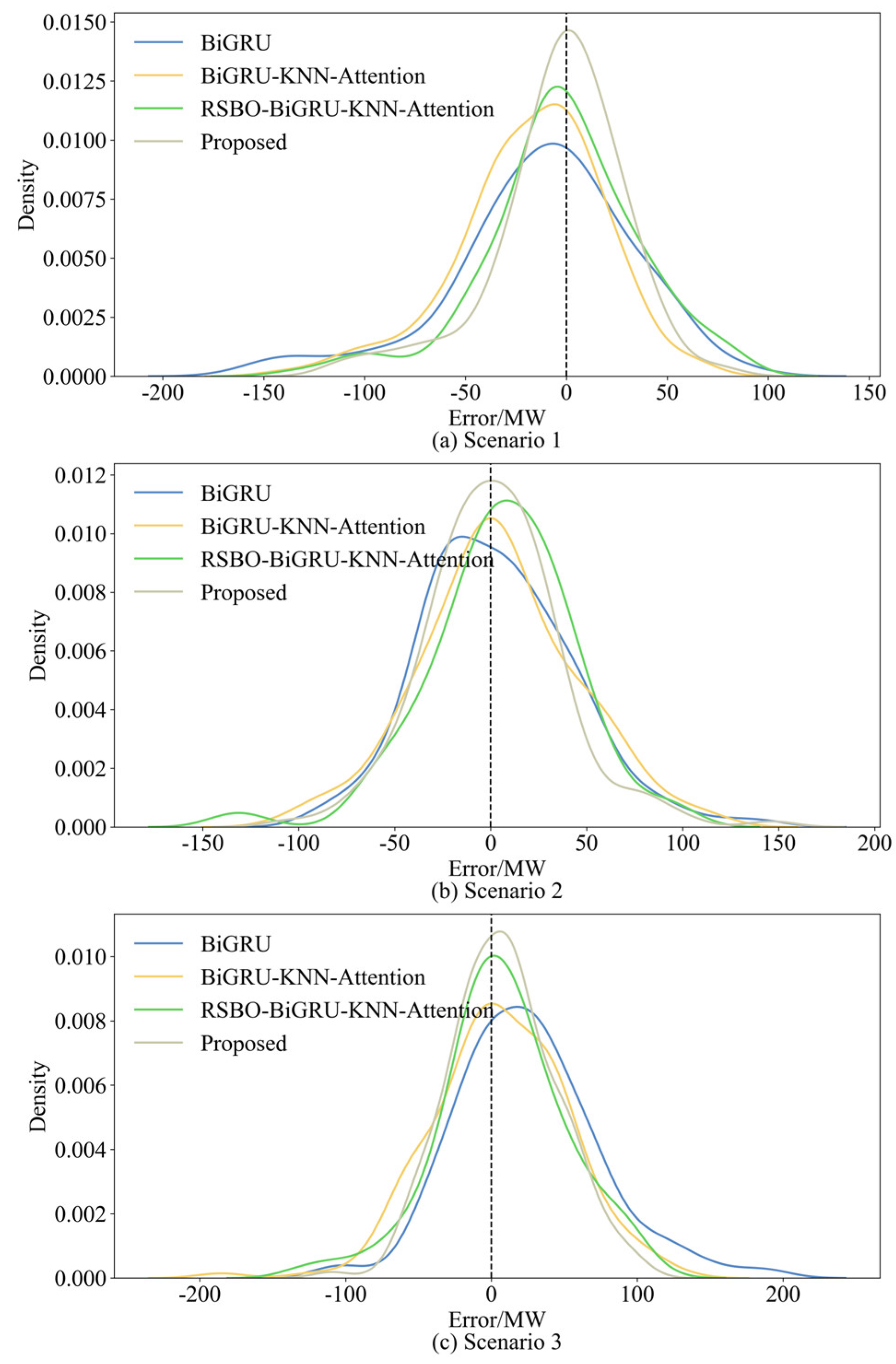
3.3. Ablation Study
3.4. Supplementary Case Study Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Wang, J.; Sun, J.; Sun, R.; Qin, D. Power load forecasting system of iron and steel enterprises based on deep kernel–multiple kernel joint learning. Processes 2025, 13, 584. [Google Scholar] [CrossRef]
- Cui, J.; Kuang, W.; Geng, K.; Bi, A.; Bi, F.; Zheng, X.; Lin, C. Advanced short-term load forecasting with XGBoost-RF feature selection and CNN-GRU. Processes 2024, 12, 2466. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, W.; Sun, Y.; Trivedi, A.; Chung, C.; Srinivasan, D. Wind power forecasting in the presence of data scarcity: A very short-term conditional probabilistic modeling framework. Energy 2024, 291, 130305. [Google Scholar] [CrossRef]
- Zimmermann, M.; Ziel, F. Efficient mid-term forecasting of hourly electricity load using generalized additive models. Appl. Energy 2025, 388, 125444. [Google Scholar] [CrossRef]
- Shah, S.A.H.; Ahmed, U.; Bilal, M.; Khan, A.R.; Razzaq, S.; Aziz, I.; Mahmood, A. Improved electric load forecasting using quantile long short-term memory network with dual attention mechanism. Energy Rep. 2025, 13, 2343–2353. [Google Scholar] [CrossRef]
- Yeganefar, A.; Amin-Naseri, M.R.; Sheikh-El-Eslami, M.K. Improvement of representative days selection in power system planning by incorporating the extreme days of the net load to take account of the variability and intermittency of renewable resources. Appl. Energy 2020, 272, 115224. [Google Scholar] [CrossRef]
- Zhu, X.; Yu, Z.; Liu, X. Security constrained unit commitment with extreme wind scenarios. J. Mod. Power Syst. Clean Energy 2020, 8, 464–472. [Google Scholar] [CrossRef]
- Xiaoxuan, X.; Dunwei, G.; Xiaoyan, S.; Yong, Z.; Rui, L. Short-term load forecasting of integrated energy system based on reconstruction error and extreme patterns recognition. Proc. CSEE 2022, 44, 3476–3488. [Google Scholar]
- Son, J.; Cha, J.; Kim, H.; Wi, Y.-M. Day-ahead short-term load forecasting for holidays based on modification of similar days’ load profiles. IEEE Access 2022, 10, 17864–17880. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, S.; Sun, Y.; Wu, Y.; Xie, D. Ultra-short-term forecasting of wind power based on dual derivation of hybrid features and error correction. Autom. Electr. Power Syst. 2024, 48, 68–76. [Google Scholar]
- Tang, Y.; Lin, D.; Ni, C.; Zhao, B. XGBoost based bi-layer collaborative real-time calibration for ultra-short-term photovoltaic forecasting. Autom. Electr. Power Syst. 2021, 45, 18–27. [Google Scholar]
- Wang, Q.; Wang, Y.; Zhang, K.; Liu, Y.; Qiang, W.; Han Wen, Q. Artificial intelligent power forecasting for wind farm based on multi-source data fusion. Processes 2023, 11, 1429. [Google Scholar] [CrossRef]
- Ferreira, A.B.A.; Leite, J.B.; Salvadeo, D.H.P. Power substation load forecasting using interpretable transformer-based temporal fusion neural networks. Electr. Power Syst. Res. 2025, 238, 111169. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Li, Y.; Feng, C.; Chen, P. Interval forecasting method of aggregate output for multiple wind farms using LSTM networks and time-varying regular vine copulas. Processes 2023, 11, 1530. [Google Scholar] [CrossRef]
- Niu, D.; Yu, M.; Sun, L.; Gao, T.; Wang, K. Short-term multi-energy load forecasting for integrated energy systems based on CNN-BiGRU optimized by attention mechanism. Appl. Energy 2022, 313, 118801. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X.; Wang, F.; Lin, M.; Chang, S.; Li, H.; Jin, R. Kvt: k-nn attention for boosting vision transformers. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 285–302. [Google Scholar]
- Upadhyay, R.; Phlypo, R.; Saini, R.; Liwicki, M. Sharing to learn and learning to share; fitting together meta, multi-task, and transfer learning: A meta review. IEEE Access 2024, 12, 148553–148576. [Google Scholar] [CrossRef]
- Cheng, K.; Peng, X.; Xu, Q.; Wang, B.; Liu, C.; Che, J. Short-term wind power forecasting based on feature selection and multi-level deep transfer learning. High Volt. Eng. 2022, 48, 497–503. [Google Scholar]
- Yin, H.; Ou, Z.; Fu, J.; Cai, Y.; Chen, S.; Meng, A. A novel transfer learning approach for wind power forecasting based on a serio-parallel deep learning architecture. Energy 2021, 234, 121271. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, F.; Gou, F.; Cao, W. Study on short-term electricity load forecasting based on the modified simplex approach sparrow search algorithm mixed with a bidirectional long- and short-term memory network. Processes 2024, 12, 1796. [Google Scholar] [CrossRef]
- Kottath, R.; Singh, P. Influencer buddy optimization: Algorithm and its application to electricity load and price forecasting problem. Energy 2023, 263, 125641. [Google Scholar] [CrossRef]
- Han, X.; Gao, Y.; Chen, Z.; Chen, Q.; Dong, X.; Sun, Y. An extreme scenario reduction algorithm for multi-time scale net-load. In Proceedings of the 2023 IEEE 7th Conference on Energy Internet and Energy System Integration (EI2), Hangzhou, China, 15–18 December 2023; pp. 225–230. [Google Scholar]
- Granell, R.; Axon, C.J.; Wallom, D.C.H. Impacts of raw data temporal resolution using selected clustering methods on residential electricity load profiles. IEEE Trans. Power Syst. 2014, 30, 3217–3224. [Google Scholar] [CrossRef]
- Hu, M.; Ge, D.; Telford, R.; Stephen, B.; Wallom, D.C.H. Classification and characterization of intra-day load curves of PV and non-PV households using interpretable feature extraction and feature-based clustering. Sustain. Cities Soc. 2021, 75, 103380. [Google Scholar] [CrossRef]
- Guo, H.; Chen, L.; Zhang, Q.; Huang, H.; Ma, Q.; Wang, J. Research and response to extreme scenarios in new power system: A review from perspective of electricity and power balance. Power Syst. Technol. 2024, 48, 3975–3991. [Google Scholar]

| Model | Parameter | Number |
|---|---|---|
| LSTM | Hidden layer dimensions | 128 |
| Batch size | 32 | |
| Learning rate | 0.001 | |
| GRU | Hidden layer dimensions | 128 |
| Batch size | 32 | |
| Learning rate | 0.001 | |
| Transformer | Embedding dimension | 64 |
| Number of heads | 4 | |
| Batch size | 32 | |
| Learning rate | 0.001 | |
| Proposed | Hidden layer dimensions | 128 |
| Topk | 5 | |
| Batch size | 32 | |
| Learning rate | 0.001 |
| Scenario | Model | Accuracy | RMSE | MAE |
|---|---|---|---|---|
| Scenario 1 | LSTM | 0.994 | 56.519 | 42.133 |
| GRU | 0.995 | 51.767 | 38.409 | |
| Transformer | 0.983 | 95.670 | 74.969 | |
| Proposed | 0.998 | 32.547 | 23.260 | |
| Scenario 2 | LSTM | 0.978 | 58.577 | 47.577 |
| GRU | 0.984 | 49.887 | 39.863 | |
| Transformer | 0.968 | 70.529 | 53.835 | |
| Proposed | 0.992 | 35.117 | 26.460 | |
| Scenario 3 | LSTM | 0.974 | 80.605 | 61.650 |
| GRU | 0.985 | 61.092 | 45.540 | |
| Transformer | 0.973 | 81.477 | 60.390 | |
| Proposed | 0.995 | 36.871 | 29.175 |
| Scenario | Model | Accuracy | RMSE | MAE |
|---|---|---|---|---|
| Scenario 1 | 1 | 0.996 | 46.531 | 34.234 |
| 2 | 0.996 | 43.171 | 30.827 | |
| 3 | 0.997 | 40.862 | 30.180 | |
| 4 | 0.997 | 38.250 | 28.235 | |
| 5 | 0.998 | 32.547 | 23.260 | |
| Scenario 2 | 1 | 0.989 | 40.963 | 31.445 |
| 2 | 0.988 | 43.014 | 31.986 | |
| 3 | 0.990 | 39.257 | 30.827 | |
| 4 | 0.990 | 38.509 | 29.215 | |
| 5 | 0.992 | 35.117 | 26.460 | |
| Scenario 3 | 1 | 0.988 | 54.668 | 41.075 |
| 2 | 0.989 | 49.867 | 37.190 | |
| 3 | 0.991 | 46.348 | 36.077 | |
| 4 | 0.992 | 44.177 | 33.465 | |
| 5 | 0.995 | 36.871 | 29.175 |
| Scenario | Model | Accuracy | RMSE | MAE |
|---|---|---|---|---|
| Scenario 1 | LSTM | 0.995 | 126.317 | 102.913 |
| GRU | 0.998 | 86.614 | 69.757 | |
| Transformer | 0.993 | 144.996 | 119.019 | |
| Proposed | 0.998 | 72.469 | 56.915 | |
| Scenario 2 | LSTM | 0.993 | 151.609 | 114.417 |
| GRU | 0.996 | 108.187 | 83.884 | |
| Transformer | 0.995 | 132.964 | 104.810 | |
| Proposed | 0.997 | 94.547 | 70.428 | |
| Scenario 3 | LSTM | 0.986 | 113.758 | 90.610 |
| GRU | 0.989 | 101.175 | 78.109 | |
| Transformer | 0.980 | 136.947 | 104.998 | |
| Proposed | 0.993 | 80.547 | 59.388 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liang, J.; Li, J.; Sun, Y.; Tao, H.; Wang, Q.; Yu, T. Ultra-Short-Term Load Forecasting for Extreme Scenarios Based on DBSCAN-RSBO-BiGRU-KNN-Attention with Fine-Tuning Strategy. Processes 2025, 13, 1161. https://doi.org/10.3390/pr13041161
Wang L, Liang J, Li J, Sun Y, Tao H, Wang Q, Yu T. Ultra-Short-Term Load Forecasting for Extreme Scenarios Based on DBSCAN-RSBO-BiGRU-KNN-Attention with Fine-Tuning Strategy. Processes. 2025; 13(4):1161. https://doi.org/10.3390/pr13041161
Chicago/Turabian StyleWang, Leibao, Jifeng Liang, Jiawen Li, Yonghui Sun, Hongzhu Tao, Qiang Wang, and Tengkai Yu. 2025. "Ultra-Short-Term Load Forecasting for Extreme Scenarios Based on DBSCAN-RSBO-BiGRU-KNN-Attention with Fine-Tuning Strategy" Processes 13, no. 4: 1161. https://doi.org/10.3390/pr13041161
APA StyleWang, L., Liang, J., Li, J., Sun, Y., Tao, H., Wang, Q., & Yu, T. (2025). Ultra-Short-Term Load Forecasting for Extreme Scenarios Based on DBSCAN-RSBO-BiGRU-KNN-Attention with Fine-Tuning Strategy. Processes, 13(4), 1161. https://doi.org/10.3390/pr13041161







