Analysis of the Influence of Alternating Stress in the Multi-Cycle Injection Production Process
Abstract
1. Introduction
- Stress sensitivity was not taken into account;
- Only permeability stress sensitivity was considered;
- Both permeability and fracture conductivity stress sensitivity were considered. Based on the simulation results, the appropriate proppant was selected. When the gas production rate declined, the secondary cushion gas process was simulated, and the gas injection pressure was increased to improve the gas production rate.
2. Stress Sensitivity Characteristics of Fracture Conductivity and Reservoir Permeability Under Multi-Cycle Injection–Production Conditions
2.1. Testing of Fracture Conductivity Under Multi-Cycle Injection and Production Alternating Stress
2.2. Reservoir Permeability Evaluation Under Multi-Cycle Injection–Production Conditions
3. Mathematical Models
4. Establishment of the Capacity Prediction Model
5. Influence of Stress Sensitivity on the Effect of Air Compression Energy Storage Injection and Production
5.1. Analysis of Injection and Production Effect of Ceramsite Proppant Considering Stress Sensitivity
5.2. Analysis of the Injection and Production Effect of Quartz Sand Considering Stress Sensitivity
6. Analysis of Injection and Production Parameter Adjustments
6.1. Analysis of the Working System for the Secondary Gas Cushion of the Ceramsite Proppant
6.2. Analysis of the Working System for the Secondary Gas Cushion of Quartz Sand
7. Conclusions
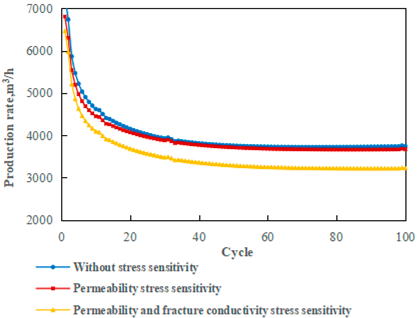
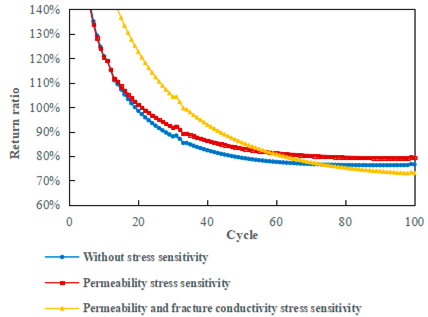
- The multi-cycle stress sensitivity effect on reservoir permeability and fracture conductivity can result in a suboptimal injection–production performance, with the impact on permeability being relatively minor.
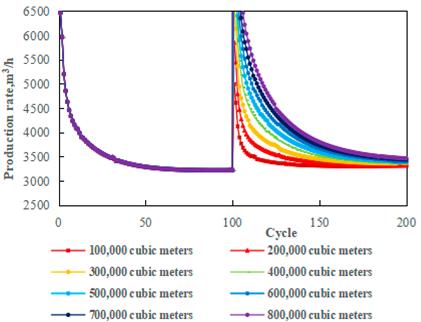
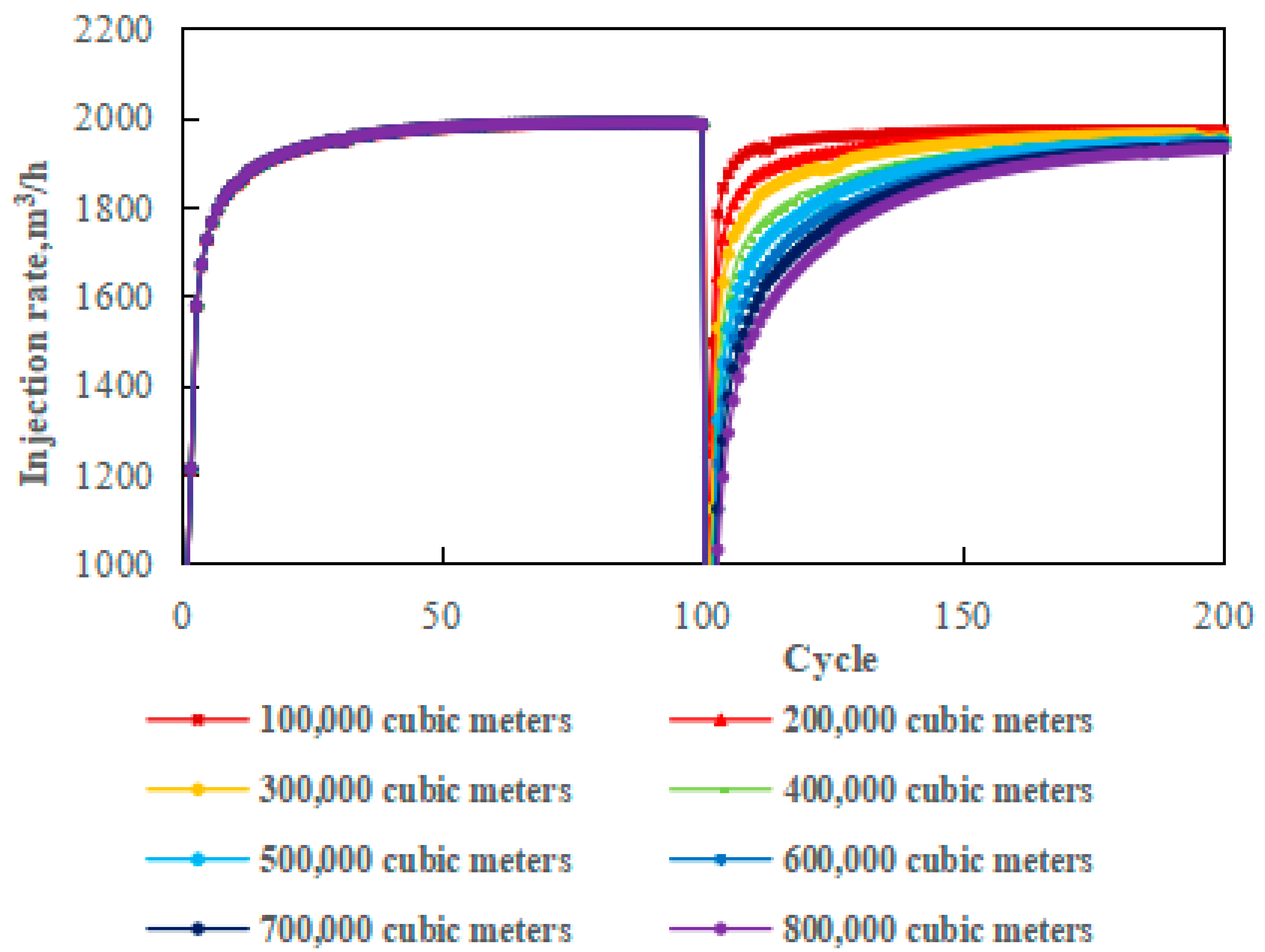
- Under alternating stress conditions, the strength of the rock and the compressive strength of the proppant will decline, which will lead to a significant reduction in reservoir permeability and fracture conductivity, and consequently, the gas production rate tends to decrease. To maintain a high gas production rate, a secondary gas cushion is required. Specifically, for a single well using the 30–50 mesh ceramsite proppant, the secondary gas cushion should exceed 500,000 cubic meters, while for a single well using the 20–40 mesh quartz sand, it should exceed 800,000 cubic meters to ensure effective injection and production.
- Compared to the quartz sand, the ceramsite proppant is less affected by the alternating stress, but the fracture conductivity can be maintained at a high level. Under the same secondary cushion gas, the gas production rate of the ceramsite proppant is significantly higher than the quartz sand proppant. Therefore, the 30–50 mesh ceramsite is recommended as the preferred choice.
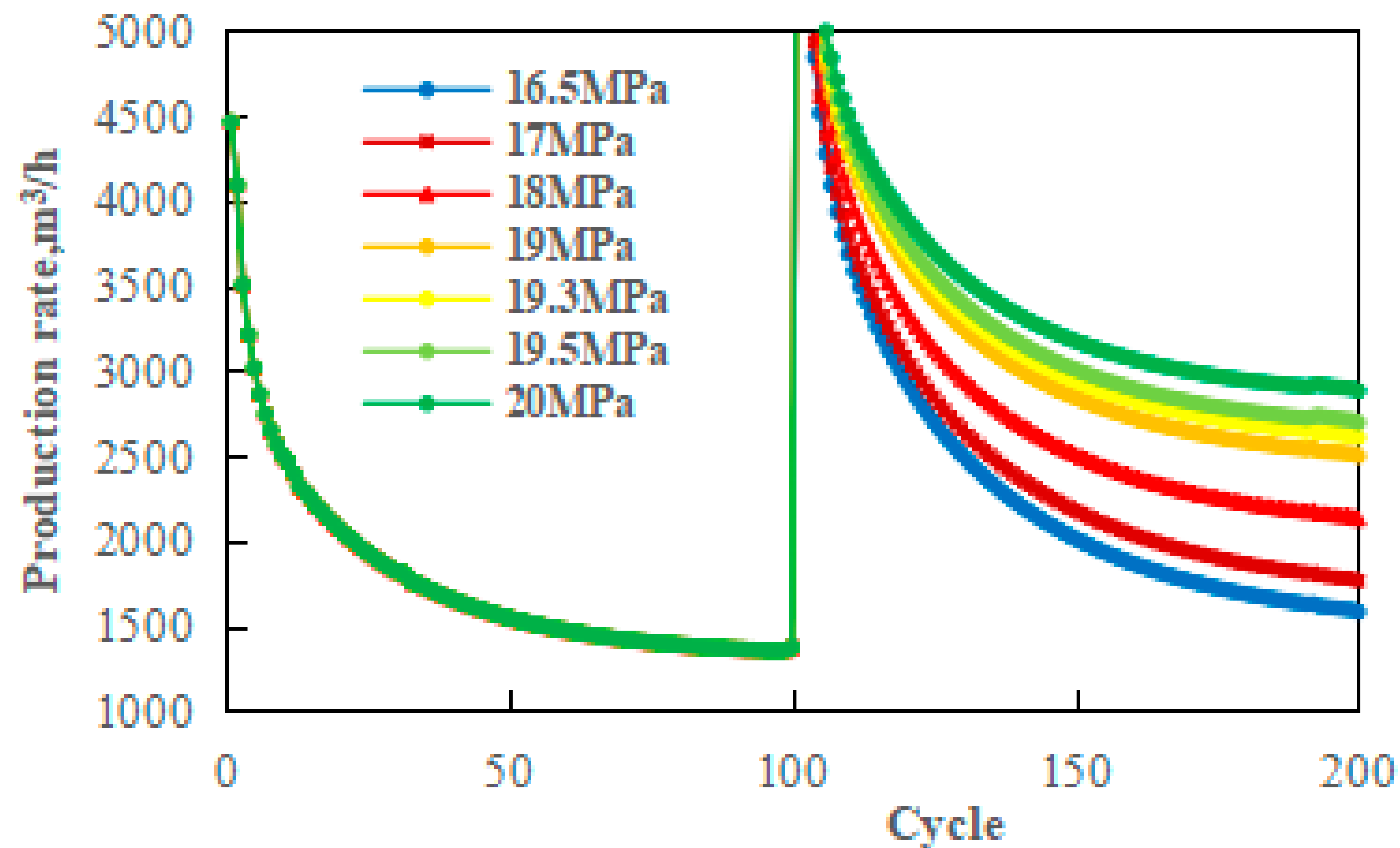
- The gas production rate will continue to decline in the later stage of injection and production. To maintain a long-term gas production rate, it is necessary to increase the gas injection pressure. For the ceramsite proppant, the gas injection pressure should be adjusted to over 17 MPa, whereas for quartz sand, it should be increased to over 19.3 MPa.
- This paper can provide certain guidance for research on the periodic stress sensitivity and has reference value for the adjustment of the injection–production system of air compression energy storage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Zhang, Y.; Mo, K. Development and Outlook of New Technologies for Energy Storage. China Heavy Equip. 2022, 4, 27–32. [Google Scholar]
- Yu, L.Z.; Hong, L.; Hui, L.Z.; Tao, H.J. The development status and application prospect of compressed air energy storage. Resour. Econ. Environ. Prot. 2023, 8, 5–8. [Google Scholar] [CrossRef]
- Shao, J.; You, L.; Kang, Y.; Gao, X.; Chen, M.; Meng, S.; Zhang, N. Experimental study on stress sensitivity of underground gas storage. J. Pet. Sci. Eng. 2020, 195, 107577. [Google Scholar] [CrossRef]
- Cao, N.; Lei, G. Stress sensitivity of tight reservoirs during pressure loading and unloading process. Pet. Explor. Dev. 2019, 46, 132–138. [Google Scholar] [CrossRef]
- Wang, Z.W.; Zhang, N.S.; Lu, H.B. Formation Damage Mechanisms of Low-permeability Gas Reservoir and Its Preventive Measures. Nat. Gas Ind. 2003, 23, 28–31. [Google Scholar]
- Lei, Q.; Xiong, W.; Yuan, J.; Cui, Y.; Wu, Y.S. Analysis of stress sensitivity and its influence on oil production from tight reservoirs. In Proceedings of the SPE Eastern Regional Meeting, Lexington, KY, USA, 17 October 2007. [Google Scholar]
- Tan, X.H.; Liu, C.Y.; Li, X.P.; Wang, H.Q.; Deng, H. A stress sensitivity model for the permeability of porous media based on bi-dispersed fractal theory. Int. J. Mod. Phys. C 2018, 29, 1850019. [Google Scholar] [CrossRef]
- Zhan, S.; Qi, L.; Zhang, Y.; Li, L.; Zhao, Z. Changes in porosity and permeability with net overburden pressure in tight sandstone reservoirs. Complex Hydrocarb. Reserv. 2015, 8, 52–56. [Google Scholar]
- Yang, B.; Hou, D.; Long, G.; Ren, C. Research and application of stress sensitive experiment on low permeable reservior. Reserv. Eval. Dev. 2012, 2, 41–45. [Google Scholar] [CrossRef]
- Yang, S.; Yang, Q.; Xiao, X.; Wang, X. Stress Sensitivity of Rock and Its Influence on Productivity for Gas Reservoirs with Abnormal High Pressure. Nat. Gas Ind. 2005, 25, 94–95. [Google Scholar]
- Ouyang, W.; Sun, H.; Zhang, M. Well test analysis for multistage fractured horizontal wells in tight gas reservoir considering stress sensitivity. Acta Pet. Sin. 2018, 39, 570–577. [Google Scholar]
- Weiming, W.E.; Shaopeng, Z.H.; Mao, L.I. Stress sensitivity features and productivity equations of offshore abnormal high-pressure gas reservoirs: A case study from the Yinggehai Basin. Nat. Gas Ind. 2014, 34, 59–63. [Google Scholar]
- Yuan, Z.; Hua, J.; Yuan, W.K.; Zhang, B.-B. Experimental study on long term conductivity decline of hydraulic fracturing fracture. Unconv. Oil Gas 2022, 9, 78–82. [Google Scholar]
- Yang, Z.; Chen, M.; Xu, Y.; Meng, C.; Xu, Z. An experimental study of long-term flow conductivity of volcanic rock core plate. Nat. Gas Ind. 2010, 30, 42–44. [Google Scholar]
- Luo, R.-L.; Lei, Q.; Fan, J.-W.; Liao, H.M.; Wang, Z. The influence of stress sensitivity on production of hydraulically-fractured tight gas wells. J. Chongqing Univ. (Nat. Sci. Ed.) 2011, 34, 95–99. [Google Scholar]
- Zhu, H.; Shen, J.; Zhou, H. Numerical simulation on propped fracture conductivity. Acta Pet. Sin. 2018, 39, 1410–1420. [Google Scholar]
- Daoyong, Z.H.; Ping, G.; Jianfen, D. Laboratory researches on stress sensibility of underground gas storage. Nat. Gas Ind. 2006, 26, 122–124. [Google Scholar]
- Wang, B.-H.; Yan, X.-Z.; Liu, X.-D.; Yang, X.-J. Study on the Migration Law of the Underground Gas Storage Reservoir in Aquifer in Fluid-solid Coupling. Sci. Technol. Eng. 2014, 14, 29–33. [Google Scholar]
- Shunli, H.; Chengquan, M.; Jiashen, Z. Study on Percolation Characteristics of Reservoirs’ Injection-Production in Dazhangtuo Underground Gas Storage. Nat. Gas Ind. 2006, 26, 90–92. [Google Scholar]
- Liu, C.J. Study on Injection-Production Seepage Mechanism of Wen 96 Underground Gas Storage. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2014. [Google Scholar]
- Kong, Q.; Wang, H.L.; Xu, W.Y. Experimental study on permeability and porosity evolution of sandstone under cyclic loading and unloading. Chin. J. Geotech. Eng. 2015, 37, 1893–1900. [Google Scholar]
- Li, J.; Zhao, G.; Qi, Z.; Yin, B.; Xu, X.; Fang, F.; Yang, S.; Qi, G. Stress sensitivity of formation during multi-cycle gas injection and production in an underground gas storage rebuilt from gas reservoirs. Pet. Explor. Dev. 2021, 48, 835–842. [Google Scholar] [CrossRef]
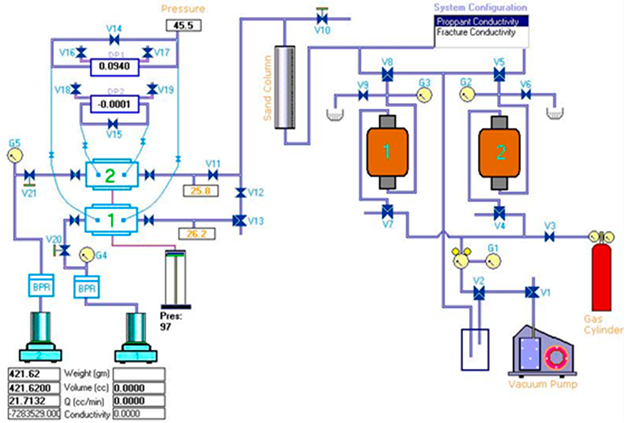

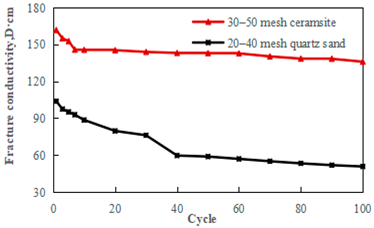

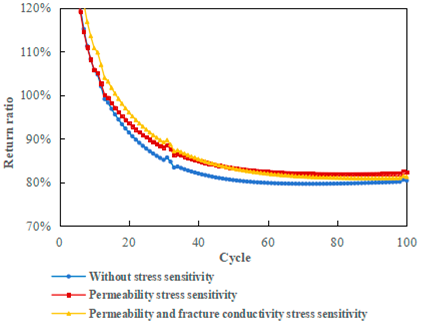





| Core Number | Initial Value of Permeability (mD) | Final Value of Permeability (mD) |
| Core1 | 0.00077 | 0.00070 |
| Core2 | 0.00061 | 0.00057 |
| Core3 | 0.00064 | 0.00034 |
| Parameter | Value |
|---|---|
| Top depth of reservoir (m) | 1317 |
| Porosity (%) | 0.07 |
| Formation permeability (mD) | 0.0067 |
| Original formation pressure (MPa) | 11 |
| Stress Sensitivity Is Not Considered | Permeability Stress Sensitivity | Permeability and Fracture Conductivity Stress Sensitivity | |
|---|---|---|---|
| Accumulated gas production of 9 wells/104m3 | 1437.56 | 1407.89 | 1259.15 |
| Accumulated gas injection of 9 wells/104m3 | 1645.22 | 1573.90 | 1394.10 |
| Cushion gas/104m3 | 1000 | 1000 | 1000 |
| Bottom hole pressure after gas cushion/MPa | 18.77 | 18.77 | 18.77 |
| Final gas injection rate/m3/h | 2330.83 | 2231.32 | 1984.89 |
| Final gas production rate/(m3/h) | 3746.36 | 3671.32 | 3224.12 |
| Return ratio | 80.36% | 82.26% | 81.21% |
| Pressure spread range/km2 | 0.422 | 0.401 | 0.394 |
| Stress Sensitivity Is Not Considered | Permeability Stress Sensitivity | Permeability and Fracture Conductivity Stress Sensitivity | |
|---|---|---|---|
| Accumulated gas production of 9 wells/104m3 | 1054.55 | 1050.38 | 631.32 |
| Accumulated gas injection of 9 wells/104m3 | 1180.46 | 1139.88 | 629.88 |
| Cushion gas/104m3 | 1000 | 1000 | 1000 |
| Bottom hole pressure after gas cushion/MPa | 20.29 | 20.29 | 20.29 |
| Final gas injection rate/(m3/h) | 1692.49 | 1635.38 | 923.44 |
| Final gas production rate/(m3/h) | 2592.09 | 2594.46 | 1348.65 |
| Return ratio | 76.57% | 79.32% | 73.03% |
| Pressure spread range/km2 | 0.400 | 0.383 | 0.360 |
| Secondary gas cushion volume/104m3 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| Accumulated gas production of 9 wells/104m3 | 2477.35 | 2523.81 | 2568.47 | 2613.32 | 2656.52 | 2699.99 | 2741.80 | 2783.97 |
| Accumulated gas injection of 9 wells/104m3 | 1404.03 | 1383.96 | 1369.14 | 1347.47 | 1330.43 | 1310.21 | 1295.74 | 1279.40 |
| Bottom hole pressure after gas cushion/MPa | 18.58 | 19.10 | 19.50 | 19.85 | 20.17 | 20.48 | 20.76 | 21.04 |
| Final gas injection rate/m3/h | 1970.21 | 1963.61 | 1955.30 | 1952.17 | 1947.41 | 1943.08 | 1934.07 | 1928.22 |
| Final gas production rate/m3/h | 3309.48 | 3328.57 | 3368.75 | 3376.45 | 3399.03 | 3405.15 | 3439.09 | 3461.99 |
| Return ratio | 84.00% | 84.79% | 86.18% | 86.35% | 87.32% | 87.58% | 88.80% | 89.64% |
| Pressure spread range/km2 | 0.536 | 0.551 | 0.564 | 0.576 | 0.589 | 0.602 | 0.616 | 0.628 |
| Secondary gas cushion volume/104m3 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Accumulated gas production of 9 wells/104m3 | 1256.98 | 1303.15 | 1348.08 | 1392.43 | 1435.99 | 1478.93 | 1521.16 | 1562.72 |
| Accumulated gas injection of 9 wells/104m3 | 628.49 | 616.41 | 604.92 | 593.68 | 582.75 | 572.14 | 561.77 | 551.81 |
| Bottom hole pressure after gas cushion/MPa | 24.64 | 24.92 | 25.26 | 25.57 | 25.87 | 26.15 | 26.49 | 26.68 |
| Final gas injection rate/(m3/h) | 911.91 | 907.38 | 902.68 | 898.07 | 893.44 | 889.18 | 884.58 | 880.95 |
| Final gas production rate/(m3/h) | 1430.77 | 1460.77 | 1491.97 | 1523.17 | 1554.68 | 1577.87 | 1609.65 | 1660.00 |
| Return ratio | 78.45% | 80.49% | 82.64% | 84.80% | 87.01% | 88.73% | 90.98% | 94.22% |
| Pressure spread range/km2 | 0.503 | 0.524 | 0.541 | 0.559 | 0.575 | 0.591 | 0.607 | 0.622 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhao, E.; Ma, B.; Liu, H.; Yang, J.; Sui, G.; Yuan, X.; Ma, X.; Wang, L. Analysis of the Influence of Alternating Stress in the Multi-Cycle Injection Production Process. Processes 2025, 13, 1158. https://doi.org/10.3390/pr13041158
Liu S, Zhao E, Ma B, Liu H, Yang J, Sui G, Yuan X, Ma X, Wang L. Analysis of the Influence of Alternating Stress in the Multi-Cycle Injection Production Process. Processes. 2025; 13(4):1158. https://doi.org/10.3390/pr13041158
Chicago/Turabian StyleLiu, Shiduo, Endong Zhao, Bin Ma, Huan Liu, Jianxuan Yang, Guojie Sui, Xin Yuan, Xinfang Ma, and Lei Wang. 2025. "Analysis of the Influence of Alternating Stress in the Multi-Cycle Injection Production Process" Processes 13, no. 4: 1158. https://doi.org/10.3390/pr13041158
APA StyleLiu, S., Zhao, E., Ma, B., Liu, H., Yang, J., Sui, G., Yuan, X., Ma, X., & Wang, L. (2025). Analysis of the Influence of Alternating Stress in the Multi-Cycle Injection Production Process. Processes, 13(4), 1158. https://doi.org/10.3390/pr13041158





