Optimizing Energy Storage Participation in Primary Frequency Regulation: A Novel Analytical Approach for Virtual Inertia and Damping Control in Low-Carbon Power Systems
Abstract
1. Introduction
- Establishing the second-order model of load frequency control based on aggregation theory to replace the original complex multi-unit model and enabling analysis of the time-domain frequency trajectory.
- Developing a fast analytical method based on the compensation principle to calculate DERs’ virtual inertia and damping coefficients and guaranteeing a desired frequency overshoot and steady-state offset.
- Proposing a flexible regulation scheme for energy storage systems involved in frequency control, and dynamically adjusting synthetic inertia and damping coefficients according to state of charge (SOC) levels.
2. System Dynamical Models
2.1. Design Ideas
2.2. Synchronous-Generator Dynamics
2.3. Frequency-Responsive DER Model
2.4. Reduced Second-Order Model
3. Designing Inertia and Damping Coefficients
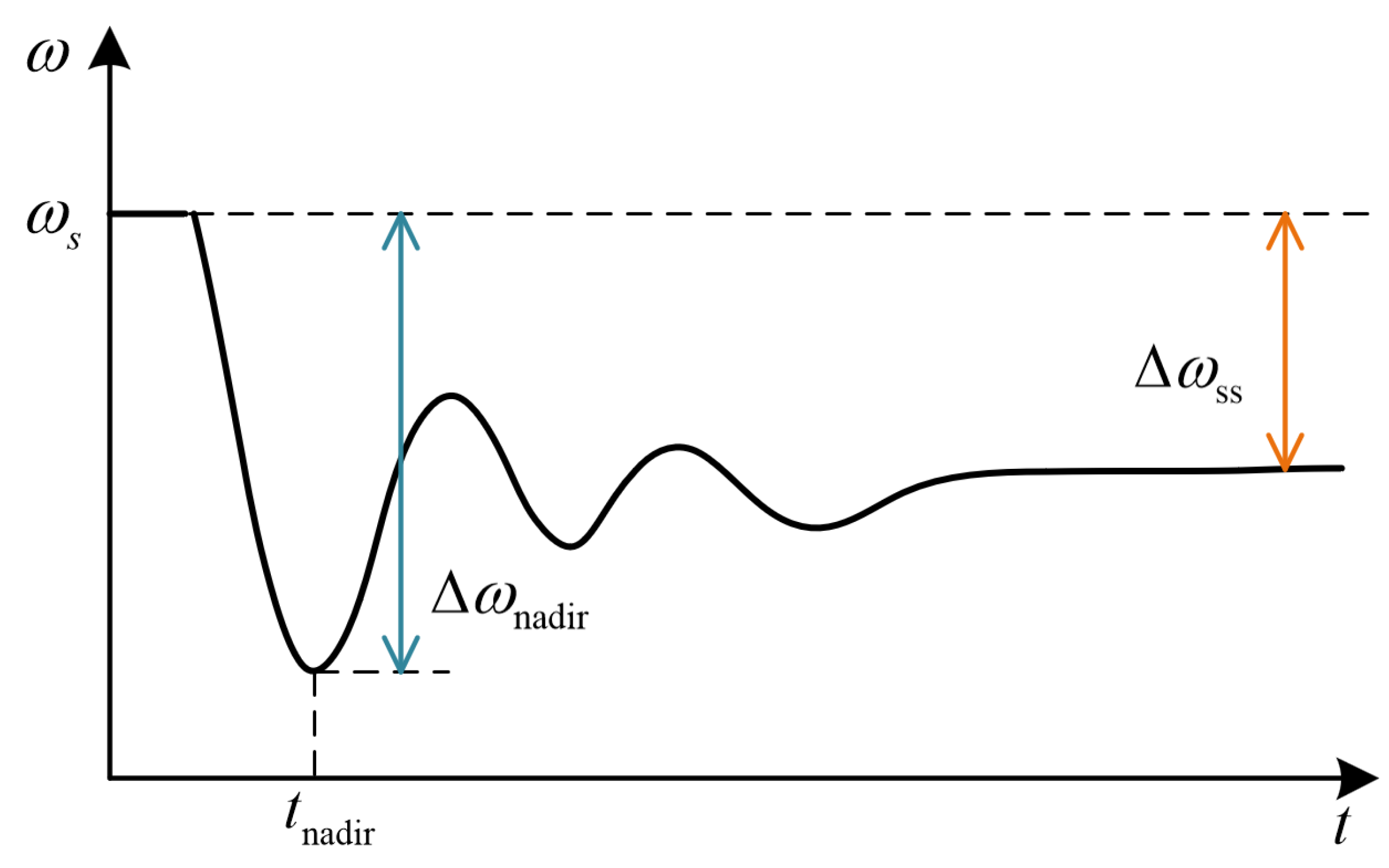
3.1. Transfer Function from Load Disturbance to Frequency Response
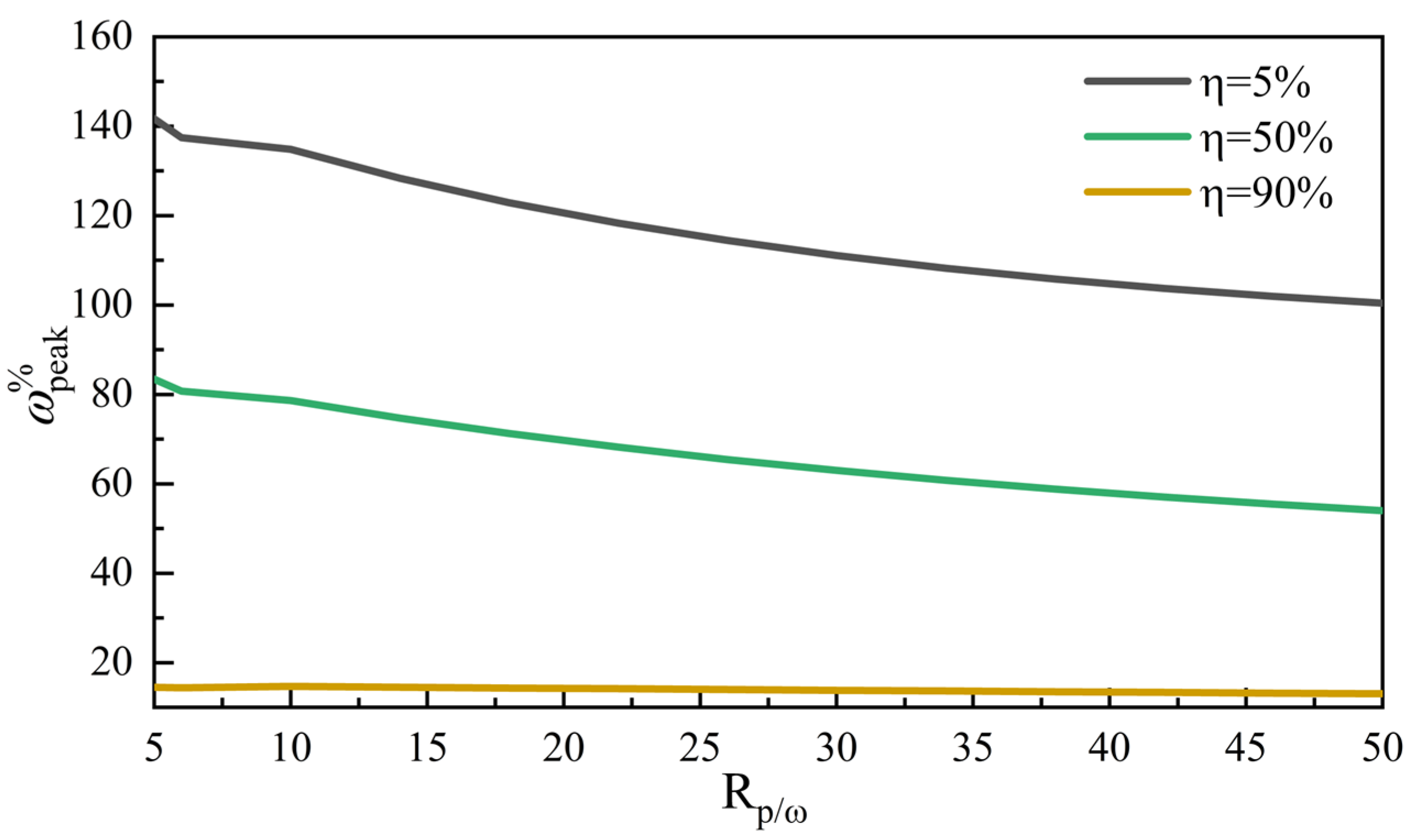
3.2. Determine Damping and Inertia Coefficients
4. SOC-Based Adaptive Optimization
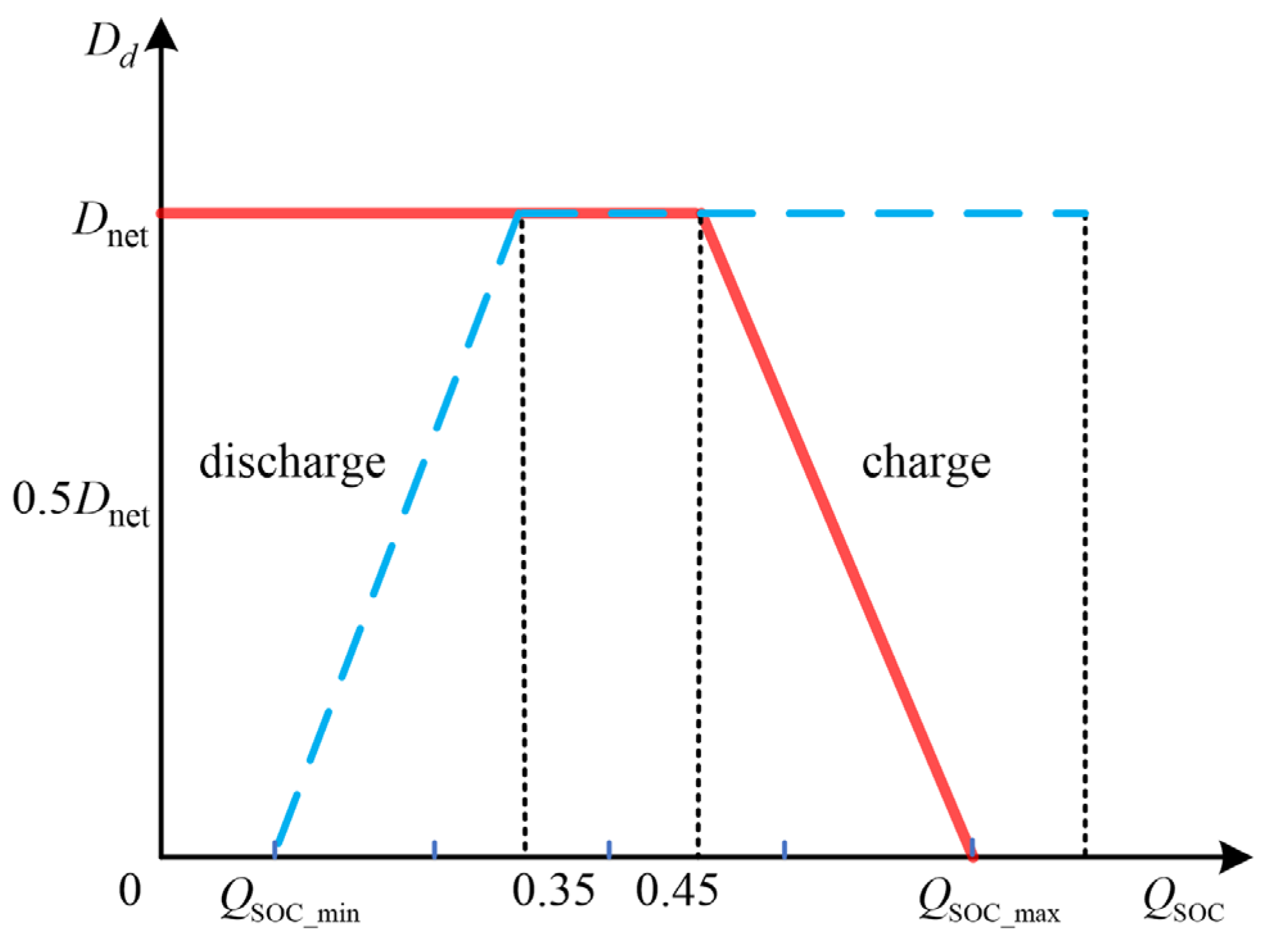
4.1. Response Mode Incorporating SOC
4.2. Design of Scaling Factors
4.3. Parameter Optimization Involving SOC
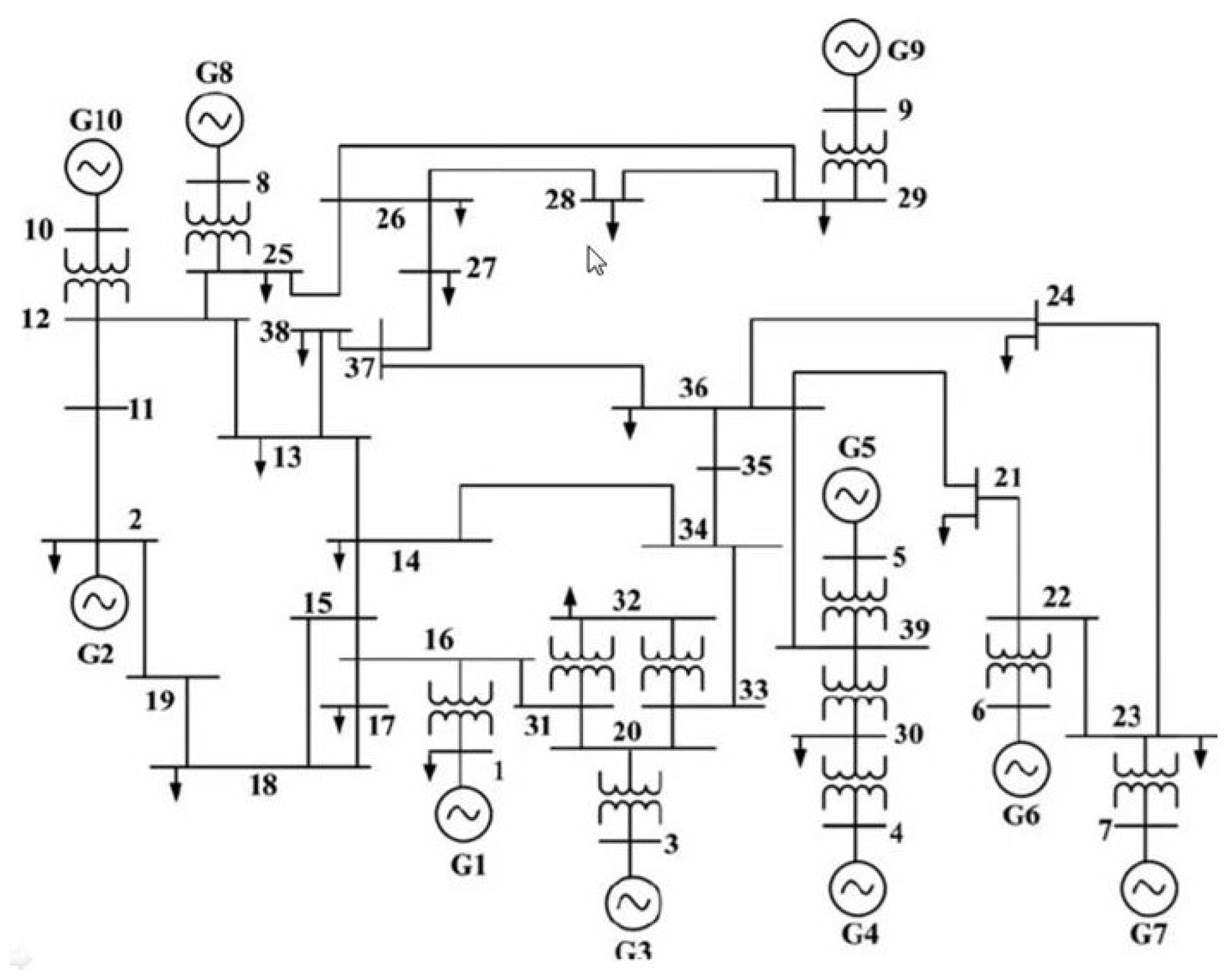
5. Simulation Results and Analysis
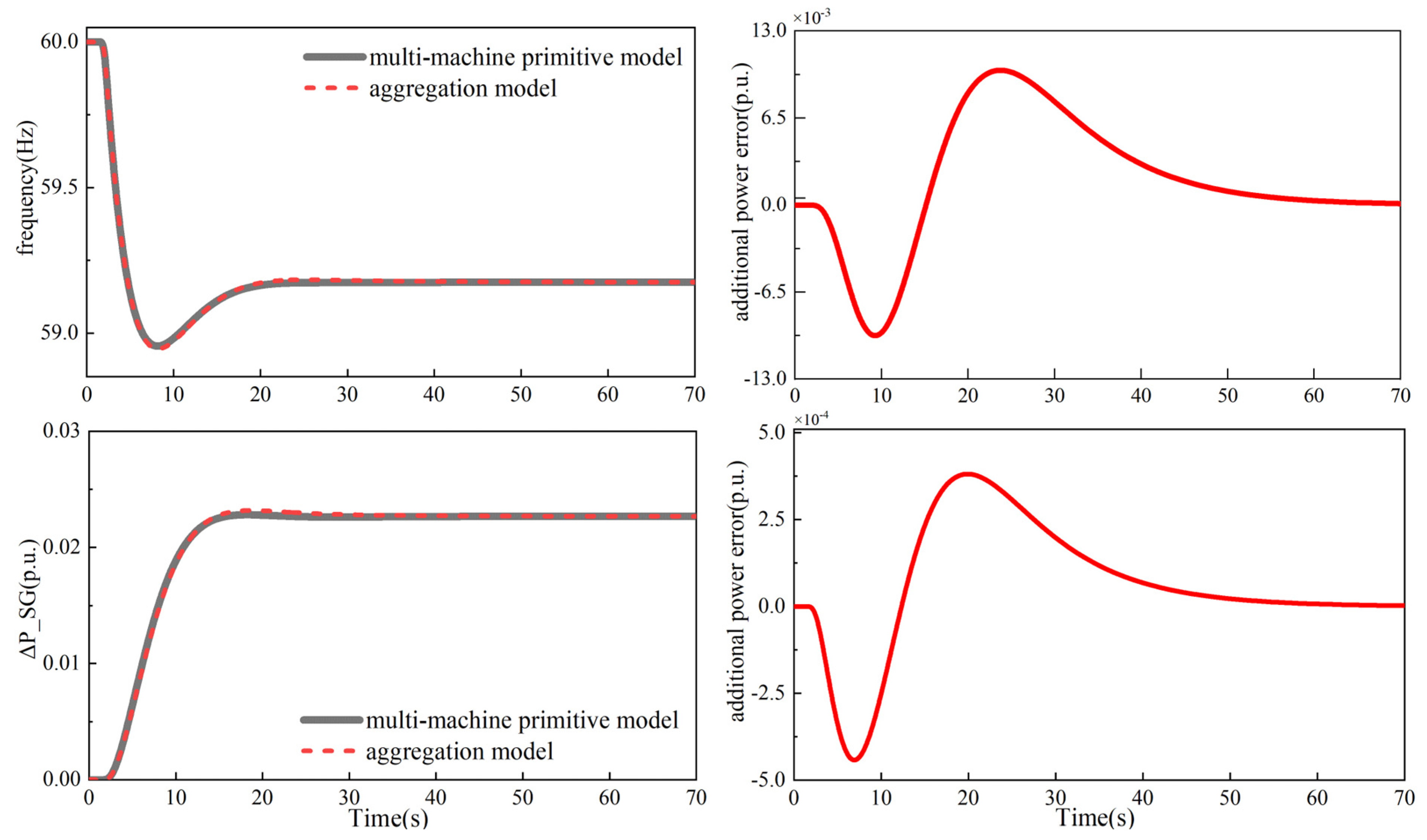
5.1. Aggregation Model Validation
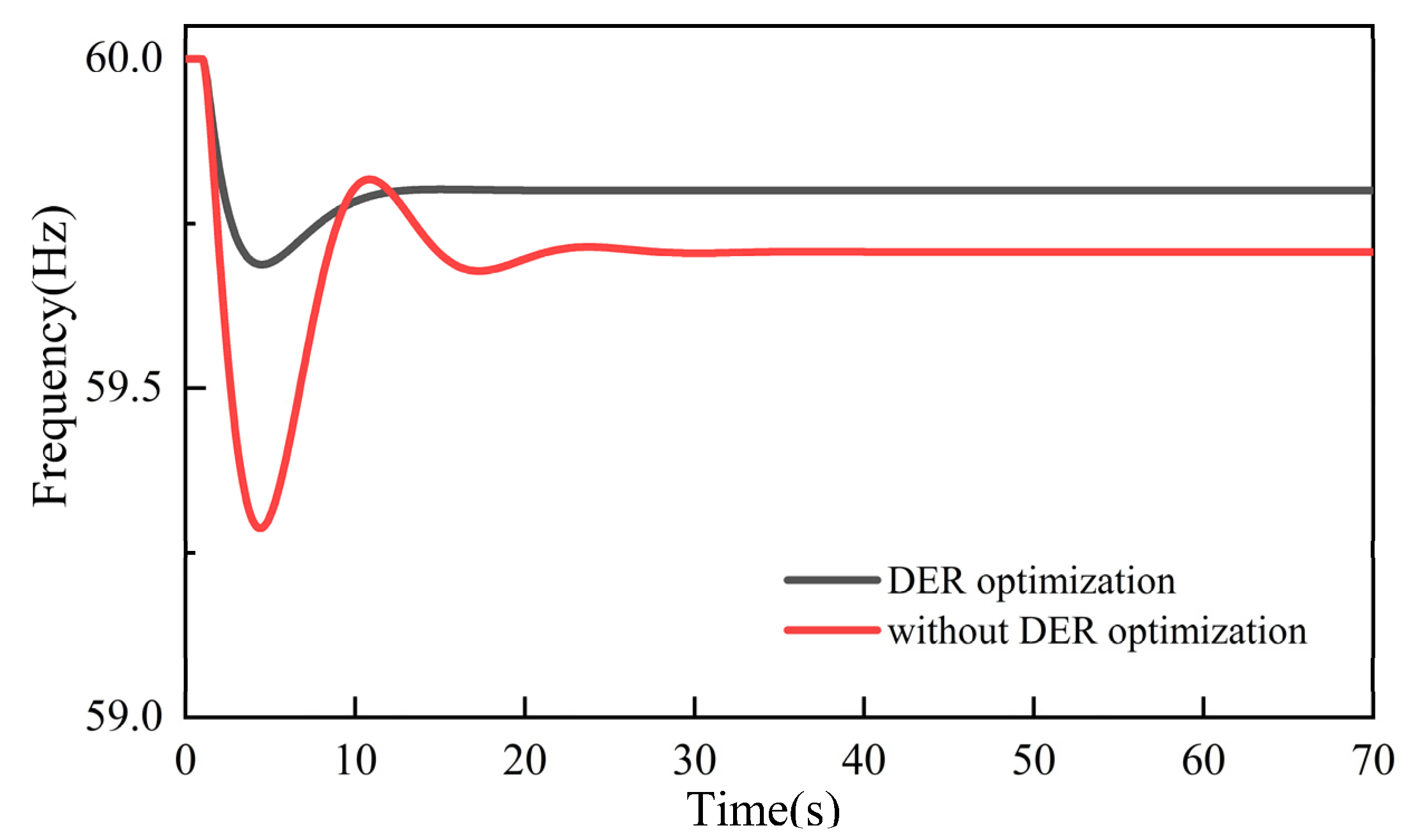
5.2. Impact of DER in Inertial and Primary Frequency Response
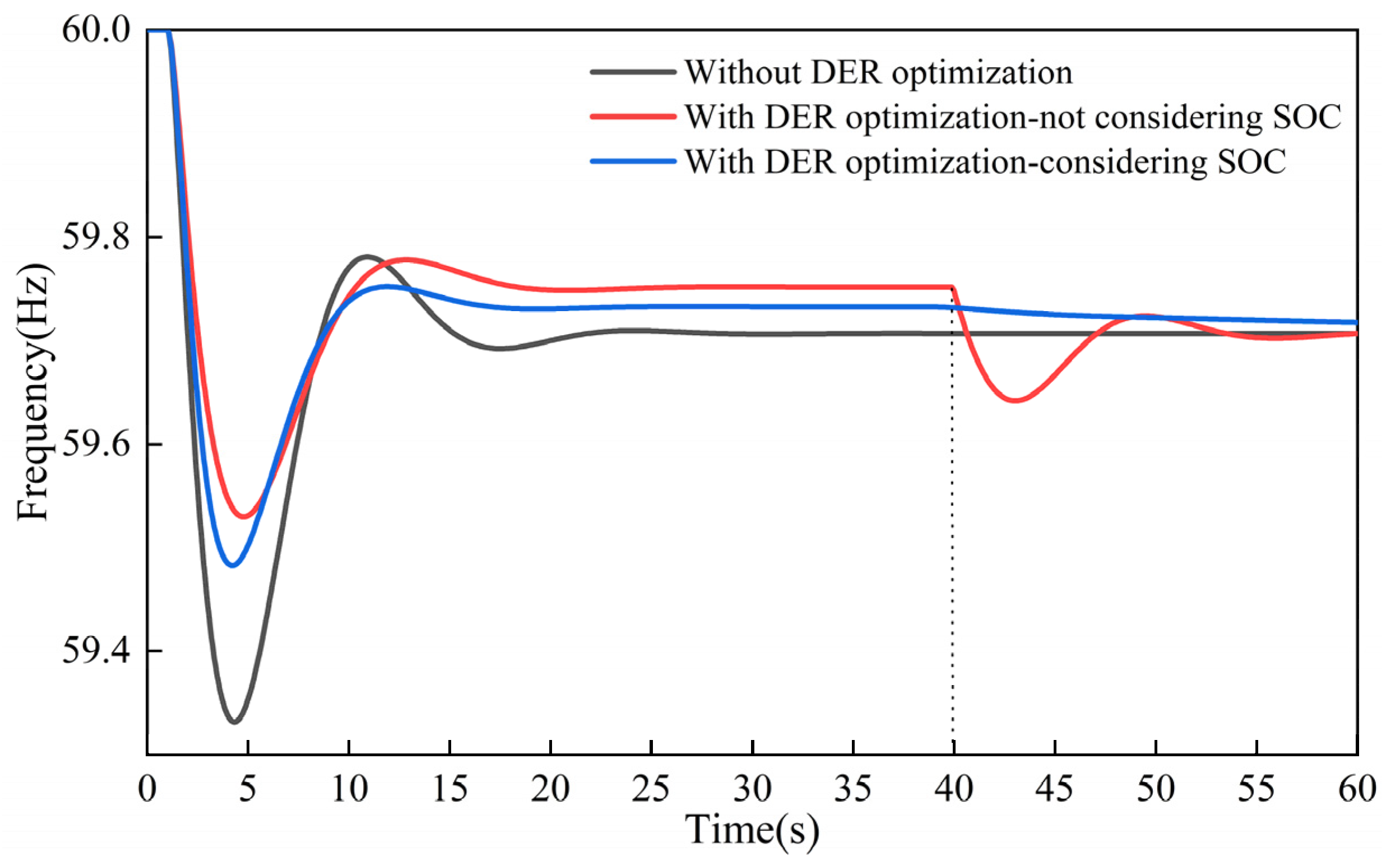
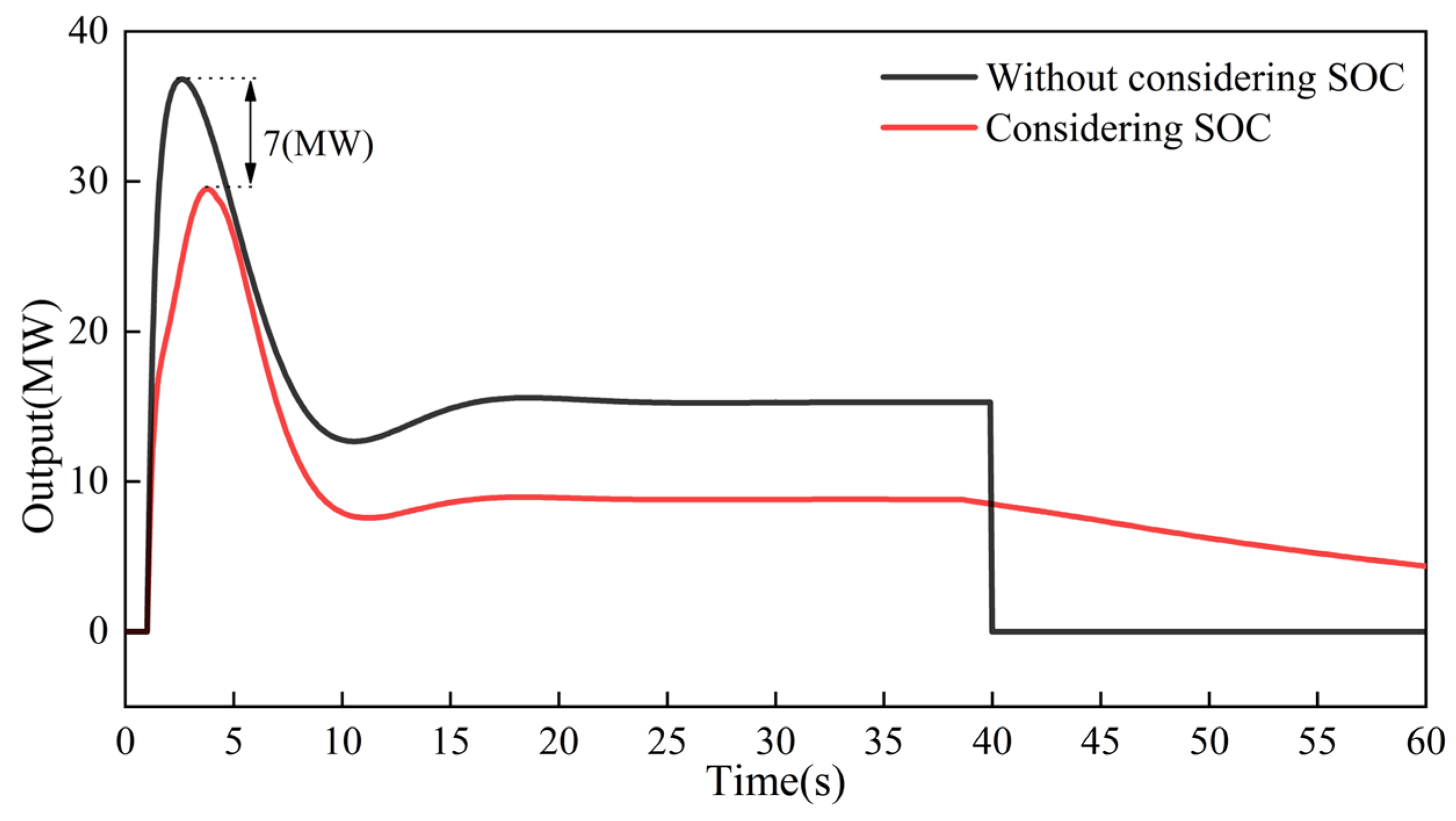
5.3. Adaptive Auxiliary Frequency Modulation with Energy Storage Considering SOC
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sadorsky, P. Wind energy for sustainable development: Driving factors and future outlook. J. Clean. Prod. 2021, 289, 125779. [Google Scholar] [CrossRef]
- Cheng, L.; Yu, T. A new generation of AI: A review and perspective on machine learning technologies applied to smart energy and electric power systems. Int. J. Energy Res. 2019, 43, 1928–1973. [Google Scholar] [CrossRef]
- Shabestari, P.M.; Mehrizi-Sani, A. Frequency response improvement of PMSG wind turbines using a washout filter. Energies 2020, 13, 4797. [Google Scholar] [CrossRef]
- Li, M.; Huang, W.; Tai, N.; Yang, L.; Duan, D.; Ma, Z. A dual-adaptivity inertia control strategy for virtual synchronous generator. IEEE Trans. Power Syst. 2019, 35, 594–604. [Google Scholar] [CrossRef]
- Zhang, Y.; Weng, Y.; Li, H.; Zhou, Z.; Li, X. Research on China’s Electricity Market and Photovoltaic and Electrochemical Energy Storage Industry. In Proceedings of the 2023 8th Asia Conference on Power and Electrical Engineering (ACPEE), Tianjin, China, 14–16 April 2023; pp. 949–953. [Google Scholar]
- Ranjan, M.; Shankar, R. A literature survey on load frequency control considering renewable energy integration in power system: Recent trends and future prospects. J. Energy Storage 2022, 45, 103717. [Google Scholar] [CrossRef]
- Cheng, L.; Huang, P.; Zou, T.; Zhang, M.; Peng, P.; Lu, W. Evolutionary game-theoretical approaches for long-term strategic bidding among diverse stakeholders in large-scale and local power markets: Basic concept, modelling review and future vision. Int. J. Electr. Power Energy Syst. 2025, 166, 110589. [Google Scholar] [CrossRef]
- Cheng, L.; Peng, P.; Lu, W.; Sun, J.; Wu, F.; Shi, M.; Yuan, X.; Chen, Y. The evolutionary game equilibrium theory on power market bidding involving renewable energy companies. Int. J. Electr. Power Energy Syst. 2025, 167, 110588. [Google Scholar] [CrossRef]
- Hamid, B.; Hussain, I.; Iqbal, S.J.; Singh, B.; Das, S.; Kumar, N. Optimal MPPT and BES control for grid-tied DFIG-based wind energy conversion system. IEEE Trans. Ind. Appl. 2022, 58, 7966–7977. [Google Scholar] [CrossRef]
- Xu, B.; Gao, X.; Jing, S.; Yang, Z.; Guo, R. A Coordinated Control Strategy for the Wind Turbine Generator-Energy Storage Device Integrated System. In Proceedings of the 2023 International Conference on Power System Technology (PowerCon), Jinan, China, 21–22 September 2023; pp. 1–6. [Google Scholar]
- Sun, M.; Min, Y.; Chen, L.; Hou, K.; Xia, D.; Mao, H. Optimal auxiliary Frequency control of wind turbine generator and coordination with synchronous generator. CSEE J. Power Energy Syst. 2021, 7, 78–85. [Google Scholar]
- Thakallapelli, A.; Nair, A.R.; Biswas, B.D.; Kamalasadan, S. Frequency regulation and control of grid-connected wind farms based on online reduced-order modeling and adaptive control. IEEE Trans. Ind. Appl. 2020, 56, 1980–1989. [Google Scholar] [CrossRef]
- Li, X.; Huang, Y.; Huang, J.; Tan, S.; Wang, M.; Xu, T.; Cheng, X. Modeling and control strategy of battery energy storage system for primary frequency regulation. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 543–549. [Google Scholar]
- Engels, J.; Claessens, B.; Deconinck, G. Combined stochastic optimization of frequency control and self-consumption with a battery. IEEE Trans. Smart Grid 2017, 10, 1971–1981. [Google Scholar] [CrossRef]
- Rajan, R.; Fernandez, F.M.; Yang, Y. Primary frequency control techniques for large-scale PV-integrated power systems: A review. Renew. Sustain. Energy Rev. 2021, 144, 110998. [Google Scholar] [CrossRef]
- Rajan, R.; Fernandez, F.M. Power control strategy of photovoltaic plants for frequency regulation in a hybrid power system. Int. J. Electr. Power Energy Syst. 2019, 110, 171–183. [Google Scholar] [CrossRef]
- Li, J.; Wen, B.; Wang, H. Adaptive virtual inertia control strategy of VSG for micro-grid based on Iimproved bang-bang control strategy. IEEE Access 2019, 7, 39509–39514. [Google Scholar] [CrossRef]
- De Siqueira, L.M.S.; Peng, W. Control strategy to smooth wind power output using battery energy storage system: A review. J. Energy Storage 2021, 35, 102252. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Wang, M.; Xu, Z.; Peng, Y.; Li, M. Coordinated VSG control of photovoltaic/battery system for maximum power output and grid supporting. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 301–309. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, L.; Cheng, H.; Liu, D.; Zhang, J.; Li, G. Frequency-constrained co-planning of generation and energy storage with high-penetration renewable energy. J. Mod. Power Syst. Clean Energy 2021, 9, 760–775. [Google Scholar] [CrossRef]
- Meng, J.; Wang, Y.; Fu, C.; Wang, H. Adaptive virtual inertia control of distributed generator for dynamic frequency support in microgrid. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–5. [Google Scholar]
- Andalib-Bin-Karim, C.; Liang, X.; Zhang, H. Fuzzy-secondary-controller-based virtual synchronous generator control scheme for interfacing inverters of renewable distributed generation in microgrids. IEEE Trans. Ind. Appl. 2018, 54, 1047–1061. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Zhao, C.; Tang, W.; Low, S.H. Profit-maximizing planning and control of battery energy storage systems for primary frequency control. IEEE Trans. Smart Grid 2018, 9, 712–723. [Google Scholar] [CrossRef]
- Carrion, M.; Dvorkin, Y.; Pandzic, H. Primary frequency response in capacity expansion with energy storage. IEEE Trans. Power Syst. 2018, 33, 1824–1835. [Google Scholar] [CrossRef]
- Purba, V.; Dhople, S.V.; Jafarpour, S.; Bullo, F.; Johnson, B.B. Reduced-order structure-preserving model for parallel-connected three-phase grid-tied inverters. In Proceedings of the 2017 IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, CA, USA, 9–12 July 2017; pp. 1–7. [Google Scholar]
- Cheng, L.; Yu, T. Smart dispatching for energy internet with complex cyber-physical-social systems: A parallel dispatch perspective. Int. J. Energy Res. 2019, 43, 3080–3133. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Yang, Y.; Kim, K.A.; Rodriguez, J. Power electronics technology for large-scale renewable energy generation. Proc. IEEE 2023, 111, 335–355. [Google Scholar] [CrossRef]
- Guggilam, S.S.; Zhao, C.; Dall, E.; Chen, Y.C.; Dhople, S.V. Engineering inertial and primary-frequency response for distributed energy resources. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, Australia, 12–15 December 2017; pp. 5112–5118. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Guggilam, S.S.; Zhao, C.; Dall’Anese, E.; Chen, Y.C.; Dhople, S.V. Optimizing DER participation in inertial and primary-frequency response. IEEE Trans. Power Syst. 2018, 33, 5194–5205. [Google Scholar] [CrossRef]
- Zhao, C.; Sun, D.; Nian, H.; Wang, M.; Yang, L. Analysis on the contribution of virtual synchronous generator controlled energy storage system to primary frequency modulation. In Proceedings of the 2021 4th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 23–25 April 2021; pp. 869–874. [Google Scholar]
- Pai, A. Energy Function Analysis for Power System Stability; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Milano, F.; Vanfretti, L.; Morataya, J.C. An open source power system virtual laboratory: The PSAT Case and Experience. IEEE Trans. Educ. 2008, 51, 17–23. [Google Scholar] [CrossRef]




| Type | Number | ||||
|---|---|---|---|---|---|
| SG | G1 | 4 | 0.217 | 0.1302 | 0.0434 |
| G2 | 4 | 0.217 | 0.1302 | 0.0434 | |
| G3 | 5 | 0.1984 | 0.1203 | 0.0343 | |
| G4 | 6 | 0.1798 | 0.1203 | 0.0343 | |
| G10 | 4 | 0.217 | 0.1302 | 0.0434 | |
| G5 | 7 | 0.1612 | 0.1203 | 0.0343 | |
| G6 | 8 | 0.1426 | 0.1203 | 0.0343 | |
| G7 | 9 | 0.1240 | 0.1302 | 0.0434 | |
| G8 | 10 | 0.1054 | 0.1302 | 0.0434 | |
| G9 | 10 | 0.0868 | 0.1302 | 0.0434 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Tan, E.; Cheng, L.; Zhang, K.; Liu, W. Optimizing Energy Storage Participation in Primary Frequency Regulation: A Novel Analytical Approach for Virtual Inertia and Damping Control in Low-Carbon Power Systems. Processes 2025, 13, 1146. https://doi.org/10.3390/pr13041146
Lu W, Tan E, Cheng L, Zhang K, Liu W. Optimizing Energy Storage Participation in Primary Frequency Regulation: A Novel Analytical Approach for Virtual Inertia and Damping Control in Low-Carbon Power Systems. Processes. 2025; 13(4):1146. https://doi.org/10.3390/pr13041146
Chicago/Turabian StyleLu, Wentian, Enkai Tan, Lefeng Cheng, Kuozhen Zhang, and Wenjie Liu. 2025. "Optimizing Energy Storage Participation in Primary Frequency Regulation: A Novel Analytical Approach for Virtual Inertia and Damping Control in Low-Carbon Power Systems" Processes 13, no. 4: 1146. https://doi.org/10.3390/pr13041146
APA StyleLu, W., Tan, E., Cheng, L., Zhang, K., & Liu, W. (2025). Optimizing Energy Storage Participation in Primary Frequency Regulation: A Novel Analytical Approach for Virtual Inertia and Damping Control in Low-Carbon Power Systems. Processes, 13(4), 1146. https://doi.org/10.3390/pr13041146








