Mathematical Modeling and Dynamic Simulation of a Tower Reactor for Intensified Ethanol Fermentation with Immobilized Yeasts and Simultaneous Gas Removal
Abstract
1. Introduction
2. Materials and Methods
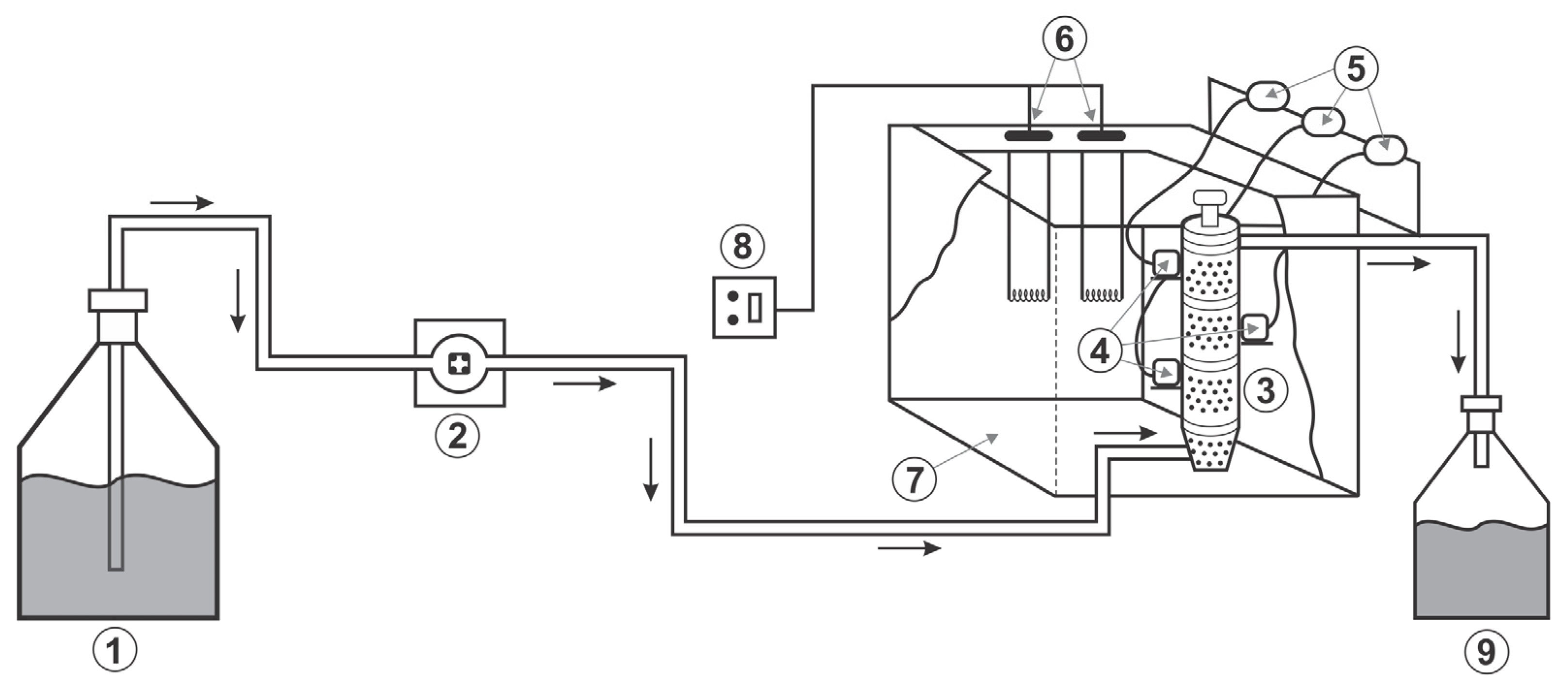
2.1. Experimental Data
2.2. Mathematical Modeling
2.2.1. Solid Phase Model
- Mass balance of cells
- Mass balance of substrate
- Mass balance of product (ethanol)
2.2.2. Fluid Phase Model
- Mass balance of substrate
- Mass balance of product (ethanol)
2.3. Numerical Methods
2.4. Kinetic and Yield Parameter Estimation
3. Results and Discussion
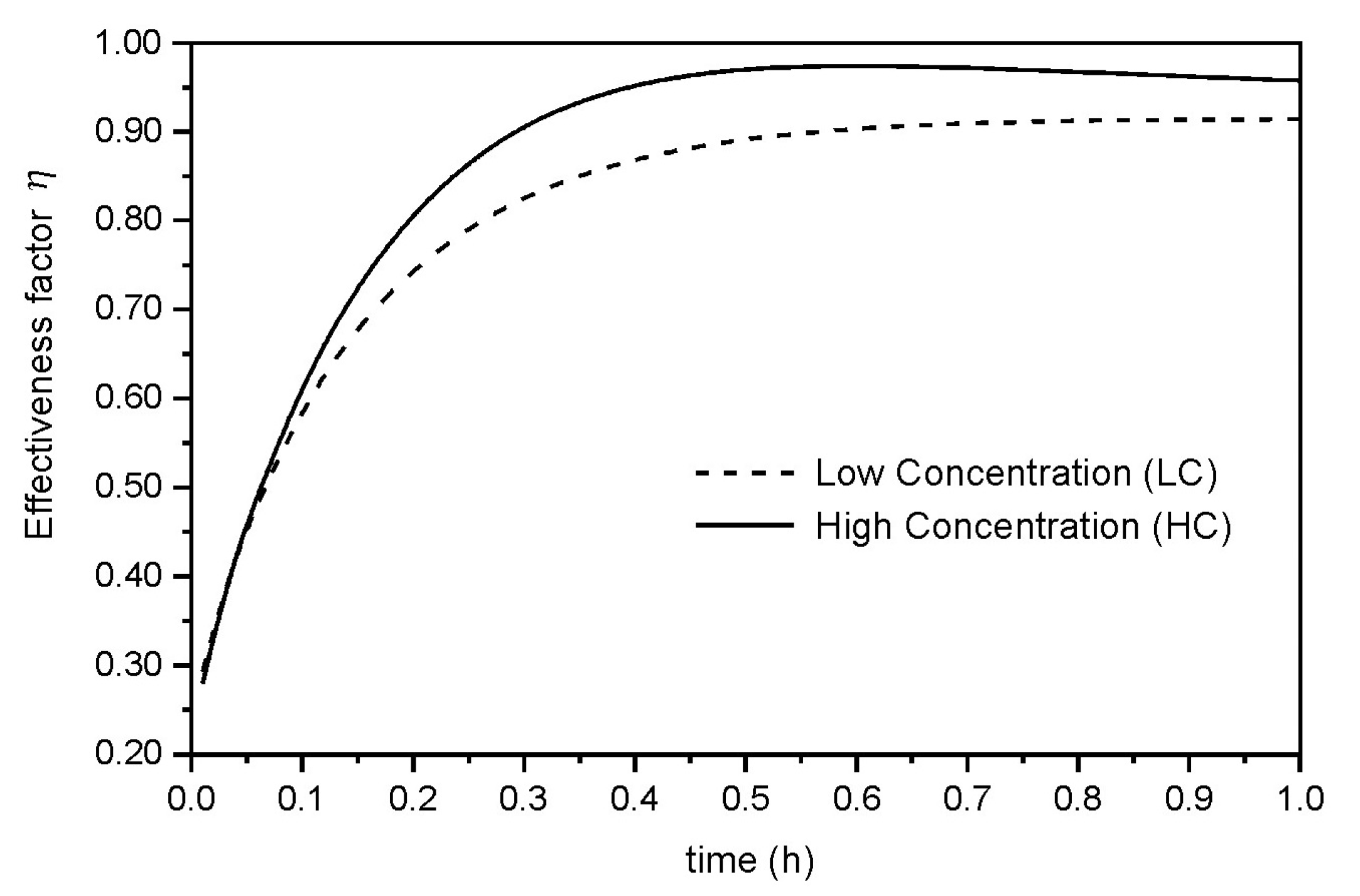
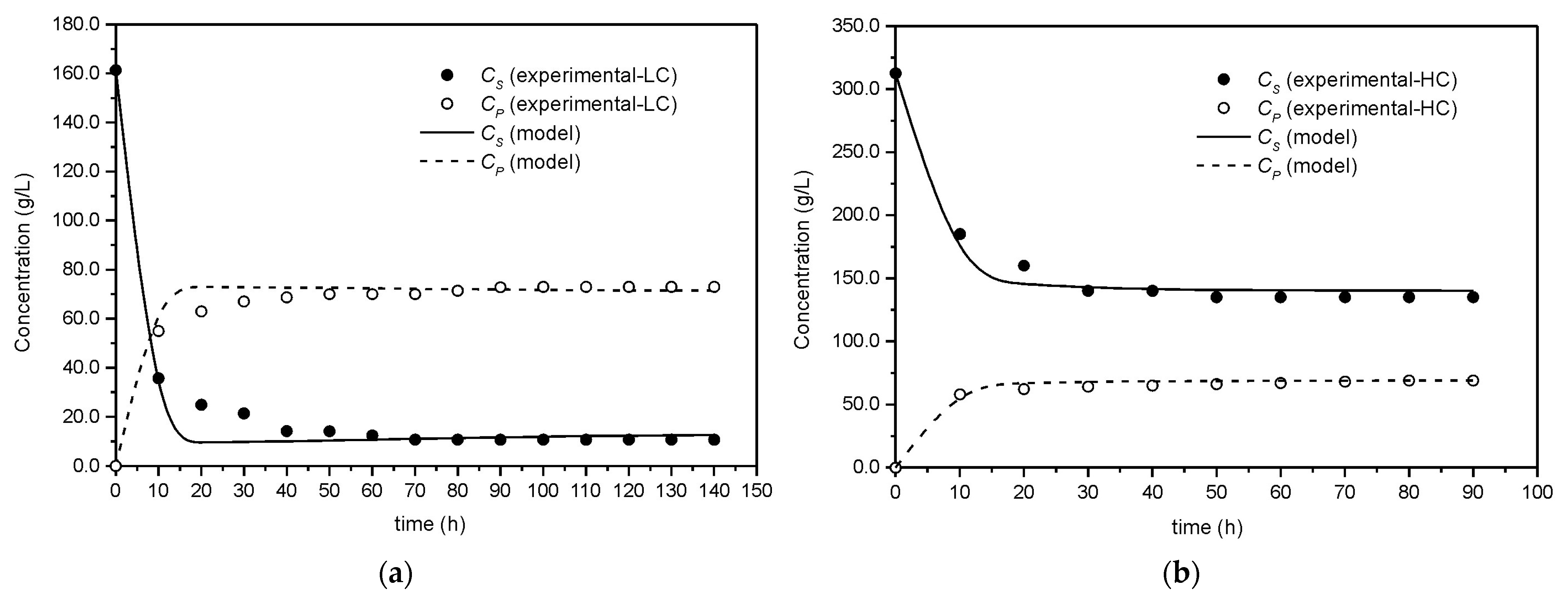
3.1. Bioprocess Start-Up
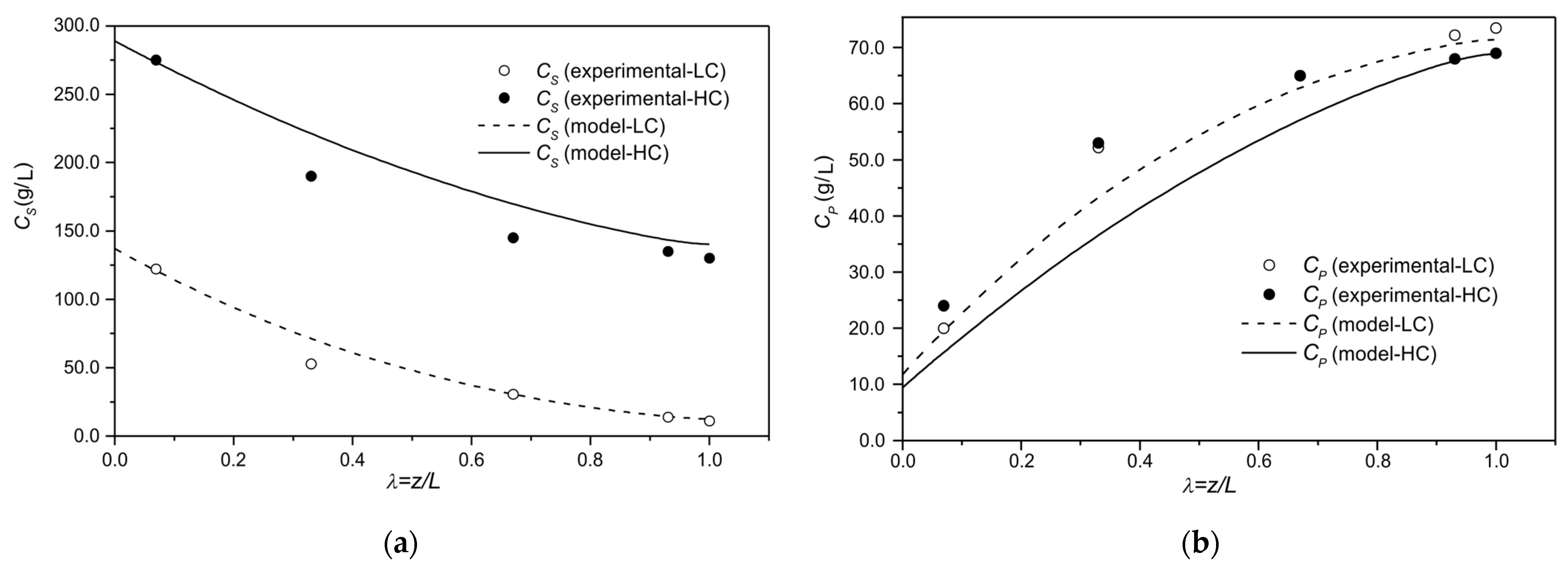
3.2. Bioreactor Simulation
4. Conclusions
- The proposed model adequately reproduced the behavior trend of the main bioprocess state variables. However, it is possible to improve the model’s predictions by optimizing its parameters since they had not been optimized in a preliminary step of parameter estimation;
- To reduce the computational effort required to estimate the parameters, the current mathematical model needs to be simplified by developing a simpler, more conservative model that incorporates the essential behavior of the bioprocess;
- Since the effects of intraparticle mass transfer are negligible, a convenient strategy, simplifying the mathematical model, would be to neglect the concentration gradients within the particle;
- Another strategy would be to replace the axial dispersion model with the tanks in series model to describe the bioreactor’s hydrodynamic behavior. These two combined strategies would reduce the current set of partial differential equations to a set of ordinary differential equations, significantly simplifying the mathematical model;
- The application of such reduction strategies represents the main potential for advancement of this study aimed at accurately estimating the model’s parameters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Area per unit volume of the particle (dm−1) |
| Surface area of the particle (dm2) | |
| Concentration of cells within the particle (g/L) | |
| Concentration of substrate within the particle (g/L) | |
| Concentration of product (ethanol) inside the particle (g/L) | |
| Concentration of substrate on the particle surface (g/L) | |
| Concentration of product on the particle surface (g/L) | |
| Maximum concentration of cells within the particle (g/L) | |
| Concentration of cells in the fluid phase (g/L) | |
| Concentration of substrate in the fluid phase (g/L) | |
| Concentration of product in the fluid phase (g/L) | |
| Substrate concentration in the feed stream (g/L) | |
| Bioreactor diameter (dm) | |
| Particle diameter (dm) | |
| Coefficient of axial dispersion (dm2/h) | |
| Diffusion coefficient of the substrate (dm2/h) | |
| Diffusion coefficient of the product (dm2/h) | |
| Coefficient of axial dispersion based on the bed porosity (dm2/h) | |
| Parameter defined in Equation (22) (-) | |
| Chilton-Colburn factor for mass transfer (-) | |
| Coefficient of mass transfer of component j (dm/h) | |
| Coefficient of mass transfer of substrate (dm/h) | |
| Coefficient of mass transfer of product (dm/h) | |
| Specific rate of cell death (g/g·h) | |
| Inhibition parameter for substrate according to Andrews’ model (g/L) | |
| Substrate saturation constant (g/L) | |
| Inhibition parameter for product (g/L) | |
| L | bioreactor length (dm) |
| m | Specific rate of substrate consumption for cell maintenance (g/g·h) |
| Q | Feed volumetric flow rate (dm3/h) |
| r | Radial coordinate in the particle (dm) |
| Rate of cell death (g/L·h) | |
| Rate of product formation (g/L·h) | |
| Substrate consumption rate per unit particle volume (g/L·h) | |
| Value of on the particle surface (g/L·h) | |
| Substrate consumption rate per unit volume of fluid (g/L·h) | |
| Particle radius (dm) | |
| Reynolds number (-) | |
| Schmidt number (-) | |
| Time (h) | |
| Duration time of the transient regime for fermentation with high substrate concentration in the feed stream (h) | |
| Duration time of the transient regime for fermentation with low substrate concentration in the feed stream (h) | |
| Superficial velocity of the fluid (dm/h) | |
| Interstitial velocity of the fluid (dm/h) | |
| Particle volume (dm3) | |
| Apparent yield coefficient for substrate-to-cell conversion (g/g) | |
| Apparent yield coefficient for substrate-to-product conversion (g/g) | |
| z | Axial coordinate in the bioreactor (dm) |
| α | Parameter related to the product formation associated with cell growth (g/g) |
| β | Parameter related to product formation not associated with cell growth (g/g·h) |
| σ, δ | Characteristic parameters of Jacobi polynomials (-) |
| ε | bed porosity (-) |
| Dimensionless axial coordinate in the bioreactor (-) | |
| Maximum specific rate of cell growth (g/g·h) | |
| Specific rate of cell growth (g/g·h) | |
| Specific rate of substrate consumption (g/g·h) | |
| Specific rate of product formation (g/g·h) | |
| Absolute viscosity of the fluid (g/dm·h) | |
| η | Effectiveness factor of the catalytic particles (-) |
| Dimensionless radial coordinate in the particle (-) | |
| Fluid density (g/dm3) |
Appendix A
References
- Polona, Z.P. Biocatalytic process intensification via efficient biocatalyst immobilization, miniaturization, and process integration, Current Opinion. Green Sustain. Chem. 2021, 32, 100546, ISSN 2452-2236. [Google Scholar] [CrossRef]
- Stankiewicz, A.I.; Moulijn, J.A. Process Intensification: Transforming Chemical Engineering. Chem. Eng. Prog. 2000, 96, 22–34. [Google Scholar]
- Gutiérrez-Antonio, C.; Romero-Izquierdo, A.G.; Gómez-Castro, F.I.; Hernández, S. Process intensification and integration in the production of biojet fuel. In Production Processes of Renewable Aviation Fuel; Romero-Izquierdo, A.G., Gómez-Castro, F.I., Hernández, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 171–199. [Google Scholar] [CrossRef]
- Nakasaki, K.; Murai, T.; Akiyama, T. Dynamic modeling of immobilized cell reactor: Application to ethanol fermentation. Biotechnol. Bioeng. 1989, 33, 1317–1323. [Google Scholar] [CrossRef]
- Fukuda, H. Immobilized microorganisms bioreactors. In Bioreactor System Design; Asenjo, J.A., Merchuk, J.C., Eds.; Marcel Dekker: New York, NY, USA, 1995; pp. 339–373. [Google Scholar]
- Laca, A.; Quirós, C.; García, L.A.; Diaz, M. Modeling and description of internal profiles in immobilized cells systems. Biochem. Eng. J. 1998, 1, 225–232. [Google Scholar]
- Toda, K.; Ohtake, H.; Asakura, T. Ethanol production in horizontal bioreactor. Appl. Microbiol. Biotechnol. 1986, 24, 97–101. [Google Scholar]
- Wöhrer, W. A horizontal bioreactor for ethanol production by immobilized cells. Bioprocess Eng. 1989, 4, 105–111. [Google Scholar]
- Parekh, S.R.; Wayman, M. Performance of a novel continuous dynamic immobilized cell bioreactor in ethanolic fermentation. Enzyme Microb. Technol. 1987, 9, 406–410. [Google Scholar]
- Shiotani, T.; Yamané, T. A horizontal packed-bed bioreactor to reduce CO2 gas holdup in the continuous production of ethanol by immobilized yeast cells. European J. Appl. Microbiol. Biotechnol. 1981, 13, 96–101. [Google Scholar]
- Converti, A.B.M.; Sommariva, C. Ethanol production in an entrapped yeast cell column. Chem. Eng. J. 1991, 47, B1–B10. [Google Scholar] [CrossRef]
- Sanromán, A.; Chamy, R.; Núnez, M.J.; Lema, J.M. Enzymatic hydrolysis of starch in a fixed-bed pulsed-flow reactor. Appl. Biochem. Biotechnol. 1991, 28/29, 527–538. [Google Scholar]
- Belincanta, J.; Alchorne, J.A.; Teixeira da Silva, M. The brazilian experience with ethanol fuel: Aspects of production, use, quality and distribution logistics. Braz. Chem. Eng. J. 2016, 33, 1091–1102. [Google Scholar]
- Oliveira, S.C.; Stremel, D.P.; Dechechi, E.C.; Pereira, F.M. Kinetic modeling of 1-G ethanol fermentations. In Fermentation Processes; Jozala, A.F., Ed.; InTech: Rijeka, Croatia, 2017; pp. 93–117. [Google Scholar]
- Zanin, G.M.; Santana, C.C.; Bom, E.P.; Giordano, R.C.L.; de Moraes, F.F.; Andrietta, S.R.; de Carvalho Neto, C.C.; Macedo, I.C.; Fo, D.L.; Ramos, L.P.; et al. Brazilian bioethanol program. Appl. Biochem. Biotechnol. 2000, 84–86, 1147–1161. [Google Scholar] [CrossRef] [PubMed]
- Vasconcelos, J.N.; Lopes, C.E.; França, F.P. Continuous ethanol production using yeast immobilized on sugar-cane stalks. Braz. Chem. Eng. J. 2004, 21, 357–365. [Google Scholar] [CrossRef]
- Scott, F.; Conejeros, R.; Aroca, G. Attainable region analysis for continuous production of second generation bioethanol. Biotechnol. Biofuels 2013, 6, 171. [Google Scholar] [CrossRef]
- Lee, C.W.; Chang, H.N. Examination of immobilized cell in a rotating packed drum reactor for the production of ethanol from D-glucose. Enzyme Microb. Technol. 1985, 7, 561–563. [Google Scholar] [CrossRef]
- Admassu, W.; Korus, R.A.; Heimsch, R.C. Ethanol fermentation with a flocculating yeast. Chem. Eng. J. 1985, 31, B1–B8. [Google Scholar] [CrossRef]
- Baptista, C.M.S.G.; Cóias, J.M.A.; Oliveira, A.C.M.; Oliveira, N.M.C.; Rocha, J.M.S.; Dempsey, M.J.; Lannigan, K.C.; Benson, P.S. Natural immobilisation of microorganisms for continuous ethanol production. Enzyme Microb. Technol. 2006, 40, 127–131. [Google Scholar] [CrossRef]
- Oliveira, S.C.; de Castro, H.F.; Visconti, A.E.S.; Giudici, R. Mathematical modeling of a continuous alcoholic fermentation process in a two-stage tower reactor cascade with flocculating yeast recycle. Bioprocess Biosyst. Eng. 2015, 38, 469–479. [Google Scholar] [CrossRef]
- Setiadi, T.; Larsen, V.F. Modelling concentration profiles in tower fermenter: The influence of the axial dispersion coefficient. Biotech. Lett. 1991, 13, 647–652. [Google Scholar] [CrossRef]
- Ivancic, M.; Santek, B.; Novak, S.; Horvart, P.; Maric, V. Bioprocess kinetics in a horizontal rotating tubular bioreactor. Bioprocess Biosyst. Eng. 2004, 26, 169–175. [Google Scholar] [CrossRef]
- Cardona, C.A.; Sánchez, O.J. Fuel ethanol production: Process design trends and integration opportunities. Bioresour. Technol. 2007, 98, 2415–2457. [Google Scholar] [PubMed]
- Elnashaie, S.S.E.H.; Fakeeha, A.H.; Helal, E.; Abashar, M.E. A mathematical model achieving the twin objectives of simplicity and accuracy for the simulation of immobilized packed bed fermenters. Math. Comput. Modell. 1994, 19, 105–114. [Google Scholar] [CrossRef]
- Oliveira, S.C.; Oliveira, R.C.; Tacin, M.V.; Gattás, E.A.L. Kinetic modeling and optimization of a batch ethanol fermentation process. J. Bioprocess. Biotech. 2016, 6, 266. [Google Scholar]
- Gòdia, F.; Casas, C.; Solá, Ç. Mathematical modelization of a packed-bed reactor performance with immobilized yeast for ethanol fermentation. Biotechnol. Bioeng. 1987, 30, 836–843. [Google Scholar] [CrossRef]
- Melick, M.R.; Karim, M.N.; Linden, J.C.; Dale, B.E.; Mihaltz, P. Mathematical modeling of ethanol production by immobilized Zymomonas mobilis in a packed bed fermenter. Biotechnol. Bioeng. 1987, 29, 370–382. [Google Scholar] [CrossRef]
- Nath, S.; Chand, S. Mass transfer and biochemical reaction in immobilized cell packed bed reactors: Correlation of experiment with theory. J. Chem. Tech. Biotechnol. 1996, 66, 286–292. [Google Scholar] [CrossRef]
- Converti, A.; del Borghi, M. A new kinetic approach to the fermentation of multisubstrate complex media. Appl. Biochem. Biotechnol. 1991, 30, 361–373. [Google Scholar]
- Lee, C.G.; Kim, C.H.; Rhee, S.K. A kinetic model and simulation of starch saccharification and simultaneous ethanol fermentation by amyloglucosidase and Zymomonas mobilis. Bioprocess Eng. 1992, 7, 335–341. [Google Scholar] [CrossRef]
- Liu, D.; Xu, L.; Xiong, W.; Zhang, H.T.; Lin, C.C.; Jiang, L.; Xu, B. Fermentation process modeling with Levenberg-Marquardt algorithm and Runge-Kutta method on ethanol production by Saccharomyces cerevisiae. Math. Prob. Eng. 2014, 2014, 289492. [Google Scholar] [CrossRef]
- Vásquez, J.E.; Quintero, J.C.; Ochoa-Cácere, S. Modeling of a simultaneous saccharification and fermentation process for ethanol production from lignocellulosic wastes by Kluyveromyces marxianus. DYNA 2014, 81, 107–115. [Google Scholar]
- Oliveira, S.C.; Paiva, T.C.B.; Visconti, A.E.S.; Giudici, R. Discrimination between ethanol inhibition models in a continuous alcoholic fermentation process using flocculating yeast. Appl. Biochem. Biotechnol. 1998, 74, 161–172. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.I.C.; Cooney, C.L.; Demain, A.L.; Dunnill, P.; Humphrey, A.E.; Lilly, M.D. Fermentation and Enzyme Technology; John Wiley: New York, NY, USA, 1979. [Google Scholar]
- Bailey, J.E.; Ollis, D.F. Biochemical Engineering Fundamentals, 2nd ed.; Mc. Graw-Hill: New York, NY, USA, 1986. [Google Scholar]
- Hannoun, B.J.; Stephanopoulos, G. Diffusion coefficients of glucose and ethanol in cell-free and cell-occupied calcium alginate membranes. Biotechnol. Bioeng. 1986, 28, 829–835. [Google Scholar] [CrossRef] [PubMed]
- Blanch, H.W.; Clark, D.S. Biochemical Engineering; Marcel Dekker: New York, NY, USA, 1997. [Google Scholar]
- Pereira, F.M.; Oliveira, S.C. Occurrence of dead core in catalytic particles containing immobilized enzymes: Analysis for the Michaelis-Menten kinetics and assessment of numerical methods. Bioprocess. Biosyst. Eng. 2016, 39, 1717–1727. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Oliveira, S.C. Evaluation of effectiveness factor of immobilized enzymes using Runge-Kutta-Gill method: How to solve mathematical undetermination at particle center point. Bioprocess Eng. 1999, 20, 185–187. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Froment, G.F.; Bischoff, K.B.; De Wilde, J. Chemical Reactor Analysis and Design, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Fogler, E.H. Elements of Chemical Reaction Engineering, 3rd ed.; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Ramirez, W.F. Computational Methods for Process Simulation, 2nd ed.; Butterworth Publishers: Oxford, UK, 1997. [Google Scholar]
- Rice, R.G.; Do, D.D. Applied Mathematics and Modeling for Chemical Engineers; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Hamamci, H.; Ryu, D.D.Y. Performance of tapered column co-packed bed bioreactor for ethanol production. Biotechnol. Bioeng. 1987, 29, 994–1002. [Google Scholar] [CrossRef]
- Ramakrishna, S.V.; Prema, P.; Sai, P.S.T. Performance of cell immobilized packed bed bioreactor for continuous fermentation of alcohol. Bioprocess Eng. 1991, 6, 117–121. [Google Scholar] [CrossRef]
- Himmelblau, D.M. Process Analysis by Statistical Methods; John Wiley & Sons: New York, NY, USA, 1970. [Google Scholar]
- Constantinides, A.M.N. Numerical Methods for Chemical Engineers with MATLAB Applications; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Gencer, M.A.; Muthrasan, R. Ethanol Fermentation in a yeast immobilized tubular fermentor. Biotech. Bioeng. 1983, 25, 2243–2261. [Google Scholar] [CrossRef]
- Jiménez-Islas, D.; Páez-Lerma, J.; Soto-Cruz, N.O.; Gracida, J. Modelling of Ethanol Production from Red Beet Juice by Saccharomyces cerevisiae under Thermal and Acid Stress Conditions. Food Technol. Biotechnol. 2014, 52, 93–100. [Google Scholar]
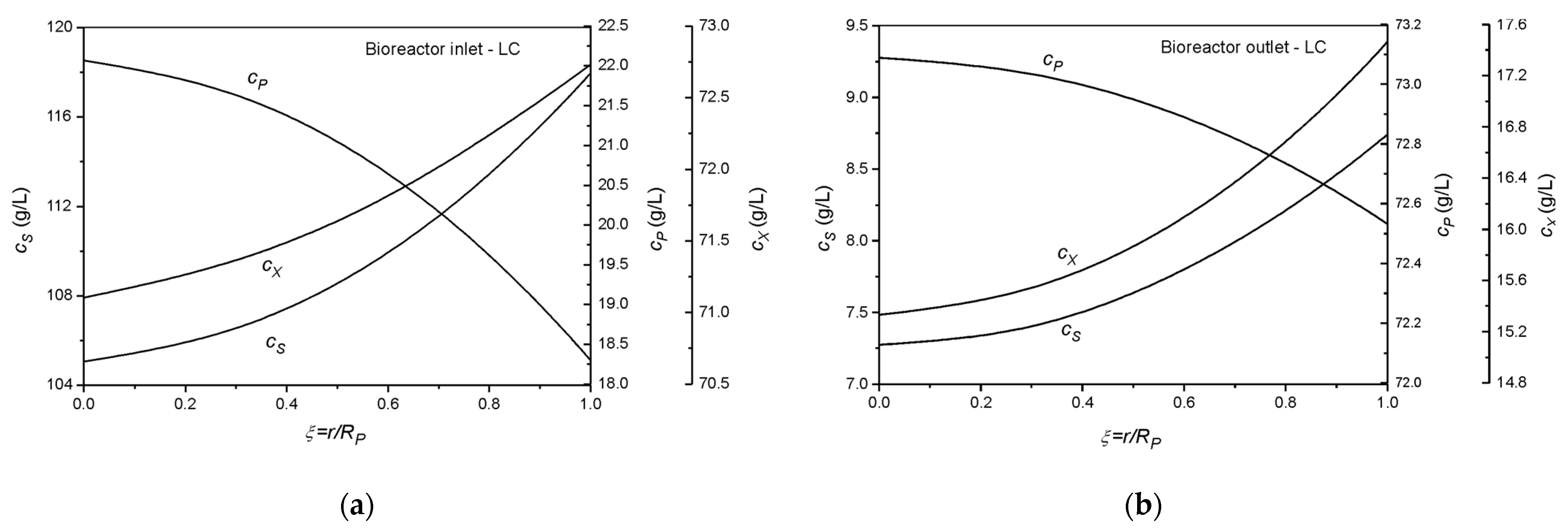
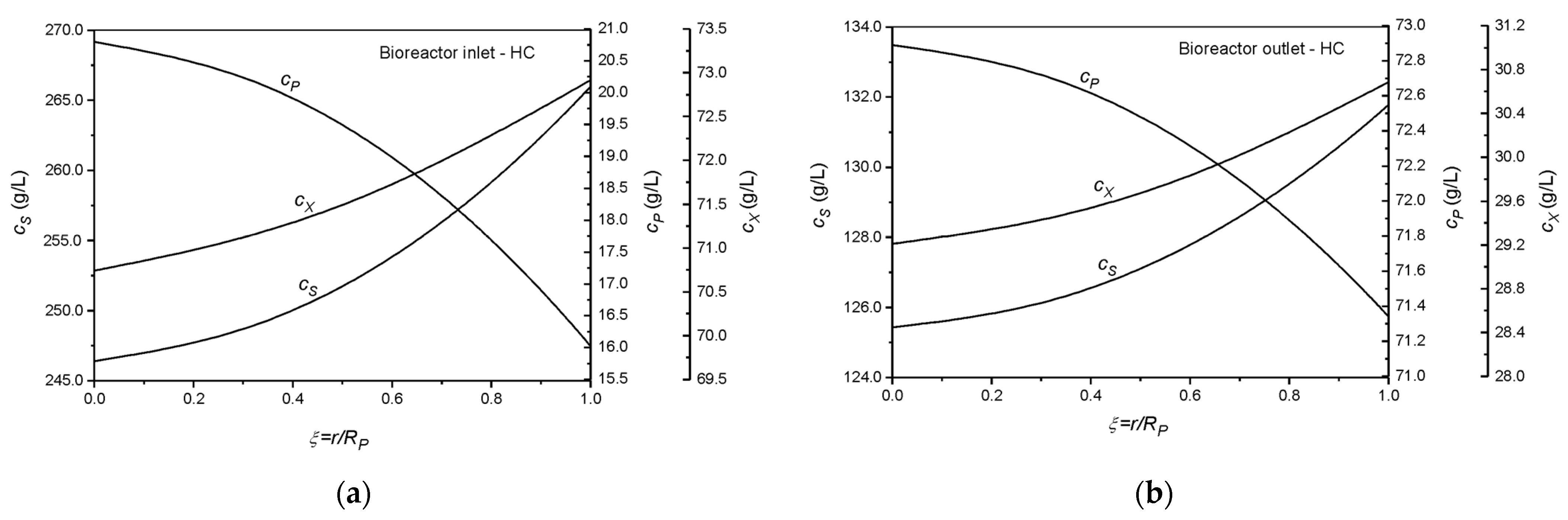
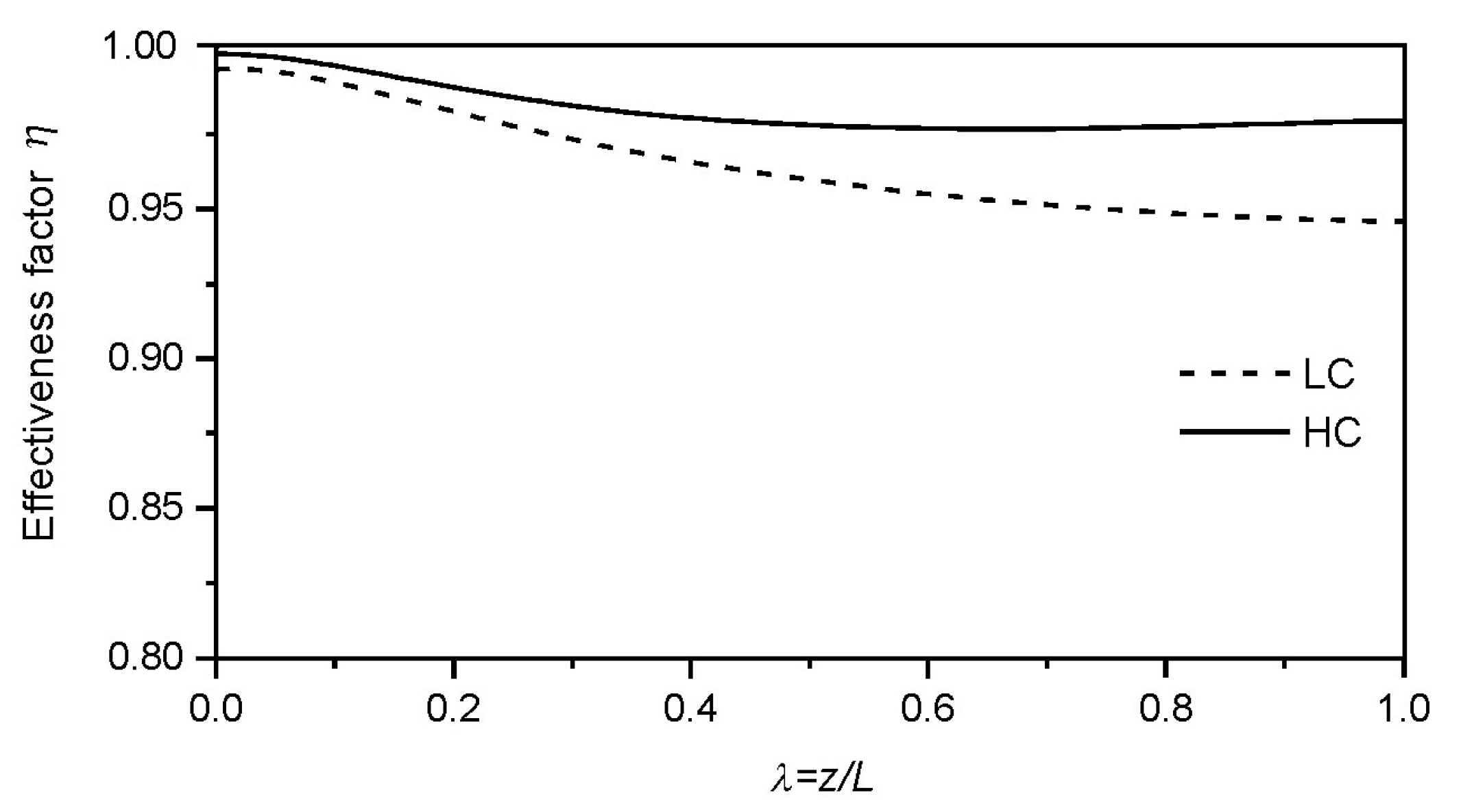
| Collocation Point | ξ = r/Rp (Particle) | λ = z/L (Reactor) | W (Weight) |
|---|---|---|---|
| 1 | - | 0.0000000 | - |
| 2 | 0.2957658 | 0.0694318 | 0.02509 |
| 3 | 0.5652353 | 0.3300095 | 0.07925 |
| 4 | 0.7844835 | 0.6699905 | 0.11520 |
| 5 | 0.9340014 | 0.9305682 | 0.09562 |
| 6 | 1.0000000 | 1.0000000 | 0.01818 |
| Kinetic Parameters | Physical Parameters | Operating Conditions |
|---|---|---|
| (including the headspace) | ||
| Variable | R2 | Feed Substrate Concentration/Position/State |
|---|---|---|
| 0.98 | LC/Exit Reactor/Transient State | |
| 0.98 | HC/Exit Reactor/Transient State | |
| 0.96 | LC/Exit Reactor/Transient State | |
| 0.97 | HC/Exit Reactor/Transient State | |
| 0.96 | LC/Axial Position/Steady State | |
| 0.90 | HC/Axial Position/Steady State | |
| 0.96 | LC/Axial Position/Steady State | |
| 0.90 | HC/Axial Position/Steady State |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stremel, D.; Pulitano, V.; Oliveira, S. Mathematical Modeling and Dynamic Simulation of a Tower Reactor for Intensified Ethanol Fermentation with Immobilized Yeasts and Simultaneous Gas Removal. Processes 2025, 13, 1122. https://doi.org/10.3390/pr13041122
Stremel D, Pulitano V, Oliveira S. Mathematical Modeling and Dynamic Simulation of a Tower Reactor for Intensified Ethanol Fermentation with Immobilized Yeasts and Simultaneous Gas Removal. Processes. 2025; 13(4):1122. https://doi.org/10.3390/pr13041122
Chicago/Turabian StyleStremel, Dile, Valéria Pulitano, and Samuel Oliveira. 2025. "Mathematical Modeling and Dynamic Simulation of a Tower Reactor for Intensified Ethanol Fermentation with Immobilized Yeasts and Simultaneous Gas Removal" Processes 13, no. 4: 1122. https://doi.org/10.3390/pr13041122
APA StyleStremel, D., Pulitano, V., & Oliveira, S. (2025). Mathematical Modeling and Dynamic Simulation of a Tower Reactor for Intensified Ethanol Fermentation with Immobilized Yeasts and Simultaneous Gas Removal. Processes, 13(4), 1122. https://doi.org/10.3390/pr13041122








