Abstract
The randomness, volatility, and intermittency of renewable energy sources such as wind and solar energy present significant challenges to energy management in microgrids, resulting in low management efficiency and poor accuracy. This paper proposes an energy optimization method for microgrids based on an uncertainty-aware deep deterministic policy gradient (DDPG) algorithm. First, considering the uncertainty of renewable energy output, an uncertainty awareness model is constructed based on information gap decision theory (IGDT). Second, the DDPG algorithm is employed to optimize the energy scheduling strategy, incorporating a bidirectional feedback collaborative optimization framework. The uncertainty radius is used for forward feedback adjustment of the optimization step size of the DDPG model, while the risk-aversion coefficient of the IGDT model is adjusted via backward feedback based on the DDPG optimization results. This approach enables adaptive regulation in dynamic and complex environments. The research demonstrates that the proposed algorithm significantly enhances the robustness, convergence, and adaptability of the microgrid in uncertain environments, improving peak shaving and valley filling performance as well as the adaptability to fluctuations in renewable energy sources. The proposed method demonstrates significant improvements in robustness, convergence speed, and adaptability when applied to microgrid energy management. Numerical results show a 5.44% and 70.26% improvement in total microgrid revenue compared to baseline algorithms, highlighting the effectiveness of the uncertainty-aware DDPG algorithm in dynamic and uncertain environments.
1. Introduction
With the deepening reforms in power systems, traditional large-scale centralized energy supply models are undergoing a transformation towards more flexible and efficient microgrid and smart grid models [1]. A microgrid is a regional energy interconnection network that builds a smaller-scale power system based on local distribution networks [2]. This system enables efficient energy distribution within a limited area and features flexibility and reliability. Unlike traditional grid models, which rely on large-scale centralized power deployment, microgrids, which integrate distributed energy sources such as wind and solar energy, offer significant potential for improving energy efficiency and sustainability. Additionally, with the help of distributed generators and energy storage facilities, microgrids effectively balance local energy generation and user consumption. Research on microgrid energy management is essential for flexibly adjusting power generation, transmission, distribution, and consumption equipment in response to variations in energy demand and environmental conditions [3]. This, in turn, ensures the stability and reliability of the power supply. However, the integration of renewable energy sources into microgrids introduces significant challenges due to the inherent randomness, volatility, and intermittency of these sources [4]. These characteristics lead to source–load fluctuations that make it difficult to accurately control energy demand and output variations, resulting in low energy management efficiency and poor accuracy. Uncertainty awareness, by quantifying and evaluating the uncertainty of renewable energy output, enables the adjustment of energy management strategies, significantly improving the economy and robustness [5,6]. However, existing energy optimization methods for microgrids often fail to adequately address these uncertainties, leading to suboptimal performance. Therefore, there is an urgent need to develop advanced energy optimization strategies that can effectively incorporate uncertainty awareness to enhance the robustness, adaptability, and overall efficiency of microgrids. This highlights the need for advanced energy management strategies that can effectively address these uncertainties and improve the overall performance of microgrids.
Deep reinforcement learning (DRL) offers advantages such as automatic feature learning, strong adaptability to complex environments, and effective handling of high-dimensional state spaces, making it widely applied in microgrid energy management. Zhou et al. proposed a generalized dynamic non-smooth control framework combined with the deep actor–critic (DAC) algorithm, which uses the adaptability of non-smooth control to achieve DC microgrid control [7]. A real-time scheduling strategy was developed to realize economic scheduling for microgrid energy storage based on a dual deep Q-network (DQN) algorithm [8]. Compared to DAC and DQN, the deep deterministic policy gradient (DDPG) algorithm has clear advantages in handling continuous action spaces, improving sample efficiency, and enhancing stability, making it more suitable for microgrid energy optimization scenarios. Buraimoh et al. proposed a real-time energy management method based on distributed DDPG, which dynamically adjusts power generation and storage usage. It can ensure efficient energy utilization within the microgrid and adapt to different microgrid configurations [9]. A real-time microgrid optimization method based on the DDPG algorithm was proposed to achieve optimal scheduling strategies through offline training and online decision-making, addressing the impact of non-linear constraints from distributed renewable energy on microgrids [10]. However, these studies generally fail to incorporate comprehensive uncertainty awareness mechanisms. As a result, they are highly susceptible to disturbances caused by load fluctuations and the inherent intermittency and volatility of renewable energy sources. This limitation leads to several critical issues: First, the optimization strategies for microgrid energy management may become unstable under dynamic operating conditions, resulting in frequent and unpredictable adjustments to the energy scheduling plans. Second, the lack of robustness against uncertainties can degrade the overall performance of the algorithms, reducing their convergence speed and accuracy. Finally, without proper uncertainty awareness, these methods may struggle to balance economic efficiency and system stability, especially in the face of severe fluctuations in renewable energy output and load demand. Overall, these shortcomings highlight the necessity for a more adaptive and uncertainty-aware approach to enhance the reliability and effectiveness of microgrid energy optimization.
To enhance the scheduling capabilities of microgrids in uncertain environments, many scholars have proposed various uncertainty optimization methods, such as robust optimization, chance-constrained optimization, and conditional value-at-risk (CVaR) optimization. The robust optimization method guarantees that the system maintains good performance under extreme uncertainties by optimizing decisions for the worst-case scenario. Nishida et al. proposed a robust optimization model to address the regulation risks introduced by the fluctuations in wind and solar energy outputs. It also ensures the stability and reliability of the system by considering optimal solutions under different uncertainty scenarios [11]. Liu et al. proposed a trading energy framework for the coordinated energy management of interconnected microgrids in future distribution systems. The distribution network operator does not directly coordinate signals and fixed pricing schemes, but organizes a trading market with MG to coordinate energy management in operation. In addition, an algorithm based on distributed robust optimization has been developed to provide robust solutions for detailed scheduling decisions in the proposed trading energy framework under uncertainty [12]. The chance-constrained optimization method optimizes the system operation by modeling uncertainty under a specified reliability level. A microgrid energy scheduling strategy based on the chance-constrained optimization model was constructed to satisfy demand with high probability, effectively reducing the system energy scheduling risks [13]. The CVaR optimization method optimizes losses at a specific confidence level by quantifying risk. Ran et al. proposed a microgrid scheduling method based on CVaR by considering uncertainties and risks, which ensures the system can maintain acceptable operation performance for unforeseen fluctuations [14]. Although the above methods have made progress in addressing uncertainty issues, they often rely on assumptions about the probabilistic distributions of uncertain variables, which are difficult to be obtained accurately in practical applications. In contrast, information gap decision theory (IGDT) offers a novel approach to addressing this challenge. IGDT does not require the exact probabilistic distributions of uncertain variables. Instead, it optimizes decisions by setting information gaps, i.e., constraining the uncertainty intervals, thereby enhancing decision flexibility and adaptability. A wide-area power system robust stabilizer based on IGDT was designed by considering the power output fluctuations from wind farms and transmission line interruptions, effectively improving the robustness of wind farm regulation [15]. Nasr et al. introduced an energy management system considering the optimal power flow framework for linking unit commitment. This system effectively handles uncertainties caused by generator switching states and power flow constraints through IGDT [16]. Li et al. proposed a 5G BS integrated BS aggregation regulation and collaborative scheduling method that considers PV load uncertainty, in which a PV load uncertainty model was established based on IGDT [17]. However, the aforementioned studies generally lack sophisticated dynamic feedback mechanisms, which prevents real-time adjustments to model parameters based on current states and empirical performance. This limitation leads to several challenges: First, these models cannot adaptively respond to rapid changes in microgrid conditions, such as fluctuations in renewable energy generation or load demand. Second, the absence of real-time adjustments restricts the models’ ability to learn from past performance and optimize parameters, which is crucial for maintaining accuracy and efficiency. Third, the static nature of these models makes them less robust and more prone to errors in complex, time-varying microgrid scenarios. Overall, these shortcomings highlight the need for advanced feedback mechanisms to enhance adaptability, responsiveness, and performance in microgrid applications.
In summary, the current research on microgrid energy optimization still faces the following challenges: First, there is a lack of effective uncertainty awareness mechanisms, making it difficult to address the uncertainty risks brought by the volatility and intermittency of renewable energy integration. Second, traditional DDPG algorithms suffer from poor convergence performance and unstable optimization processes in microgrid scenarios with uncertainty factors, which affect the algorithm optimization efficiency. Finally, traditional IGDT models and DDPG algorithms lack suitable feedback mechanisms and cannot dynamically adapt to environmental changes, thus impacting the accuracy and robustness of optimization results.
To address the above challenges, this paper proposes an energy optimization strategy for microgrids based on uncertainty-aware DDPG. First, a microgrid revenue and cost model is constructed to reasonably model each microgrid entity and establish the energy management optimization problem aimed at maximizing the microgrid operation revenue. Next, a microgrid energy management algorithm based on uncertainty-aware DDPG is introduced, which designs the uncertainty awareness model using IGDT theory and addresses energy optimization strategies through the uncertainty-aware DDPG model. This method also introduces a bidirectional feedback collaborative optimization mechanism. The optimization step size of the DDPG model is forward-fed according to the uncertainty radius calculated by the IGDT model. In parallel, based on the DDPG optimization results, the risk-aversion coefficient of the IGDT model is adjusted through backward feedback, considering the current uncertainty state and historical performance data. This enhances the algorithm’s adaptability to dynamic, time-varying microgrid environments. Finally, simulation results are provided to validate the superiority and feasibility of the proposed method. The innovations of this work are as follows:
- An uncertainty awareness model of renewable energy output based on IGDT is proposed, employing uncertainty intervals for decision optimization without relying on precise probability distribution assumptions. This enhances the robustness and stability of the microgrid for renewable energy volatility and other uncertainties.
- A microgrid energy optimization algorithm based on uncertainty-aware DDPG is proposed. Through forward feedback of equivalent uncertainty radius, the optimization step size is adaptively adjusted. When the environment uncertainty is high, the step size is reduced to improve stability, while under low uncertainty, the step size is increased to accelerate the decision-making process. This method better addresses external fluctuations and improves the economy, stability, and overall operation efficiency of the microgrid.
- An IGDT risk-aversion coefficient adaptive adjustment method based on the backward feedback of DDPG optimization results is proposed. Based on the DDPG optimization results, this method adjusts the risk-aversion coefficient considering current uncertainty state and historical performance data. It increases the real-time decision-making and uncertainty-aware capabilities of the microgrid in complex environments, improving optimization efficiency while ensuring system stability.
2. Microgrid Revenue and Cost Model
Optimization time includes T time slots, represented by the set , with each time slot having a duration of . In each time slot, the microgrid utilizes an energy management system to implement unified management and regulation of internal resources, which include micro gas turbines (MGTs), photovoltaic arrays (PVAs), wind turbines (WTs), energy storage units (ESs), and loads. Specifically, is dynamically adjusted according to the volatility of renewable energy and load fluctuations. When the uncertainty is high, a smaller step size is used to improve stability and avoid overshooting during the optimization process; when it is more stable, a larger step size is used to speed up the convergence.
2.1. Micro Gas Turbines Model
In a microgrid, MGTs are characterized by stable power generation and quick response, making them suitable as a backup power source for the system to enhance its stability. The revenue from MGT represents the revenue earned from electricity sales, which is expressed as
where denotes the revenue from MGTs, represents the real-time electricity price in time slot t, and denotes the output power of the MGT in time slot t.
The cost of MGT consists of three components: fuel expenses required for their operation, device maintenance costs, and treatment costs of pollutants, which is expressed as
where denotes the cost of MGTs and and are the fuel gas selling price per unit and the lower heating value of fuel gas, respectively. represents the power generation efficiency of MGTs in the microgrid. is the index for different types of pollutants generated during the operation of MGTs. denotes the cost of treating per unit mass of pollutant i. is the mass of pollutant i emitted by MGTs when generating unit power. is the operation and maintenance cost coefficients per unit time for MGTs and denotes the operation and maintenance cost of MGTs in time slot t.
To ensure that the MGT does not exceed its designed performance limits, its output power cannot surpass its nominal maximum rated power. Additionally, to prevent the device from operation under no-load conditions, thereby avoiding unnecessary wear and tear and inefficiency, a minimum output power limit should also be set. Therefore, the power constraint condition for MGTs is expressed as
where and are the upward and downward ramp rate limits, respectively, for the MGTs in the microgrid.
2.2. Photovoltaic Arrays and Wind Turbines Model
The revenue of PVAs and WTs consists of two parts: revenue from photovoltaic power generation transactions and revenue from wind power transactions. The revenue of PVAs and WTs is expressed as
where denotes the revenue of PVAs and WTs, represents the output power of the PVAs in time slot t, and denotes the output power of the WTs in time slot t.
The cost of PVAs and WTs consists of three parts: maintenance costs for PVAs and WTs, curtailment costs for unused solar energy, and curtailment costs for unused wind energy, which is expressed as
where denotes the cost of PVAs and WTs, represents the operation and maintenance cost for PVAs and WTs in time slot t, and represents the operation and maintenance cost parameter per unit time. is the curtailment cost for unused solar energy, represents the penalty parameter per unit of curtailed solar energy in the microgrid. denotes the output power of PVAs in time slot t. is the curtailment cost for unused wind energy and and represents the penalty parameter per unit of curtailed wind energy in the microgrid. denotes the output power of WTs in time slot t.
The constraints that the output of PVAs and WTs should follow are expressed as
2.3. Energy Storage Model
The ES device possesses dual attributes: during charging, it acts as a load, and during discharging, it serves as a power source. It can alleviate the temporal and spatial mismatch between renewable energy output and load demand, primarily playing a role in balancing power and reducing peak loads and filling valleys. The revenue from ES in a microgrid represents the income earned from selling surplus power to the grid, which is
where denotes the revenue from ES. is an indicator variable for the charging and discharging of ES, taking a value of 1 when ES is discharging and 0 otherwise. represents the discharging power of ES in time slot t.
The cost of ES is mainly composed of two parts: the cost of purchasing electricity from the grid and the operation and maintenance cost of the ES device, which is expressed as
where denotes the cost of ES. represents the charging power of ES in time slot t. is the operation and maintenance cost parameter per unit time for the ES device. denotes the operation and maintenance cost of the ES device in time slot t.
The constraints that the output of ES should follow are expressed as
where denotes the charged capacity of the ES in time slot t, denotes the prescriptive minimum capacity of the ES, is the maximum charging power of the ES, and is the maximum discharging power.
2.4. User Load Model
In microgrid systems, users’ electricity demand is classified into dispatchable flexible loads and critical important loads. Important loads, due to their necessity and urgency, are typically fixed and constrained, and they are not discussed in this context. Flexible loads refer to those that can adjust their electricity consumption patterns according to grid operation conditions and demand changes. These loads can flexibly increase or decrease electricity usage under the guidance of grid dispatch, contributing to mitigating the difference of peak and valley. Through coordinated cooperation with ES systems, flexible loads can effectively increase the utilization rate of renewable energy.
The cost of flexible loads mainly consists of three main components, including electricity consumption cost, discomfort cost, and device operation and maintenance cost. The cost of users’ flexible loads is expressed as
where is the index for different flexible loads, denotes the actual power consumption of the l-th flexible load in time slot t and is the discomfort cost, reflecting the economic impact of reduced user comfort due to restrictions or adjustments in electricity use. is the planned electricity consumption of the l-th flexible load in time slot t, and is the willingness parameter for the l-th flexible load; a higher value of this parameter indicates that the user is more inclined to follow the original electricity consumption plan. is the operation and maintenance cost parameter per unit time for user load equipment and denotes the operation and maintenance cost of user load equipment in time slot t.
2.5. Formulation of Optimization Problem
This paper addresses the key issue of coordinated energy management for multiple types of resources in a microgrid. By jointly optimizing the output power of MGTs, PVAs, and WTs; the charging and discharging power of ES; and the actual power consumption of flexible loads, the operation revenue of the microgrid is maximized. The optimization problem is formulated as
where represents the time-series decomposition value of the optimization objective, which will be used in subsequent algorithm solving to improve the model’s dynamic adjustment capability.
3. Energy Optimization Algorithm for Microgrids Based on Uncertainty-Aware DDPG
The problem of microgrid energy optimization is highly complex, especially after the integration of renewable energy sources such as wind and solar power. The randomness and dynamics of these energy sources introduce volatility and intermittency, posing significant challenges to energy management. Traditional DDPG methods, while performing well in continuous action spaces and dynamic environments, overly rely on deterministic models or models with uncertainty assumptions. This leads to issues such as sensitivity to optimization step size parameters and poor adaptability to uncertainty, resulting in unstable training in complex environments and affecting optimization efficiency.
To address the aforementioned issues, this paper proposes an energy optimization algorithm for microgrids based on uncertainty-aware DDPG. The principle of the algorithm is illustrated in Figure 1. Firstly, an IGDT-based uncertainty awareness model is constructed, and an uncertainty-aware DDPG model is introduced to solve the energy management strategy. On this basis, a bidirectional feedback collaborative optimization framework is designed. The uncertainty radius calculated by the IGDT model is used for forward feedback adjustment of the optimization step size of the DDPG model. Combining the optimization results of DDPG, the risk-aversion coefficient of the IGDT model is adjusted through backward feedback based on the current uncertainty state and historical performance data, in order to improve the algorithm’s adaptability, stability, and optimization efficiency in uncertain environments.
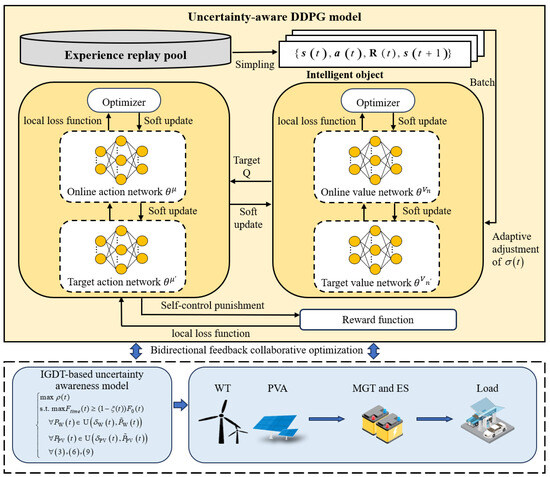
Figure 1.
Energy optimization algorithm schematic diagram for microgrids based on uncertainty-aware DPGG.
3.1. IGDT-Based Uncertainty Awareness Model
The IGDT method effectively deals with uncertainty by analyzing the mechanism of uncertainty risk and quantifying the error between the predicted and actual values of uncertain parameters. IGDT represents uncertainty as a function of predictive variables. After obtaining the predicted values of wind and solar power output through calculation, it adds a description of the fluctuation in the predicted values of uncertain parameters, thereby constructing the corresponding uncertainty set.
In deterministic models, the probability density of WT output is expressed as
where d represents the shape parameter of the probability density distribution curve for WT output, is the scale parameter, and is the predicted value with the highest probability density for WT output in time slot t.
The output of PVAs is positively correlated with irradiance. It is assumed that the probability density of irradiance in the microgrid follows a Beta distribution [18]. Therefore, the probability density of the output of PVAs is expressed as
where and are the shape parameters of the probability density distribution curve for PVA output, which are calculated based on the characteristics of the probabilistic distribution of irradiance. denotes the Gamma function. is the predicted value of PVA output where the probability density is maximized.
Using the envelope boundary uncertainty model to mechanistically model the uncertainty of wind and solar power output, the corresponding uncertainty set is expressed as
where and are the uncertainty radii for WT and PVA output, respectively. and represent the fluctuation ranges of the uncertain parameters for WT and PVA output, respectively.
The risk-averse robust model provided by IGDT can cater to the needs of conservative decision-makers. Its purpose is to identify the largest set of uncertain variables that can meet predefined objectives, thereby mitigating risks associated with uncertainty. Fluctuations in energy sources and loads mostly exert adverse effects on energy optimization outcomes. In response to this, this paper adopts a risk-averse robust model, assigning different weights to the uncertainty radii of uncertain parameters for PVAs and WTs. The uncertainties are unified through a weighted sum approach, resulting in an equivalent uncertainty radius for the combined uncertain parameters. The specific model is defined as
where denotes the uncertainty radius of the equivalent uncertain parameter and and are the weights of the uncertainty radii for the power output fluctuations of WTs and PVAs, respectively, satisfying the condition that .
The risk-averse robust model can be expressed as
where is the benchmark value, representing the operation revenue of the microgrid when the uncertain parameters of wind and solar power take their predicted values. is the risk-aversion coefficient, which reflects the preference for robustness in decision-making and will be introduced in detail later with its feedback process. Equation (16) represents a bi-level scheduling model. The objective function at the upper level is to maximize the uncertainty radius of the power output of PVAs and WTs under the constraints of the regulation decisions at the lower level. A larger value of indicates better robustness of the system, but correspondingly, reduces the achievable revenue of the microgrid. The objective function at the lower level is to optimize the operation revenue of the microgrid through risk-averse decisions, intending to restrict the energy optimization decisions in the model within the uncertainty set.
3.2. Uncertainty-Aware DDPG Model with Forward Feedback
Addressing the aforementioned energy optimization problem, this section constructs a Markov decision process (MDP) model to solve it using reinforcement learning algorithms. An MDP model is generally represented by a 3-tuple ,where denotes the state space, denotes the action space, and R denotes the reward function. Below is the specific modeling process.
- (1)
- State Space: The state space includes the real-time output of PVAs and WTs, the state of charge of ES, the planned electricity consumption of flexible loads, real-time electricity prices, and the optimization time slot of the microgrid operation environment, which is expressed as
- (2)
- Action Space: The action space encompasses the output power of MGTs, the output power of PVAs and WTs, the charging and discharging states of ES, the charging and discharging power of ES, and the actual power consumption of flexible loads, which is expressed as
- (3)
- Reward Function: The reward function is denoted as .
The DDPG algorithm is based on the actor–critic (AC) algorithm framework, with the actor network serving as the policy network and the critic network serving as the value network. Additionally, the DDPG algorithm adopts the experience replay mechanism and the separate target network structure from the DQN algorithm. The policy network consists of an online network and a target network, denoted as and , respectively, where represents the parameters of the online policy network and represents the parameters of the target policy network. During the exploration and learning process of the DDPG algorithm, when the current state of the microgrid operation environment is input into the current policy network, the network will output an action based on a deterministic policy , which is expressed as
The task of the value network is to evaluate the generated actions by fitting the value function. It includes two parts: an online network and a target network, denoted as and , respectively, where represents the parameters of the online value network and represents the parameters of the target value network. Under a given state , the online value network generates an action , and after obtaining a reward , the action together with the state form an experience tuple that is stored in the experience replay buffer as a training sample. The specific training process is as follows.
Firstly, after the experience replay buffer reaches a certain size, N random samples of experience tuples are drawn from the experience replay. The target value and the loss function are then computed using the online value network, which are expressed as
where n denotes the index of the sampled training sample.
Then, the online policy network is updated using a gradient descent strategy and by minimizing the loss function, which is expressed as
where represents the current optimization step size. To enhance the uncertainty awareness capability of the DDPG model, this paper incorporates forward feedback based on the equivalent uncertainty radius calculated by the IGDT model at the beginning of time slot t. This feedback enables adaptive adjustment of the optimization step size, which is expressed as
where denotes the base step size under no uncertainty. The equation implies that if the uncertainty radius is large, indicating significant fluctuations in the external environment, the step size should be reduced to enhance the stability of the decision. Conversely, if the uncertainty radius is small, suggesting a relatively stable environment, the step size can be appropriately increased to accelerate the optimization process and improve the efficiency of finding the optimal solution. Thus, this approach can enhance the awareness and adaptability of the DDPG algorithm to the highly uncertain environment of microgrids.
Finally, the target policy network and the target value network are updated using a soft update method, which is expressed as
where denotes the rate of soft update for the target networks.
3.3. IGDT Risk-Aversion Coefficient Adaptive Adjustment Method Based on Backward Feedback of DDPG Optimization Results
Considering that traditional IGDT models primarily deal with static uncertain parameters, this paper proposes an adaptive adjustment method for the IGDT risk-aversion coefficient based on the backward feedback of DDPG optimization results. This method aims to improve the algorithm’s decision-making capability under complex conditions, enabling the microgrid to maintain efficient and stable operation in a real-time changing environment. The specific process is expressed as
where denotes the adjustment magnitude of the risk-aversion coefficient at time slot represents the adjustment magnitude considering uncertainty fluctuations. If the uncertainty fluctuation level at the time slot is high, is increased to elevate the risk-aversion coefficient at time slot , allowing for better handling of uncertainty risks. Conversely, if the fluctuation level is low, the risk-aversion coefficient is decreased to enhance system flexibility. denotes the adjustment magnitude considering historical performance. If the DDPG optimization results at time slot t have a positive impact on historical performance, the risk-aversion coefficient at time slot is reduced to pursue economic efficiency. Otherwise, the risk-aversion coefficient is increased to promote robust decision-making by the system. and are weight coefficients that balance the two adjustment terms. The algorithm flow is shown in Figure 2.
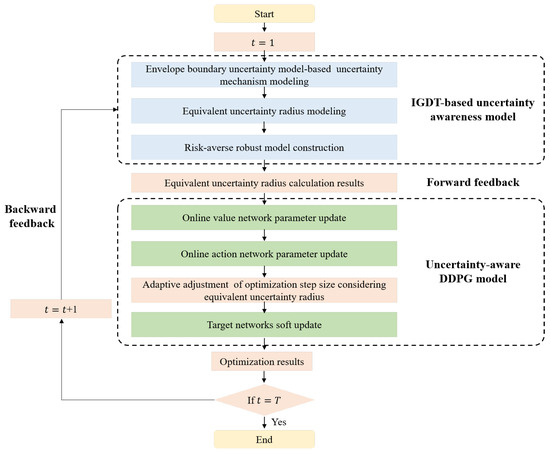
Figure 2.
The proposed algorithm flowchart.
3.4. Algorithm Complexity Analysis
The time complexity of the DDPG model is generally related to the size of the neural network, the number of training episodes, and the number of time steps per episode. Assuming there are E training episodes in total, and the total number of parameters in the DDPG neural network is N, then the time complexity can be expressed as . In comparison, the data complexity of the forward feedback process for optimizing the step size mainly arises from the calculation of the uncertainty radius, with a complexity of . This complexity is negligible compared to the overall complexity of the DDPG algorithm.
For the IGDT-based uncertainty awareness model, similar to the forward feedback process, its complexity arises from the uncertainty modeling of WT and PVA output. The computational complexity is of constant order, having a minor impact on the overall complexity of the algorithm. Therefore, the microgrid energy optimization algorithm based on uncertainty-aware DDPG has a complexity approximately equal to .
4. Simulation
In order to verify the validity of the proposed model, the typical daily load data of a microgrid in summer are selected for simulation. This dataset contains daily load data from 1 June 2023 to 30 June 2023, with a time range covering the summer peak load period. There are a total of 3000 data entries covering 24 h of daily load records. Each record item contains the load value and its corresponding timestamp. Table 1 and Table 2 list the main parameters. The simulation was carried out using MATLAB R2022a (9.12.0.1884302), 64-bit version (released on 16 February 2022).

Table 1.
Main parameters [19].

Table 2.
Time-of-use electricity price.
Figure 3 and Figure 4 depict the distribution of microgrid user load and the output distribution of wind and solar power, respectively. These figures provide a comprehensive overview of the temporal variations in load demand and renewable energy supply, which are essential for understanding the operational dynamics of the microgrid. These insights are critical for evaluating the effectiveness of the proposed energy management strategy. To systematically assess the proposed algorithm, we conducted a comparative analysis using two established baselines. Baseline 1 employs a DDPG algorithm augmented with uncertainty considerations [20], while Baseline 2 utilizes the conventional DDPG algorithm without any feedback mechanisms [21]. Both baselines share the same optimization objective as the proposed algorithm: to maximize the operational revenue of the microgrid. Specifically, Baseline 1 incorporates forward feedback but lacks backward feedback, whereas Baseline 2 does not feature any feedback mechanisms. Through this comparative analysis, we elucidate the superior adaptability of the proposed algorithm in addressing the inherent volatility and uncertainty associated with renewable energy sources, thereby enhancing the robustness and economic efficiency of microgrid operations.
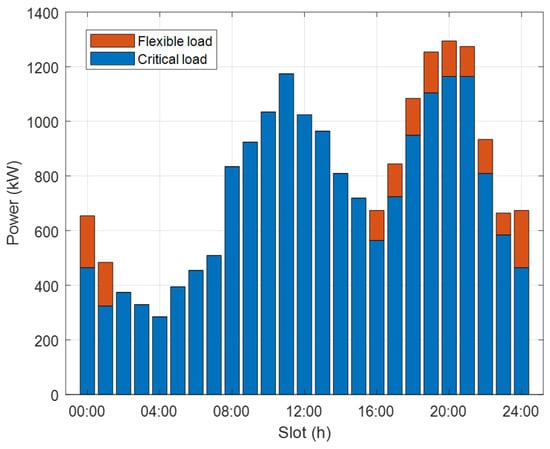
Figure 3.
Microgrid user load distribution.
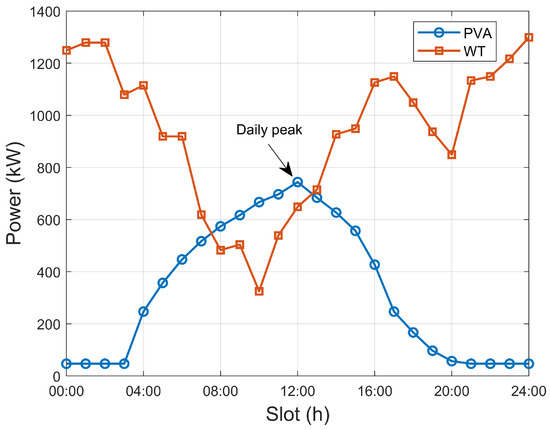
Figure 4.
Microgrid wind and solar power output distribution.
Figure 5 illustrates the comparison of the microgrid user load curve after optimization adjustment. As shown in the figure, the power consumption of users decreases during the periods of 00:00–01:00, 09:00–10:00, and 15:00–21:00, while it increases during the periods of 08:00–10:00 and 21:00–24:00. These changes reflect the rational adjustment and redistribution of flexible loads while ensuring that the basic electricity demand is met. Through this optimized scheduling, some of the peak-hour loads are successfully transferred to the off-peak hours of 04:00–16:00, effectively balancing the load peaks and valleys. Therefore, the optimization strategy proposed in this paper not only alleviates the power supply pressure of the microgrid system to a certain extent but also enhances the system’s stability and operational efficiency through peak shaving and valley filling. Additionally, this optimization strategy reduces the reliance on traditional fossil fuels and improves the utilization rate of renewable energy sources, offering significant economic and environmental benefits.
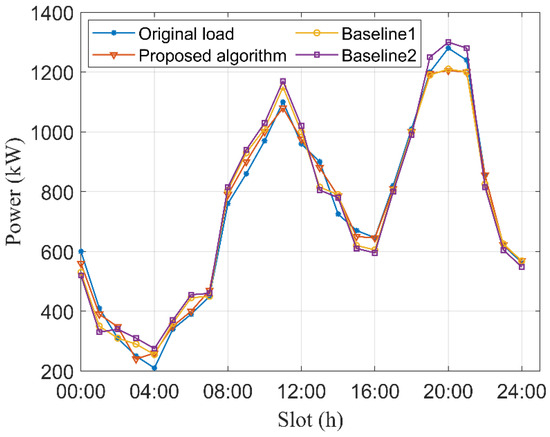
Figure 5.
Microgrid user load curve comparison after optimization adjustment.
Figure 6 presents a comparison of the convergence performance in microgrid energy management optimization. The results indicate that the proposed algorithm achieves superior convergence for microgrid gain optimization, reaching the fastest convergence speed at the 12th iteration. Moreover, the proposed algorithm attains the highest total microgrid revenue after 20 iterations, which is 5.44% and 70.26% higher than Baseline 1 and Baseline 2, respectively. This enhanced performance is attributed to the joint optimization of the IGDT and DDPG algorithms, where the update step of the DDPG algorithm is dynamically adjusted based on the uncertainty radius. Additionally, the introduction of a bidirectional feedback mechanism enables the algorithm to adapt more effectively to environmental changes, thereby improving optimization efficiency. In practical applications, the rapid convergence and high optimization efficiency demonstrated by the proposed algorithm imply that microgrids can achieve optimal energy scheduling strategies within a shorter timeframe. This not only enhances the economic viability and stability of the system but also reduces reliance on traditional energy sources and increases the utilization efficiency of renewable energy, offering significant economic and environmental benefits.
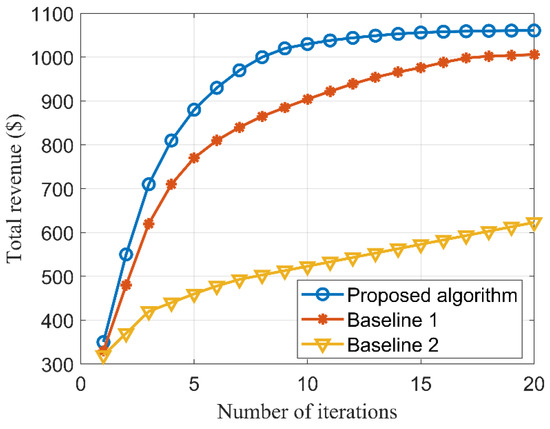
Figure 6.
Comparison of microgrid energy management convergence.
Table 3 shows the comparison between the total training time and optimal performance of the three algorithms. It can be seen from the table that, in terms of total training time, the total training time of the proposed method is the longest, and that of Baseline 2 is the shortest, because the proposed method has a mechanism of forward feedback and backward feedback, while Baseline 1 only considers forward feedback, and Baseline 2 does not consider any feedback. However, the total training time of the proposed method is only 8.87% longer than that of Baseline 2. In terms of optimal performance, the total revenue of the proposed method is 7.39% and 67.08% higher than that of Baseline 1 and Baseline 2, respectively. Combined with the results of Figure 6, although the proposed algorithm requires more computational time due to the enhanced feedback mechanism, its improvement in convergence speed and optimization performance fully proves the necessity of increasing computational time.

Table 3.
Total training time and optimal performance.
Figure 7 illustrates the variation of microgrid total revenue and risk-aversion coefficient with the equivalent uncertainty radius. As shown in the figure, the total revenue of both the proposed algorithm and Baseline 1 decreases as the equivalent uncertainty radius increases. However, the proposed algorithm exhibits a slower rate of revenue decline when the equivalent uncertainty radius is larger. This indicates that the proposed algorithm is more capable of maintaining system economic viability in the face of higher uncertainty. During this process, the risk-aversion coefficient of the proposed algorithm initially increases and then stabilizes, whereas that of Baseline 1 continues to rise. This difference arises because both algorithms account for uncertainty, but the proposed algorithm incorporates a bidirectional feedback mechanism. When the microgrid revenue significantly decreases, the bidirectional feedback mechanism delays the increase in the risk-aversion coefficient, thereby slowing down the reduction in revenue. From a practical standpoint, this characteristic implies that the proposed algorithm can better balance the economic viability and robustness of the microgrid in environments with high uncertainty. By dynamically adjusting the risk-aversion coefficient, the algorithm not only meets the stability requirements of the microgrid but also minimizes revenue loss as uncertainty increases. This capability is crucial for the economic operation and sustainable development of microgrids.
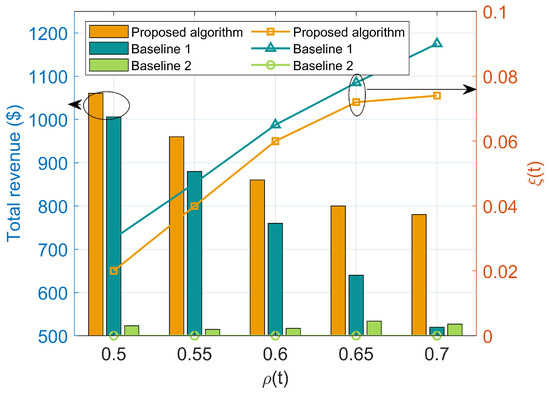
Figure 7.
The variation of microgrid total revenue and risk-aversion coefficient with equivalent uncertainty radius.
Figure 8 illustrates the power output of each component in the microgrid. During the period from 00:00 to 09:00, the output of renewable energy is sufficiently abundant to meet the power demand of users. Consequently, there is no need to activate the micro gas turbines (MGTs), which helps to reduce fossil fuel consumption and environmental pollution. Particularly from 01:00 to 04:00, the high output of renewable energy provides an optimal charging period for energy storage (ES) devices, enabling flexible load adjustment and transfer. In contrast, during the period from 19:00 to 21:00, the output of wind and photovoltaic power generation may not fully satisfy user demand due to natural conditions. In such cases, MGTs must be activated to provide additional power support, ensuring adequate electricity supply. Meanwhile, ES devices switch from charging to discharging mode to release previously stored power, maintaining the continuity and stability of the power supply. These observations demonstrate that the proposed algorithm, through uncertainty awareness and the integration of forward and backward feedback mechanisms, significantly enhances the adaptability of the microgrid to source–load fluctuations. In practical applications, this capability enables the microgrid to more efficiently utilize renewable energy across different time periods, reduce reliance on traditional energy sources, and optimize the charging and discharging strategies of ES devices to cope with dynamic changes in power supply and demand. This not only reduces operational costs but also enhances the reliability and environmental sustainability of the microgrid. The apparent negative power of the ES devices in the figure is due to the time period during which the ES is charging. Specifically, following the convention in the figure, the power output of the ES during the charging state is shown as negative.
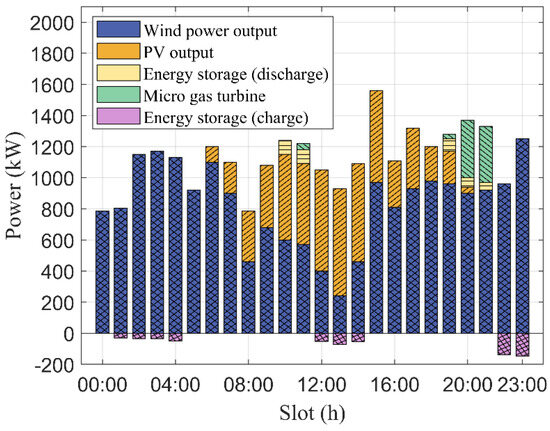
Figure 8.
The power output of each component in microgrids.
5. Conclusions
In this paper, an energy optimization strategy for microgrids based on an uncertainty-aware DDPG algorithm has been proposed. The strategy aims to address the challenges posed by the uncertainty of renewable energy sources and improve the robustness and stability of microgrid operations. The main conclusions are summarized as follows:
- (1)
- An uncertainty awareness model for wind power output based on information gap decision theory (IGDT) has been constructed. This model employs uncertainty intervals for decision optimization without relying on precise probability distribution assumptions. As a result, it provides a flexible and robust framework for describing and coping with uncertainty. This approach enhances the robustness and stability of microgrids when facing the volatility of renewable energy sources and other uncertainty factors.
- (2)
- The DDPG algorithm has been utilized to optimize the energy management strategy. The algorithm adaptively adjusts the optimization step size based on the forward feedback of the equivalent uncertainty radius. When the environmental uncertainty is large, the step size is reduced to improve stability. Conversely, when the uncertainty is small, the step size is increased to accelerate the decision-making process. This mechanism allows the microgrid to better cope with external fluctuations, thereby improving the economy, stability, and overall operational efficiency.
- (3)
- Based on the DDPG optimization results, the risk-aversion coefficient has been dynamically adjusted using backward feedback from the current uncertainty state and historical performance data. This adjustment mechanism enhances the real-time decision-making capabilities of microgrids in complex environments. It improves the balance between economic efficiency and robustness while ensuring system stability and optimal performance.
Simulation results demonstrate the superiority of the proposed algorithm over traditional optimization methods in terms of both total microgrid revenue and convergence speed. Specifically, at an iteration number of 20, the optimization effect of the proposed algorithm is improved by 5.44% and 70.26% compared to Baseline 1 and Baseline 2, respectively. These results highlight the enhanced adaptability, robustness, and convergence capabilities of the proposed strategy in microgrid energy optimization.
The main limitations of the paper are as follows:
- (1)
- Our approach assumes that the uncertainty in renewable energy output (wind and solar) can be adequately modeled using IGDT. However, this model assumes that the uncertainty bounds can be estimated with reasonable accuracy, which may not always be the case in real-world applications due to the dynamic nature of renewable energy sources. Further research could explore more accurate models for uncertainty estimation.
- (2)
- In our model, ES is simplified by assuming that it operate with perfect charging and discharging efficiencies. This simplification may not hold true in practice due to degradation and efficiency losses over time, which could influence the overall performance of the microgrid. Future work could incorporate more realistic modeling of ES behavior.
In the future, further research will focus on extending this work to address more complex scenarios. This includes the regulation and control of multi-energy flow coupling in microgrids and the cooperative optimization of large-scale multi-microgrid systems. These research directions aim to further improve the economy, stability, and adaptability of microgrid systems, ensuring their efficient operation in diverse and dynamic environments.
Author Contributions
Conceptualization, T.W. and H.L.; methodology, T.W., H.L. and M.S.; software, T.W. and M.S.; validation, T.W., H.L. and M.S.; formal analysis, T.W., H.L. and M.S.; investigation, T.W.; data curation, T.W.; writing—original draft preparation, T.W.; writing—review and editing, H.L. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, Hongchen Liu, upon reasonable request.
Acknowledgments
We would like to thank Ming Su for his valuable contributions to this research, particularly in the areas of methodology, software development, validation, formal analysis, and manuscript writing—review and editing. Ming Su’s expert guidance and collaboration have played a crucial role in the successful progression and completion of this work.
Conflicts of Interest
Author Tao Wang was employed by State Grid Weihai Supply Company. Author Ming Su was employed by Shandong Huake Information Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The companies had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Ma, H.; Liu, Y. An IGDT-Based Intraday Scheduling Strategy Method Considering Wind Power Ramp Event. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Al-Wajih, Y.A.; Shafiullah, M.; Al-Dhaifallah, M.M.; Sonbul, A. Efficient Energy Scheduling for Microgrids Under Uncertainty. In Proceedings of the 2024 21st International Multi-Conference on Systems, Signals & Devices (SSD), Erbil, Iraq, 22–25 April 2024; pp. 230–238. [Google Scholar]
- Liao, H.; Zhou, Z.; Jia, Z.; Shu, Y.; Tariq, M.; Rodriguez, J.; Frascolla, V. Ultra-Low AoI Digital Twin-Assisted Resource Allocation for Multi-Mode Power IoT in Distribution Grid Energy Management. IEEE J. Sel. Areas Commun. 2023, 41, 3122–3132. [Google Scholar]
- Hamanah, W.M.; Shafiullah, M.; Alhems, L.M.; Alam, M.S.; Abido, M.A. Realization of Robust Frequency Stability in Low-Inertia Islanded Microgrids with Optimized Virtual Inertia Control. IEEE Access 2024, 12, 58208–58221. [Google Scholar]
- Li, Z.; Wu, L.; Xu, Y.; Moazeni, S.; Tang, Z. Multi-Stage Real-Time Operation of a Multi-Energy Microgrid with Electrical and Thermal Energy Storage Assets: A Data-Driven MPC-ADP Approach. IEEE Trans. Smart Grid 2022, 13, 213–226. [Google Scholar]
- Alam, M.S.; Hossain, M.A.; Shafiullah, M.; Islam, A.; Choudhury, M.; Faruque, M.O.; Abido, M.A. Renewable Energy Integration with DC Microgrids: Challenges and Opportunities. Electr. Power Syst. Res. 2024, 234, 110548. [Google Scholar]
- Zhou, L.; Zhang, C.; Ge, J.; Dong, X.; Cui, C. A Generalized Dynamic Nonsmooth Control Design for DC Microgrids Based on Deep Reinforcement Learning. In Proceedings of the 2023 IEEE 18th Conference on Industrial Electronics and Applications (ICIEA), Ningbo, China, 18–22 August 2023; pp. 1257–1262. [Google Scholar]
- Shu, Y.; Bi, W.; Dong, W.; Yang, Q. Dueling Double Q-Learning Based Real-Time Energy Dispatch in Grid-Connected Microgrids. In Proceedings of the 2020 19th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), Xuzhou, China, 16–19 October 2020; pp. 42–45. [Google Scholar]
- Buraimoh, E.; Ozkan, G.; Timilsina, L.; Muriithi, G.; Arsalan, A.; Papari, B.; Moghassemi, A.; Edrington, C.; Ozden, M. Distributed Deep Deterministic Policy Gradient Agents for Real-Time Energy Management of DC Microgrid. In Proceedings of the 2024 IEEE Sixth International Conference on DC Microgrids (ICDCM), Columbia, SC, USA, 5–8 August 2024; pp. 1–5. [Google Scholar]
- Chen, W.; Wu, N.; Huang, Y. Real-Time Optimal Dispatch of Microgrid Based on Deep Deterministic Policy Gradient Algorithm. In Proceedings of the 2021 International Conference on Big Data and Intelligent Decision Making (BDIDM), Guilin, China, 23–25 July 2021; pp. 24–28. [Google Scholar]
- Nishida, N.; Takahashi, Y.; Wakao, S. Robust Design Optimization Approach by Combination of Sensitivity Analysis and Sigma Level Estimation. IEEE Trans. Magn. 2008, 44, 998–1001. [Google Scholar]
- Liu, Z.; Wang, L.; Ma, L. A Transactive Energy Framework for Coordinated Energy Management of Networked Microgrids with Distributionally Robust Optimization. IEEE Trans. Power Syst. 2020, 35, 395–404. [Google Scholar] [CrossRef]
- Yang, T.; Song, B.; Jiang, S.; Wang, B. Steady-State Security Region-Based Chance-Constrained Optimization for Integrated Energy Systems. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October 2020; pp. 1307–1312. [Google Scholar]
- Ran, X.; Zhang, J.; Liu, K. An Interval–Probabilistic CVaR (IP-CVaR) and Modelling for Unknown Probability Distribution of Some Random Variables. IEEE Trans. Power Syst. 2023, 38, 2035–2045. [Google Scholar] [CrossRef]
- Ke, D.; Shen, F.; Chung, C.Y.; Zhang, C.; Xu, J.; Sun, Y. Application of Information Gap Decision Theory to the Design of Robust Wide-Area Power System Stabilizers Considering Uncertainties of Wind Power. IEEE Trans. Sustain. Energy 2018, 9, 805–817. [Google Scholar]
- Nasr, M.A.; Nasr-Azadani, E.; Nafisi, H.; Hosseinian, S.H.; Siano, P. Assessing the Effectiveness of Weighted Information Gap Decision Theory Integrated with Energy Management Systems for Isolated Microgrids. IEEE Trans. Ind. Inform. 2020, 16, 5286–5299. [Google Scholar]
- Li, C.; Liu, J.; Ding, T.; Liu, X.; Zhou, Z.; Sun, Z. Aggregated Regulation and Coordinated Scheduling of PV-Storage Integrated 5G Base Stations Considering PV-Load Uncertainty. Int. J. Electr. Power Energy Syst. 2024, 162, 110306. [Google Scholar] [CrossRef]
- Li, Z.; Wu, L.; Xu, Y.; Wang, L.; Yang, N. Distributed Tri-Layer Risk-Averse Stochastic Game Approach for Energy Trading Among Multi-Energy Microgrids. Appl. Energy 2023, 331, 120282. [Google Scholar] [CrossRef]
- Wu, N.; Wang, Z.; Li, X.; Lei, L.; Qiao, Y.; Linghu, J.; Huang, J. Research on Real-Time Coordinated Optimization Scheduling Control Strategy with Supply-Side Flexibility in Multi-Microgrid Energy Systems. Renew. Energy 2025, 238, 121976. [Google Scholar] [CrossRef]
- Wenjun, L.; Shuaihu, L.; Rui, M.; Shuyun, H. Multi-Objective DDPG Optimal Dispatch for Low-Voltage Distribution Station Area Flexible Interconnection System. Smart Power 2024, 52, 62–70. [Google Scholar]
- Zhang, H.; Yue, D.; Dou, C.; Hancke, G.P. A Three-Stage Optimal Operation Strategy of Interconnected Microgrids with Rule-Based Deep Deterministic Policy Gradient Algorithm. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 1773–1784. [Google Scholar] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).