Numerical Study on Hydraulic Fracture Propagation in Coalbed Methane Considering Coal Seam Cleats
Abstract
1. Introduction
2. Method
2.1. Mathematical Modeling
- (1)
- Displacement boundary: Uz = 0 in the Z direction at the bottom of the constrained model to simulate the rigid support of the coal seam floor; the normal displacement constraint is applied to the side of the model, and the displacement Ux = 0 in the X-axis direction and Uy = 0 in the Y-axis direction to avoid rigid body displacement.
- (2)
- Stress boundary: The vertical stress is calculated according to the formation density. The position of the model centroid is 600 m, the stress gradient is 25 MPa/km, and the horizontal stress is the maximum horizontal principal stress of 15 MPa and the minimum horizontal principal stress of 12 MPa according to the measured data.
- (3)
- Fluid pressure boundary: The initial pore pressure is 9.8 MPa/km.
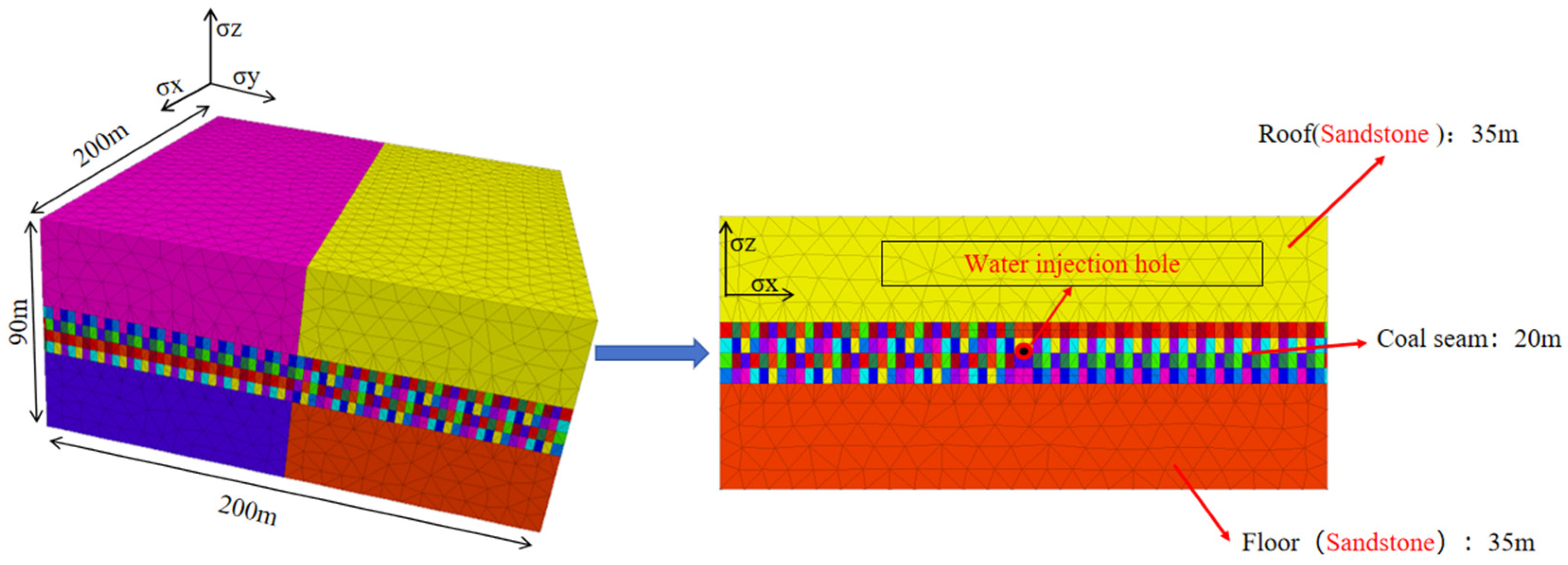
2.2. Geometric Modeling
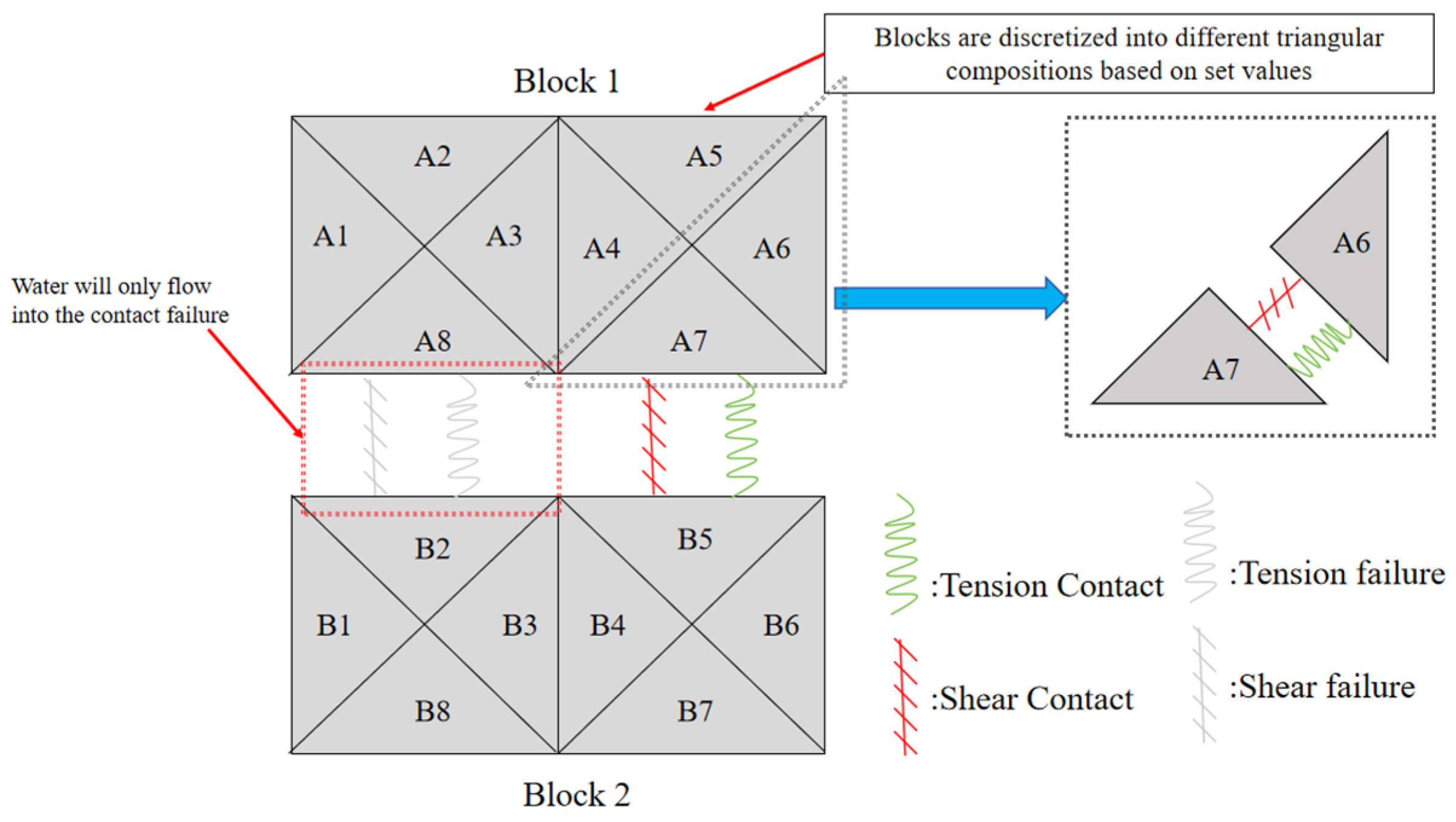
2.2.1. Three-Dimensional Coalbed Methane Fracture Propagation Modeling with Coal Cleats
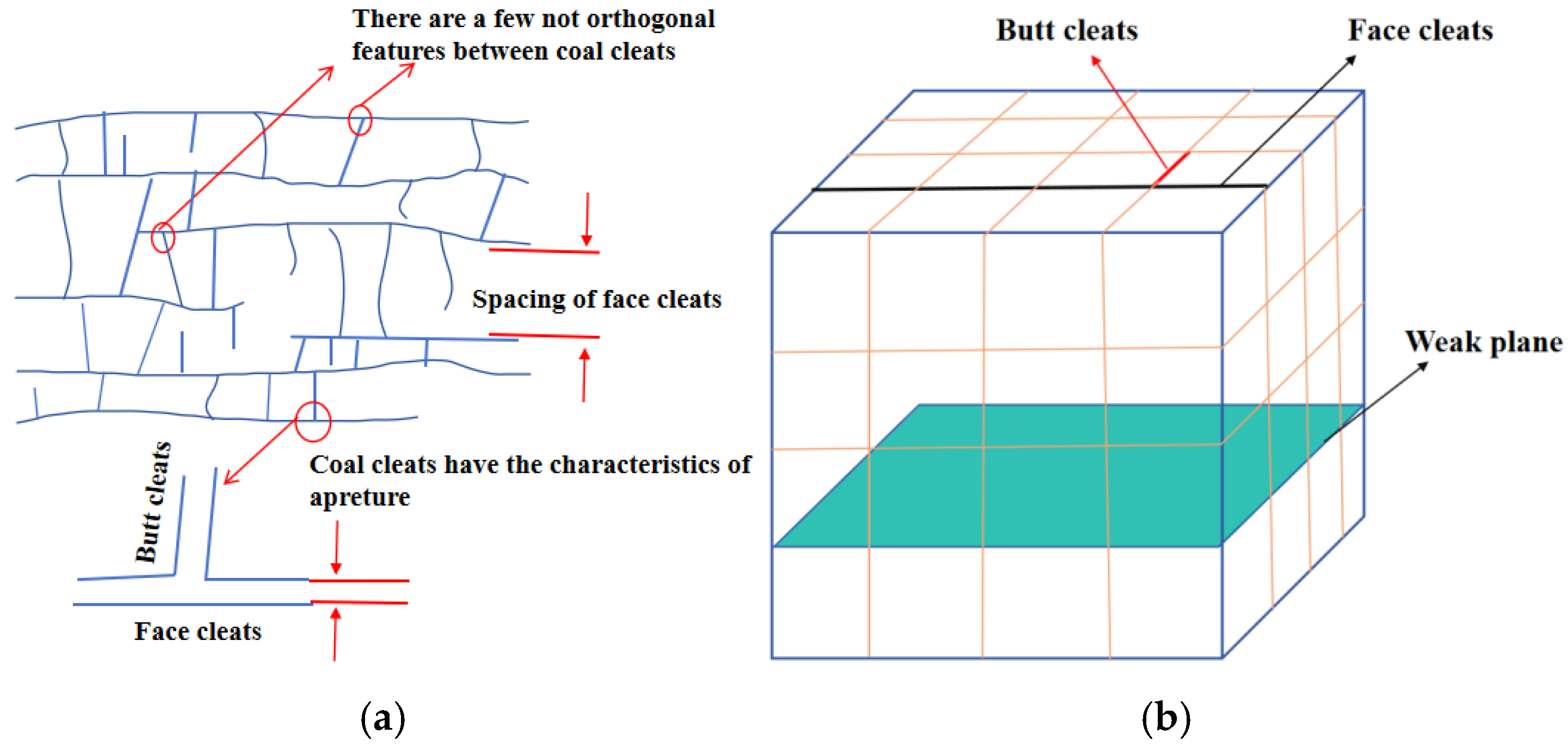
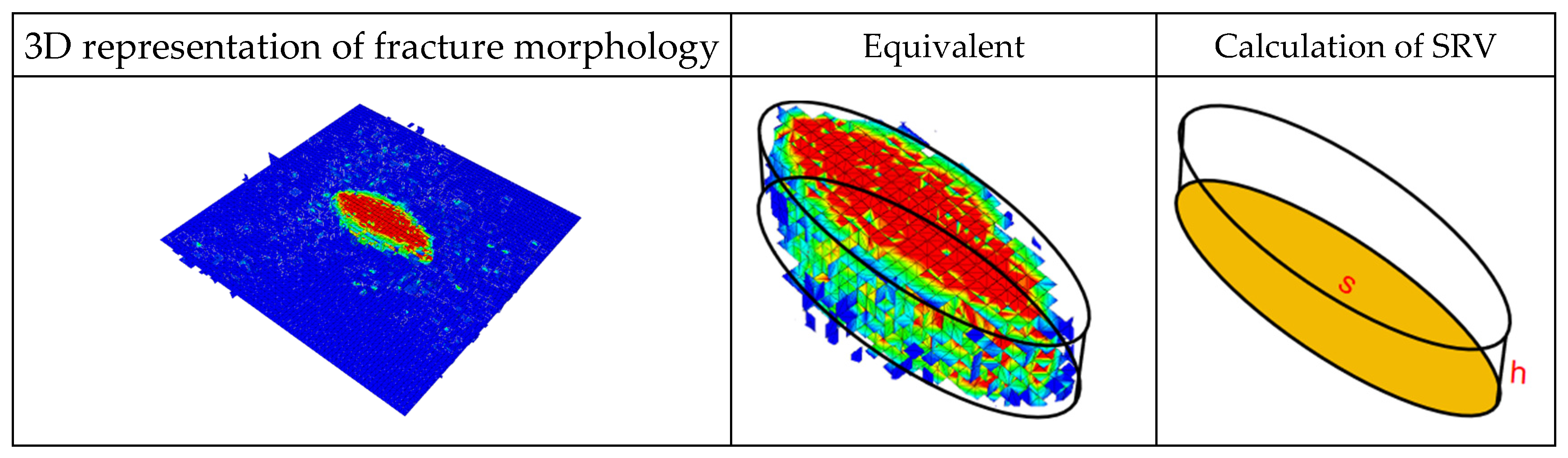
2.2.2. Geometrical Modeling of Coal Cleats
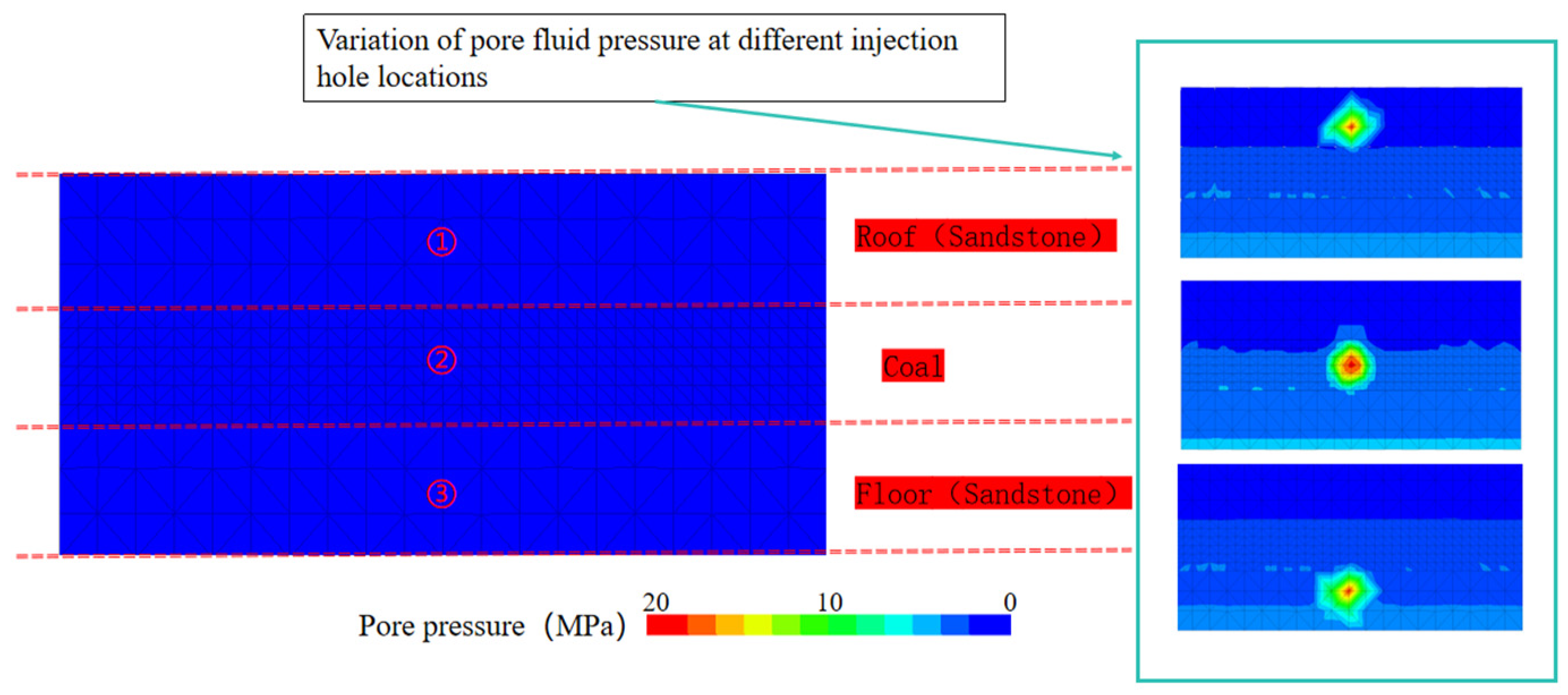
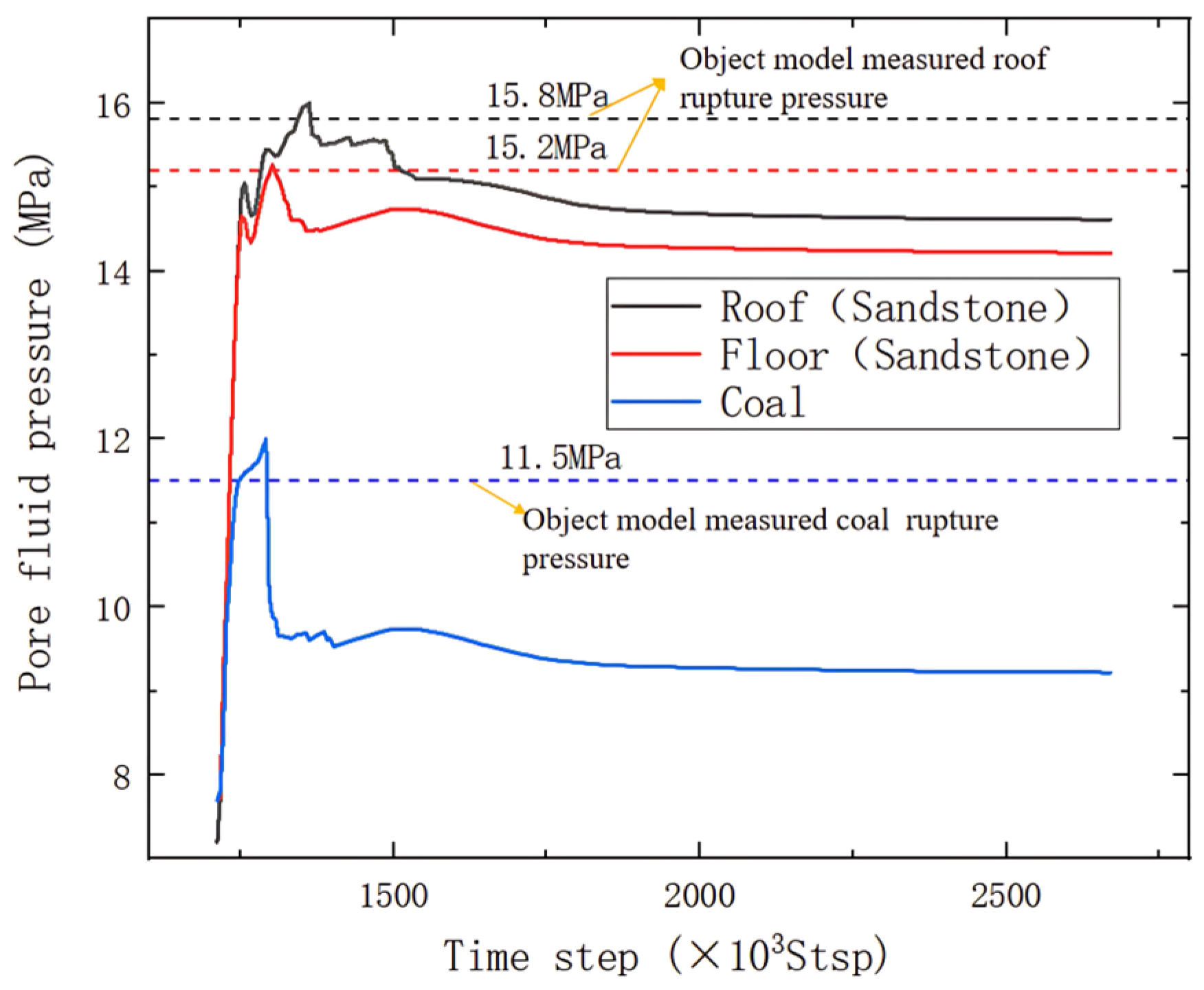
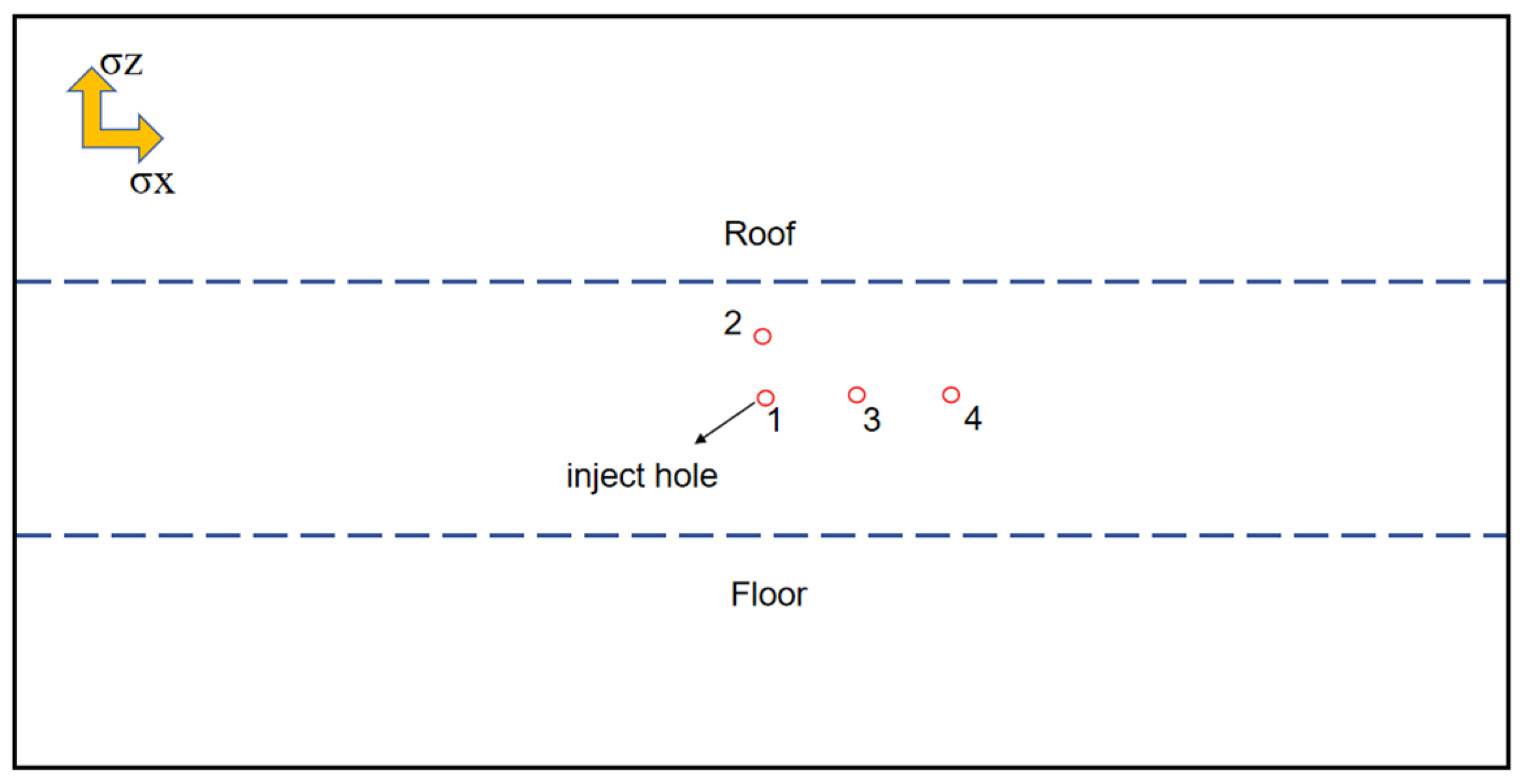
3. Model Validation
4. Analysis and Discussion of Results
4.1. Effect of Cleats in Coal Seams on Hydraulic Fracture Propagation
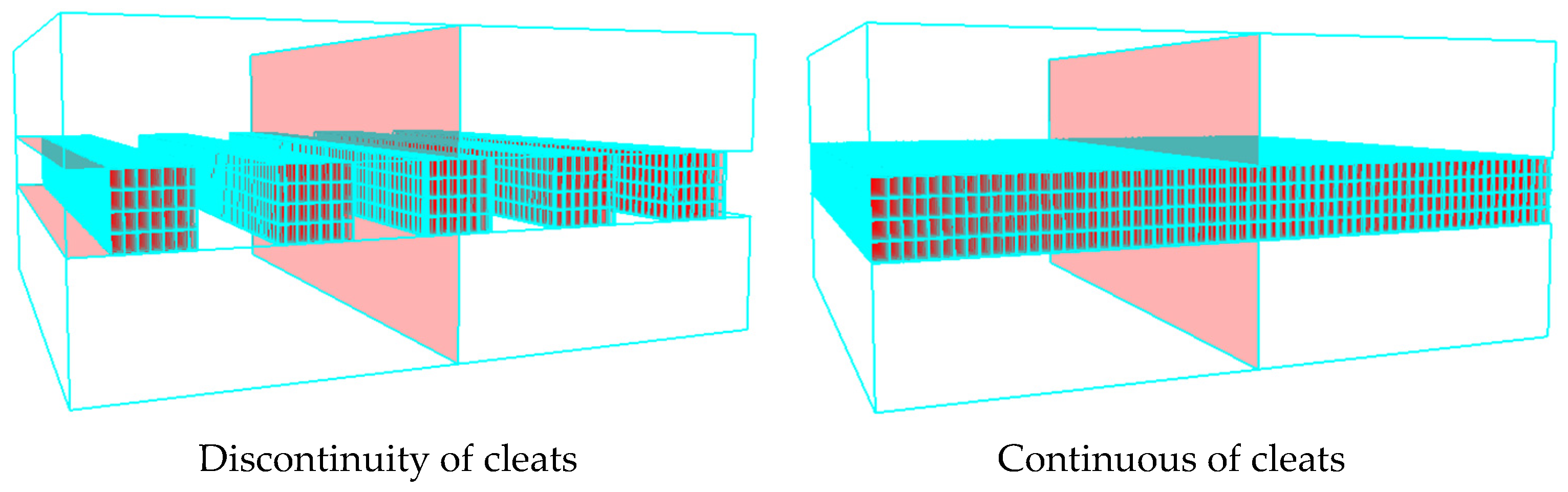
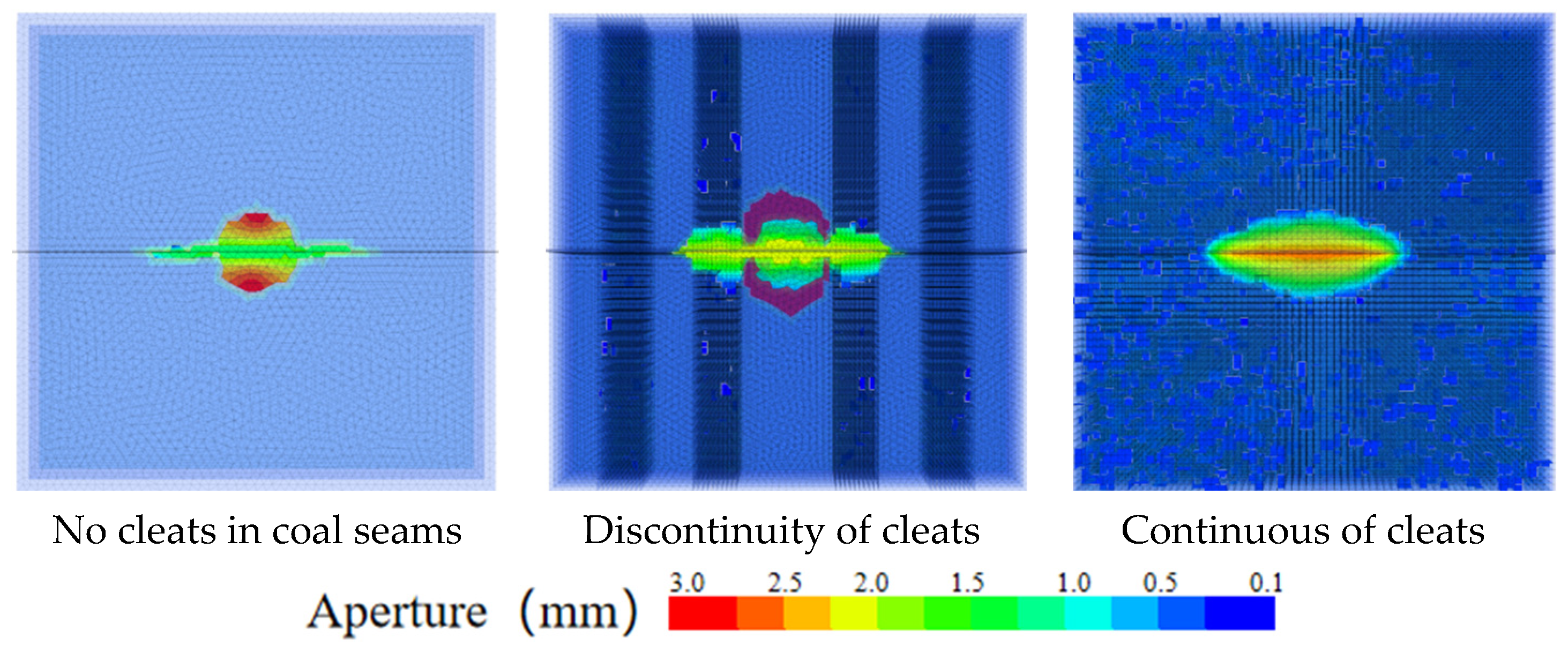
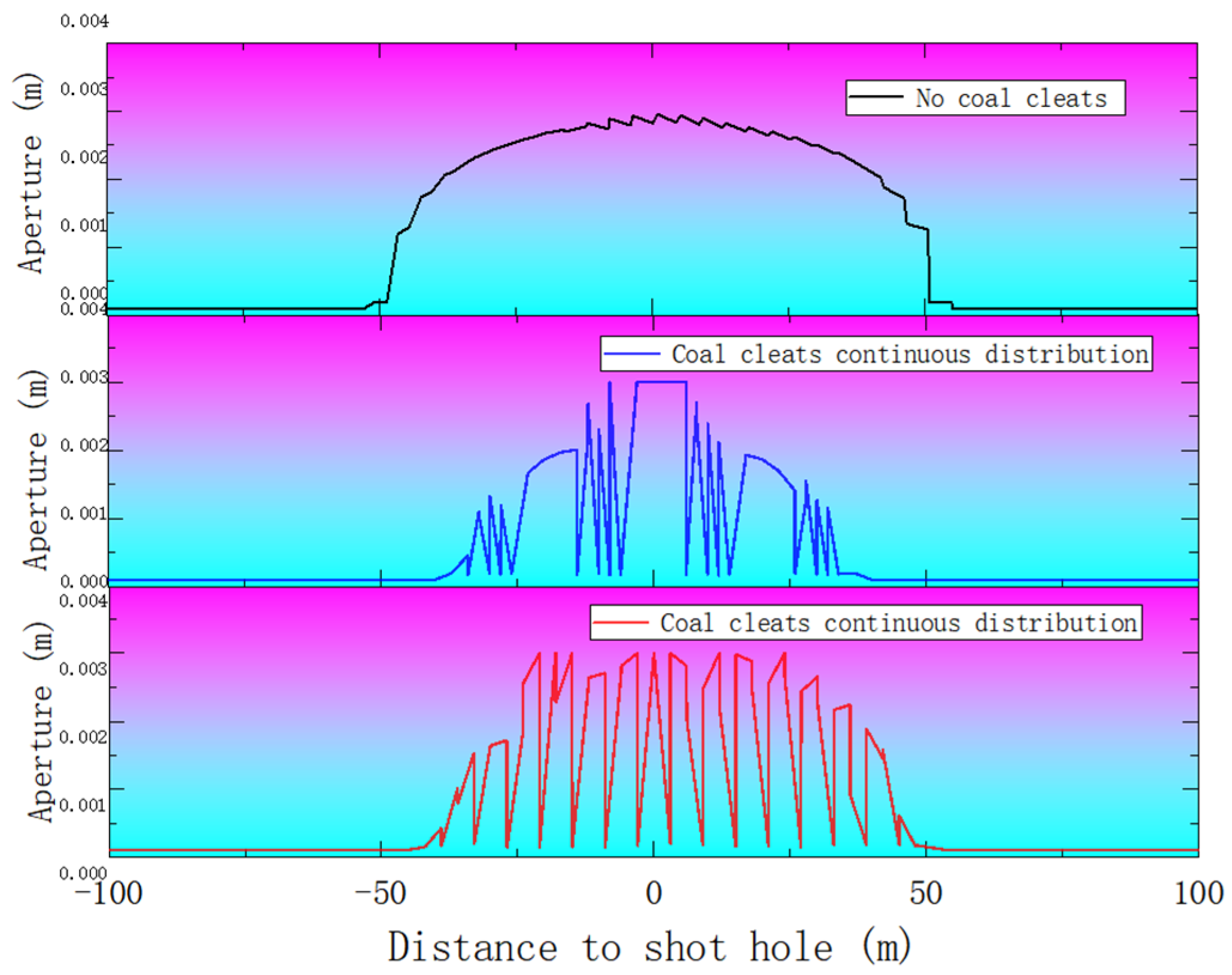
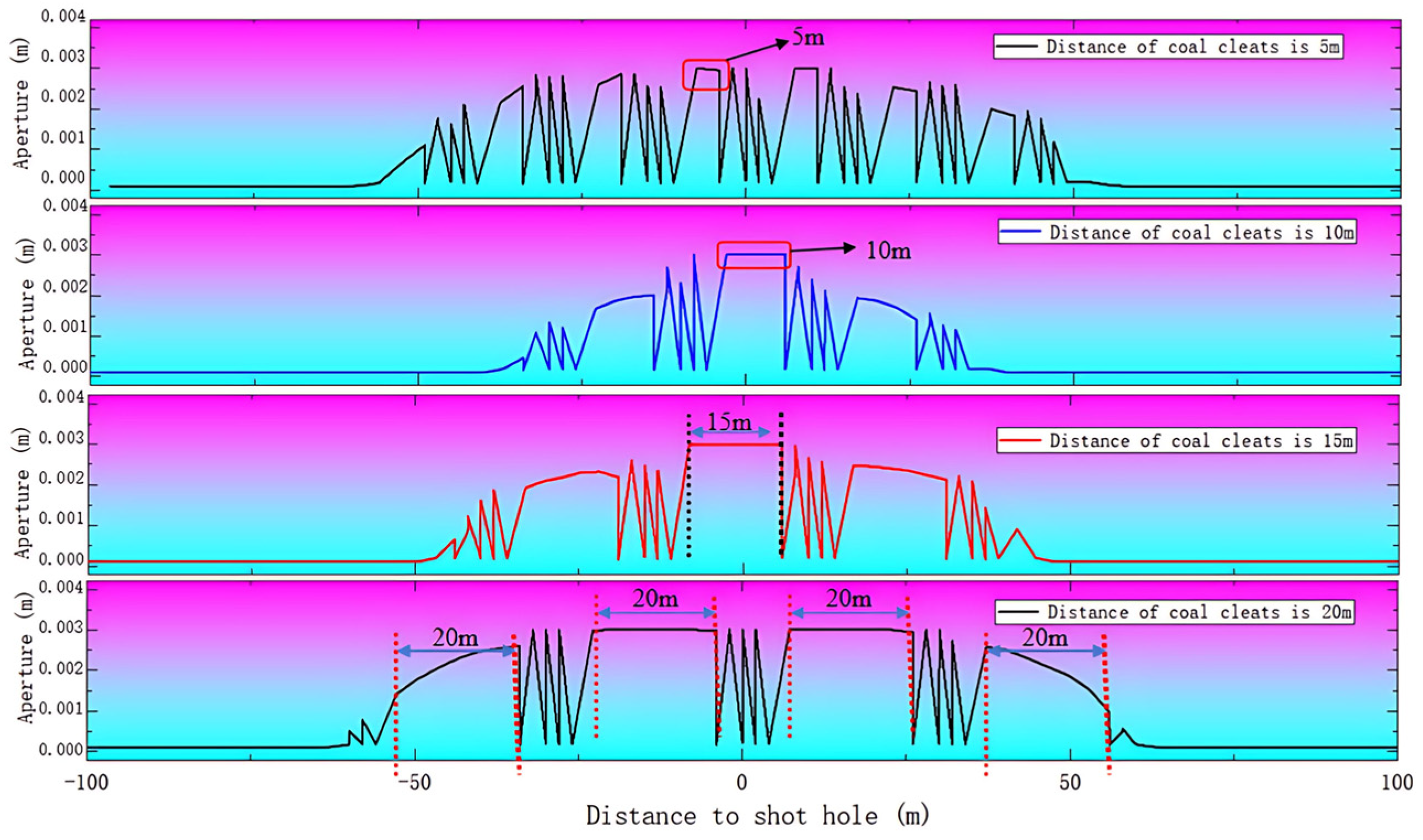
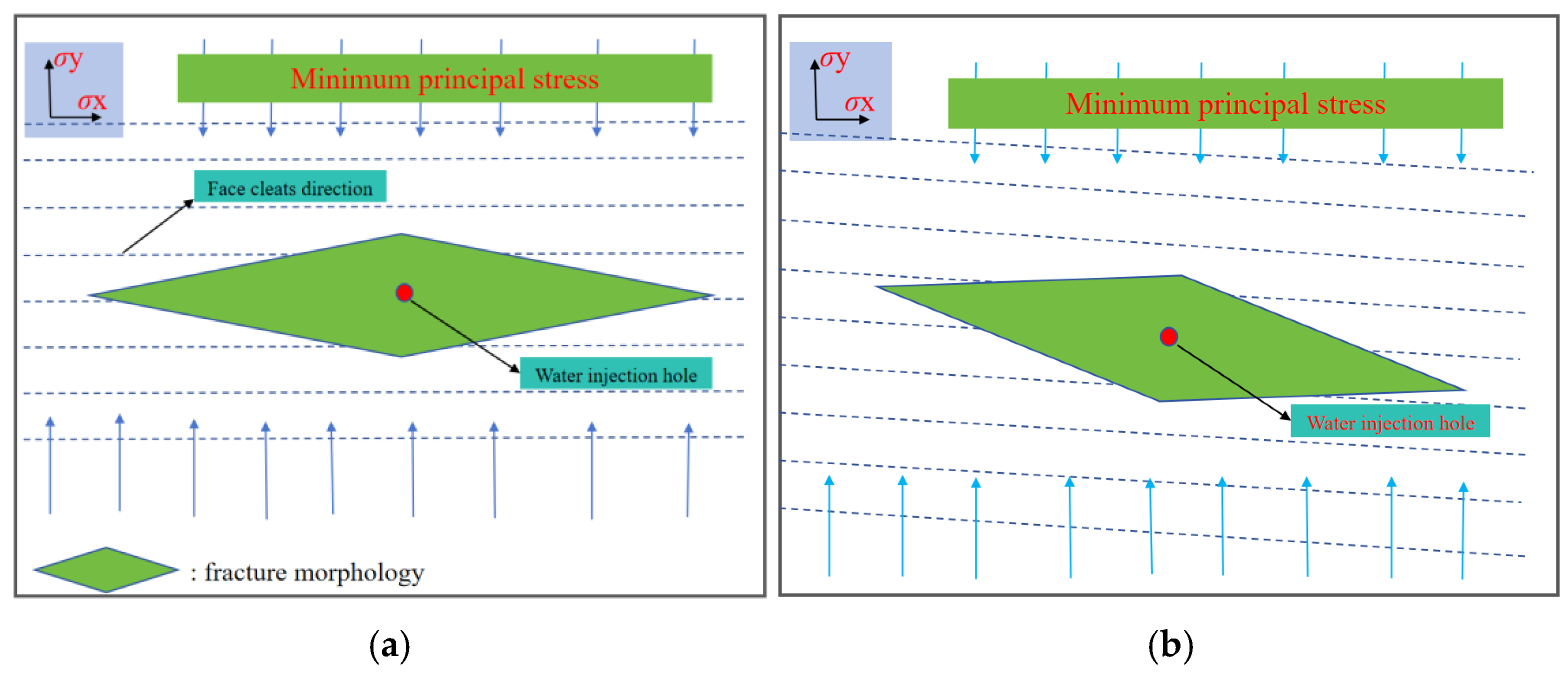
4.1.1. Continuity of Cleats
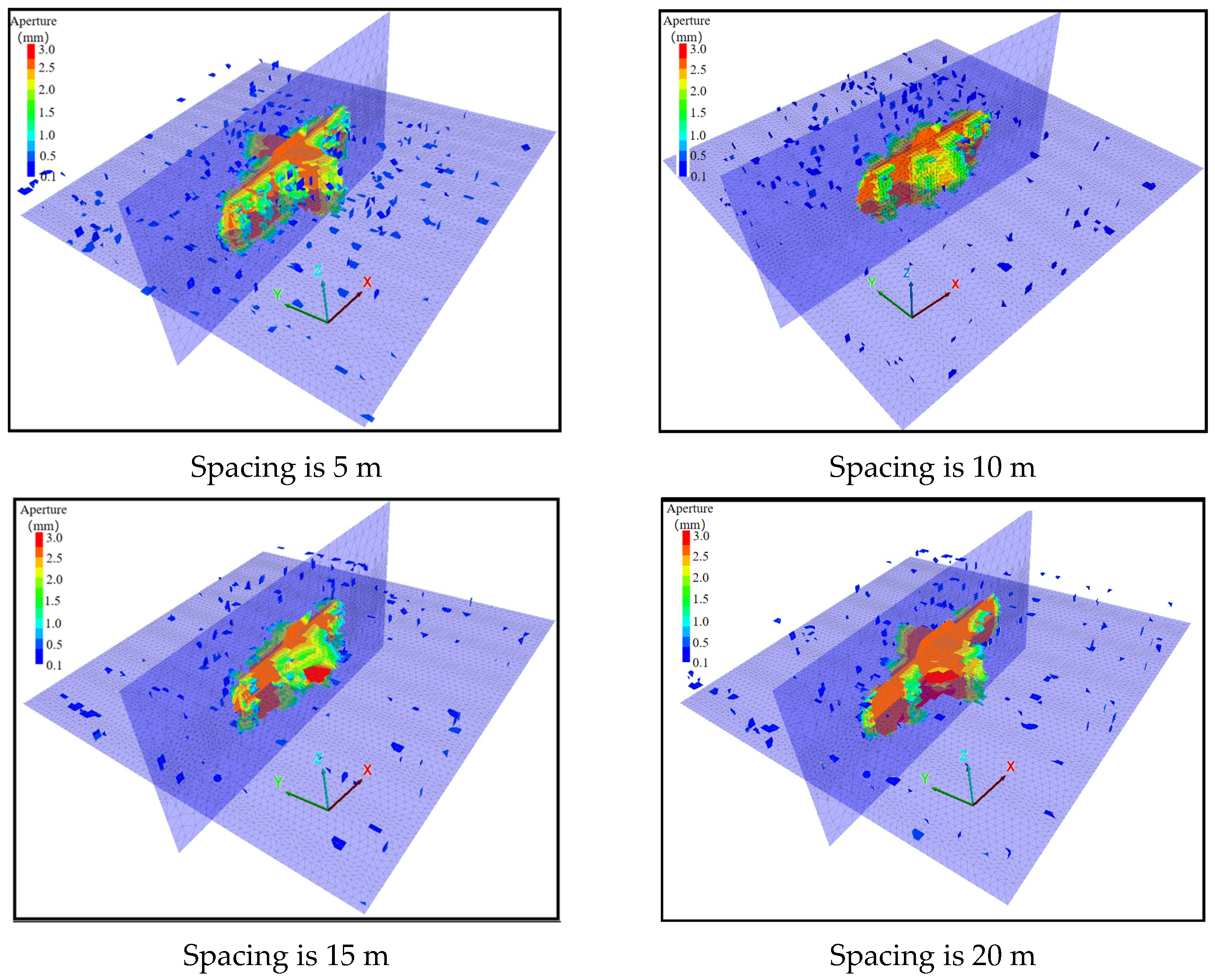
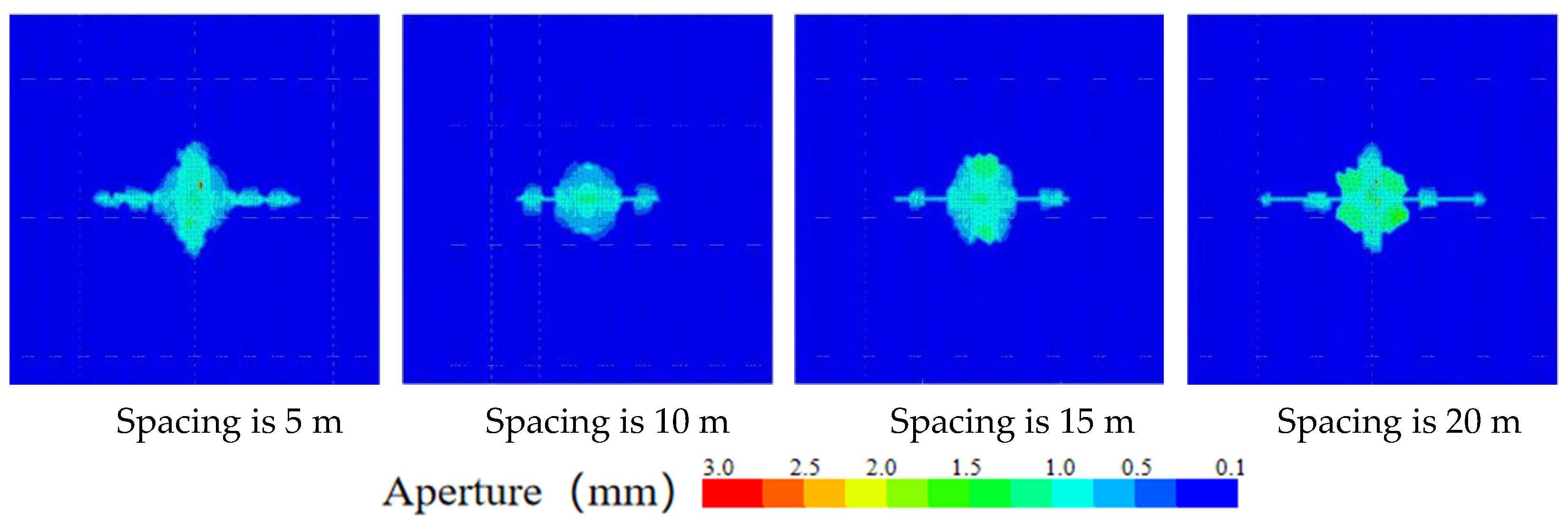
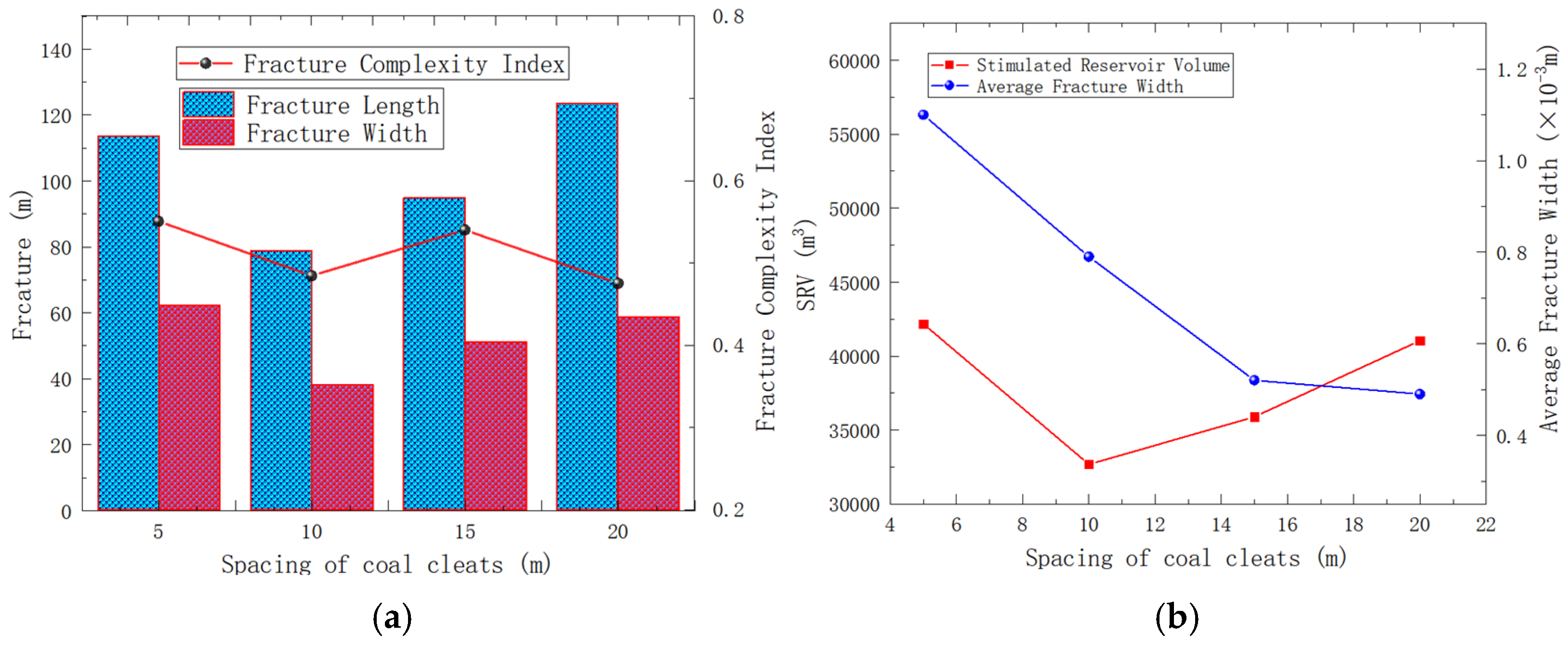
4.1.2. The Influence of Spacing of the Cleat System
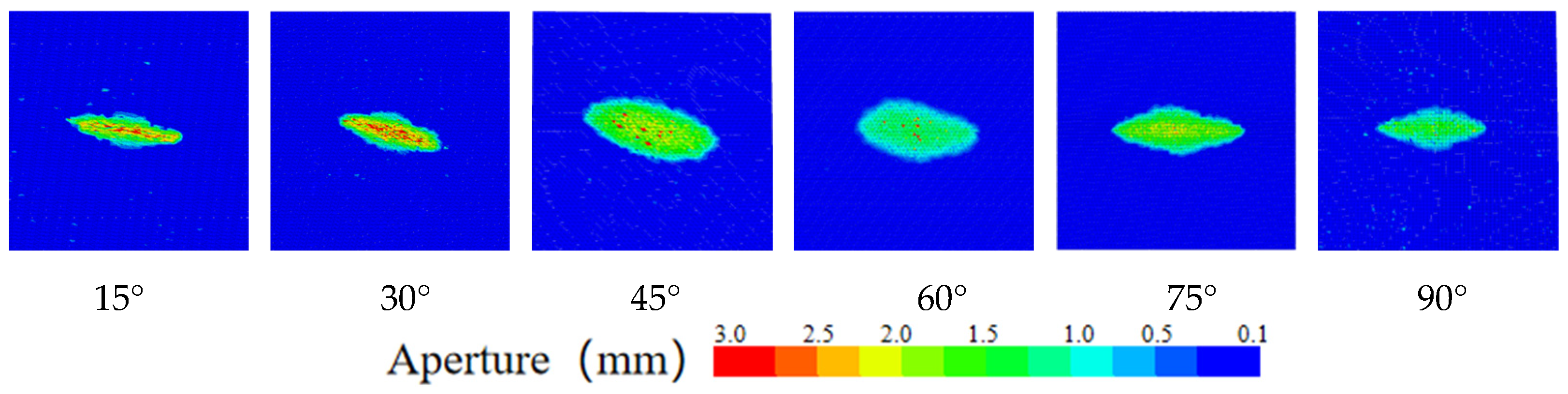
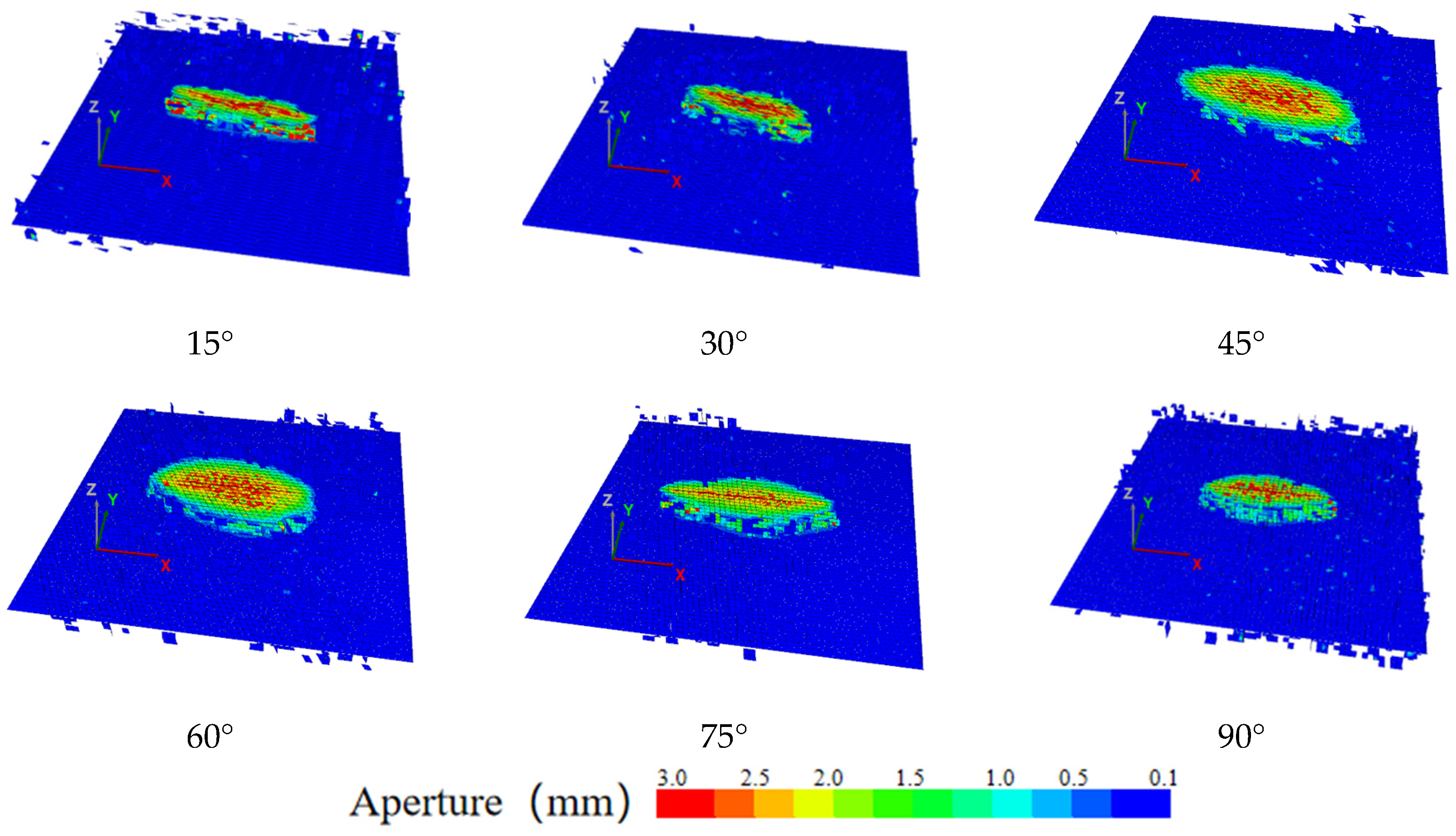
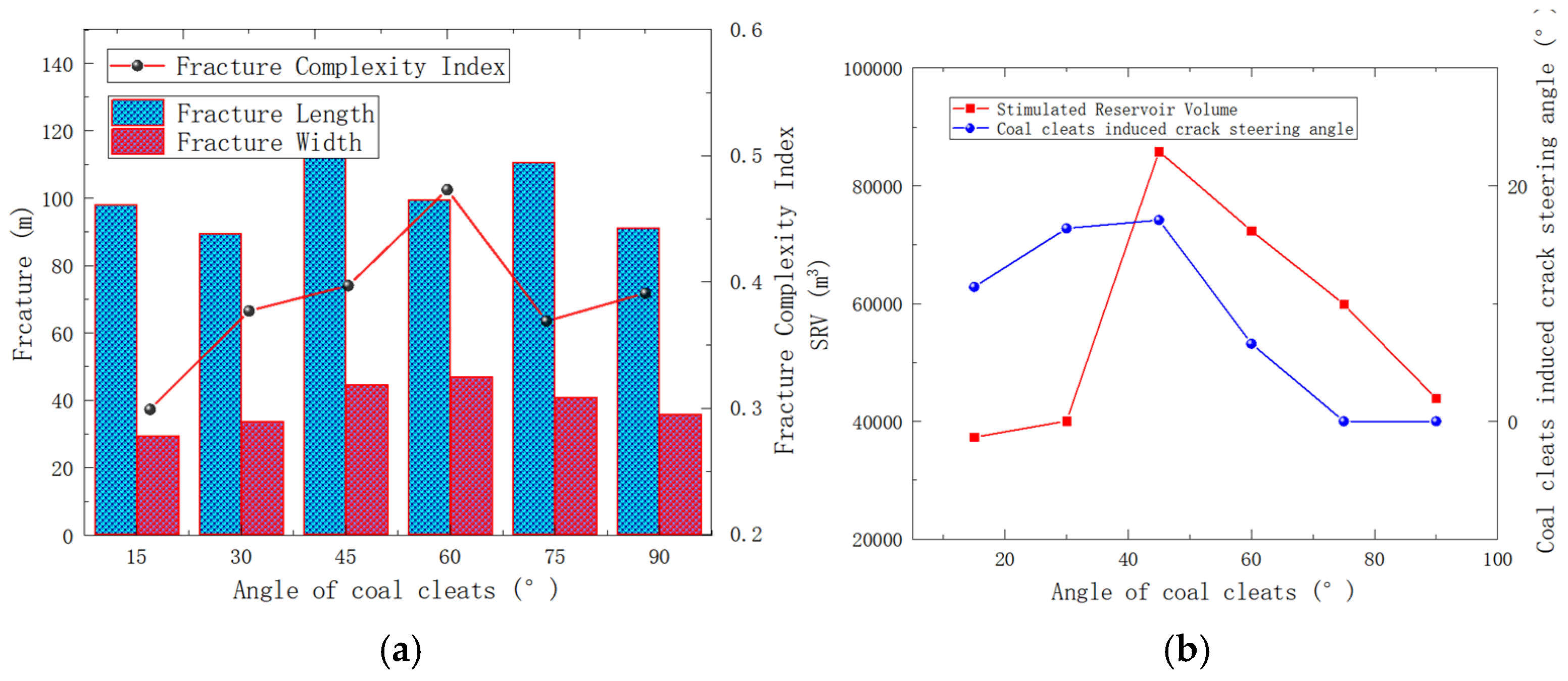
4.1.3. The Influence of Angle Face Cleat and Butt Cleat
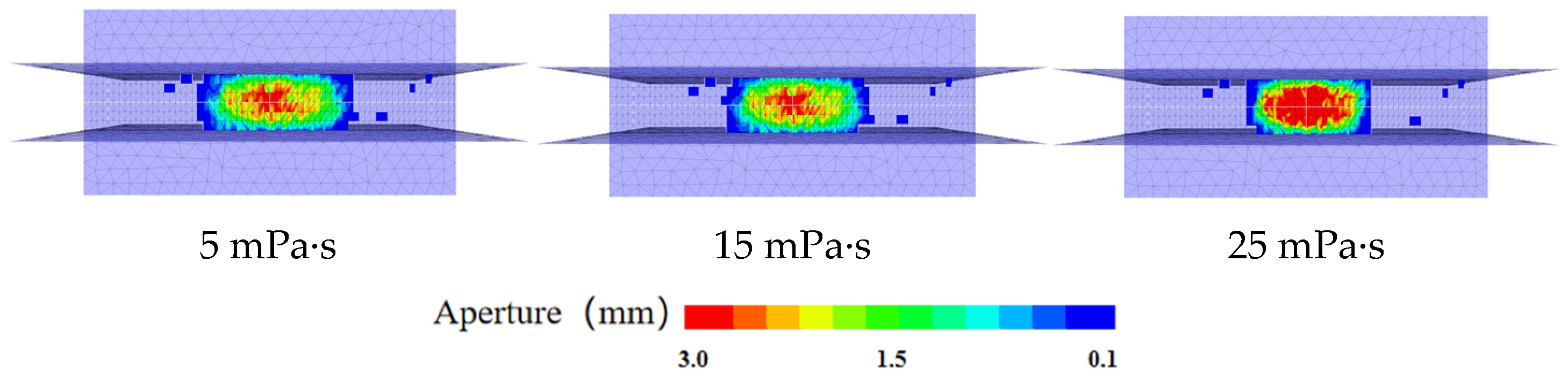
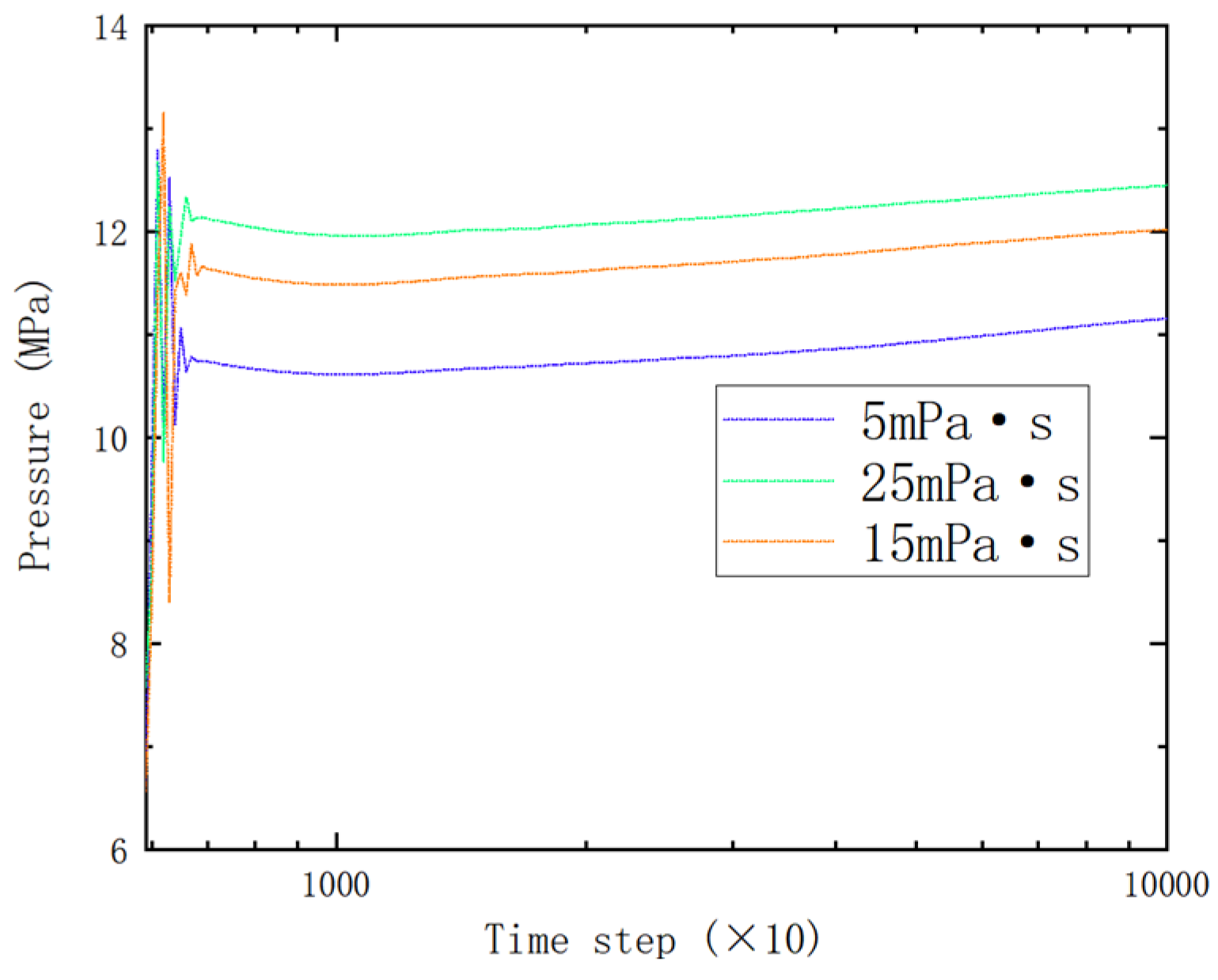
4.2. Effect of Different Viscosity of Liquid in Coal Seams on Hydraulic Fracture Propagation
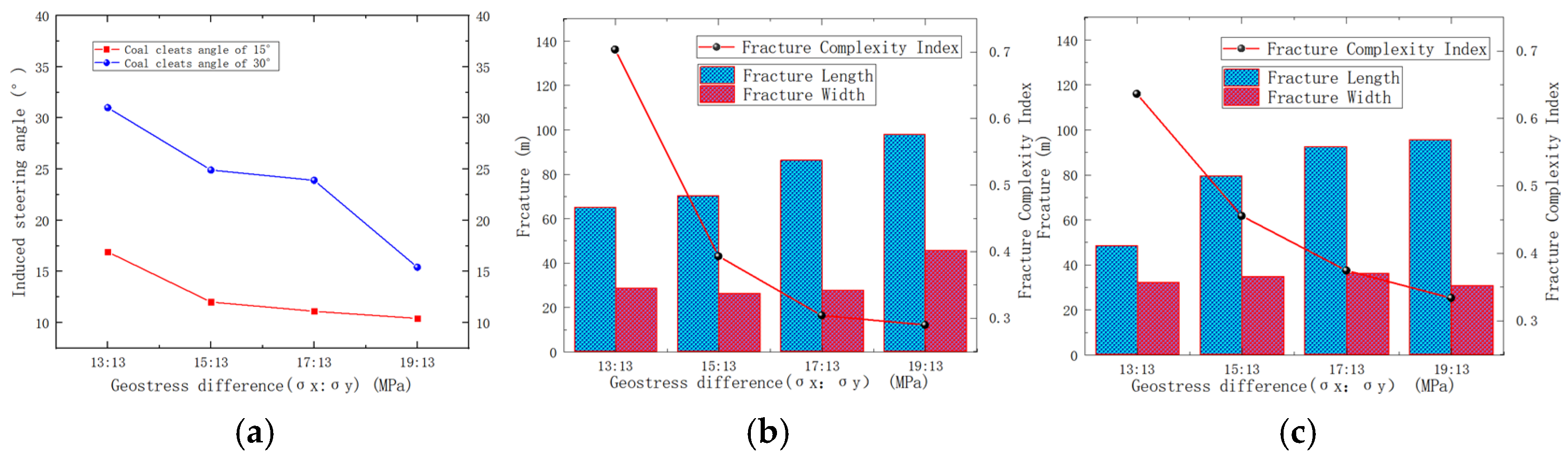
4.3. Effect of Geostress Difference in Coal Seams on Hydraulic Fracture Propagation
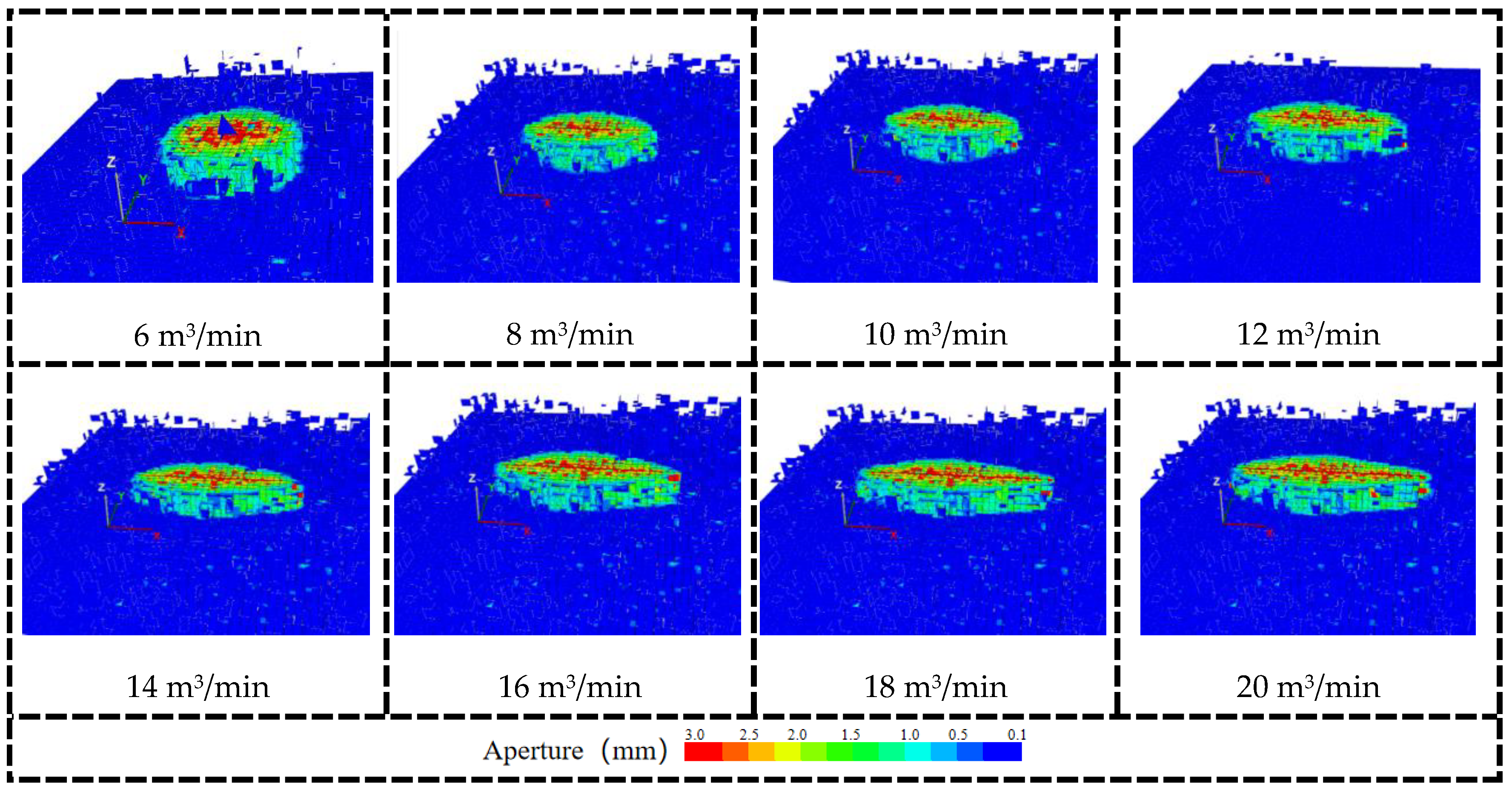
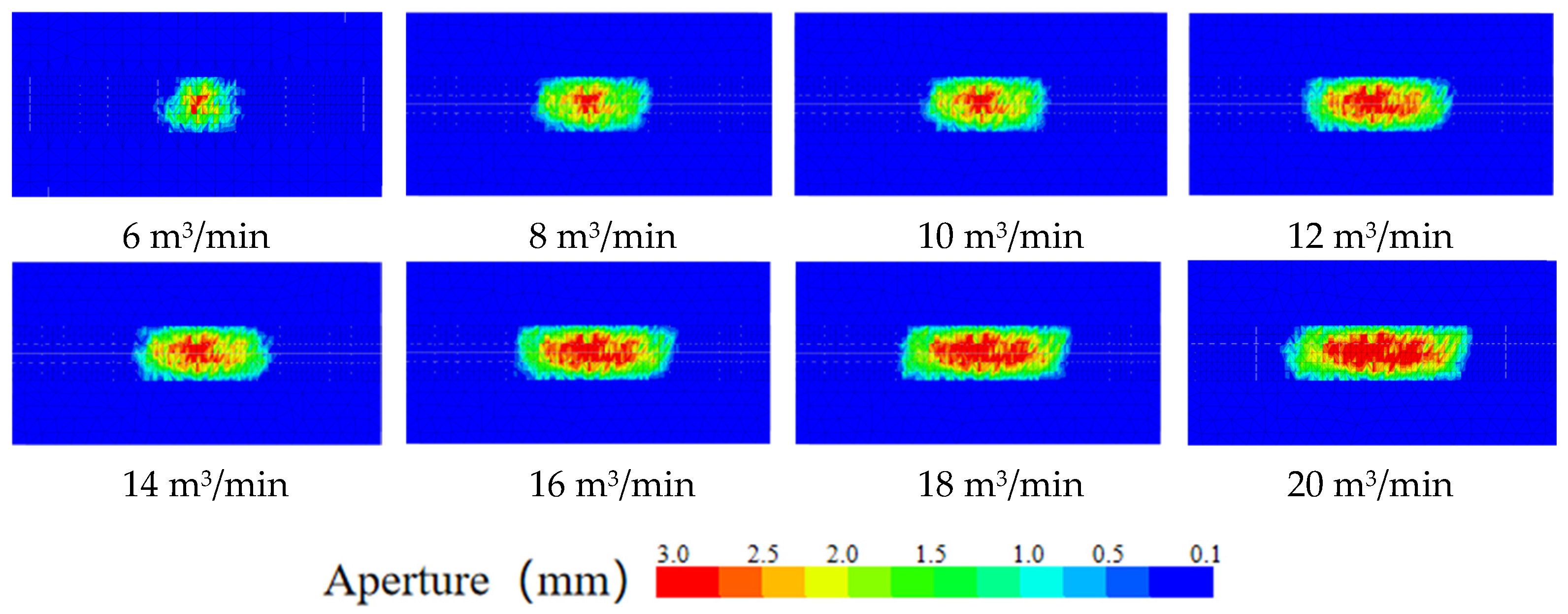
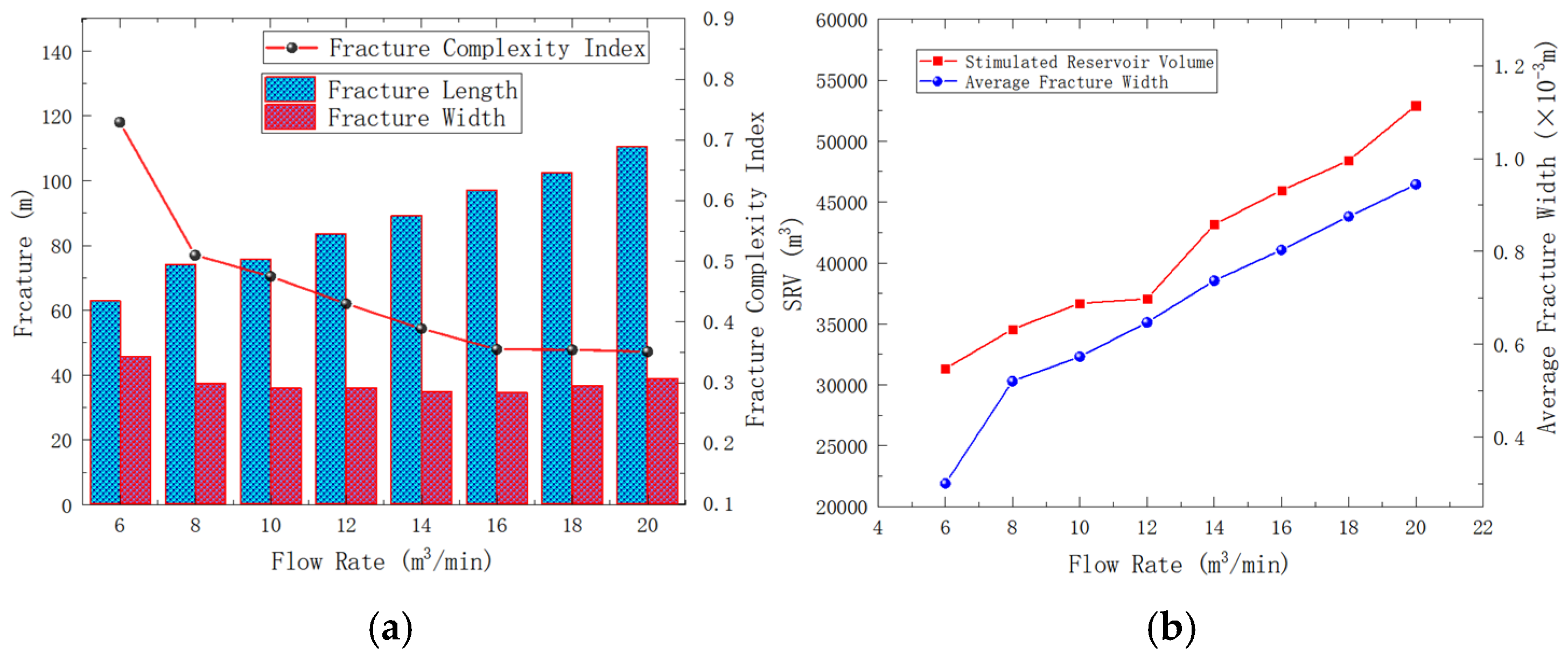
4.4. Effect of the Liquid Injection Rate in Coal Seams on Hydraulic Fracture Propagation
5. Conclusions
- (1)
- When the injection hole is on the cleats, the hydraulic fracture preferentially extends along the cleats system, and the hydraulic fracture shows a “cross” propagation. The coal cleats have an inducing effect on the direction of hydraulic fracture propagation; the coal cleats have a small effect on SRV but have a large effect on the fracture width. The coal reservoir hardly gains a large reforming volume away from the injection hole; the angle of the cleat is from 0° to 45°, and the steering angle of cleats-induced fractures increases to 17.1°, and the cleat angle is from 0° to 45°, and the steering angle of cleats-induced fracture increases to 17.1°. The cleat angle has a great influence on the hydraulic fracture propagation direction, and when the cleat angle is from 45° to 90°, the coal cleat gradually loses its inducing effect on the hydraulic fracture propagation direction.
- (2)
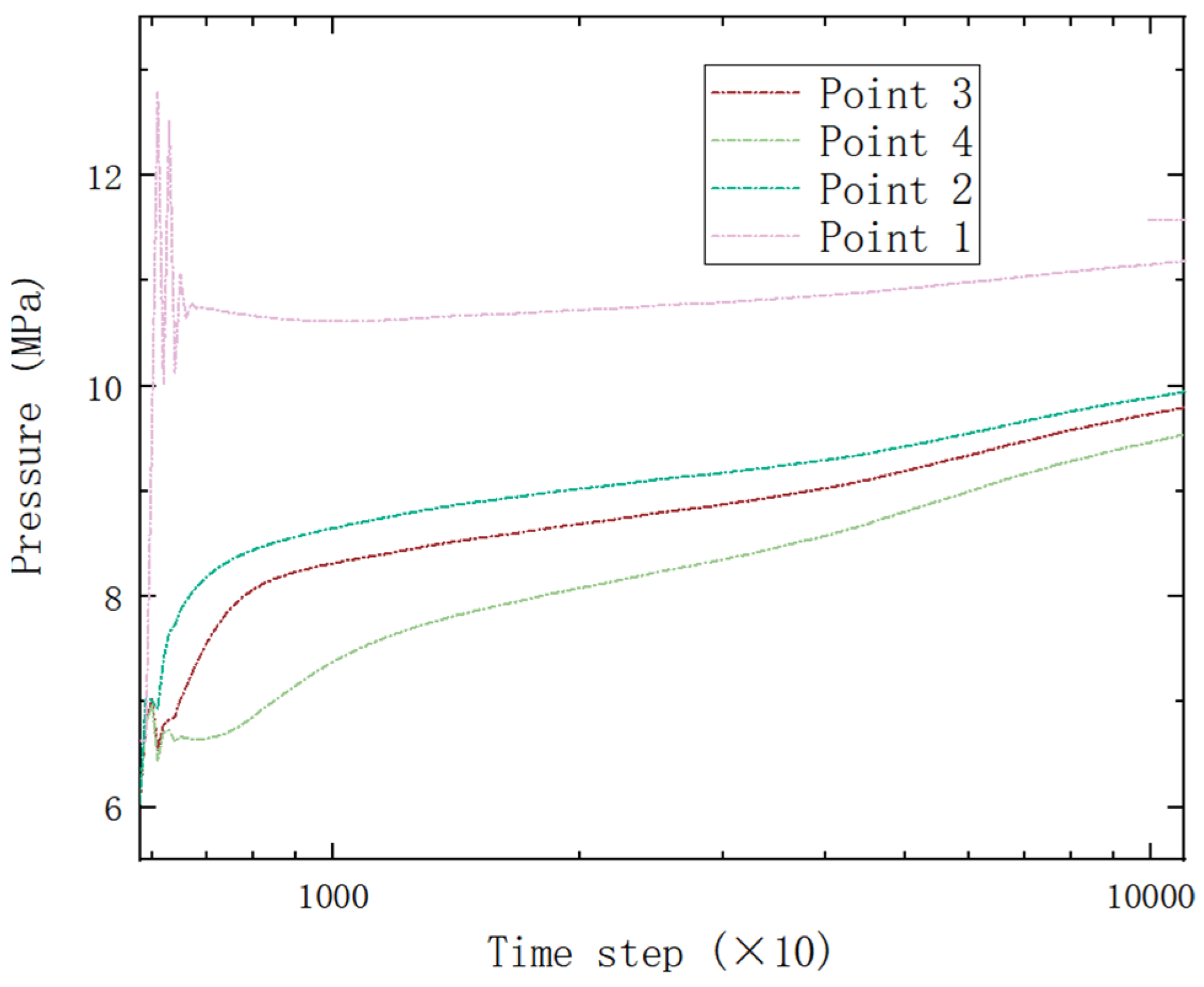
- High viscosity liquid will limit the fracture length but will increase the fracture width; it also increases the extension pressure of the fracture. Under the influence of cleats, the pore pressure is unstable at the initial water injection hole.
- (3)
- The influence of maximum principal stress on the propagation direction of hydraulic fractures is greater than that of the direction of cleats. With the increase of the geostress difference, the fracture length gradually becomes smaller, the fracture width gradually becomes larger, and the Ifc decreases. The smaller the angle between the direction of the face cleat and the direction of maximum principal stress is, the larger the fracture length is and the smaller the fracture width is.
- (4)
- In coal seam fracturing operations where the seam thickness exceeds 20 m, due to the significantly greater fracture strength of the caprock compared to the coal seam rock, it is nearly impossible for hydraulic fractures to penetrate the caprock. Higher pumping rates can also result in increased fracture width, which benefits the entry of proppants.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohamed, T.; Mehana, M. Coalbed methane characterization and modeling: Review and outlook. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 47, 2874–2896. [Google Scholar] [CrossRef]
- Ting, F.T.C. Origin and Spacing of Cleats in Coal Beds. ASME J. Press. Vessel Technol. 1977, 99, 624–626. [Google Scholar] [CrossRef]
- Zhang, J. Numerical simulation of hydraulic fracturing coalbed methane reservoir. Fuel 2014, 136, 57–61. [Google Scholar] [CrossRef]
- Huang, T.; Wang, Z. A novel numerical reconstruction method of coal based on characteristics of the cleat system. Fuel 2024, 372, 132213. [Google Scholar] [CrossRef]
- Mostaghimi, P.; Armstrong, R.T.; Gerami, A.; Hu, Y.; Jing, Y.; Kamali, F.; Liu, M.; Liu, Z.; Lu, X.; Ramandi, H.L.; et al. Cleat-scale characterisation of coal: An overview. J. Nat. Gas Sci. Eng. 2017, 39, 143–160. [Google Scholar] [CrossRef]
- Cheng, X.; Luan, H.; Chen, L.; Jiang, Y.; Han, W. Numerical investigation on mechanical properties of inhomogeneous coal under uniaxial compression and the role of cleat distribution. Bull. Eng. Geol. Environ. 2021, 80, 7009–7027. [Google Scholar] [CrossRef]
- Fan, T.; Zhang, G.; Cui, J. The impact of cleats on hydraulic fracture initiation and propagation in coal seams. Pet. Sci. 2014, 11, 532–539. [Google Scholar]
- Li, Q.; Li, Y.; Cheng, Y.; Li, Q.; Wang, F.; Wei, J.; Liu, Y.; Zhang, C.; Song, B.; Yan, C.; et al. Numerical simulation of fracture reorientation during hydraulic fracturing in perforated horizontal well in shale reservoirs. Energy Sources Part A Recovery Util. Environ. Eff. 2018, 40, 1807–1813. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Cao, H.; Wu, J.; Wang, F.; Wang, Y. The Crack Propagation Behaviour of CO2 Fracturing Fluid in Unconventional Low Permeability Reservoirs: Factor Analysis and Mechanism Revelation. Processes 2025, 13, 159. [Google Scholar] [CrossRef]
- Tan, P.; Fu, S.; Huang, L.; Chen, Z.; Cao, J. Effects of orthogonal cleat structures on hydraulic fracture evolution behavior. Geoenergy Sci. Eng. 2024, 241, 213119. [Google Scholar]
- Yang, T.H.; Jia, P.; Shi, W.H.; Wang, P.T.; Liu, H.L.; Yu, Q.L. Seepage-stress coupled analysis on anisotropic characteristics of the fractured rock mass around roadway. Tunn. Undergr. Space Technol. 2014, 43, 11–19. [Google Scholar] [CrossRef]
- Wenli, Y.; Sharifzadeh, M.; Yang, Z.; Xu, G.; Fang, Z. Assessment of fracture characteristics controlling fluid flow performance in discrete fracture networks (DFN). J. Pet. Sci. Eng. 2019, 178, 1104–1111. [Google Scholar] [CrossRef]
- Jing, Y.; Armstrong, R.T.; Ramandi, H.; Mostaghimi, P. Coal cleat reconstruction using micro-computed tomography imaging. Fuel 2016, 181, 286–299. [Google Scholar] [CrossRef]
- Hui, G.; Chun, F.; Zhu, X. Three-dimensional hydraulic fracturing analysis of coal bed methane based on continuous-discontinuous element method. J. Shandong Univ. (Eng. Sci.) 2021, 51, 119–128. [Google Scholar]
- Tao, X.; Su, G.; Chi, B.; Sun, P. Feasibility Study of Separate Layer Fracturing and Multi-layer Drainage for CBM in Sange Area, Eastern Margin of Ordos Basin. Coal Geol. China 2013, 25, 52–54. [Google Scholar]
- Zou, J.; Chen, W.; Yuan, J.; Yang, D.; Yang, J. 3-D numerical simulation of hydraulic fracturing in a CBM reservoir. J. Nat. Gas Sci. Eng. 2017, 37, 386–396. [Google Scholar] [CrossRef]
- Huang, S.; Lu, Y.; Ge, Z.; Zhou, Z.; Guan, Y.; Chen, X. Fracture Mechanism of Coal Seams Induced by a Multibranched Borehole Drilling (MBBD) Technique to Enhance Coalbed Methane (CBM) Extraction. Energy Fuels 2023, 37, 13034–13047. [Google Scholar]
- Zheng, Y.; He, R.; Huang, L.; Bai, Y.; Wang, C.; Chen, W.; Wang, W. Exploring the effect of engineering parameters on the penetration of hydraulic fractures through bedding planes in different propagation regimes. Comput. Geotech. 2022, 146, 104736. [Google Scholar]
- Itasca Consulting Group, Inc. 3DEC, Version 5.2; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2016. Available online: https://www.itascacg.com/software/3dec (accessed on 16 February 2025).
- Xiong, D.; He, J.; Ma, X.; Qu, Z.; Guo, T.; Ma, S. Breakthrough, future challenges and countermeasures of deep coalbed methane in the eastern margin of Ordos Basin: A case study of Linxing-Shenfu block. J. China Coal Soc. 2023, 49, 1827. [Google Scholar] [CrossRef]
- Laubach, S.; Marrett, R.; Olson, J.; Scott, A. Characteristics and origins of coal cleat: A review. Int. J. Coal Geol. 1998, 35, 175–207. [Google Scholar]
- Karimpouli, S.; Tahmasebi, P.; Ramandi, H.L. A review of experimental and numerical modeling of digital coalbed methane: Imaging, segmentation, fracture modeling and permeability prediction. Int. J. Coal Geol. 2020, 228, 103552. [Google Scholar] [CrossRef]
- Ramandi, H.L.; Mostaghimi, P.; Armstrong, R.T.R.T. Digital rock analysis for accurate prediction of fractured media permeability. J. Hydrol. 2017, 554, 817–826. [Google Scholar] [CrossRef]
- Zheng, X. Study on Hydraulic Fracture Propagation Law of Coal Considering Soft Interlaye and Coal Fracture Conductivity. Master’s Thesis, Chongqing University, Chongqing, China, 2021. [Google Scholar] [CrossRef]
- Cipolla, C.L.; Warpinski, N.R.; Mayerhofer, M.J.; Lolon, E.P.; Vincent, M.C. The relationship between fracture complexity, reservoir properties, and fracture treatment design. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008. SPE-115769-MS. [Google Scholar]
- Hubbert, M.K.; Willis, D.G. Mechanics of hydraulic fracturing. Trans. AIME 1957, 210, 153–168. [Google Scholar] [CrossRef]






| Coal Seam | Roof and Floor | ||
|---|---|---|---|
| Input parameters | Values | Input parameters | Values |
| Modulus of elasticity E (GPa) | 10 | Modulus of elasticity E (GPa) | 25 |
| Poisson’s ratio μ (%) | 0.25 | Poisson’s ratio μ (%) | 0.2 |
| Rock density (kg/m3) | 1200 | Rock density (kg/m3) | 2590 |
| Rock tensile strength (MPa) | 1.5 | Rock tensile strength (MPa) | 5 |
| Block normal stiffness kn (GPa) | 1 | Block normal stiffness (GPa) | 5 |
| Block shear stiffness ks (GPa) | 1 | Block shear stiffness (GPa) | 5 |
| Input Parameters | Values |
|---|---|
| Fluid bulk modulus K (GPa) | 3 |
| Fluid density (kg/m3) | 1000 |
| Fluid viscosity η (Pa·s) | 0.0015 |
| Input Parameters | Values |
|---|---|
| Stress gradient (MPa/km) | 25 |
| Depth of center of mass (m) | 600 |
| Horizontal minimum principal stress (MPa) | 12 |
| Horizontal maximum principal stress (MPa) | 15 |
| Block | Rock Type | Compressive Strength (MPa) | Young’s Modulus (GPa) | Poisson’s Ratio | Fracture Pressure (MPa) | Horizontal Minimum Principal Stress (MPa) | Horizontal Maximum Principal Stress (MPa) | Vertical Principal Stress (MPa) |
|---|---|---|---|---|---|---|---|---|
| Daijiatian No. 16 Coal Seam | Roof (siltstone) | 25.1 | 3.2 | 0.19 | 15.8 | 15.1 | 16.5 | 16.9 |
| Coal | 6.6 | 0.9 | 0.21 | 11.5 | 11.6 | 14.2 | 17 | |
| Floor (muddy siltstone) | 17.8 | 2.7 | 0.17 | 15.2 | 14.7 | 16.1 | 17.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, H.; Zhang, H.; Wang, H.; Xie, X.; Wang, C.; Liu, J. Numerical Study on Hydraulic Fracture Propagation in Coalbed Methane Considering Coal Seam Cleats. Processes 2025, 13, 1036. https://doi.org/10.3390/pr13041036
Xiao H, Zhang H, Wang H, Xie X, Wang C, Liu J. Numerical Study on Hydraulic Fracture Propagation in Coalbed Methane Considering Coal Seam Cleats. Processes. 2025; 13(4):1036. https://doi.org/10.3390/pr13041036
Chicago/Turabian StyleXiao, Hui, Han Zhang, Hongsen Wang, Xin Xie, Chunbing Wang, and Junchen Liu. 2025. "Numerical Study on Hydraulic Fracture Propagation in Coalbed Methane Considering Coal Seam Cleats" Processes 13, no. 4: 1036. https://doi.org/10.3390/pr13041036
APA StyleXiao, H., Zhang, H., Wang, H., Xie, X., Wang, C., & Liu, J. (2025). Numerical Study on Hydraulic Fracture Propagation in Coalbed Methane Considering Coal Seam Cleats. Processes, 13(4), 1036. https://doi.org/10.3390/pr13041036







