Physical Simulation Tests on Deformation and Instability of Composite Roof in Large-Section Coal Roadway Under Different Burial Depths
Abstract
1. Introduction
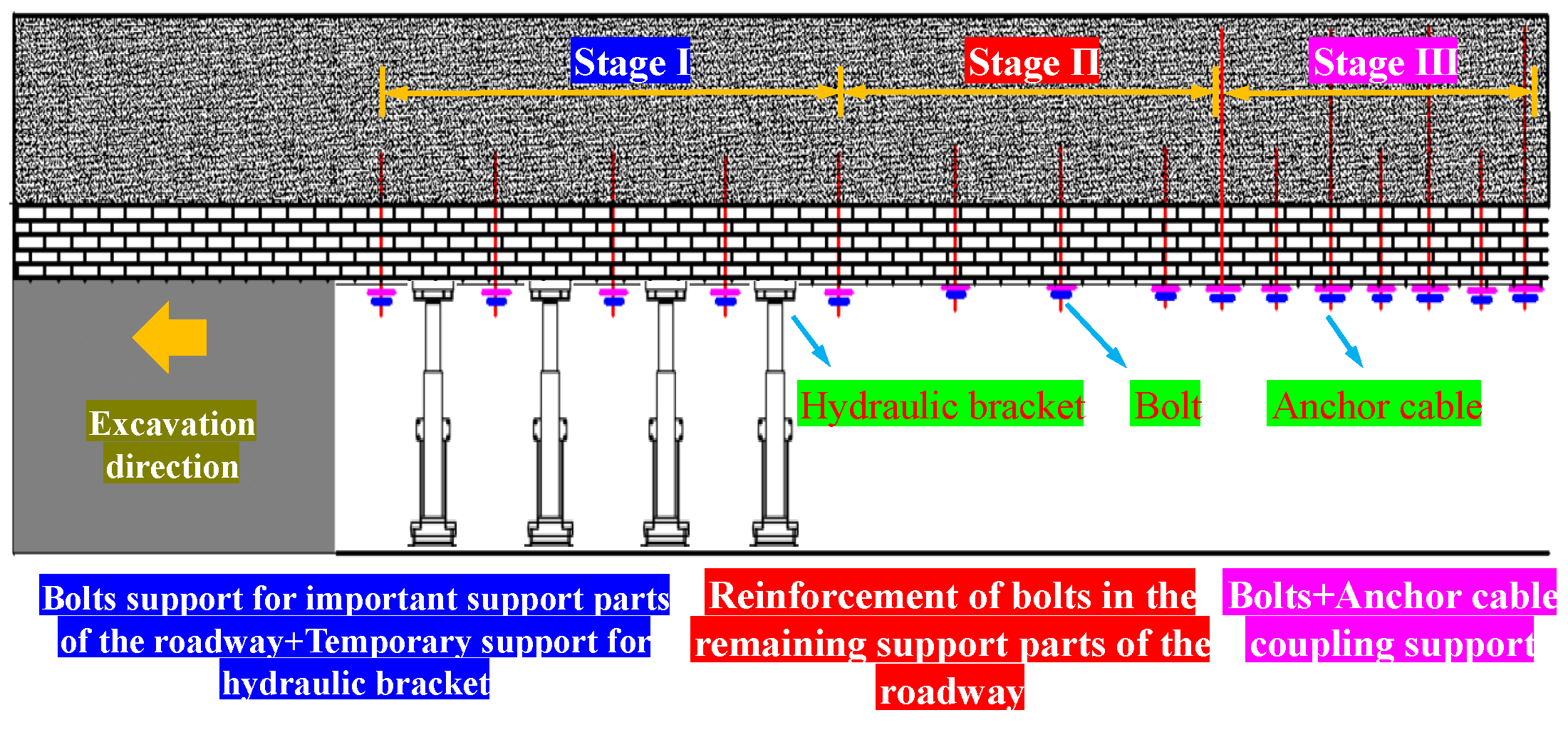
2. Principle of Staged Control of Coal Roadway Composite Roof
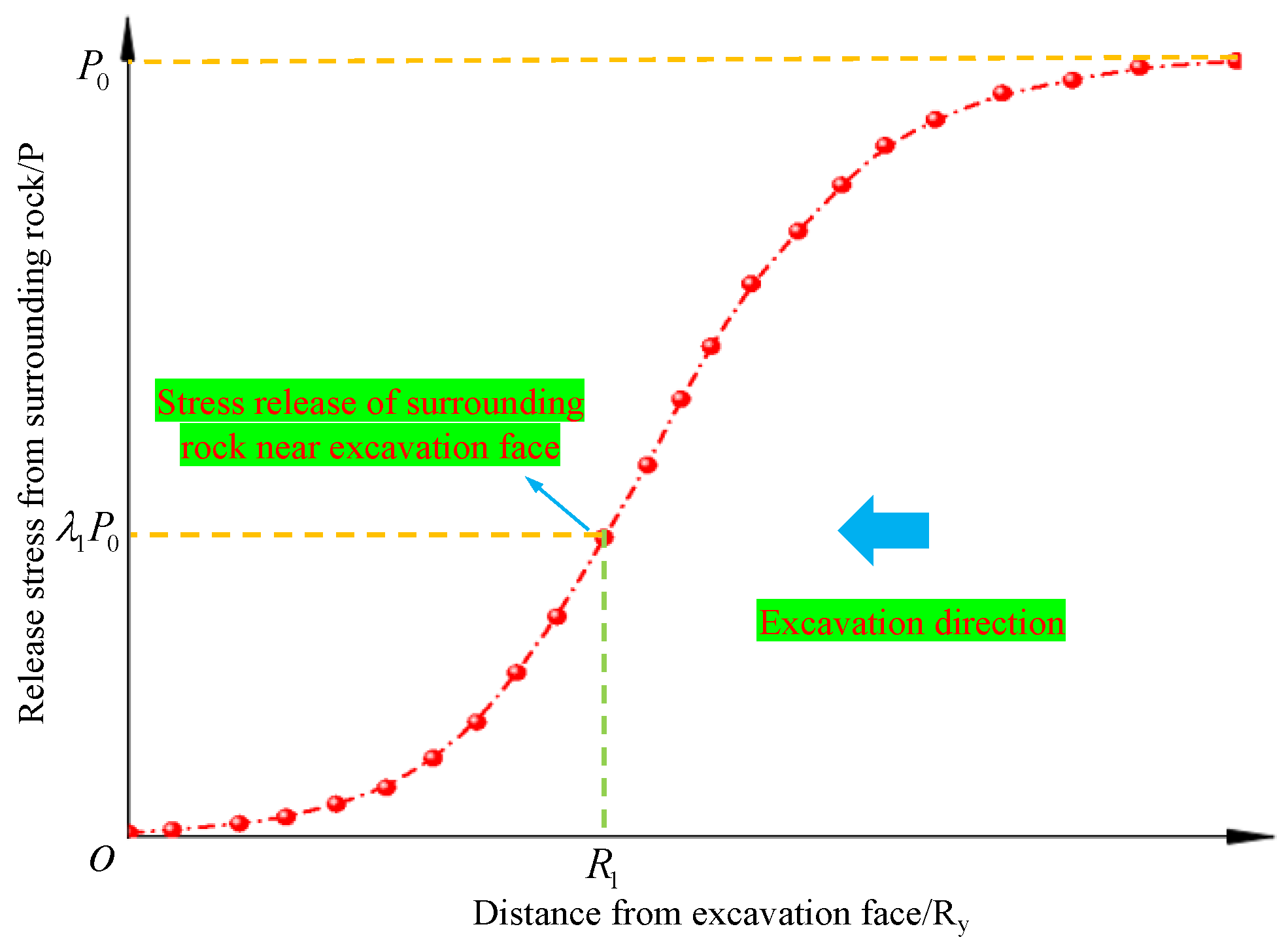
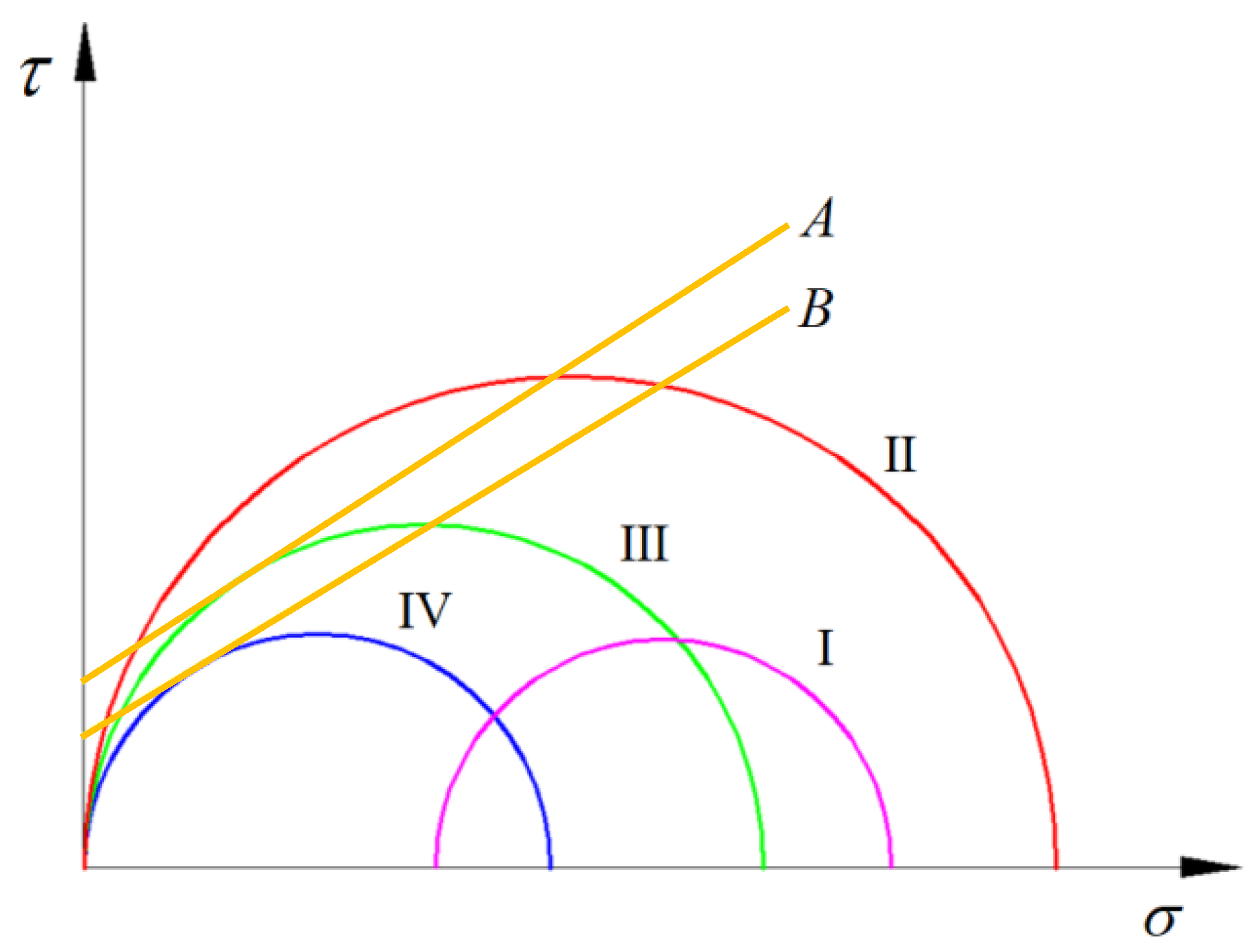
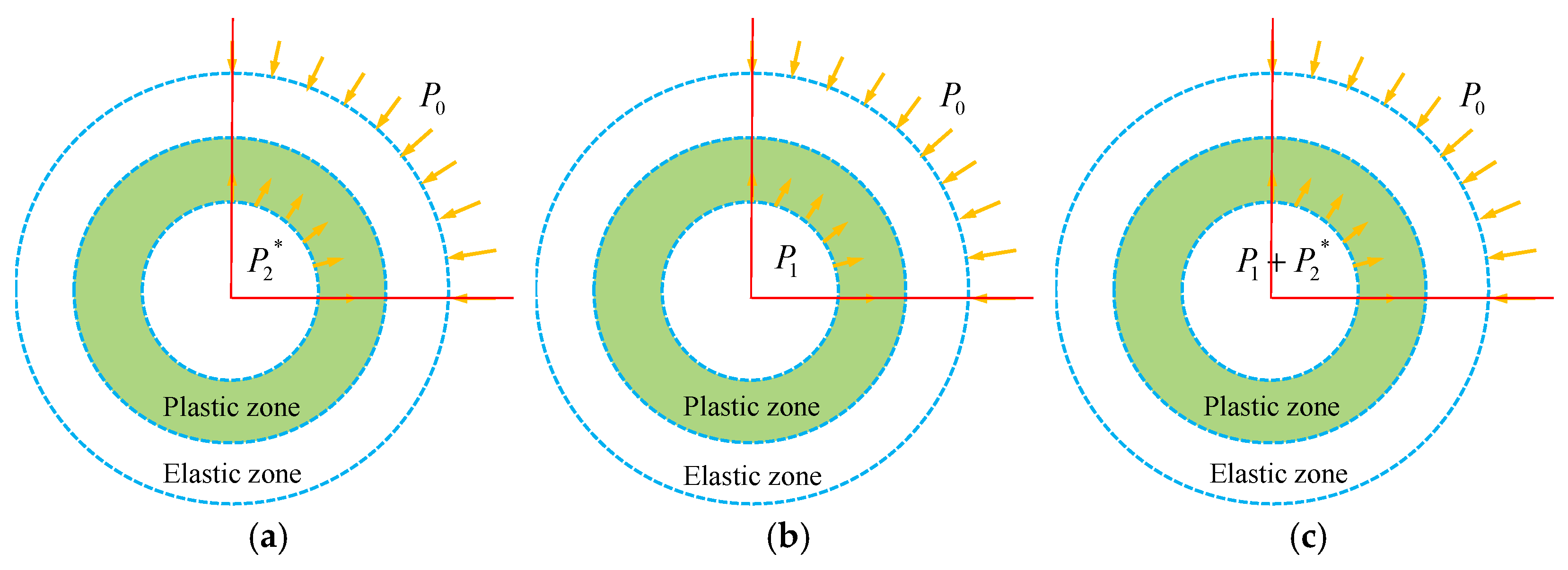
2.1. Characteristics of Spatiotemporal Effects on Excavation Face
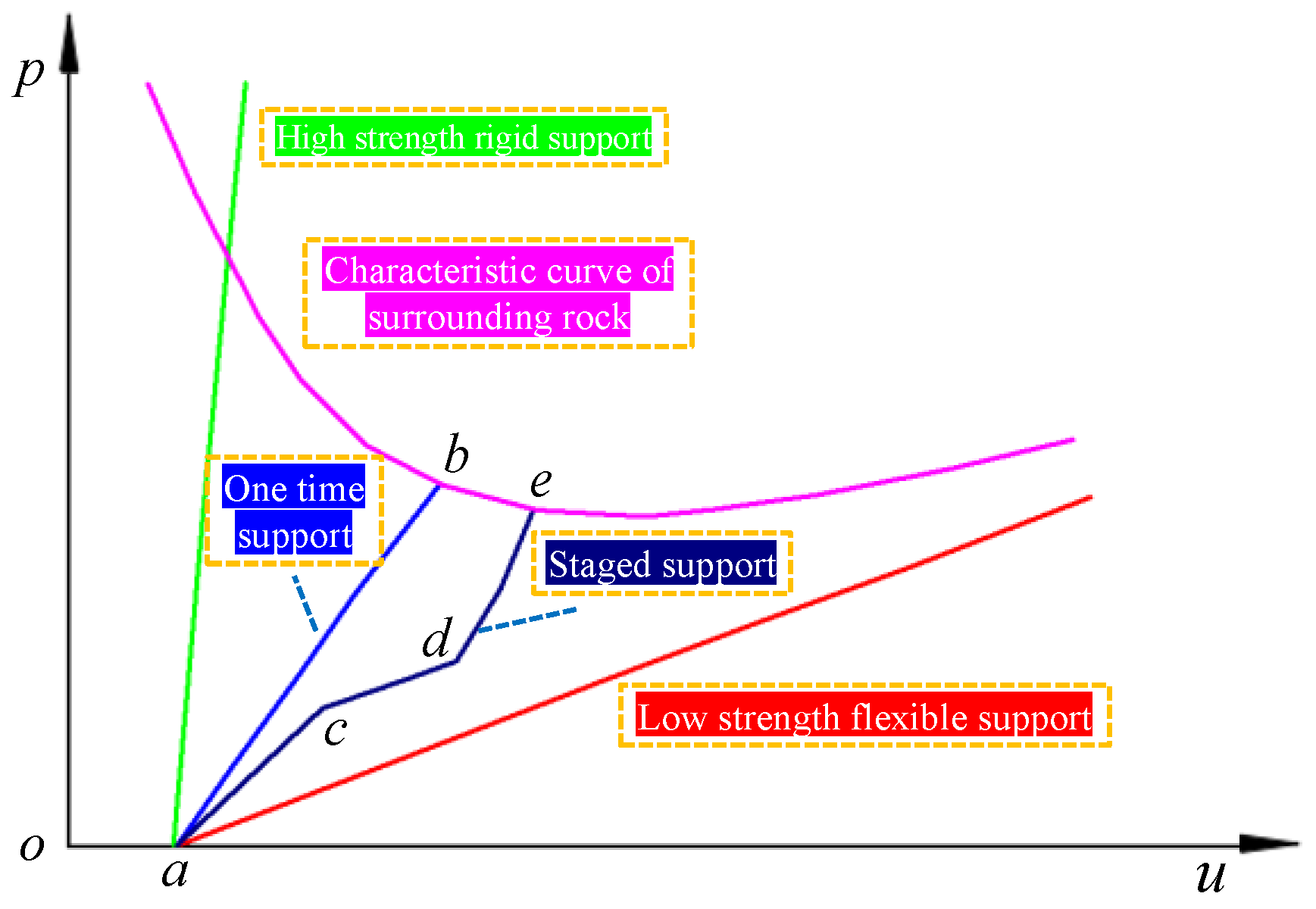
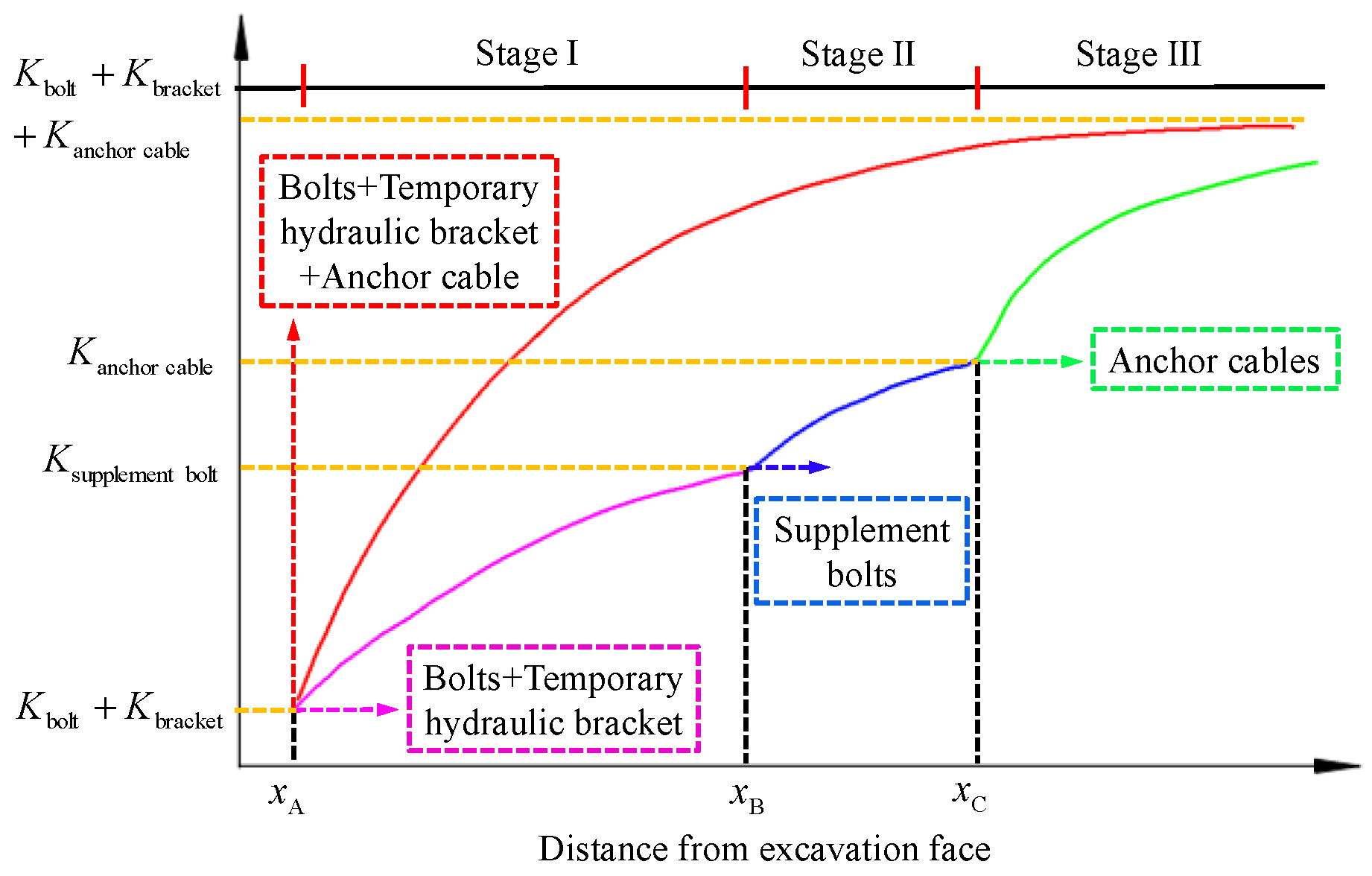
2.2. Stiffness Characteristics of Supporting Structures
3. Physical Similarity Simulation Test Scheme
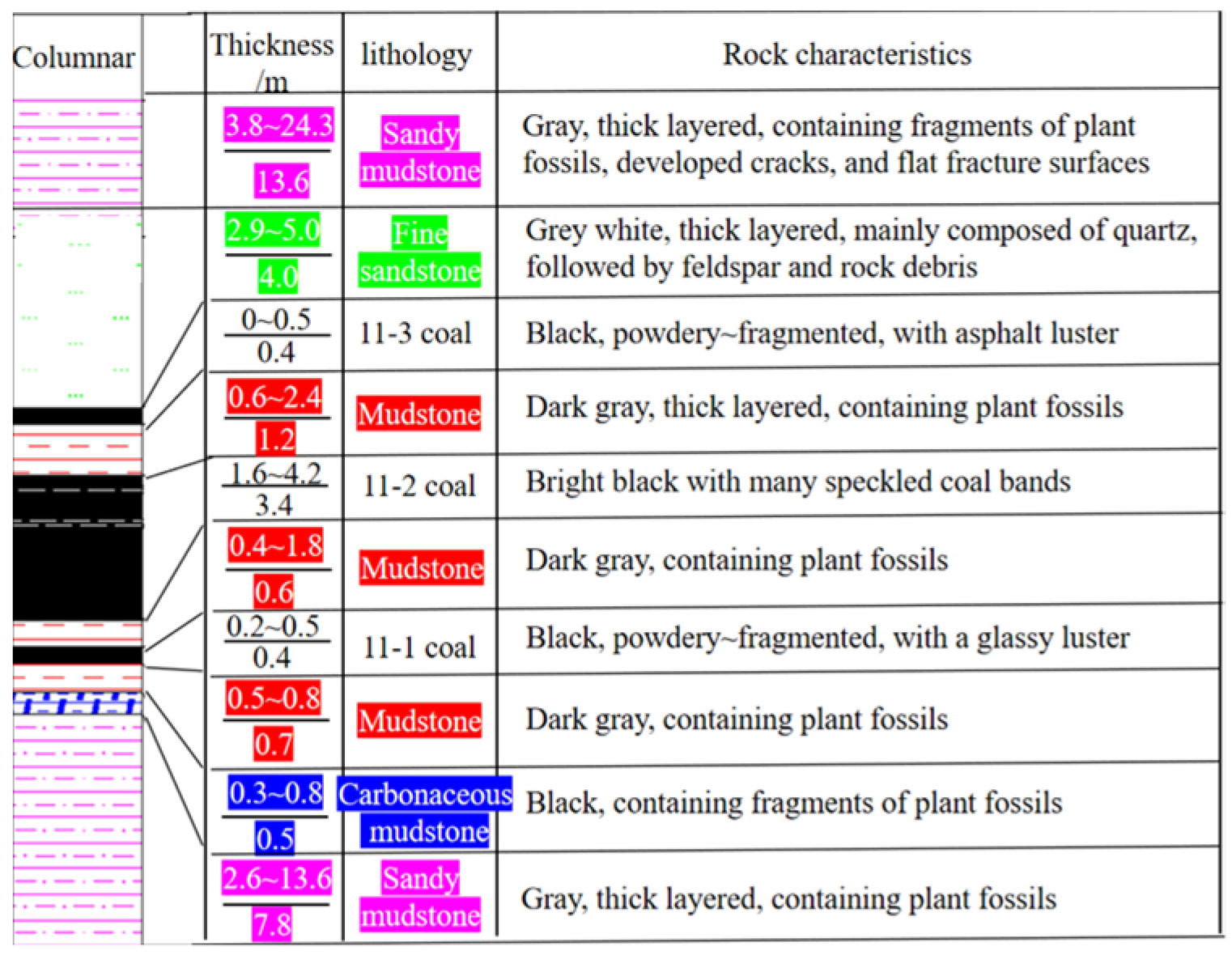
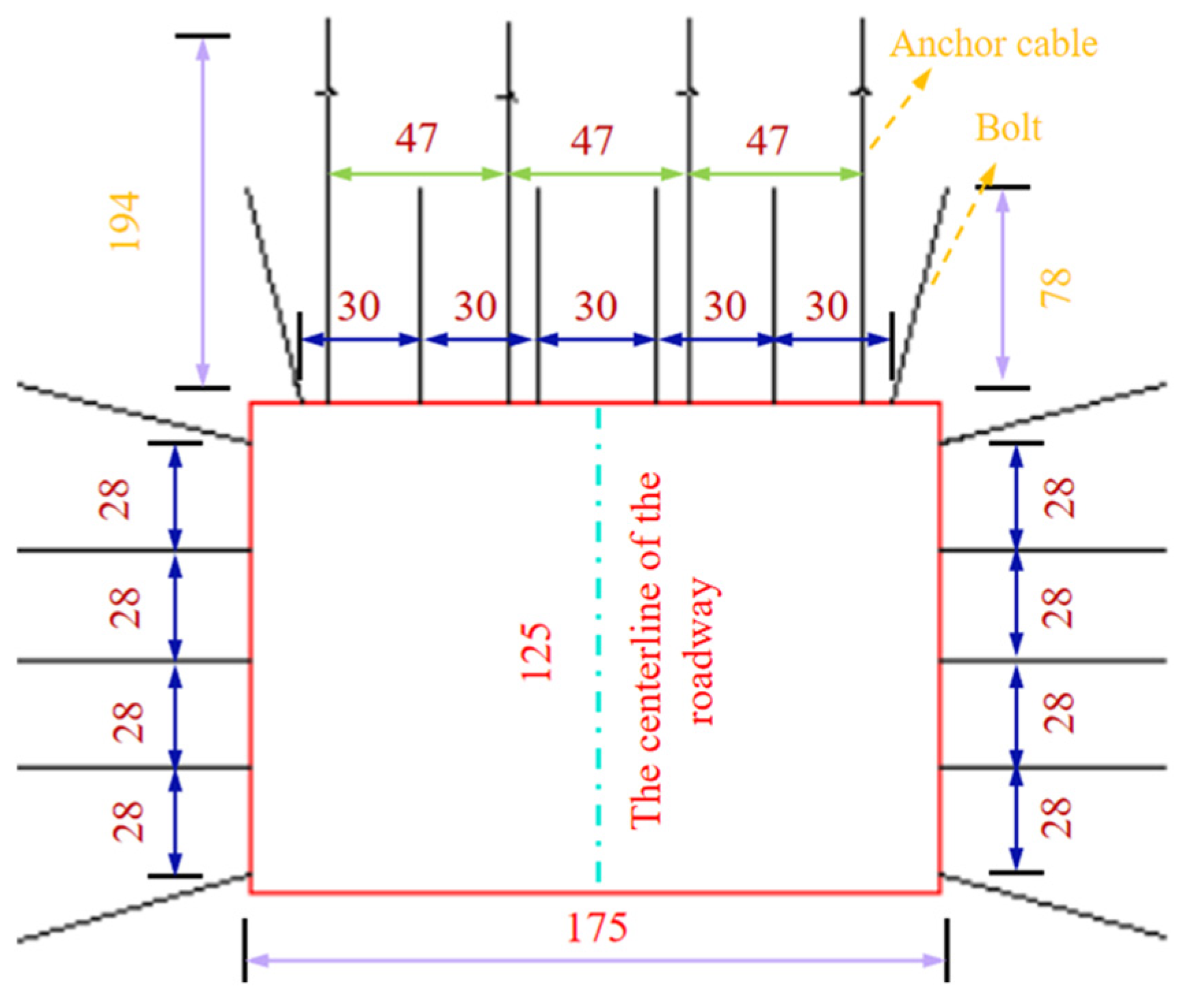
3.1. Overview of Prototype Engineering
3.2. Design of Similar Simulation Test Scheme
- (1)
- Determination of similar parameters
- (a)
- Geometric similarity ratio
- (b)
- Stress similarity ratio
- (c)
- The ratio of excavation time between prototype and model
- (d)
- Similar model test materials
- (e)
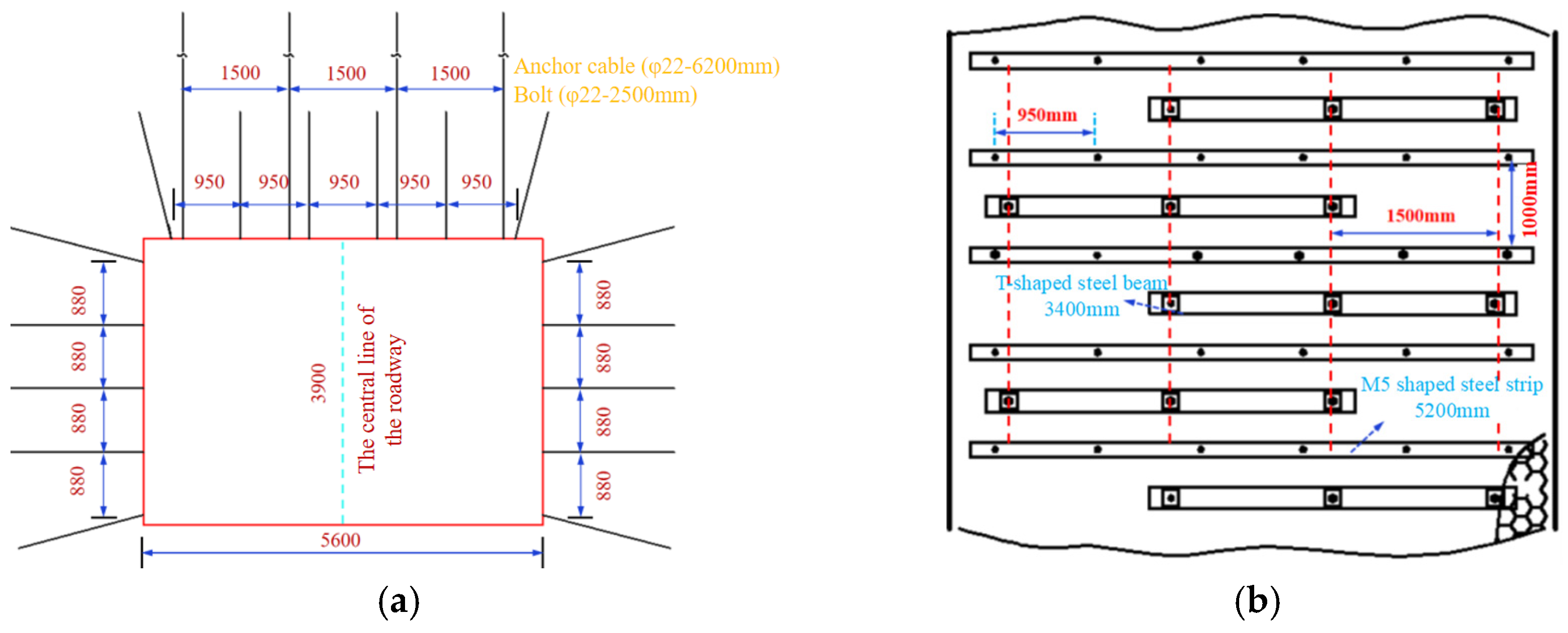
- Model roadway support process parameters
- (2)
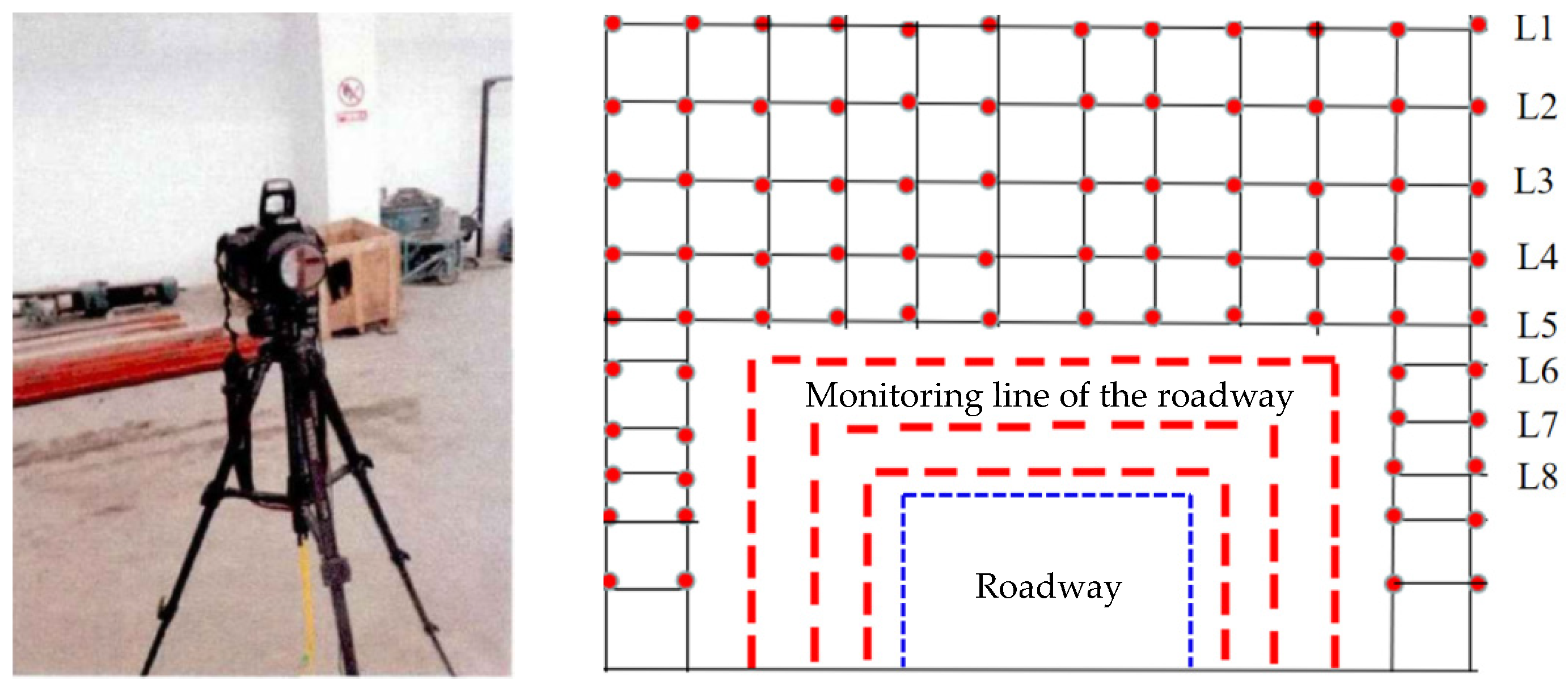
- Stress and displacement monitoring
- (3)
- Model making and loading process
4. Test Results and Analysis
4.1. Evolution of Roof Stress and Displacement
- (1)
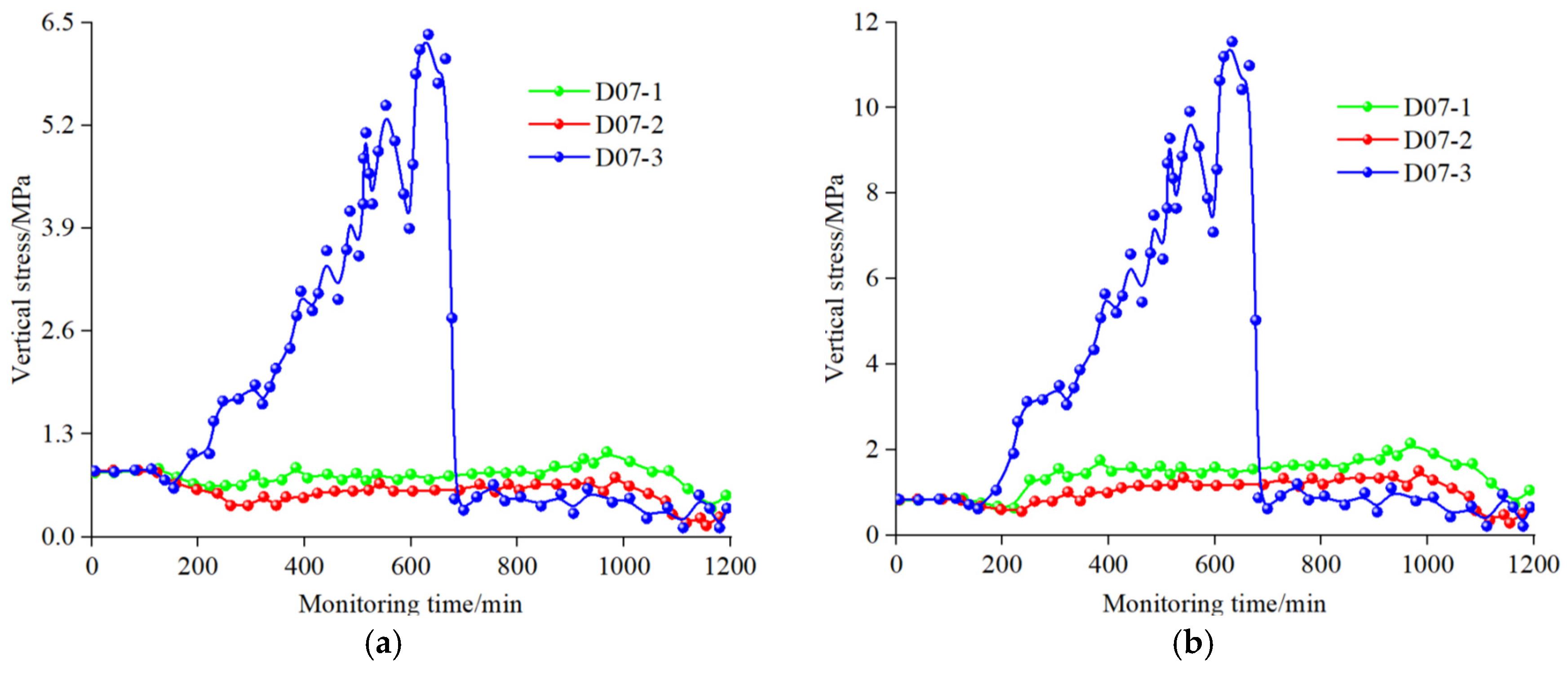
- Evolution of roof stress
- (2)
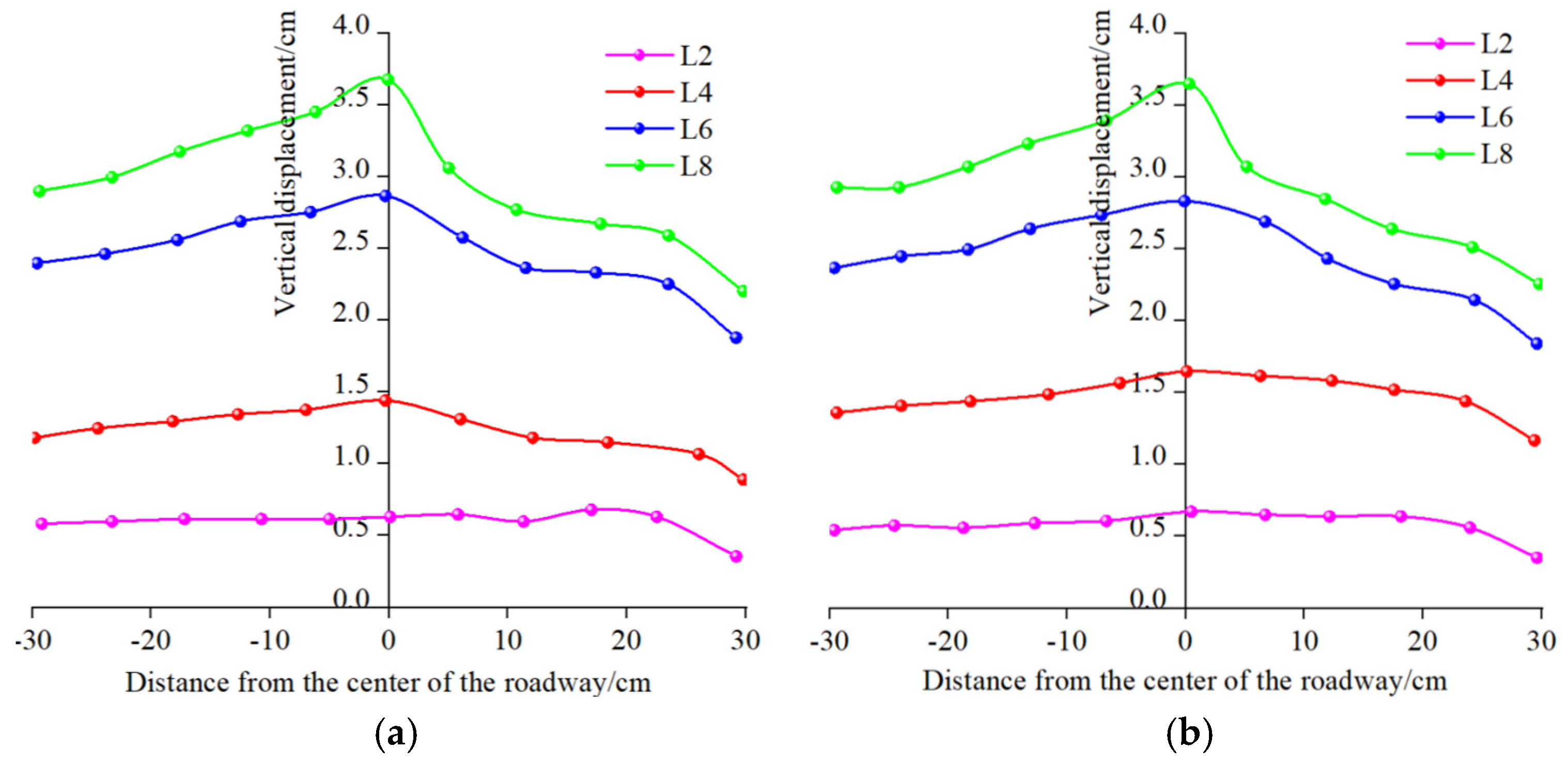
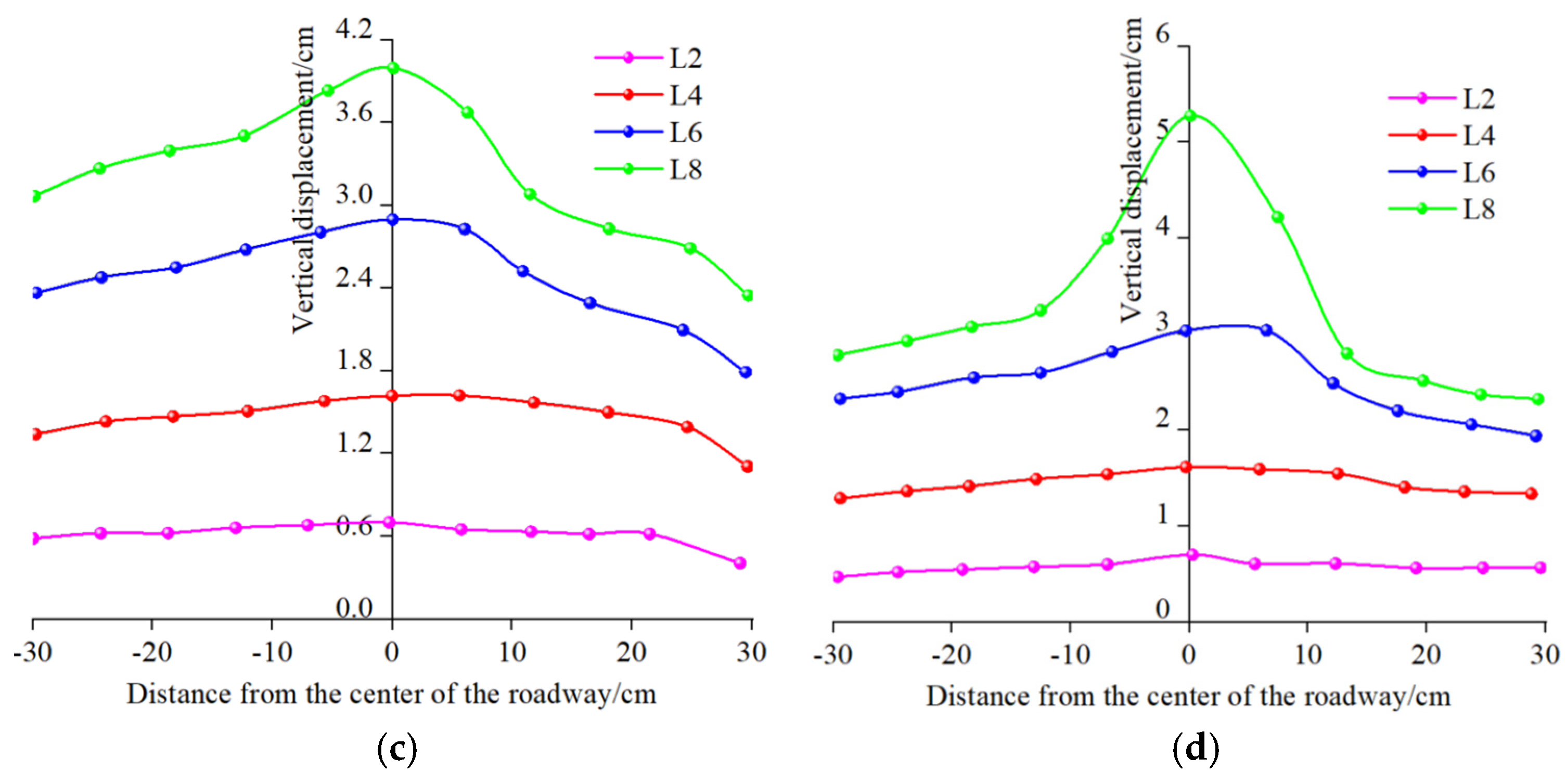
- Evolution of roof displacement
4.2. Analysis of Roof Failure Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheluszka, P. Numerical studies of the dynamics of the roadheader equipped with an automatic control system during cutting of rocks with different mechanical properties. Energies 2021, 14, 7353. [Google Scholar] [CrossRef]
- Wang, E.Y.; Chen, G.B.; Yang, X.J.; Zhang, G.F.; Guo, W.B. Study on the failure mechanism for coal roadway stability in jointed rock mass due to the excavation unloading effect. Energies 2020, 13, 2515. [Google Scholar] [CrossRef]
- Wang, J.H. China mechanized road header status and bolt support technology in mine seam roadway. Coal Sci. Technol. 2004, 1, 6–10. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.L.; Zhang, X.F. Theory and technology of integrated and efficient excavation and anchoring. J. China Coal Soc. 2020, 45, 2021–2030. [Google Scholar] [CrossRef]
- Kaiser, P. Phenomenological model for rock with time dependent strength. Int. J. Rock Mech. Min. Sci. Geomech. 1985, 18, 153–165. [Google Scholar] [CrossRef]
- Guo, H.; Ji, M.; Li, H.; Zhang, K.; Wang, H.; Liang, A. Research and application on support technology of coal seam roadway with high stress. J. Mines Met. Fuels 2019, 67, 82–89. [Google Scholar]
- Hayati, A.N.; Ahmadi, M.M.; Hajjar, M.; Kashighandi, A. Unsupported advance length in tunnels constructed using New Austrian Tunnelling Method and ground surface settlement. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 2170–2185. [Google Scholar] [CrossRef]
- Jia, H.S.; Ma, N.J.; Zhu, Q.K. Mechanism and control method of wing leaf plastic zone penetration induced collapse in roadway roof. J. China Coal Soc. 2016, 41, 1384–1392. [Google Scholar]
- Jing, W.; Zhou, J.; Yuan, L.; Jin, R.C.; Jing, L.W. Deformation and failure mechanism of surrounding rock in deep soft rock tunnels considering rock rheology and different strength criteria. Rock Mech. Rock Eng. 2024, 57, 545–580. [Google Scholar] [CrossRef]
- Tang, B.; Mao, A.; Li, T.G.; Cheng, H.; Tao, W.B.; Liu, B.; Hou, J.L. Mechanical behaviors of steel segment support structures for TBM-excavated coal mine tunnels: Experimental and numerical study. Int. J. Civ. Eng. 2024, 23, 345–359. [Google Scholar] [CrossRef]
- Yasitli, N.E. Numerical modeling of surface settlements at the transition zone excavated by New Austrian Tunneling Method and Umbrella Arch Method in weak rock. Arab. J. Geosci. 2013, 6, 2699–2708. [Google Scholar] [CrossRef]
- Aygar, E.B. Evaluation of new Austrian tunnelling method applied to Bolu tunnel’s weak rocks. J. Rock Mech. Geotech. Eng. 2020, 12, 541–556. [Google Scholar] [CrossRef]
- Wibisono, D.Y.; Gutierrez, M.; Majumder, D. Experimental investigation of tunnel damage and spalling in brittle rock using a true-triaxial cell. Int. J. Rock Mech. Min. Sci. 2024, 182, 105884. [Google Scholar] [CrossRef]
- Chu, X.W.; Wu, Y.Z.; Wu, Z.G.; Hao, D.Y.; Feng, Y.L.; Li, W.Z.; Meng, X.Z. Characteristics of roof deformation in excavating face and determination method of reasonable non-support distance. J. Min. Saf. Eng. 2020, 37, 908–917. [Google Scholar] [CrossRef]
- Zhou, H.; Hu, S.C.; Lu, J.J.; Wang, Z.C.; Zhang, C.Q. In situ testing of surrounding rock deformation and failure during the entire process of coal mine deep well roadway excavation. Geotech. Mech. 2015, 36, 3523–3530. [Google Scholar] [CrossRef]
- Sofianos, A.I.; Kapenis, A.P. Effect of strata thickness on the stability of an idealized bolted underground roof. Mine Plan. Equip. Sel. 1996, 1996, 275–279. [Google Scholar]
- Zhao, M.Z. Stability Mechanism and Safety Control Technology of Compound Roof in Fully Mechanized Coal Roadway of Zhaozhuang Mine; China University of Mining and Technology: Xuzhou, China, 2022. [Google Scholar]
- Yu, Y.; Wang, X.Y.; Bai, J.B.; Zhang, L.Y.; Xia, H.C. Deformation mechanism and stability control of roadway surrounding rock with compound roof: Research and applications. Energies 2020, 13, 1350. [Google Scholar] [CrossRef]
- Guo, Y.X. Linkage Effect of Surrounding Rock Layers in Deep Large Section Coal Roadway and Roof Support Control Technology; China University of Mining and Technology: Xuzhou, China, 2024. [Google Scholar]
- Wang, B. Research on graded support and rapid excavation technology of bolt(cable) in coal mine roadway. Xi’an Univ. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Sun, J. Progress in Rock Rheological Mechanics and Its Engineering Applications. J. Rock Mech. Eng. 2007, 6, 1081–1106. [Google Scholar]
- Zhou, Z.L.; Tan, Z.S.; Li, L.F.; Lei, K. Research on the dynamic interaction mechanism between surrounding rock and support in TBM tunnel. J. Railw. Sci. Eng. 2024, 22, 284. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Underground Excavations in Rock; Institution of Mining and Metallurgy: London, UK, 1980. [Google Scholar]
- Oreste, P.P. Analysis of structural interaction in tunnels using the covergence-confinement approach. Tunn. Undergr. Space Technol. 2003, 18, 347–363. [Google Scholar] [CrossRef]






| Rock Layer Name | Ratio Number (Sand:Lime:Gypsum) | Average Compressive Strength of Samples/MPa | Rock Compressive Strength/MPa |
|---|---|---|---|
| Fine sandstone | 6:5:5 | 1.192 | 54.84 |
| Sandy mudstone | 7:7:3 | 0.674 | 31.45 |
| Coal | 10:5:5 | 0.163 | 5.49 |
| Mudstone | 8:6:4 | 0.357 | 16.42 |
| Siltstone | 9:5:5 | 1.152 | 53.41 |
| NO. | Lithology | Thickness/m | Density/kg·m−3 | Layers | Ratio Number | Weight of Each Layer/kg | |||
|---|---|---|---|---|---|---|---|---|---|
| Sand | Lime | Gypsum | Water | ||||||
| 10 | Sandy mudstone | 15.0 | 2280 | 7 | 773 | 167.9 | 16.8 | 7.2 | 19.2 |
| 9 | Fine sandstone | 5.0 | 2630 | 5 | 655 | 88.6 | 7.4 | 7.4 | 10.3 |
| 8 | 11-3 coal | 0.5 | 1500 | 1 | 1055 | 26.8 | 1.3 | 1.3 | 2.9 |
| 7 | Mudstone | 0.9 | 1690 | 2 | 864 | 26.5 | 1.9 | 1.3 | 2.9 |
| 6 | 11-2 coal | 4.0 | 1380 | 4 | 1055 | 49.3 | 2.5 | 2.5 | 5.4 |
| 5 | Mudstone | 2.0 | 1690 | 2 | 864 | 59.1 | 4.4 | 2.9 | 6.6 |
| 4 | 11-1 coal | 0.5 | 1400 | 1 | 1055 | 25.0 | 1.3 | 1.3 | 2.8 |
| 3 | Mudstone | 0.8 | 1690 | 1 | 864 | 47.2 | 3.5 | 2.4 | 5.3 |
| 2 | Charcoal mudstone | 0.5 | 1600 | 1 | 1237 | 29.0 | 0.7 | 1.7 | 3.1 |
| 1 | Sandy mudstone | 10.8 | 2280 | 4 | 773 | 211.6 | 21.2 | 9.1 | 2.4 |
| Loading Level | Time Interval | Vertical Loading |
|---|---|---|
| Step 1 | 1 h (Preloading) | 5.98 kN |
| Step 2 | 1 h (Preloading) | 11.95 kN |
| Step 3 | 1 h | Wait for the pressure to stabilize and start extracting the wooden strips |
| Step 4 | 2 h | 16.3 kN |
| Step 5 | 2 h | 23.9 kN |
| Step 6 | 2 h | 29.8 kN |
| Step 7 | 2 h | 36.3 kN |
| Step 8 | 1 h | Excavate the coal seam in front of the roadway |
| Step 9 | 2 h | 36.3 × 1.3 kN (Mining impact) |
| Step 10 | 2 h | 36.3 × 1.5 kN (Mining impact) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Ma, L.; Wei, W.; Huang, S. Physical Simulation Tests on Deformation and Instability of Composite Roof in Large-Section Coal Roadway Under Different Burial Depths. Processes 2025, 13, 1003. https://doi.org/10.3390/pr13041003
Yang S, Ma L, Wei W, Huang S. Physical Simulation Tests on Deformation and Instability of Composite Roof in Large-Section Coal Roadway Under Different Burial Depths. Processes. 2025; 13(4):1003. https://doi.org/10.3390/pr13041003
Chicago/Turabian StyleYang, Sen, Liqiang Ma, Weilong Wei, and Shunjie Huang. 2025. "Physical Simulation Tests on Deformation and Instability of Composite Roof in Large-Section Coal Roadway Under Different Burial Depths" Processes 13, no. 4: 1003. https://doi.org/10.3390/pr13041003
APA StyleYang, S., Ma, L., Wei, W., & Huang, S. (2025). Physical Simulation Tests on Deformation and Instability of Composite Roof in Large-Section Coal Roadway Under Different Burial Depths. Processes, 13(4), 1003. https://doi.org/10.3390/pr13041003








