Thermal Performance and Entropy Generation of Unsteady Natural Convection in a Trapezoid-Shaped Cavity
Abstract
1. Introduction
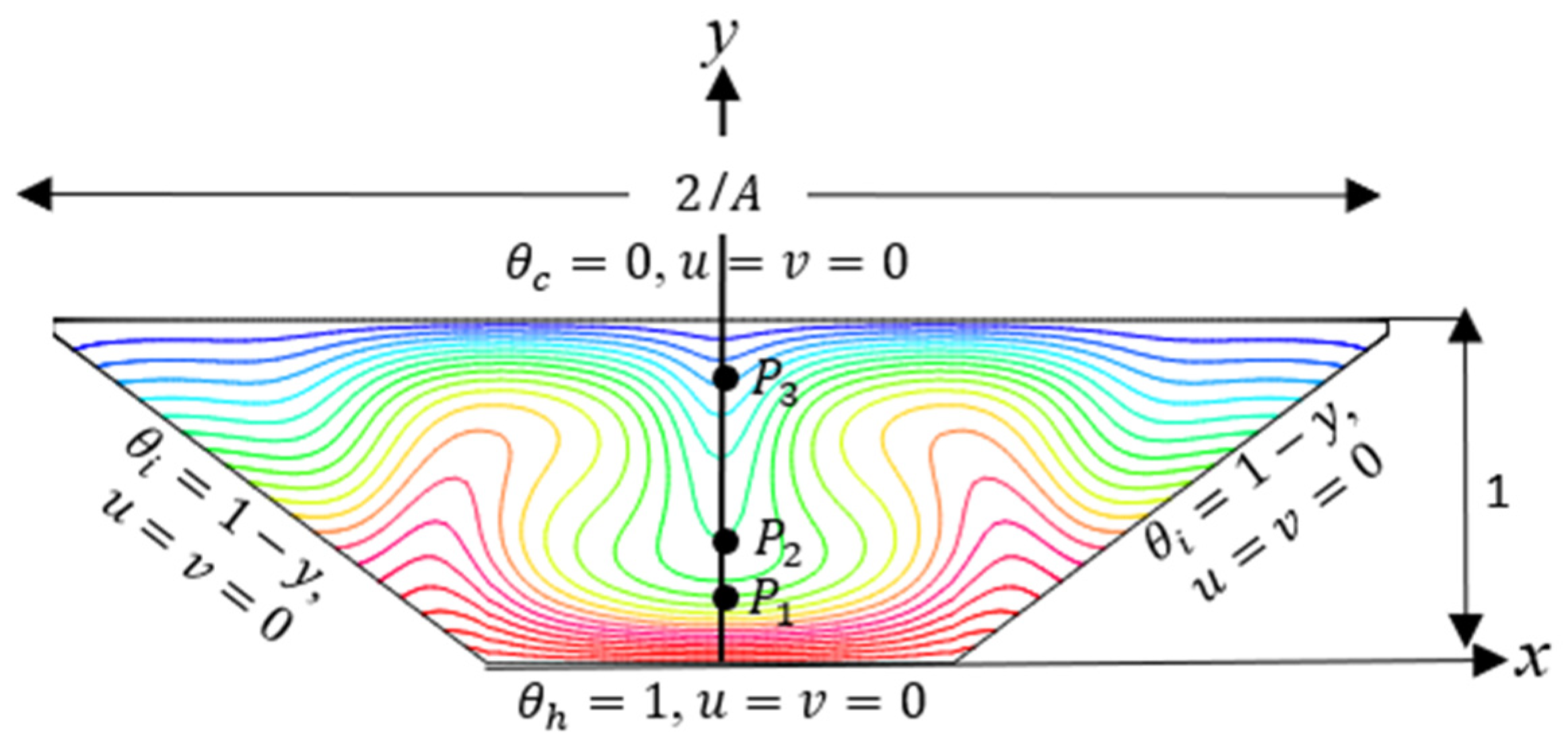
2. Problem Formulations
| Property (Unit) | Water |
|---|---|
| k (W/m K) | 0.566 |
| ρ (kg/m3) | 998.4 |
| Cp (J/kg K) | 4182 |
| μ (kg/m s) | 9.4748 × 10−4 |
| β (1/K) | 3.109 × 10−4 |
3. Numerical Model
4. Grid and Time Step Dependent Tests
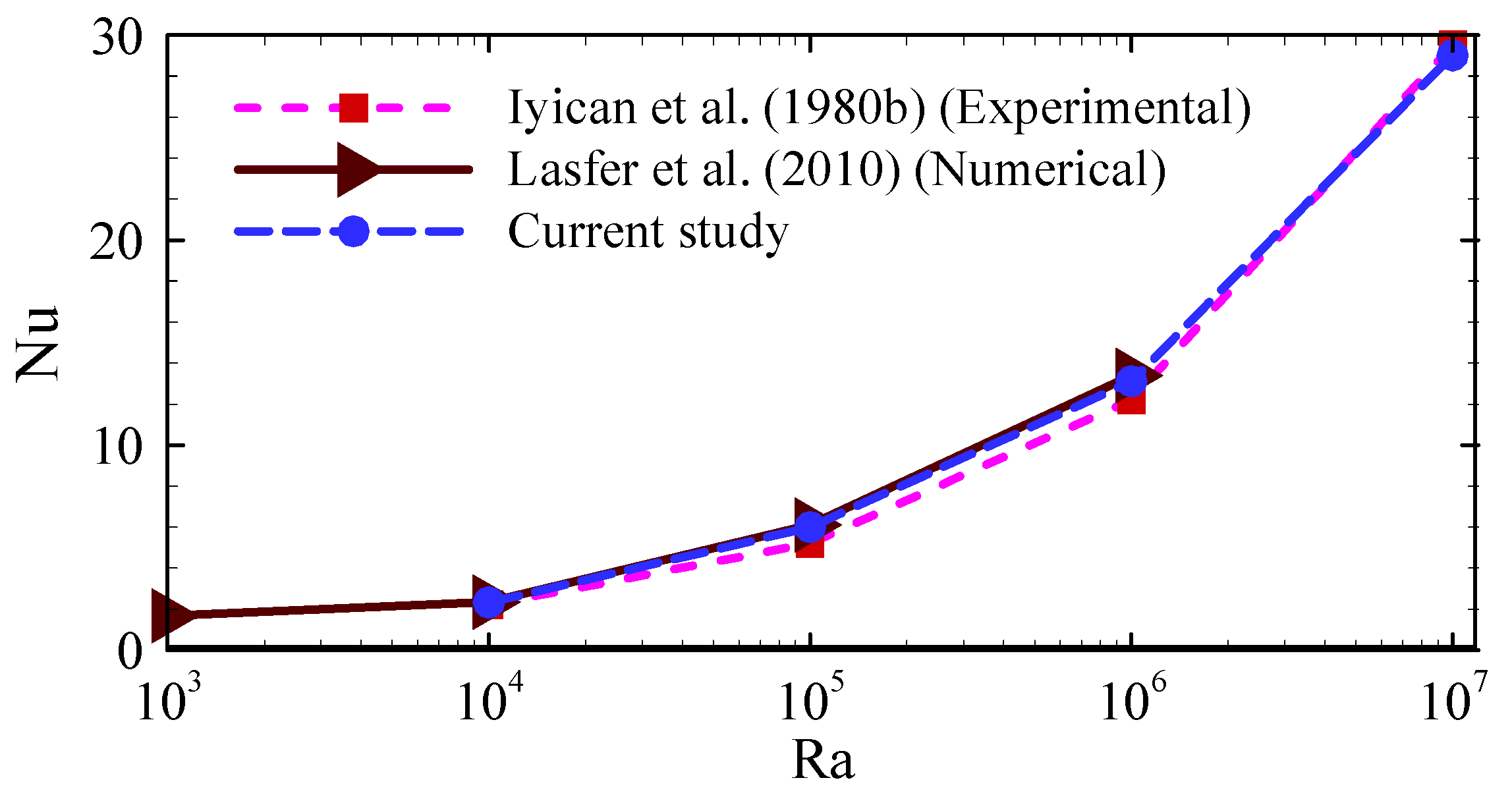
5. Model Validation
6. Results and Discussions
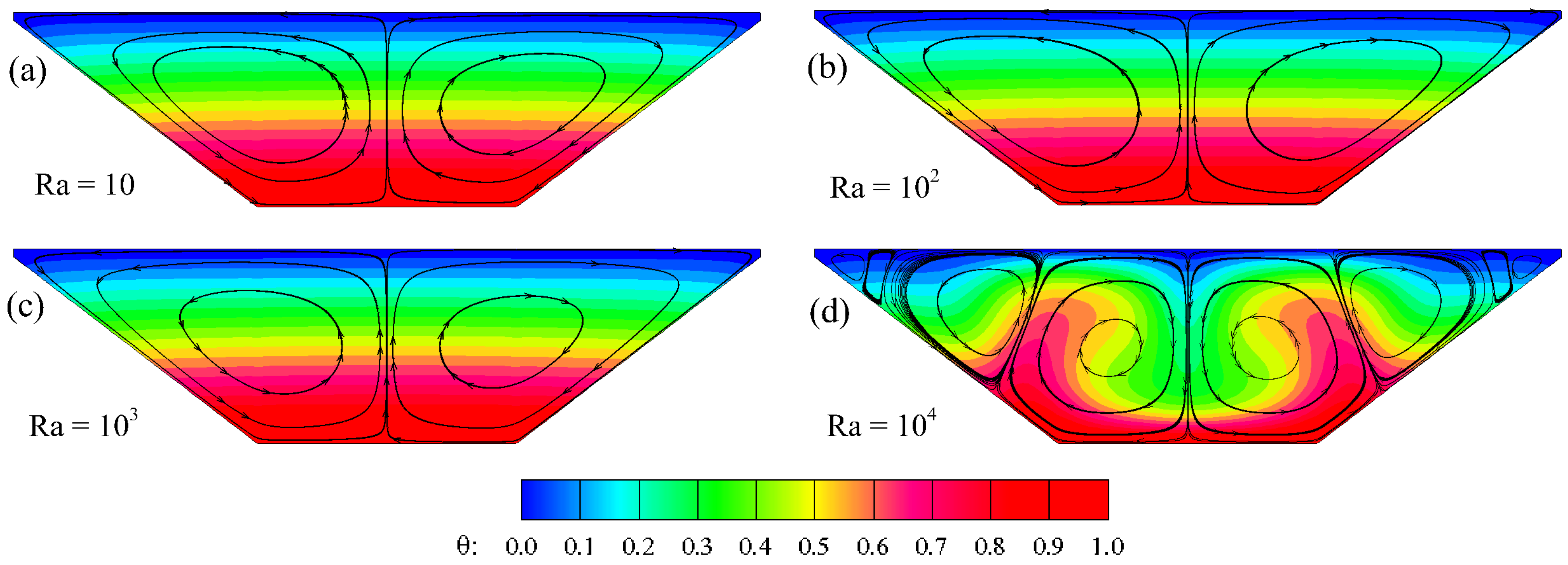
6.1. Development of Symmetrical Flow
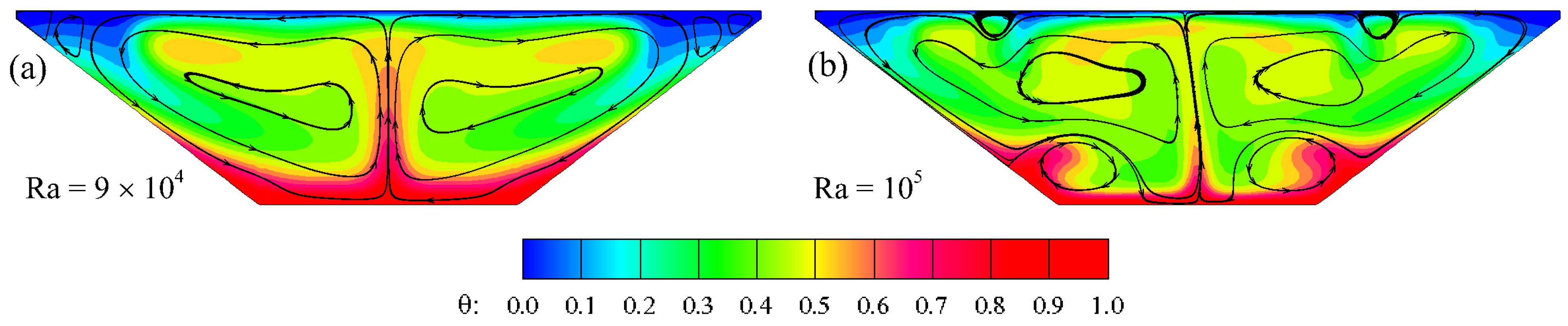
6.2. Development of Asymmetrical Flow
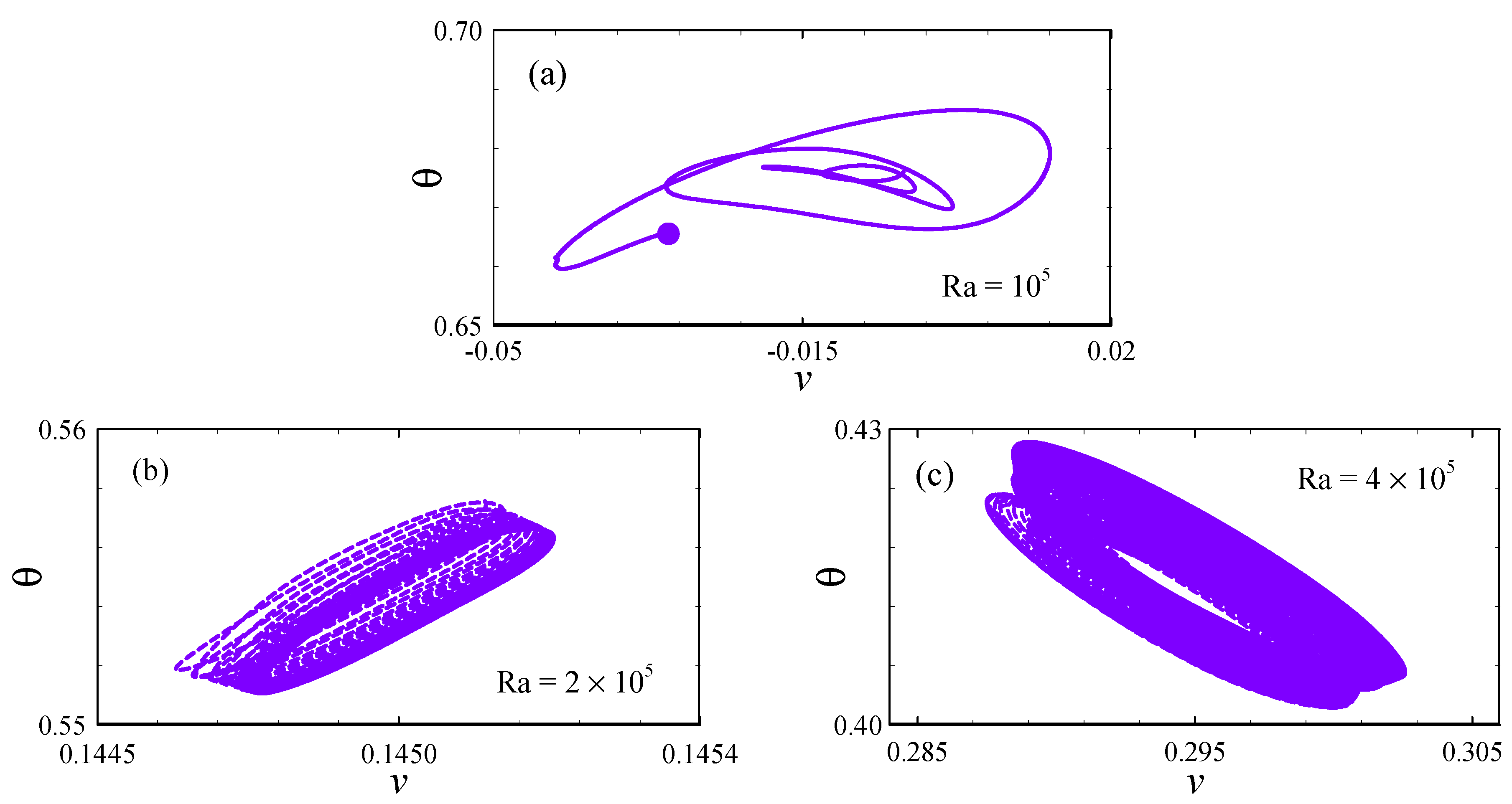
6.3. Development of Unsteady Flow
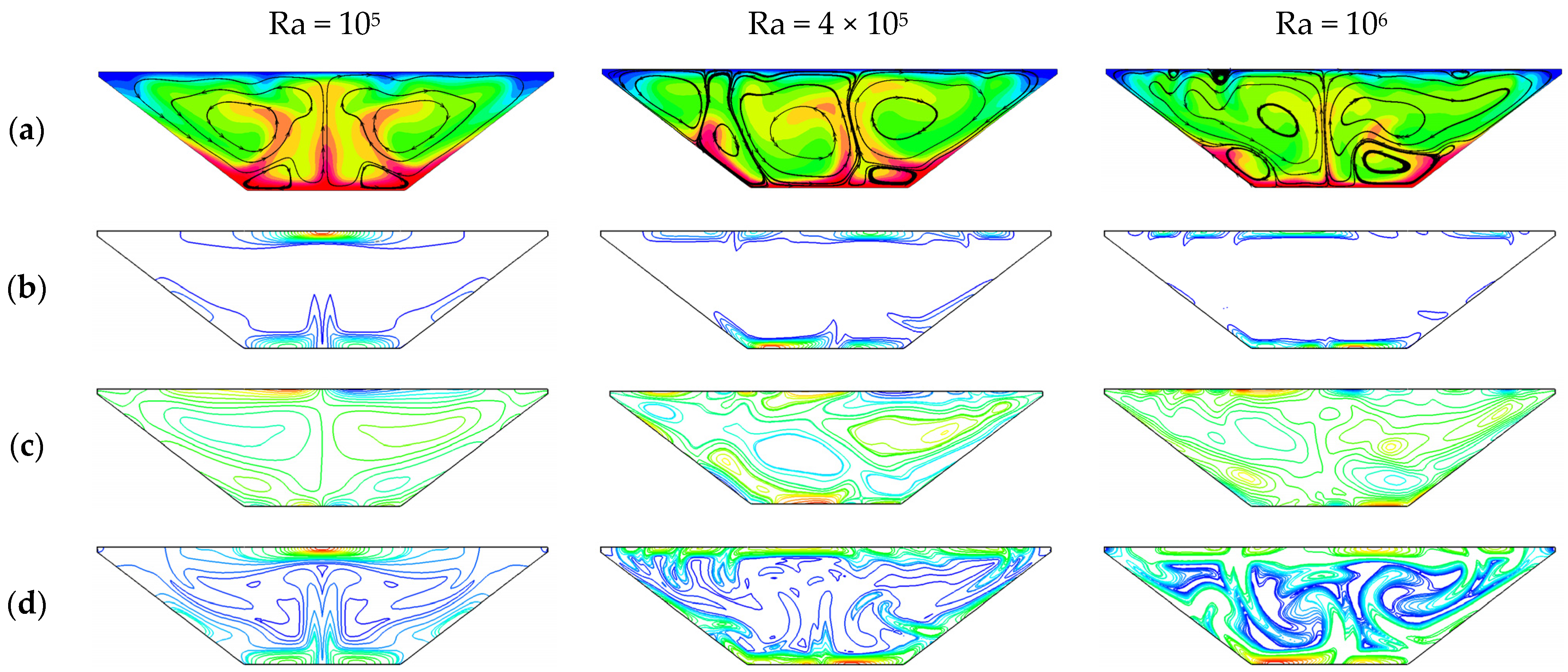
6.4. Effects of Ra on Fluid Flow and EG
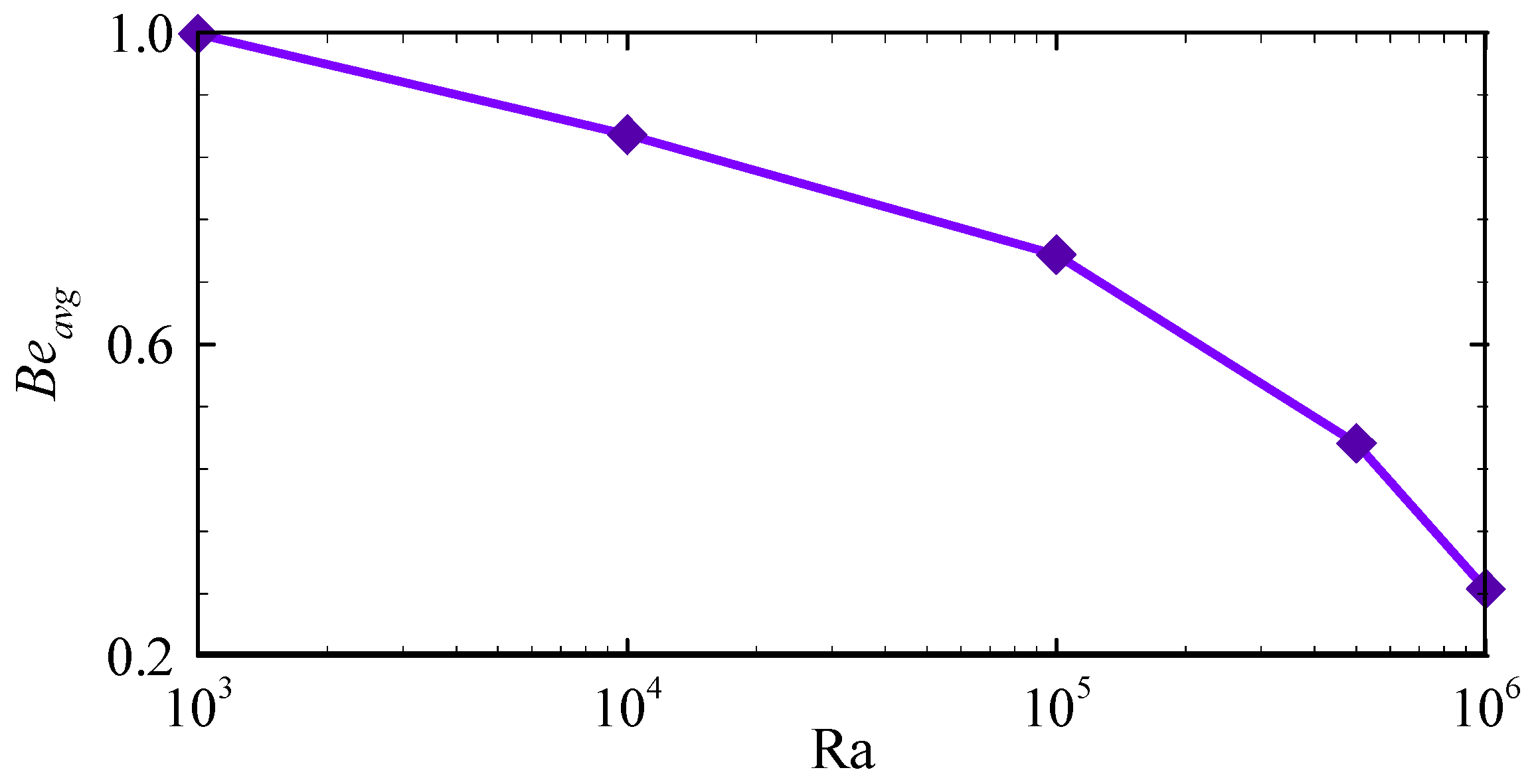
6.5. Variation of Average Bejan Number
6.6. Heat Transfer
6.7. Variation of Nu, Eavg, and ECOP for Different Ra
7. Conclusions
- In the beginning, the flow is marked by the development of thermal boundary layers along all internal surfaces and the onset of primary circulations. During the transitional stage, convective instabilities appear as rising and falling thermal plumes, leading to the construction of cellular flow patterns.
- The steady-state flow at Ra < 9 × 104 is marked by symmetric flow around the cavity’s symmetrical plane.
- The shift of the flow from a symmetrical to an asymmetrical state due to pitchfork bifurcation occurs between the Rayleigh numbers of 9 × 104 and 105.
- The shift of the flow from an asymmetric steady state to a periodic state due to Hopf bifurcation occurs between the Rayleigh numbers of 105 and 2 × 105.
- The shift of the flow from a periodic to a chaotic state due to another bifurcation occurs between the Rayleigh numbers of 4 × 105 and 5 × 105.
- As Ra increases from 103 to 106, the rate of increment in Nu is 81.13%, and the average entropy generation is 94.97%.
- For the Ra values of 103 to 105, Beavg > 0.5, signifying that EG due to HT dominates over EG due to FF. However, for higher Ra values of 5 × 105 to 106, Beavg < 0.5, indicating that EG due to FF becomes more significant than EG due to HT.
- As the Ra value increases from 103 to 106, it results in a decrease in energy efficiency and an increased environmental impact.
8. Limitations and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AR | aspect ratio | Beavg | average Bejan number |
| L, H | half-length and height of the cavity (m) | k | thermal conductivity (W/(m·K)) |
| g | gravitational force (m/s2) | X, Y | coordinates |
| t | time (s) | x, y | dimensionless coordinates |
| Cp | specific heat (J/kg·K) | U, V | velocity components (m/s) |
| P | pressure (N/m2) | u, v | dimensionless velocity components |
| p | dimensionless pressure | ||
| T | temperature (K) | Greek symbols | |
| T∞ | environmental temperature (K) | κ | thermal diffusivity (m2/s) |
| Th | temperature of the bottom wall (K) | θ | dimensionless temperature |
| Tc | temperature of the top wall (K) | ν | kinematic viscosity (m2/s) |
| Ti | temperature of the inclined walls (K) | ψ | irreversibility distribution ratio |
| φ | inclination angle | ||
| ΔT | temperature difference, (Th − Tc) | ρ | density (kg/m3) |
| Gr | Grashof number, gβ(Th − Tc)H3/ν2 | Eθ | entropy generation due to heat transfer |
| Pr | Prandtl number | ||
| Egen | entropy generation | τ | dimensionless time |
| Ra | Rayleigh number, gβ(Th − Tc)H3/νκ | Δτ | dimensionless time step |
| Nu | Nusselt number | θi | dimensionless temperature of the inclined walls |
| Ef | entropy generation due to fluid friction | ||
| El | local entropy generation | θc | dimensionless temperature of the top wall |
| Nuavg | average Nusselt number | ||
| Eavg | average entropy generation | θh | dimensionless temperature of the bottom wall |
| Bel | local Bejan number | ||
References
- Nourdanesh, N.; Hossainpour, S.; Adamiak, K. Numerical simulation and optimization of natural convection heat transfer enhancement in solar collectors using electrohydrodynamic conduction pump. Appl. Therm. Eng. 2020, 180, 115825. [Google Scholar]
- Letan, R.; Dubovsky, V.; Ziskind, G. Passive ventilation and heating by natural convection in a multi-storey building. Build. Environ. 2003, 38, 197–208. [Google Scholar]
- Chen, H.T.; Hsieh, Y.L.; Chen, P.C.; Lin, Y.F.; Liu, K.C. Numerical simulation of natural convection heat transfer for annular elliptical finned tube heat exchanger with experimental data. Int. J. Heat Mass Transf. 2018, 127, 541–554. [Google Scholar]
- Rath, S.; Dash, S.K. Thermal performance of a wavy annular finned horizontal cylinder in natural convection for electronic cooling application. Int. Commun. Heat Mass Transf. 2021, 128, 105623. [Google Scholar]
- Vogel, J.; Felbinger, J.; Johnson, M. Natural convection in high temperature flat plate latent heat thermal energy storage systems. Appl. Energy 2016, 184, 184–196. [Google Scholar]
- Bhavsar, H.P.; Patel, C.M. Performance investigation of natural and forced convection cabinet solar dryer for ginger drying. Mater. Today Proc. 2021, 47, 6128–6133. [Google Scholar]
- Saha, S.C. Unsteady natural convection in a triangular enclosure under isothermal heating. Energy Build. 2011, 43, 695–703. [Google Scholar] [CrossRef]
- Bhowmick, S.; Saha, S.C.; Qiao, M.; Xu, F. Transition to a chaotic flow in a V-shaped triangular cavity heated from below. Int. J. Heat Mass Transf. 2019, 128, 76–86. [Google Scholar]
- Wang, X.; Bhowmick, S.; Tian, Z.F.; Saha, S.C.; Xu, F. Experimental study of natural convection in a V-shape-section cavity. Phys. Fluids 2021, 33, 014104. [Google Scholar] [CrossRef]
- Bhowmick, S.; Xu, F.; Molla, M.M.; Saha, S.C. Chaotic phenomena of natural convection for water in a V-shaped enclosure. Int. J. Therm. Sci. 2022, 176, 107526. [Google Scholar]
- Chen, C.C.; Eichhorn, R. Natural convection from a vertical surface to a thermally stratified fluid. ASME J. Heat Transf. 1976, 98, 446–451. [Google Scholar] [CrossRef]
- Chen, C.C.; Eichhorn, R. Natural Convection from Simple Bodies Immersed in Thermally Stratified Fluids; Report No. UKY TR 105-ME 14-77; ORES Publications, College of Engineering, University of Kentucky Lexington: Lexington, KY, USA, 1977. [Google Scholar]
- Eichhorn, R. Natural convection in a thermally stratified fluid. Prog. Heat Mass Transf. 1969, 2, 41–53. [Google Scholar]
- Eichhorn, R.; Lienhard, J.H.; Chen, C.C. Natural convection from isothermal spheres and cylinders immersed in a stratified fluid. In International Heat Transfer Conference Digital Library; Begel House Inc.: Danbury, CT, USA, 1974. [Google Scholar]
- Angirasa, D.; Peterson, G.P. Natural convection heat transfer from an isothermal vertical surface to a fluid saturated thermally stratified porous medium. Int. J. Heat Mass Transf. 1997, 40, 4329–4335. [Google Scholar] [CrossRef]
- Tripathi, R.K.; Nath, G. Unsteady natural convection flow over a vertical plate embedded in a stratified medium. Int. J. Heat Mass Transf. 1993, 36, 1125–1128. [Google Scholar] [CrossRef]
- Hossain, M.A.; Paul, S.C.; Mandal, A.C. Natural convection flow along a vertical circular cone with uniform surface temperature and surface heat flux in a thermally stratified medium. Int. J. Numer. Methods Heat Fluid Flow 2002, 12, 290–305. [Google Scholar] [CrossRef]
- Lin, W.; Armfield, S.W.; Morgan, P.L. Unsteady natural convection boundary-layer flow along a vertical isothermal plate in a linearly stratified fluid with Pr > 1. Int. J. Heat Mass Transf. 2002, 45, 451–459. [Google Scholar] [CrossRef]
- Shapiro, A.; Fedorovich, E. Prandtl number dependence of unsteady natural convection along a vertical plate in a stably stratified fluid. Int. J. Heat Mass Transf. 2004, 47, 4911–4927. [Google Scholar] [CrossRef]
- Shapiro, A.; Fedorovich, E. Unsteady convectively driven flow along a vertical plate immersed in a stably stratified fluid. J. Fluid Mech. 2004, 498, 333–352. [Google Scholar] [CrossRef]
- Shapiro, A.; Fedorovich, E. Natural convection in a stably stratified fluid along vertical plates and cylinders with temporally periodic surface temperature variations. J. Fluid Mech. 2006, 546, 295–311. [Google Scholar] [CrossRef]
- Patterson, J.; Imberger, J. Unsteady natural convection in a rectangular cavity. J. Fluid Mech. 1980, 100, 65–86. [Google Scholar] [CrossRef]
- Kuhn, D.; Oosthuizen, P.H. Unsteady natural convection in a partially heated rectangular cavity. J. Heat Transf. 1987, 109, 798–801. [Google Scholar] [CrossRef]
- Lei, C.; Armfield, S.W.; Patterson, J.C. Unsteady natural convection in a water-filled isosceles triangular enclosure heated from below. Int. J. Heat Mass Transf. 2008, 51, 2637–2650. [Google Scholar]
- Ma, J.; Xu, F. Unsteady natural convection and heat transfer in a differentially heated cavity with a fin for high Rayleigh numbers. Appl. Therm. Eng. 2016, 99, 625–634. [Google Scholar] [CrossRef]
- Xu, F.; Patterson, J.C.; Lei, C. Unsteady flow and heat transfer adjacent to the sidewall wall of a differentially heated cavity with a conducting and an adiabatic fin. Int. J. Heat Fluid Flow 2011, 32, 680–687. [Google Scholar]
- Elkhazen, M.I.; Hassen, W.; Gannoun, R.; Hussein, A.K.; Borjini, M.N. Numerical study of electroconvection in a dielectric layer between two cofocal elliptical cylinders subjected to unipolar injection. J. Eng. Phys. Thermophys. 2019, 92, 1318–1329. [Google Scholar]
- Elkhazen, M.I.; Hassen, W.; Kolsi, L.; Oztop, H.F.; Al-Rashed, A.A.; Borjini, M.N.; Abu-Hamdeh, N. Heat transfer intensification induced by electrically generated convection between two elliptical cylinders. Int. J. Therm. Sci. 2019, 135, 523–532. [Google Scholar]
- Hassen, W.; Elkhazen, M.I.; Traore, P.; Borjini, M.N. Numerical study of the electro–thermo-convection in an annular dielectric layer subjected to a partial unipolar injection. Int. J. Heat Fluid Flow 2014, 50, 201–208. [Google Scholar]
- Rejeb, S.; Hassen, W.; Kolsi, L.; Estellé, P. Heat transfer by oil natural convection in an annular space under combined effects of carbon nanotubes and electric field. Int. Commun. Heat Mass Transf. 2022, 138, 106345. [Google Scholar] [CrossRef]
- Hassen, W.; Elkhazen, M.I.; Traore, P.; Borjini, M.N. Charge injection in horizontal eccentric annuli filled with a dielectric liquid. Eur. J. Mech.-B/Fluids 2018, 72, 691–700. [Google Scholar]
- Elkhazen, M.I.; Hassen, W.; Öztop, H.F.; Kolsi, L.; Al-Rashed, A.A.; Borjini, M.N.; Ali, M.E. Electro-thermo-convection in dielectric liquid subjected to partial unipolar injection between two eccentric cylinders. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 78–93. [Google Scholar]
- Akrour, D.; Elkhazen, M.I.; Hassen, W.; Kriaa, K.; Maatki, C.; Hadrich, B.; Kolsi, L. Numerical Investigation of the Electro-Thermo Convection in an Inclined Cavity Filled with a Dielectric Fluid. Processes 2023, 11, 2506. [Google Scholar] [CrossRef]
- Iyican, L.; Bayazitoglu, Y.; Witte, L.C. An analytical study of natural convective heat transfer within a trapezoidal enclosure. J. Heat Transf. 1980, 102, 640–647. [Google Scholar]
- Iyican, L.; Witte, L.C.; Bayazitoglu, Y. An experimental study of natural convection in trapezoidal enclosures. J. Heat Transf. 1980, 102, 648–653. [Google Scholar]
- Lam, S.W.; Gani, R.; Symons, J.G. Experimental and numerical studies of natural convection in trapezoidal cavities. J. Heat Transf. 1989, 111, 372–377. [Google Scholar] [CrossRef]
- Lee, T.S. Numerical experiments with fluid convection in tilted nonrectangular enclosures. Numer. Heat Transf. Part A Appl. 1991, 19, 487–499. [Google Scholar]
- Perić, M. Natural convection in trapezoidal cavities. Numer. Heat Transf. Part A Appl. 1993, 24, 213–219. [Google Scholar]
- Kuyper, R.A.; Hoogendoorn, C.J. Laminar natural convection flow in trapezoidal enclosures. Numer. Heat Transf. Part A Appl. 1995, 28, 55–67. [Google Scholar] [CrossRef]
- Moukalled, F.; Darwish, M. Natural convection in a partitioned trapezoidal cavity heated from the side. Numer. Heat Transf. Part A Appl. 2003, 43, 543–563. [Google Scholar]
- Moukalled, F.; Darwish, M. Natural convection in a trapezoidal enclosure heated from the side with a baffle mounted on its upper inclined surface. Heat Transf. Eng. 2004, 25, 80–93. [Google Scholar]
- Moukalled, F.; Darwish, M. Buoyancy-induced heat transfer in a trapezoidal enclosure with offset baffles. Numer. Heat Transf. Part A Appl. 2007, 52, 337–355. [Google Scholar]
- Natarajan, E.; Roy, S.; Basak, T. Effect of various thermal boundary conditions on natural convection in a trapezoidal cavity with linearly heated side wall (s). Numer. Heat Transf. Part B Fundam. 2007, 52, 551–568. [Google Scholar]
- Natarajan, E.; Basak, T.; Roy, S. Natural convection flows in a trapezoidal enclosure with uniform and non-uniform heating of bottom wall. Int. J. Heat Mass Transf. 2008, 51, 747–756. [Google Scholar]
- Basak, T.; Roy, S.; Pop, I. Heat flow analysis for natural convection within trapezoidal enclosures based on heatline concept. Int. J. Heat Mass Transf. 2009, 52, 2471–2483. [Google Scholar]
- Basak, T.; Roy, S.; Singh, A.; Pandey, B.D. Natural convection flow simulation for various angles in a trapezoidal enclosure with linearly heated side wall (s). Int. J. Heat Mass Transf. 2009, 52, 4413–4425. [Google Scholar]
- Lasfer, K.; Bouzaiane, M.; Lili, T. Numerical study of laminar natural convection in a side-heated trapezoidal cavity at various inclined heated sidewalls. Heat Transf. Eng. 2010, 31, 362–373. [Google Scholar]
- Rahaman, M.M.; Titab, R.; Bhowmick, S.; Mondal, R.N.; Saha, S.C. Unsteady 2D flow in an initially stratified air-filled trapezoid. Jagannath Univ. J. Sci. 2022, 8, 1–6. [Google Scholar]
- Rahaman, M.M.; Bhowmick, S.; Mondal, R.N.; Saha, S.C. Unsteady natural convection in an initially stratified air-filled trapezoidal enclosure heated from below. Processes 2022, 10, 1383. [Google Scholar] [CrossRef]
- Rahaman, M.M.; Bhowmick, S.; Mondal, R.N.; Saha, S.C. A Computational Study of Chaotic Flow and Heat Transfer within a Trapezoidal Cavity. Energies 2023, 16, 5031. [Google Scholar] [CrossRef]
- Rahaman, M.M.; Bhowmick, S.; Mondal, R.N.; Saha, S.C. Transient 2D Flow in a Stratified Air-Filled Trapezoidal Cavity. 2024. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4874263 (accessed on 12 February 2025).
- Rahaman, M.M.; Bhowmick, S.; Mondal, R.N.; Saha, S.C. Unsteady Natural Convection Flow Within a Trapezoidal Enclosure. 2024. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4951897 (accessed on 12 February 2025).
- Bejan, A. Second law analysis in heat transfer. Energy 1980, 5, 720–732. [Google Scholar]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar]
- Biswal, P.; Basak, T. Entropy generation vs energy efficiency for natural convection based energy flow in enclosures and various applications: A review. Renew. Sustain. Energy Rev. 2017, 80, 1412–1457. [Google Scholar]
- Goh, L.H.K.; Hung, Y.M.; Chen, G.M.; Tso, C.P. Entropy generation analysis of turbulent convection in a heat exchanger with self-rotating turbulator inserts. Int. J. Therm. Sci. 2021, 160, 106652. [Google Scholar]
- Magherbi, M.; Abbassi, H.; Brahim, A.B. Entropy generation at the onset of natural convection. Int. J. Heat Mass Transf. 2003, 46, 3441–3450. [Google Scholar]
- Ilis, G.G.; Mobedi, M.; Sunden, B. Effect of aspect ratio on entropy generation in a rectangular cavity with differentially heated vertical walls. Int. Commun. Heat Mass Transf. 2008, 35, 696–703. [Google Scholar]
- Varol, Y.; Oztop, H.F.; Koca, A. Entropy generation due to conjugate natural convection in enclosures bounded by vertical solid walls with different thicknesses. Int. Commun. Heat Mass Transf. 2008, 35, 648–656. [Google Scholar]
- Varol, Y.; Oztop, H.F.; Pop, I. Entropy generation due to natural convection in non-uniformly heated porous isosceles triangular enclosures at different positions. Int. J. Heat Mass Transf. 2009, 52, 1193–1205. [Google Scholar]
- Basak, T.; Kaluri, R.S.; Balakrishnan, A.R. Entropy generation during natural convection in a porous cavity: Effect of thermal boundary conditions. Numer. Heat Transf. Part A Appl. 2012, 62, 336–364. [Google Scholar]
- Siavashi, M.; Yousofv, R.; Rezanejad, S. Nanofluid and porous fins effect on natural convection and entropy generation of flow inside a cavity. Adv. Powder Technol. 2018, 29, 142–156. [Google Scholar]
- Rahaman, M.M.; Bhowmick, S.; Saha, G.; Xu, F.; Saha, S.C. Transition to chaotic flow, bifurcation, and entropy generation analysis inside a stratified trapezoidal enclosure for varying aspect ratio. Chin. J. Phys. 2024, 91, 867–882. [Google Scholar]
- Saha, S.C.; Patterson, J.C.; Lei, C. Natural convection and heat transfer in attics subject to periodic thermal forcing. Int. J. Therm. Sci. 2010, 49, 1899–1910. [Google Scholar]
- Rahaman, M.M.; Bhowmick, S.; Ghosh, B.P.; Xu, F.; Mondal, R.N.; Saha, S.C. Transient natural convection flows and heat transfer in a thermally stratified air-filled trapezoidal cavity. Therm. Sci. Eng. Prog. 2024, 47, 102377. [Google Scholar]
- Saha, S.C.; Gu, Y. Natural convection in a triangular enclosure heated from below and non-uniformly cooled from top. Int. J. Heat Mass Transf. 2015, 80, 529–538. [Google Scholar]






| References | Parameters | Key Findings |
|---|---|---|
| Iyican et al. [34] | φ = 0–180° Pr = 0.71 | Described how the flow structures and HT are influenced by the inclination of the walls and the Ra. |
| Iyican et al. [35] | φ = 0–180° | Developed correlations for the Nu as a function of the Ra. These correlations agree with the findings of the earlier analytical study. |
| Lam et al. [36] | φ = 0–25° Pr = 0.71 | Examined the effect of the Ra and the sloped angle on fluid flow and HT. |
| Lee [37] | AR = 3–6 φ = 22.5°, 45°, 77.5° Pr = 0.001–100 | Investigated the effect of the Ra, Pr, and sloped angle on fluid flow and HT. |
| Perić [38] | φ = 0°, 90°, 180°, 270° Pr = 0.7 | Analyzed Lee’s results and observed that the outcomes differed both quantitatively and qualitatively. |
| Kuyper and Hoogendoorn [39] | φ = 0–45° Pr = 0.71 | Discovered the impact of the sloped angle and Ra on fluid flow and HT. |
| Moukalled and Darwish [40,41] | AR = 0.5 Pr = 0.7, 10, 130 | Revealed the influence of the baffle position and the Pr on fluid flow and HT. |
| Moukalled and Darwish [42] | AR = 0.5 Pr = 0.7, 10, 130 | Discovered the effect of two offset baffles and the Pr on fluid flow and HT. |
| Natarajan et al. [43,44] | φ = 30° Pr = 0.7–100 | Revealed that the effect of the Pr on HT is more significant for Pr values between 0.07 and 0.7 than for values between 10 and 100. |
| Basak et al. [45] | φ = 45°, 30°, 0° Pr = 0.026–1000 | Demonstrated that the HT rate is higher for uniform heating of the bottom wall compared to non-uniform heating of the bottom wall. |
| Basak et al. [46] | φ = 0–45° Pr = 0.7–100 | Discovered that the HT rate remained unchanged due to the uneven heating of the bottom walls. |
| Lasfer et al. [47] | AR = 0.5, 1.0, 1.5 φ = 60°–120° Pr = 0.71 | Showed that the flow and HT depend significantly on the sloped angle, AR, and thermal strength. |
| Rahaman et al. [48,49] | AR = 0.5 Pr = 0.71 | Described the flow transition from a steady to a chaotic state with a higher Ra and demonstrated how different Ra values influence the flow and heat transfer characteristics. |
| Rahaman et al. [50] | AR = 0.5 Pr = 0.71 | Provided detailed insights into fluid flow behavior, including vortex formation, oscillatory patterns, and chaotic flow. |
| Rahaman et al. [51] | AR = 1.0 Pr = 0.71 | Discovered a series of bifurcations involved in the shifting of convective flows from a symmetric steady state to an unsteady state. |
| Rahaman et al. [52] | AR = 0.2 Pr = 0.71 | Revealed fluid flow and HT behavior within the cavity for lower AR. |
| Rahaman et al. [63] | AR = 0.2, 0.5, 1.0 Pr = 0.71 | Studied the critical Ra value for each AR in the transition from a symmetric to a chaotic state and illustrated how thermal performance depends on AR. |
| Current study | AR = 0.5 Pr = 7.01 | Considered a Pr of 7.01 to investigate fluid flow, HT rates, and the transition from a steady to a chaotic state. Also demonstrated how the energy efficiency and environmental impact depend on the Ra. |
| Ra | 103 | 104 | 105 | 5 × 105 | 106 |
| Nu | 2.8299 | 5.2002 | 7.0909 | 11.9060 | 14.9935 |
| Eavg | 3.6043 | 7.9591 | 12.6171 | 42.2933 | 71.5994 |
| ECOP | 0.78515 | 0.65337 | 0.56201 | 0.28151 | 0.20941 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahaman, M.M.; Bhowmick, S.; Saha, S.C. Thermal Performance and Entropy Generation of Unsteady Natural Convection in a Trapezoid-Shaped Cavity. Processes 2025, 13, 921. https://doi.org/10.3390/pr13030921
Rahaman MM, Bhowmick S, Saha SC. Thermal Performance and Entropy Generation of Unsteady Natural Convection in a Trapezoid-Shaped Cavity. Processes. 2025; 13(3):921. https://doi.org/10.3390/pr13030921
Chicago/Turabian StyleRahaman, Md. Mahafujur, Sidhartha Bhowmick, and Suvash C. Saha. 2025. "Thermal Performance and Entropy Generation of Unsteady Natural Convection in a Trapezoid-Shaped Cavity" Processes 13, no. 3: 921. https://doi.org/10.3390/pr13030921
APA StyleRahaman, M. M., Bhowmick, S., & Saha, S. C. (2025). Thermal Performance and Entropy Generation of Unsteady Natural Convection in a Trapezoid-Shaped Cavity. Processes, 13(3), 921. https://doi.org/10.3390/pr13030921








