Numerical Investigation of Vertical Hydraulic Fracture Propagation and Fracturing Parameter Optimization in Deep Coalbed Methane Reservoirs
Abstract
1. Introduction
2. Numerical Model Development
3. Numerical Simulation Results
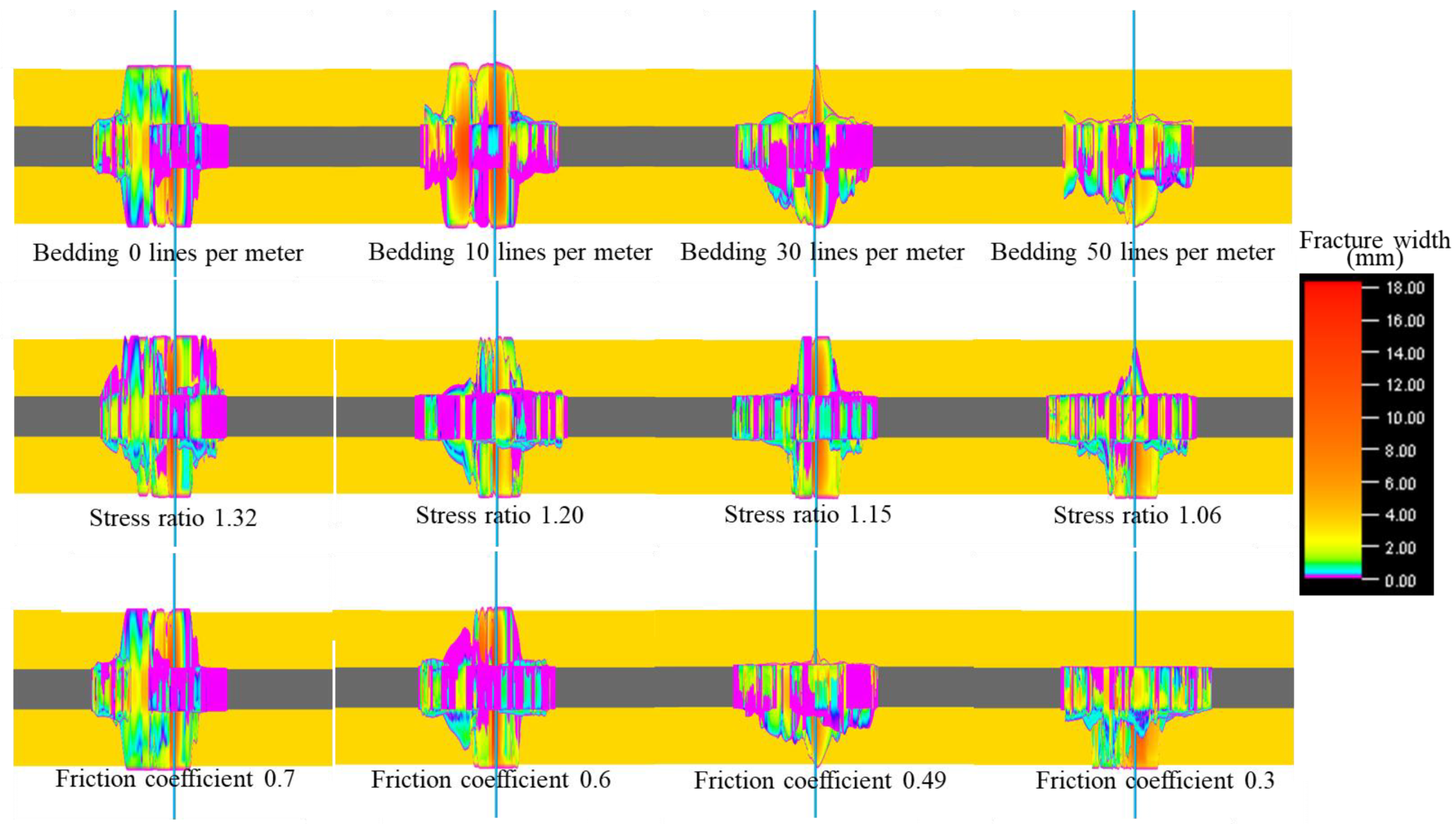
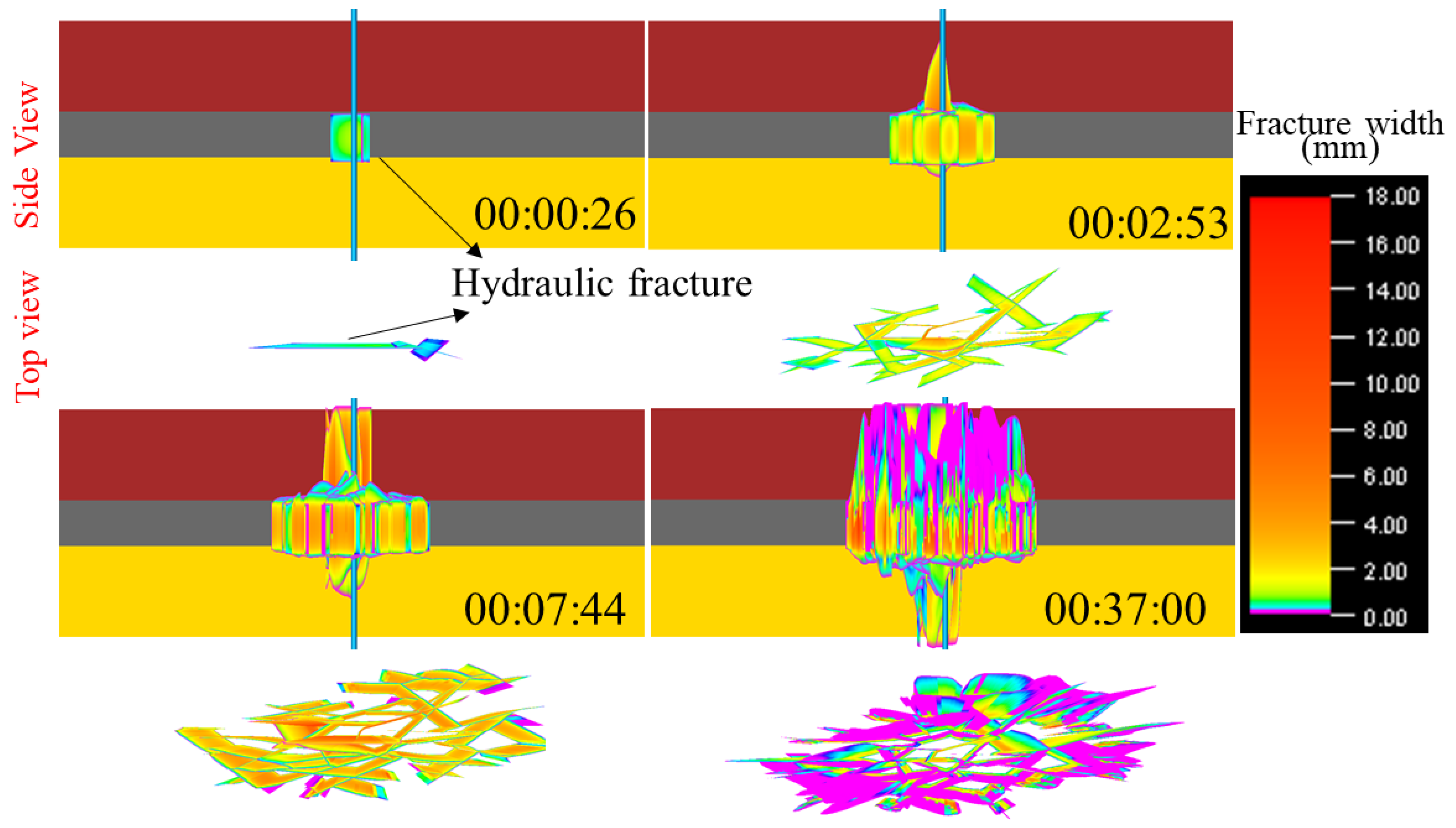
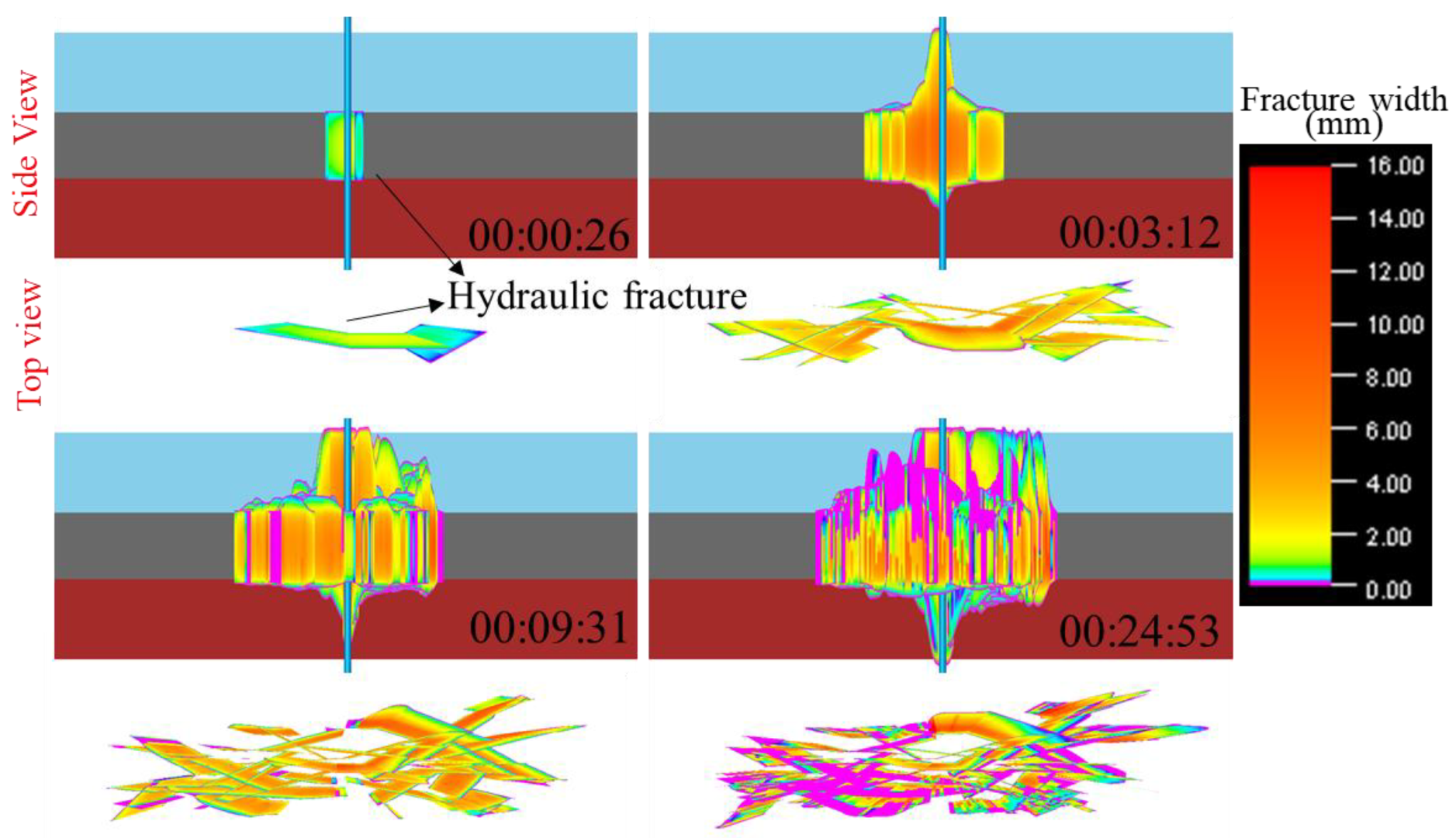
3.1. Discussion of Simulation Results for Combination 1
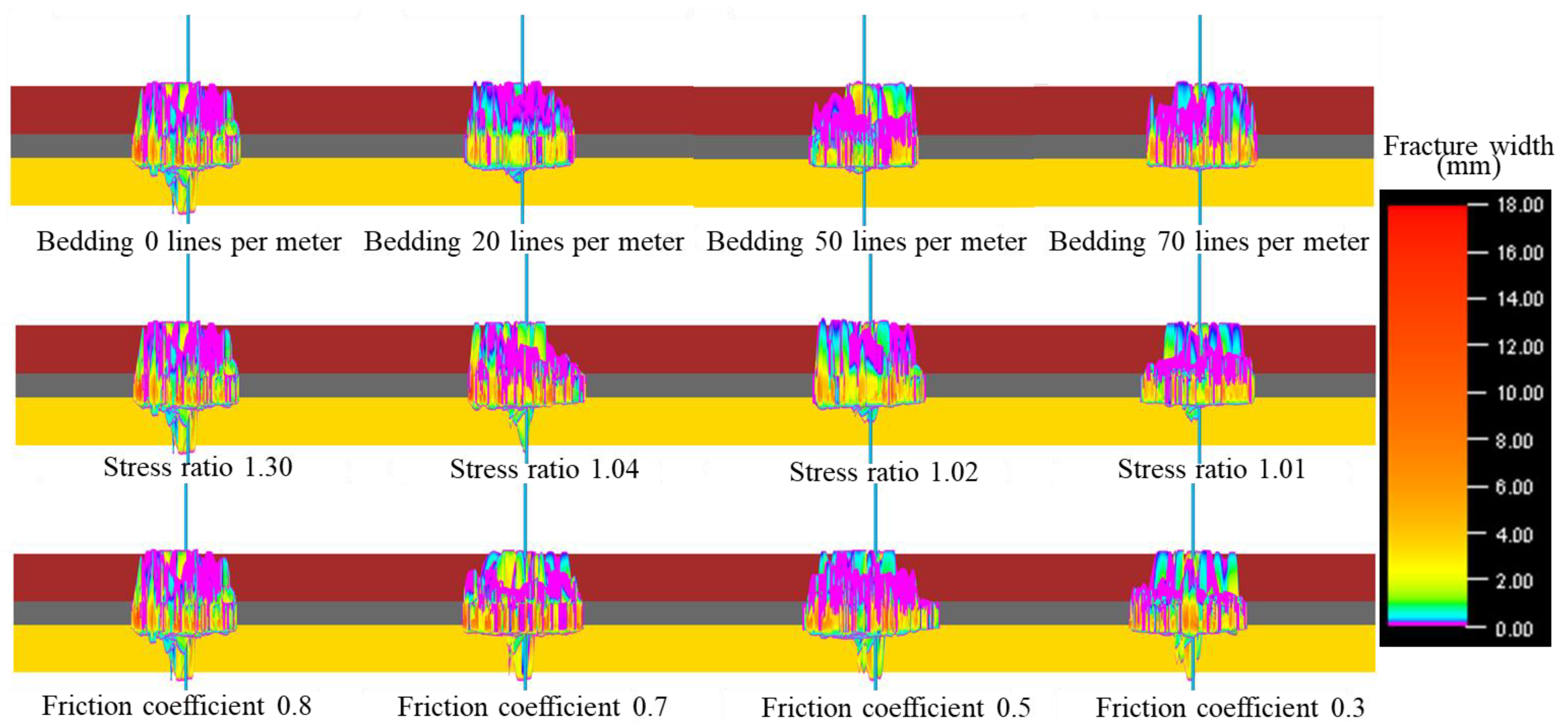
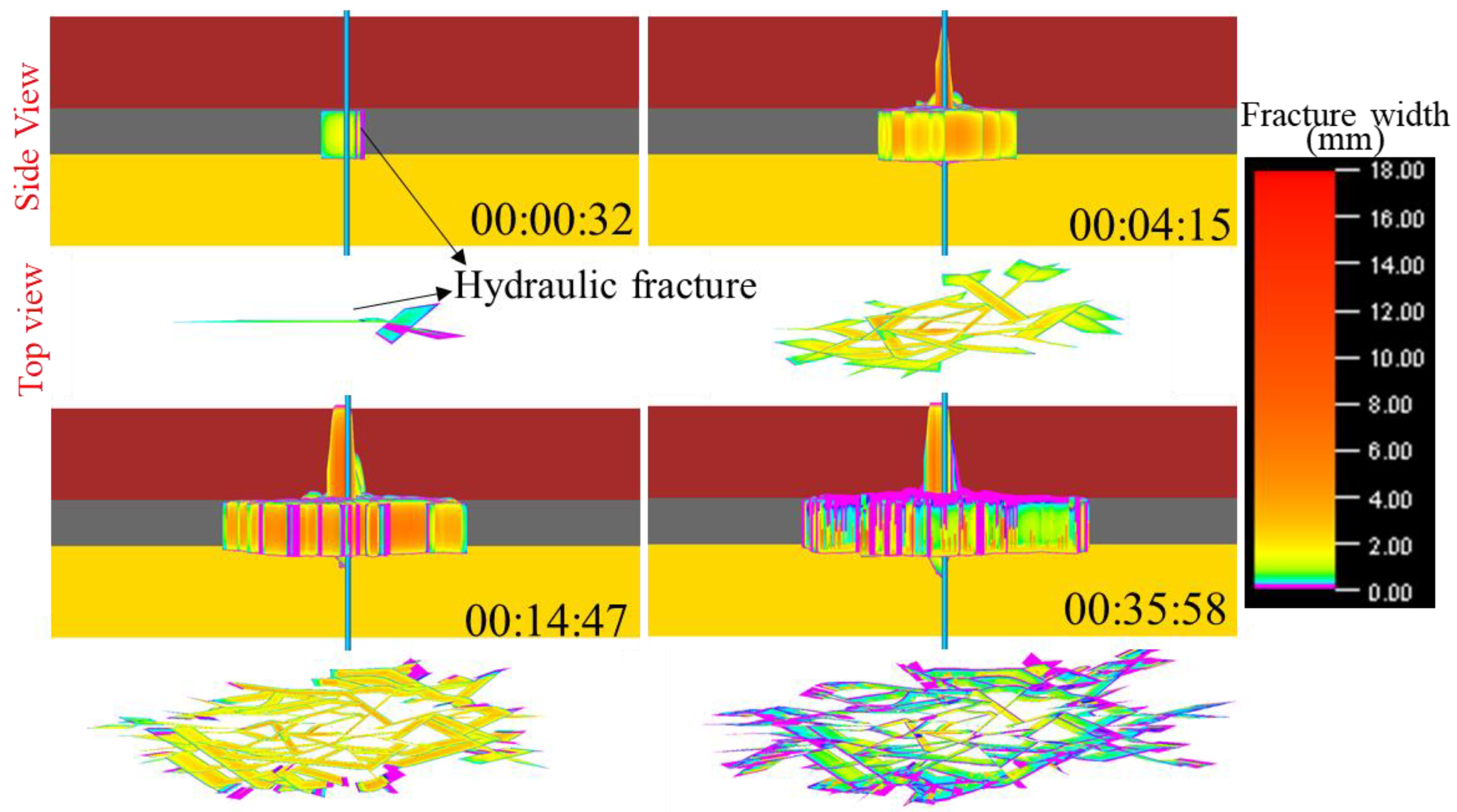
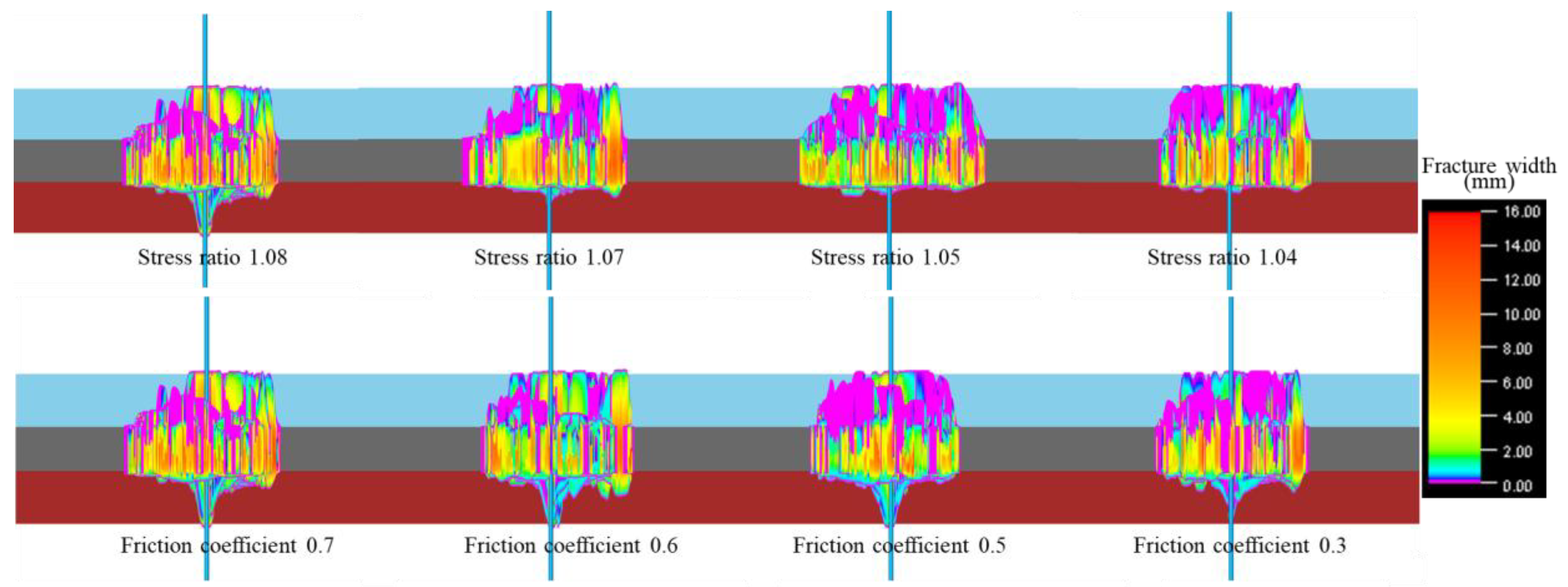
3.2. Discussion of Combination 2 Simulation Results
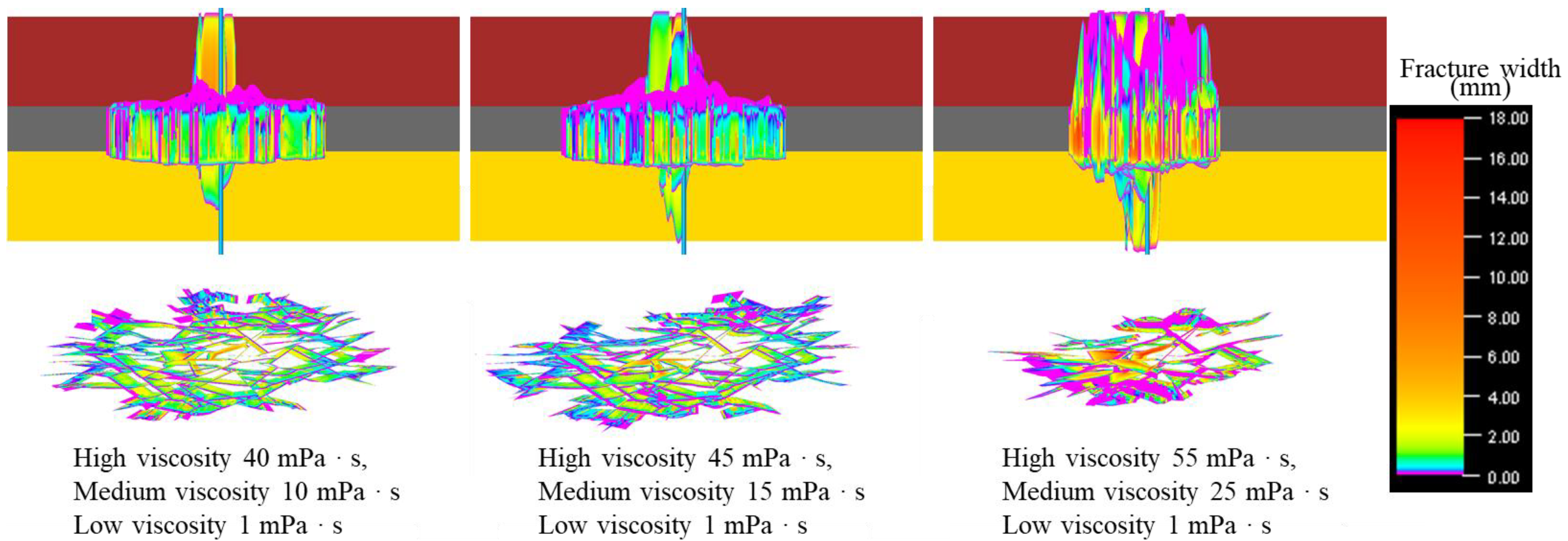
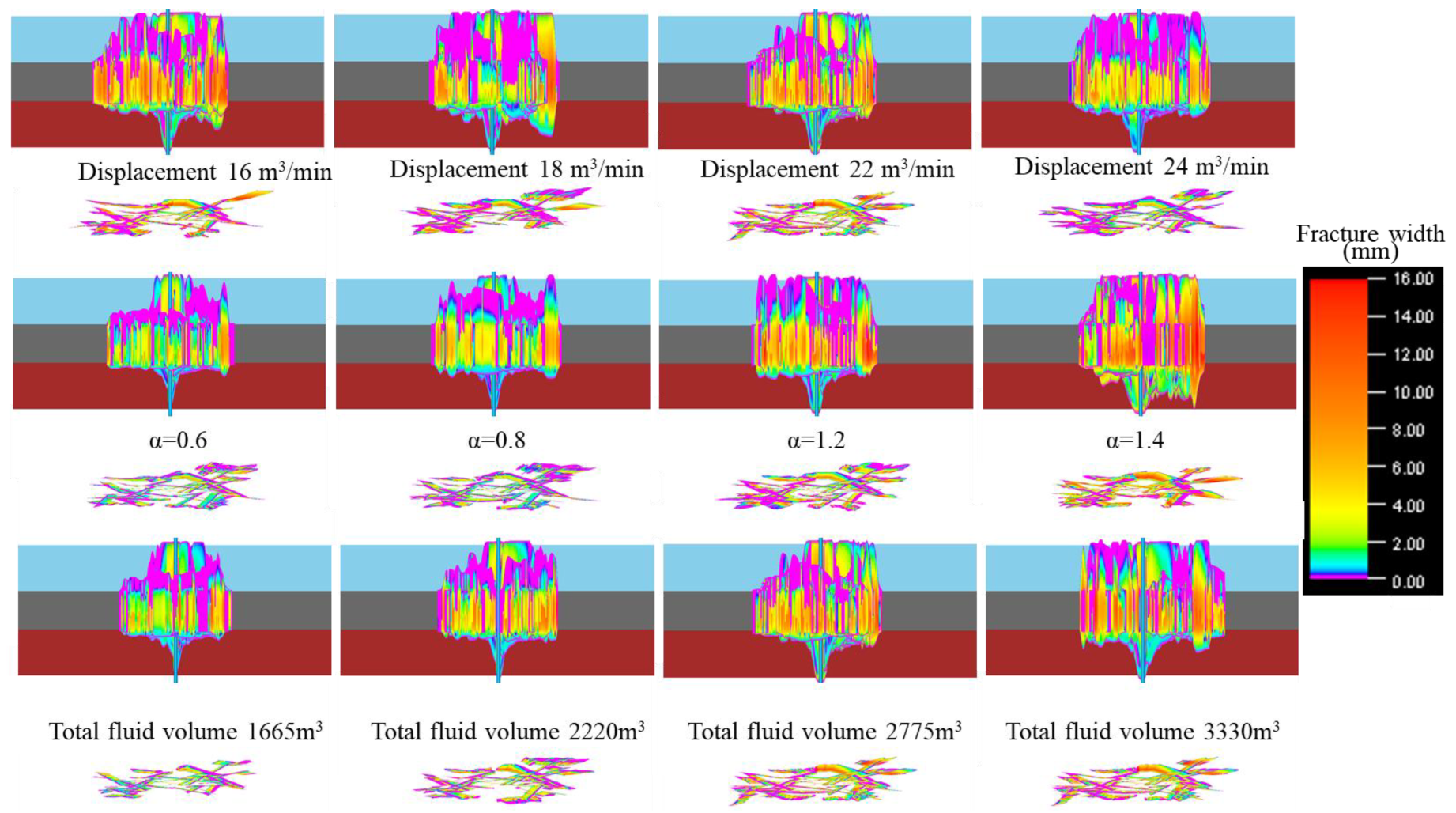
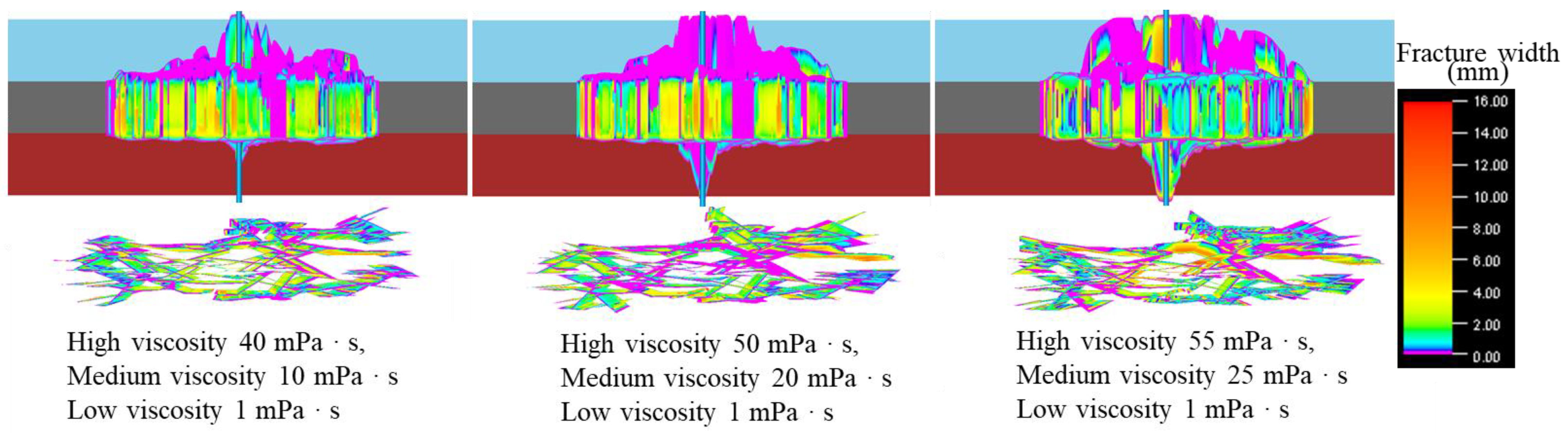
3.3. Discussion of Combined Simulation 3 Results
4. Conclusions
- (1)
- During the fracturing process in coal seams, hydraulic fractures first propagate from the wellbore and penetrate the cap rock or bottom rock of the coal seam, simultaneously initiating branch fractures that form a complex fracture network. The branch fractures may penetrate the cap rock and bottom rock, but after penetration, the overall fracture width remains relatively small.
- (2)
- Under different lithological combinations, the effects of layer density, stress ratio, and rock friction coefficient on hydraulic fracture through-layer vary. When the layer distribution in the mudstone is relatively dense, it can effectively restrict fracture through-layer. A smaller stress ratio and rock friction coefficient are favorable for preventing fractures from propagating through the cap rock or bottom rock.
- (3)
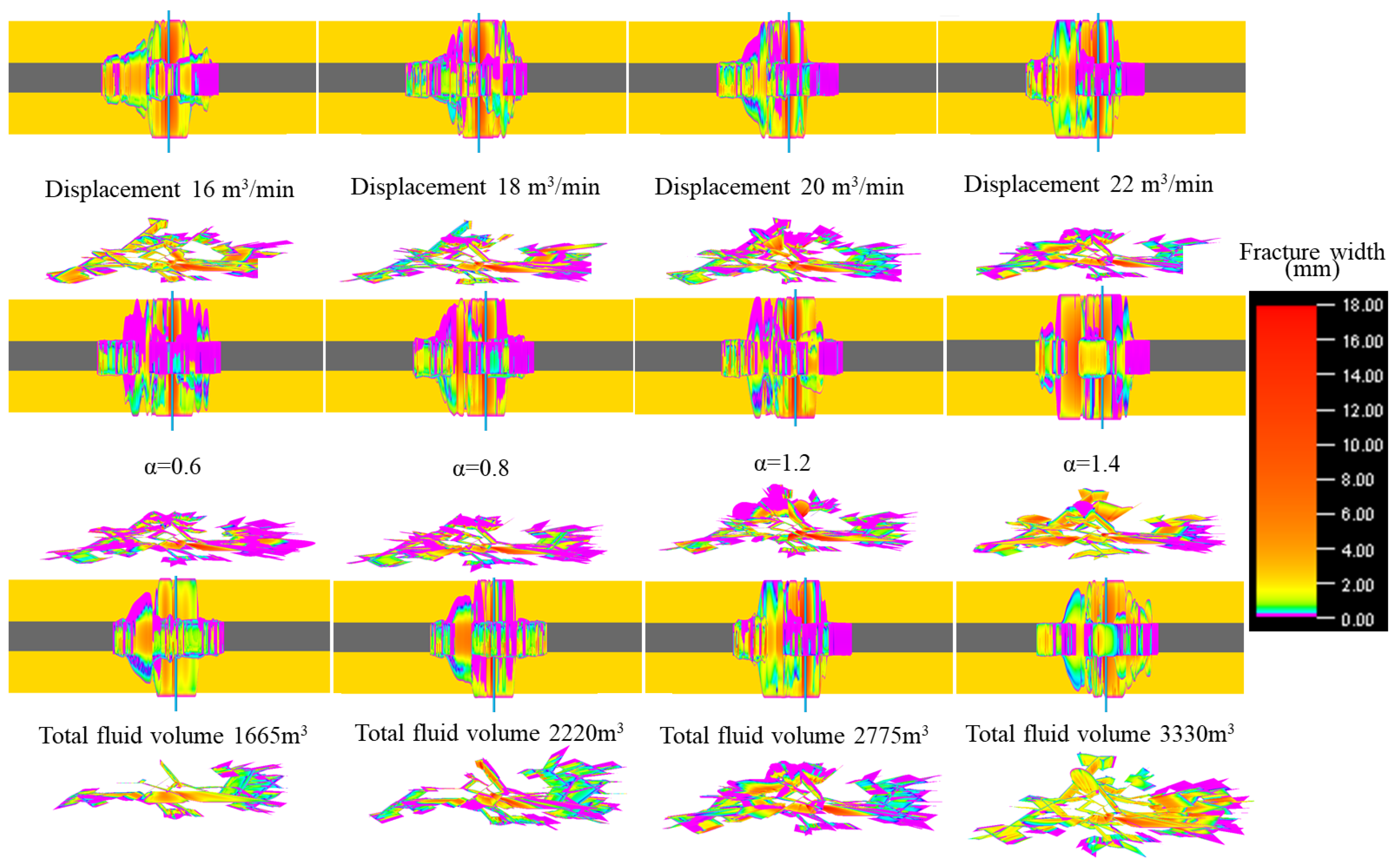
- Reducing the fracturing fluid injection rate and sand concentration, while selecting an appropriate total fracturing fluid volume, can effectively control the hydraulic fracture’s ability to propagate through the cap rock or bottom rock of the coal seam. A low-viscosity fracturing fluid system, compared to a high-viscosity fracturing fluid system, can effectively weaken the fracture through-layer effect and initiate more natural fractures within the coal seam interval.
- (4)
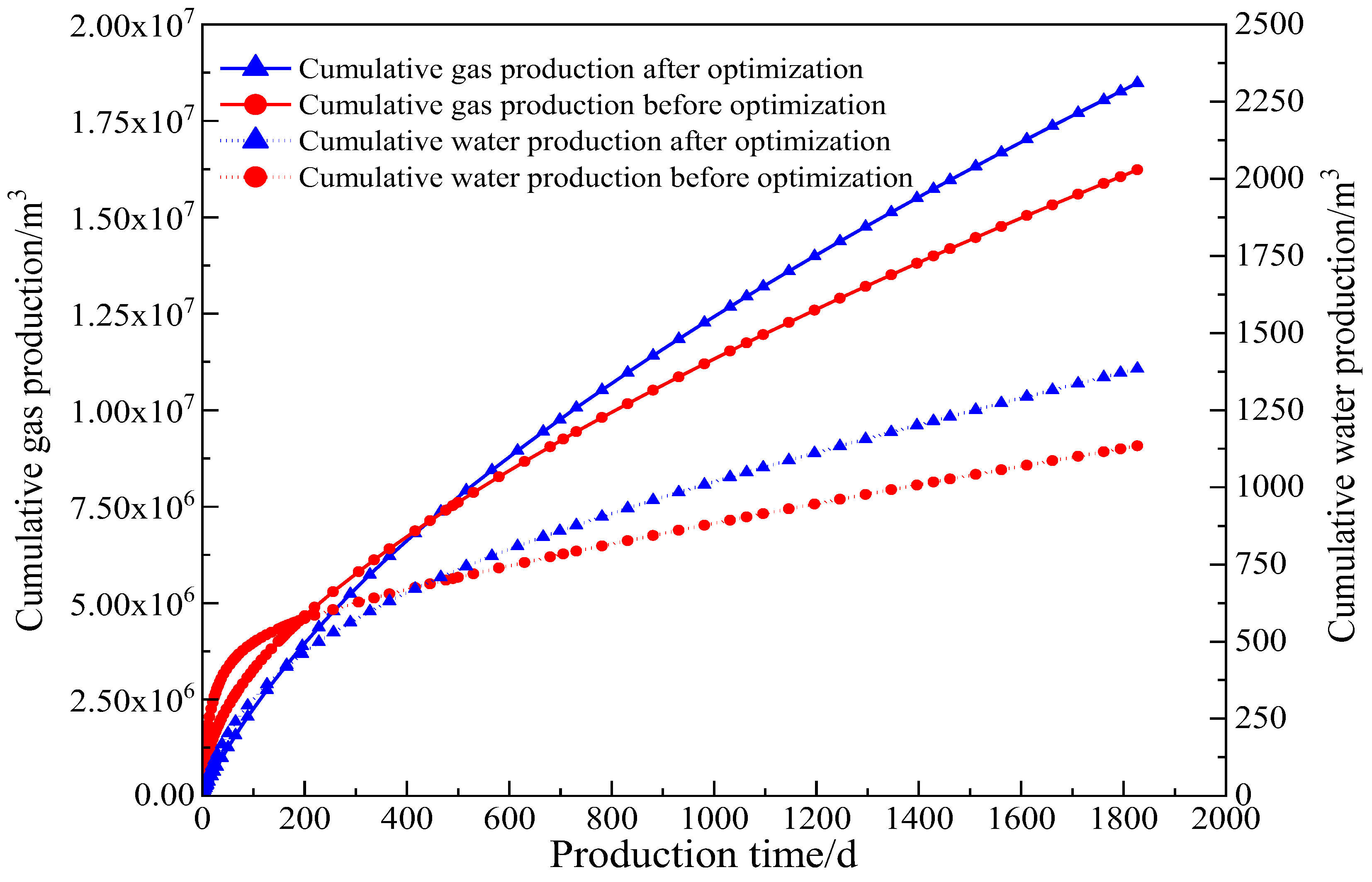
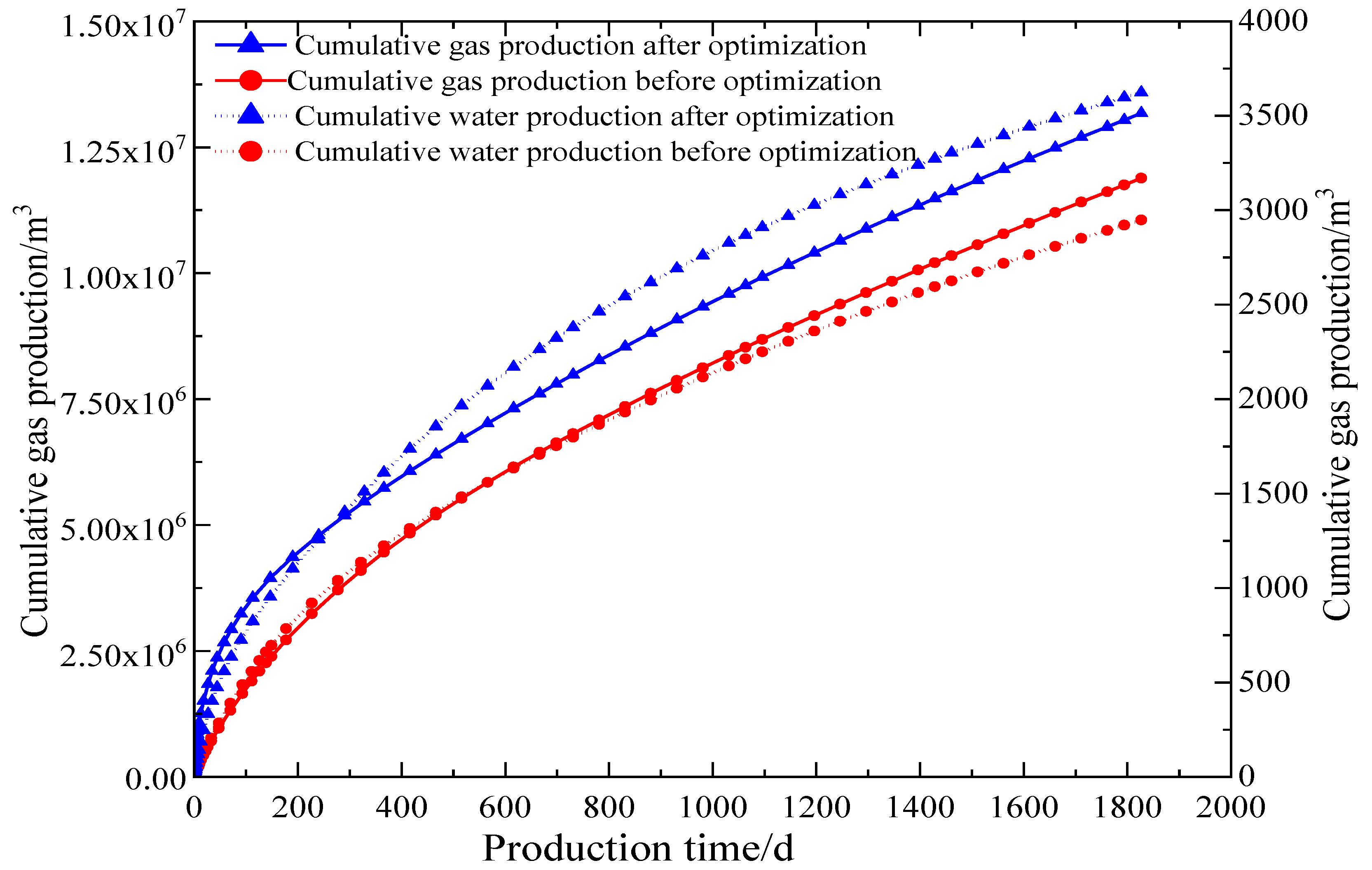
- For deep coalbed methane reservoirs with different lithological combinations, optimizing the fracturing operational parameters can increase the complexity of the fracture network within the coal seam interval and effectively control the stimulated volume. The cumulative gas production per well over 5 years can be increased by more than 1 million cubic meters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CBM | coalbed methane |
Appendix A
| Fracturing Procedure | Fluid Type | Injection Volume (m3) | Proppant Type | Sand Concentration (kg/m3) | Injection Rate (m3/min) |
|---|---|---|---|---|---|
| Pre-Fluid | Active Water | 20 | 2 | ||
| 15% Hydrochloric Acid | 15 | 2 | |||
| Active Water | 10 | 4 | |||
| High-viscosity Slickwater (55.0 mPa·s) | 120 | 22 | |||
| Low-viscosity Slickwater (1.0 mPa·s) | 20 | 200-mesh quartz sand | 88.10 | 22 | |
| High-viscosity Slickwater | 100 | 22 | |||
| Low-viscosity Slickwater | 33.3 | 200-mesh quartz sand | 105.83 | 22 | |
| High-viscosity Slickwater | 90 | 22 | |||
| Low-viscosity Slickwater | 42.9 | 200-mesh quartz sand | 123.22 | 22 | |
| High-viscosity Slickwater | 80 | 22 | |||
| Proppant-Laden Fluid | Medium-viscosity Slickwater (25.0 mPa·s) | 100 | 200-mesh quartz sand | 176.20 | 22 |
| Medium-viscosity Slickwater | 108.3 | 200-mesh quartz sand | 211.51 | 22 | |
| Medium-viscosity Slickwater | 121.4 | 200-mesh quartz sand | 246.74 | 22 | |
| Medium-viscosity Slickwater | 178.6 | 100-mesh quartz sand | 224.22 | 22 | |
| Medium-viscosity Slickwater | 200 | 100-mesh quartz sand | 256.30 | 22 | |
| Medium-viscosity Slickwater | 194.4 | 100-mesh quartz sand | 288.40 | 22 | |
| Medium-viscosity Slickwater | 200 | 100-mesh quartz sand | 304.35 | 22 | |
| Medium-viscosity Slickwater | 200 | 100-mesh quartz sand | 320.37 | 22 | |
| Medium-viscosity Slickwater | 200 | 100-mesh quartz sand | 336.39 | 22 | |
| Medium-viscosity Slickwater | 204.5 | 100-mesh quartz sand | 352.48 | 22 | |
| Medium-viscosity Slickwater | 120 | 40/70-mesh quartz sand | 334.00 | 22 | |
| Medium-viscosity Slickwater | 142.9 | 40/70-mesh quartz sand | 350.59 | 22 | |
| Medium-viscosity Slickwater | 172.7 | 30/50-mesh quartz sand | 373.61 | 22 | |
| Medium-viscosity Slickwater | 75 | 30/50 Mesh Ceramic Proppant + Coated Ceramic Proppant | 320.10 | 22 | |
| Displacement Fluid | Low-viscosity Slickwater | 26 | 22 | ||
| Total | 2775 |
References
- Li, Y.; Wang, Y.; Ding, J.; Yu, J.; Wu, P.; Song, Y. Pore-Scale Permeability Characteristics of Deep Coalbed Methane Reservoirs. Energy Fuels 2024, 38, 16149–16158. [Google Scholar] [CrossRef]
- Chen, B.; Li, S.; Tang, D.; Pu, Y.; Zhong, G. Evaluation of recoverable potential of deep coalbed methane in the Linxing Block, Eastern Margin of the Ordos Basin. Sci. Rep. 2024, 14, 9192. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Hou, S.; Wang, X.; Yuan, Y.; Dang, Z.; Tu, M. Geological and hydrological controls on the pressure regime of coalbed methane reservoir in the Yanchuannan field: Implications for deep coalbed methane exploitation in the eastern Ordos Basin, China. Int. J. Coal Geol. 2024, 294, 104619. [Google Scholar] [CrossRef]
- Zhang, C.; Li, M.; Hu, Q.; Jia, H.; Li, K.; Wang, Q.; Yang, R. Moderately deep coalbed methane reservoirs in the southern Qinshui Basin: Characteristics and technical strategies for exploitation. Coal Geol. Explor. 2024, 52, 122–133. [Google Scholar] [CrossRef]
- Fu, H.; Huang, L.; Hou, B.; Weng, D.; Guan, B.; Zhong, T.; Zhao, Y. Experimental and Numerical Investigation on Interaction Mechanism Between Hydraulic Fracture and Natural Fracture. Rock Mech. Rock Eng. 2024, 57, 10571–10582. [Google Scholar] [CrossRef]
- Huang, L.; Liao, X.; Fan, M.; Wu, S.; Tan, P.; Yang, L. Experimental and numerical simulation technique for hydraulic fracturing of shale formations. Adv. Geo-Energy Res. 2024, 13, 83–88. [Google Scholar] [CrossRef]
- Yu, J.; Li, N.; Hui, B.; Zhao, W.; Li, Y.; Kang, J.; Hu, P.; Chen, Y. Experimental simulation of fracture propagation and extension in hydraulic fracturing: A state-of-the-art review. Fuel 2024, 363, 131021. [Google Scholar] [CrossRef]
- Guo, X.; Yu, Z. Experimental and numerical simulation study on hydraulic fracture propagation law of coal seam. Pet. Sci. Technol. 2024, 42, 2063–2085. [Google Scholar] [CrossRef]
- Liao, S.; Hu, J.; Zhang, Y. Mechanism of hydraulic fracture vertical propagation in deep shale formation based on elastic–plastic model. Eng. Fract. Mech. 2024, 295, 109806. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, X.; Liang, L. Analysis of Factors Influencing Three-Dimensional Multi-Cluster Hydraulic Fracturing Considering Interlayer Effect. Appl. Sci. 2024, 14, 5330. [Google Scholar] [CrossRef]
- Tan, P.; Chen, Z.-W.; Huang, L.-K.; Zhao, Q.; Shao, S.-R. Evaluation of the combined influence of geological layer property and in-situ stresses on fracture height growth for layered formations. Pet. Sci. 2024, 21, 3222–3236. [Google Scholar] [CrossRef]
- Du, B.; Zhang, F.; Zhang, C. Distinct element modeling of hydraulic fracture propagation with discrete fracture network at Gonghe enhanced geothermal system site, northwest China. J. Rock Mech. Geotech. Eng. 2024, in press. [CrossRef]
- Wang, H.; Zhou, D.; Zou, Y.; Zheng, P. Effect mechanism of seepage force on the hydraulic fracture propagation. Int. J. Coal Sci. Technol. 2024, 11, 43. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, D. Mechanistic study on the effect of seepage force on hydraulic fracture initiation. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 1602–1619. [Google Scholar] [CrossRef]
- Yinghao, D.; Yang, X.; Di, W.; Yan, J. A study of Hydraulic fracture propagation in laminated shale using extended finite element method. Comput. Geotech. 2024, 166, 105961. [Google Scholar] [CrossRef]
- Zhang, Z.-P.; Zou, Y.-S.; Zhu, H.-Y.; Zhang, S.-C. Investigation of interaction behavior between hydraulic fractures and gravels in heterogeneous glutenite using a grain-based discrete element method. Pet. Sci. 2025, 22, 348–369. [Google Scholar] [CrossRef]
- Fu, W.; Deng, Q.; Ge, Z.; Jia, Y.; Ma, Z.; Shang, C.; Zheng, J.; Hou, Y. Numerical Investigation of Tree-Type Hydraulic Fracturing for Balanced Permeability Enhancement of Heterogenous Coal Seams Based on the Finite-Discrete Element Method Model. ACS Omega 2024, 9, 22090–22101. [Google Scholar] [CrossRef]
- Liao, Z.; Rabiee, H.; Ge, L.; Li, X.; Yang, Z.; Xue, Q.; Shen, C.; Wang, H. Revelling pore microstructure impacts on the compressive strength of porous proppant based on finite and discrete element method. J. Mater. Sci. Technol. 2024, 211, 72–81. [Google Scholar] [CrossRef]
- Liu, X.; Tao, W.; Liu, B.; Wang, S.; Deng, W.; Fan, Y. Study on direct shear mechanical characteristics of grouted-filled jointed coal using discrete element method. Eng. Anal. Bound. Elem. 2024, 169, 106048. [Google Scholar] [CrossRef]
- Lu, S.; Jia, N. Coal seam penetration enhancement technology integrating hydraulic fracturing fracture development theory. Appl. Earth Sci. 2024, 133, 162–173. [Google Scholar] [CrossRef]
- Chen, B.; Li, S.; Tang, D. Numerical simulation study on hydraulic fracture propagation of multi-cluster fracturing of horizontal well in deep fractured coal seams. Eng. Fract. Mech. 2025, 318, 110983. [Google Scholar] [CrossRef]
- Han, L.; Zhou, X. Numerical Simulations of the Hydraulic Fracture Propagation in Poroelastic Media Using the Coupled Hydro-Mechanical Field-Enriched Finite Element Method. Rock Mech. Rock Eng. 2025, 58, 245–274. [Google Scholar] [CrossRef]
- Huang, L.; Li, B.; Wu, B.; Li, C.; Wang, J.; Cai, H. Study on the extension mechanism of hydraulic fractures in bedding coal. Theor. Appl. Fract. Mech. 2024, 131, 104431. [Google Scholar] [CrossRef]
- Lecampion, B. An extended finite element method for hydraulic fracture problems. Commun. Numer. Methods Eng. 2009, 25, 121–133. [Google Scholar] [CrossRef]
- Zheng, P.; Xia, Y.; Yao, T.; Jiang, X.; Xiao, P.; He, Z.; Zhou, D. Formation mechanisms of hydraulic fracture network based on fracture interaction. Energy 2022, 243, 123057. [Google Scholar] [CrossRef]
- Cheng, S.; Zhang, M.; Zhang, X.; Wu, B.; Chen, Z.; Lei, Z.; Tan, P. Numerical study of hydraulic fracturing near a wellbore using dual boundary element method. Int. J. Solids Struct. 2022, 239–240, 111479. [Google Scholar] [CrossRef]
- Li, P.; Liu, Y.; Cai, M.; Miao, S.; Dai, L.; Gorjian, M.J.A.i.G.-E.R. Accurate stress measurement using hydraulic fracturing in deep low-permeability reservoirs: Challenges and research directions. Adv. Geo-Energy Res. 2024, 14, 165–169. [Google Scholar] [CrossRef]
- Ismail, A.; Azadbakht, S.J.I.J.f.N.; Geomechanics, A.M.i. A comprehensive review of numerical simulation methods for hydraulic fracturing. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 1433–1459. [Google Scholar] [CrossRef]
- Jahandideh, A.; Jafarpour, B. Optimization of hydraulic fracturing design under spatially variable shale fracability. J. Pet. Sci. Eng. 2016, 138, 174–188. [Google Scholar] [CrossRef]
- Starovoitova, B.N.; Golovin, S.V.; Paderin, G.V.; Shel, E.V.; Kavunnikova, E.A.; Krivtsov, A.M. Design optimization of hydraulic fracturing. IOP Conf. Ser. Earth Environ. Sci. 2018, 193, 012011. [Google Scholar] [CrossRef]
- Duplyakov, V.M.; Morozov, A.D.; Popkov, D.O.; Shel, E.V.; Vainshtein, A.L.; Burnaev, E.V.; Osiptsov, A.A.; Paderin, G.V. Data-driven model for hydraulic fracturing design optimization. Part II: Inverse problem. J. Pet. Sci. Eng. 2022, 208, 109303. [Google Scholar] [CrossRef]
- Wang, L.; Yao, Y.; Wang, K.; Adenutsi, C.D.; Zhao, G.; Lai, F. Data-driven multi-objective optimization design method for shale gas fracturing parameters. J. Nat. Gas Sci. Eng. 2022, 99, 104420. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Z.; Lai, F.; Li, H.; Adenutsi, C.D.; Wang, K.; Yang, S.; Xu, W. Integrated optimization design for horizontal well placement and fracturing in tight oil reservoirs. J. Pet. Sci. Eng. 2019, 178, 82–96. [Google Scholar] [CrossRef]
- Wang, H.; Yang, S.; Zhang, L.; Xiao, Y.; Su, X.; Yu, W.; Zhou, D. Experimental Analysis of the Mechanical Properties and Failure Behavior of Deep Coalbed Methane Reservoir Rocks. Processes 2024, 12, 1125. [Google Scholar] [CrossRef]
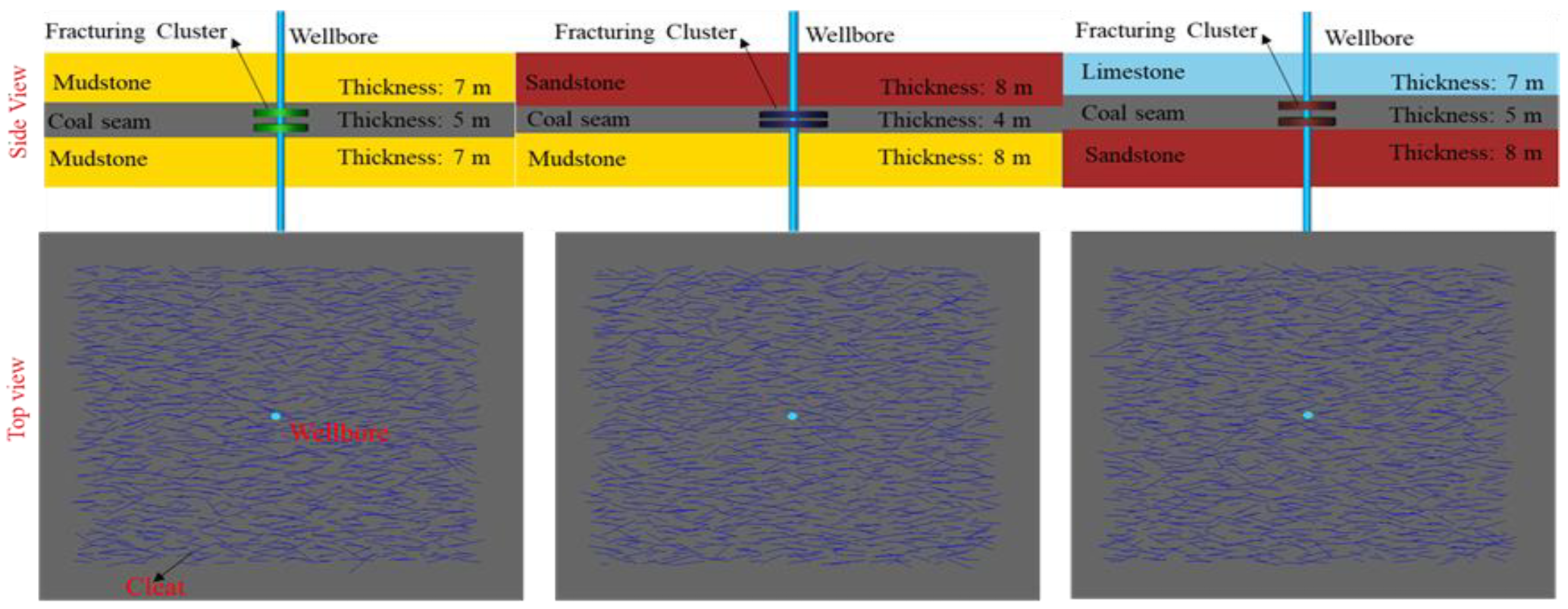








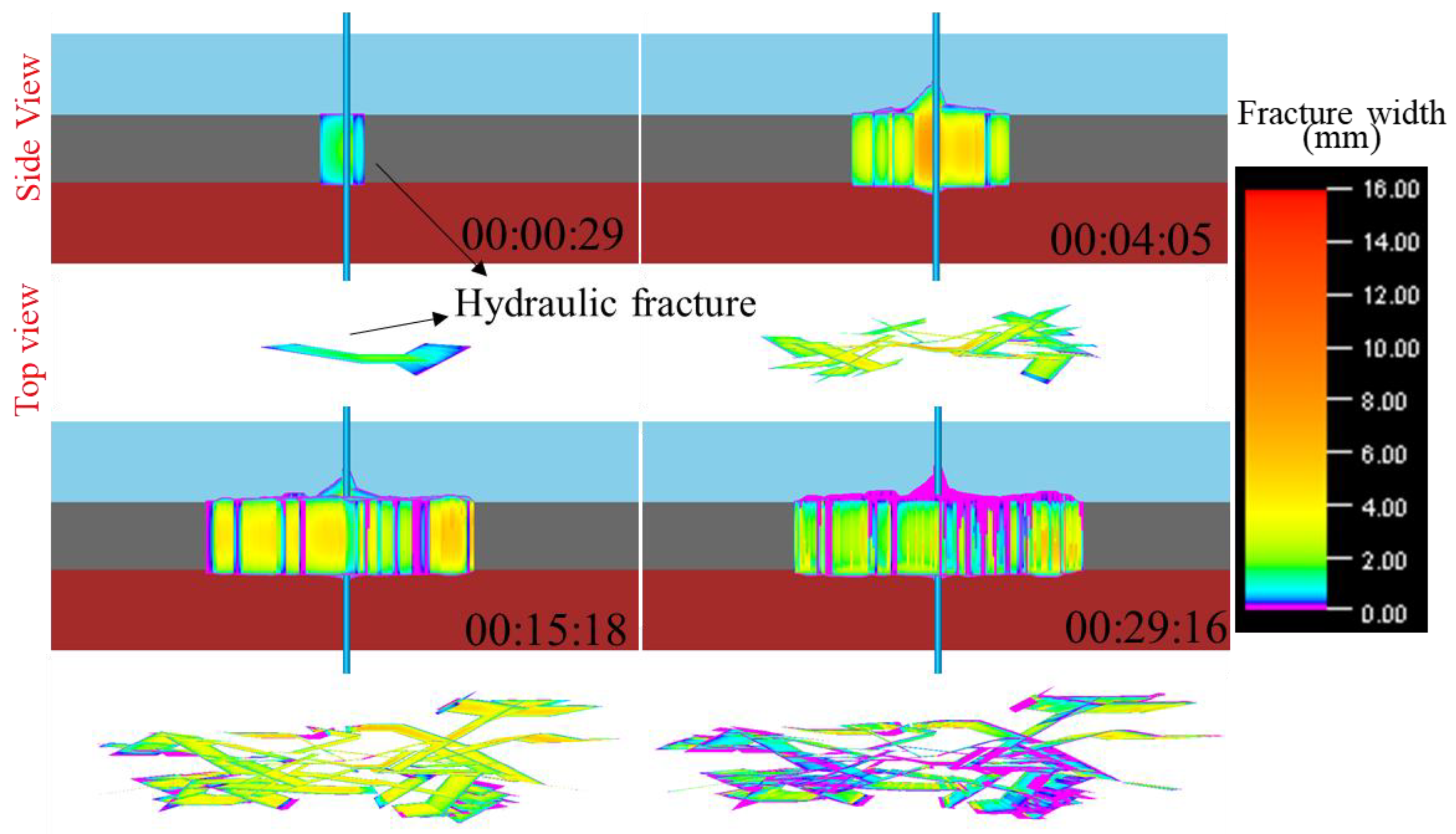
| Combination Category | Lithology | Porosity Φ/% | Permeability /mD | Young’s Modulus E/GPa | Poisson’s Ratio/ν | Friction Coefficient | In Situ Stress/MPa |
|---|---|---|---|---|---|---|---|
| Combination 1 | Mudstone | 5 | 0.01 | 22.9 | 0.32 | 0.78 | SV = 54, SH = 52, Sh = 44 |
| Coal | 7 | 0.075 | 2.9 | 0.39 | 0.67 | SV = 54, SH = 38, Sh = 37 | |
| Mudstone | 5 | 0.01 | 22.9 | 0.32 | 0.60 | SV = 54, SH = 52, Sh = 44 | |
| Combination 2 | Sandstone | 8 | 0.025 | 32.0 | 0.28 | 0.83 | SV = 55, SH = 55, Sh = 44 |
| Coal | 7 | 0.075 | 2.9 | 0.39 | 0.55 | SV = 55, SH = 38, Sh = 37 | |
| Mudstone | 5 | 0.01 | 22.8 | 0.32 | 0.81 | SV = 55, SH = 48, Sh = 42 | |
| Combination 3 | Limestone | 3 | 0.005 | 24.3 | 0.15 | 0.75 | SV = 56, SH = 56, Sh = 46 |
| Coal | 7 | 0.075 | 4.7 | 0.32 | 0.40 | SV = 56, SH = 38, Sh = 36 | |
| Sandstone | 8 | 0.025 | 18.0 | 0.25 | 0.70 | SV = 56, SH = 59, Sh = 52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, L.; Liu, E.; Sun, D.; Dong, Q.; Qiao, L.; Bai, X.; Wang, Z.; Su, X.; Wang, H.; Zhou, D. Numerical Investigation of Vertical Hydraulic Fracture Propagation and Fracturing Parameter Optimization in Deep Coalbed Methane Reservoirs. Processes 2025, 13, 909. https://doi.org/10.3390/pr13030909
Qiao L, Liu E, Sun D, Dong Q, Qiao L, Bai X, Wang Z, Su X, Wang H, Zhou D. Numerical Investigation of Vertical Hydraulic Fracture Propagation and Fracturing Parameter Optimization in Deep Coalbed Methane Reservoirs. Processes. 2025; 13(3):909. https://doi.org/10.3390/pr13030909
Chicago/Turabian StyleQiao, Lianlian, Erhu Liu, Dong Sun, Qiaosen Dong, Linsheng Qiao, Xiaofang Bai, Zhaohuan Wang, Xu Su, Haiyang Wang, and Desheng Zhou. 2025. "Numerical Investigation of Vertical Hydraulic Fracture Propagation and Fracturing Parameter Optimization in Deep Coalbed Methane Reservoirs" Processes 13, no. 3: 909. https://doi.org/10.3390/pr13030909
APA StyleQiao, L., Liu, E., Sun, D., Dong, Q., Qiao, L., Bai, X., Wang, Z., Su, X., Wang, H., & Zhou, D. (2025). Numerical Investigation of Vertical Hydraulic Fracture Propagation and Fracturing Parameter Optimization in Deep Coalbed Methane Reservoirs. Processes, 13(3), 909. https://doi.org/10.3390/pr13030909






