The Geometric Effect on the Two-Fluid Mixing in Planetary Centrifugal Mixer During Spin-Up: A Numerical Study
Abstract
1. Introduction
2. Materials and Methodologies
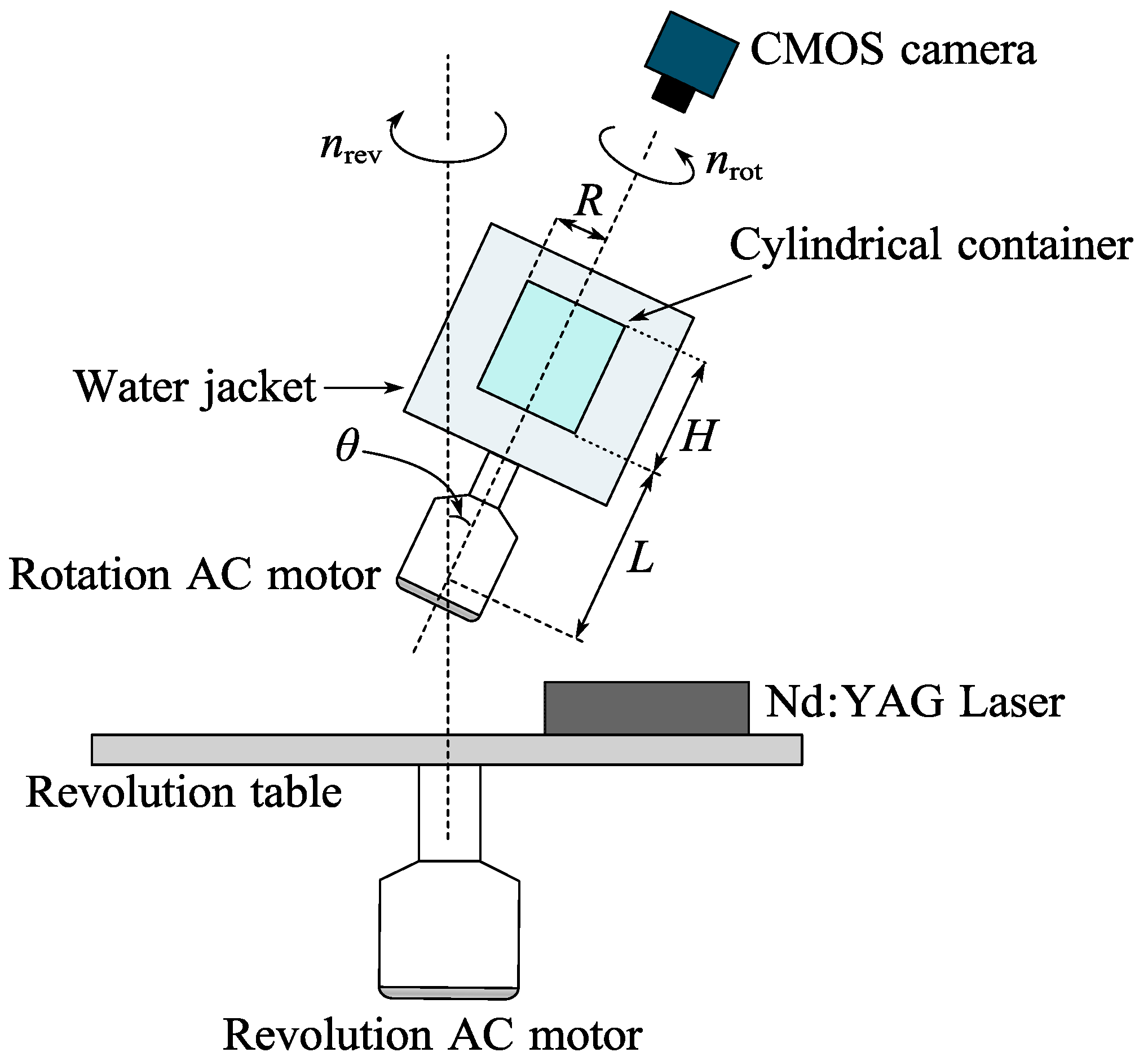
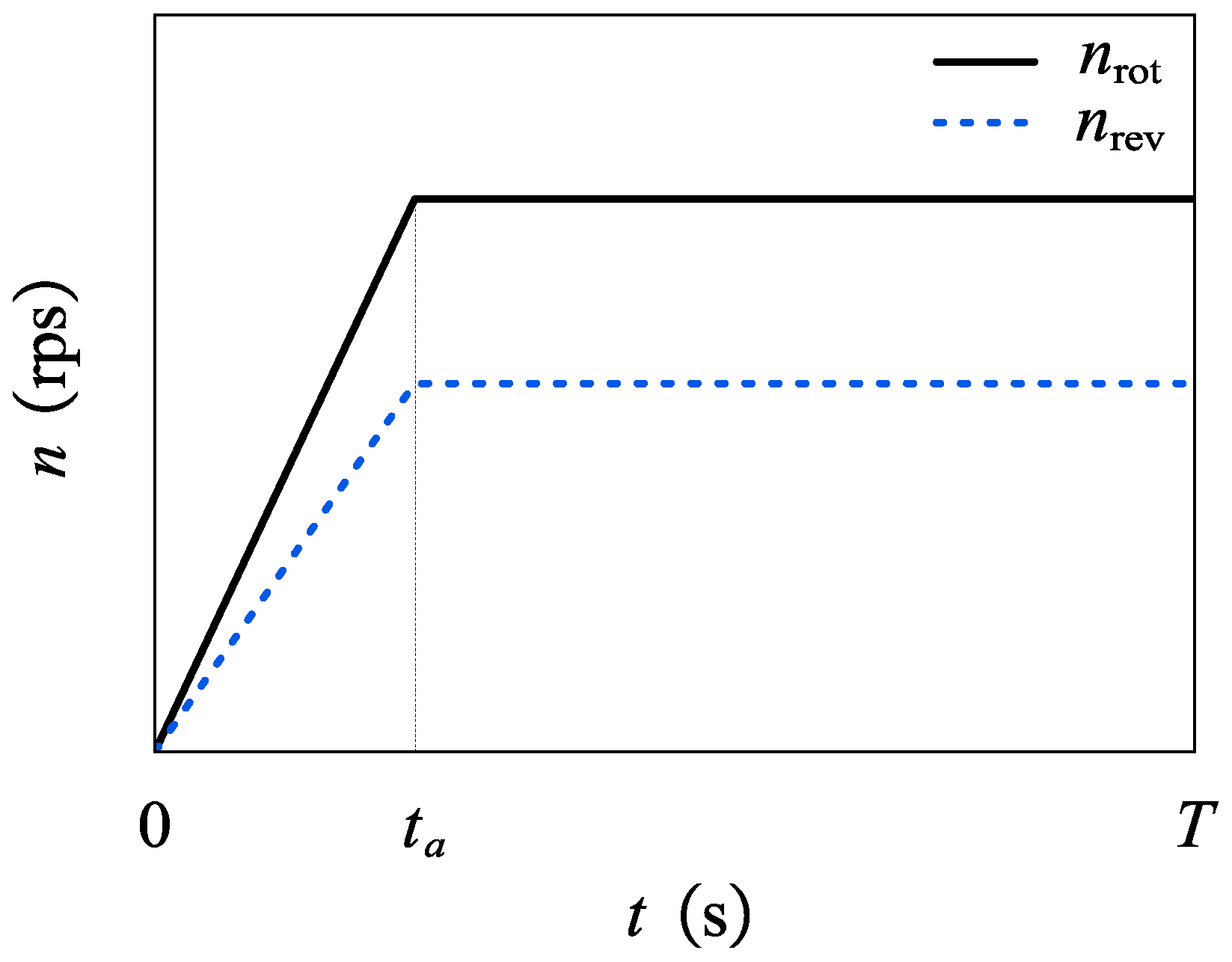
2.1. Experiment Setup
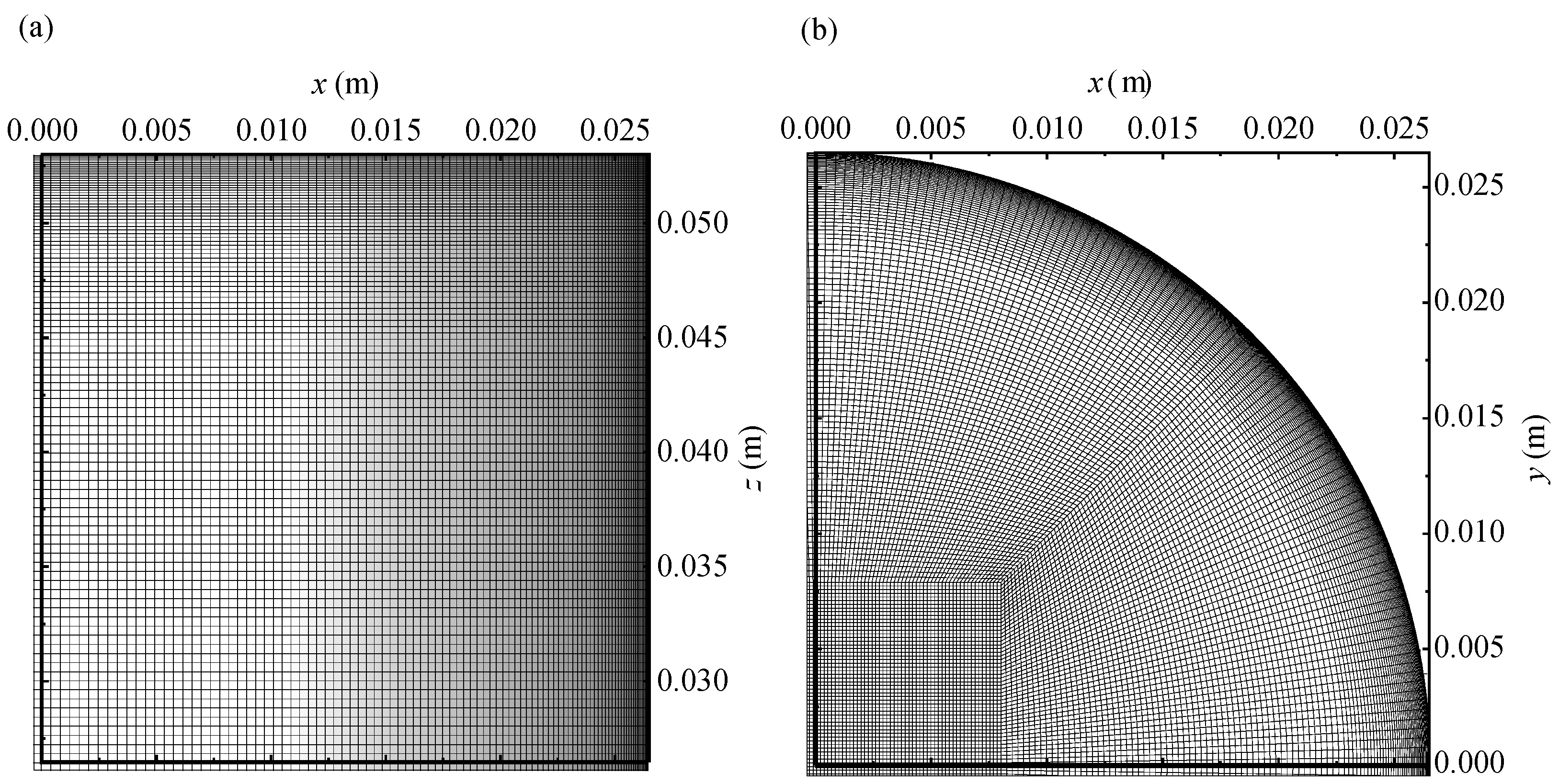
2.2. Numerical Methodologies
3. Results and Discussion
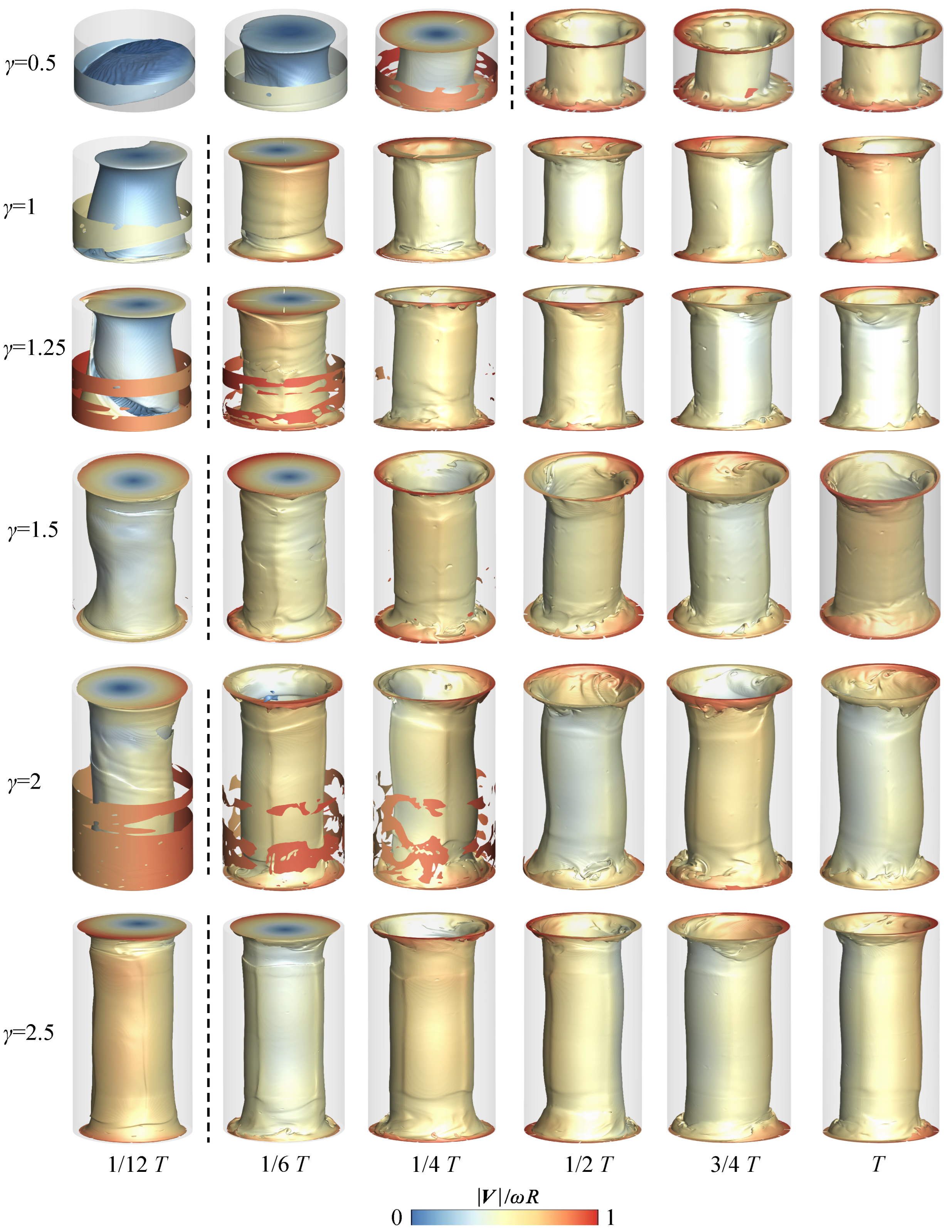
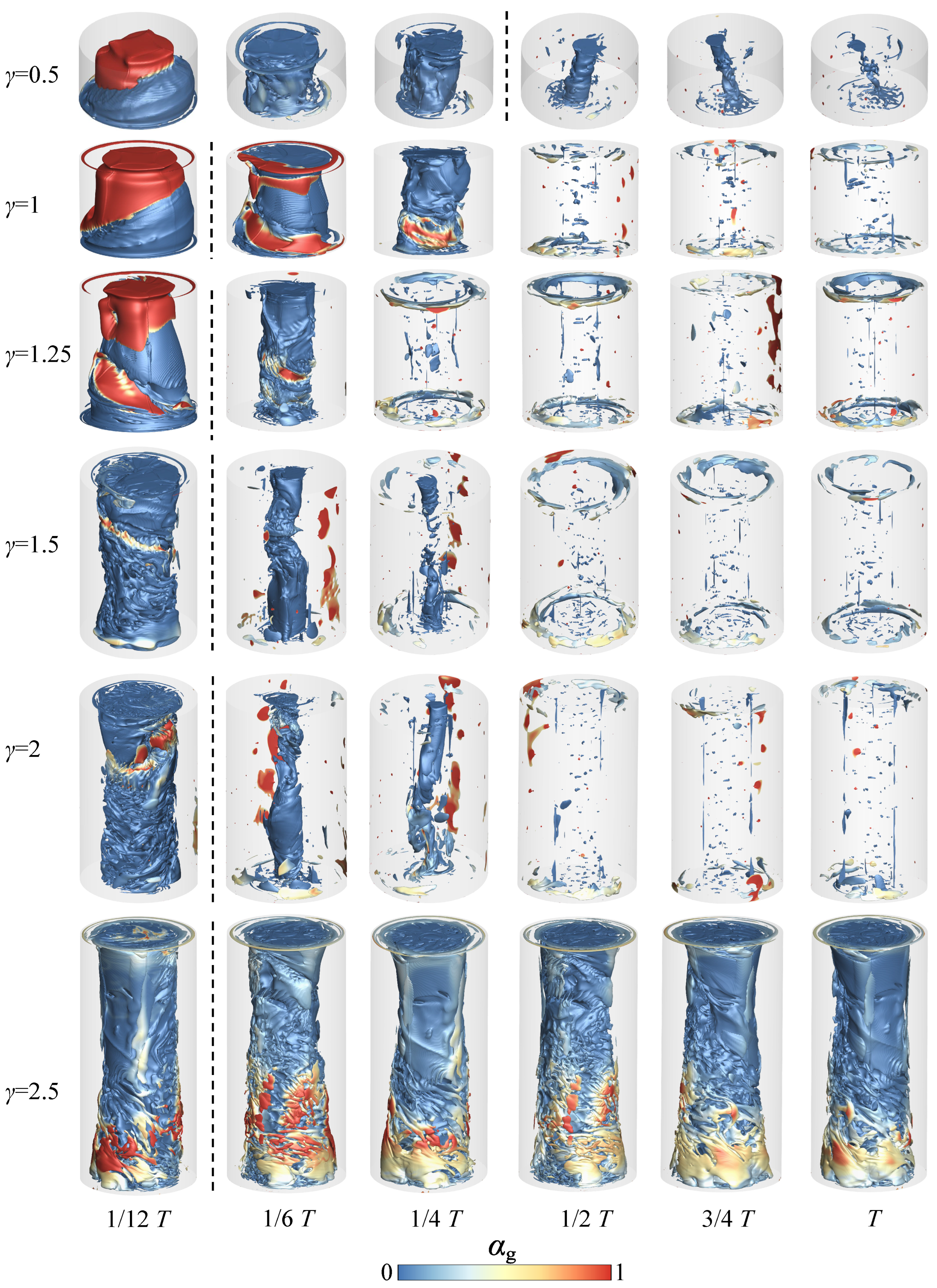
3.1. Interface Evolution
3.2. Vortex Development
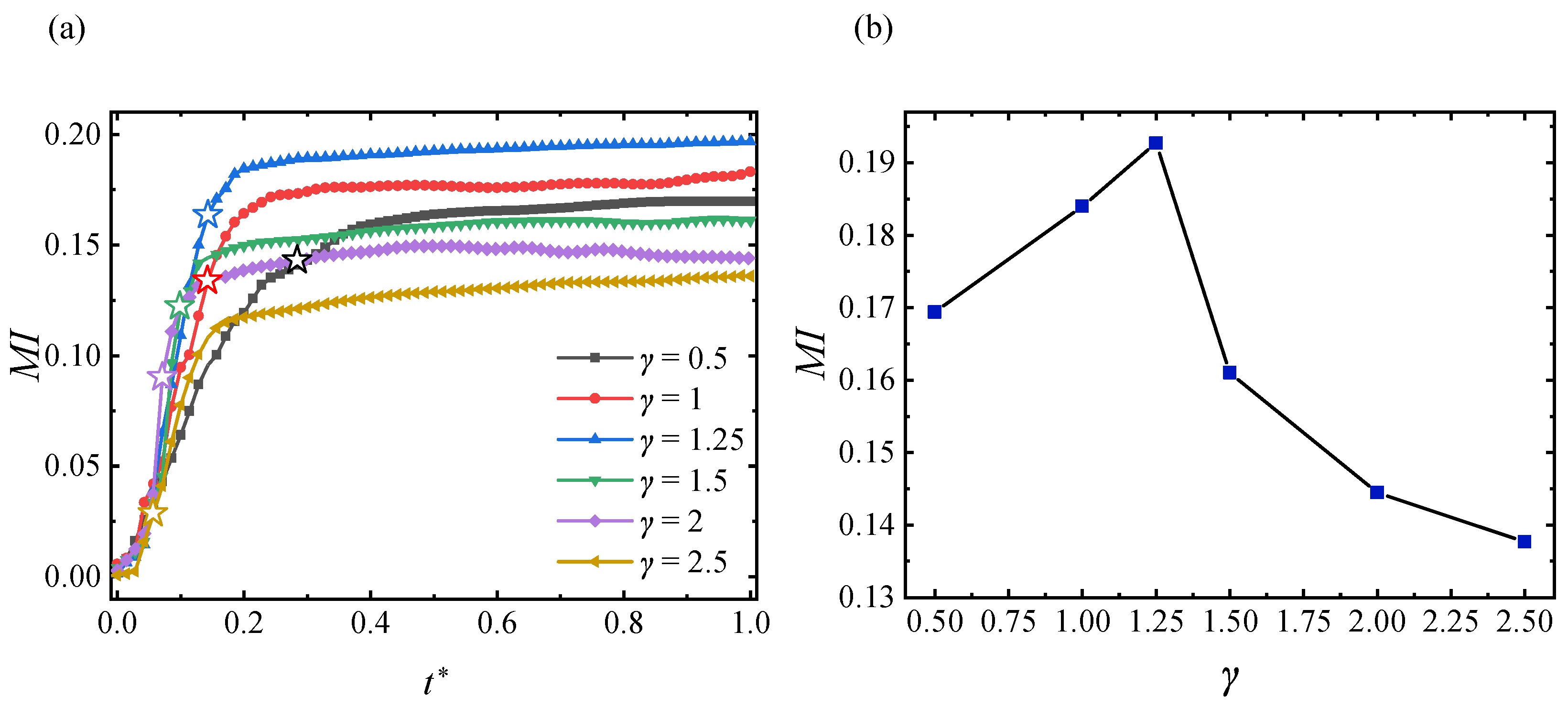
3.3. Mixing Performance
4. Conclusions
- The configurations with smaller aspect ratios (e.g., ) or larger ones (e.g., ) relatively suppress the vortex development and mixing efficiency.
- The mixing performance reaches a peak value at , with a of 0.196 at the end of spin-up. This geometric configuration introduces intense vortex fragmentation, obvious interface shrinking, small low-velocity regions, and strong chaotic convection.
- The correlation between vortex dissipation, interface collapse, and low-velocity regions was elucidated. At , intense vortex fragmentation and minimal low-velocity regions promote interfacial stretching, enhancing turbulent energy dissipation (average ).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
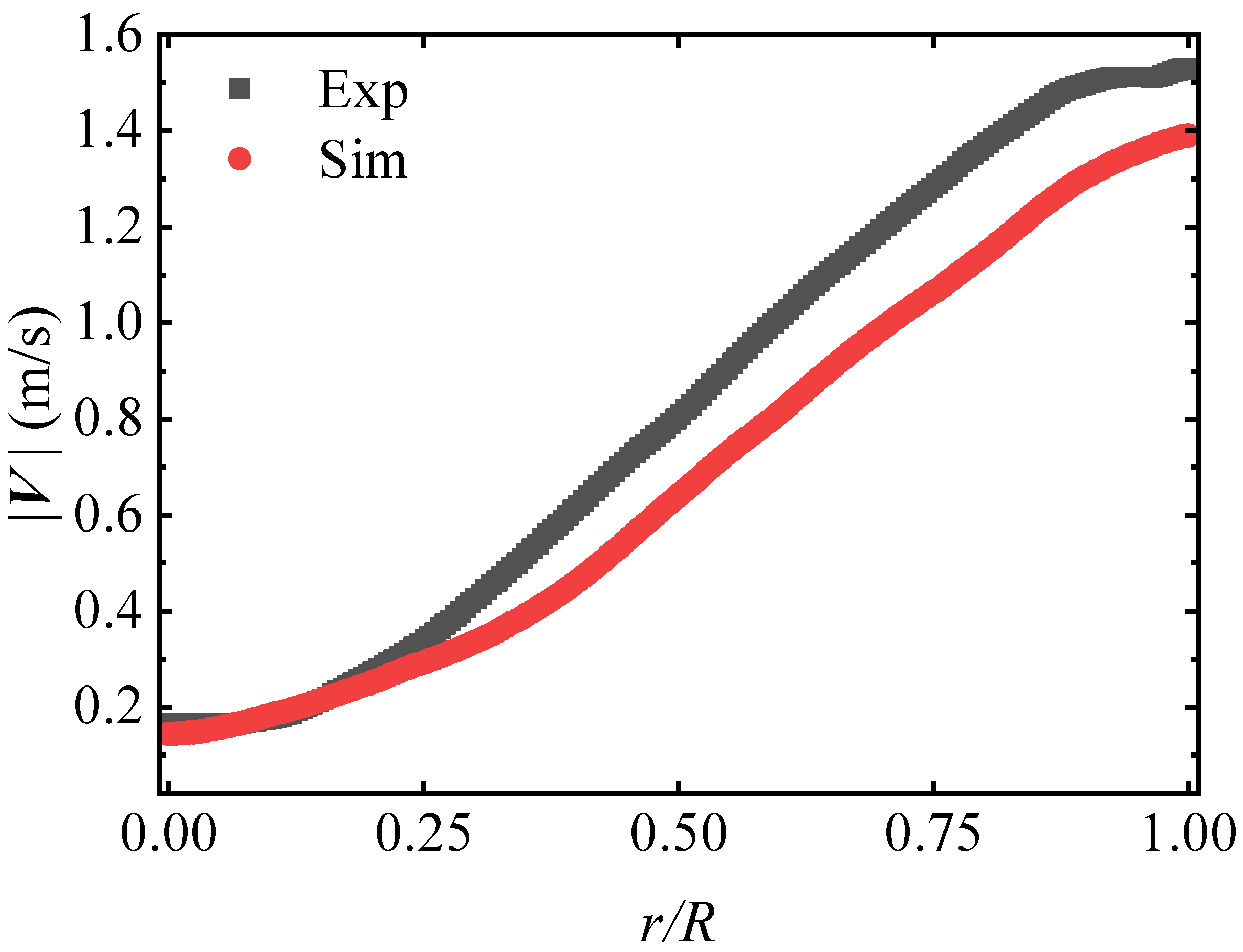
Appendix A. Numerical Validation with Literature
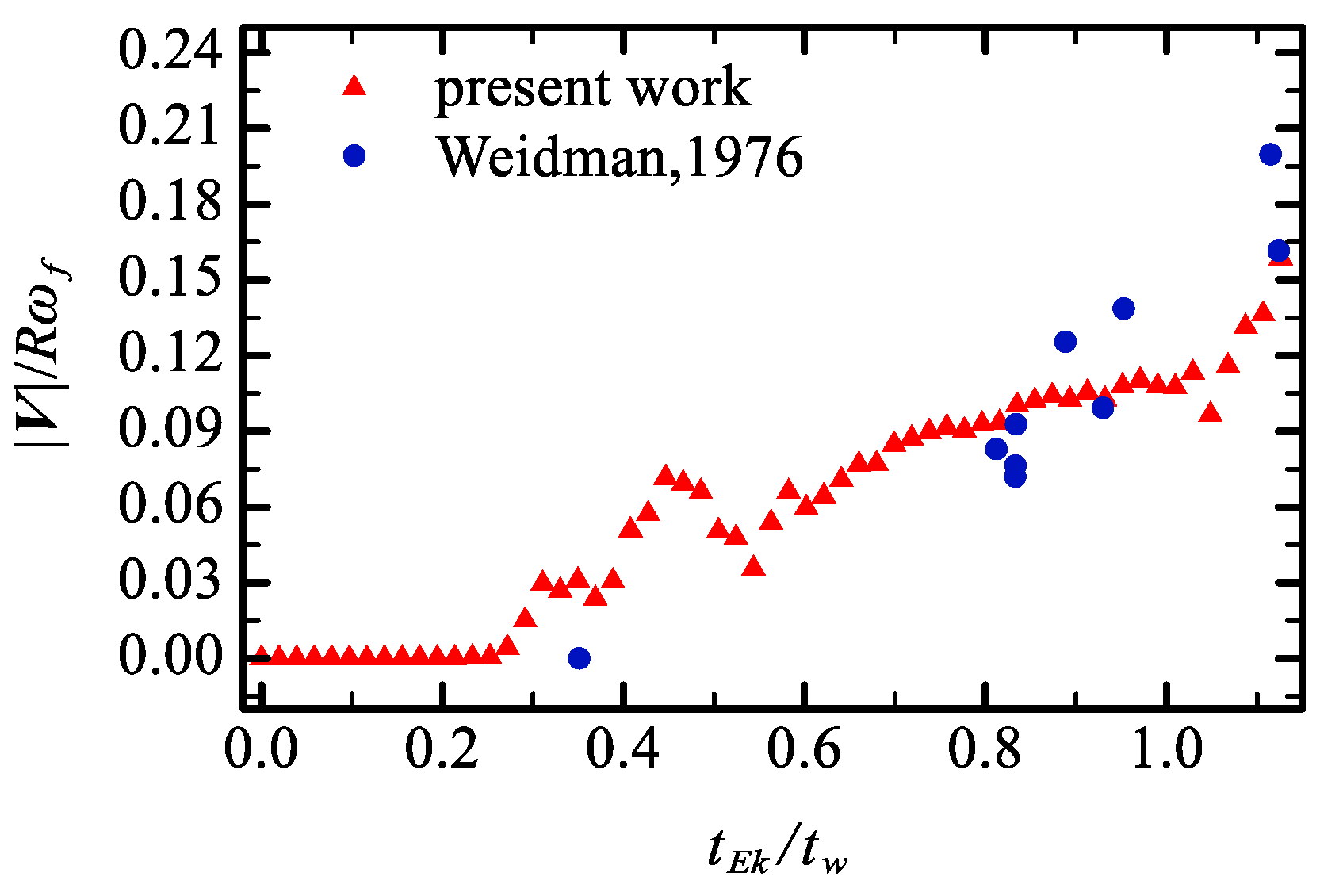
References
- Son, K.J. A numerical study of the influence of rheology of cohesive particles on blade-free planetary mixing. Korea-Aust. Rheol. J. 2018, 30, 199–209. [Google Scholar] [CrossRef]
- Son, K.J. A numerical study of the influence of operating conditions of a blade-free planetary mixer on blending of cohesive powders. Korea-Aust. Rheol. J. 2019, 31, 15–23. [Google Scholar] [CrossRef]
- Peerhossaini, H. Effects of turbulent mixing and orbitally shaking on cell growth and biomass production in active fluids. Am. J. Biomed. Sci. Res. 2022, 15, 396–404. [Google Scholar] [CrossRef]
- Yamagata, T.; Sugisawa, H.; Fujisawa, N. Experimental study on laminar mixing in planetary mixer. Exp. Fluids 2021, 62, 28. [Google Scholar] [CrossRef]
- Yamagata, T.; Fujisawa, N. Effect of rotation and revolution on performance of blade-free planetary mixer. J. Flow Cont. Meas. Vis. 2019, 7, 1–10. [Google Scholar] [CrossRef]
- Weheliye, W.; Ducci, A.; Weheliye, W.; Yianneskis, M.; Ducci, A. PIV measurements in a shaken cylindrical bioreactor. In Proceedings of the 16th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 9–12 July 2012; pp. 9–12. [Google Scholar]
- Chergui, N.; Lateb, M.; Lacroix, É.; Dufresne, L. CFD study of flow dynamics in a blade free planetary mixer (BFPM)—A qualitative flow study. Chem. Eng. Res. Des. 2015, 102, 100–115. [Google Scholar] [CrossRef]
- Shen, B.; Zhan, X.; He, Y.; Sun, Z.; Long, J.; Yang, Y.; Li, X. Computational fluid dynamic analysis of mass transfer and hydrodynamics in a planetary centrifugal bioreactor. Korean J. Chem. Eng. 2021, 38, 1358–1369. [Google Scholar] [CrossRef]
- Shen, B.; Zhan, X.; Sun, Z.; He, Y.; Long, J.; Li, X. Piv experiments and CFD simulations of liquid-liquid mixing in a planetary centrifugal mixer (PCM). Chem. Eng. Sci. 2022, 259, 117764. [Google Scholar] [CrossRef]
- Wang, G.; Liu, C.; Li, X.; Lou, J.; Li, J. Numerical study on influence of material characteristics on mixing performance of planetary centrifugal mixer. J. Mech. Electr. Eng 2022, 39, 627–633. [Google Scholar]
- Kaiser, F.; Wahl, T.; Gatti, D.; Rival, D.E.; Kriegseis, J. Vorticity propagation for spin-up and spin-down in a rotating tank. In Proceedings of the 18th International Symposium on the Application of Laser and Imaging Techniques to Fluid Mechanics, Lisbon, Portugal, 4–7 July 2016. [Google Scholar]
- Hewitt, R.E.; Foster, M.R.; Davies, P.A. Spin-up of a two-layer rotating stratified fluid in a variable-depth container. J. Fluid Mech. 2001, 438, 379–407. [Google Scholar] [CrossRef]
- Benton, E.R. Vorticity dynamics in spin-up from rest. Phys. Fluids 1979, 22, 1250–1251. [Google Scholar] [CrossRef]
- Park, J.S.; Hyun, J.M. Review on open-problems of spin-up flow of an incompressible fluid. J. Mech. Sci. Technol. 2008, 22, 780–787. [Google Scholar] [CrossRef]
- Greenspan, H.P.; Howard, L.N. On a time-dependent motion of a rotating fluid. J. Fluid Mech. 1963, 17, 385–404. [Google Scholar] [CrossRef]
- Meunier, P.; Hourigan, K. Mixing in a vortex breakdown flow. J. Fluid Mech. 2013, 731, 195–222. [Google Scholar] [CrossRef]
- Eloy, C.; Gal, P.L.; Dizés, S.L. Elliptic and triangular instabilities in rotating cylinders. J. Fluid Mech. 2003, 476, 357–388. [Google Scholar] [CrossRef]
- Ferreira, A.G.; Egas, A.P.; Fonseca, I.M.; Costa, A.C.; Abreu, D.C.; Lobo, L.Q. The viscosity of glycerol. J. Chem. Thermodyn. 2017, 113, 162–182. [Google Scholar] [CrossRef]
- Takamura, K.; Fischer, H.; Morrow, N.R. Physical properties of aqueous glycerol solutions. J. Petrol. Sci. Eng. 2012, 98–99, 50–60. [Google Scholar] [CrossRef]
- OpenCFD Limited. OpenFOAM The Open Source CFD Toolbox Tutorial Guide; OpenCFD Limited: Bracknell, UK, 2024; pp. 16–40. [Google Scholar]
- Manninen, M.; Taivassalo, V.; Energy, V.; Kallio, S. On the Mixture Model for Multiphase Flow; Altion Teknillinen Tutkimuskeskus: Espoo, Finland, 1996; pp. 16–48. [Google Scholar]
- Hernandez-Perez, V.; Abdulkadir, M.; Azzopardi, B.J. Grid generation issues in the cfd modelling of two-phase flow in a pipe. J. Comput. Multiph. Flows 2011, 3, 13–26. [Google Scholar] [CrossRef]
- Nishijima, Y.; Oster, G. Diffusion in Glycerol-Water Mixture. Bull. Chem. Soc. Jpn. 1960, 33, 1649–1651. [Google Scholar] [CrossRef]
- Hemmingsen, C.S.; Ingvorsen, K.M.; Mayer, S.; Walther, J.H. LES And URANS simulations of the swirling flow in a dynamic model of a uniflow-scavenged cylinder. Int. J. Heat Fluid Flow 2016, 62, 213–223. [Google Scholar] [CrossRef]
- Markatos, N.C. The mathematical modelling of turbulent flows. Appl. Math. Model. 1986, 10, 190–220. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Rashkovan, A.; Amar, S.D.; Bieder, U.; Ziskind, G. Analysis of polygonal vortex flows in a cylinder with a rotating bottom. Appl. Sci. 2021, 11, 1348. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Shang, Z.; Emerson, D.R.; Gu, X. Numerical investigations of cavitation around a high speed submarine using OpenFOAM with les. Int. J. Comput. Methods 2012, 9, 1250040. [Google Scholar] [CrossRef]
- Shang, Z. Numerical investigations of supercavitation around blunt bodies of submarine shape. Appl. Math. Model. 2013, 37, 8836–8845. [Google Scholar] [CrossRef]
- Naumov, I.V.; Sharifullin, B.R.; Tsoy, M.A.; Shtern, V.N. Dual vortex breakdown in a two-fluid confined flow. Phys. Fluids 2020, 32, 061706. [Google Scholar] [CrossRef]
- Weidman, P.D. On the spin-up and spin-down of a rotating fluid. Part 2. Measurements and stability. J. Fluid Mech. 1976, 77, 709–735. [Google Scholar] [CrossRef]
- Eisenga, A.H.; Verzicco, R.; Heijst, G.J.V. Dynamics of a vortex ring moving perpendicularly to the axis of a rotating fluid. J. Fluid Mech. 1998, 354, 69–100. [Google Scholar] [CrossRef]
- Pacheco, J.R.; Verzicco, R. Formation of columnar baroclinic vortices in thermally stratified nonlinear spin-up. J. Fluid Mech. 2012, 702, 265–285. [Google Scholar] [CrossRef]
- Han, H.; Geng, D.; Qian, Z.; Ren, Z.; Zuo, Z.; Liu, S. On cavitation caused by tip clearance of a flat-plate hydrofoil. Phys. Fluids 2024, 36, 113345. [Google Scholar] [CrossRef]
- Zhan, J.M.; Li, Y.T.; Wai, W.H.O.; Hu, W.Q. Comparison between the q criterion and rortex in the application of an in-stream structure. Phys. Fluids 2019, 31, 121701. [Google Scholar] [CrossRef]
- Yu, Y.; Shrestha, P.; Alvarez, O.; Nottage, C.; Liu, C. Investigation of correlation between vorticity, Q, λci, λ2, Δ and liutex. Comput. Fluids 2021, 225, 104977. [Google Scholar] [CrossRef]
- Ijichi, T.; St. Laurent, L.; Polzin, K.L. How Variable Is Mixing Efficiency in the Abyss? Geophys. Res. Lett. 2020, 47, e2019GL086813. [Google Scholar] [CrossRef]
- Klema, M.R.; Venayagamoorthy, S.K. Mixing rates in stably stratified flows with respect to the turbulent froude number and turbulent scales. Environ. Fluid Mech. 2023, 23, 1037–1049. [Google Scholar] [CrossRef]
- Qin, L.; Lu, X.; Li, L.; Han, H.; Yan, X.; Chen, S.; Wang, H.; Ma, W. Optimization of G1 micromixer structure in two-fluid mixing based on CFD and response surface methodology. Processes 2024, 12, 122. [Google Scholar] [CrossRef]
- Samancoğlu, U.E.; Koşar, A.; Cetkin, E. Optimization of y-shaped micro-mixers with a mixing chamber for increased mixing efficiency and decreased pressure drop. Asme J. Heat Mass Transf. 2024, 146, 043201. [Google Scholar] [CrossRef]






| Component | Density () | Viscosity () | Surface Tension () |
|---|---|---|---|
| water | 0.99 | 1010 | 72.00 |
| glycerol | 1.26 | 1410 | 61.90 |
| T/s | |||||
|---|---|---|---|---|---|
| 10 | 1 | 1 | 10 | 0.5, 1, 1.25, 1.5, 2, 2.5 | 3.52, 7.04, 8.80, 10.56, 14.08, 17.61 |
| Width of Mixing Region/mm | Volume Fraction of Low Velocity Region | Average /() | ||
|---|---|---|---|---|
| 0.5 | 6.761 | 0.313 | 0.169 | |
| 1 | 6.662 | 0.301 | 0.184 | |
| 1.25 | 8.894 | 0.225 | 0.196 | |
| 1.5 | 6.433 | 0.259 | 0.161 | |
| 2 | 5.612 | 0.368 | 0.145 | |
| 2.5 | 2.232 | 0.422 | 0.138 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, L.; Han, H.; Lu, X.; Li, L.; Liu, J.; Yan, X.; Zhang, Y. The Geometric Effect on the Two-Fluid Mixing in Planetary Centrifugal Mixer During Spin-Up: A Numerical Study. Processes 2025, 13, 874. https://doi.org/10.3390/pr13030874
Qin L, Han H, Lu X, Li L, Liu J, Yan X, Zhang Y. The Geometric Effect on the Two-Fluid Mixing in Planetary Centrifugal Mixer During Spin-Up: A Numerical Study. Processes. 2025; 13(3):874. https://doi.org/10.3390/pr13030874
Chicago/Turabian StyleQin, Liang, Huan Han, Xiaoxia Lu, Lei Li, Jianghai Liu, Xiaofang Yan, and Yinze Zhang. 2025. "The Geometric Effect on the Two-Fluid Mixing in Planetary Centrifugal Mixer During Spin-Up: A Numerical Study" Processes 13, no. 3: 874. https://doi.org/10.3390/pr13030874
APA StyleQin, L., Han, H., Lu, X., Li, L., Liu, J., Yan, X., & Zhang, Y. (2025). The Geometric Effect on the Two-Fluid Mixing in Planetary Centrifugal Mixer During Spin-Up: A Numerical Study. Processes, 13(3), 874. https://doi.org/10.3390/pr13030874






