Design and Optimization of Stem Mustard Cutting Device Based on Response Surface Methodology (RSM)
Abstract
1. Introduction
2. Materials and Methods
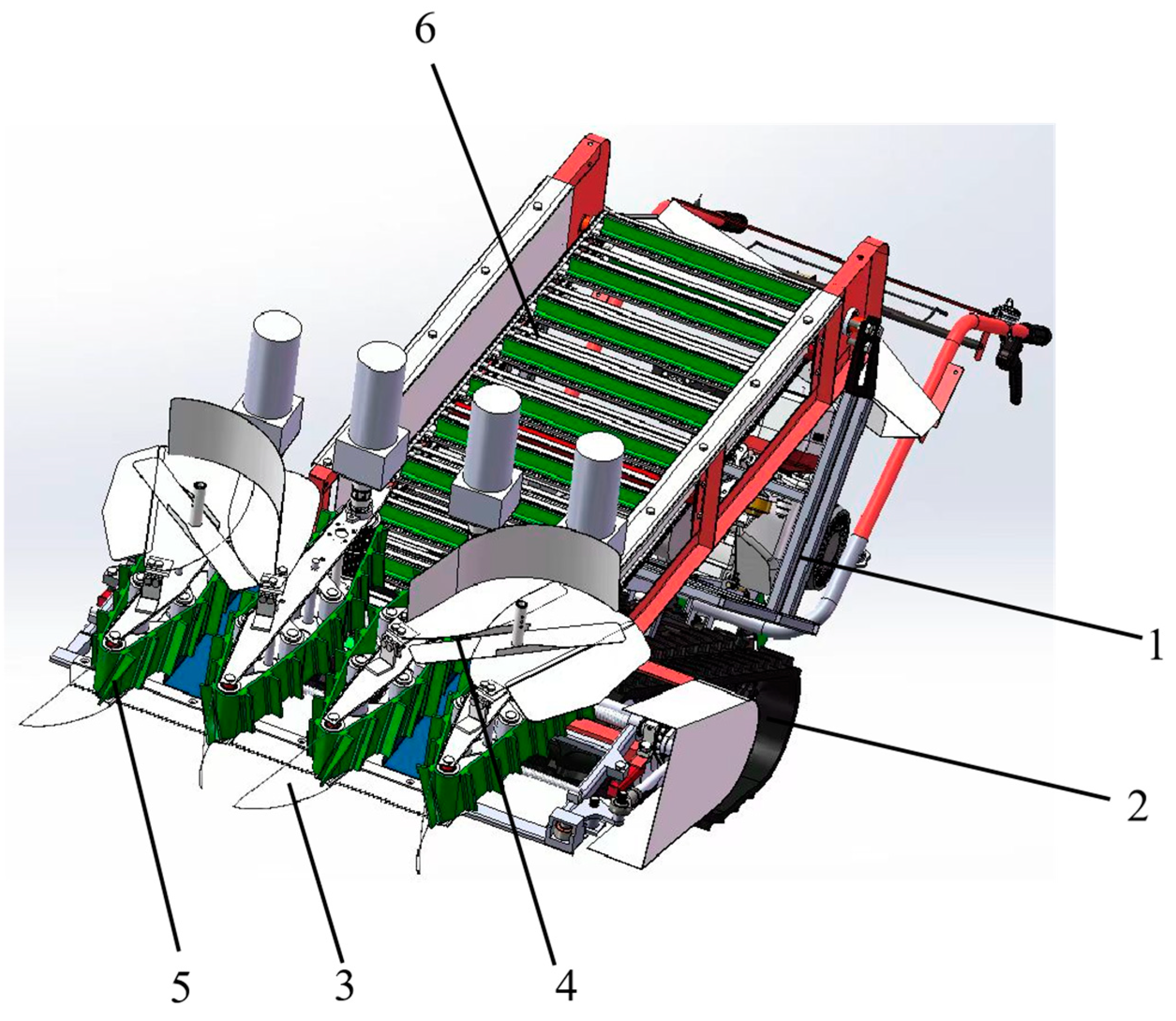
2.1. Machine Structure
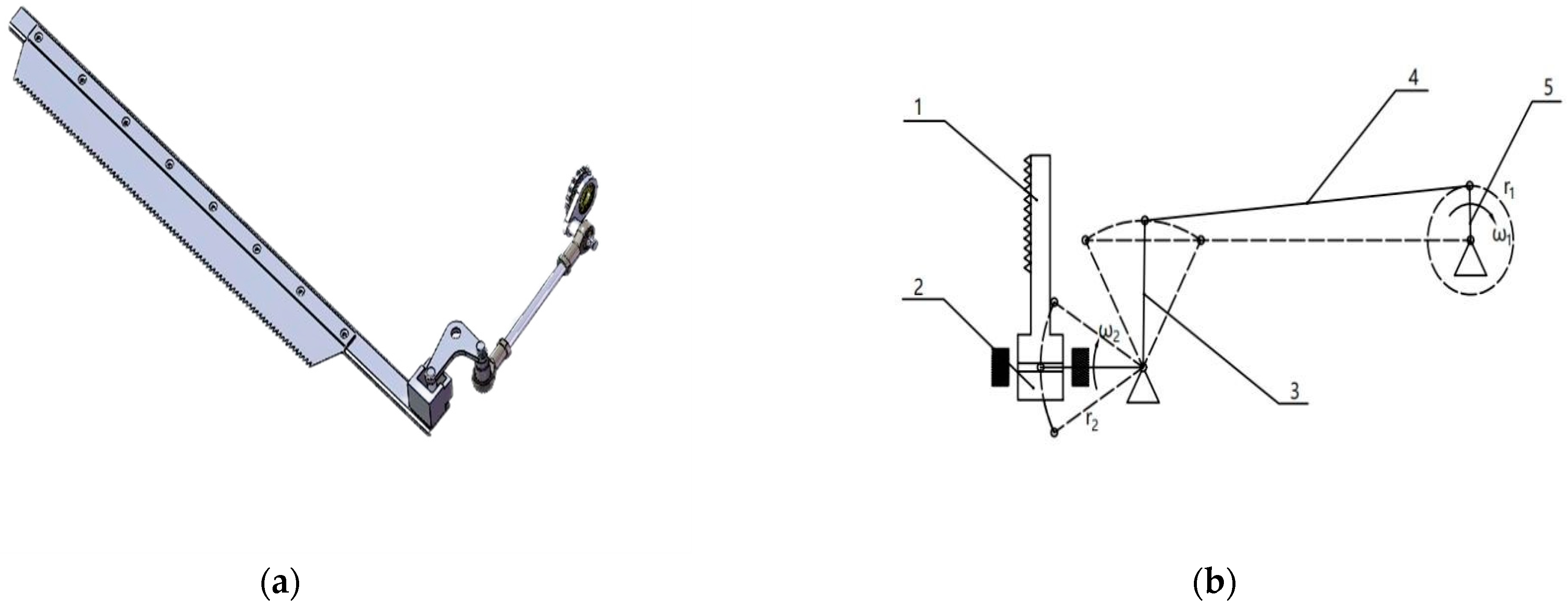
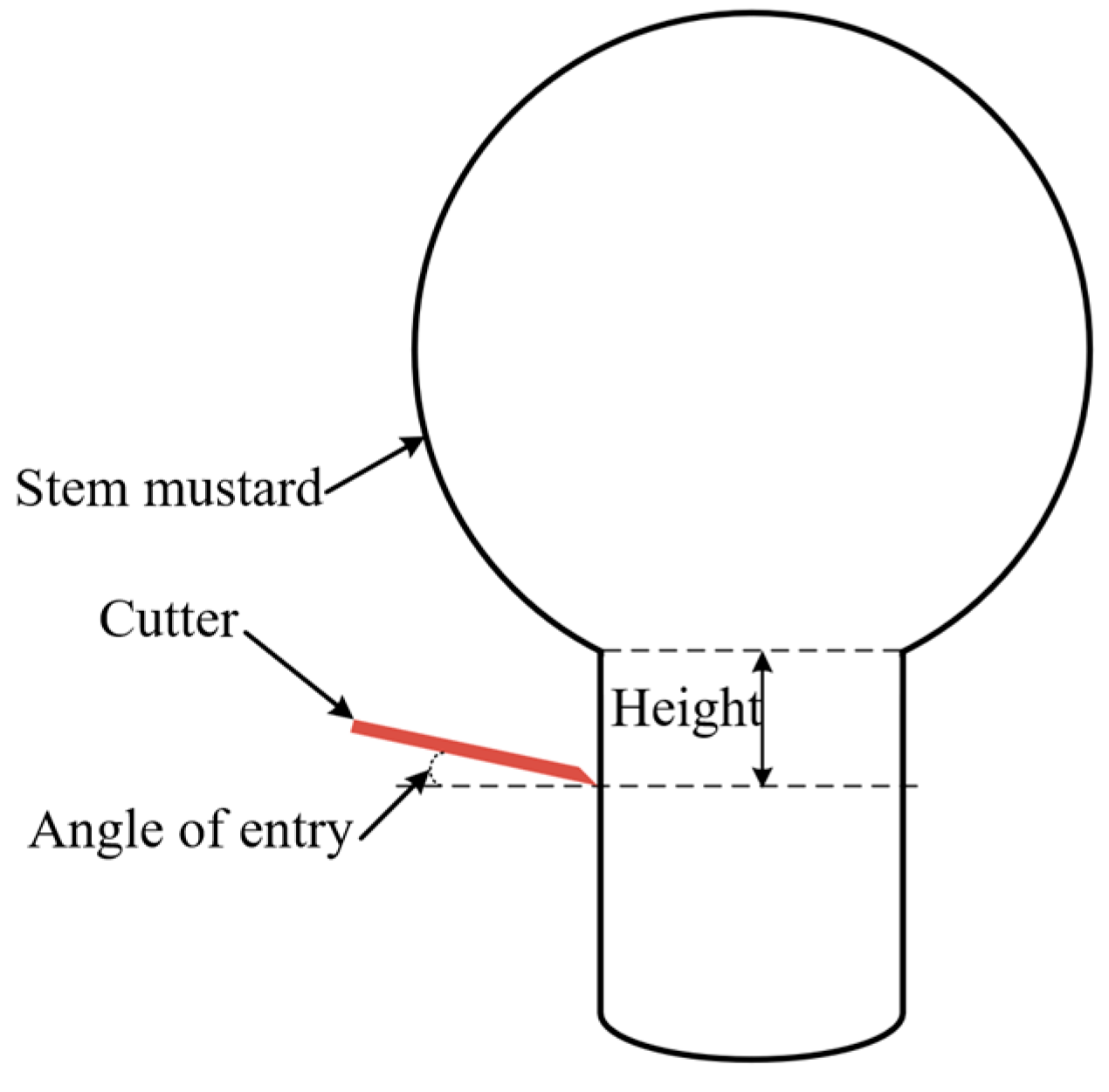
2.2. Design of Cutting Mechanism for Stem Mustard
2.3. Cutter Modelling and Analysis
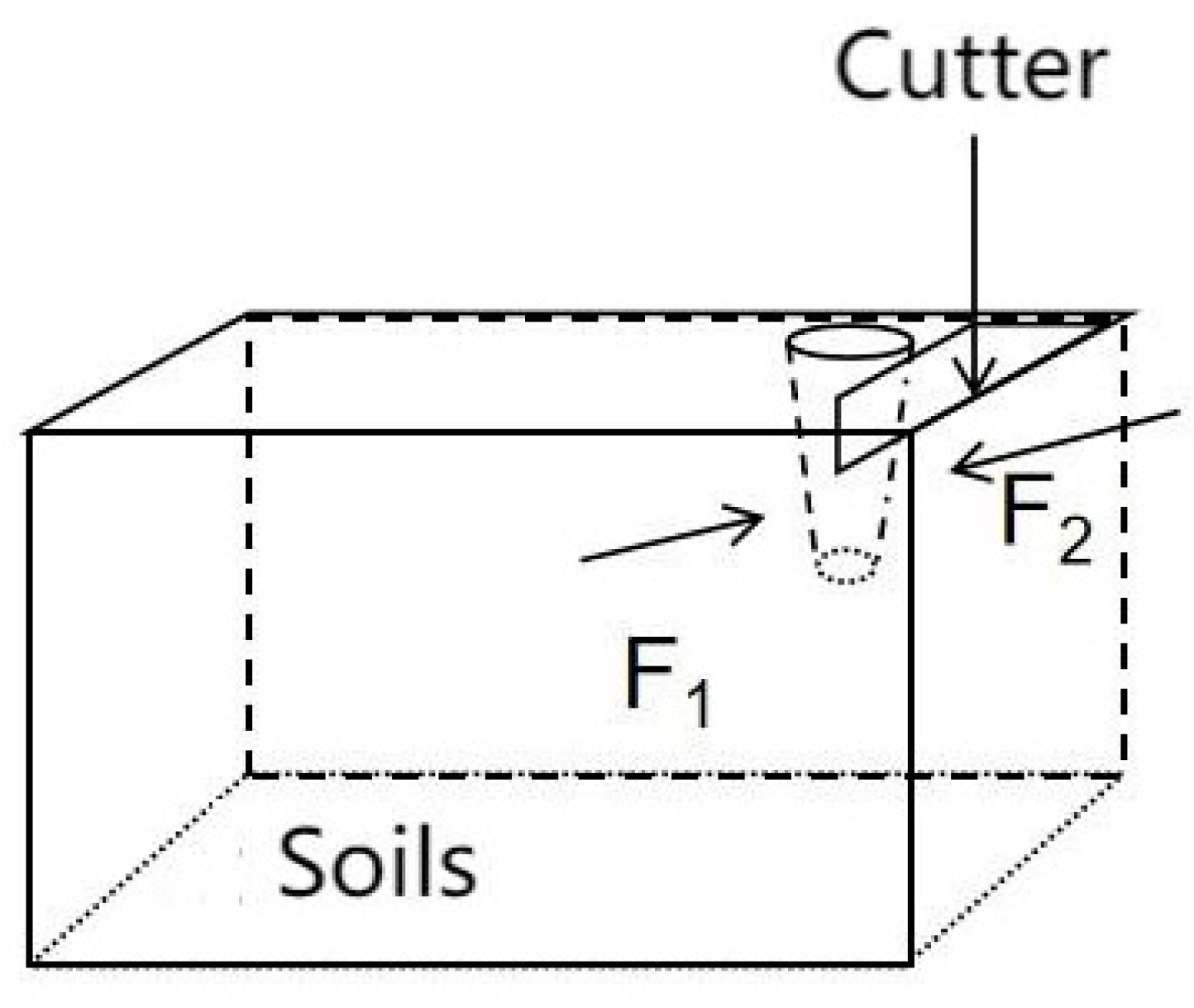
2.3.1. Cutter Cutting Force Analysis
2.3.2. Finite Element Modelling
- (1)
- Cutter and soils
- (2)
- Stem mustard
- (3)
- Material properties
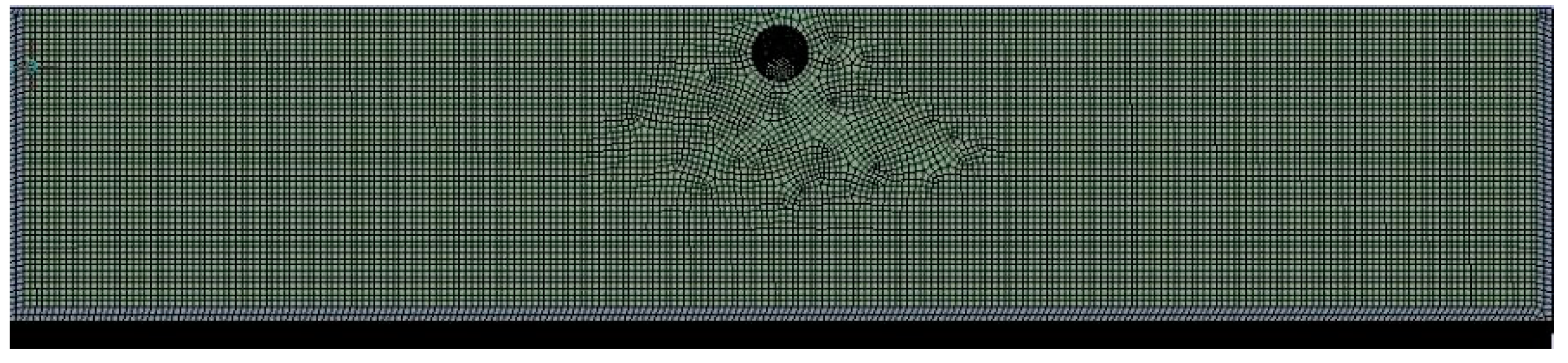
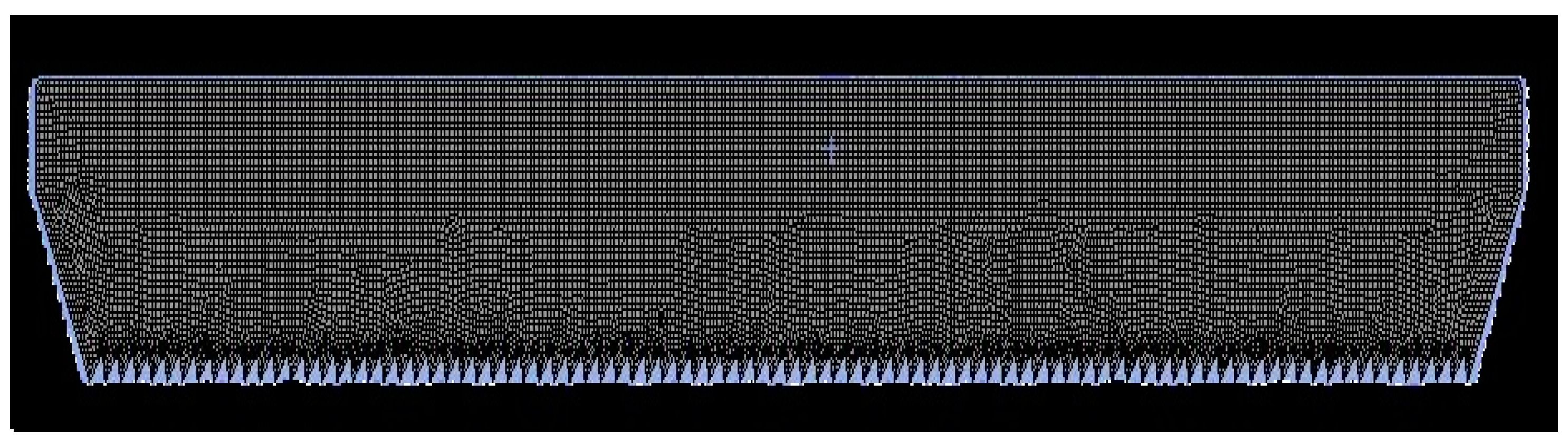
2.3.3. Model Meshing
- (1)
- The geometry of the truncated stem exhibits a larger diameter at the upper section and a reduced diameter at the lower section, while the configuration of the lower portion is more intricate. During the cutting process, the interface between the truncated stem and the stem tumor constitutes the cutting region. Consequently, the model representing this cutting region can be approximated as a cylindrical shape, thereby enhancing meshing efficiency.
- (2)
- The single run displacement of the cutter remains unaffected by external variables.
- (3)
- There is an absence of elastic deformation in the cutter, as well as a lack of misalignment during its movement.
- (4)
- The soil composition is unaffected by external influences, exhibiting no contaminants, and each segment of the soil possesses uniform characteristics.
2.4. Cutting Impact Factors and Evaluation Indicators
3. Results
3.1. Analysis of the Results of the Single Factor Cutting Experiment
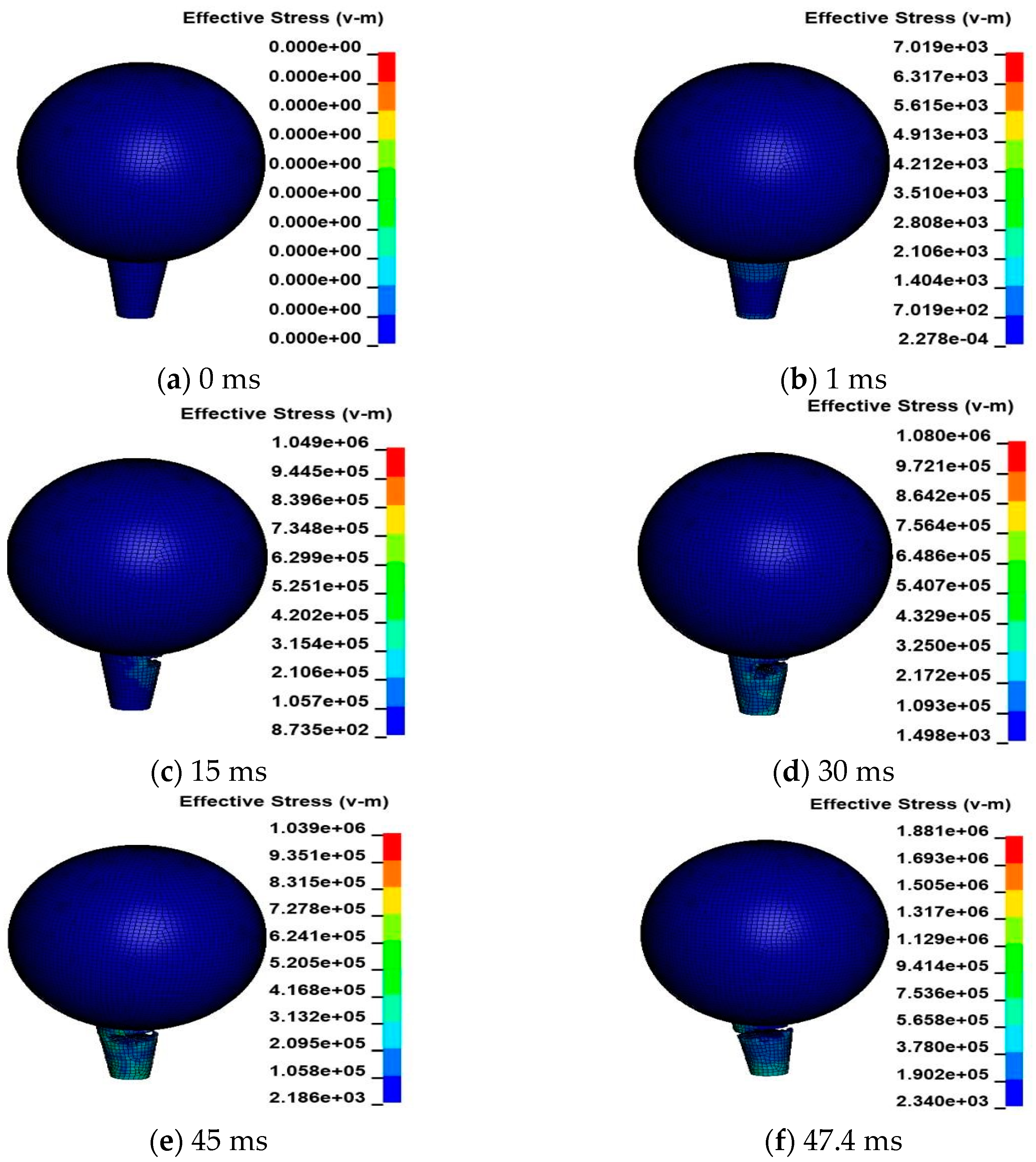
3.1.1. Simulation Analysis of the Cutting Process
3.1.2. Analysis of Power Consumption
3.2. Results and Analyses of Multifactorial Regression Cutting Experiments
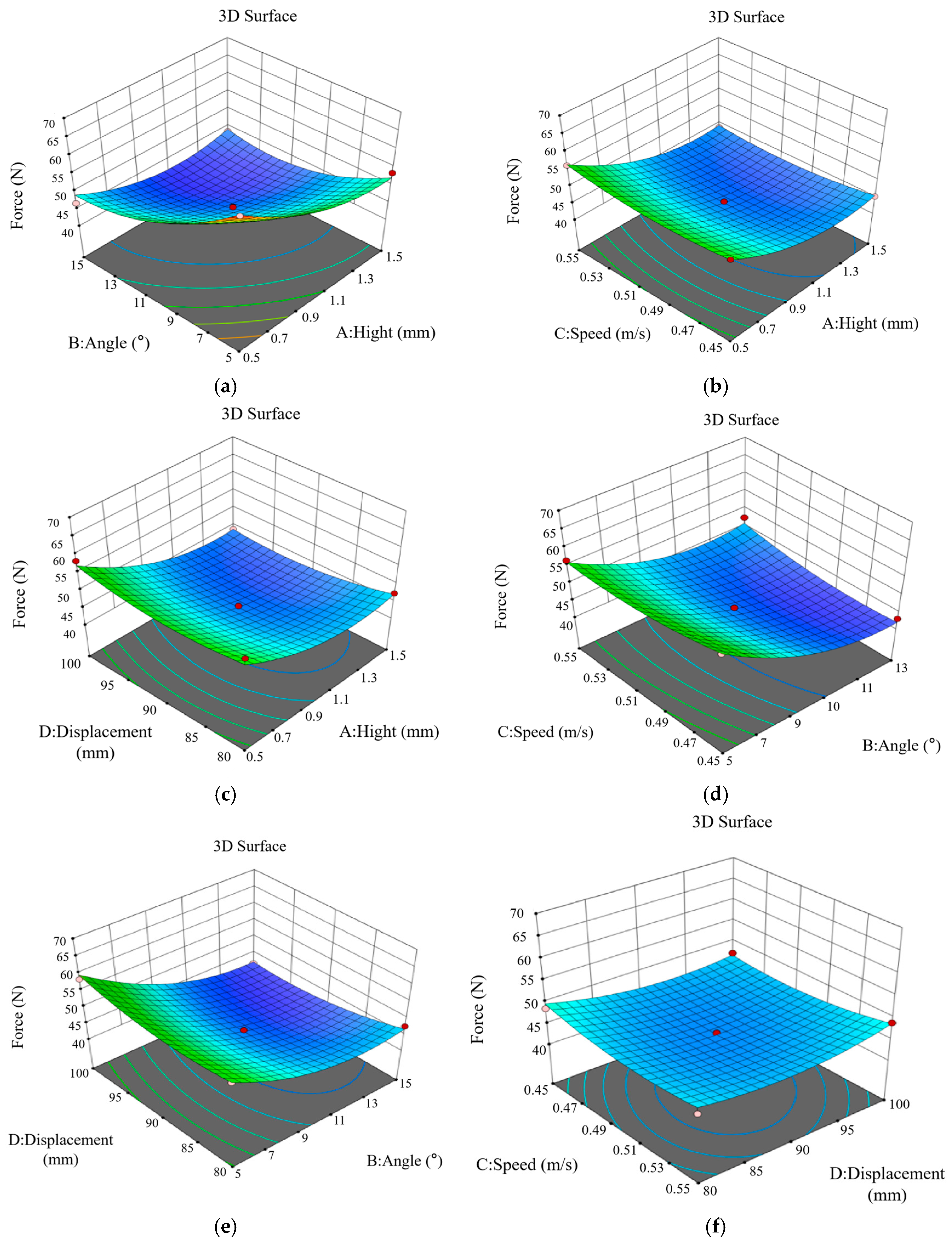
3.2.1. Analysis of Cutting Force
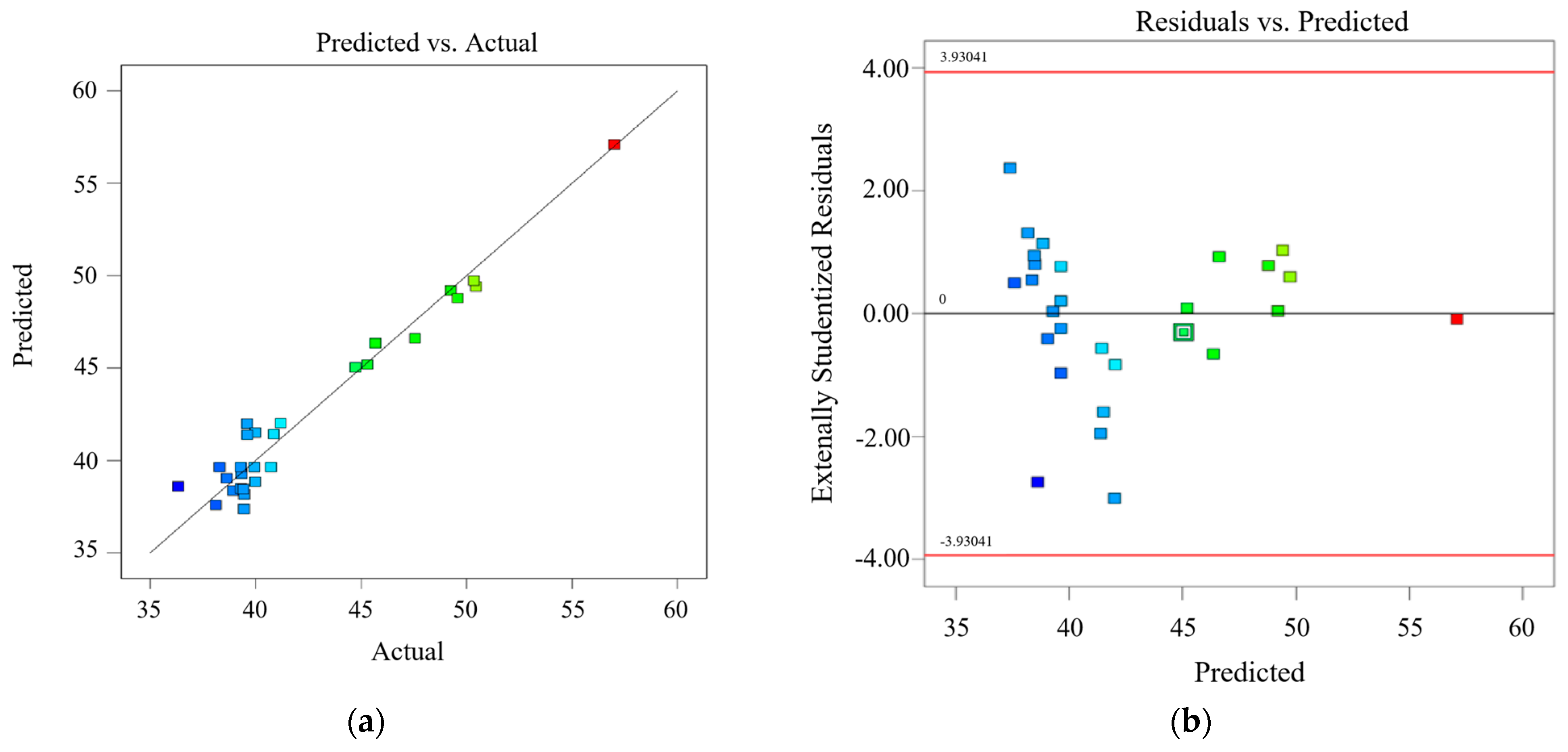
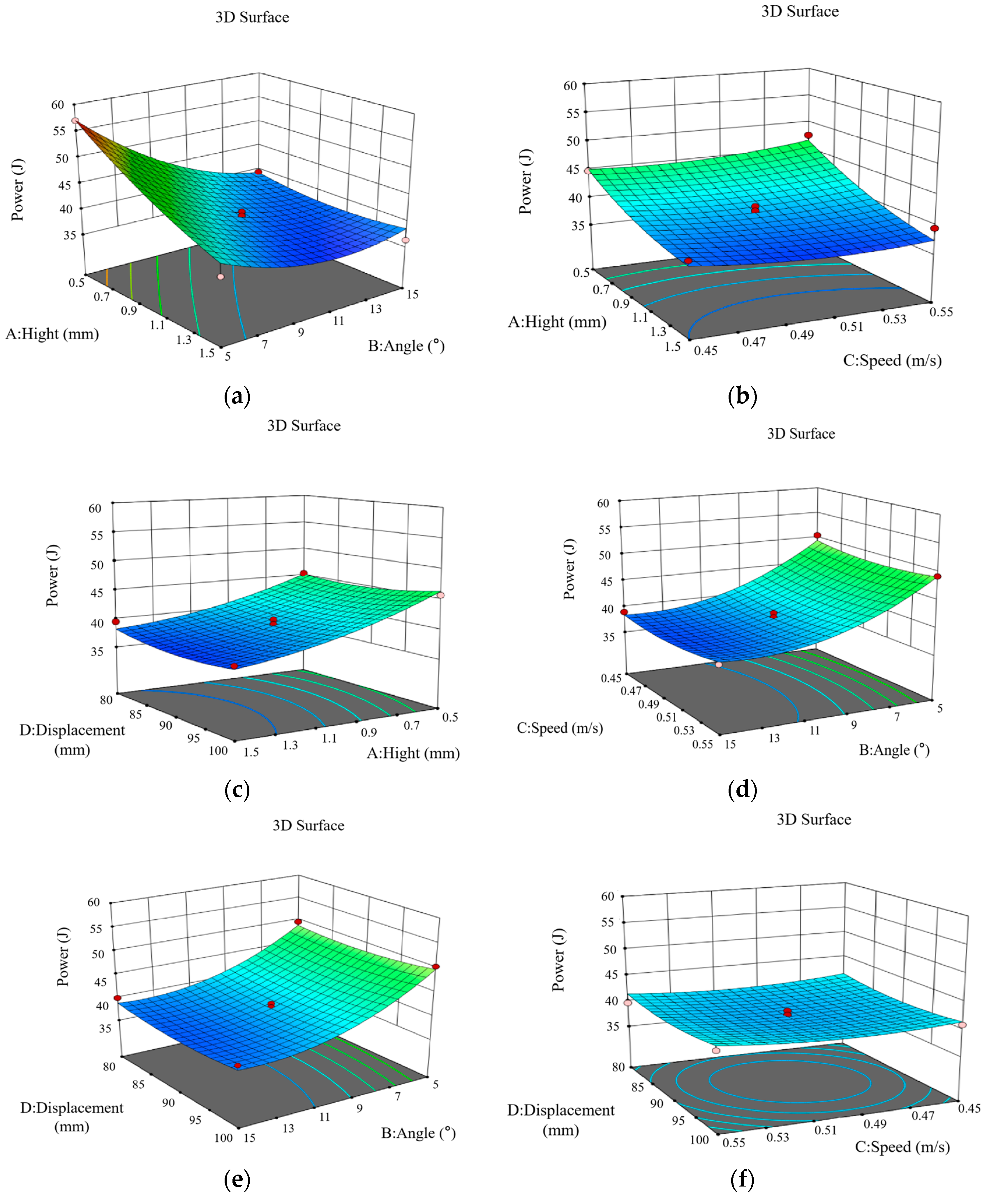
3.2.2. Analysis of Cutting Power
3.2.3. Optimization of Cutting Parameters
3.3. Experimental Verification
4. Conclusions
- (1)
- The reciprocating cutter model was developed using ANSYS/LS-DYNA (https://lsdyna.ansys.com/, accessed on 18 December 2024), with the cutting height (X1), angle of entry (X2), forward speed (X3), and single run displacement (X4) of the cutter applied to stem mustard identified as the key influencing parameters. An analysis was conducted to assess the effects of these factors on F and p, and regression equations were formulated to account for the interactions among the multiple factors. The cutting force (F) and cutting power (p) were obtained by applied derivation of regression equations were 41.4 N and 37.755 W.
- (2)
- The multifactor quadratic regression orthogonal combination testing framework was established utilizing the Box–Behnken design methodology. The software Design-Expert was employed to conduct analysis of variance and response surface analysis on the outcomes of the simulation tests, leading to the identification of optimal operational parameters for the cutting tool used on stem mustard, specifically: X1 = 1.45 mm, X2 = 12°, X3 = 0.5 m/s and X4 = 93 mm. Furthermore, an analysis of multiple sets of field experiments utilizing these optimal cutting parameter combinations revealed that the reciprocating cutting device achieved a success rate of 94% and a damage rate of only 6% during the cutting operations of stem mustard.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xue, X.L.; Zheng, H.; Ye, Y.X. Design and test of a fixed-blade sliding-cutting type squash harvester. Chin. J. Agric. Mech. Chem. 2023, 44, 48–55. [Google Scholar]
- Xiang, W.; Sun, Y.H.; Liu, F.Y.; Li, M.; Xie, S.; Ke, C.; Haung, Y. Development of sliding cutter for shortened stalk of green vegetable. Trans. Chin. Soc. Agric. Eng. 2023, 39, 266–275. [Google Scholar]
- Wang, L.B.; Ye, J.; Yang, S. Design and test of plucking and conveying mechanism of squash harvester. Agric. Mech. Res. 2018, 40, 138–141+246. [Google Scholar]
- Xue, Y.P.; Chen, J.J.; Ye, J. Research on physical and mechanical properties of stem mustards. J. Southwest Univ. 2017, 39, 147–152. [Google Scholar]
- Zheng, Z.Q.; He, J.; Li, H.W. Design and test of movable and static knife-supported slip-cutting straw crushing device. J. Agric. Mach. 2016, 47, 108–116. [Google Scholar]
- Zhou, H.; Zhang, W.L.; Yang, Q.J. Design and test of slip-cutting type self-excited vibration dampening deep pine device. J. Agric. Mach. 2019, 50, 71–78. [Google Scholar]
- Yuan, J.; Li, J.G.; Zou, L.L. Optimisation design and test of spinach harvester root cutting shovel based on discrete elements. J. Agric. Mach. 2020, 51, 85–98. [Google Scholar]
- Kang, F.; Tong, S.Y.; Zhang, H.S. Analysis and test of reciprocating cutting and pruning parameters of apple branches. J. Agric. Eng. 2020, 36, 9–16. [Google Scholar]
- Zhang, T.; Li, Y.; Song, S. Design and test of a flexible clamping based stem mustards harvester. J. Agric. Mach. 2020, 51, 162–169+190. [Google Scholar]
- Jin, Y.; Xiao, H.R.; Song, Z.Y. Design and test of walk-behind self-propelled stem mustards combine harvester. Chin. J. Agric. Mech. Chem. 2020, 41, 45–50. [Google Scholar]
- Du, D.D.; Fei, G.Q.; Wang, J.; Huang, J.; You, X. Design and test of self-propelled kale harvester. J. Agric. Eng. 2015, 31, 16–23. [Google Scholar]
- Du, D.D.; Wang, J.; Qiu, S.S. Experimental study on optimisation of cutting site and method of kale root and stem. J. Agric. Eng. 2014, 30, 34–40. [Google Scholar]
- Wang, J.W.; Guan, R.; Gao, P.X. Design and test of single disc top cutting device for carrot combine harvester. J. Agric. Mach. 2020, 51, 73–81. [Google Scholar]
- Urschel, W.E. Spinach Harvesting Machine. U.S. Patent 2,210,273, 29 April 1941. [Google Scholar]
- Shepardson, E.; Markwardt, E.; Millier, W. Mechanical harvesting of fruits and vegetables. New York’s Food Life Sci. Bull. 1970, 5, 2–12. [Google Scholar]
- Didamony, M.I.E.; Shal, A.M.E. Fabrication and Evaluation of a Cabbage Harvester Prototype. Agriculture 2020, 10, 631. [Google Scholar] [CrossRef]
- Yasmeen, Z.; Ashraf, M.; Ahmad, S.; Ahmad, M.; Sabir, I. Development and economic evaluation of carrot harvester cum trimmer. J. Agric. Res. 2023, 61, 65–76. [Google Scholar] [CrossRef]
- Li, K.; Ye, J.; Yue, G. Design and Experimental study on cutting device of vegetable head harvester. Agric. Mech. Res. 2019, 140–144. [Google Scholar] [CrossRef]




| Cutting Properties | Value | Soils | Value | Stem Mustard | Value |
|---|---|---|---|---|---|
| Material | 65 Mn | Density (kg/m3) | 1630 | Density (kg/m3) | 976 |
| Density (kg/m3) | 7850 | Shear modulus (MPa) | 7.4 | Young’s modulus X direction (MPa) | 4.1 |
| Young’s modulus (MPa) | 2 × 108 | Bulk modulus (MPa) | 16 | Young’s modulus Y direction (MPa) | 4.9 |
| Poisson’s ratio | 0.3 | Water content | 3.5% | Young’s modulus Z direction (MPa) | 3.1 |
| Friction coefficient | 0.2 | Cohesion | 1.53 × 104 | Poisson’s ratio XY | 0.38 |
| Friction angle (rad) | 0.5759 | Poisson’s ratio YZ | 0.031 | ||
| Poisson’s ratio XZ | 0.028 | ||||
| Shear modulus XY (MPa) | 3.59 | ||||
| Shear modulus YZ (MPa) | 4.09 | ||||
| Shear modulus XZ (MPa) | 2.4 |
| Factor | Coding | Horizontal Coding | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| Hight (mm) | X1 | 0.5 | 1 | 1.5 |
| Angle of entry (°) | X2 | 5 | 10 | 15 |
| Forward speed (m/s) | X3 | 0.45 | 0.5 | 0.55 |
| Single run displacement of cutter (mm) | X4 | 80 | 90 | 100 |
| No. | SS | Significance | ||||
|---|---|---|---|---|---|---|
| Cutting Height | Angle of Entry | Forward Speed | Single Run Displacement | Cutting Force | Cutting Power | |
| 1 | 1.5 | 5 | 0.5 | 90 | 53.6 | 39.593 |
| 2 | 0.5 | 10 | 0.55 | 90 | 56.3 | 47.549 |
| 3 | 1 | 15 | 0.45 | 90 | 43.1 | 38.935 |
| 4 | 1 | 10 | 0.5 | 90 | 44.6 | 39.935 |
| 5 | 0.5 | 10 | 0.45 | 90 | 55.3 | 44.733 |
| 6 | 1.5 | 10 | 0.45 | 90 | 45.2 | 39.297 |
| 7 | 1 | 10 | 0.55 | 80 | 46.2 | 39.604 |
| 8 | 0.5 | 10 | 0.5 | 80 | 57.3 | 45.299 |
| 9 | 1 | 10 | 0.5 | 90 | 44.7 | 38.294 |
| 10 | 1 | 5 | 0.55 | 90 | 56.6 | 49.253 |
| 11 | 1 | 10 | 0.45 | 80 | 48.6 | 39.988 |
| 12 | 1 | 15 | 0.55 | 90 | 47.3 | 38.626 |
| 13 | 1 | 5 | 0.5 | 80 | 56.9 | 49.577 |
| 14 | 0.5 | 5 | 0.5 | 80 | 68.7 | 57.008 |
| 15 | 1 | 5 | 0.5 | 100 | 58.4 | 50.349 |
| 16 | 1 | 10 | 0.5 | 90 | 44.6 | 39.297 |
| 17 | 0.5 | 15 | 0.5 | 90 | 46.7 | 39.33 |
| 18 | 1.5 | 15 | 0.5 | 90 | 43.3 | 36.332 |
| 19 | 1 | 10 | 0.45 | 100 | 47 | 40.86 |
| 20 | 1.5 | 10 | 0.5 | 80 | 47.4 | 39.457 |
| 21 | 1 | 10 | 0.5 | 90 | 44.6 | 40.725 |
| 22 | 1.5 | 10 | 0.55 | 90 | 43.6 | 39.446 |
| 23 | 0.5 | 10 | 0.5 | 100 | 58.4 | 45.679 |
| 24 | 1 | 15 | 0.5 | 80 | 47.6 | 39.98 |
| 25 | 1 | 10 | 0.55 | 100 | 48.9 | 41.187 |
| 26 | 1 | 10 | 0.5 | 90 | 42.6 | 39.944 |
| 27 | 1.5 | 10 | 0.5 | 100 | 43.6 | 38.108 |
| 28 | 1 | 5 | 0.45 | 90 | 59.5 | 50.448 |
| 29 | 1 | 15 | 0.5 | 100 | 41.4 | 39.415 |
| Source | Sum of Squares (SS) | Degrees of Freedom (DF) | Mean Square (MS) | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Model | 1275.74 | 14 | 91.12 | 46.61 | <0.0001 | significance |
| X1 | 363 | 1 | 363 | 185.67 | <0.0001 | |
| X2 | 592.21 | 1 | 592.21 | 302.91 | <0.0001 | |
| X3 | 0.0033 | 1 | 0.0033 | 0.0017 | 0.9676 | |
| X4 | 3.31 | 1 | 3.31 | 1.69 | 0.2144 | |
| X1X2 | 34.22 | 1 | 34.22 | 17.5 | 0.0009 | |
| X1X3 | 1.69 | 1 | 1.69 | 0.8644 | 0.3683 | |
| X1X4 | 6 | 1 | 6 | 3.07 | 0.1016 | |
| X2X3 | 12.6 | 1 | 12.6 | 6.45 | 0.0236 | |
| X2X4 | 14.82 | 1 | 14.82 | 7.58 | 0.0115 | |
| X3X4 | 4.62 | 1 | 4.62 | 2.36 | 0.1464 | |
| X12 | 128.11 | 1 | 128.11 | 65.53 | <0.0001 | |
| X22 | 156.16 | 1 | 156.16 | 79.88 | <0.0001 | |
| X32 | 19.7 | 1 | 19.7 | 9.81 | 0.0074 | |
| X42 | 32.30 | 1 | 32.30 | 16.52 | 0.0012 | |
| Residual | 27.37 | 14 | 1.96 | |||
| Lack of Fit | 24.08 | 10 | 2.41 | 2.93 | 0.1559 | not significance |
| Pure Error | 3.29 | 4 | 0.8220 | |||
| Cor Total | 1303.11 | 28 |
| Source | SS | DF | MS | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Model | 656.53 | 14 | 46.89 | 19.42 | <0.0001 | significance |
| X1-hight | 186.95 | 1 | 186.95 | 77.43 | <0.0001 | |
| X2-angle | 337.19 | 1 | 337.19 | 139.66 | <0.0001 | |
| X3-speed | 0.1643 | 1 | 0.1643 | 0.0680 | 0.7980 | |
| X4-frequency | 0.2389 | 1 | 0.2389 | 0.0989 | 0.7578 | |
| X1X2 | 51.96 | 1 | 51.96 | 21.52 | 0.0004 | |
| X1X3 | 1.78 | 1 | 1.78 | 0.7365 | 0.4052 | |
| X1X4 | 0.7474 | 1 | 0.7474 | 0.3095 | 0.5867 | |
| X2X3 | 0.1962 | 1 | 0.1962 | 0.0813 | 0.7797 | |
| X2X4 | 0.4469 | 1 | 0.4469 | 0.1851 | 0.6736 | |
| X3X4 | 0.1264 | 1 | 0.1264 | 0.0523 | 0.8223 | |
| X12 | 9.98 | 1 | 9.98 | 4.13 | 0.0614 | |
| X22 | 73.55 | 1 | 73.55 | 30.46 | <0.0001 | |
| X32 | 6.52 | 1 | 6.52 | 2.70 | 0.1226 | |
| X42 | 5.85 | 1 | 5.85 | 2.42 | 0.1419 | |
| Residual | 33.80 | 14 | 2.41 | |||
| Lack of Fit | 30.51 | 10 | 3.05 | 3.71 | 0.1008 | not significance |
| Pure Error | 3.29 | 4 | 0.8215 | |||
| Cor Total | 690.33 | 28 |
| Item | Evaluation Indicators | |
|---|---|---|
| Cutting Force (N) | Cutting Power (W) | |
| Theoretical optimization value | 41.4 | 36.756 |
| Simulation value | 41.5 | 38.046 |
| Relative error (%) | 0.24 | 3.39 |
| Experimental Group | Number of Stem Mustards | Cutting Success Rate | Cutting Damage Rate |
|---|---|---|---|
| 1 | 50 | 92% | 12% |
| 2 | 50 | 88% | 6% |
| 3 | 50 | 80% | 10% |
| 4 | 50 | 94% | 8% |
| 5 | 50 | 86% | 8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Zhang, L.; Wu, Y.; Shao, W.; Liu, W.; Li, B.; Zeng, Z.; Pang, Y. Design and Optimization of Stem Mustard Cutting Device Based on Response Surface Methodology (RSM). Processes 2025, 13, 845. https://doi.org/10.3390/pr13030845
Song S, Zhang L, Wu Y, Shao W, Liu W, Li B, Zeng Z, Pang Y. Design and Optimization of Stem Mustard Cutting Device Based on Response Surface Methodology (RSM). Processes. 2025; 13(3):845. https://doi.org/10.3390/pr13030845
Chicago/Turabian StyleSong, Shumin, Lei Zhang, Yu Wu, Weixing Shao, Wenshu Liu, Bin Li, Zhiheng Zeng, and Youlun Pang. 2025. "Design and Optimization of Stem Mustard Cutting Device Based on Response Surface Methodology (RSM)" Processes 13, no. 3: 845. https://doi.org/10.3390/pr13030845
APA StyleSong, S., Zhang, L., Wu, Y., Shao, W., Liu, W., Li, B., Zeng, Z., & Pang, Y. (2025). Design and Optimization of Stem Mustard Cutting Device Based on Response Surface Methodology (RSM). Processes, 13(3), 845. https://doi.org/10.3390/pr13030845








