Enhanced Local Search for Bee Colony Optimization in Economic Dispatch with Smooth Cost Functions

Abstract

This study introduces an Enhanced Local Search (ELS) technique integrated into the Bee Colony Optimization (BCO) algorithm to address the Economic Dispatch (ED) problem characterized by a continuous cost function. This paper combines Lambda Iteration and Golden Section Search with Bee Colony Optimization (BCO) into a more efficient method called Enhanced Local Search for Bee Colony Optimization (ELS-BCO). The proposed methodology seeks to enhance search efficiency and solution quality. One of the main challenges with standard BCO is random initialization, which can lead to slow convergence. The ELS-BCO algorithm overcomes this issue by using Lambda Iteration for better initial estimation and Golden Section Search to refine the movement direction of the bees. These enhancements significantly improve the algorithm’s capacity to identify optimal solutions. The performance of ELS-BCO was evaluated on two benchmark systems with three and six power generators, and the results were compared with those of the original BCO, LI-BCO, GS-BCO, and traditional optimization methods such as Particle Swarm Optimization (PSO), Hybrid PSO, Lambda Iteration with Simulated Annealing, the Sine Cosine Algorithm, Mountaineering Team-Based Optimization, and Teaching–Learning-Based Optimization. The results demonstrate that ELS-BCO achieves faster convergence and higher-quality solutions than these existing methods.

1. Introduction

Economic dispatch plays a critical role in reducing the operational expenses of power plants by minimizing fuel costs for generators, which is confirmed by economic principles, research studies, mathematical simulations, and practical applications in the power industry. Effective power system management necessitates the resolution of the economic dispatch problem, which aims to optimize energy production costs while considering transmission line losses and ensuring that both equality and inequality constraints are met. Investigating the economic dispatch problem is essential, as it offers a pathway to significant reductions in operating costs.

Various classical methods, including quadratic programming [1], lambda iteration [2], gradient methods [3], Lagrangian relaxation [4], dynamic programming [5], and linear programming [6], have been utilized in ED situations. Nevertheless, these approaches often struggle with finding global optimal solutions and are prone to becoming trapped in local optima. To address these shortcomings, metaheuristic optimization techniques have gained popularity, providing a more robust framework for solving ED challenges in power systems.

Notable metaheuristic methods include Tabu search (TS) [7], which leverages memory to avoid revisiting previously explored solutions, and simulated annealing (SA) [8,9], which explores new solutions by simulating a cooling process to escape local minima. The Cuckoo Search Algorithm (CSA) [10,11], inspired by the brood parasitism of cuckoos, and the Shuffled Frog Leaping Algorithm (SFLA) [12,13], modeled on frogs searching for food, have also been applied. Other algorithms like the Genetic Algorithm (GA) [14,15], which follows Darwin’s theory of natural selection, and Ant Colony Optimization (ACO) [16,17], which is based on ant foraging behavior, have shown promise. Particle Swarm Optimization (PSO) [18,19,20,21], which mimics social behavior in animal groups, and Bee Colony Optimization (BCO) [22,23,24], which replicates bee swarm behavior, are also widely used for ED problems.

While these algorithms have existed for decades, newer algorithms like Adaptive Fitness–Distance Balance-based Artificial Rabbits Optimization (AFDB-ARO) [25], Artificial Ecosystem Optimization (AEO) [26], and the Social Optimization Algorithm (SOA) [27] have introduced innovative strategies to improve performance. These approaches excel in achieving global optimization while balancing solution quality and speed.

Among metaheuristic approaches, BCO has gained prominence owing to its adaptive search mechanism and global optimization efficacy. Inspired by the foraging activity of honeybees, BCO effectively balances exploration and exploitation, rendering it a promising method for addressing ED problems. Notwithstanding its benefits, typical BCO encounters considerable constraints, including sluggish convergence, suboptimal initial solution quality, and challenges in managing real-world limitations such as ramp–rate restrictions and forbidden operating zones. Rectifying these deficiencies is essential for enhancing the efficacy and relevance of BCO in power system optimization. As a result, enhancing convergence and avoiding local optima have become critical goals in BCO research, leading to numerous BCO variants [28,29,30,31].

Aurasopon and Khamsen [32] introduced an improved BCO method by integrating lambda iteration and golden section search to enhance the search efficiency to address the ED problem within fundamental generation constraints. Their approach, known as ILS-BCO, showed significant improvements in both convergence speed and solution quality when applied to systems with smooth cost functions and basic generation limits. However, real-world power systems frequently operate under more complex constraints, such as ramp–rate limits and prohibited operating zones (POZs), which are essential for maintaining system stability and meeting operational regulations. Ramp–rate limits restrict the rate at which power output can change, while POZs define operationally forbidden regions for certain generation units.

In this paper, we propose an ELS-BCO algorithm, which builds upon the work of Aurasopon and Khamsen [32]. The motivation behind this study is to enhance the performance of BCO in solving the ED problem, thus addressing these more complex constraints. While ELS-BCO incorporates lambda iteration and golden section search, it is uniquely designed to handle both ramp–rate limits and prohibited operating zones, making it more applicable to practical, real-world ED scenarios. The method is tested on systems with both smooth cost functions and dynamic constraints, demonstrating that ELS-BCO achieves faster convergence and higher-quality solutions in these challenging environments. Specifically, we hypothesize that integrating Lambda Iteration and the Golden Section Search method into BCO will enhance optimization efficiency by reducing search randomness and improving local search performance. To validate this hypothesis, ELS-BCO was evaluated against benchmark algorithms under various test scenarios, ensuring a comprehensive performance assessment.

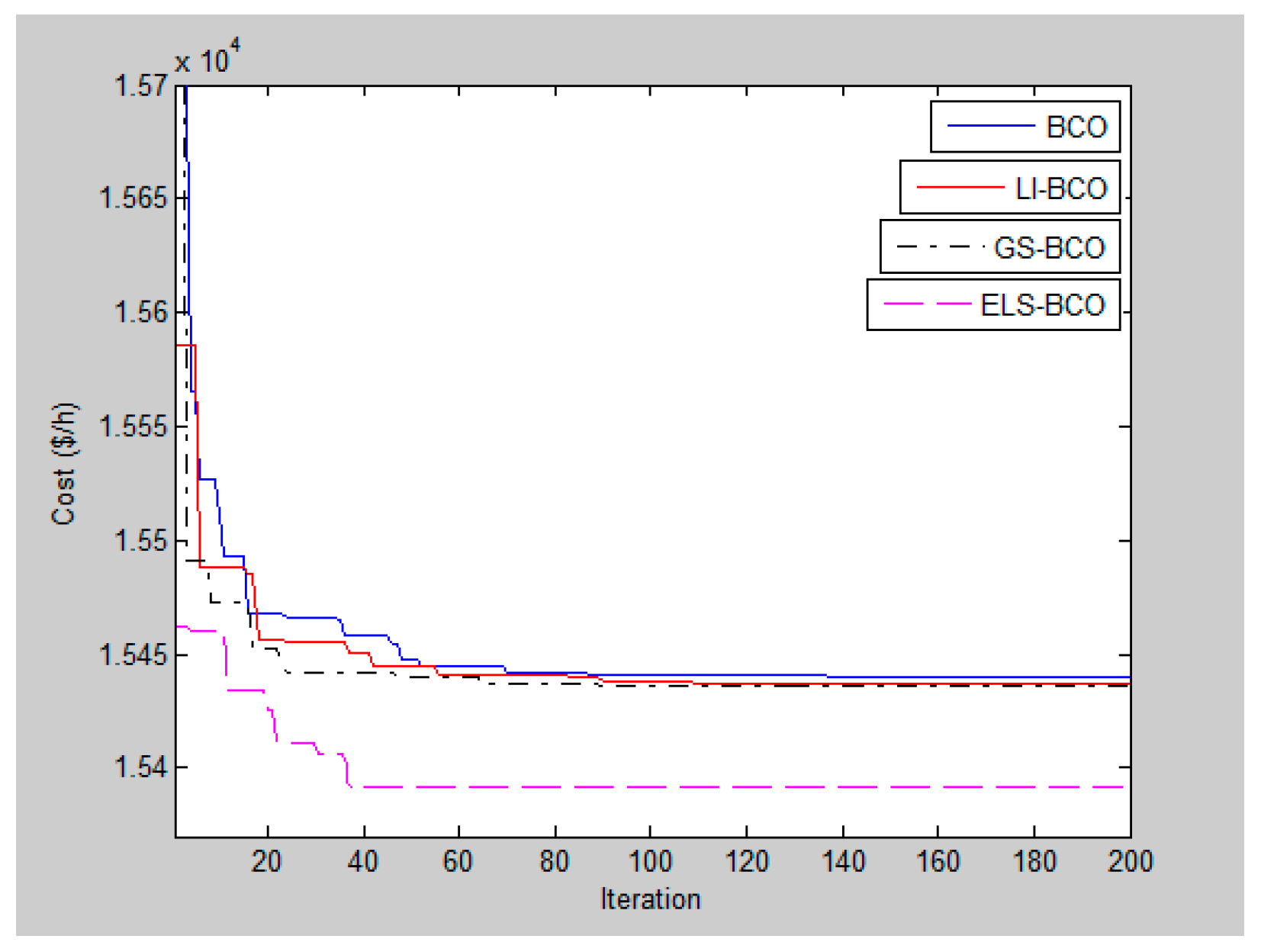
Two case studies on ED were undertaken to evaluate the efficacy of ELS-BCO. The initial study examined a continuous cost function, whereas the subsequent one included ramp–rate constraints and restricted working regions. The outcomes were juxtaposed with various standard algorithms, such as PSO, Hybrid PSO, Multiple Hybrids of Lambda Iteration and Simulated Annealing (MHLSA), the Sine Cosine Algorithm (SCA), Mountaineering Team-Based Optimization (MTBO), and Teaching–Learning-Based Optimization (TLBO). The comparisons demonstrated that ELS-BCO surpasses these methods in identifying optimal solutions and attaining quicker convergence. This document is structured as follows: Section 2 provides a summary of the economic dispatch issue. Section 3 and Section 4 examine the improved local search within the Bee Colony Optimization technique and its implementation in the economic dispatch problem. Section 5 presents the simulation results and analysis, confirming the efficacy of the proposed strategy, with conclusions provided in the last section.

2. Economic Dispatch Problem Formula

The objective of the ED problem is to calculate the total power output of all generators to meet the energy demand at any given time. This involves allocating the load across the system to efficiently operate a set of generators within a given time frame. The process must comply with both physical constraints and operational requirements. The following variables are essential to the system’s conditions.

2.1. Objective Function

The principal aim of the ED problem is to reduce fuel expenses while complying with the operating limits of the power production system. The following equation represents this purpose:

$$\mathrm{Minimize}: F_T={\sum }_{i=1}^N{F}_i\left(P_i\right)$$

(1)

where $F_T$ denotes the total generation cost, N signifies the number of generators, and $F_i$ indicates the cost of power generation for the $i^{th}$ generator. The cost function for each generator is generally represented as a quadratic polynomial defined by:

$$F_i\left(P_i\right)=a_i{P}_i^2+b_i{P}_i+c_i$$

(2)

where $a_i$, $b_i$, and $c_i$ represent the coefficients of the quadratic equation, and $P_i$ denotes the power output of the $i^{th}$ generator. This mathematical expression represents the smooth cost function and delineates the correlation between power output and generation costs. To approximate the input–output characteristics of generators or their cost functions, the projected unit incremental cost curve is often linearized, with incremental cost values increasing in small, uniform steps. This approximation simplifies the optimization process while capturing the essential behavior of the cost function.

2.2. Constraints

2.2.1. Power Balance Constraint

In Equation (3), the total load capacity is defined as the combined total of electricity demand and transmission system energy losses, as follows:

$${\sum }_{i=1}^N\left(P_i\right)=P_D+P_{loss}$$

(3)

where $P_D$ signifies the load demand, while$P_{loss}$ indicates the overall losses in the transmission lines. Both variables are contingent upon the power output of each unit and can be articulated using B coefficients as follows:

$$P_{loss}={\sum }_{i=1}^N{\sum }_{j=1}^N{P}_i{B}_{ij}{P}_j+{\sum }_{j=1}^N{B}_{0i}{P}_i+B_{00}$$

(4)

2.2.2. Generator Rating Constraint

The power output of each generating unit must lie within a specified range, as shown by the following two inequality constraints:

$$P_i^{min}\le P_i\le +P_i^{max}$$

(5)

where $P_i^{min}$ and $P_i^{max}$ denote the minimum and maximum power outputs of the generating unit, respectively, and $P_i$ represents the actual power output of that unit.

2.2.3. Ramp–Rate Limits and Prohibited Operating Zone

Mechanical inertia in thermal units restricts how quickly the output power can change. As a result, decisions made in the present impact future decisions due to changing power demands over time. The operation of the units results in two possible scenarios—an increase or decrease in generation. These conditions are expressed by the following equations:

$$P_i-P_i^o\le +U{R}_i$$

(6)

$$P_i^o-P_i\le +D{R}_i$$

(7)

In these equations, $P_i^o$ denotes the output power of the generating unit in the prior phase, while $D{R}_i$ and $U{R}_i$ represent the decrease and increase boundary values, respectively. Based on this, the operational capability of the generators within these constraints is defined as:

$$\max (P_i^{min},P_i^o-D{R}_i)\le P_i\le min{(P}_i^{max},P_i^o+U{R}_i)$$

(8)

Thermal power generators’ efficiency is limited in prohibited operating zones due to steam valve malfunctions during these intervals. Consequently, the generators should avoid operating during this time. Therefore, economic dispatch issues involving prohibited operating zones and unit operational boundary values are resolved as shown in the following equation:

$$P_i=\left\{\begin{array}{c}{P}_i^{min}\le P_i\le P_{i,1}^l\\ P_{i,j-1}^u\le P_i\le P_{i,j}^l \\ P_{i,n}^u\le P_i\le P_{i,1}^{max}\end{array}\right. j=2,3,\dots ,n_i$$

(9)

3. Enhanced Local Search of Bee Colony Optimization

In ELS-BCO, methods from the lambda iteration and golden section ratio techniques are combined to form a novel search strategy. Based on the concept of equal cost lambda (λ), this approach provides an initial estimate, defines the boundary limits around λ values, and improves bee movement using the golden section method, which is a local search strategy. The objective is to attain equilibrium between exploration and the identification of food venues. Each step in this process is performed according to the BCO method. The following sections will detail the ELS-BCO approaches to solving the ED problem.

3.1. Economic Dispatch Problem with Bee Colony Optimization

The BCO algorithm, developed by Karaboga [33], was influenced by the natural foraging behavior of honeybees. Much like bees searching for flowers to collect food, the BCO algorithm mimics this process to efficiently find optimal dispatch values in the economic dispatch problem. In nature, bees are categorized into the following two primary groups: scout bees and worker bees. Scout bees randomly investigate new areas to identify prospective food sources, while worker bees collect food from these identified spots. When scout bees find flowers rich in pollen, they return to the hive and use distinct dances to communicate the quantity and location of the food. This communication system enables worker bees to relocate to better food sources. The number of worker bees varies depending on the distance and richness of the nectar at the discovered sites.

The BCO algorithm is structured around the following parameters:

• n: the aggregate quantity of scout bees,
• m: the quantity of nectar sources identified by the scouts
• e: the count of top nectar sources identified
• nep: the quantity of worker bees assigned to the top e nectar sources
• nsp: the quantity of worker bees randomly assigned to the remaining m-e sources

The BCO algorithm follows a defined process, outlined in the following steps:

Step 1: Establish the parameters for the BCO algorithm.

Step 2: Initially, allocate the scout bees (n) randomly across the search field. The placement of each bee must adhere to the specified regulation formula:

$$P_i=P_{i,min}+\left(\right(P_{i,max}-P_{i,min})\times rand(\mathrm{0,1})$$

(10)

Step 3: Scout bees evaluate the suitability of the locations they visit and rank them from highest to lowest efficiency.

Step 4: Select the top m solutions out of the total n solutions.

Step 5: Among the selected m solutions, choose the e best ones. Divide the remaining m-e solutions into two groups: One group contains the e best solutions, while the other includes the remaining m-e solutions.

Step 6: Based on the results from Step 5, there are two types of food sources—

e and m-e. Worker bees in the nep group search in the vicinity of the e sources, while those in the nsp group search around the m-e sources. Worker bees use the first food source $x_i$ to locate the next food source $v_i$ using the following formula:

$$v_i=x_i+{\mathsf{\varphi }}_i\times (x_k-x_i)$$

(11)

Here, $x_k$ represents a food source randomly chosen from the population, and ${\varphi }_i$ is a uniformly distributed random variable inside the interval [−1, 1], produced for each iteration.

Step 7: Assess the quality of the results and perform a comparative analysis of each component. Decide on the most appropriate approach or solution based on the current conditions and parameters.

Step 8: Determine if the solution meets the minimum requirements. If so, present the best option; otherwise, return to Step 2.

3.2. Lambda Iteration

Lambda Iteration is a technique employed in power generation systems to reduce total generation expenses while satisfying power demand. It entails calibrating the power output of several generators so that the incremental cost of generating an additional unit of power is uniform among all operational generators. The marginal cost is denoted by Lambda (λ) and is ascertained by an iterative procedure. An initial estimate of λ is assumed, and the power output of each generator is then changed based on this value. Upon modifying the generating capacity, the whole cost is assessed, and the value of λ is re-evaluated. The procedure is reiterated until the system attains equilibrium, characterized by equal marginal costs across all generators and reduced overall costs. Through Lambda Iteration, the system guarantees power generation at minimal cost by assigning greater output to lower-cost generators and reduced output to higher-cost generators. The fuel expense for power production of each generator can be calculated using Equation (2). The additional cost is determined by the subsequent differential equation:

$${\displaystyle \frac{d\left(F_i\left(P_i\right)\right)}{d\left(P_i\right)}}=\lambda$$

(12)

When λ is consistent across all generators, the total fuel cost is minimized. The initial λ value for the system can be calculated using:

$$\lambda ={\displaystyle \frac{P_D+\sum _{i=1}^N\frac{b_i}{2a_i}}{\sum _{i=1}^N\frac{1}{2a_i}}}$$

(13)

The amount of electric power generated by each generator can then be calculated using:

$$P_i={\displaystyle \frac{\lambda -b_i}{2a_i}}$$

(14)

3.3. Golden Section Ratio

The golden section ratio is a technique that progressively reduces the range of values to determine the extreme (either the minimum or maximum) of a strictly unimodal function. This technique refines the search range iteratively by evaluating function values at points that maintain a golden ratio between their distances. Named for this property, the method was introduced by Kiefer in 1953 [34]. It is regarded as a traditional local search technique, especially efficient for non-differentiable fitness functions.

The golden section ratio approach is utilized to ascertain the best scale factor within a defined range. Specifically, for a range [a, b] with initial values set at −1 and 1, the method generates two intermediate points:

$$F_1=b-{\displaystyle \frac{b-a}{\delta }}$$

(15)

$$F_2=a-{\displaystyle \frac{b-a}{\delta }}$$

(16)

where $\delta$ is the golden section ratio, defined as:

$$\delta ={\displaystyle \frac{1+\sqrt{5}}{2}}$$

(17)

The values ${f(F}_1)$ and ${f(F}_2)$ are evaluated. If ${f(F}_2)$ is greater than ${f(F}_1)$, $F_2$ is replaced with $F_1$, and the process is repeated with a more refined interval [a, b]. This iterative approach helps to accurately calculate the upper and lower boundaries of the scaling factor.

3.4. Solving the Economic Dispatch Problem Using Lambda Iteration and Bee Colony Optimization

The Bee Colony Optimization (BCO) algorithm is augmented by incorporating the Lambda Iteration technique to boost its efficacy in addressing the Economic Dispatch (ED) problem. A primary disadvantage of traditional BCO is its dependence on random initialization, which may result in sluggish convergence and unsatisfactory outcomes. Lambda Iteration alleviates this problem by offering a well-informed preliminary calculation of the power generation distribution, so ensuring that the search process commences in a favorable area of the solution space. Incorporating Lambda Iteration provides multiple advantages to BCO. Compared to the Enhanced Preliminary Solution, rather than commencing with a wholly arbitrary distribution of solutions, Lambda Iteration computes an initial estimate derived from the system’s cost function and power balance restrictions. Accelerated Convergence, as the starting answer, is nearer to the ideal region, and the method necessitates fewer iterations to attain the best solution. Enhanced Solution Quality with integration of Lambda Iteration and BCO mitigates the likelihood of entrapment in local optima, resulting in enhanced accuracy and stability of outcomes. The hybrid methodology, designated as Lambda Iteration-Based Bee Colony Optimization (LI-BCO), improves the optimization process by utilizing the advantages of both techniques—the global search efficacy of BCO and the accurate assessment of Lambda Iteration. The procedure is as follows:

Step 1: Establish the settings for the LI-BCO algorithm.

Step 2: Compute the initial value of λ for the scout bees’ system setup utilizing Equation (13).

Step 3: Define the upper and lower limits for the $i^{th}$ generating unit by delineating the range λ as follows:

$$P_i^{max}={\displaystyle \frac{\lambda -b_i}{c_i}}+\left[{\displaystyle \frac{\lambda -b_i}{c_i}}\times rank\right]$$

(18)

$$P_i^{min}={\displaystyle \frac{\lambda -b_i}{c_i}}-\left[{\displaystyle \frac{\lambda -b_i}{c_i}}\times rank\right]$$

(19)

where ‘rank’ is a factor that defines the magnitude of the reaction, with a value between zero and one. Based on various tests, a rank value of 0.15 is specified.

Step 4: Implement the BCO algorithm, repeating Steps 2 through 8 as described previously.

By integrating the Lambda Iteration technique with BCO, the initial values and bounds are better aligned with the optimal solution, enhancing the algorithm’s efficiency and convergence rate.

3.5. The Golden Section Ratio with Bee Colony Optimization Solves the Economic Dispatch Problem

Follow the steps of the BCO algorithm outlined in Section 3.1 from step 1 to step 5.

Step 6: Enhance the search for food sources by using the worker bees to explore additional solutions. This is performed using the formula:

$$v_i=x_i+F(x_k-x_i)$$

(20)

where F represents the scaling factor ascertained by the golden section ratio approach. Assess and retain the optimal solution determined by this methodology. The process of generating new food sources is influenced by the scaling factor F, as well as the values of a and b. It is crucial to carefully choose the scaling factor to ensure the creation of high-quality solutions that will benefit future generations. After this, repeat Steps 7 and 8 of the BCO method.

4. Enhancing the Local Search of Bee Colony Optimization to Solve the Economic Dispatch Problem

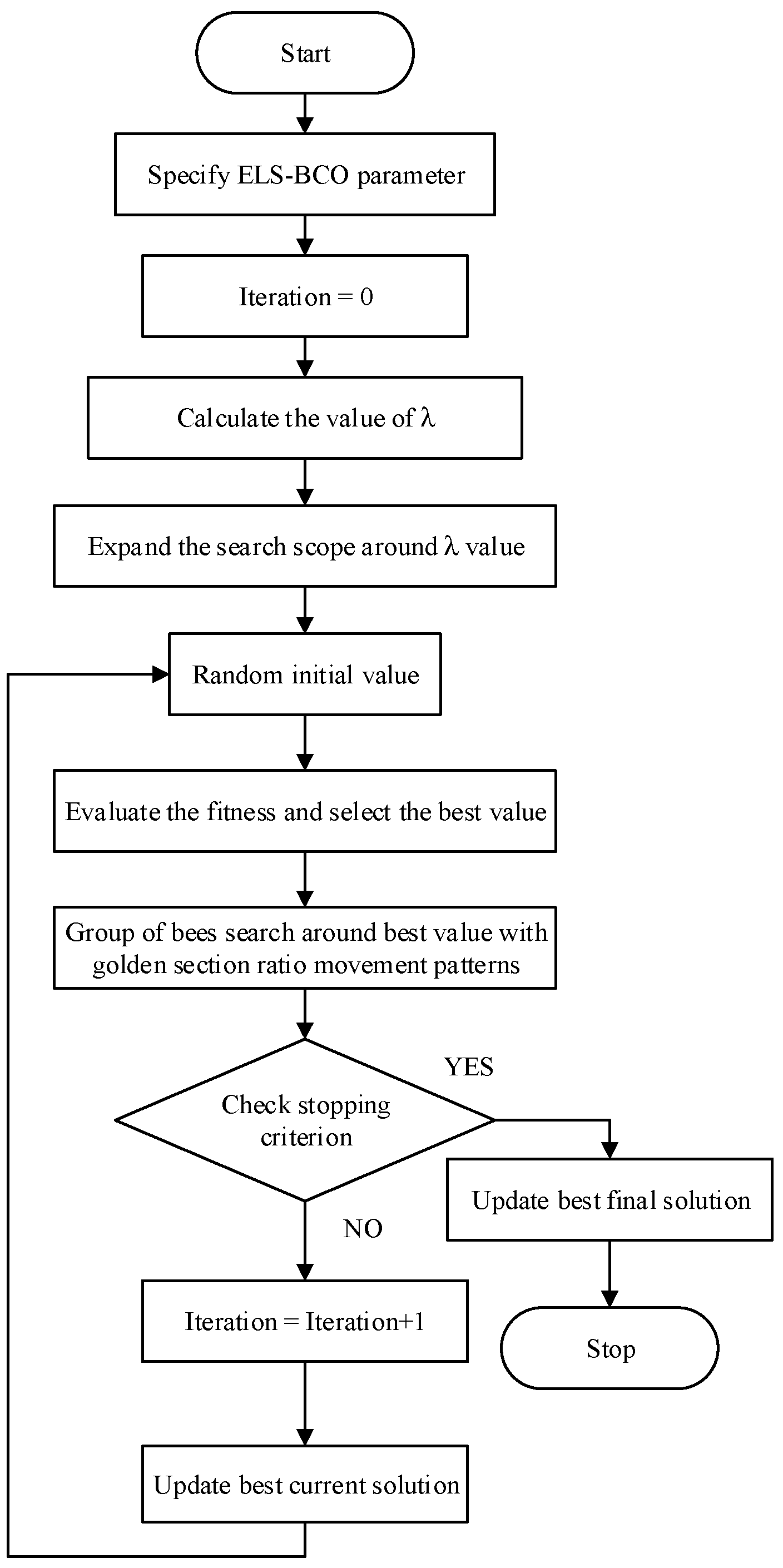
The ELS-BCO approach is designed to augment the local search efficiency of the BCO algorithm and enhance its exploitation capabilities. It incorporates several key strategies, including lambda iteration for better initial population estimation, narrowing the search scope, and the golden section ratio to optimize bee movement. Figure 1 depicts the flowchart of the proposed ELS-BCO method.

The following steps detail the ELS-BCO approach for addressing the economic dispatch (ED) problem:

Step 1: Configure the settings for the ELS-BCO algorithm as delineated in

Table 1. The parameters utilized in ELS-BCO.

Parameters	Number
Initial population density of bees (n)	30
The number of top-notch picks (m)	20
The total number of top destinations (e)	10
The number of bees found in the areas with the best locations (nep)	30
The number of bees found in and around various locations (nsp)	30

. The parameters, refined via experimentation, encompass values for n, m, e, nep, and nsp. The suggested ranges for these values are:

• n and m: 5 to 50
• e: 3 to 30
• nep and nsp: 10 to 100

The optimal settings for achieving the best results with minimal iterations and repetitions are detailed in Table 1.

Step 2: Determine the initial lambda (λ) value for the scout bees’ system configuration utilizing Equation (14).

Step 3: Ascertain the minimum and maximum values for the $i^{th}$-generating unit based on the range of λ given in Equations (18) and (19).

Step 4: Initialize the BCO algorithm with a random distribution of scout bees (n) across the search space, ensuring compliance with the system’s regulatory constraints.

Step 5: Assess the suitability of the sites explored by the scout bees and rank them based on fitness, from highest to lowest.

Step 6: Select the top m solutions from the n options and arrange them in descending order of fitness.

Step 7: Select the optimal solution from the top m solutions for the quantity e. Divide these into two groups—one consisting of the e optimal solutions and the other comprising the residual m-e solutions.

Step 8: Deploy nep worker bees to search around the e solutions and nsp worker bees to explore the m-e solutions. Improve their movements using the golden section ratio method, as explained in Equation (20).

Step 9: Evaluate the options and contrast each element to identify the optimal strategy that satisfies the requirements.

Step 10: Verify the downtime threshold. Should the conditions be satisfied, provide the ideal solution; otherwise, revert to Step 4.

To ensure a fair comparison, the parameter settings for ELS-BCO and benchmark algorithms were carefully selected based on prior research and empirical tuning. The key parameters for ELS-BCO, such as the numbers of scout bees, employed bees, and onlooker bees, were optimized through preliminary sensitivity analysis. A grid search approach was used to determine the optimal values, minimizing convergence time while maintaining solution quality. Additionally, multiple experimental runs were conducted to assess the stability of parameter selection, ensuring robustness across different test cases.

5. Results and Discussion

5.1. Case Studies

The ELS-BCO approach was tested in two unique scenarios, one of which addressed the economic dispatch problem with forbidden operation zones. The case studies included systems with varying configurations—a three-unit arrangement and a six-unit arrangement. All optimization methods were conducted in MATLAB 2024a on an Intel Core i5 CPU operating at 2.30 GHz with 8 GB of RAM.

5.1.1. First Case Study

The initial case study analyzed the IEEE 6-Bus, 3-generator system, which has ramp–rate constraints and a prohibited zone. The primary emphasis was on a system with a 300 MW load requirement. System parameters are detailed in

Table 2. Generator data for case 1.

Unit	ai	bi	ci	${\mathit{P}}_{\mathit{i}}^{\mathit{m}\mathit{i}\mathit{n}}$	${\mathit{P}}_{\mathit{i}}^{\mathit{m}\mathit{a}\mathit{x}}$
1	0.00525	8.663	328.13	50	250
2	0.00609	10.04	136.91	5	150
3	0.00592	9.76	59.16	15	100

and

Table 3. Ramp–rate limits and prohibited zone for case 1.

Unit	${\mathit{P}}_{\mathit{i}}^{\mathit{o}}$	$\mathit{U}{\mathit{R}}_{\mathit{i}}$	$\mathit{D}{\mathit{R}}_{\mathit{i}}$	Prohibited Zone
				Zone 1	Zone 2
1	215	55	95	[105–117]	[165–177]
2	72	55	78	[50–60]	[92–102]
3	98	45	64	[25–32]	[60–67]

, and the matrix of loss coefficients is presented below [35].

$$B_{ij}={10}^{-5}\left[\begin{array}{c}13.6 1.75 18.4\\ 1.75 15.4 28.3\\ 1.84 28.3 161\end{array}\right]$$

The results of this method were evaluated in the following two key areas: (1) its convergence speed compared to those of the BCO, LI-BCO, and GS-BCO methods, and (2) its optimal solution quality compared to those of the PSO, HPSO, and MHLSA methods.

5.1.2. Second Case Study

This case study examined a test system of 6 thermal units, 26 buses, and 46 transmission lines, all subject to output constraints, fuel cost coefficients, ramp–rate limitations, and restricted operation zones. Transmission line losses were calculated with a B matrix following the method described in [36].

Table 4. Generator data for case 2.

Unit	ai	bi	ci	${\mathit{P}}_{\mathit{i}}^{\mathit{m}\mathit{i}\mathit{n}}$	${\mathit{P}}_{\mathit{i}}^{\mathit{m}\mathit{a}\mathit{x}}$
1	0.0070	7.00	240	100	500
2	0.0095	10.0	200	50	200
3	0.0090	8.50	220	80	300
4	0.0090	11.0	200	50	150
5	0.0080	10.5	220	50	200
6	0.0075	12.0	190	50	120

and

Table 5. Ramp–rate limits and prohibited zone for case 2.

Unit	${\mathit{P}}_{\mathit{i}}^{\mathit{o}}$	$\mathit{U}{\mathit{R}}_{\mathit{i}}$	$\mathit{D}{\mathit{R}}_{\mathit{i}}$	Prohibited Zone
				Zone 1	Zone 2
1	440	80	120	[210–240]	[350–380]
2	170	50	90	[90–110]	[140–160]
3	200	65	100	[150–170]	[210–240]
4	150	50	90	[80–90]	[110–120]
5	190	50	90	[90–110]	[140–150]
6	150	50	90	[75–85]	[100–105]

in [36] present the details of the six thermal units.

$${\mathrm{B}}_{\mathrm{i}\mathrm{j}}={10}^{-1}\left[\begin{array}{l}0.017 0.012 0.007 -0.001 -0.005 -0.002\\ 0.012 0.014 0.009 0.001 -0.006 -0.001\\ 0.007 0.009 0.031 0.000 -0.010 -0.006\\ -0.001 0.001 0.000 0.240 -0.006 -0.008\\ -0.005 -0.006 -0.010 -0.006 0.129 -0.002\\ -0.002 0.001 -0.006 -0.008 -0.002 0.150\end{array}\right]$$

$$B_{ij}={10}^{-2}\times \left[-0.3908-0.127 0.7047 0.0591 0.2161-0.6635\right]$$

$$B_{00}=0.056$$

The results of this method were analyzed in two key aspects—convergence speed, where it was compared to the BCO, LI-BCO, and GS-BCO methods, and solution optimality, where it was evaluated against the SCA, MTBO, and TLBO methods.

5.2. Simulation Results

The viability of employing BCO, LI-BCO, GS-BCO, and ELS-BCO methodologies to address the ED issue was assessed in two power generation scenarios, including one with three units and another with six. Each optimization method was initialized randomly, and all algorithms were executed concurrently to assess their performance. The method that achieved the fastest convergence was deemed the most effective, as quick convergence is essential due to the time-consuming nature of simulations. The parameters for BCO, LI-BCO, GS-BCO, and ELS-BCO utilized in this test are presented in Table 1. The benchmark algorithms selected for comparison included PSO, HPSO, SCA, MTBO, and TLBO. These methods were chosen because they represent diverse optimization approaches, including swarm intelligence, evolutionary computation, and ecosystem-based strategies. By comparing ELS-BCO against these well-established techniques, we ensure a comprehensive evaluation of its performance in terms of convergence speed, solution accuracy, and robustness.

5.2.1. Simulation Results in Case 1

Four methodologies—BCO, LI-BCO, GS-BCO, and ELS-BCO—were evaluated in this instance.

Table 6. Results of the three-unit system for case 1.

Unit	BCO	LI-BCO	GS-BCO	ELS-BCO
P1 (MW)	199.58	203.07	202.57	204.23
P2 (MW)	79.24	75.65	75.96	72.50
P3 (MW)	34.00	34.00	34.07	34.00
PT (MW)	312.82	312.72	312.60	310.73
FT ($/h)	3634.79	2632.97	3631.63	3611.03
Ploss (MW)	12.82	12.72	12.60	10.73

shows the best solutions to system constraints after 250 trial runs. The ELS-BCO method demonstrated a lower overall cost and reduced transmission line loss compared to the BCO, LI-BCO, and GS-BCO systems. Figure 2 illustrates the computation and convergence times. The ELS-BCO approach found the solution with fewer iterations and faster convergence than the other methods. Additionally, the results were comparable to those achieved using PSO [37] and HPSO [37]. (Refer to

Table 7. Results and comparison to other methods for case 1.

Unit	PSO	HPSO	ELS-BCO
P1 (MW)	190.59	200.18	204.23
P2 (MW)	85.77	76.26	72.50
P3 (MW)	34.80	34.40	34.00
PT (MW)	311.16	310.84	310.73
FT ($/h)	3631.10	3623.11	3611.03
Ploss (MW)	11.16	10.84	10.73

for details.)

Four methods—BCO, LI-BCO, GS-BCO, and ELS-BCO—were applied in this case study. The simulation was run with the selected parameters, and 200 trial runs were conducted. Table 6 presents the most successful solutions that met the system’s requirements. The ELS-BCO method demonstrated a lower overall cost and reduced transmission line loss compared to the BCO, LI-BCO, and GS-BCO systems. Figure 2 shows the computation and convergence times. The ELS-BCO approach achieved the solution with fewer iterations and faster convergence than the other methods, with results comparable to those of PSO and HPSO (see Table 7).

Table 6 illustrates that the ELS-BCO algorithm outperformed BCO, LI-BCO, and the proposed GS-BCO methods in locating optimal solutions within the search space. For the optimal scenario, ELS-BCO produced a cost of 3611.03, which is competitive compared to the other values in the table. In terms of convergence, the BCO method reached an optimal cost after 185 iterations, LI-BCO after 90 iterations, GS-BCO after 50 iterations, and ELS-BCO in fewer than 30 iterations. While the cost function’s value remained relatively stable across methods, ELS-BCO had the fastest convergence. Additionally, the ELS-BCO approach delivered a significantly better cost function outcome than the PSO and HPSO methods (see Table 7).

5.2.2. Simulation Results in Case 2

The four methodologies—BCO, LI-BCO, GS-BCO, and ELS-BCO—were implemented in the second test system, where each power generator (PG) possessed six output levels. The approaches were evaluated for the 1263 MW power demand based on the lowest production cost and computational efficiency.

Table 8. Results of the six-unit system in case 2.

Unit	BCO	LI-BCO	GS-BCO	ELS-BCO
P1 (MW)	467.44	469.05	468.90	467.25
P2 (MW)	176.31	164.03	169.66	170.52
P3 (MW)	262.70	255.78	252.10	254.35
P4 (MW)	123.38	120.30	122.41	132.49
P5 (MW)	173.79	173.38	171.13	156.89
P6 (MW)	71.50	92.17	90.44	89.67
PT (MW)	1275.12	1274.71	1274.64	1217.18
FT ($/h)	15,441.1	15,436.50	15,435.4	15,390.7
Ploss (MW)	12.12	11.71	11.64	8.18

delineates the techniques that yielded optimal solutions, and Figure 2 depicts the convergence characteristics of all approaches for the six-unit system. The ELS-BCO results were also compared with those of SCA [38], MTBO [39], and TLBO [40], as outlined in

Table 9. Results and comparison to other methods for case 2.

Unit	SCA	MTBO	TLBO	ELS-BCO
P1 (MW)	443.5177	447.0448	470.0	467.25
P2 (MW)	174.7330	173.1765	160.0	170.52
P3 (MW)	264.1966	263.9628	269.4	254.35
P4 (MW)	143.9844	139.0569	128.0	132.49
P5 (MW)	163.7919	165.5902	163.1	156.89
P6 (MW)	85.1836	86.5847	95.6	89.67
PT (MW)	1275.41	1275.4154	1273.0	1217.18
FT ($/h)	15,444.30	15,442.675	15,393.0	15,390.70
Ploss (MW)	12.41	12.4154	10.0	8.18

. The results indicate that ELS-BCO not only provides the lowest cost but also has the smallest convergence iterations, suggesting higher solution stability than that of other optimization techniques.

The simulation results for the BCO, LI-BCO, GS-BCO, and ELS-BCO techniques were analyzed based on the selected parameters. Out of 200 trial runs conducted for this case study, Table 8 displays the solutions that best met the system conditions. The ELS-BCO approach achieved reduced transmission line losses and lower overall costs compared to the BCO, LI-BCO, and GS-BCO methods. Figure 3 illustrates the computation and convergence times, with the ELS-BCO strategy reaching a solution more quickly and with fewer iterations than the other methods. The results were comparable to those of SCA, MTBO, and TLBO (Table 9).

As shown in Table 8, the ELS-BCO algorithm outperformed BCO, LI-BCO, and GS-BCO in identifying optimal locations in the search space. The ELS-BCO method achieved a cost of 15,390.7 for the optimal scenario, which is comparable to the other numbers in the table. The BCO method achieved an optimal cost after 140 iterations, LI-BCO after 110 iterations, and GS-BCO after 90 iterations, and ELS-BCO after fewer than 40 iterations. Although the cost function values did not vary significantly across methods, ELS-BCO demonstrated the fastest convergence. Similarly, Table 9 shows that the ELS-BCO method resulted in a significantly better cost function than the SCA, MTBO, and TLBO approaches.

6. Conclusions

The Bee Colony Optimization (BCO) algorithm integrates lambda iteration and the golden section ratio. Lambda iteration was employed to refine the search parameters, while the golden section ratio enhanced swarm dynamics. The integration of Lambda Iteration and Golden Section Search into BCO has significantly improved both convergence speed and solution quality. Collectively, these methodologies improved the local search proficiency of the BCO algorithm. The algorithm’s effectiveness was demonstrated through two case studies, both of which addressed complex economic dispatch (ED) problems. The proposed algorithm exhibited superior convergence to the optimal cost in both case studies. When applied to three and six generating units, the results showed that the enhanced algorithm outperformed traditional BCO methods by producing high-quality solutions with stable convergence characteristics. This improved stability was evident in the consistently better solutions found by the proposed approach. The ability to handle ramp–rate limits and prohibited operating zones makes it suitable for constraints. Additionally, the method reduced execution time, further demonstrating its efficiency. In the case studies, the suggested approach outperformed four other methods under the test conditions. The numerical results clearly indicated that the proposed method yielded superior outcomes, making it an excellent choice for optimizing economic dispatch problems.