An Interphase Short-Circuit Fault Location Method for Distribution Networks Considering Topological Flexibility
Abstract
1. Introduction
2. Physical Layer Predictive Fault Set Construction
2.1. Distribution Network Topology Identification
2.2. Characterization of Short-Circuit Fault Currents Between Phases
2.3. Characterization of Short-Circuit Fault Currents Between Phase and Ground
2.4. Switching Function Construction
3. Information Layer Fault Current Information Feature Modelling
3.1. Fault Current Array Construction
3.2. Information Perturbation Processing
- Information distortion:
- 2.
- Transmission delay:
- 3.
- Information failure:
- (1)
- When the feeder segment with information failure is located on the system power supply side, report 1 for this lost point information;
- (2)
- When the feeder segment with information failure is located on the distributed power supply side, the loss point information is reported as −1;
- (3)
- When the feeder segment with information failure is located in the middle part of the distribution network and the information of the switch FTUs in two neighbouring positions upstream and downstream is the same, the information of the neighbouring position is used to fill in the missing position information;
- (4)
- When the feeder segment with the failed information is located in the middle part of the distribution network and the switch FTU information of two neighbouring positions upstream and downstream of the switch is not consistent, the system reports the missing point information as 0.
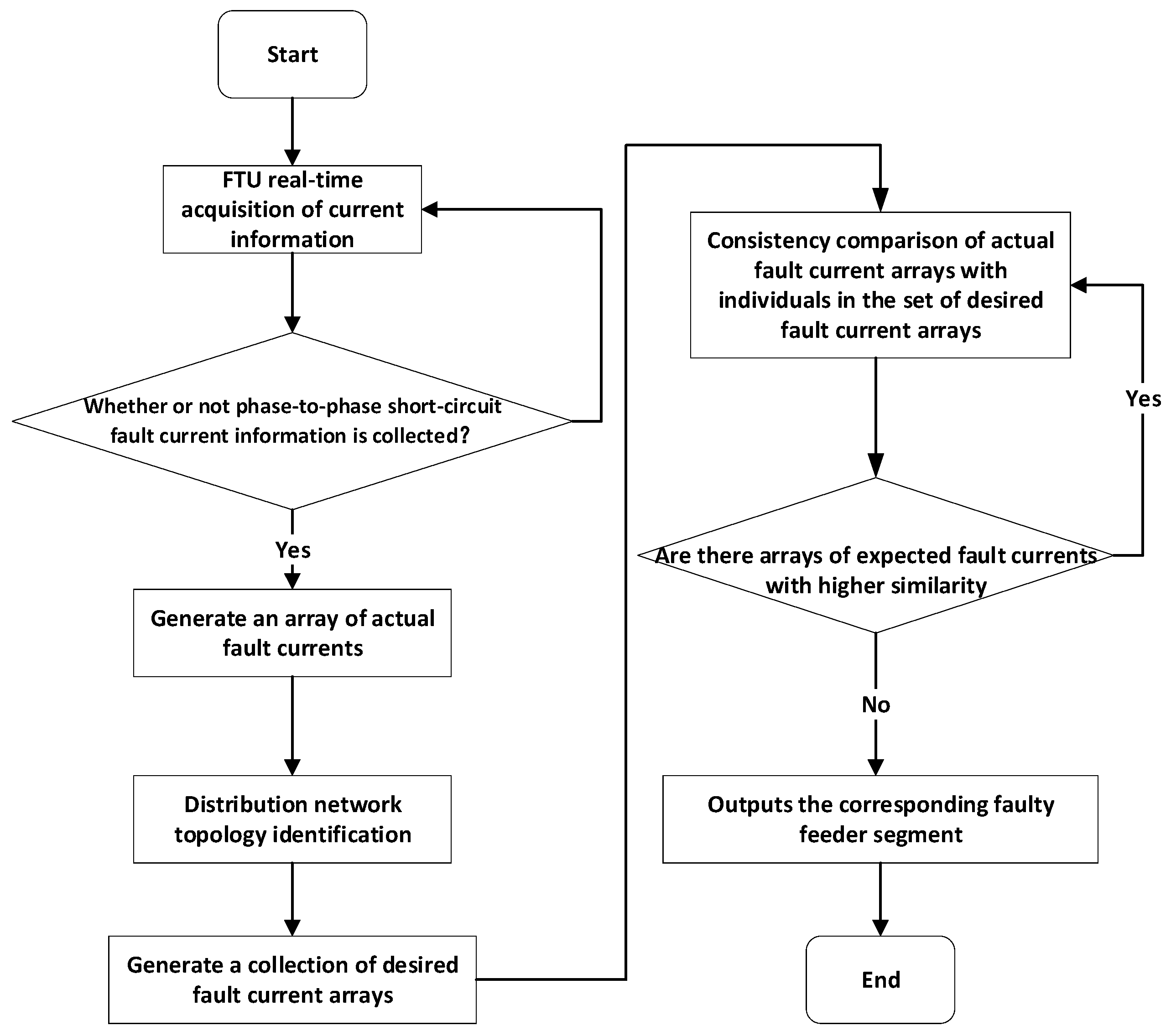
4. Location Method Based on Fault Feature Similarity
4.1. Construction of Similarity Function
4.2. Solution Algorithm
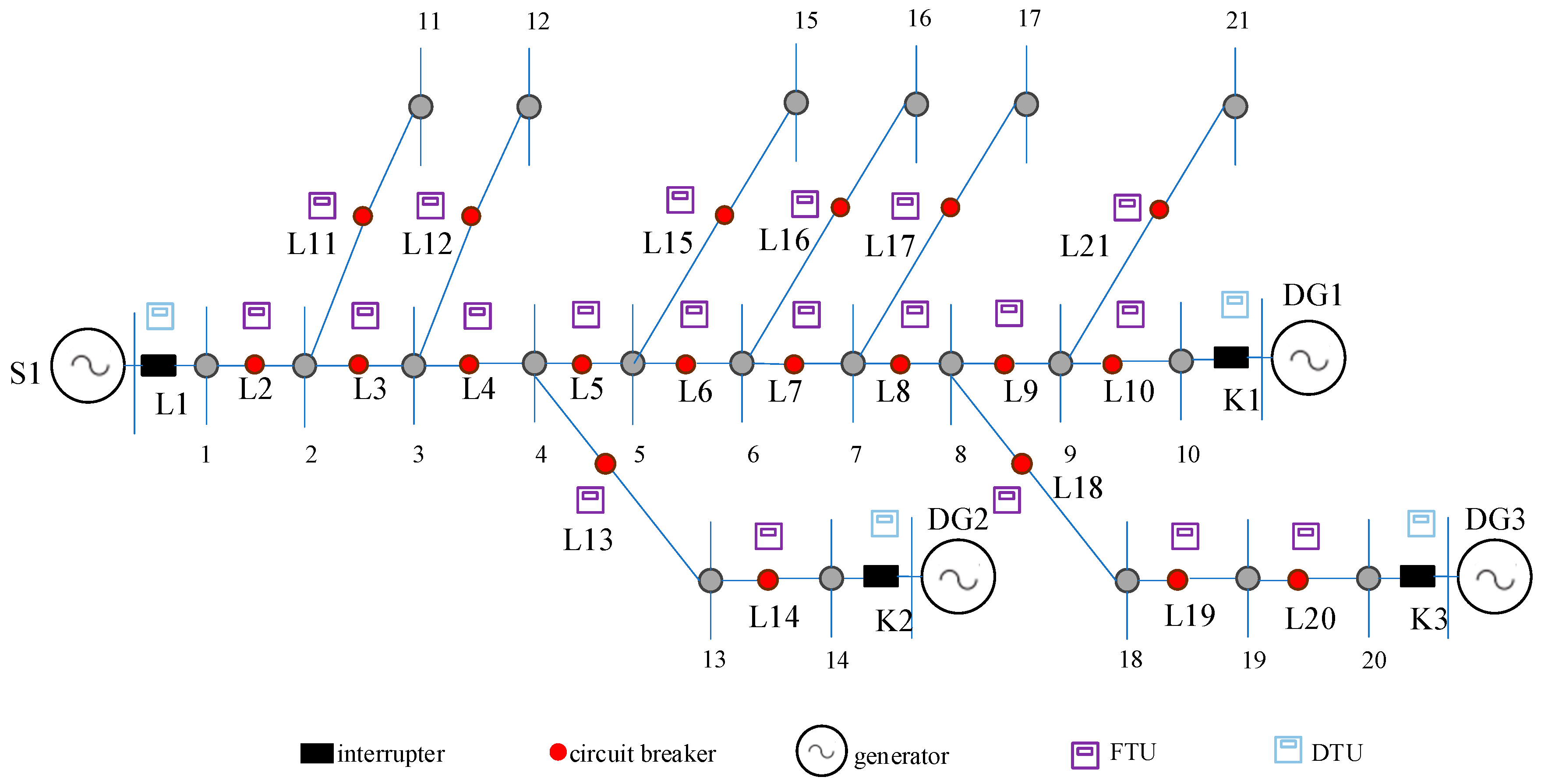
5. Case Analysis
5.1. Analysis of Methodological Validity
- 1.
- Unperturbed information scenarios:
- 2.
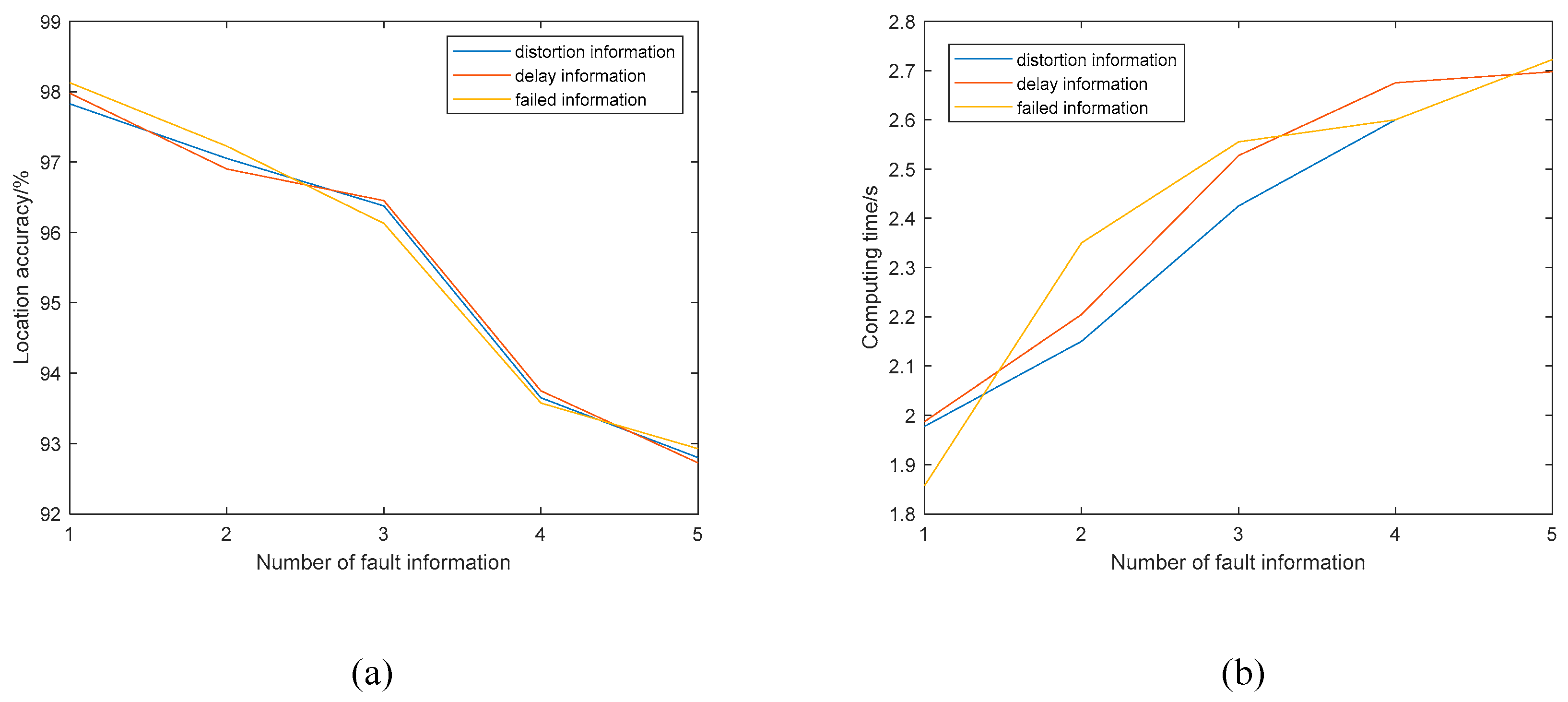
- Perturbed information scenarios:
- (1)
- Information distortion:
- (2)
- Information delay:
- (3)
- Information failure:
5.2. Analysis of Methodological Applicability
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bango, O.; Misra, S.; Jonathan, O.; Ahuja, R. Power system protection on smart grid monitoring faults in the distribution network via IoT. In New Frontiers in Cloud Computing and Internet of Things; Springer: Berlin/Heidelberg, Germany, 2022; pp. 343–363. [Google Scholar]
- Qin, J.; Yu, D.; Wang, H. Research on distribution network monitoring and fault location based on edge computing. Water Lect. Notes Electr. Eng. 2024, 1132, 260–265. [Google Scholar]
- Zhang, C.; Liu, Z.; Wang, J.; Wang, Z. Fast fault detection and location system for distribution network lines based on power electronic disturbance signals. J. Circuits Syst. Comput. 2021, 30, 2150187. [Google Scholar] [CrossRef]
- Ma, T.; Hu, Z.; Xu, Y.; Dong, H. Fault location based on comprehensive grey correlation degree analysis for flexible DC distribution network. Energies 2022, 15, 7820. [Google Scholar] [CrossRef]
- An, D.; Zhang, F.; Cui, F.; Yang, Q. Toward data integrity attacks against distributed dynamic state estimation in smart grid. IEEE Trans. Autom. Sci. Eng. 2024, 21, 881–894. [Google Scholar]
- Huang, C.; He, H.; Wang, Y.; Miao, R.; Ke, Z.; Chen, K. Low-voltage characteristic voltage based fault distance estimation method of distribution network. Front. Energy Res. 2024, 12, 1357459. [Google Scholar] [CrossRef]
- Ngoc-Hung, T. A new method for estimating fault location in radial medium voltage distribution network only using measurements at feeder beginning. Arch. Electr. Eng. 2023, 72, 503–520. [Google Scholar]
- Shu, H.; Liu, X.; Tan, X. Single-ended fault location for hybrid feeders based on charaeterislie distribution of traveling wave along a line. IEEE Trans. Power Deliv. 2021, 36, 339–351. [Google Scholar] [CrossRef]
- Li, L.; Gao, H.; Yuan, T.; Peng, F.; Xue, Y. Location method of high-impedance fault based on transient zero-sequence factor in non-effectively grounded distribution network. Electr. Power Syst. Res. 2024, 226, 109912. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, S.; Chen, Y.; Li, B.; Mei, S. Cyber-physical coordinated risk mitigation in smart grids based on attack-defense game. IEEE Trans. Power Syst. 2022, 37, 530–542. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, Q.; Xie, D.; Shao, N.; Ding, W.; Dong, Y. Novel faulted-section location method for active distribution networks of new-type power systems. Appl. Sci. 2023, 13, 8521. [Google Scholar] [CrossRef]
- An, J.; Deng, Z.; Chen, H.; Mu, G. Fault location detection of transmission lines in noise environments based on random matrix theory. CSEE J. Power Energy Syst. 2022, 8, 1233–1241. [Google Scholar]
- Liu, Z.; Chen, K.; Xie, J.; Wu, X.; Lu, W. Active distribution network fault section location method based on characteristic wave coupling. IET Renew. Power Gener. 2024, 18, 3020–3039. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, K. Fault location of distribution network with distributed generation based on Karrenbauer transform and support vector machine regression. Arch. Electr. Eng. 2023, 72, 461–481. [Google Scholar]
- Wang, D.; Yu, D.; Gao, H.; Peng, F.; Lin, J.; Wang, J. Frequency modification algorithm-based traveling wave fault location approach for overhead transmission lines with structural changes. Prot. Control of Mod. Power Syst. 2025, 10, 1–12. [Google Scholar] [CrossRef]
- Kanwal, S.; Jiriwibhakorn, S. Artificial intelligence based faults identification, classification, and localization techniques in transmission lines-a review. IEEE Lat. Am. Trans. 2024, 21, 1291–1305. [Google Scholar] [CrossRef]
- Niu, S.; Zhao, Q.; Niu, S.; Jian, L. A comprehensive investigation of thermal risks in wireless EV chargers considering spatial misalignment from a dynamic perspective. IEEE J. Emerg. Sel. Top. Ind. Electron. 2024, 4, 1560–1571. [Google Scholar] [CrossRef]
- Azizivahed, A.; Arefi, A.; Ghavidel, S.; Shafie-khah, M.; Li, L.; Zhang, J.; Catalao, J. Energy management strategy in dynamic distribution network reconfiguration considering renewable energy resources and storage. IEEE Trans. Sustain. Energy 2020, 11, 662–673. [Google Scholar] [CrossRef]
- Fan, B.; Shu, N.; Li, Z.; Li, F. Critical nodes identification for power grid based on electrical topology and power flow distribution. IEEE Syst. J. 2023, 17, 4874–4884. [Google Scholar] [CrossRef]
- Wang, H.; Gu, C.; Zhao, W.; Wang, S.; Zhang, X.; Buticchi, G.; Gerada, C.; Zhang, H. Fault-tolerant control for single-phase open-circuit and short-circuit fault in five-phase PMSM with third-order harmonic back EMF using coefficients reconfiguration. IEEE Trans. Energy Convers. 2024, 39–51, 782–792. [Google Scholar] [CrossRef]
- Gutierrez-Rojas, D.; Christou, I.; Dantas, D.; Narayanan, A.; Nardelli, P.; Yang, Y. Performance evaluation of machine learning for fault selection in power transmission lines. Knowl. Inf. Syst. 2022, 64, 859–883. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, J.; Ma, Z.; Chen, J.; Ren, H. A fault recovery strategy for distribution networks considering distributed energy storage and information systems. In Proceedings of the 11th Frontier Academic Forum of Electrical Engineering (FAFEE2024), Chongqing, China, 21 June 2024. [Google Scholar]
- Samal, S.; Samantaray, S. A novel sequence component based fault detection index for microgrid protection. Electr. Power Syst. Res. 2024, 232, 110380. [Google Scholar] [CrossRef]
- Das, C.; Bass, O.; Kothapalli, G.; Mahmoud, T.; Habibi, D. Optimal placement of distributed energy storage systems in distribution networks using artificial bee colony algorithm. Appl. Energy 2018, 232, 212–228. [Google Scholar] [CrossRef]
- GB/T 42151.5-2022; Communication Networks and Systems for Power Utility Automation—Part 5: Communication Requirements for Functions and Device Models. Standardization Administration of China: Beijing, China, 2022.
- Liu, B.; Chen, J.; Li, J. Distribution network topology identification method based on state estimation with mixed integer programming and structural equation model. Int. J. Electr. Power Energy Syst. 2024, 162, 110251. [Google Scholar] [CrossRef]
- Xu, H.; Feng, B.; Wang, C.; Guo, C.; Qiu, J.; Sun, M. Exact box-constrained economic operating region for power grids considering renewable energy sources. J. Mod. Power Syst. Clean Energy 2024, 12, 514–523. [Google Scholar] [CrossRef]
- Xu, D.; Wu, Z.; Xu, J.; Hu, Q. Data-Model Hybrid Driven Topology Identification Framework for Distribution Networks. CSEE J. Power Energy Syst. 2024, 10, 1478–1490. [Google Scholar]
- Sheng, W.; Liu, K.; Li, Z.; Ye, X. Collaborative fault recovery and network reconstruction method for cyber-physical-systems based on double layer optimization. CSEE J. Power Energy Syst. 2023, 9, 380–392. [Google Scholar]

| K1, K2, K3 Switching State | Total Number of Faulty Lines | Location Accuracy/% | Computing Time/s |
|---|---|---|---|
| [0,0,0] | 1 | 100 | 1.39 |
| 2 | 99.5 | 1.65 | |
| 4 | 98.6 | 1.69 | |
| 6 | 98.8 | 1.73 | |
| [0,0,1] | 1 | 100 | 1.38 |
| 2 | 98.3 | 1.64 | |
| 4 | 99.2 | 1.71 | |
| 6 | 98.5 | 1.81 | |
| [0,1,0] | 1 | 100 | 1.38 |
| 2 | 98.2 | 1.52 | |
| 4 | 98.2 | 1.64 | |
| 6 | 98.2 | 1.83 | |
| [0,1,1] | 1 | 100 | 1.34 |
| 2 | 98.4 | 1.89 | |
| 4 | 98.7 | 1.87 | |
| 6 | 98.7 | 1.89 | |
| [1,0,0] | 1 | 100 | 1.36 |
| 2 | 98.2 | 1.74 | |
| 4 | 98.7 | 1.84 | |
| 6 | 98.7 | 1.83 | |
| [1,0,1] | 1 | 100 | 1.39 |
| 2 | 98.4 | 1.64 | |
| 4 | 98.2 | 1.72 | |
| 6 | 98.2 | 1.81 | |
| [1,1,0] | 1 | 100 | 1.38 |
| 2 | 99.2 | 1.74 | |
| 4 | 98.7 | 1.77 | |
| 6 | 98.4 | 1.87 | |
| [1,1,1] | 1 | 100 | 1.38 |
| 2 | 98.4 | 1.69 | |
| 4 | 98.2 | 1.76 | |
| 6 | 97.5 | 1.77 |
| Number of Distortion Information | Total Number of Faulty Lines | Location Accuracy/% | Computing Time/s |
|---|---|---|---|
| 1 | 1 | 98.7 | 1.69 |
| 2 | 98.1 | 1.87 | |
| 4 | 97.2 | 2.02 | |
| 6 | 97.3 | 2.33 | |
| 2 | 1 | 97.9 | 1.78 |
| 2 | 97.3 | 2.06 | |
| 4 | 96.8 | 2.25 | |
| 6 | 96.2 | 2.51 | |
| 3 | 1 | 97.6 | 2.08 |
| 2 | 96.8 | 2.36 | |
| 4 | 95.9 | 2.52 | |
| 6 | 95.2 | 2.74 | |
| 4 | 1 | 94.4 | 2.24 |
| 2 | 93.8 | 2.52 | |
| 4 | 93.3 | 2.71 | |
| 6 | 93.1 | 2.93 | |
| 5 | 1 | 93.6 | 2.31 |
| 2 | 92.9 | 2.59 | |
| 4 | 92.6 | 2.86 | |
| 6 | 92.1 | 3.13 |
| Number of Delayed Information | Total Number of Faulty Lines | Location Accuracy/% | Computing Time/s |
|---|---|---|---|
| 1 | 1 | 98.4 | 1.63 |
| 2 | 98.5 | 1.87 | |
| 4 | 97.7 | 2.14 | |
| 6 | 97.3 | 2.31 | |
| 2 | 1 | 97.7 | 1.73 |
| 2 | 97.4 | 2.19 | |
| 4 | 96.3 | 2.26 | |
| 6 | 96.2 | 2.64 | |
| 3 | 1 | 97.9 | 2.17 |
| 2 | 96.6 | 2.43 | |
| 4 | 95.9 | 2.69 | |
| 6 | 95.4 | 2.82 | |
| 4 | 1 | 94.7 | 2.33 |
| 2 | 93.3 | 2.58 | |
| 4 | 93.5 | 2.83 | |
| 6 | 93.5 | 2.96 | |
| 5 | 1 | 93.7 | 2.42 |
| 2 | 92.4 | 2.49 | |
| 4 | 92.6 | 2.79 | |
| 6 | 92.2 | 3.07 |
| Number of Failed Information | Total Number of Faulty Lines | Location Accuracy/% | Computing Time/s |
|---|---|---|---|
| 1 | 1 | 98.9 | 1.56 |
| 2 | 98.7 | 1.77 | |
| 4 | 97.5 | 1.95 | |
| 6 | 97.4 | 2.15 | |
| 2 | 1 | 97.9 | 1.80 |
| 2 | 97.5 | 2.23 | |
| 4 | 96.9 | 2.64 | |
| 6 | 96.6 | 2.73 | |
| 3 | 1 | 97.1 | 2.21 |
| 2 | 96.9 | 2.47 | |
| 4 | 95.3 | 2.66 | |
| 6 | 95.2 | 2.88 | |
| 4 | 1 | 94.7 | 2.24 |
| 2 | 93.4 | 2.52 | |
| 4 | 93.1 | 2.71 | |
| 6 | 93.1 | 2.93 | |
| 5 | 1 | 93.7 | 2.31 |
| 2 | 92.9 | 2.59 | |
| 4 | 92.7 | 2.86 | |
| 6 | 92.4 | 3.13 |
| K1, K2, K3 Switching State | Total Number of Faulty Lines | Location Accuracy/% | Computing Time/s |
|---|---|---|---|
| [0,0,0] | 1 | 100 | 1.36 |
| 2 | 99.5 | 1.84 | |
| 4 | 98.6 | 1.79 | |
| 6 | 98.8 | 1.92 | |
| [0,0,1] | 1 | 100 | 1.37 |
| 2 | 98.3 | 1.66 | |
| 4 | 99.2 | 1.74 | |
| 6 | 98.5 | 1.83 | |
| [0,1,0] | 1 | 100 | 1.34 |
| 2 | 98.2 | 1.48 | |
| 4 | 98.2 | 1.67 | |
| 6 | 98.2 | 1.82 | |
| [0,1,1] | 1 | 100 | 1.41 |
| 2 | 98.4 | 1.92 | |
| 4 | 98.7 | 1.86 | |
| 6 | 98.7 | 1.99 | |
| [1,0,0] | 1 | 100 | 1.41 |
| 2 | 98.2 | 1.71 | |
| 4 | 98.7 | 1.79 | |
| 6 | 98.7 | 1.82 | |
| [1,0,1] | 1 | 100 | 1.36 |
| 2 | 98.4 | 1.66 | |
| 4 | 98.2 | 1.74 | |
| 6 | 98.2 | 1.83 | |
| [1,1,0] | 1 | 100 | 1.34 |
| 2 | 99.2 | 1.78 | |
| 4 | 98.7 | 1.79 | |
| 6 | 98.4 | 1.86 | |
| [1,1,1] | 1 | 100 | 1.37 |
| 2 | 98.4 | 1.54 | |
| 4 | 98.2 | 1.79 | |
| 6 | 97.5 | 1.82 |
| System Example | Total Number of Faulty Lines | Location Accuracy/% | Computing Time/s |
|---|---|---|---|
| IEEE-9 | 1 | 99.5 | 1.15 |
| 2 | 98.7 | 1.22 | |
| 4 | 98.3 | 1.25 | |
| IEEE-33 | 1 | 99.2 | 1.64 |
| 2 | 98.6 | 1.84 | |
| 4 | 98.1 | 2.03 | |
| 6 | 98.0 | 2.14 | |
| IEEE-160 | 1 | 99.8 | 3.42 |
| 5 | 98.9 | 3.55 | |
| 10 | 97.9 | 3.73 | |
| 15 | 96.5 | 3.94 | |
| 30 | 94.3 | 4.17 |
| Algorithms | Accuracy/% | Iteration Time/s |
|---|---|---|
| VBC | 100 | 1.36 |
| IA | 69.9 | 3.86 |
| GA | 59.4 | 2.91 |
| QGA | 100 | 2.44 |
| BDA | 95.2 | 1.40 |
| SM | 95.2 | 1.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, H.; Liu, Z.; Li, K.; Chen, Q.; Yang, C.; Li, T. An Interphase Short-Circuit Fault Location Method for Distribution Networks Considering Topological Flexibility. Processes 2025, 13, 782. https://doi.org/10.3390/pr13030782
Xie H, Liu Z, Li K, Chen Q, Yang C, Li T. An Interphase Short-Circuit Fault Location Method for Distribution Networks Considering Topological Flexibility. Processes. 2025; 13(3):782. https://doi.org/10.3390/pr13030782
Chicago/Turabian StyleXie, Hua, Zhe Liu, Kai Li, Qifang Chen, Chao Yang, and Tong Li. 2025. "An Interphase Short-Circuit Fault Location Method for Distribution Networks Considering Topological Flexibility" Processes 13, no. 3: 782. https://doi.org/10.3390/pr13030782
APA StyleXie, H., Liu, Z., Li, K., Chen, Q., Yang, C., & Li, T. (2025). An Interphase Short-Circuit Fault Location Method for Distribution Networks Considering Topological Flexibility. Processes, 13(3), 782. https://doi.org/10.3390/pr13030782






