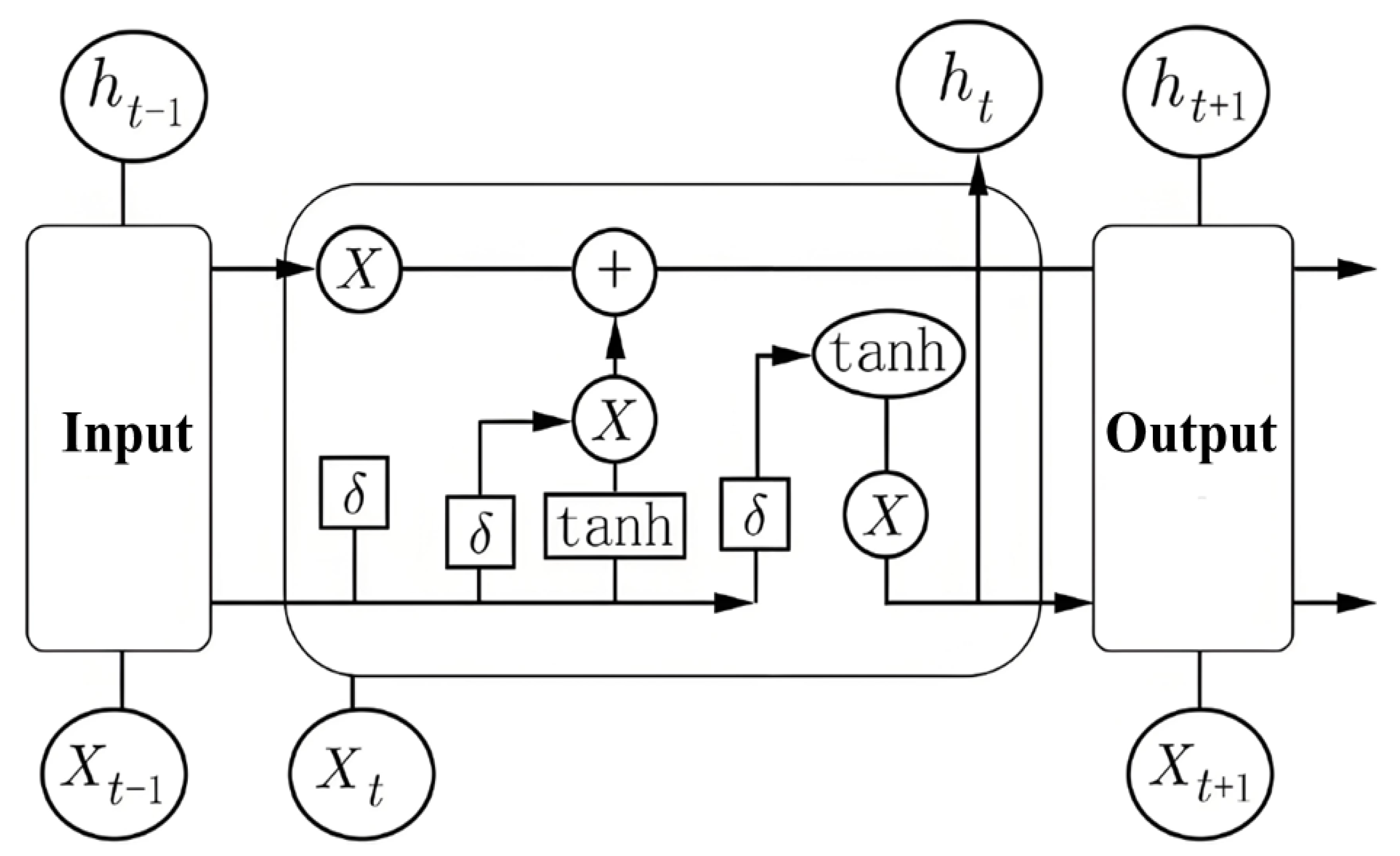
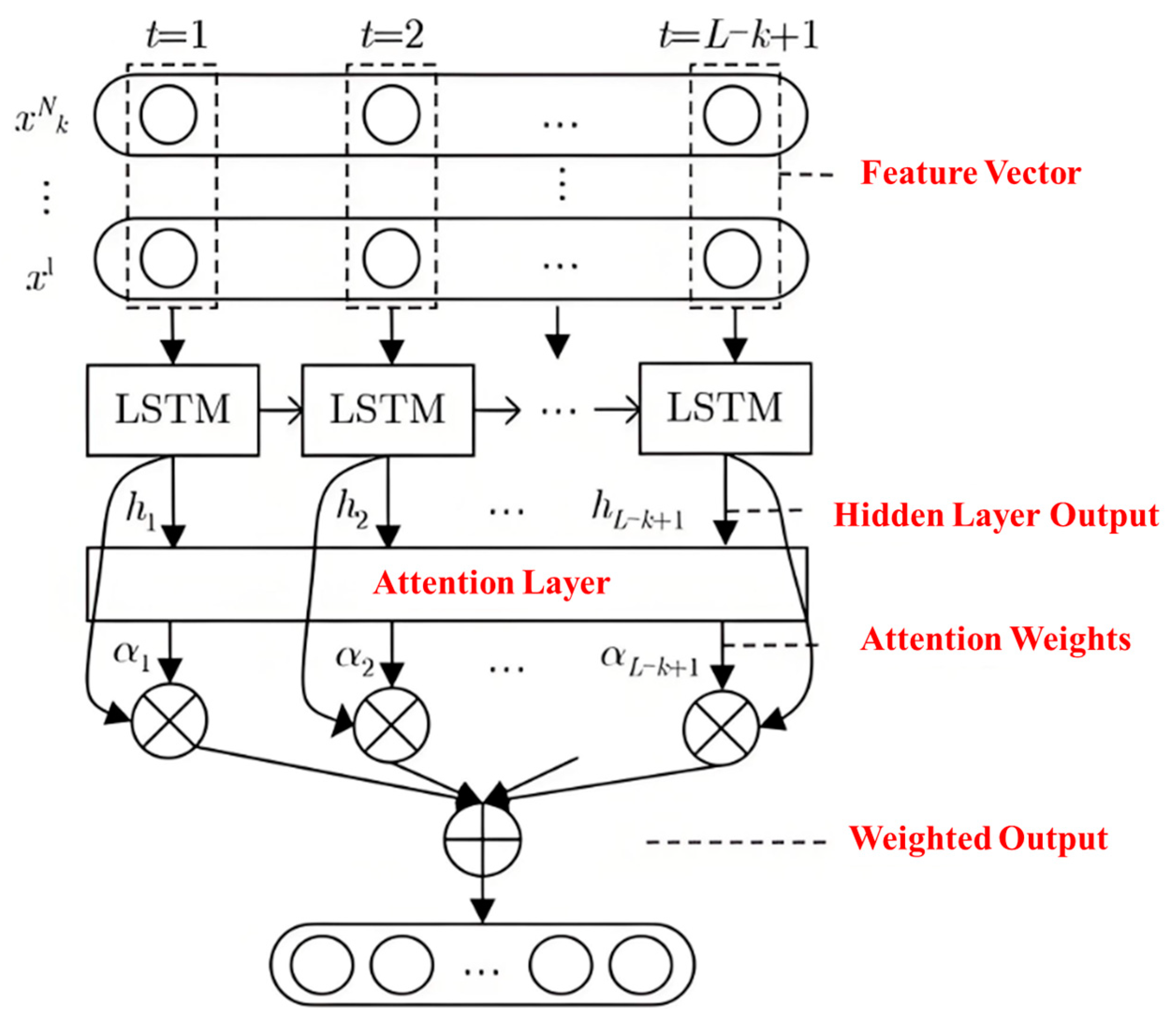
4.1. Effectiveness Verification of Single-Type Disturbance Identification
To demonstrate the effectiveness and feasibility of the proposed method in this paper, simulations were performed using MATLAB software. Five types of power quality disturbances were considered, namely voltage swells, voltage sags, voltage interruptions, transient impulses, and transient oscillations. The normal voltage waveform is sinusoidal, as shown in Equation (20). The mathematical models of each disturbance are presented in Equations (21)–(25). Using the random data generation functions in MATLAB, a large dataset was constructed. For each operating condition, 1000 data samples were randomly generated, with 600 samples used as the training set and the remaining 400 samples serving as the testing set. For the CNN-LSTM model, due to its complex network structure and numerous parameters, high-performance CPUs or GPUs are usually required to accelerate computations. For real-time or near-real-time applications, servers or embedded systems equipped with high-performance computing devices can be used to ensure low-latency processing. In this paper, the relevant models were implemented using MATLAB R2024B software installed on a desktop computer, with the computational configuration being an Intel(R) Core(TM) i5-9500 CPU @ 3.00 GHz and 8 GB of RAM made in the USA.
The following
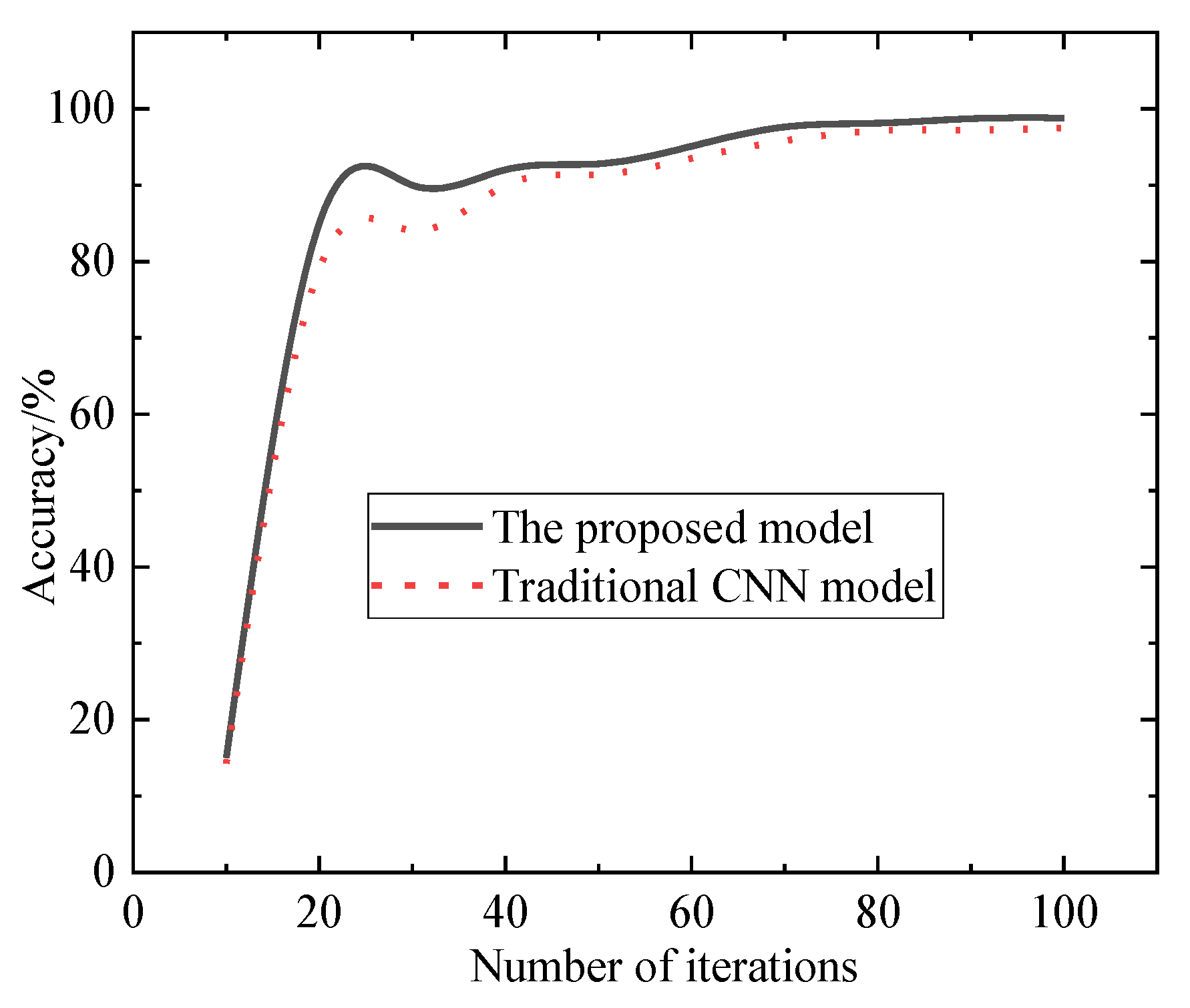
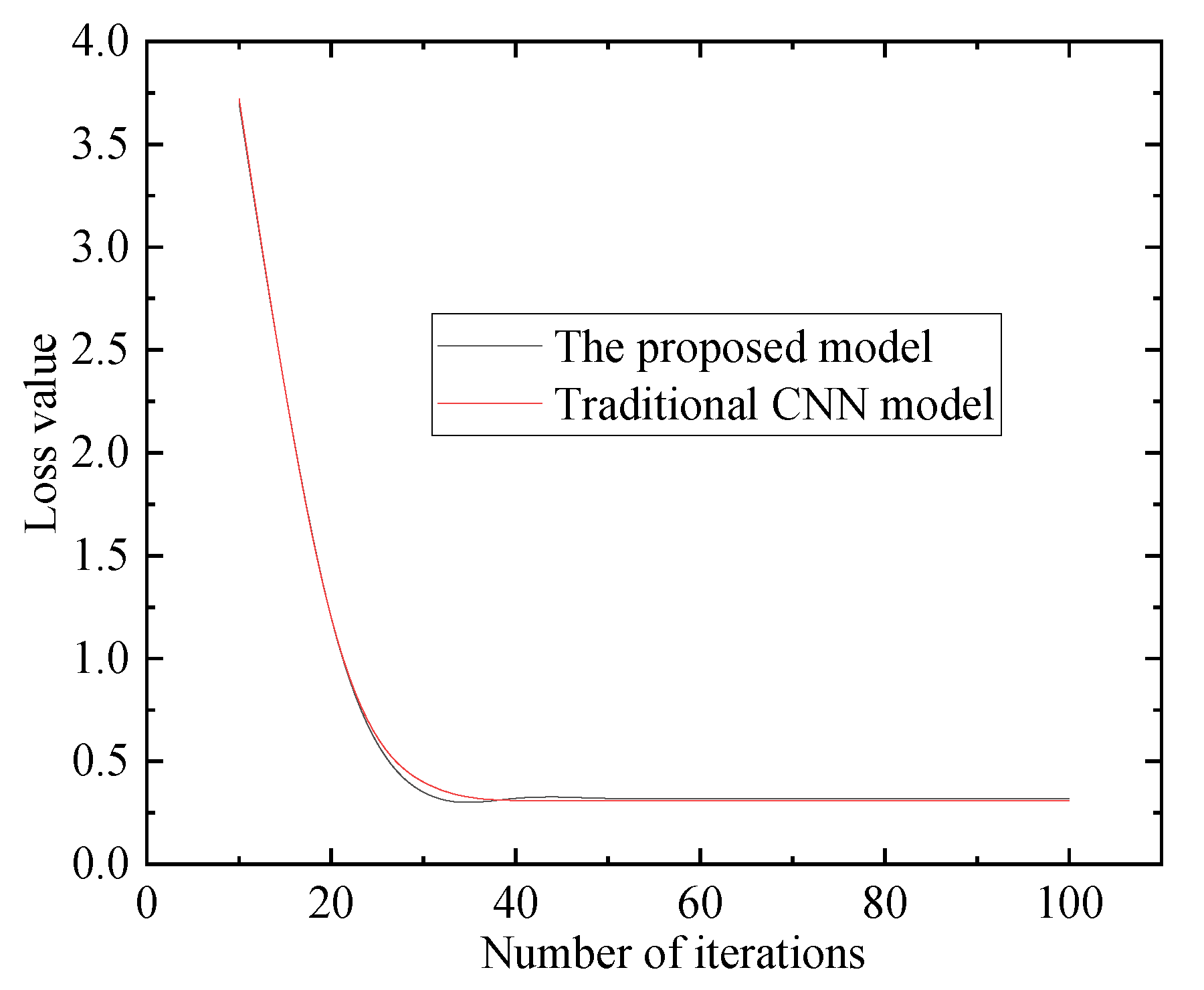
Figure 4 and
Figure 5 present a comparison of the discrimination accuracy and loss values between the proposed model in this paper and the traditional CNN model.
As can be observed from the figures above, the proposed method in this paper outperforms the traditional model in terms of both recognition accuracy and loss values. LSTM is a recurrent neural network model particularly suitable for processing time-series data. With its memory and learning capabilities, LSTM can capture long-term dependencies in data. In the classification of power quality disturbances, power signals often possess the characteristics of time series, and the introduction of LSTM can better handle such temporal data, thereby improving the accuracy of classification. CNN excels at capturing spatial information, i.e., local features of data. The hybrid LSTM-CNN model combines the advantages of LSTM and CNN, capable of capturing both spatial and temporal information of data. This dual-capturing ability enables the model to comprehend the characteristics of power quality disturbance signals more comprehensively, thus improving the classification accuracy.
Meanwhile, the gated mechanism of LSTM can prevent the model from overfitting during the training process, avoiding excessive fitting to the training data and losing the generalization ability for unseen data. The pooling layer of CNN also helps reduce the risk of overfitting. In the hybrid LSTM-CNN model, the combination of these two mechanisms can further enhance the robustness of the model and reduce the occurrence of overfitting. LSTM extracts temporal features from data through its unique memory mechanism, which is crucial for understanding the time-varying characteristics of power quality disturbance signals. By combining these two feature extraction capabilities, the hybrid LSTM-CNN model achieves more comprehensive feature extraction and classification of power quality disturbance signals, thereby improving the classification accuracy.
In summary, the hybrid LSTM-CNN model exhibits significant advantages in the field of power quality disturbance classification and identification, outperforming the traditional CNN model in terms of recognition accuracy and loss values. This is mainly attributed to LSTM’s ability to process time-series data, CNN’s capability to capture spatial information, their complementary roles in preventing overfitting, and their complementary strengths in feature extraction and classification.
In practical applications, power disturbance signals are often accompanied by a significant amount of noise interference. To further demonstrate the robustness of the proposed method in this paper, a comparison with some other common model methods under different noise interference conditions has been conducted. The relevant identification results are presented in
Table 2 below.
Observing the table above, it can be found that the proposed LSTM-CNN hybrid model maintains high accuracy under different noise conditions. LSTM excels at processing sequential data and capturing long-term dependencies within sequences. This is particularly advantageous for data with time-series characteristics, such as power quality disturbance signals, as it can better grasp patterns in the time series. Meanwhile, CNN is adept at extracting local features from image data and capturing spatial information. In the classification of power quality disturbances, CNN can extract spatial features from the disturbance signals, while LSTM captures temporal information. The combination of the two allows for the consideration of both spatial and temporal information, thereby enhancing the model’s accuracy. In summary, the CNN-LSTM hybrid model combines the strengths of CNN and LSTM, taking into account both temporal and spatial information of the data. This enables the model to more accurately capture temporal dependencies and spatial patterns in historical data when predicting power quality disturbances, thus improving diagnostic accuracy.
To illustrate the rationality of selecting the SSA. Comparisons are made in terms of identification accuracy and optimization time, with the relevant results shown in
Table 3 below.
Observing
Table 3 above, it can be seen that SSA optimization achieves the highest identification accuracy while ensuring computational efficiency. Compared to Genetic Algorithm (GA) and Bayesian Optimization, the identification accuracy is improved by 3.9% and 2.8%, respectively. By simulating the foraging behavior of sparrows, SSA effectively balances exploration (searching for new areas) and exploitation (conducting fine searches in known promising areas) within the search space. This balance is crucial for hyperparameter optimization, as it allows the algorithm to conduct an extensive search for the optimal solution while also making fine adjustments near potential optimal solutions. Compared to other optimization algorithms, SSA is relatively insensitive to the setting of initial parameters. This means that SSA can exhibit good performance without the need for extensive parameter tuning, which is particularly important for rapid deployment in practical applications and reducing tuning costs. Through its unique leader–follower strategy, SSA maintains high diversity in the search space, thereby enhancing its global search capability. This is particularly advantageous for finding optimal solutions in complex, multimodal search spaces. Although computational efficiency may vary depending on problem size and algorithm implementation, SSA typically provides relatively fast convergence speeds while maintaining high search quality. This is particularly critical for hyperparameter optimization in large-scale datasets and real-time applications. SSA can flexibly adapt to various problems and constraints. In the power quality disturbance classification strategy proposed in this paper, SSA can handle the complexity and nonlinear characteristics of the CNN-LSTM model, thereby finding the optimal combination of hyperparameters suitable for specific datasets and tasks. In contrast, although GA is also a global optimization algorithm, its crossover and mutation operations may lead to a loss of diversity in the search process, causing the algorithm to fall into local optimal solutions. While Bayesian Optimization performs well in high-dimensional spaces, it relies on information from previously evaluated points to construct a surrogate model and therefore may lack sufficient exploratory capabilities in the initial stages. In the specific problem addressed in this paper, these advantages of SSA enable it to more effectively optimize the hyperparameters of the CNN-LSTM model, thereby improving the accuracy and generalization ability of power quality disturbance classification. Furthermore, by incorporating an enhanced learning mechanism, SSA can further adapt to the complexity and non-stationarity of power quality signals, maintaining stable classification performance under load fluctuations.
4.2. Effectiveness Verification of Complex Dynamic Environment
In power quality disturbance identification, the difficulty of identifying mixed disturbances of multiple types is significantly greater than that of a single type of disturbance. Single disturbances typically exhibit relatively clear and independent characteristics that are easy to identify. However, when multiple disturbances occur simultaneously, their characteristics may overlap or generate new composite features. For example, when a voltage sag occurs concurrently with harmonics, it may obscure the originally clear characteristics of the voltage sag, thereby increasing the difficulty of identification. Voltage signals in actual power systems are often affected by noise to varying degrees. For single disturbances, their characteristics can be relatively easily extracted through appropriate filtering and signal-processing techniques. However, for mixed disturbances, noise may simultaneously affect the characteristics of multiple disturbances, making feature extraction more challenging. Additionally, noise may obscure certain weak disturbance characteristics, preventing the identification system from accurately recognizing them. Most current power quality disturbance identification algorithms are based on specific mathematical models or feature extraction methods. For single disturbances, these algorithms usually achieve good identification results. However, for mixed disturbances, due to the complexity of their characteristics and the interference of noise, these algorithms may fail to accurately extract the characteristics of all disturbances, leading to a decrease in identification accuracy. In practical applications, samples of mixed disturbances are often more difficult to obtain than those of single disturbances. Therefore, during the training of identification systems, there may be a lack of sufficient samples of mixed disturbances, resulting in limited identification capabilities for mixed disturbances.
To further validate the effectiveness of the method proposed in this paper under complex disturbances, the authors increased the identification accuracy in scenarios involving complex and mixed types of disturbances, as shown in
Table 4 below.
Observation of the table above reveals that the method proposed in this paper maintains a diagnostic accuracy of over 92% even under multiple types of fault disturbances. The FST is an effective signal processing tool capable of efficiently analyzing power quality disturbance signals while effectively preserving their time–frequency characteristics. This is particularly important for composite disturbances, which often contain features of multiple frequencies and times. By providing a clear time–frequency representation, FST enables more precise feature extraction, aiding the identification system in distinguishing between different types of disturbances, even when they occur simultaneously, while maintaining high identification accuracy. Traditional CNNs excel in processing image or time-series data but may have limitations when dealing with power quality disturbances with complex time dependencies. The introduction of LSTM networks partially enhances the model’s ability to process time-series data, especially its capacity to capture long-term dependencies. This hybrid CNN-LSTM model combines CNN’s spatial feature extraction capabilities with LSTM’s time-series analysis capabilities, thereby improving the identification accuracy for composite disturbances. Additionally, it cannot be overlooked that the method proposed in this paper can operate effectively even in high-noise environments. As a feature extraction tool, FST’s efficiency is not only reflected in its computational speed but also in its sensitivity to signal features and its ability to suppress noise. By extracting key time–frequency features, FST assists the model in identifying useful signal components in high-noise environments. The CNN-LSTM model integrates mechanisms, meaning that the physical mechanisms and characteristics of power quality disturbances are considered during model design and training. This integration enables the model to more specifically address power quality disturbances, enhancing its performance in complex and noisy environments.
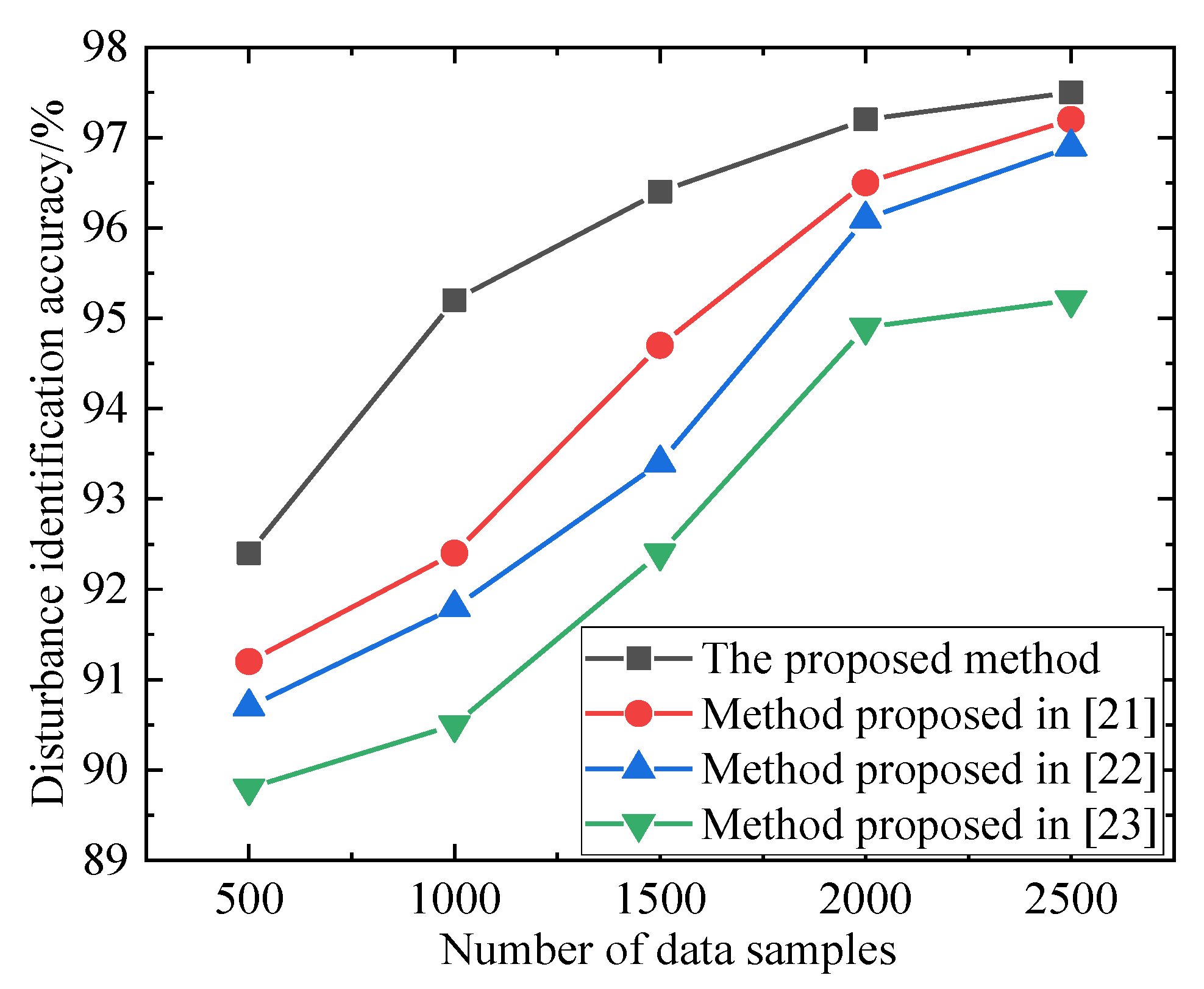
This paper further compares the identification accuracy of the current mainstream methods under different data sample sizes. Currently, methods such as the plug Hilbert transform method [
20], the multi-dimensional spectral convolutional neural fusion network [
21], and the weighted recursive layer aggregation (WRLA) network [
22] are widely used in power quality detection and have achieved good results. This paper further tests the composite power quality disturbance diagnosis accuracy of each method under different data sample sizes, as shown in
Figure 6 below. In this paper, the data values used for power quality detection all represent voltage amplitudes containing disturbance information. It should be noted that these data are collected by power grid measurement devices and power quality analyzers. Power quality analyzers are generally equipped with specialized software, USB interfaces, and wireless transmission capabilities for exporting and analyzing data. They are capable of capturing voltage and current waveforms in real time, thereby extracting disturbance information. The relevant data samples can be downloaded from the CSDN website [
24].
Observing the above figure, it is not difficult to find that under the condition of small data samples, the advantages of the method proposed in this paper are more prominent, with an identification accuracy nearly 3.2% higher than that of existing methods. Meanwhile, as the number of data samples further increases, the diagnostic accuracy of various methods shows little difference. The FST adopted in this paper can efficiently analyze and extract features from power quality disturbance signals while effectively preserving the time–frequency characteristics of the signals. This is particularly important for small data samples because the limited number of samples requires the feature extraction method to capture the key information of the signals as accurately as possible, and FST excels in this aspect. Compared with other methods, the method proposed in this paper may have better adaptability when dealing with small data samples. This is because the combination of FST with CNN-LSTM can more flexibly capture and utilize key features in the signals while reducing the dependence on a large amount of training data. In the case of small data samples, complex models may be prone to overfitting due to excessive parameters, and the WRLA network may be affected by sample size limitations when processing sequential data. In contrast, the method in this paper improves adaptability to small data samples by simplifying the feature extraction process and enhancing the model’s learning ability.
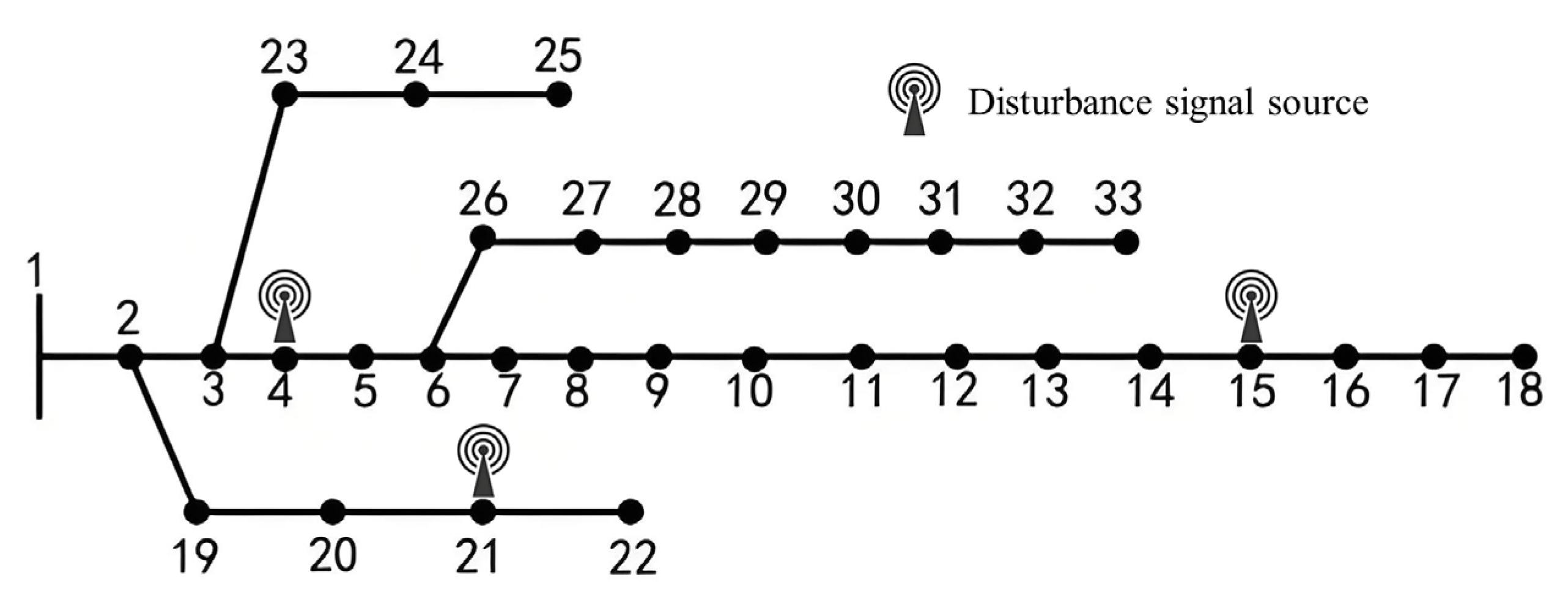
On the other hand, a time-varying dynamic power grid test environment is also used to verify the practicality of the method proposed in this paper. The modified IEEE-33-node distribution network is employed for testing, with the network structure shown in
Figure 7 below. Three disturbance signal sources are installed at nodes 4, 15, and 21, respectively.
Table 5 below presents the disturbance identification accuracy under different load fluctuation rates.
Observing the table above, it can be found that the method proposed in this paper still performs well under different load fluctuation rates. However, for all methods, as the load fluctuation rate increases, the accuracy of disturbance diagnosis tends to decline. This is because load fluctuations complicate the time–frequency characteristics of power quality signals, making feature extraction more difficult. The random variations in load impart non-stationarity to power quality data, which traditional methods may struggle to accurately capture. The classification accuracy of power quality disturbances can be affected by load fluctuation interference, leading to misclassification or missed classification. The plug Hilbert transform method can provide instantaneous frequency and amplitude information of signals, which is helpful for analyzing power quality disturbances. However, it has poor adaptability to load fluctuations and may fail to accurately capture the characteristics of dynamic changes. Additionally, this method has high computational complexity and is not suitable for real-time processing. The multi-dimensional spectral convolutional neural fusion network can automatically extract multi-dimensional features and has strong processing capabilities for complex signals. Through convolutional operations, it can capture local features and improve classification accuracy. However, in cases of load fluctuations, a large amount of training data may be required to optimize model parameters and avoid overfitting. The model structure is complex, and the training time is relatively long. The Weighted Recurrent Layer Aggregation Network can process sequential data and capture long-term dependencies in time series. By utilizing weighted recurrent layers, it can better exploit historical information. In situations with large load fluctuations, it may be difficult to accurately capture the dynamic changes of signals. This method demands high computational resources and is not suitable for resource-constrained environments. In contrast, the method proposed in this paper combines the advantages of CNNs in feature extraction with the capabilities of LSTMs in handling long-term dependencies in sequential data. By introducing an enhanced sparrow search algorithm and a learning mechanism, the classification performance and generalization ability of the model are further improved.
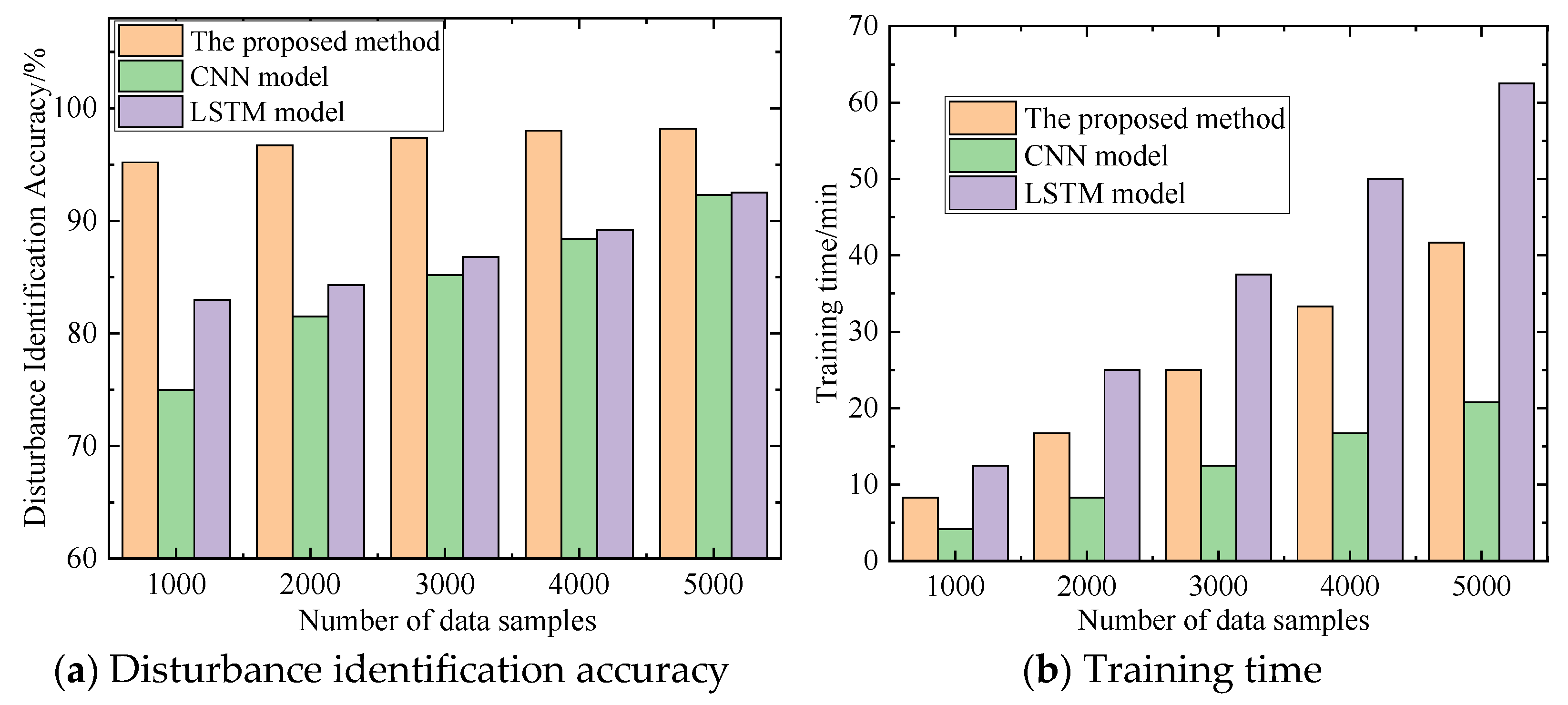
To provide a more intuitive comparison with traditional CNN and LSTM models, this paper analyzes the differences from two perspectives: identification accuracy and training time. The relevant data results are shown in
Figure 8a,b below.
It should be noted here that power quality disturbance identification mainly consists of three key steps: FST processing, model training, and inference. The time consumption for FST processing and model inference is minimal, generally completed within a few seconds. Therefore, this paper mainly compares the model training time. Observing
Figure 8, it can be found that the diagnostic accuracy of the method proposed in this paper is significantly better than that of traditional LSTM and CNN models. The training time increases linearly with the number of data samples. Among them, the CNN model has the shortest training time, while the LSTM model has a longer training time compared to CNN due to its higher time complexity. However, considering that model training can be done offline and only model inference and result output are required in the real-time stage, the above models can all meet the time requirements for online applications. Therefore, this paper mainly focuses on identification accuracy.
Although the power quality disturbance classification strategy based on the FST and the improved CNN-LSTM model proposed in the paper has achieved positive results in experimental validation, there are still some limitations. These limitations may stem from the size of the dataset, the complexity of the model, and the challenges of practical deployment. The complex CNN-LSTM model contains a large number of parameters, which increases the risk of overfitting. When the dataset size is insufficient to fully cover various possible disturbance scenarios, the model may learn noise or specific patterns in the dataset rather than the true disturbance characteristics. The CNN-LSTM model requires high-performance computing resources to support real-time or near-real-time processing. In practical deployment, specialized hardware (such as GPUs) may be needed to meet these requirements, which increases deployment costs. With the increasing complexity of power systems and the introduction of new types of power electronic equipment, power quality disturbances may change. Therefore, the model needs to be regularly updated to adapt to these changes, which requires continuous maintenance and updating capabilities. Lastly, it cannot be overlooked that although CNN-LSTM models perform well in classification, they are often considered “black box” models lacking interpretability. This may make it difficult to understand and trust the decision-making process of the model in practical deployment.