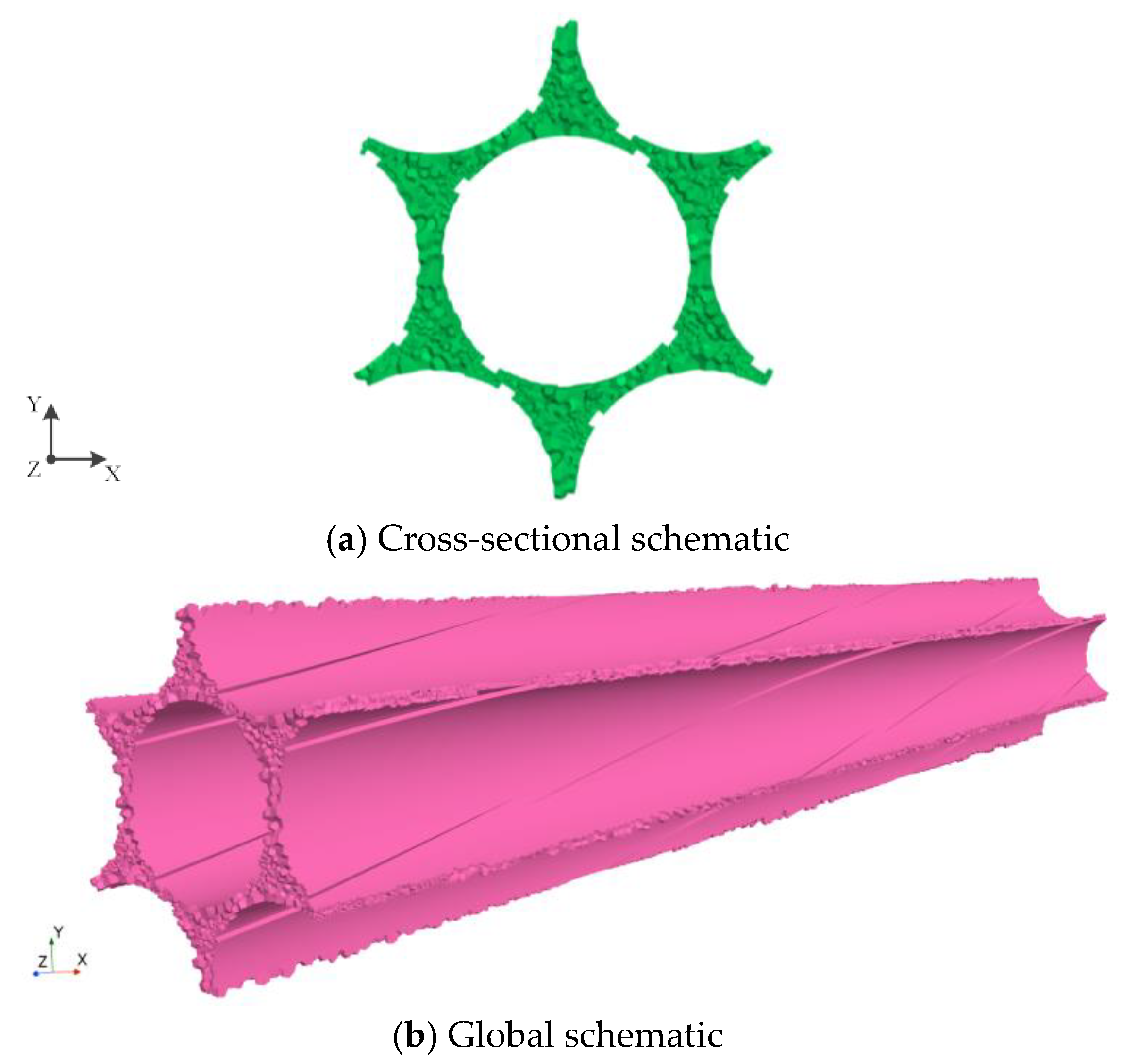
Numerical Study on Flow Characteristics of Spiral Channel with Coiled Wire
Abstract
1. Introduction
2. Experimental Facility
2.1. Experimental Loop
2.2. Instrumentation Systems
2.3. Uncertainty Analysis
3. Numerical Methods
3.1. Mathematical Model
- Continuity Equation:
3.2. Mesh Independence Verification
3.3. Validation of Model Accuracy
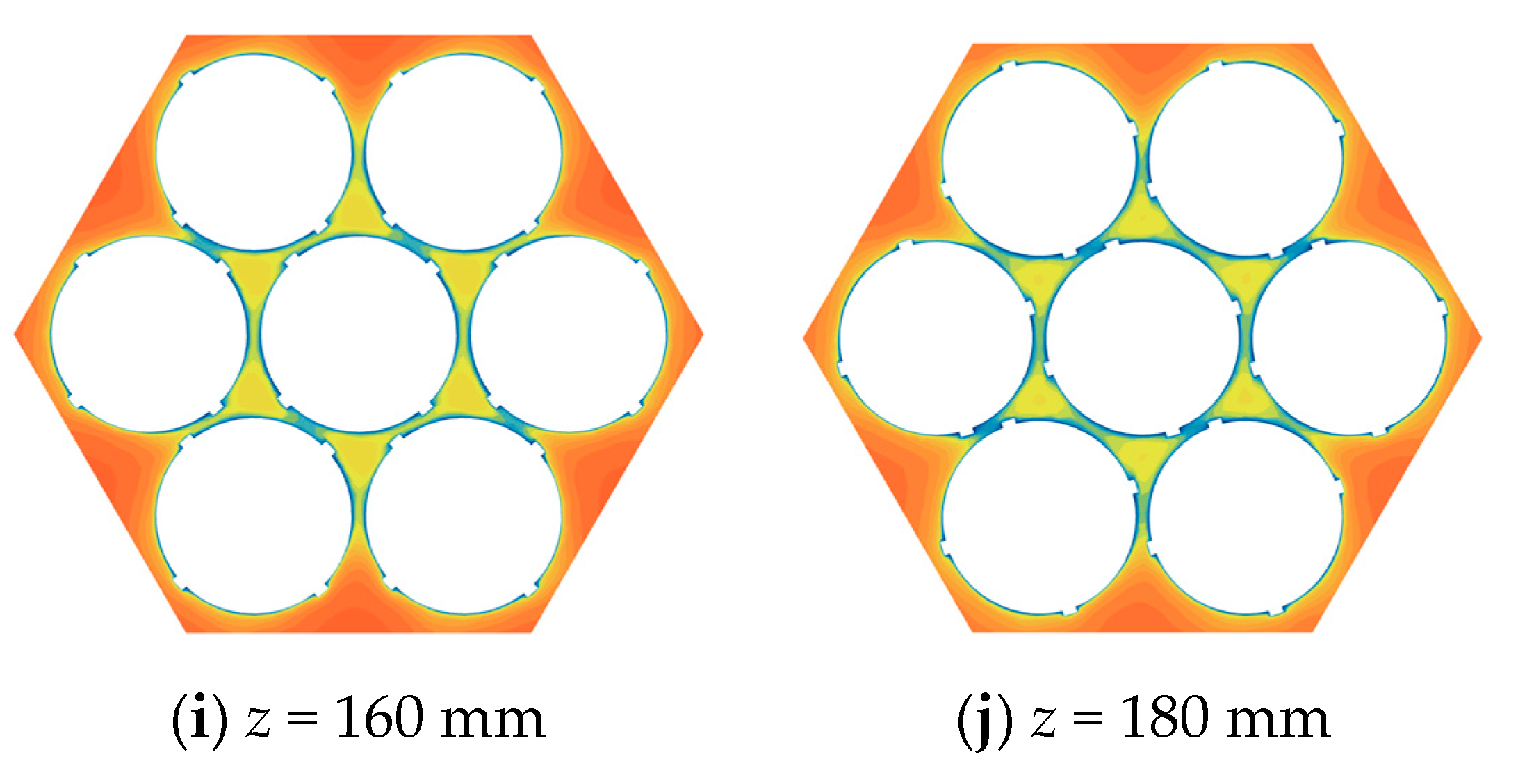
4. Determination of the Fully Developed Section
5. Results and Discussion
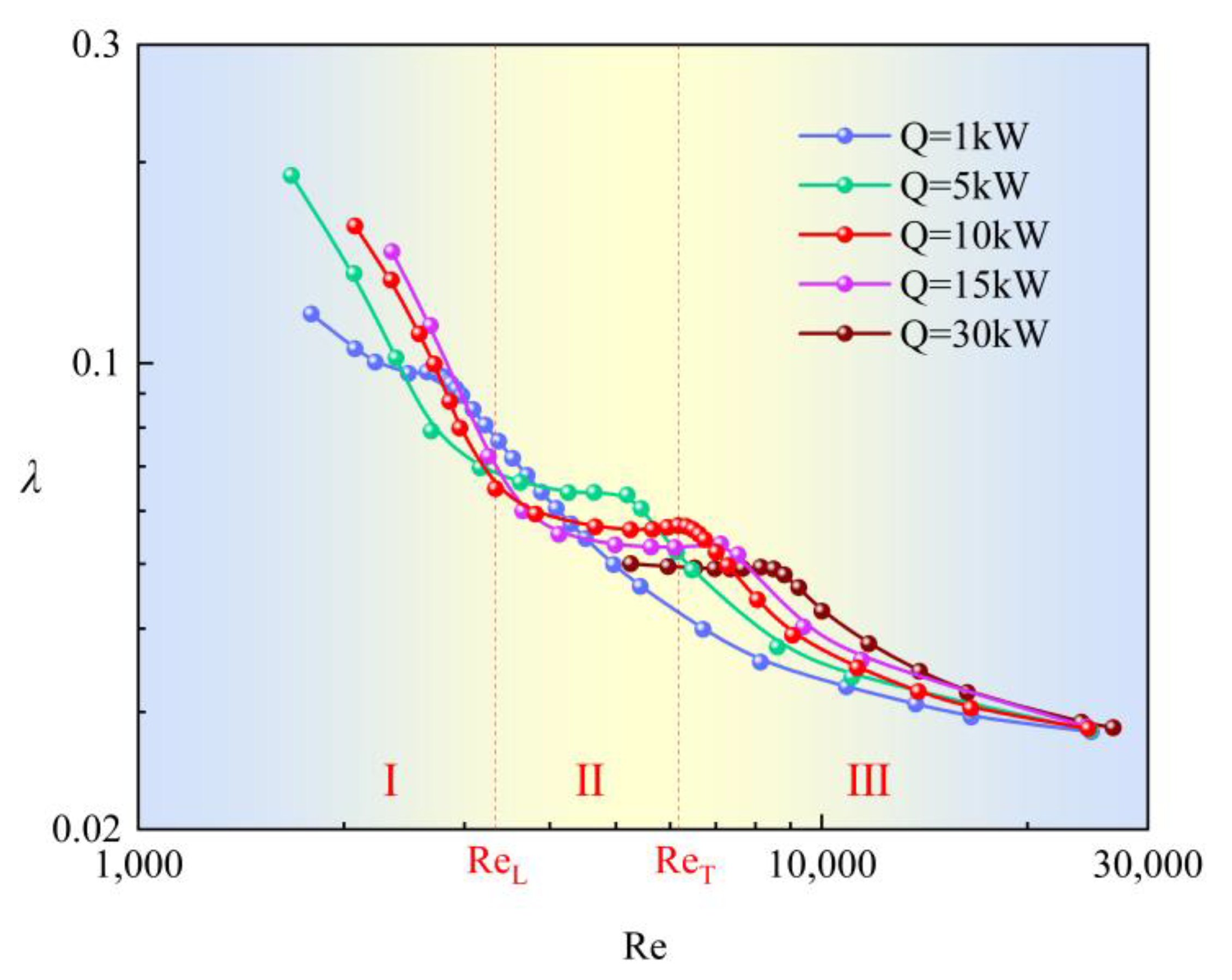
5.1. Numerical Analysis of Resistance Characteristics in Spiral Channel with Coiled Wire
- I.
- Laminar Region
- II.
- Transition Region
- III.
- Turbulent Region
5.2. Detailed Study of Axial Resistance Characteristics
5.2.1. Axial Frictional Resistance Characteristics in Laminar Region
5.2.2. Axial Frictional Resistance Characteristics in Transition Region
5.2.3. Axial Frictional Resistance Characteristics in Turbulent Region
6. Conclusions
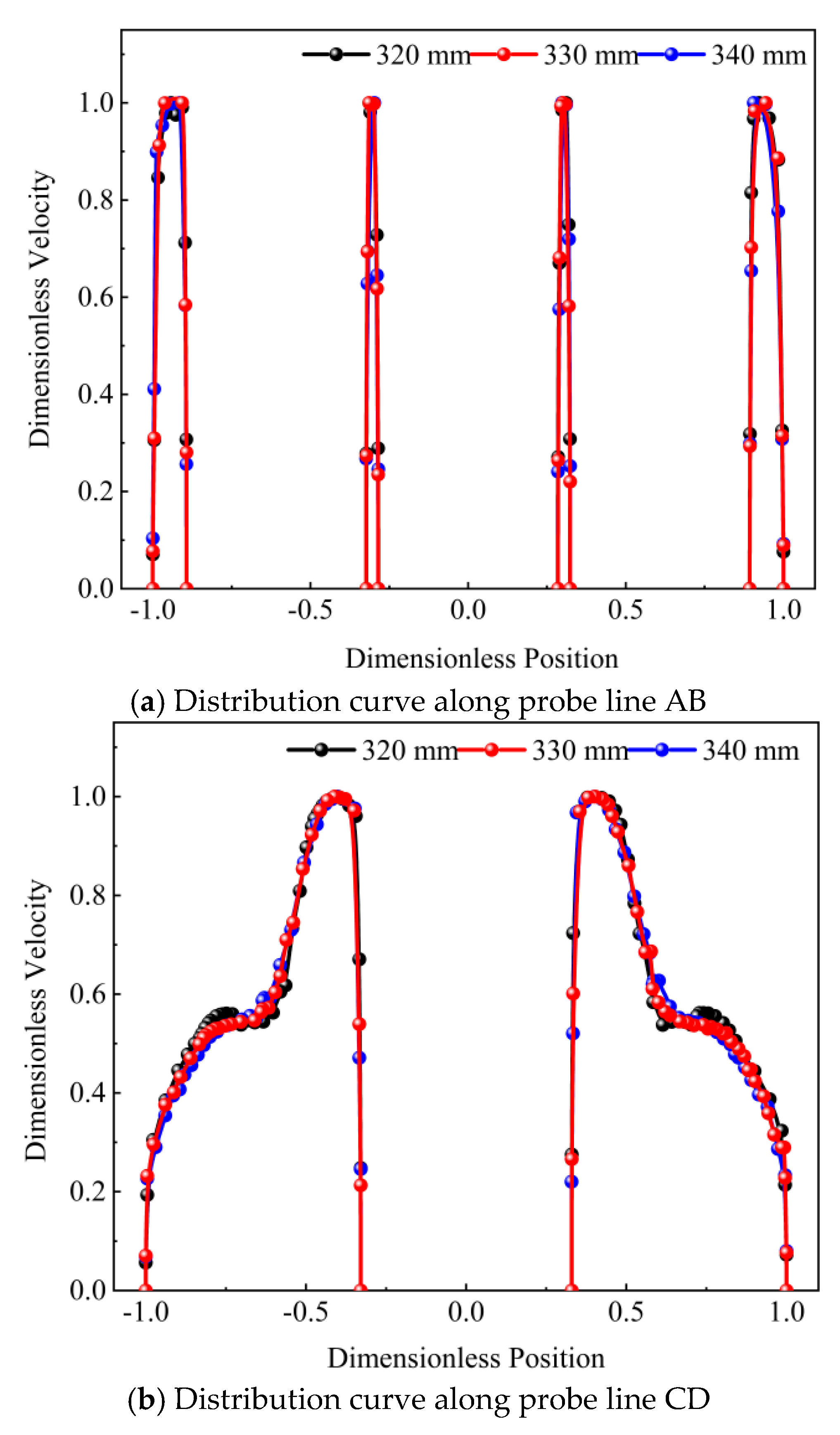
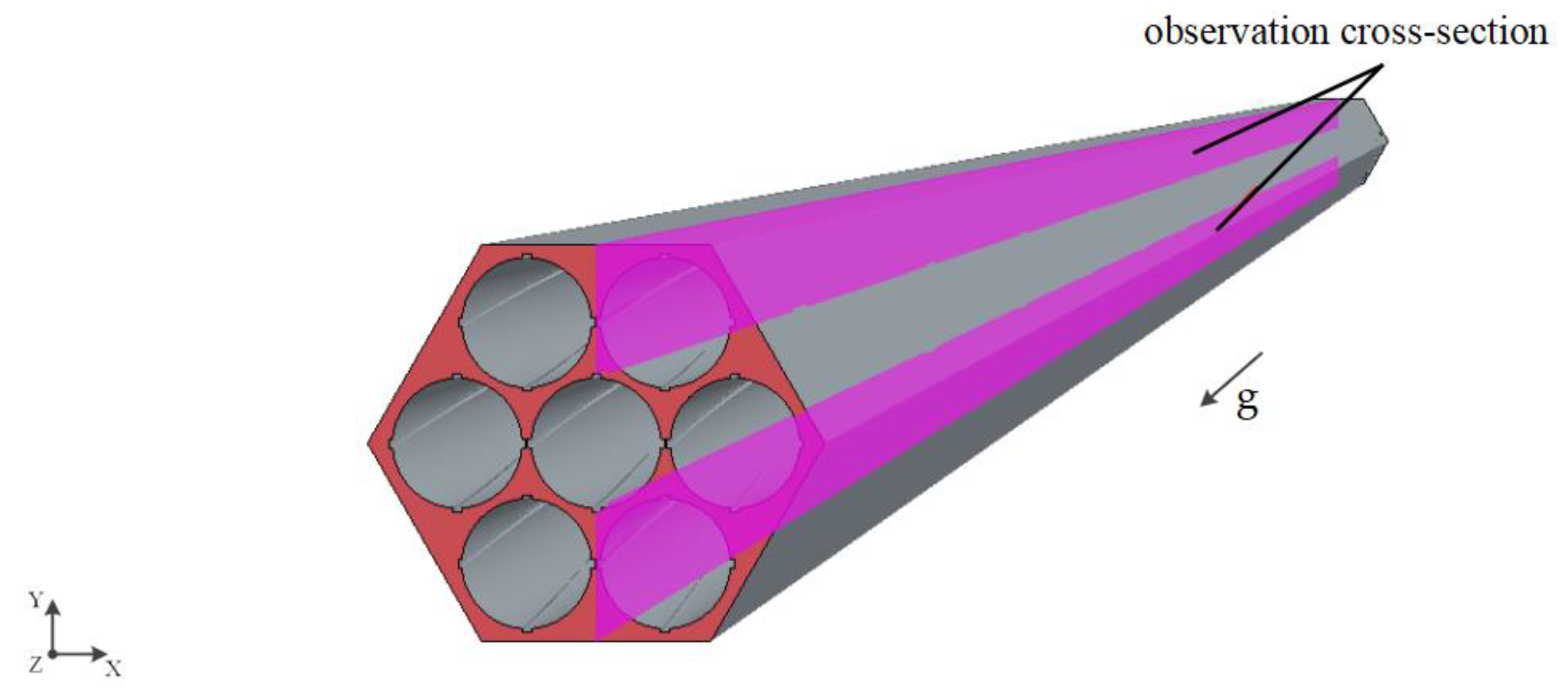
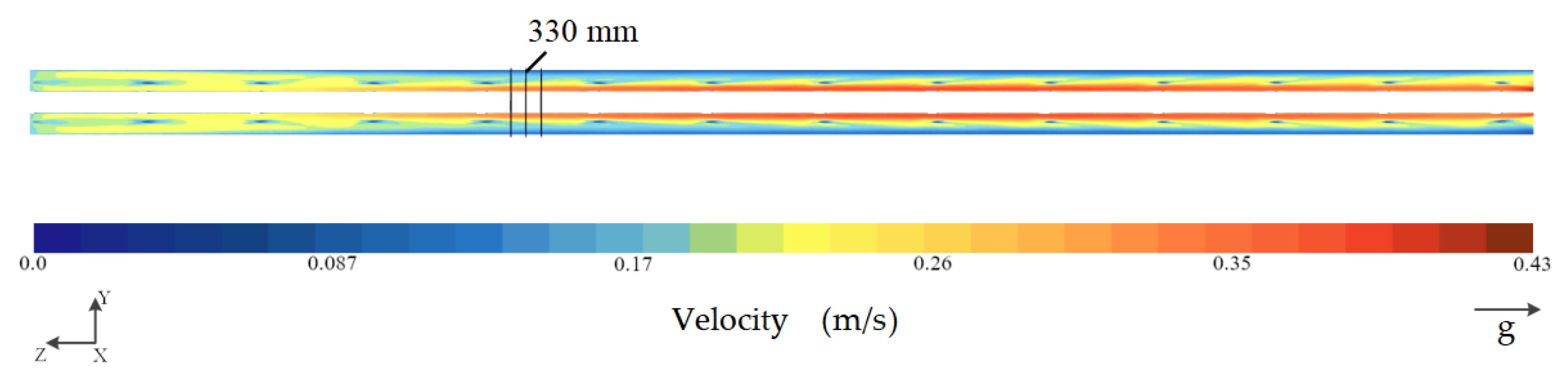
- By calculating the dimensionless velocities along two types of probe lines at different heights from the channel inlet and assessing the overlap of the dimensionless velocity curves at different heights, it is determined whether the fluid has reached full development. The variation of the velocity field along the axial direction of the channel is also considered to judge whether the fluid has fully developed. An evaluation criterion for the velocity distribution of fully developed fluid is provided. By calculating the ratio of the transverse fluctuating velocity to the mainstream velocity at different cross-sections from the channel inlet, it is concluded that full development is achieved when the ratio is below 11.5%. The study results show that for the coiled wire spiral channel on the primary side of the casing once-through steam generator, the inlet section length is L∗ = 80De.
- A numerical study under vertical conditions is conducted for a broad range of Reynolds numbers. The characteristic curve of the frictional resistance of the coiled wire spiral channel is divided into three regions based on the different characteristics of the frictional resistance under different Reynolds number ranges: laminar region, transition region, and turbulent region.
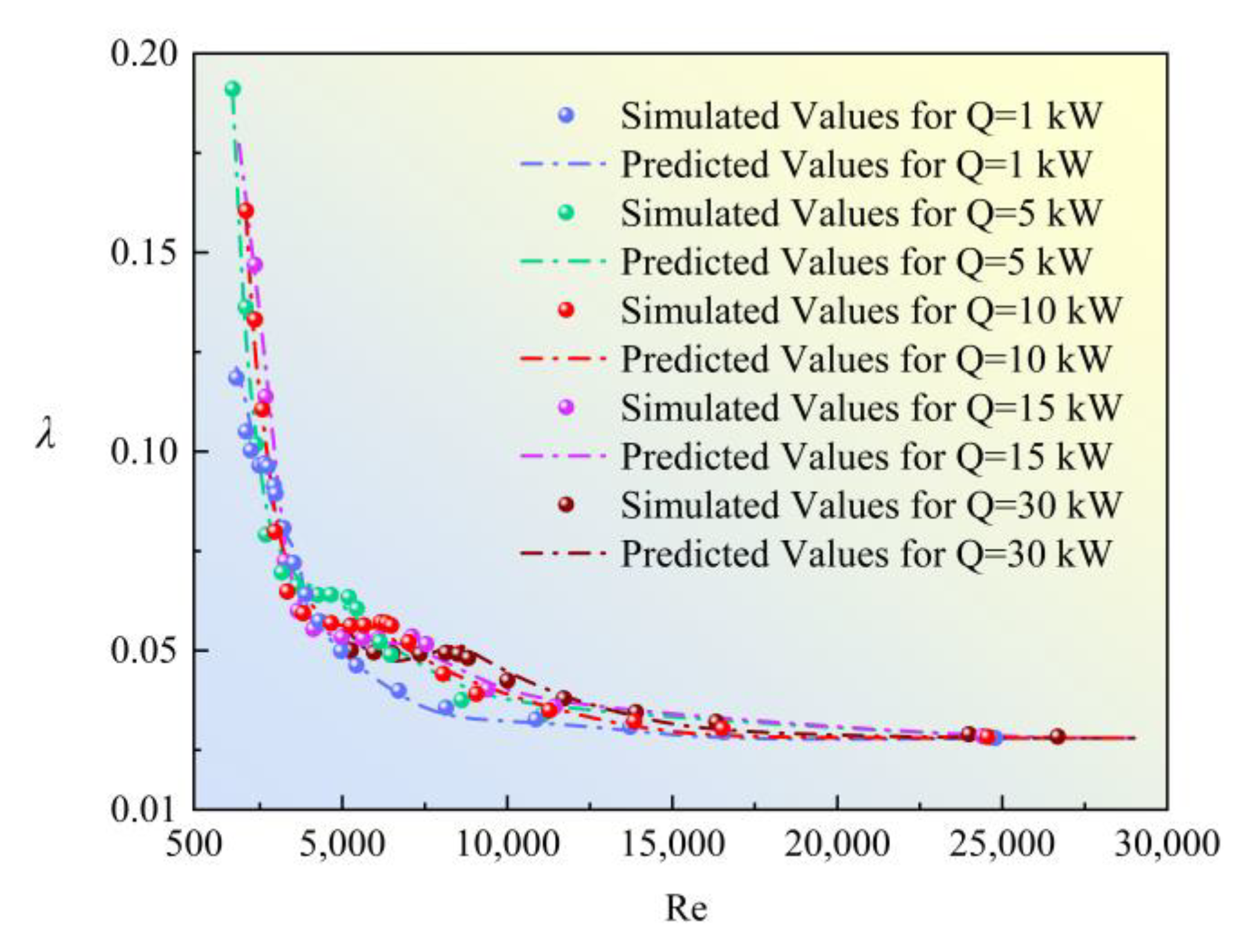
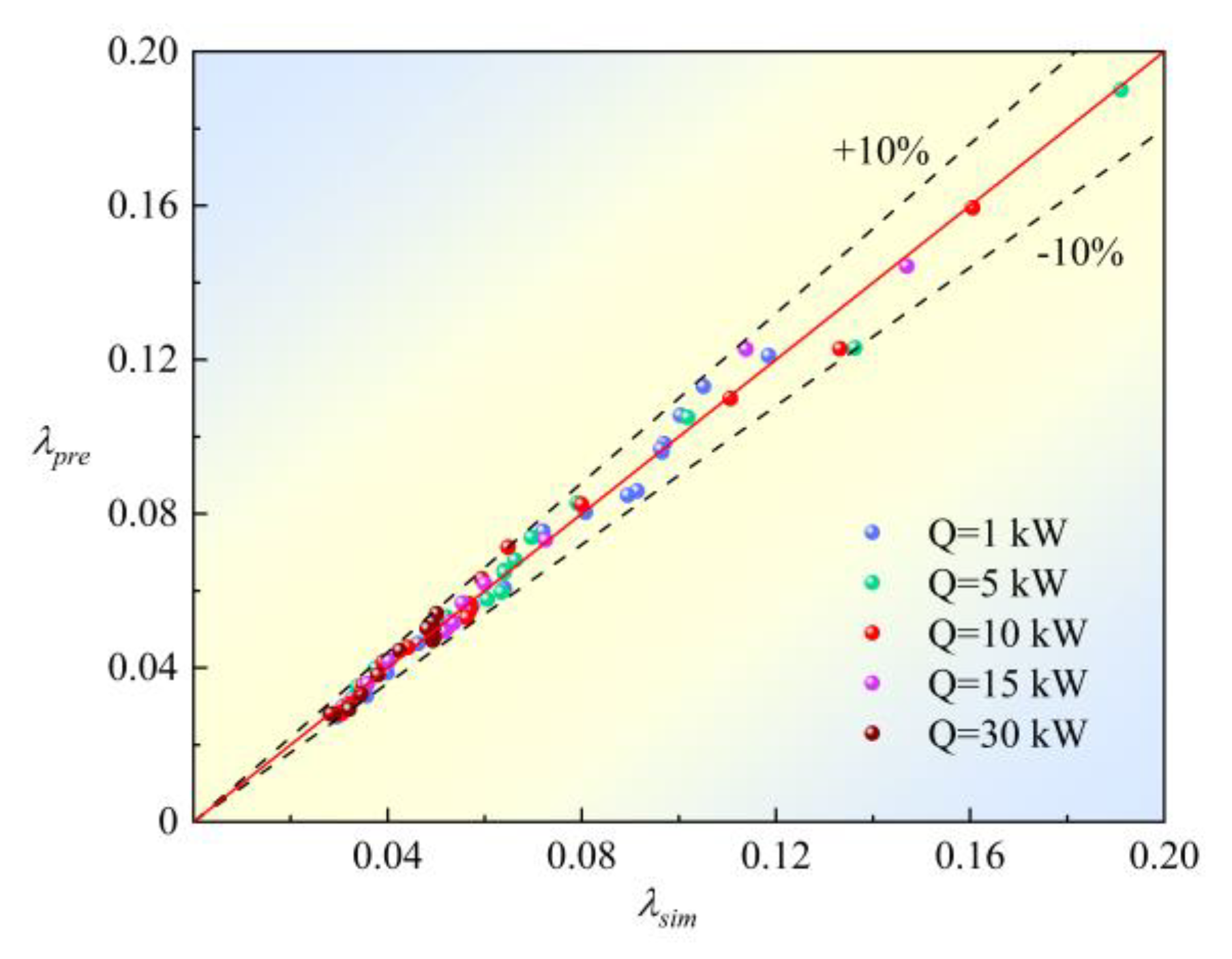
- The frictional resistance coefficient within the coiled wire spiral channel under vertical conditions is related to the fluid velocity, fluid property parameters, and channel structural parameters. Under the same heat transfer power, the frictional resistance coefficient of the coiled wire spiral channel decreases gradually with the increase of Reynolds number. By analyzing the data results under different heat transfer powers, a kinematic viscosity correction factor is introduced, and an expression for the frictional resistance coefficient of the channel is obtained. This predictive expression fits well with the frictional resistance characteristic curve of the coiled wire spiral channel, with a relative error within ±10%.
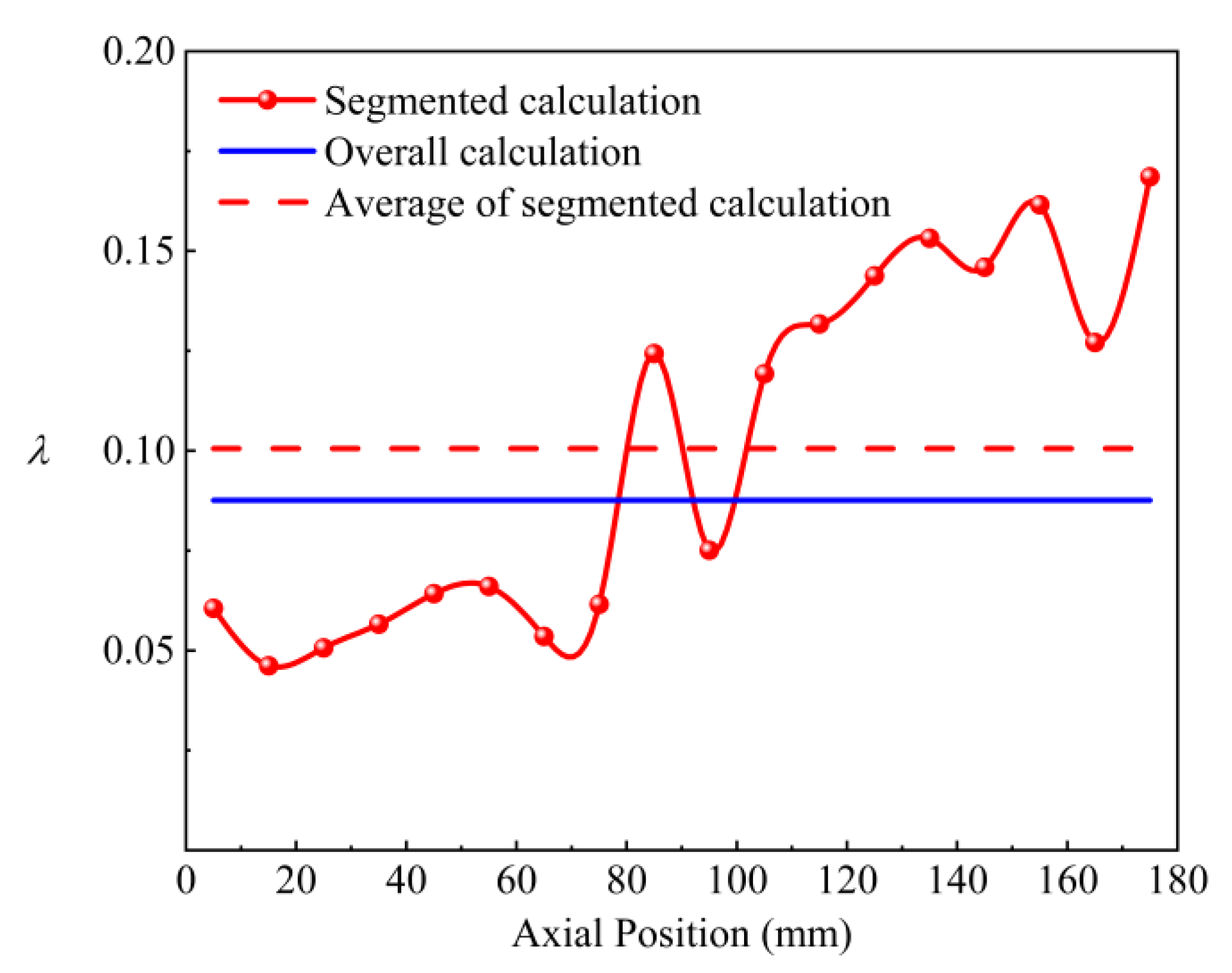
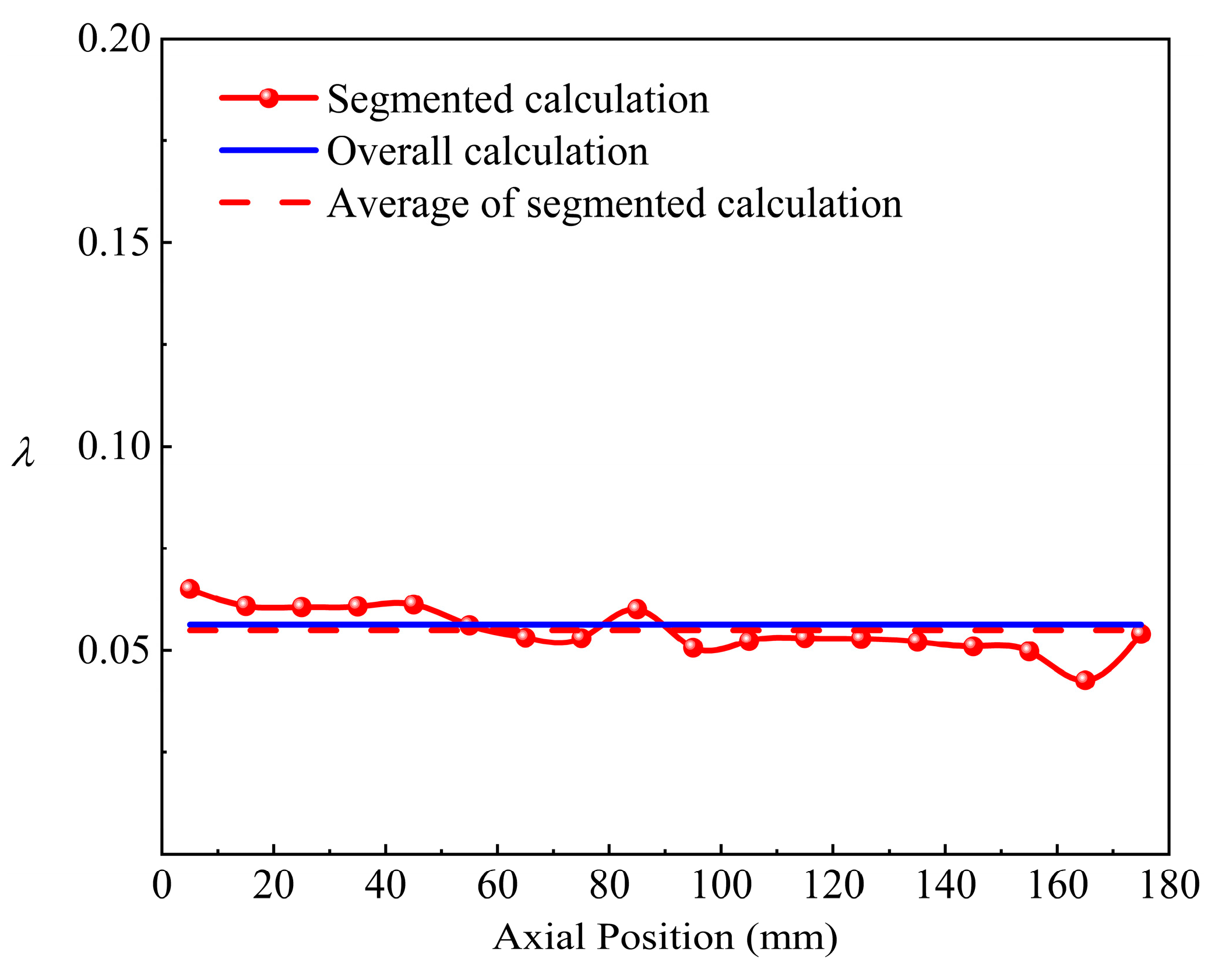
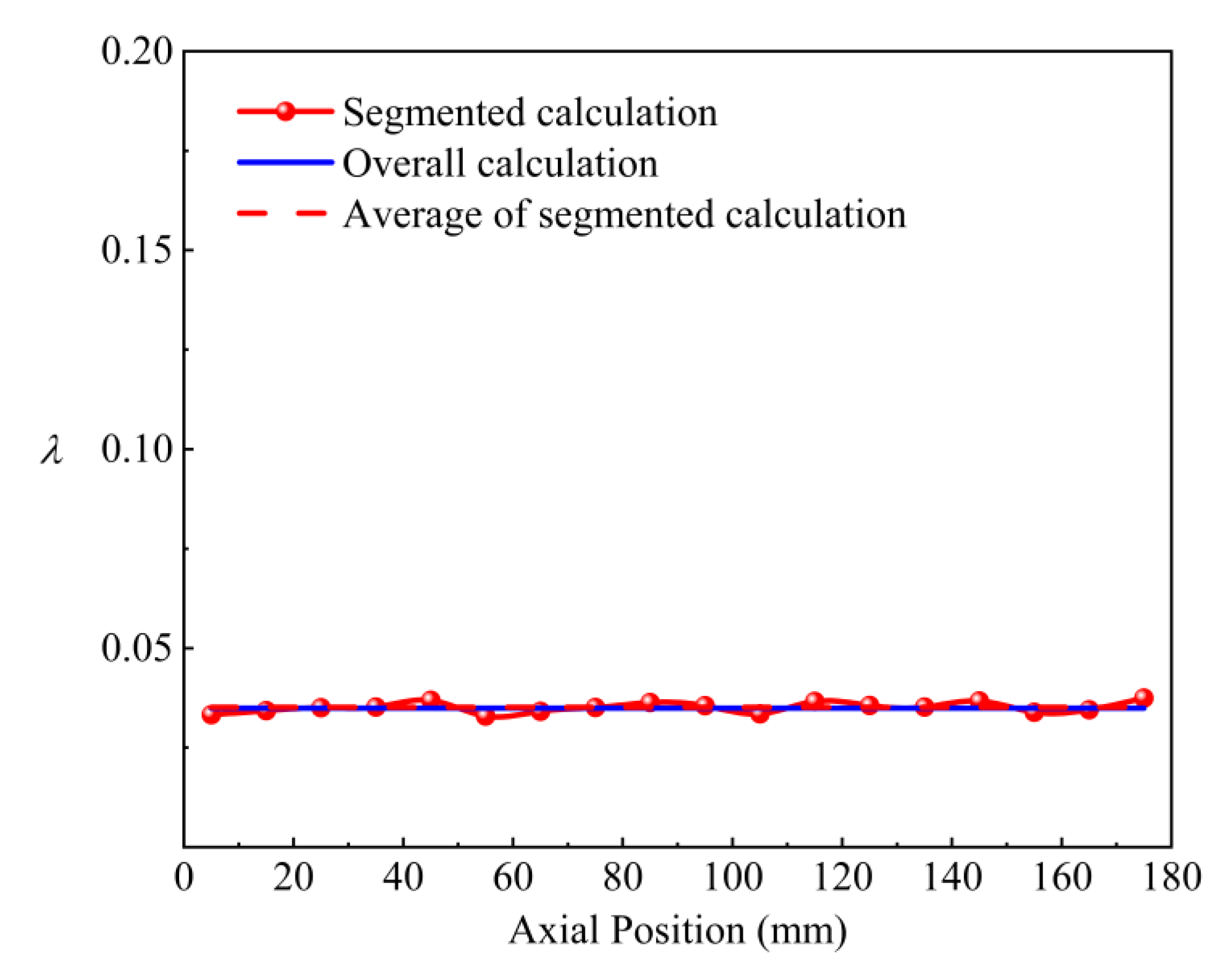
- It is found through the study of the frictional resistance coefficient along the axial direction of the coiled wire spiral channel under vertical conditions that, due to continuous heat transfer in the channel, the frictional resistance coefficient fluctuates at different positions along the channel. In the laminar condition, the fluid velocity is low, and the frictional resistance coefficient fluctuates significantly due to the strong influence of heat transfer conditions. The frictional resistance coefficient in the channel increases overall in the direction of fluid flow. In the transition condition, the fluid velocity is slightly higher, and the influence of heat transfer conditions is reduced, leading to smaller fluctuations in the frictional resistance coefficient, which decreases overall in the direction of fluid flow. In the turbulent condition, the fluid velocity is the highest, and the influence of heat transfer conditions is the smallest, resulting in the smallest fluctuations in the frictional resistance coefficient, which remains essentially constant in the direction of fluid flow. The frictional resistance coefficient of the heat transfer channel calculated using the segmented method is more accurate than that obtained from traditional algorithms and better reflects the changes along the flow direction of the channel. The more segments used in the calculation, the closer the results are to the actual conditions. When the fluid velocity is high, the traditional algorithm can ensure the credibility of the frictional resistance coefficient calculation results to some extent.
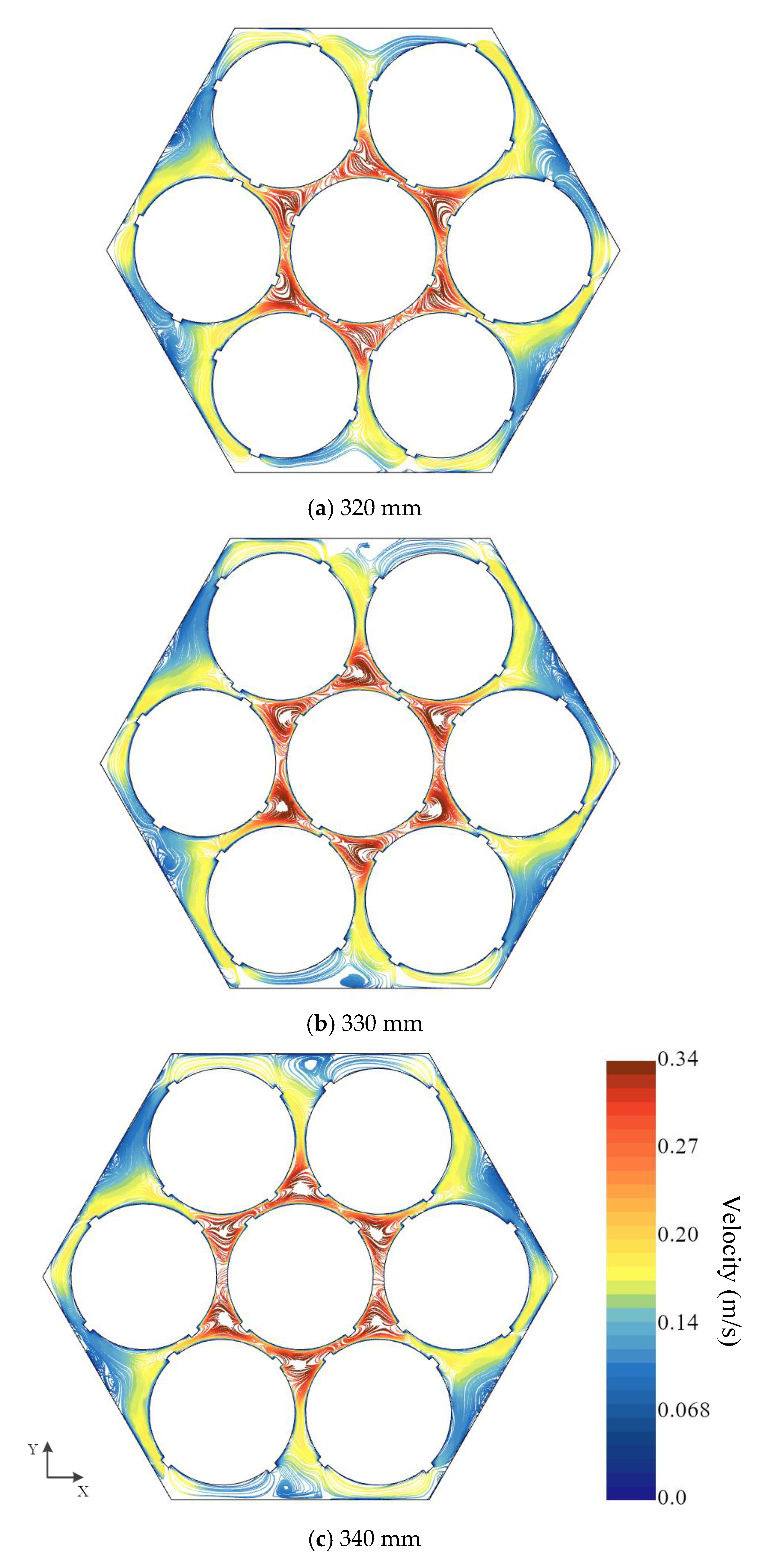
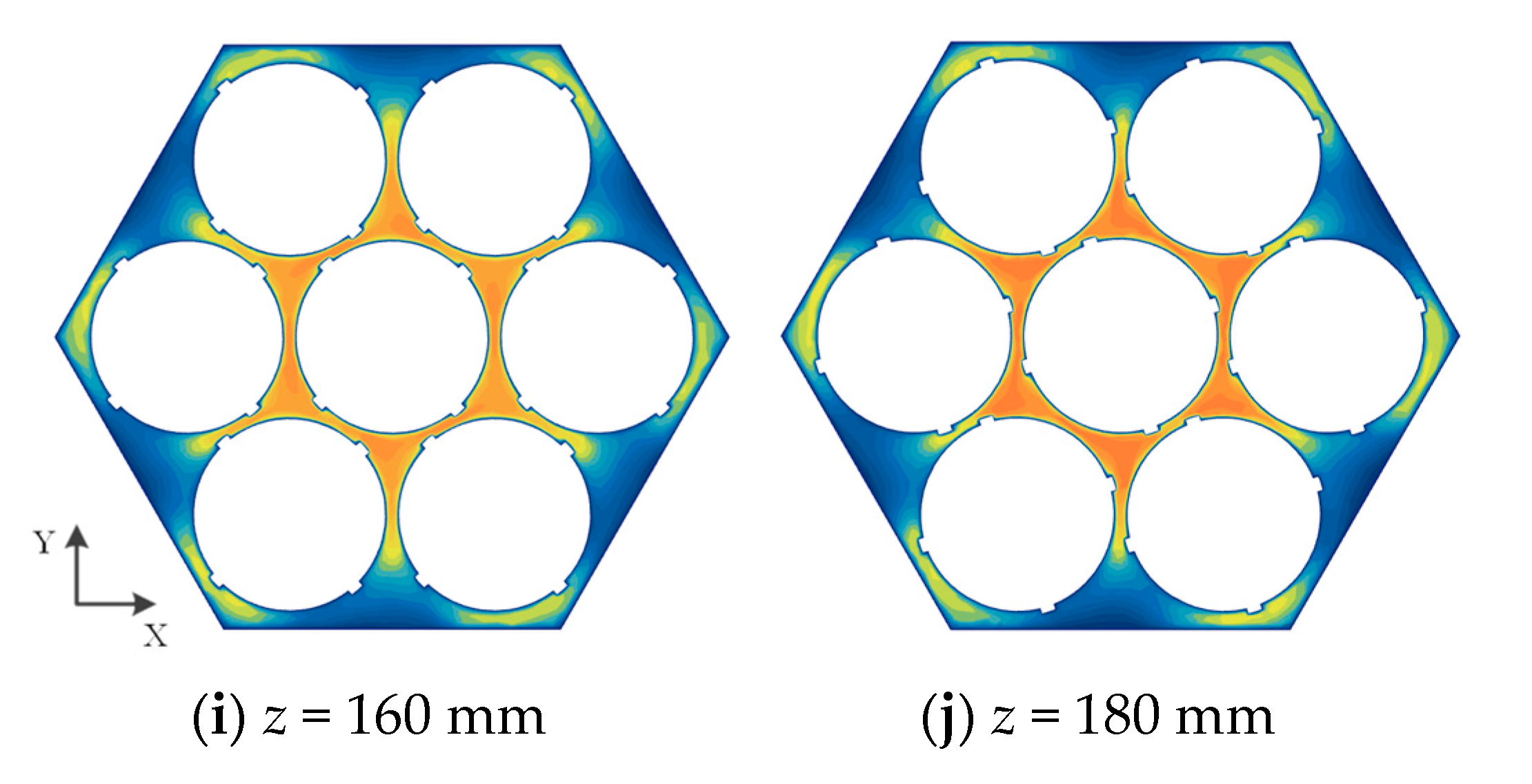
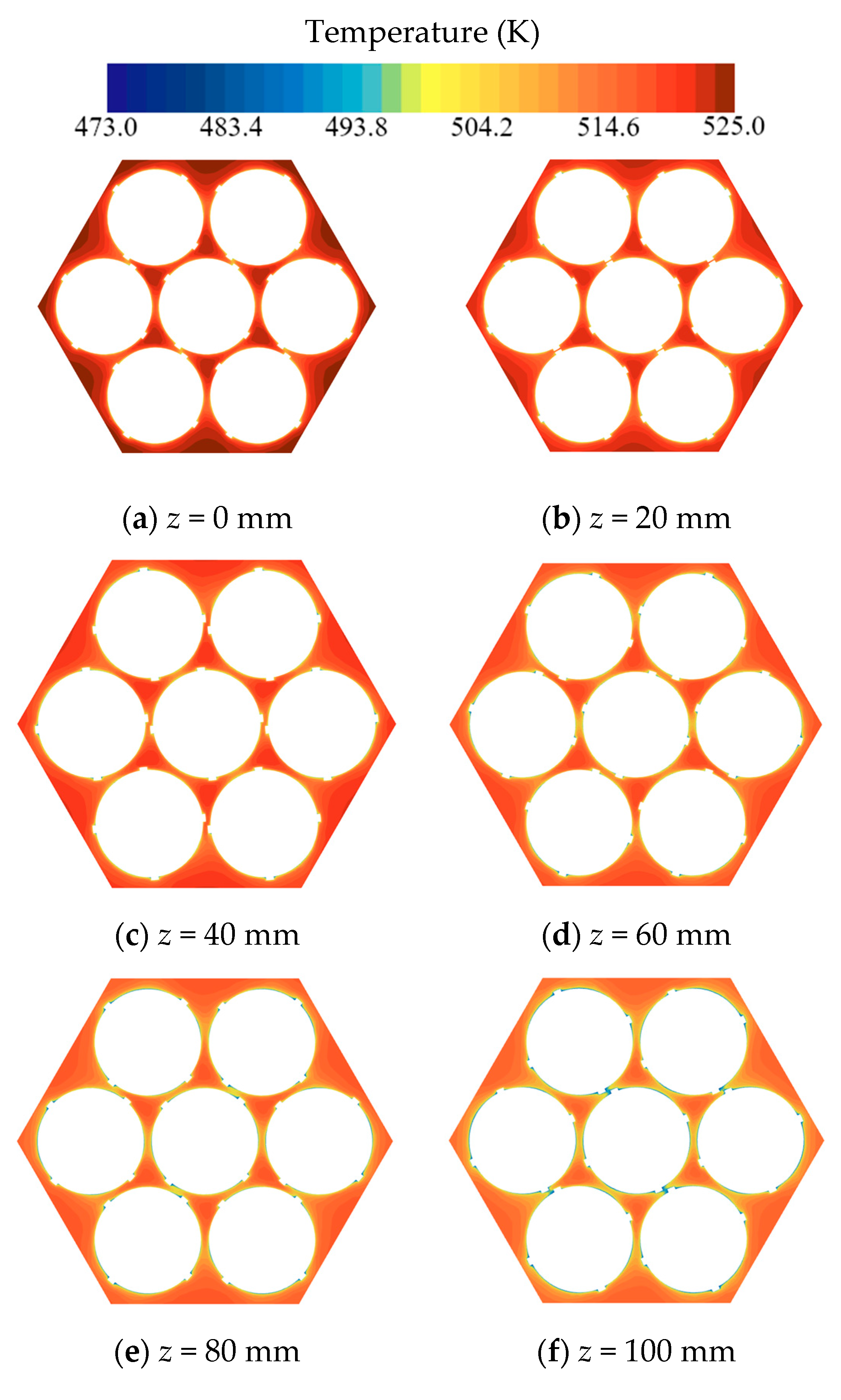
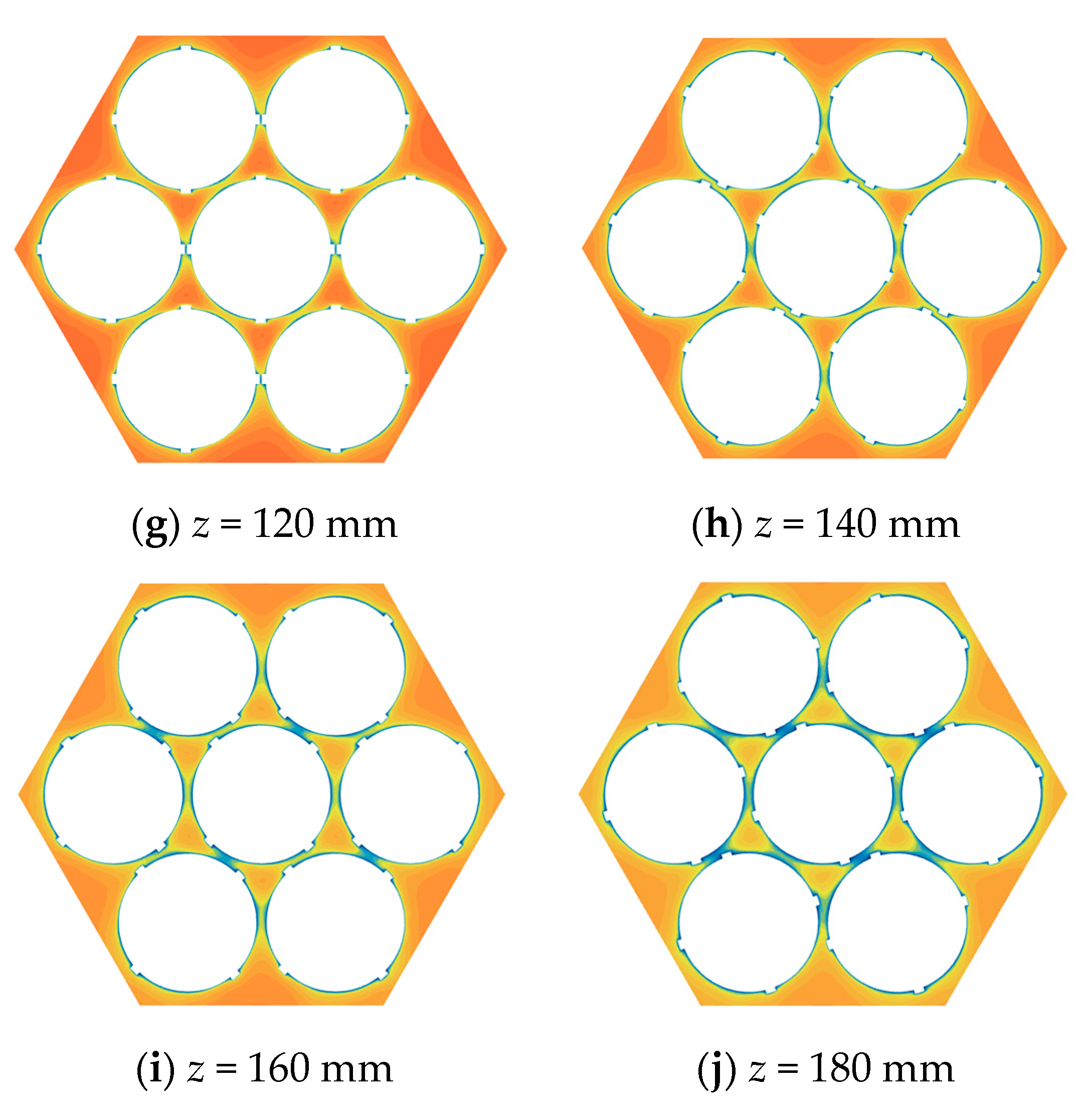
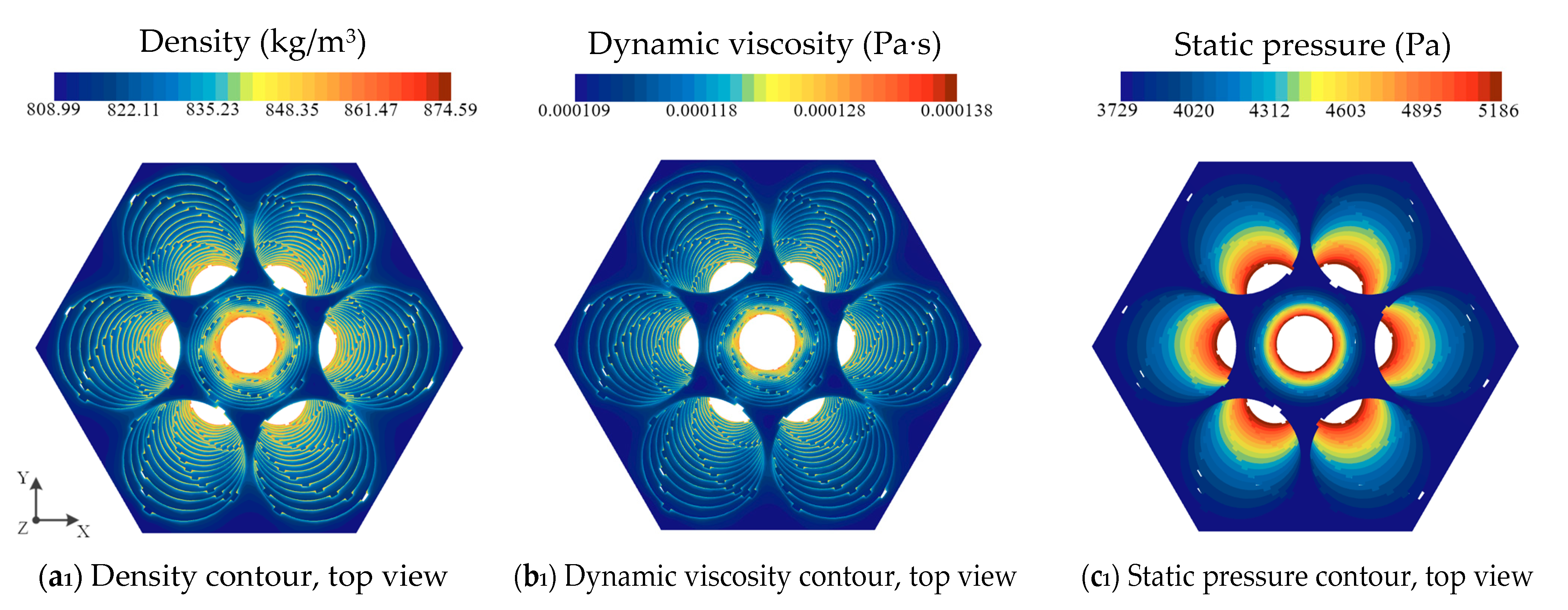
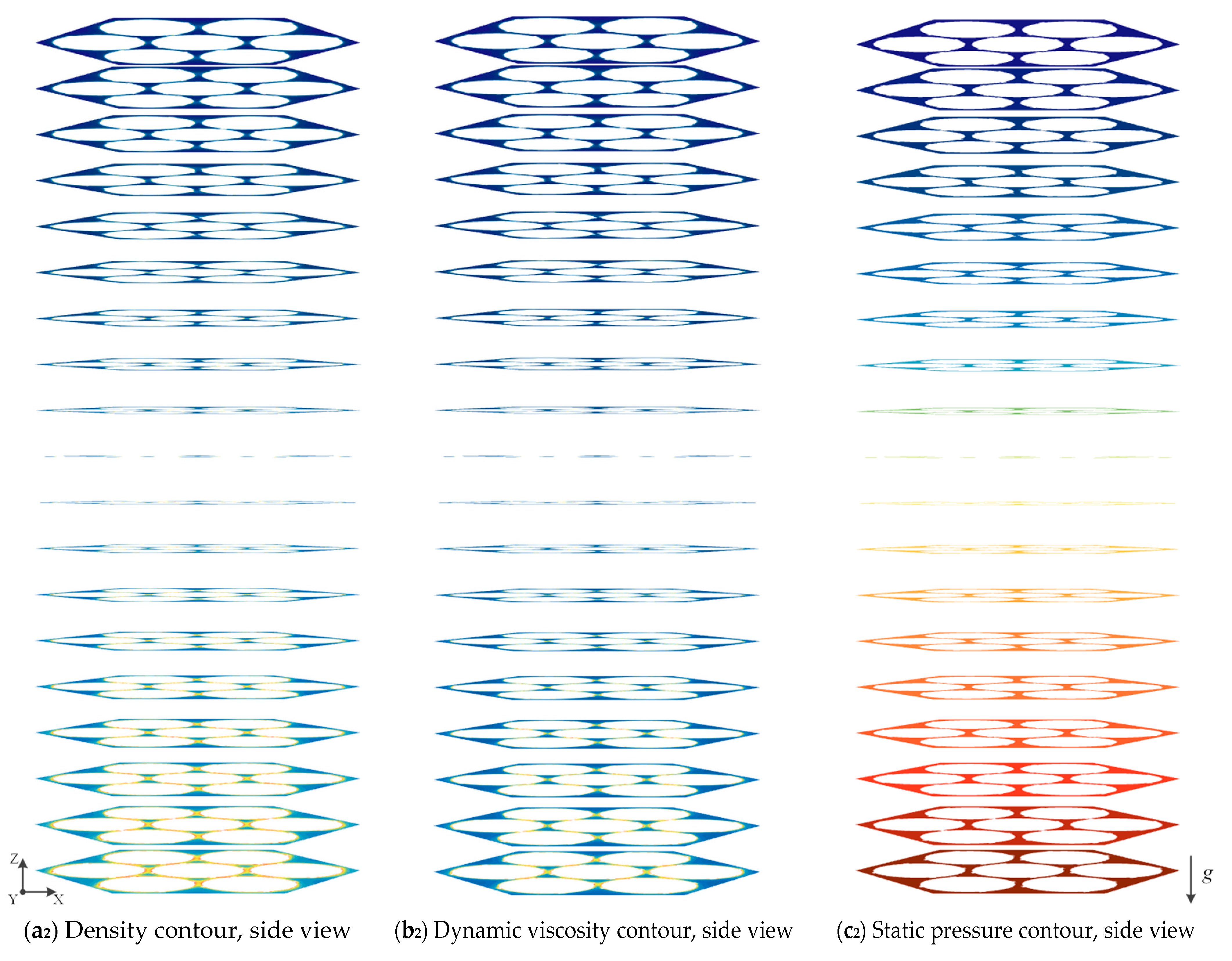
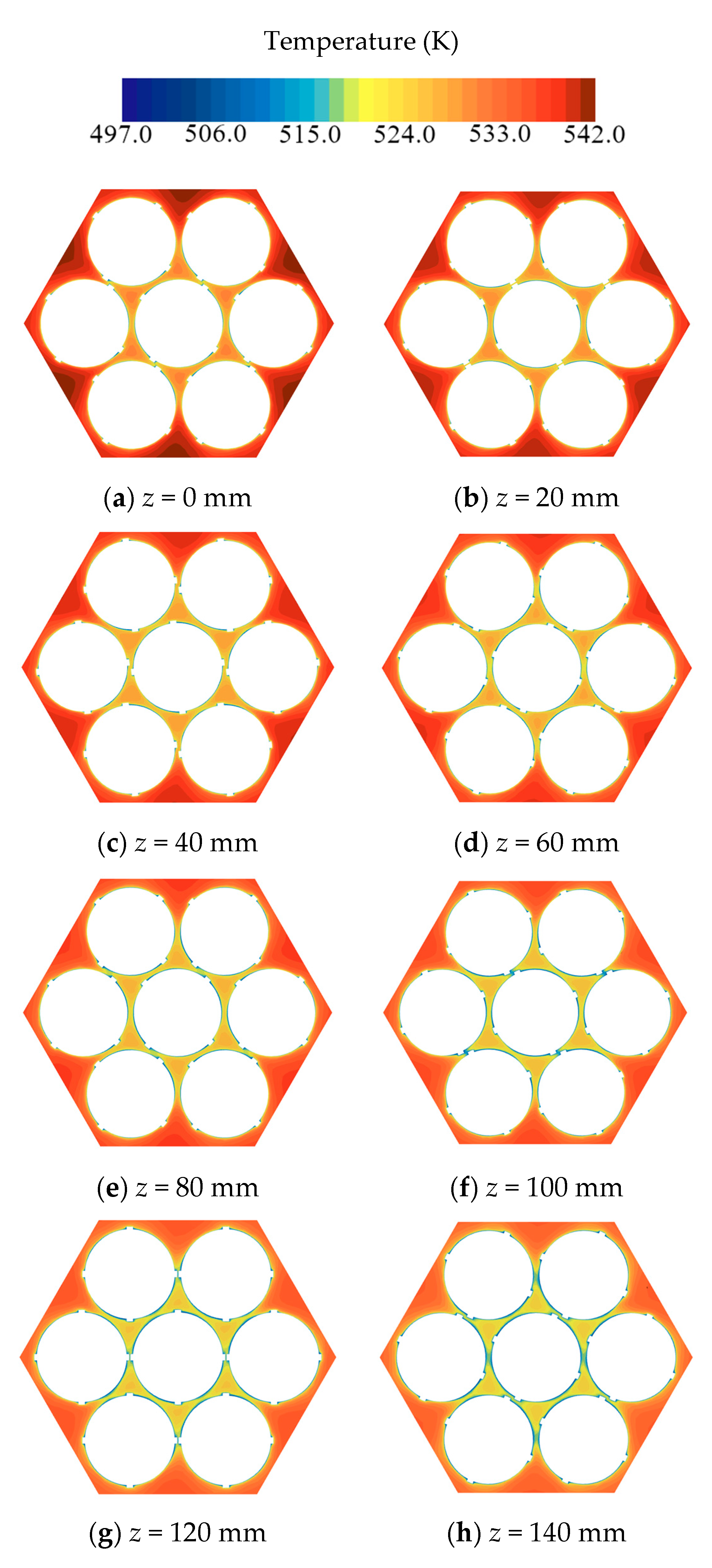
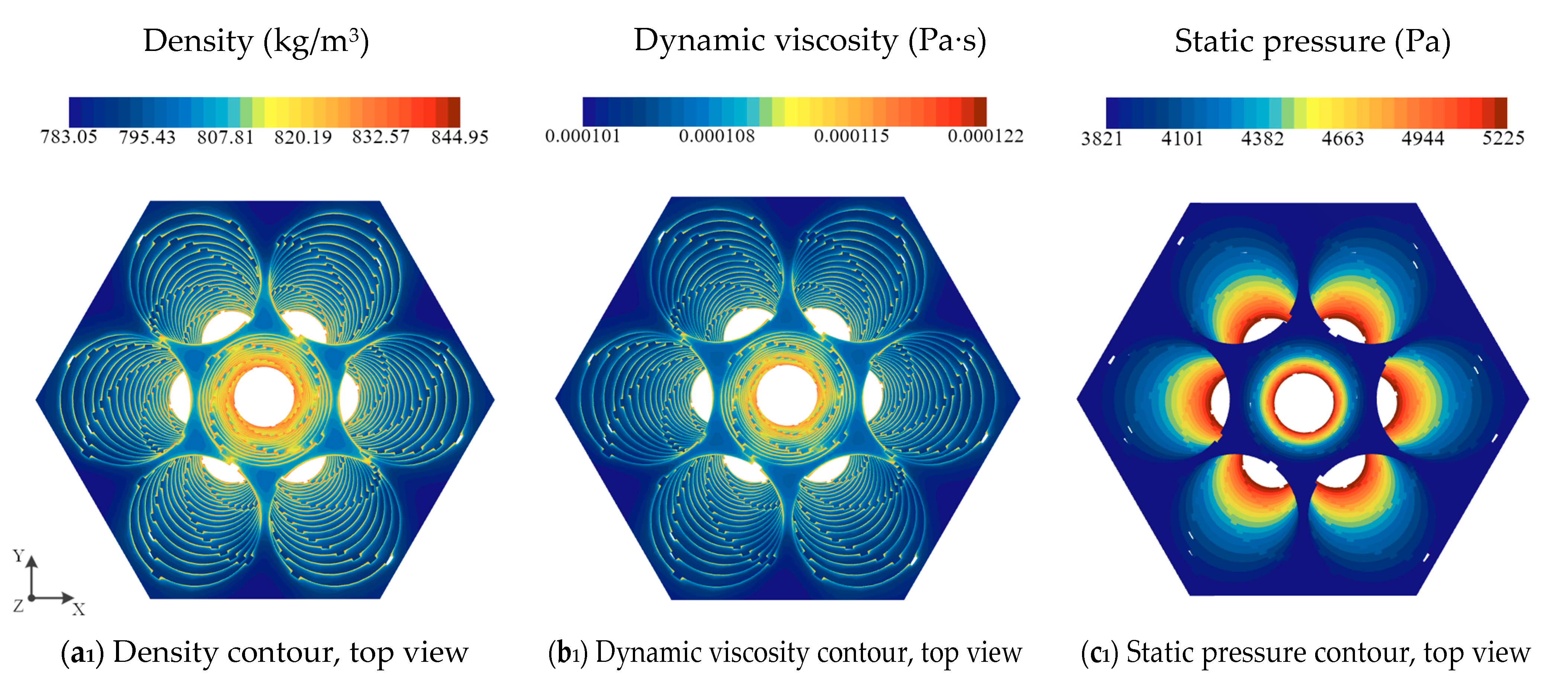
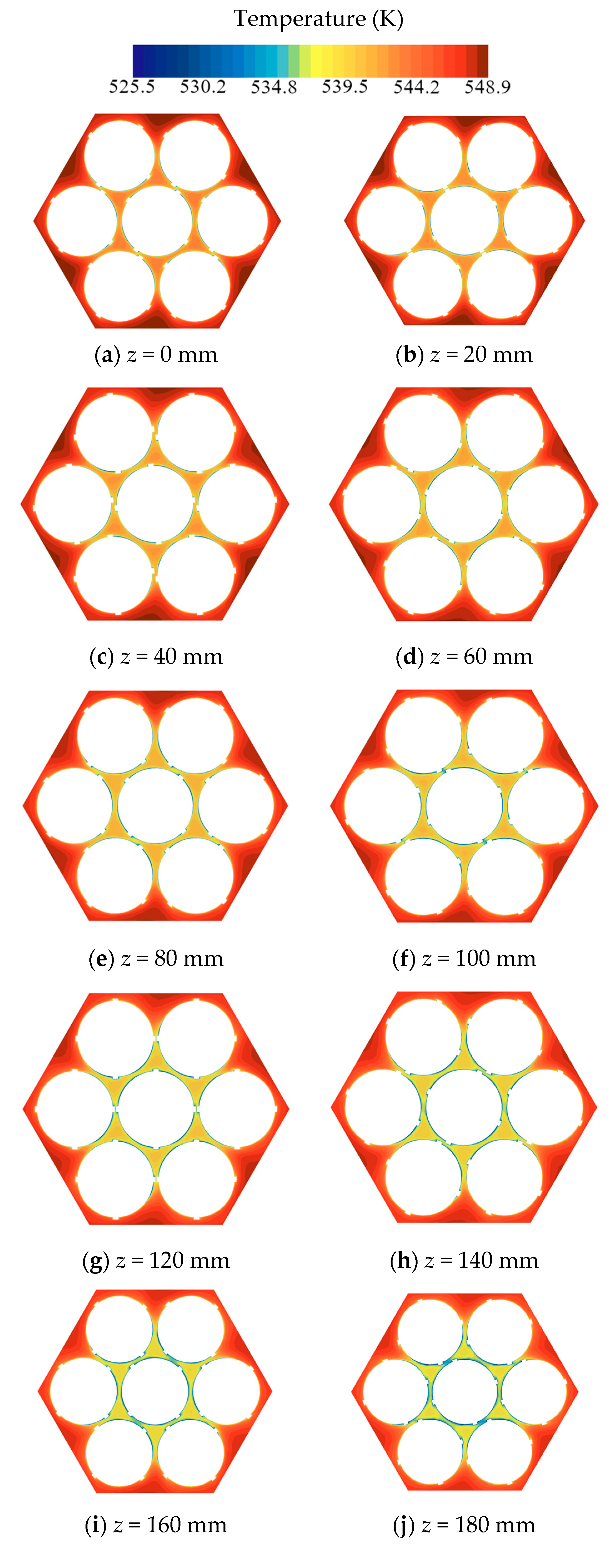
- Through the analysis of the flow field at different axial positions along the cooling channel, a deeper understanding of the variation patterns of flow along the axial direction of the heat transfer channel is achieved. As the fluid in the coiled wire spiral channel is continuously cooled, for the velocity field, the fluid velocity in the central sub-channels decreases gradually in the laminar condition, increases gradually in the transition condition, and remains essentially unchanged in the turbulent condition. The maximum velocity distribution at different cross-sections occurs at the center of the central sub-channels in the laminar and transition conditions, while it occurs at the boundary sub-channels in the turbulent condition. For the temperature field, the fluid temperature near the heat transfer wall decreases first. When the wires meet, the fluid temperature decreases further. Under the influence of the coiled wire, the fluid mixing is more thorough, and heat transfer is enhanced, making the fluid temperature in the channel more uniform. This leads to an overall decrease in the fluid temperature in the central sub-channels, followed by a decrease in the fluid temperature in the corner and boundary sub-channels.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | cross-sectional flow area, m2 |
| C | constant |
| ct | kinematic viscosity correction coefficient |
| De | equivalent diameter, m |
| E | total energy per unit mass, kJ/kg |
| body force, N/m3 | |
| G | mass flux, kg/m2·s |
| unit tensor | |
| L | channel total length, m |
| L2 | second piezometric section length, m |
| L∗ | entrance length, m |
| Q | heat transfer power, kW |
| heat flux, kW/m2 | |
| p | pressure, Pa |
| Re | Reynolds number |
| heat source per unit volume, kW/m3 | |
| T | temperature, K |
| viscous stress tensor, kJ/m3 | |
| trace of the Reynolds stress tensor | |
| v | velocity, m/s |
| V | dimensionless velocity |
| w | uncertainty |
| ΔP | pressure drop, Pa |
| ΔPf | frictional pressure drop, Pa |
| Greek letters | |
| χ | wetted perimeter, m |
| ρ | density, kg/m3 |
| υ | kinematic viscosity, m2/s |
| λ | frictional resistance coefficient |
| second-order tensor, kJ/m3 | |
| ϕ | intermittency factor |
| Subscripts | |
| i | inlet |
| o | outlet |
| m | maximum |
| L | laminar |
| T | turbulent |
| w | wall |
| f | fluid |
| Abbreviations | |
| COTSG | Casing Once-Through Steam Generator |
| CFD | Computational Fluid Dynamics |
| RST | Reynolds stress transport |
| RANS | Reynolds-Averaged Navier-Stokes |
References
- Yang, C.; Fang, C.; Tong, J. Necessity of Developing Nuclear Energy in China. Nucl. Power Eng. 2014, 35 (Suppl. 1), 200–202. [Google Scholar]
- Cheng, S.K.; Todreas, N.E. Hydrodynamic models and correlations for bare and wire-wrapped hexagonal rod bundles—Bundle friction factors, subchannel friction factors and mixing parameters. Nucl. Eng. Des. 1986, 92, 227–251. [Google Scholar] [CrossRef]
- Gu, H. Study on Mechanism of Heat Transfer Enhancement of Vortex Flow in Complex Channels. Southeast University, 2021. Available online: https://cdmd.cnki.com.cn/Article/CDMD-10286-1022462780.htm (accessed on 23 February 2025).
- Ghobadi, M.; Muzychka, Y.S. Pressure drop in mini-scale coiled tubing. Exp. Therm. Fluid Sci. 2014, 57, 57–64. [Google Scholar] [CrossRef]
- Zhang, L.; Xing, Y.; Wu, J. Flow characteristics in helical duct with rectangular cross section. J. Chem. Ind. Eng. 2010, 61, 1089–1096. [Google Scholar]
- Nobari, M.R.H.; Shiniyan, B.; Mirzaei, M. Mixed convection in a vertical helical annular pipe. Int. J. Heat Mass Transf. 2014, 73, 468–482. [Google Scholar] [CrossRef]
- Liu, L.; Shen, C.; Liu, M.; Xiao, Y.; Cong, T.; Gu, H. Numerical simulation of the thermal-hydraulic characteristics of the liquid metal flow across the single-start helical coiled tube bundles. Prog. Nucl. Energy 2024, 173, 105270. [Google Scholar] [CrossRef]
- Wang, C.; Chen, S.; Tian, W.; Su, G.; Qiu, S. Thermal-hydraulic analysis of He–Xe gas mixture in 2×2 rod bundle wrapped with helical wires. Nucl. Eng. Technol. 2023, 55, 2534–2546. [Google Scholar] [CrossRef]
- Yang, Y. Thermal-hydraulic characteristics of FLiBe in annuli with helical wire. Int. J. Mech. Sci. 2023, 243, 108056. [Google Scholar] [CrossRef]
- Yuan, X.; Guo, Y.; Zhou, J.; Zhang, B.; Wei, J.; Tan, W.; Chen, Y.; Yang, S. Numerical study on the thermal hydraulic characteristics in mixed pattern of wire-wrapped bundle for fast reactor annular fuel assembly. Ann. Nucl. Energy 2023, 181, 109541. [Google Scholar] [CrossRef]
- Saha, G.; Paul, M.C. Investigation of the characteristics of nanofluids flow and heat transfer in a pipe using a single phase model. Int. Commun. Heat Mass Transf. 2018, 93, 48–59. [Google Scholar] [CrossRef]
- Saha, G.; Paul, M.C. Numerical analysis of the heat transfer behaviour of water based Al2O3 and TiO2 nanofluids in a circular pipe under the turbulent flow condition. Int. Commun. Heat Mass Transf. 2014, 56, 96–108. [Google Scholar] [CrossRef]
- Saha, G.; Paul, M.C. Heat transfer and entropy generation of turbulent forced convection flow of nanofluids in a heated pipe. Int. Commun. Heat Mass Transf. 2015, 61, 26–36. [Google Scholar] [CrossRef]
- Saha, G.; Paul, M.C. Analysis of Heat Transfer and Entropy Generation of TiO2-Water Nanofluid Flow in a Pipe under Transition. Procedia Eng. 2015, 105, 381–387. [Google Scholar] [CrossRef][Green Version]
- Islam, M.Z.; Saha, G.; Chin, Y.S.; Saha, S.C. Heat transfer intensification in a horizontal tube utilizing hexagonal perforated tube inserts. J. Nav. Archit. Mar. Eng. 2024, 21, 155–168. [Google Scholar]
- Golam, A.S. Experimental and Numerical Investigation of the Performance of Turbulent Heat Transfer in Tubes with Different Cross-Sectioned Wire Coils. Front. Heat Mass Transf. 2024, 22, 633–653. [Google Scholar] [CrossRef]
- Mousavi Ajarostaghi, S.S.; Basem, A.; Al-Mansoori, K.W.; Sultan, A.J.; Al-Yasiri, M.; Karouei, S.H.H.; Ahangaran, H. Numerical evaluation of the impact of using spiral innovative turbulator on improving the thermal performance of a helical double-pipe heat exchanger. Int. J. Thermofluids 2024, 24, 100830. [Google Scholar] [CrossRef]
- Ali, E.; Park, C.; Kim, D.; Park, H. Performance improvement of high voltage direct current devices by using a novel vortex generating heat sink design. Int. J. Therm. Sci. 2025, 210, 109624. [Google Scholar] [CrossRef]
- Jasim, D.J.; Mahdi, M.S.; Mahdy, O.S.; Basem, A.; Karouei, S.H.H.; Alinia-Kolaei, M. Hydrothermal analysis of hybrid nanofluid flow inside a shell and double coil heat exchanger; Numerical examination. Int. J. Thermofluids 2024, 23, 100770. [Google Scholar] [CrossRef]
- Elboughdiri, N.; Salih, S.Q.; Chauhan, B.S.; Albani, A.; Almujibah, H.; Islam, S.; Alturise, F.; El-Shorbagy, M.; Aouaini, F.; Deifalla, A. Numerical analysis of thermohydraulic and exergetic performance in corrugated spiral tubes with diverse arc corrugation configurations. Case Stud. Therm. Eng. 2023, 51, 103605. [Google Scholar] [CrossRef]
- Xu, H.; Liu, X.; Yu, W. Comparison study on thermo-hydraulic performance of circular and airfoil shaped wire-wrapped rod bundle. Nucl. Eng. Des. 2023, 414, 112651. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, P.; He, X.; Chen, C.; Wang, Q.; Tian, C. Numerical analysis of flow resistance characteristics in an inclined rod bundle channel. Prog. Nucl. Energy 2020, 122, 103247. [Google Scholar] [CrossRef]
- Cunningham, M.J. Measurement Errors and Instrument Inaccuracies; Springer: New York, NY, USA, 1990. [Google Scholar]
- Holman, J.P.; Gajda, W.J. Experimental Methods for Engineers; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Cd-Adapco. STAR-CCM+, version 18.04; User Guide. Reynolds-Averaged Navier-Stokes (RANS) Turbulence Models; Siemens Digital Industries Software: Plano, TX, USA, 2023; pp. 8403–8407. [Google Scholar]
- Fan, X.; Peng, T.; Fan, D.; Zhu, Y.; Cai, Y.; Gu, L. Study on Periodicity of Cross Flow in Gaps of a Lead-based FastReactor Fuel Assembly. Nucl. Phys. Rev. 2018, 35, 216–223. [Google Scholar]
- Nivedita, N.; Ligrani, P.; Papautsky, I. Dean Flow Dynamics in Low-Aspect Ratio Spiral Microchannels. Sci. Rep. 2017, 7, 44072. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Gu, H.; Tang, W.; Chen, B.; Shi, Y. Experimental Study of Flow and Heat Transfer Characteristicsin Helically-coiled Tube and Evaluation of Empirical Formulas. At. Energy Sci. Technol. 2025, 59, 100–109. [Google Scholar]
- Ferraris, D.L.; Marcel, C.P. Two-phase flow frictional pressure drop prediction in helical coiled tubes. Int. J. Heat Mass Transf. 2020, 162, 120372. [Google Scholar] [CrossRef]
- Sieder, E.N.; Tate, G.E. Heat Transfer and Pressure Drop of Liquids in Tubes. Ind. Eng. Chem. Res. 1936, 28, 1429–1435. [Google Scholar] [CrossRef]
- Zhan, H.H. Research and Phenomenon of Secondary Flow. J. Zhuzhou Inst. Technol. 2001, 15, 27–29. [Google Scholar]




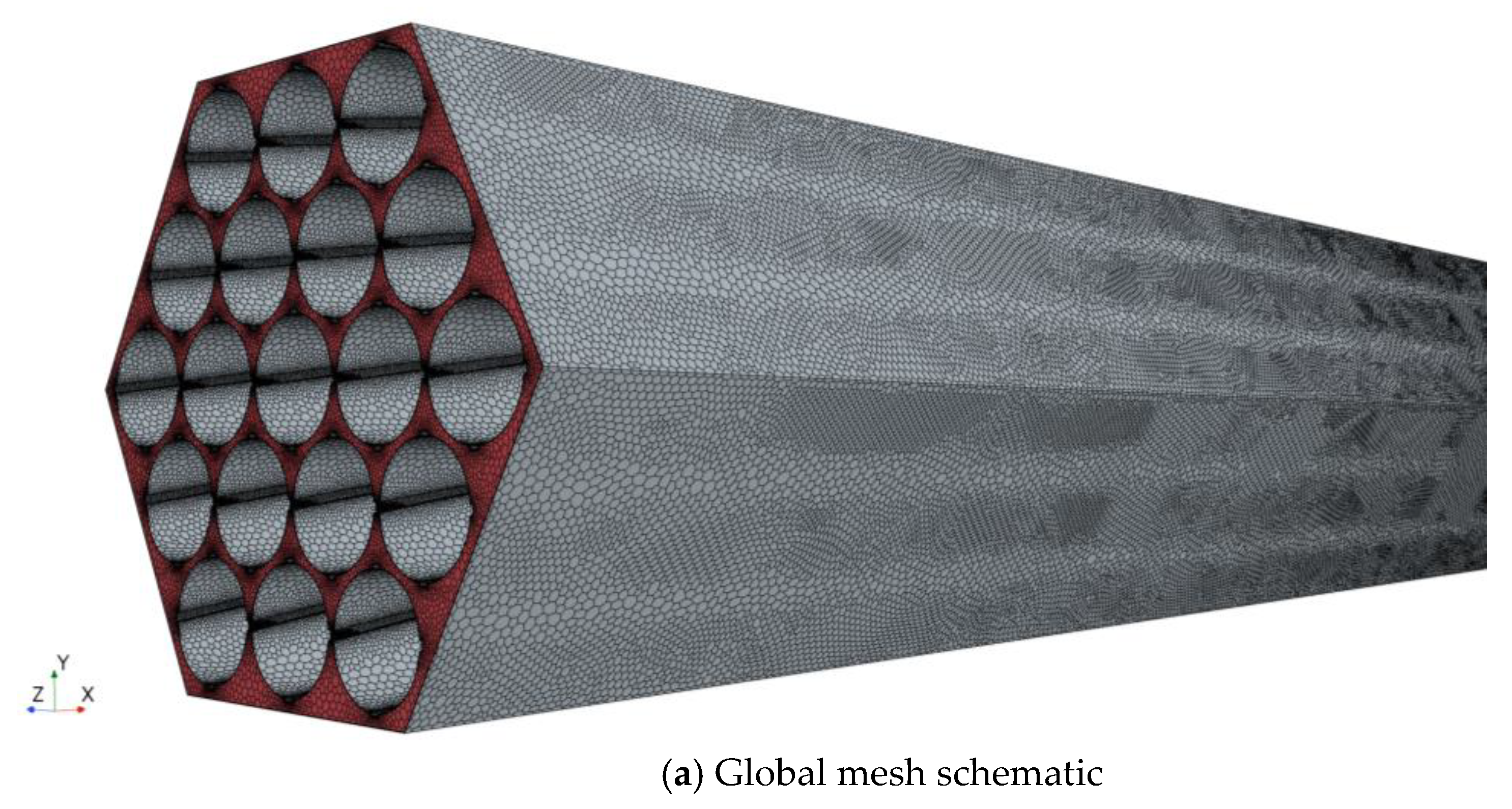
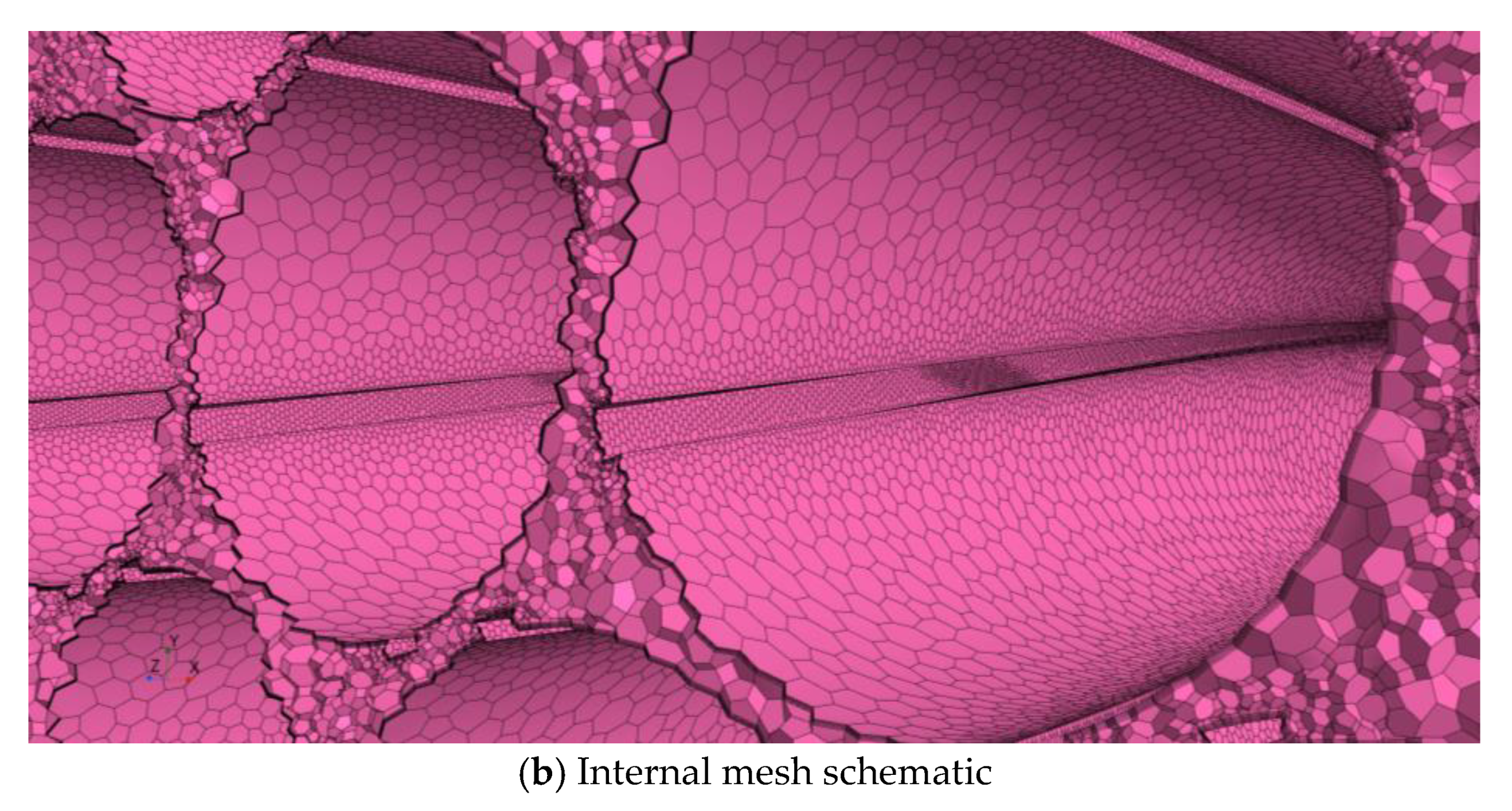
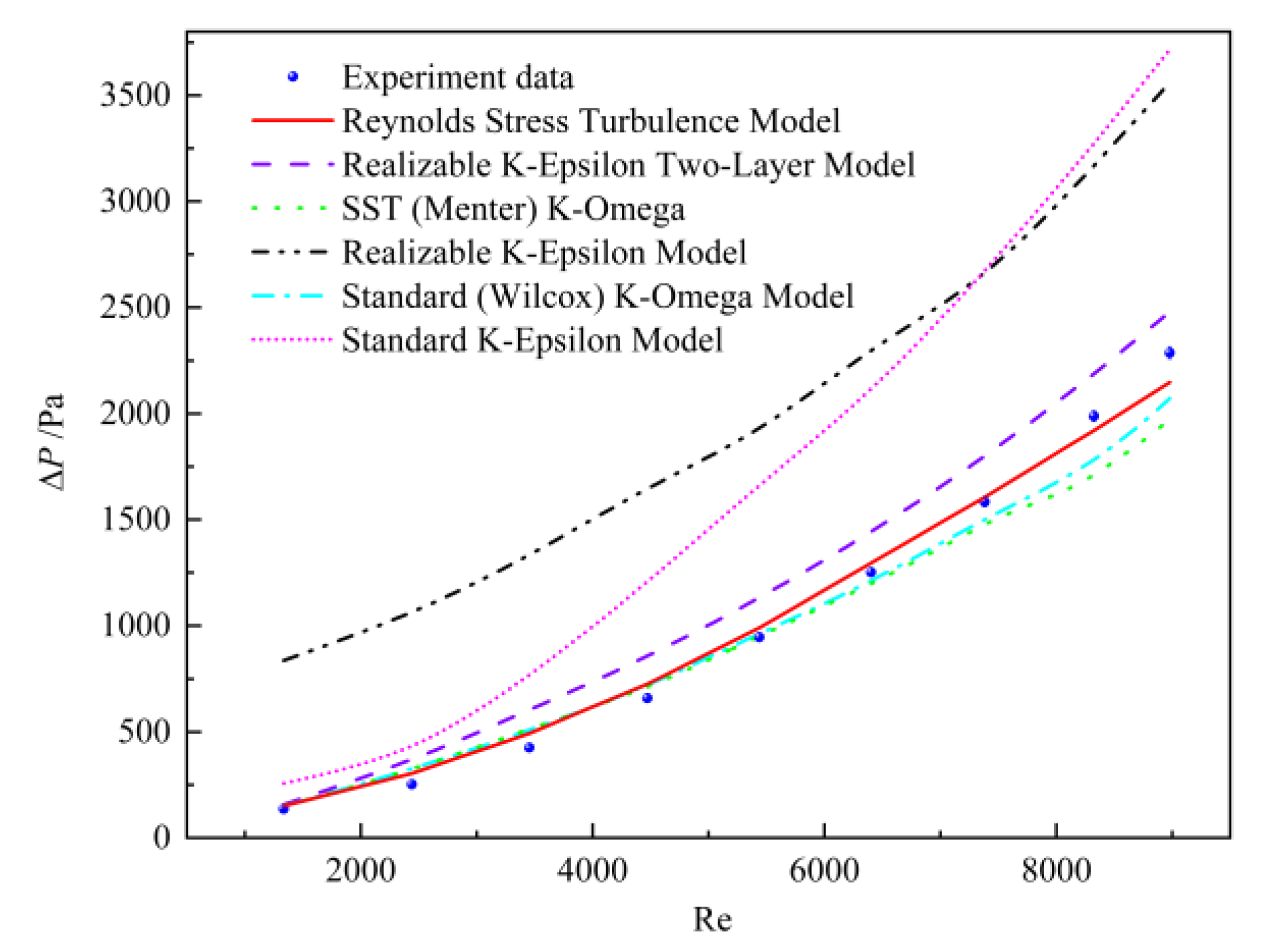

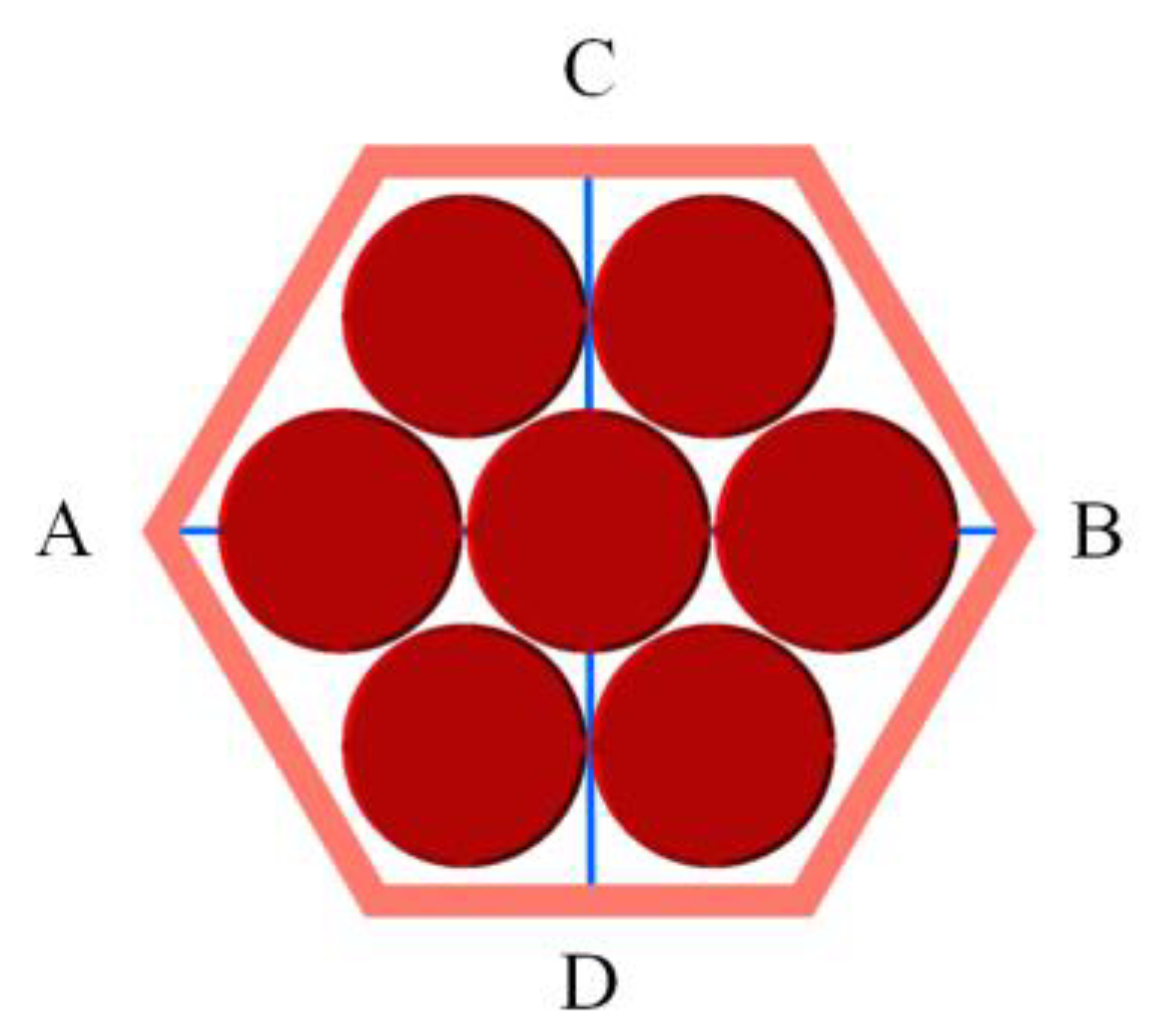





| Measurement Parameters | Instrument | Range | Error |
|---|---|---|---|
| Mass flow rate | Electromagnetic flowmeter | 0–100,00 kg/h | ±0.1% |
| Pressure drop | Differential pressure transducer | 0–10 kPa | ±0.1% |
| Pressure | Pressure transmitter | 0–1 MPa | ±0.04% |
| Fluid temperature | K-type armored thermocouple | 0–100 °C | ±1.0 °C |
| Channel size | Vernier caliper | 0–1000 mm | ±0.02 mm |
| Model | Grid Number | ΔP [Pa] | vo [m/s] | To [K] |
|---|---|---|---|---|
| #1 | 14,149,427 | 1879.31 | 1.79626 | 299.6508 |
| #2 | 21,023,326 | 1920.016 | 1.792078 | 299.6508 |
| #3 | 24,788,095 | 1921.149 | 1.792958 | 299.6508 |
| #4 | 36,049,558 | 1921.631 | 1.792805 | 299.6507 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Jiang, J.; Fu, S.; Liu, J.; Liu, X.; Feng, L.; Li, A.; Liu, P.; Chen, Y.; Cai, Q. Numerical Study on Flow Characteristics of Spiral Channel with Coiled Wire. Processes 2025, 13, 667. https://doi.org/10.3390/pr13030667
Zhang Y, Jiang J, Fu S, Liu J, Liu X, Feng L, Li A, Liu P, Chen Y, Cai Q. Numerical Study on Flow Characteristics of Spiral Channel with Coiled Wire. Processes. 2025; 13(3):667. https://doi.org/10.3390/pr13030667
Chicago/Turabian StyleZhang, Yinxing, Jiahang Jiang, Shengwei Fu, Jialei Liu, Xiaoya Liu, Li Feng, Ang Li, Pengfei Liu, Yuqing Chen, and Qi Cai. 2025. "Numerical Study on Flow Characteristics of Spiral Channel with Coiled Wire" Processes 13, no. 3: 667. https://doi.org/10.3390/pr13030667
APA StyleZhang, Y., Jiang, J., Fu, S., Liu, J., Liu, X., Feng, L., Li, A., Liu, P., Chen, Y., & Cai, Q. (2025). Numerical Study on Flow Characteristics of Spiral Channel with Coiled Wire. Processes, 13(3), 667. https://doi.org/10.3390/pr13030667





