Abstract
The present study evaluates the heat transfer performance of an immersion liquid cooling system, utilizing copper-water (Cu-water) nanofluids under various flow and geometric conditions, including different Reynolds and Rayleigh numbers, nanoparticle volume fractions, and block spacing configurations. To this end, numerical simulations were conducted to assess the impact of these parameters on the system’s temperature distribution and overall cooling efficiency. The findings indicate that augmenting the Reynolds number from 100 to 500, and the nanoparticle volume fraction from 0% to 5%, at a Rayleigh number of 105, results in substantial enhancements in heat transfer, with improvements reaching up to 193.8%. Furthermore, an increase in the Rayleigh number from 103 to 106, in conjunction with elevated nanoparticle concentrations at a Reynolds number of 500, yielded a heat transfer enhancement of up to 36.3%. These findings demonstrate that higher Reynolds and Rayleigh numbers promote better heat dissipation through increased convective flow and buoyancy-driven convection. Furthermore, the study underscores the pivotal function of block spacing in maximizing cooling efficacy. While closer spacing results in higher temperatures, wider spacing improves heat transfer efficiency by reducing thermal interference between blocks. The study emphasizes the synergistic effect of an enhanced thermal conductivity, strong convective flow, and optimal geometric configurations in maximizing cooling efficiency. These findings are of crucial importance for the design of more efficient thermal management systems, with applications in electronics cooling, energy systems, and industrial processes.
1. Introduction
Immersion liquid cooling systems represent a sophisticated approach to maintaining optimal thermal conditions for high-performance computing hardware. Conventional cooling methods rely on fans and heat sinks, whereas immersion cooling employs a distinct strategy. This method involves submerging components directly in a thermally conductive liquid and leveraging its enhanced thermal conductivity to effectively dissipate heat. This approach mitigates the occurrence of hot spots and ensures consistent operating temperatures, enhancing the effectiveness and reliability of the system. The system is clever because it continuously circulates the heated liquid from the dip tank to a cooling unit, where it is cooled and then recirculated. This process is beneficial for high-performance industrial applications because it ensures consistent and uniform cooling [1,2].
Cooling systems play a vital role in a wide range of applications, regulating temperatures to prevent overheating and to protect against potential damage or loss of efficiency. They are essential in sectors such as automotive, industrial, and district cooling, ensuring optimal performance and safety [3,4,5,6,7]. In addition, the integration of nanofluids—engineered fluids containing nanoparticles suspended in a base liquid—represents a promising way to improve the thermal performance of liquid chillers. By introducing nanoparticles, typically metal or oxide nanoparticles, into the coolant, the nanofluids offer significant improvements in thermal conductivity and heat transfer properties. This enhancement facilitates more efficient heat removal from the submerged components, reduces thermal resistance, and ensures sustained cooling performance over time [8,9].
Several studies have contributed to advancing our understanding of nanofluid-enhanced cooling systems and their practical applications. Wen et al. conducted a comprehensive investigation into the use of nanofluids to improve heat transfer in liquid-cooled data centers. They evaluated the heat transfer characteristics of various nanofluids and provided valuable insights into their performance, highlighting the effectiveness of Al-FC40 nanofluids in particular. Niazmand et al. [10] contributed to the field through a focused examination of oil immersion cooling for servers, leveraging computational fluid dynamic (CFD) simulations to enhance cooling efficacy. Their research endeavors led to significant reductions in CPU temperatures, alongside the identification of optimal operational conditions. Moreover, their work offered key insights into nanofluid-enhanced cooling systems, showcasing expertise in thermal analysis, nanofluid technology, and data-driven research methodologies. Jilte et al. [11] explored the cooling performance of battery thermal management systems (BTMSs) for electric vehicles, emphasizing the critical role of effective cooling systems in ensuring battery safety. Through meticulous analysis, they compared the efficacy of liquid-filled BTMS (LfBS) and liquid-circulated BTMS (LcBS) configurations, assessing their performance across varying discharge rates and ambient temperatures. Their comprehensive study provided valuable insights into battery type selection, nanofluid thermophysical properties, and numerical scheme validation, ultimately offering recommendations for implementing BTMS arrangements, based on environmental factors and discharge rates. In a separate study, Moghaieb et al. [12] examined the effectiveness of γ-Al2O3/water nanofluid as an engine coolant, focusing on convective heat transfer characteristics. Their experiments elucidated the influence of nanoparticle concentration, bulk temperature, and flow velocity on heat transfer efficiency, highlighting the potential of nanofluid-based solutions for engine cooling applications. Catherine et al. [13], in another research endeavor, explored methods for the improvement of critical heat flow (CHF), using Cu-water and Al-water nanofluids for electronic system cooling. Their experimental investigations showcased significant CHF enhancements over traditional cooling methods, suggesting the promise of nanoparticle-enhanced nanofluids for enhancing electronic cooling efficiency. Cheng et al. [14] investigated a single-phase immersion cooling system for electronic devices, focusing on heat distribution and the effects of different flow rates and heat sink materials. Their findings provided valuable insights into designing efficient cooling systems, with implications for power densification and operational safety. Mehrizi et al. [15] explored mixed convection heat transfer in ventilated cavities, examining the effect of nanofluids and outlet port locations. Their simulations provided nuanced insights into optimizing heat transfer dynamics in similar systems. Yousefzadeh et al. [16] investigated the effect of silver nanoparticles on heat transfer in open cavities, providing valuable insights for optimizing heat transfer in industrial applications. Al-Rashed et al. [17] conducted numerical simulations to investigate the factors influencing heat transfer and entropy generation in nanofluid-filled cavities, offering insights into optimizing heat transfer processes in various engineering applications. Finally, Zhang et al. [18] studied mixed convection of nanofluids in inclined cavities, highlighting the intricate relationship between fluid dynamics and nanofluid properties in optimizing heat transfer in complex geometries.
In the field of nanofluid heat transfer simulation, two primary modeling approaches are employed: the single-phase model and the two-phase model. The single-phase model treats the nanofluid as a homogeneous mixture, assuming uniform dispersion of nanoparticles and considering the nanofluid as a single entity with effective thermophysical properties. This approach is computationally efficient and provides reasonable approximations, with deviations from experimental results typically within 5.9% when temperature-dependent properties are incorporated. However, it may fail to accurately capture the complex interactions between nanoparticles and the base fluid. In contrast, the two-phase model treats the nanoparticles and base fluid as separate phases, enabling the explicit modeling of interactions such as slip velocity, particle clustering, and dispersion. Sub-models within the two-phase framework, such as the Eulerian, Lagrange-Eulerian, and mixture models, offer higher precision in predicting convective heat transfer coefficients and often align more closely with experimental data. Nevertheless, two-phase models have been shown to overestimate the heat transfer enhancement and to introduce practical challenges, such as an increased computational cost, higher predicted pressure drops, and wall shear stresses. While the two-phase model provides a more detailed representation, the choice between these approaches depends on the desired accuracy and computational resources available [19,20,21,22].
In addition, the simulation of the heat transfer in nanofluid-based immersion cooling systems presents significant challenges. Accurate modeling of complex fluid behavior such as turbulence, cavitation and the interplay of thermodynamic and compressibility effects remains elusive. These phenomena are critical for predicting the heat transfer performance but require advanced computational models that are computationally expensive and often lack sufficient validation. In addition, traditional methods for modeling flow in complex geometries, which are common in immersion cooling systems, are inadequate. This requires the development of improved numerical techniques specifically tailored to capture the unique characteristics of nanofluids, coupled with rigorous experimental validation to ensure reliable predictions for practical applications [23,24,25].
This study addresses the challenge of effectively cooling components immersed in a Cu-water nanofluid within an adiabatic cavity. Using the Lattice Boltzmann Method, we simulate heat transfer in an immersion liquid cooling system with a bottom inlet and top outlet for the nanofluid, ensuring a continuous flow through a cavity containing four hot rectangular blocks. By varying the volume fraction of nanoparticles and investigating different Reynolds and Rayleigh numbers, we aim to optimize cooling performance, analyze flow patterns and provide practical guidelines for the design of advanced liquid cooling systems. This comprehensive approach will advance our understanding of nanofluid dynamics and its application to efficient thermal management solutions.
2. Materials and Methods
2.1. Physical Model
The present study focuses on investigating the heat transfer characteristics within an immersion fluid system, specifically an open cavity configuration as shown in Figure 1. The cavity geometry consists of inlet and outlet ports strategically positioned for the introduction and extraction of a nanofluid maintained at a cold temperature () and a predetermined velocity (). Within this cavity, four heated blocks are immersed, which form the central focus of the investigation as their effective cooling is essential.
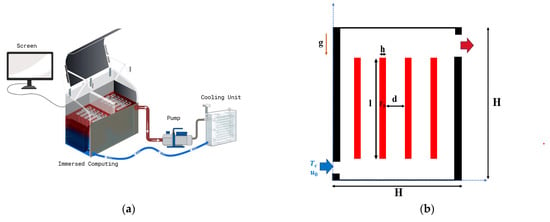
Figure 1.
(a) Schematic diagram of a system for cooling by immersion in nanofluid, (b) Schematic representation of the studied geometry and dimensional parameters.
In the present study, the range of 0% to 5% nanoparticle volume fractions is utilized, a concentration that has been widely adopted in the field of nanofluid research. This range is considered to offer an optimal balance between enhancing heat transfer and preserving manageable fluid properties. The concentrations that exceed this range can increase viscosity, leading to difficulties in pumping the fluid and the potential for sedimentation or agglomeration, which can compromise stability. Correlations for viscosity and thermal conductivity are essential in modeling nanofluids, as they facilitate the prediction of how nanoparticles enhance the fluid’s thermal properties. These correlations, which are based on experimental and theoretical data, allow for accurate simulations of nanofluid behavior under various conditions [26].
The nanofluid used consists of copper nanoparticles dispersed in a water base, with varying volume fractions ranging from 0% to 5%. The operating parameters include Reynolds numbers from 100 to 500 and Rayleigh numbers from to , reflecting different flow and thermal conditions, with:
The cavity dimensions are defined so that the height and length are equivalent (L = H), with the cavity height doubled (2 h) and the outlet positioned at four times the height (4 h) for optimum fluid flow dynamics. The heated blocks, characterized by a height (l) to length (h) ratio of and respectively, are maintained at a constant high temperature (). The introduction of a new variable, the distance (d) between the heated blocks, allows the study of three different scenarios as shown in Table 1:

Table 1.
Case Configurations.
By carefully investigating the interplay between different nanofluid concentrations, flow conditions and block configurations, this research aims to contribute to the advancement of thermal management strategies in engineering applications.
The thermophysical properties of these nanoparticles dispersed in water contribute significantly to improving the heat transfer efficiency, as detailed in Table 2.

Table 2.
Thermophysical properties.
2.2. The Numerical Simulation
2.2.1. Reviewing the LBM
The Lattice Boltzmann Method is a highly effective computational approach for simulating fluid dynamics, particularly in complex systems, where traditional methods are inadequate [27,28,29,30,31,32]. This study highlights the use of LBM in the simulation of immersion cooling systems, where four hot blocks are cooled by nanofluids.
LBM works at a mesoscopic level, using distribution functions to describe the fluid state at specific lattice points. The process involves two main steps: first, the collision step, where particle velocities are redistributed based on a collision operator; and second, the streaming step, where particles move to neighboring lattice points. The choice of collision operator, such as the Bhatnagar–Gross–Krook model, and the design of the lattice structure are crucial to ensure the accuracy and stability of the method. In this method, the solution to the energy and the Navier–Stokes equations for fluid flow and energy, respectively, is achieved through the utilization of two distribution functions of and . Furthermore, a D2Q9 lattice is employed for fluid flow, while a D2Q5 lattice is utilized for energy, as shown in Equations (1) and (2).
In this context, and represent the relaxation times for fluid flow and energy distribution, respectively. Meanwhile, and denote the equilibrium distribution functions, while signifies the discretized external force. The parameters and , on the other hand, correspond to the velocities and time step, respectively.
In order to consider the discretized external force ‘buoyancy force’ in the model, the term is written as follows:
The equilibrium distribution functions are defined in discrete form as follows. In this context, the variables ρ and T represent the density and temperature.
The equilibrium distribution functions for the flow and in the D2Q9 and D2Q5 models are derived from the following equations:
The discrete particle velocities have the following definitions:
where are the constant factors, which, for D2Q9, are shown in Equation (6), and for D2Q5 are shown in Equation (7):
The macroscopic u variables, including the density , the momentum and the temperature T, are computed using the following equations:
2.2.2. Boundary Conditions
The accurate application of boundary conditions is of paramount importance in guaranteeing the stability and accuracy of the simulations conducted using the lattice Boltzmann method. In contrast to the conventional methods based on the Navier–Stokes equations, the LBM employs the values of the density and energy distribution functions to impose these conditions. This approach affords superior control of the simulations, thereby ensuring a priori stability and accuracy in the results obtained.
Inlet boundary condition:
In the flow field, a uniform free nanofluid velocity is imposed at the inlet. The distribution functions towards the interior of the boundary region must be calculated by the appropriate equation, taking into account the specified boundary condition. The following boundary conditions proposed by Zou and He [33] are considered:
The unknown inlet temperature distribution functions are obtained using the following equations:
Outlet boundary condition:
In the outlet region, where both velocity and energy values are unknown, an open boundary condition is used to facilitate accurate simulation.
In the context of the temperature field, the walls of the cooling system are adiabatic, i.e., the adiabatic boundary condition is imposed, also the velocity in the walls is zero. The corresponding boundary conditions for the walls are:
In the Single Relaxation Time Lattice Boltzmann Method (SRT-LBM), the no-slip boundary condition is implemented through the utilization of the bounce-back scheme:
The constant temperature boundary condition for the blocks is described by the following equations:
2.3. Nanofluid Properties
Nanofluids are a game changer in the field of heat transfer due to their remarkable thermophysical properties. When it comes to accurately simulating these fluids, it is all about getting the details of the properties, such as thermal conductivity, viscosity, density, and heat capacity right. The scientific community has tried several models, including the Brinkman, Maxwell, and Namburu models for viscosity and the Patel, Chon and Maxwell models for thermal conductivity [34,35,36,37]. It is fascinating how Brownian motion plays a crucial role in increasing thermal conductivity, and it is a reminder that temperature-dependent properties cannot be ignored if we want our simulations to hit the mark. This drives home the point that choosing the right property models is key to nailing thermal management when working with nanofluids. The nanofluid description equations we will use are as follows:
Density is obtained using the following formula:
In the context of nanofluids, the symbol φ stands for the volume fraction of nanoparticles, which essentially quantifies how much of the tiny solid particles are in the fluid compared to the rest of the fluid. This measure is crucial because it directly influences the overall properties of the nanofluid. As for the effective heat capacity, it is a way of measuring how much heat the nanofluid can store, and it is calculated based on the contributions of both the nanoparticles and the base fluid.
The effective heat capacity of the nanofluid is determined as:
and thermal diffusivity can be obtained using the following formula:
In fluid mechanics, the Brinkman model and the model proposed by Patel et al. are often cited in the research focused on nanofluids [38]. These models are central to understanding and predicting the behavior of nanofluids, particularly in terms of their thermal conductivity and viscosity. The Brinkman model is well known for its approach to viscosity, taking into account the effects of particle volume fraction and particle size. On the other hand, the Patel et al. model is widely used for its comprehensive approach to thermal conductivity, which includes the influence of temperature and particle size.
Viscosity:
thermal conductivity:
The nanoparticle Brownian velocity can be determined as follows:
This equation establishes a link between the dynamics of the system and its thermal state, taking into account the Boltzmann constant, denoted by , and the temperature, expressed in Kelvin and symbolized by .
Average Nusselt number:
In the x-direction, the initial and final points of the obstacle, designated x0 and x1, respectively, are represented. Similarly, in the y-direction, y0 and y1 are used to denote the initial and final points of the obstacle:
3. Results and Discussion
This study presents a comprehensive numerical analysis of isotherm distributions and the average Nusselt number profiles in an immersion liquid cooling system employing nanofluids. The investigation focuses on the effects of the Reynolds number, Rayleigh number, nanoparticle volume fraction, and inter-block spacing on thermal performance. Three configurations of block spacing were evaluated, alongside nanoparticle volume fractions ranging from (base fluid) to , with Reynolds and Rayleigh numbers spanning Re = 100–500 and Ra = 103–106, respectively. A systematic parametric study was conducted to quantify the individual and synergistic impacts of these variables on heat transfer efficiency. The findings of this study aim to establish design guidelines for optimizing the thermal management capabilities in immersion cooling systems, particularly for high-power density applications requiring enhanced heat dissipation.
3.1. Mesh Study
A grid independence study was conducted to ascertain the optimal mesh resolution that balanced computational efficiency and numerical accuracy. A series of simulations was performed under fixed dimensionless parameters (Re = 100, Ra = 105) across a series of uniformly structured grids (n × m). As illustrated in Table 3, the average Nusselt number exhibited asymptotic convergence with the increasing grid density. The results indicate that the Nusselt number converges as the grid is refined, with minimal differences observed from the 150 × 150 to 400 × 400 grids. To ensure accurate results while minimizing computational cost, the grid size of 200 × 200 nodes is selected for all simulations, as it provides sufficiently converging results with negligible errors, compared to the finer grids.

Table 3.
Grid independence study.
3.2. Validation Model
Numerical validation is a critical step in computational research, ensuring the accuracy and reliability of model predictions through systematic comparison with experimental or theoretical benchmarks. This process establishes confidence in a model’s ability to reproduce physical phenomena while safeguarding against methodological inaccuracies, thereby strengthening the scientific validity of the results.
As shown in Figure 2, the results of this study show a strong agreement with established natural convection trends reported by Guiet et al. [39] and with forced convection data from Santra et al. [40]. Guiet et al. analyzed the natural convection in a cavity with a hot obstacle, adiabatic top/bottom boundaries and isothermal cold sidewalls. Conversely, Santra et al. studied heat transfer in Newtonian and non-Newtonian condensed nanofluids under forced convection, in a channel with uniformly heated top/bottom walls.
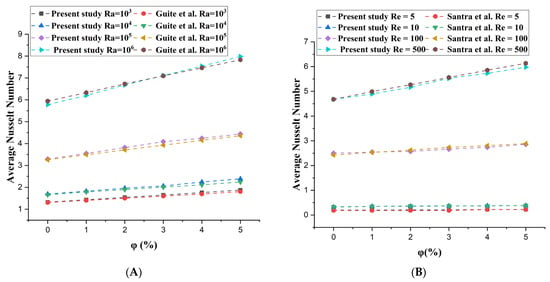
Figure 2.
Comparison of heat transfer results: present study vs. established trends, (A): natural convection Guite et al. [39] and (B): forced convection Santra et al. [40].
In the present work, the nanofluids are modeled as Newtonian fluids, assuming a constant viscosity independent of the shear rate. A comparative analysis shows that the simulated results agree with the Newtonian case of Santra et al. and Guiet et al. within a 3% deviation, confirming the consistency of the current numerical framework. This agreement underlines the robustness of the adopted methodology in simulating coupled heat transfer phenomena, while maintaining fidelity to previous experimental and theoretical benchmarks under analogous assumptions.
3.3. Impact of Reynolds Numbers and Nanoparticle Volume Fractions
The significance of the Reynolds number and nanoparticle volume fraction in enhancing the convective heat transfer within immersion cooling systems is demonstrated in this study. It is demonstrated that higher Reynolds numbers indicate stronger inertial forces, which promote increased fluid motion and more effective thermal energy transport. The inclusion of nanofluids, i.e., fluids that exhibit superior thermal conductivity due to the inclusion of nanoparticles, amplifies the heat transfer performance even further. The isothermal contours presented in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 illustrate the impact of varying Reynolds numbers, nanoparticle volume fractions, and block spacing at a constant Rayleigh number () on the thermal performance of the system. These results demonstrate how these parameters influence the heat transfer efficiency and cooling uniformity. The addition of nanoparticles significantly improves heat dissipation. For the base fluid (), the isothermal contours demonstrate the pronounced temperature gradients around the heated blocks, indicating localized heat retention and reduced thermal management efficiency. In contrast, a nanoparticle volume fraction of 5% increases the fluid’s thermal conductivity, resulting in more uniform and extended thermal plumes. This enhancement has been shown to reduce thermal resistance and improve heat transfer from the heated blocks to the cooling medium, thus highlighting the effectiveness of nanoparticle-enhanced nanofluids.
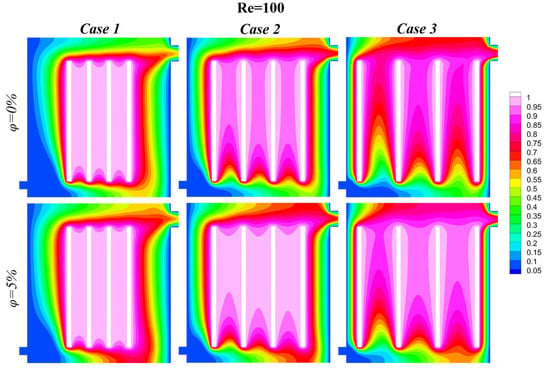
Figure 3.
Isothermal lines at , , and .
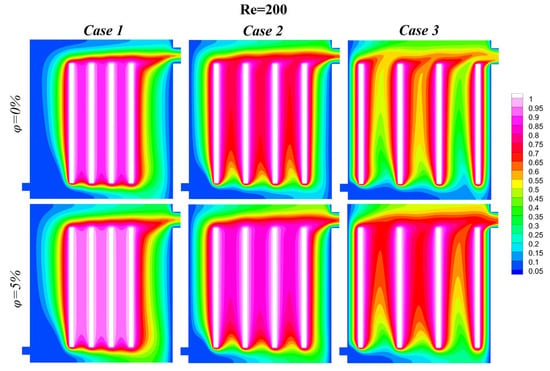
Figure 4.
Isothermal lines at , , and .
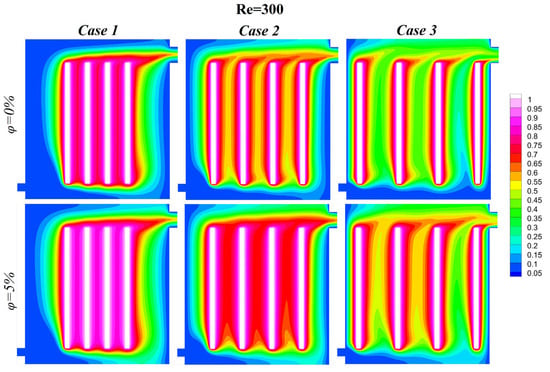
Figure 5.
Isothermal lines at , , and .
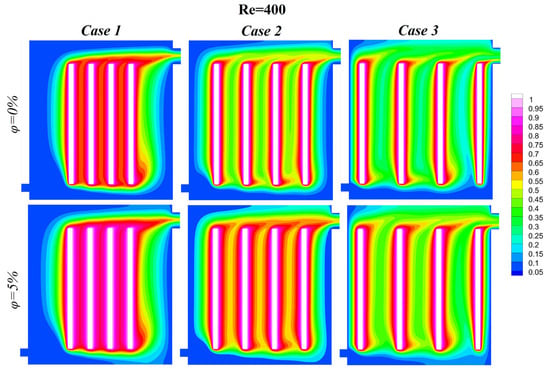
Figure 6.
Isothermal lines at , , and .
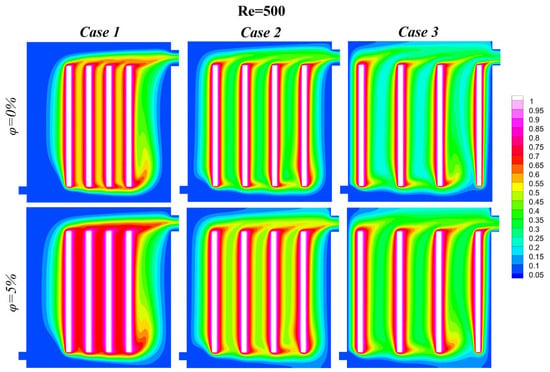
Figure 7.
Isothermal lines at , , and .
The Reynolds number is also of critical importance in determining the behavior of the heat transfer. At lower Reynolds numbers (Re = 100, 200) the flow is laminar, characterized by distinct thermal layers near the heated surfaces. In this regime, convective heat transfer is limited, and conduction dominates. Consequently, the addition of nanoparticles has a negligible impact on heat dissipation due to insufficient fluid mixing. Conversely, at higher Reynolds numbers (Re = 300, 400, 500), the flow transitions to a turbulent state, leading to the disruption of thermal boundary layers and the promotion of vigorous nanofluid mixing. This turbulence, in conjunction with the enhanced thermal conductivity of nanoparticles, results in a more uniform temperature distribution and enhanced heat transfer efficiency, as evidenced by the smoother and more extended thermal contours.
The distance between heated blocks has also been shown to affect cooling performance: in Case 1, where the blocks are closely spaced, significant thermal interactions between adjacent plumes create localized hotspots, reducing cooling efficiency; in Case 2, with moderate spacing, thermal dispersion improves as the increased distance allows plumes to spread more effectively, minimizing localized heating; and Case 3, with the largest spacing, achieves the highest cooling efficiency across all conditions. The conclusion drawn from this analysis is that the greatest spacing leads to the most effective minimization of plume interactions, thereby enabling uniform heat dissipation and optimizing the thermal management system as a whole.
The impact of the Reynolds number, nanoparticle volume fraction, and block spacing on heat transfer performance is demonstrated in Figure 8 and Figure 9, which present the variation in the average Nusselt number, with the Reynolds number and nanoparticle volume fraction for the three-block spacing configurations. The findings unequivocally demonstrate the influence of these parameters on thermal performance, with the Nusselt number increasing consistently with the Reynolds number, across all cases and nanoparticle volume fractions. At higher Reynolds numbers, the transition to turbulent flow enhances convective heat transfer by promoting fluid mixing and reducing thermal boundary layer thickness, a trend that is consistent across all configurations. This underscores the importance of flow dynamics in optimizing thermal performance.
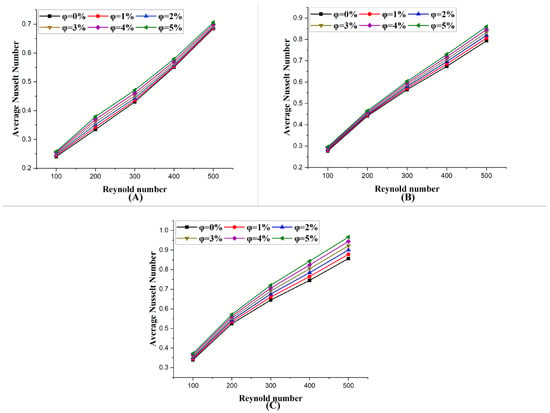
Figure 8.
Average Nusselt number variation, with Reynolds number, for different nanofluid volume fractions, at Rayleigh number in each case, (A): case 1, (B): case 2, (C): case 3.
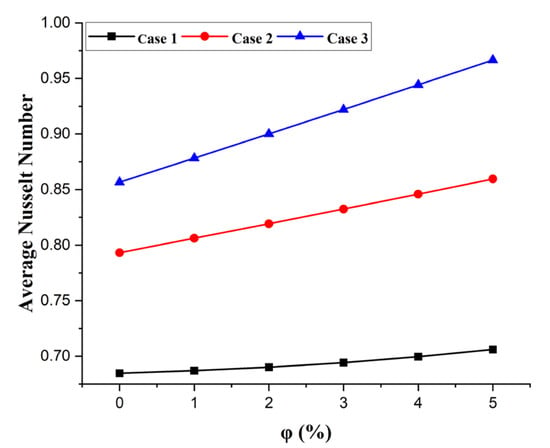
Figure 9.
Comparison of the average Nusselt numbers for the three cases, at various volume fractions, in and .
The nanoparticle volume fraction exerts a substantial influence on the Nusselt number. As , increases from 0% to 5%, there is an enhancement in the thermal conductivity of the nanofluid due to the superior heat conduction properties of the nanoparticles. This enhancement in thermal conductivity results in a gradual increase in the Nusselt number with the rising ϕ. The effect of nanoparticle volume fraction is most pronounced at higher Reynolds numbers, where turbulent flow enables a more effective utilization of the nanoparticles’ enhanced thermal conductivity, further amplifying heat transfer efficiency. Block spacing also plays a critical role in determining the heat transfer performance. In Case 3, which features the largest spacing, Nusselt umber values are consistently the highest across all Reynolds numbers and nanoparticle volume fractions. The increased spacing minimizes thermal interference between adjacent blocks, allowing thermal plumes to disperse more effectively and promoting uniform cooling. In contrast, Case 1, with the smallest spacing, exhibits the lowest Nusselt number values due to significant thermal plume interactions and the formation of localized hotspots. Case 2, with moderate spacing, performs better than Case 1 but remains inferior to Case 3, demonstrating a gradual improvement in heat transfer efficiency with increasing block spacing.
For instance, at Re = 100, and = 5%, the Nusselt number values for Case 3 is considerably higher than that for Case 1 under equivalent conditions. This underscores the combined impact of an enhanced thermal conductivity and optimized block spacing, a trend that persists across all Reynolds numbers, further reinforcing the superior heat transfer performance of Case 3.
As demonstrated in Table 4, at a constant Rayleigh number (Ra = 105), there is a substantial enhancement in the heat transfer efficiency when the Reynolds number is increased from 100 to 500, under constant conditions. This enhancement is further augmented by increasing the nanoparticle volume fraction from 0% to 5%. Specifically, the transition from Case 1 (ϕ = 0%, Re = 100) to Case 3 (ϕ = 5%, Re = 500) results in a substantial 302.3% enhancement in the heat transfer performance. These results underscore the preeminent impact of the Reynolds number on thermal performance, a phenomenon that is further accentuated by the incorporation of nanoparticles.

Table 4.
The percentage of enhancement caused by increasing the Reynolds number from to and the nanoparticle volume fraction from to at Rayleigh number .
3.4. Impact of Rayleigh Numbers and Nanoparticle Volume Fractions
To gain insight into the impact of the Rayleigh number and nanoparticle volume fraction on heat transfer performance, the variation in the average Nusselt number is examined across a range of block spacing scenarios. An increase in the Rayleigh number signifies a rise in the intensity of buoyancy-driven flows, which facilitate convective heat transfer by stimulating the fluid motion. The enhanced thermal conductivity of nanoparticles, when combined with nanofluids, serves to augment the efficiency of heat transfer.
The isothermal contours illustrated in Figure 10, Figure 11, Figure 12 and Figure 13 demonstrate the effects of varying Rayleigh numbers (Ra), nanoparticle volume fractions, and block spacing configurations, at a constant Reynolds number (Re = 500). These simulations emphasize the influence of the natural convection and nanoparticle-enhanced fluids on the thermal performance of an immersion liquid cooling system.
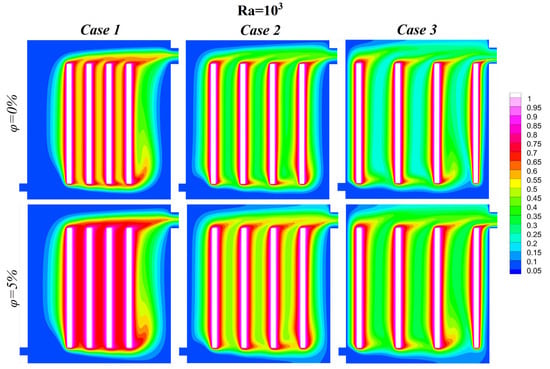
Figure 10.
Isothermal lines at , and .
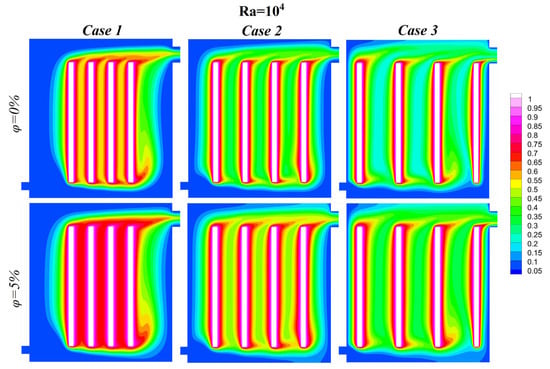
Figure 11.
Isothermal lines at , , and .
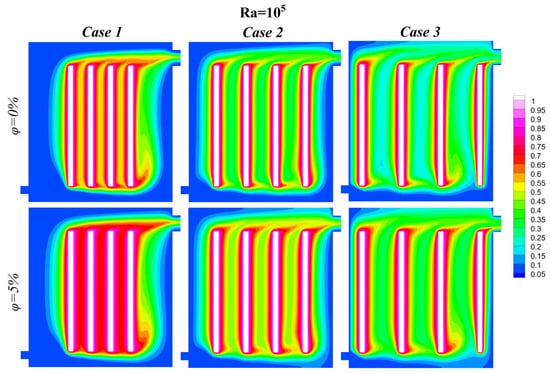
Figure 12.
Isothermal lines at , , and .
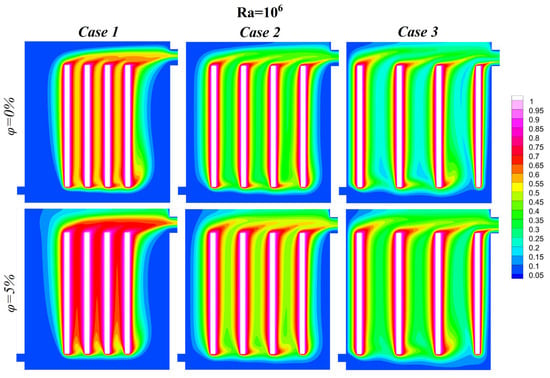
Figure 13.
Isothermal lines at , and .
As the Rayleigh number increases, the buoyancy-driven flow intensifies, thereby strengthening the natural convection mechanism. At lower Rayleigh numbers, convective flow is weak, resulting in less diffuse thermal plumes and distinct thermal layers around the heated blocks. In this regime, fluid–block surface interactions are minimal. Conversely, at higher Rayleigh numbers, stronger buoyancy forces generate vigorous convective currents, thereby enhancing fluid mixing and heat transfer. The thermal plumes become more uniform and extended, indicating improved heat dissipation from the blocks into the surrounding fluid. The addition of nanoparticles () significantly enhances the system’s thermal performance. The nanofluid’s improved thermal conductivity reduces thermal resistance, leading to a more uniform temperature distribution and smoother isothermal contours. This effect is particularly pronounced at higher Rayleigh number values, where convective forces amplify the impact of nanoparticle-enhanced conductivity. However, at lower Rayleigh number values, the influence of nanoparticles is less significant due to the dominance of conduction over convection in heat transfer.
As illustrated in Figure 10, Figure 11, Figure 12 and Figure 13, the isothermal contours demonstrate the effects of varying Rayleigh numbers, nanoparticle volume fractions, and block spacing configurations, at a constant Reynolds number (Re = 500). These simulations emphasize the influence of natural convection and nanoparticle-enhanced fluids on the thermal performance of an immersion liquid cooling system.
An increase in the Rayleigh number leads to an intensification of the buoyancy-driven flow, thereby strengthening the natural convection mechanism. Conversely, at lower Rayleigh numbers, convective flow is weak, resulting in less diffuse thermal plumes and distinct thermal layers around the heated blocks. In this regime, fluid-block surface interactions are minimal. Conversely, at higher Rayleigh numbers, stronger buoyancy forces generate vigorous convective currents, thereby enhancing fluid mixing and heat transfer. The thermal plumes become more uniform and extensive, indicating improved heat dissipation from the blocks into the surrounding fluid. The addition of nanoparticles () significantly enhances the system’s thermal performance, as the nanofluid’s improved thermal conductivity reduces thermal resistance, leading to a more uniform temperature distribution and smoother isothermal contours. This effect is particularly pronounced at higher Rayleigh number values, where convective forces amplify the impact of nanoparticle-enhanced conductivity. However, at lower Rayleigh number values, the influence of nanoparticles is less significant due to the dominance of conduction over convection in heat transfer.
This analysis aims to evaluate the influence of the Rayleigh number and nanoparticle volume fraction on heat transfer performance. Figure 14 and Figure 15 illustrate the variation in the Nusselt number as a function of nanoparticle volume fraction and Rayleigh number, as well as the impact of block spacing at a fixed Reynolds number on heat transfer efficiency. These results provide valuable insights into the interplay between natural convection, nanoparticle-enhanced thermal conductivity, and geometric configurations.
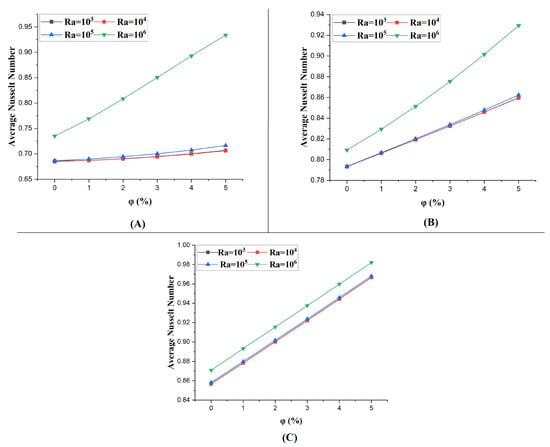
Figure 14.
Average Nusselt number variation with Rayleigh number for different nanofluid volume fractions at Reynolds number 500 in each case, (A) case 1, (B) case 2, (C) case 3.
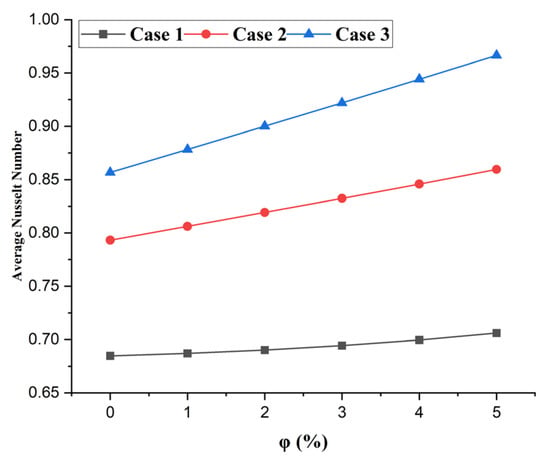
Figure 15.
Comparison of the average Nusselt numbers for the three cases, at various volume fractions, with , and .
At low Rayleigh number values (Ra = 103 and Ra = 104), the phenomenon of natural convection is relatively weak, and the buoyancy forces at play are insufficient to generate strong convective currents. In this regime, heat transfer is dominated by conduction, and the addition of nanoparticles has a minimal effect on the Nusselt number.
Consequently, the slope of the Nusselt number, with respect to nanoparticle volume fraction, is relatively flat, indicating that the enhanced thermal conductivity provided by nanoparticles is not fully utilized under conditions of weak convection. Conversely, at higher Rayleigh numbers (Ra = 105 and Ra = 106), the stronger buoyancy-driven flow promotes vigorous convective mixing, which enhances the interaction between the fluid and the heated surfaces. The enhanced convective heat transfer, in combination with the elevated thermal conductivity of the nanofluid, results in a substantial increase in the Nusselt number. The steeper slope of the Nusselt number with the increasing nanoparticle volume fraction at higher Rayleigh numbers demonstrate the synergistic effect of the stronger natural convection and nanoparticle-enhanced thermal properties.
The incorporation of nanoparticles has been demonstrated to enhance the thermal conductivity of fluids, thereby establishing additional conductive pathways for heat transfer. This phenomenon is further augmented by the random motion of nanoparticles, known as the Brownian motion, which facilitates energy transfer at the microscopic level and improves overall heat dissipation. At higher Rayleigh numbers, the enhanced thermal conductivity becomes more effective due to increased fluid motion and stronger convective currents. However, to ensure an effective heat transfer, it is essential to maintain the stability of the nanofluid, as nanoparticle agglomeration can impede the process. The selection of appropriate nanoparticle size, shape, and material properties is critical in determining the extent of thermal enhancement, and must be made with care to optimize performance.
The influence of block spacing is clearly illustrated in Figure 15, which demonstrates that Case 3 (the largest spacing) consistently achieves the highest Nusselt number values across the entire range of nanoparticle volume fractions. The increased spacing minimizes the interaction of thermal plumes between adjacent blocks, thereby facilitating a more effective heat dissipation and a uniform temperature distribution. In contrast, Case 1 (smallest spacing) exhibits the lowest Nusselt number values, which can be attributed to significant thermal interference and the formation of localized hot spots. Case 2 (moderate spacing) demonstrates an intermediate performance, indicating a gradual improvement in heat transfer efficiency as the spacing between the blocks increases. The results emphasize the necessity of minimizing plume interference to optimize the benefits of nanoparticle-enhanced thermal conductivity.
As demonstrated in Table 5, an increase in the Rayleigh number from 103 to 106, whilst maintaining a constant Reynolds number, also enhances the heat transfer. However, this effect is less pronounced than that observed in changes to the Reynolds number. Specifically, the transition from Case 1 ( Ra = 103) to Case 3 ( Ra = 106) yields a more moderate enhancement of 43.4%.While the nanoparticle volume fraction remains a crucial factor in optimizing heat transfer, the improvements driven by variations in the Rayleigh number are comparatively modest when compared to those resulting from adjustments to the Reynolds number.

Table 5.
The percentage of enhancement obtained by increasing the Rayleigh number from to 106 and the nanoparticle volume fraction from to at Rayleigh number 500.
3.5. Derivation of the Nusselt Number Correlation
The Nusselt number is found to be significantly influenced by the Rayleigh number, the Reynolds number, and the nanoparticle volume fraction (see [41]). This dependence arises from the interplay of buoyancy-driven and forced convection mechanisms, along with the thermal conductivity enhancements provided by nanoparticles. Higher Rayleigh numbers generate stronger buoyancy forces, intensifying convective currents and enhancing heat transfer efficiency. Conversely, increasing the Reynolds numbers results in higher fluid velocities, promoting convective mixing and reducing thermal resistance. The incorporation of nanoparticles into the system has been shown to enhance thermal conductivity and disrupt the thermal boundary layer, thereby augmenting the heat transfer rate. Consequently, these parameters act synergistically to enhance the thermal performance of nanofluid-based systems [41,42,43]. To establish a correlation between the Nusselt number and the aforementioned parameters, a numerical analysis was conducted, ensuring the applicability of the correlation to the specific geometric configurations, flow regimes, and nanoparticle concentrations examined.
The derived equation is presented as follows:
In the present model, C denotes the case type. The term (0.12C + 0.15) accounts for geometric differences between cases, such as block spacing. Nonlinear regression confirms that this linear scaling effectively captures its impact on the Nusselt number. Factor models the enhancement of thermal conductivity based on the presence of nanoparticles, consistent with experimental observations indicating that the Nusselt number scales weakly with nanoparticle volume fraction due to trade-offs between conductivity and viscosity. The additive terms Re0.18 and Ra0.012 capture the distinct scaling of forced and natural convection, respectively, with forced convection dominating at higher Reynolds numbers and natural convection contributing, albeit weakly, at higher Rayleigh numbers. The coefficients in the equation were determined using the Levenberg–Marquardt nonlinear regression algorithm to minimize the error between predicted and actual Nusselt number values, with 90% of the dataset used for training and 10% reserved for validation, as confirmed by our validation metrics.
The correlation was validated using the following metrics:
Mean Absolute Error (MAE):
Root Mean Squared Error (RMSE):
Mean Absolute Percentage Error (MAPE):
4. Conclusions
This study investigates the thermal performance of an immersion liquid cooling system using nanofluids, focusing on the effects of the Reynolds number, Rayleigh number, nanoparticle volume fraction, and block spacing. Using the Lattice Boltzmann Single Relaxation Time (LBM-SRT) method, simulations were conducted to analyze the heat transfer and nanofluid flow, providing insights into optimal conditions for improving the cooling efficiency. The findings reveal substantial enhancements in heat transfer with rising Reynolds and Rayleigh numbers, as well as nanoparticle incorporation, which augments the thermal conductivity of the fluid. It is noteworthy that block spacing assumes a pivotal role in attaining elevated Nusselt numbers, with larger spacings exhibiting superior thermal performance due to diminished plume interference and more uniform heat dissipation. Conversely, smaller spacings give rise to the formation of localized hot spots, thereby diminishing the overall system efficiency.
Quantitative results highlight substantial improvements: increasing the Reynolds number from 100 to 500 and the nanoparticle volume fraction from 0% to 5% resulted in heat transfer enhancements of up to 193.8% in Case 1, 210.1% in Case 2, and 184.4% in Case 3 (Table 4). Furthermore, an increase in the Rayleigh number from 103 to 106, with an unchanged nanoparticle volume fraction, resulted in enhancements of 36.3% in Case 1, 17.1% in Case 2, and 14.6% in Case 3 (see Table 5). These findings underscore the significance of nanoparticle concentration, flow conditions, and geometric configurations in optimizing the heat transfer performance of immersion cooling systems.
Whilst the study presents encouraging results, it is important to acknowledge the limitations of the research. Firstly, the numerical approach assumes idealized conditions, such as stable nanoparticle dispersion without agglomeration or settling, which may not always be achievable in real-world applications. Secondly, the study focuses on a specific nanofluid type (Cu-water) and geometric configurations, which limits the generalizability of the results to other systems or nanofluid compositions.
The findings of this study have significant implications for the design and optimization of advanced cooling systems, particularly in the domains of high-performance computing, electronics, automotive battery management, and industrial heat exchangers. The enhanced heat transfer efficiency offered by nanofluids presents a promising solution to meet the growing thermal demands of modern technologies. Further research is needed to validate these results through experimental studies, explore alternative nanofluids, and consider more complex geometries to broaden the applicability of these findings to practical cooling solutions.
It is imperative to acknowledge that the conclusions presented in this study are derived from steady-state simulations. While the Reynolds numbers range from 100 to 500 and the Rayleigh numbers span from 103 to 106, there is a possibility of flow transitioning to unsteady conditions at the higher end of these ranges. Such transitions could influence heat transfer performance due to the emergence of transient or oscillatory flow behaviors driven by inertial and buoyancy forces. It is recommended that subsequent studies examine the effect of an unsteady flow and thermal convection regimes, with a particular focus on applications operating at elevated Reynolds and Rayleigh numbers or under dynamic conditions. While the steady-state assumption undoubtedly provides valuable insights into system performance, exploring unsteady behaviors could offer a more profound understanding of transient flow dynamics and their impact on heat transfer efficiency.
Author Contributions
A.M. (Abdelilah Makaoui): Conceptualization, Investigation, Methodology, Formal analysis, Software, Validation, Writing—original draft. Y.A.: Investigation, Verification, Writing—original draft. M.A.M.: Supervision, Visualization, Methodology, Investigation, Formal analysis, Writing—review and editing. A.M. (Ahmed Mezrhab): Supervision, Investigation, Visualization, Methodology, Formal analysis, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| Distance between blocks, | |
| y-component of gravitational acceleration, | |
| Cavity height, | |
| Height of the blocks, | |
| Cavity length, | |
| Blocks length, | |
| Average Nusselt number | |
| Rayleigh number, | |
| Reynolds number, | |
| Time, | |
| Temperature of fluid, K | |
| x-component of velocity, | |
| y-component of velocity | |
| Cartesian coordinates | |
| Greek symbols | |
| Specific Heat, | |
| Thermal conductivity, | |
| Density, | |
| Diffusivity, | |
| Dynamic viscosity, | |
| Kinematic viscosity, | |
| Volume fraction, % | |
| Subscripts | |
| Cold | |
| Fluid | |
| Hot | |
| Solid | |
| Nanofluid | |
| Abbreviations | |
| Computational Fluid Dynamics | |
| Fluorocarbon liquid | |
| Lattice Boltzmann Method | |
| Single Relaxation Time |
References
- Luo, M.; Cao, J.; Liu, N.; Zhang, Z.; Fang, X. Experimental and Simulative Investigations on a Water Immersion Cooling System for Cylindrical Battery Cells. Front. Energy Res. 2022, 10, 803882. [Google Scholar] [CrossRef]
- Wakabayashi, D.; Yu, Q.; Nakamura, Y. Development of the high efficiency cooling structure of the liquid immersion cooling SR motor. In Proceedings of the 2017 IEEE 19th Electronics Packaging Technology Conference (EPTC), Singapore, 6–9 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–4. [Google Scholar]
- Xiang, H.; Wang, Y.; Zhu, L.; Han, X.; Sun, Y.; Zhao, Z. 3D numerical simulation on heat transfer performance of a cylindrical liquid immersion solar receiver. Energy Convers. Manag. 2012, 64, 97–105. [Google Scholar] [CrossRef]
- Lionello, M.; Rampazzo, M.; Beghi, A.; Varagnolo, D.; Vesterlund, M. Graph-based modelling and simulation of liquid immersion cooling systems. Energy 2020, 207, 118238. [Google Scholar] [CrossRef]
- Sarangi, S.; McAfee, E.; Damm, D.; Gullbrand, J. Thermal Characterization of Single-Phase Immersion Cooling Capability. In Proceedings of the 2023 22nd IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Orlando, FL, USA, 30 May–2 June 2023; pp. 1–6. [Google Scholar]
- Gao, T.; Tang, H.; Cui, Y.; Luo, Z. A Test Study of Technology Cooling Loop in a Liquid Cooling System. In Proceedings of the 2018 17th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), San Diego, CA, USA, 29 May–1 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 740–747. [Google Scholar]
- Joe, E.S.; Arumuga Perumal, D. Computational analysis of fluid immersed active cooling for battery thermal management using thermal lattice Boltzmann method. Eur. Phys. J. Spec. Top. 2022, 231, 2865–2877. [Google Scholar] [CrossRef]
- Saidina, D.S.; Abdullah, M.Z.; Hussin, M. Metal oxide nanofluids in electronic cooling: A review. J. Mater. Sci. Mater. Electron. 2020, 31, 4381–4398. [Google Scholar] [CrossRef]
- Ruan, H.; Xie, H.; Wang, J.; Liao, J.; Sun, L.; Gao, M.; Li, C. Numerical investigation and comparative analysis of nanofluid cooling enhancement for TEG and TEC systems. Case Stud. Therm. Eng. 2021, 27, 101331. [Google Scholar] [CrossRef]
- Niazmand, A.; Murthy, P.; Saini, S.; Shahi, P.; Bansode, P.; Agonafer, D. Numerical Analysis of Oil Immersion Cooling of a Server Using Mineral Oil and Al2O3 Nanofluid. In Proceedings of the International Electronic Packaging Technical Conference and Exhibition, Virtual, 27–29 October 2020. [Google Scholar] [CrossRef]
- Jilte, R.D.; Kumar, R.; Ahmadi, M.H. Cooling performance of nanofluid submerged vs. nanofluid circulated battery thermal management systems. J. Clean. Prod. 2019, 240, 118131. [Google Scholar] [CrossRef]
- Moghaieb, H.S.; Abdel-Hamid, H.M.; Shedid, M.H.; Helali, A.B. Engine cooling using Al2O3/water nanofluids. Appl. Therm. Eng. 2017, 115, 152–159. [Google Scholar] [CrossRef]
- Catherine Joy, R.; Albert Rajan, A.; Brusly Solomon, A.; Ramachandran, K.; Pillai, B.C. Experimental investigation on the critical heat flux of Cu-water, Al-water nanofluids for precise cooling of electronic systems. IOP Conf. Ser.Mater. Sci. Eng. 2019, 561, 012036. [Google Scholar] [CrossRef]
- Cheng, C.-C.; Chang, P.-C.; Li, H.-C.; Hsu, F.-I. Design of a single-phase immersion cooling system through experimental and numerical analysis. Int. J. Heat Mass Transf. 2020, 160, 120203. [Google Scholar] [CrossRef]
- Mehrizi, A.A.; Besharati, F.; Jahanian, O.; Hassanzadeh Afrouzi, H. Numerical investigation of conjugate heat transfer in a microchannel with a hydrophobic surface utilizing nanofluids under a magnetic field. Phys. Fluids 2021, 33, 052002. [Google Scholar] [CrossRef]
- Yousefzadeh, S.; Rajabi, H.; Ghajari, N.; Sarafraz, M.M.; Akbari, O.A.; Goodarzi, M. Numerical investigation of mixed convection heat transfer behavior of nanofluid in a cavity with different heat transfer areas. J. Therm. Anal. Calorim. 2020, 140, 2779–2803. [Google Scholar] [CrossRef]
- Al-Rashed, A.A.A.A.; Kalidasan, K.; Kolsi, L.; Velkennedy, R.; Aydi, A.; Hussein, A.K.; Malekshah, E.H. Mixed convection and entropy generation in a nanofluid filled cubical open cavity with a central isothermal block. Int. J. Mech. Sci. 2018, 135, 362–375. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, G.; Sundén, B.; Li, Y. An LBM-based investigation of thermal buoyancy and arrangement angle on flow characteristics and heat transfer over four heated square cylinders. Numer. Heat Transf. Part B Fundam. 2021, 79, 278–301. [Google Scholar] [CrossRef]
- Rajpoot, R.S.; Dhinakaran, S.; Alam, M.M. Numerical Analysis of Mixed Convective Heat Transfer from a Square Cylinder Utilizing Nanofluids with Multi-Phase Modelling Approach. Energies 2021, 14, 5485. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Sohankar, A.; Joulaei, A. Investigations of nanofluid flow and heat transfer in a rotating microchannel using single- and two-phase approaches. Numer. Heat Transf. Part A Appl. 2023, 83, 80–115. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D.; Eslami, F.; Mehmandoust, B. Entropy generation analysis of different nanofluid flows in the space between two concentric horizontal pipes in the presence of magnetic field: Single-phase and two-phase approaches. Comput. Math. Appl. 2019, 77, 662–692. [Google Scholar] [CrossRef]
- Abdelrehim, O.; Khater, A.; Mohamad, A.A.; Radwan, A. Two-phase simulation of nanofluid in a confined single impinging jet. Case Stud. Therm. Eng. 2019, 14, 100423. [Google Scholar] [CrossRef]
- Karpenko, M.; Stosiak, M.; Šukevičius, Š.; Skačkauskas, P.; Urbanowicz, K.; Deptuła, A. Hydrodynamic Processes in Angular Fitting Connections of a Transport Machine’s Hydraulic Drive. Machines 2023, 11, 355. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Wu, J.; Li, L.; Tan, D. Machinability evolution of gas–liquid-solid three-phase rotary abrasive flow finishing. Int. J. Adv. Manuf. Technol. 2024, 131, 2145–2164. [Google Scholar] [CrossRef]
- Guo, X.; Yang, M.; Li, F.; Zhu, Z.; Cui, B. Investigation on Cryogenic Cavitation Characteristics of an Inducer Considering Thermodynamic Effects. Energies 2024, 17, 3627. [Google Scholar] [CrossRef]
- Garoosi, F. Presenting two new empirical models for calculating the effective dynamic viscosity and thermal conductivity of nanofluids. Powder Technol. 2020, 366, 788–820. [Google Scholar] [CrossRef]
- Lahmer, E.B.; Benhamou, J.; Admi, Y.; Moussaoui, M.; Phanden, R. Evaluation of Heat Transfer Rate of Double-Layered Heat Sink Cooling System with High Energy Dissipation. J. Enhanc. Heat Transf. 2024, 31, 19–37. [Google Scholar] [CrossRef]
- Moussaoui, M.A.; Admi, Y.; Lahmer, E.B.; Mezrhab, A. Numerical investigation of convective heat transfer in fluid flow past a tandem of triangular and square cylinders in channel. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1091, 012058. [Google Scholar] [CrossRef]
- Admi, Y.; el Hassani, S.; Benhamou, J.; Moussaoui, M. Numerical research on the wake characteristics and drag reduction of a square cylinder in the presence of control partitions. Ocean Eng. 2024, 301, 117341. [Google Scholar] [CrossRef]
- Lahmer, E.B.; Moussaoui, M.A.; Bode, F.; Mezrhab, A. Quality of heat transfer assessment of two microprocessors by double-layered mini channel heat sink cooling system for moderate Reynolds number. Therm. Sci. Eng. Prog. 2023, 41, 101804. [Google Scholar] [CrossRef]
- Moussaoui, M.A.; Derfoufi, S.; Mezrhab, A. Radiation Effect in a Square Cavity Containing a Circular Cylinder with Discrete Bottom Heating. In Advanced Intelligent Systems for Sustainable Development (AI2SD’2020); Advances in Intelligent Systems and Computing Series; Kacprzyk, J., Balas, V.E., Ezziyyani, M., Eds.; Springer International Publishing: Cham, Switzerland, 2022; Volume 1418, pp. 615–625. ISBN 978-3-030-90638-2. [Google Scholar]
- Admi, Y.; Channouf, S.; Lahmer, E.B.; Moussaoui, M.A.; Jami, M.; Mezrhab, A. Effect of a Detached Bi-Partition on the Drag Reduction for Flow Past a Square Cylinder. Int. J. Renew. Energy Dev. 2022, 11, 902–915. [Google Scholar] [CrossRef]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Patel, H.E.; Anoop, K.B.; Sundararajan, T.; Das, S.K. A micro-convection model for thermal conductivity of nanofluids. In Proceedings of the International Heat Transfer Conference 13, Sydney, Australia, 13–18 August 2006; Begel House Inc.: Danbury, CT, USA, 2006. [Google Scholar]
- Namburu, P.K.; Kulkarni, D.P.; Misra, D.; Das, D.K. Viscosity of copper oxide nanoparticles dispersed in ethylene glycol and water mixture. Exp. Therm. Fluid Sci. 2007, 32, 397–402. [Google Scholar] [CrossRef]
- Mehta, S.; Chauhan, K.P.; Kanagaraj, S. Modeling of thermal conductivity of nanofluids by modifying Maxwell’s equation using cell model approach. J. Nanoparticle Res. 2011, 13, 2791–2798. [Google Scholar] [CrossRef]
- Chon, C.H.; Kihm, K.D. Thermal Conductivity Enhancement of Nanofluids by Brownian Motion. J. Heat Transf. 2005, 127, 810. [Google Scholar] [CrossRef]
- Brinkman, H.C. The Viscosity of Concentrated Suspensions and Solutions. J. Chem. Phys. 2004, 20, 571. [Google Scholar] [CrossRef]
- Guiet, J.; Reggio, M.; Vasseur, P. Natural Convection of Nanofluids in a Square Enclosure with a Protruding Heater. Adv. Mech. Eng. 2012, 4, 167296. [Google Scholar] [CrossRef]
- Santra, A.K.; Sen, S.; Chakraborty, N. Study of heat transfer due to laminar flow of copper–water nanofluid through two isothermally heated parallel plates. Int. J. Therm. Sci. 2009, 48, 391–400. [Google Scholar] [CrossRef]
- Mansour, R.B.; Galanis, N.; Nguyen, C.T. Experimental study of mixed convection with water–Al2O3 nanofluid in inclined tube with uniform wall heat flux. Int. J. Therm. Sci. 2011, 50, 403–410. [Google Scholar] [CrossRef]
- Albojamal, A.; Vafai, K. Analysis of single phase, discrete and mixture models, in predicting nanofluid transport. Int. J. Heat Mass Transf. 2017, 114, 225–237. [Google Scholar] [CrossRef]
- Kimouche, A.; Mataoui, A.; Oztop, H.F.; Abu-Hamdeh, N. Analysis of heat transfer of different nanofluids flow through an abrupt expansion pipe. Appl. Therm. Eng. 2017, 112, 965–974. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).