Neural Network Modeling of CuO/Au Hybrid Nanofluid Thermal Performance with Slip Effects for Advanced Process Applications

Abstract

This study explores transient magnetohydrodynamic (MHD) heat and mass transfer in the flow of a hybrid nanofluid over a stretching surface, considering both steady and unsteady scenarios. The investigation incorporates chemical reactions, slip boundary conditions, and the effects of thermal radiation. The hybrid nanofluid, composed of copper oxide (CuO) and gold (Au) nanoparticles in a water-based fluid, demonstrates enhanced thermal performance compared with base fluids. Key findings reveal that higher nanoparticle concentrations significantly improve heat transfer, highlighting the potential of hybrid nanofluids in advanced thermal management applications. Additionally, machine learning models effectively predict heat transfer characteristics with high accuracy (R² = 0.99), showcasing their effectiveness in complementing traditional numerical methods. These findings contribute to the understanding of hybrid nanofluids in complex thermal systems and highlight the utility of emerging computational tools for thermal analysis.

1. Introduction

Recently, nanofluids have gained significant attention for their wide-ranging applications, including in double-glazing systems, heat exchangers, food processing, biomedicine, transportation, and electronic-device cooling. Researchers are focused on enhancing the thermal conductivity of conventional base fluids like water, ethylene glycol, engine oils, and kerosene by incorporating various nanoparticles (NPs). Metals and oxides, such as CuO and Au NPs, are particularly effective at boosting thermal conductivity. Unlike single-component nanofluids, hybrid nanofluids combine multiple NPs to enhance heat and mass transfer. The incorporation of NPs like CuO and Au NPs improves the stability, thermal properties, and heat transfer efficiency of water-based fluids. Moreover, neural networks are increasingly used to model and optimize the thermal behavior of hybrid nanofluids, addressing the limitations of conventional methods [1].

Choi’s pioneering work in nanofluid technology has made significant advancements, revolutionizing thermal management solutions [2]. The integration of NPs, particularly metals like copper, has led to substantial improvements in the thermal conductivity of fluids, enabling valuable applications across various industries [3]. Hybrid nanofluids, which combine two or more types of NPs, offer further enhancements in fluid mechanics and heat transfer efficiency. Recent studies have highlighted the versatility and importance of hybrid nanofluids. For instance, Sreedevi et al. [4] explored the flow and heat transfer properties of hybrid nanofluids over a stretching sheet under unsteady conditions and thermal radiation, demonstrating enhanced heat and mass transfer properties. Imoro et al. [5] extended this research to biological applications, examining the performance of hybrid nanofluids in blood flow within constricted arteries where MHD effects are significant, offering new insights for biomedical devices. Ahmad et al. [6] studied the behavior of Cu-Au hybrid nanofluids on curved surfaces, emphasizing the role of MHD in enhancing stability and thermodynamic efficiency.

Alharbi et al. [7] explored the Hall effect within rotating disk systems via nanofluids, revealing critical interactions between electromagnetic fields and thermal behavior. These insights expand the applicability of nanofluids to engineering solutions, underscoring their promise for cutting-edge technologies in energy storage, thermal regulation, and biomedical fields. The ongoing research into nanofluids continues to uncover new opportunities for innovation across these domains. A recent focus in heat transfer research has been the integration of hybrid nanofluids in thermal management to improve fluid dynamics and energy efficiency. These nanofluids, which combine metal and oxide NPs in various base fluids, exhibit superior thermal properties compared with conventional nanofluids [8]. Generous et al. [9] studied the heat transfer and flow of hybrid nanofluids in ducts, highlighting their industrial applications. Additionally, advanced computational methods like artificial neural networks (ANNs) have revolutionized the analysis of heat and mass transfer. Gupta and Wakif [10] used ANN models to explore nanofluid flow between two disks, accounting for complex thermal interactions. Further investigations into hybrid nanofluids have explored their behavior under diverse conditions, including inclined magnetic fields and nonlinear boundary conditions.

Basha et al. [11] examined hybrid nanofluid flows with convective boundary conditions, highlighting the influence of heat transfer over stretching surfaces. As research has progressed, computational models developed by Mahabaleshwar et al. [12] and Hasan et al. [13] have deepened the understanding of hybrid nanofluid dynamics. These models, which utilize neural networks, forecast thermal conductivity and optimize practical applications, including engine cooling systems. The incorporation of machine learning techniques has significantly improved heat transfer simulations, contributing to enhanced energy efficiency in thermal management systems. Hybrid nanofluids are also proving to be advantageous in solar energy applications, with developments in solar collector efficiency indicating their potential to support sustainable energy solutions. This research specifically explores the thermal and frictional characteristics of hybrid nanofluids, focusing on multi-walled carbon nanotubes and iron oxide (MWCNT–Fe₃O₄) water-based nanofluids in heat transfer applications [14]. Compared with conventional fluids, hybrid nanofluids show superior thermal performance and more efficient heat management. Additionally, Jyothi et al. [15] conducted a comparative analysis of heat and mass transfer in Sisko aluminum oxide and ethylene glycol (Al₂O₃-EG) and titanium dioxide and ethylene glycol (TiO₂-EG) fluids on a stretched surface using the FEM. Their investigation examined the effects of nanoparticle concentration and stretching velocity on transfer characteristics. The FEM proved to be an effective tool for accurately modeling fluid properties and boundary conditions in these systems [16]. The challenges of stability and transport in nanofluids, including assumptions about ideal dispersion, are discussed in detail [17]. An experimental study highlighted the importance of stable dispersion and the effect of nanoparticle aggregation on thermal conductivity [18]. Dispersion stability was theoretically analyzed using specific assumptions and limitations [19]. Experimental work further demonstrated the significant impact of nanoparticle stability on heat transfer analysis [20].

Despite significant advancements in hybrid nanofluid research, the relationship between magnetic fields, thermal radiation, and fluid dynamics, particularly in deformable surfaces under slip boundary conditions, remains insufficiently explored. Existing studies primarily focus on steady-state scenarios or neglect the influence of hybrid nanoparticle combinations such as CuO and Au in water-based fluids. Additionally, the application of machine learning techniques like neural networks to simulate heat and mass transfer under these conditions is still in its early stages, limiting the predictive accuracy and optimization potential for real-world engineering applications. The objective of this study was to investigate the combined effects of magnetic fields, thermal radiation, and the unique properties of hybrid nanofluids (CuO and Au NPs in water) on fluid flow over deformable surfaces under both slip boundary conditions and steady and unsteady states. Also, using neural networks, this research aimed to improve the accuracy of heat and mass transfer predictions, ultimately enhancing the design and performance of machinery involving stretching mechanisms, centrifugal pumps, viscometers, and aerodynamic systems.

2. Mathematical Formulation of the Problem

Consider a 2D MHD boundary layer flow of a CuO and Au NP–water hybrid nanoliquid over a stretching sheet, with slip effects incorporated in the unsteady fluid flow. The x-axis denotes the flow direction and the y-axis is normal to it. The stretching velocity of the sheet, denoted as U_w (x, t), is a function of both position and time. A magnetic field of intensity B₀ is applied perpendicular to the sheet. The sheet’s surface is maintained at temperature T_w and concentration C_w while the ambient temperature and concentration are represented by T_∞ and C_∞, respectively. The nanoliquid properties are summarized in Table 1.

The governing equations for momentum, energy, and concentration are formulated under these conditions, accounting for slip velocity, thermal radiation, and chemical reaction effects. Transient states in this system are characterized by time-dependent variations in velocity, temperature, and concentration profiles, which significantly impact boundary layer dynamics. Rapid temporal changes, such as those caused by variations in the stretching rate or applied magnetic field, can result in either boundary layer amplification or suppression. These transitions affect shear stress, thermal gradients, and the overall stability of the flow [21].

Table 1. Nanofluid and base fluid thermophysical properties [22].

Fluid	ρ (Kgm−3)	Cp (J/kg K)	k (W/m-K)
Water	997.1	4179	0.613
CuO	6400	531	76.5
Au NP	19320	129.81	297.73

Table 1. Nanofluid and base fluid thermophysical properties [22].

Fluid	ρ (Kgm−3)	Cp (J/kg K)	k (W/m-K)
Water	997.1	4179	0.613
CuO	6400	531	76.5
Au NP	19320	129.81	297.73

The interplay between magnetic fields, slip effects, thermal radiation, and chemical reactions plays a pivotal role in determining the nanoliquid’s behavior. For instance, the magnetic field induces Lorentz forces, which alter the flow patterns and heat transfer characteristics. The inclusion of slip effects accounts for the relative motion between the nanoliquid and the stretching sheet, influencing velocity and thermal profiles. Furthermore, thermal radiation and chemical reactions contribute to energy and mass distribution within the boundary layer. Understanding these interactions is critical for optimizing the system’s performance in practical applications. Figure 1 provides a schematic representation of this physical problem, illustrating the flow configuration and boundary conditions.

For an incompressible fluid flow, the continuity equation is given by Equation (1).

$${\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{\partial v}{\partial y}}=0$$

(1)

Equation (2) represents the momentum equation, developed from an unsteady Navier–Stokes equation for MHD flow with a magnetic force term $({\displaystyle \frac{\sigma }{{\rho }_{hnf}}}{B}^{2}u)$ and effective density $({\rho }_{hnf})$ and viscosity $(v_{hnf})$ for hybrid nanofluids.

$${\displaystyle \frac{\partial u}{\partial t}}+u{\displaystyle \frac{\partial u}{\partial x}}+v{\displaystyle \frac{\partial u}{\partial y}}=-{\displaystyle \frac{1}{{\rho }_{hnf}}}{\displaystyle \frac{\partial p}{\partial x}}+v_{hnf}{\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}-{\displaystyle \frac{\sigma }{{\rho }_{hnf}}}{B}^{2}u$$

(2)

Equation (3) denotes the energy equation, which includes thermal diffusion via $({\displaystyle \frac{{\partial }^{2}T}{\partial y^2}})$ and radiative heat flux $({\displaystyle \frac{\partial q_r}{\partial y}})$ using the Rosseland approximation.

$${\displaystyle \frac{\partial T}{\partial t}}+u{\displaystyle \frac{\partial T}{\partial x}}+v{\displaystyle \frac{\partial T}{\partial y}}={\displaystyle \frac{K_{hnf}}{{\left({\rho }_{cp}\right)}_{hnf}}}{\displaystyle \frac{{\partial }^{2}T}{\partial y^2}}-{\displaystyle \frac{1}{{\left({\rho }_{cp}\right)}_{nf}}}{\displaystyle \frac{\partial q_r}{\partial y}}$$

(3)

Equation (4) signifies the species concentration with diffusion $(D_B{\displaystyle \frac{{\partial }^{2}C}{\partial y^2}})$ and a first-order chemical reaction $(-c_1\left(c-c_{\infty }\right))$.

$$\frac{\partial c}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_B\frac{{\partial }^{2}C}{\partial y^2}-c_1\left(c-c_{\infty }\right)$$

(4)

The boundary conditions are as follows:

At the sheet $\left(y=0\right)$:

$$u=u_w=\lambda {\displaystyle \frac{bx}{1-ct}} ; v=v_w; T=T_w+k_1{\displaystyle \frac{\partial T}{\partial y}} ;C=C_w+k_2{\displaystyle \frac{\partial C}{\partial y}}$$

(5)

Far from the sheet $(y\to \infty$):

$$u\to 0; T\to T_{\infty }; C\to C_{\infty }$$

(6)

Utilizing similarity transformations, the governing PDEs are simplified to ODEs as follows:

$$\eta =y\sqrt{\frac{a}{v_f\left(1-ct\right)}} ;\psi =y\sqrt{\frac{a{v}_f}{\left(1-ct\right)}}f\left(\eta \right); \theta \left(\eta \right)= \frac{T-T_{\infty }}{T_w-T_{\infty }}; \varnothing \left(\eta \right)= \frac{C-C_{\infty }}{C_w-C_{\infty }}$$

(7)

Velocity, temperature, magnetic field intensity, and concentration profiles are defined for time-dependent boundary conditions as follows:

$$\begin{gathered} U_w\left(x,t\right)={\displaystyle \frac{bx}{1-ct}} ; T_w\left(x,t\right)=T_{\infty }+{\displaystyle \frac{T_0{U}_{w}x}{v{\left(1-ct\right)}^{\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}}}; \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}B\left(t\right)={\displaystyle \frac{B_0}{{\left(1-ct\right)}^{\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}}}; C_w\left(x,t\right)=C_{\infty }+{\displaystyle \frac{C_0{U}_{w}x}{v{\left(1-ct\right)}^{\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}}} \end{gathered}$$

(8)

The simplification of radiative heat flux is

$$q_r=-{\displaystyle \frac{4{\sigma }^{\ast }}{3K^{\ast }}}{\displaystyle \frac{\partial T^4}{\partial z}}$$

(9)

using

$$T^4={T_{\infty }}^4+4{T_{\infty }}^3\left(T-T_{\infty }\right)+6{T_{\infty }}^2{\left(T-T_{\infty }\right)}^2+\cdots \cong 4{T_{\infty }}^{3}T-3{T_{\infty }}^4$$

(10)

Thus, substituting Equation (10) into Equation (9), it is simplified as Equation (11).

$$q_r=-{\displaystyle \frac{16{T_{\infty }}^3{\sigma }^{\ast }}{3K^{\ast }}}{\displaystyle \frac{\partial T}{\partial z}}$$

(11)

Using Equations (7)–(11), governing nonlinear PDEs and their associated boundary conditions are simplified and presented in Equations (12)–(15).

$$f^{‴}+{\displaystyle \frac{A_2}{A_1}}f f^{″}-{\displaystyle \frac{A_2}{A_1}} {\left(f^{\prime }\right)}^2-{\displaystyle \frac{A_2}{A_1}} \alpha \{f^{\prime }+{\displaystyle \frac{\eta }{2}} f^{″}\}-A_{1}M f^{\prime }=0$$

(12)

$$\left(1+A_{4}R\right){\theta }^{″}-\mathit{Pr} {\displaystyle \frac{A_3}{A_4}} {\displaystyle \frac{\alpha }{2}}\left(\eta {\theta }^{\prime }+2{\theta }^{\prime }\right)=0$$

(13)

$$S^{″}+Sc {\displaystyle \frac{\alpha }{2}}\left(\eta S^{\prime }+2S^{\prime }\right)-Cr Sc S=0$$

(14)

The boundary conditions are transformed as follows:

$$\begin{gathered} f\left(0\right)=V_0; f^{\prime }\left(0\right)=\lambda ;\theta \left(0\right)=1+ \xi \theta \prime \left(0\right); S\left(0\right)=1+ \beta S\prime \left(0\right); \\ {f}^{\prime }(\infty )\to 1; \theta (\infty )\to 0; \varnothing (\infty )\to 0 \end{gathered}$$

(15)

where the prime symbol denotes the standard derivative with respect to $\eta$. In typical mathematical notation, the expression would be written as follows:

Non-dimensional parameters:

$$\begin{gathered} Pr={\displaystyle \frac{{\nu }_f}{{\alpha }_f}}; \alpha ={\displaystyle \frac{c}{a}}; \lambda =L\sqrt{\left({\displaystyle \frac{a}{2v}}\right)};M={\displaystyle \frac{\sigma }{\rho a}}{B_0}^2; \xi =k_1\sqrt{\left({\displaystyle \frac{a}{2v}}\right)}; \beta =k_2\sqrt{\left({\displaystyle \frac{a}{2v}}\right)};Sc={\displaystyle \frac{v}{D}}; C_r={\displaystyle \frac{C_1}{a}} ; \\ R={\displaystyle \frac{16{T_{\infty }}^3{\sigma }^{\ast }}{3K^{\ast }{k}_f}}; A_1={\displaystyle \frac{1}{{\left(1-\left({\varnothing }_1+{\varnothing }_2\right)\right)}^{2.5}}} ; A_2=\left[(1-\left({\varnothing }_1+{\varnothing }_2\right)+{\varnothing }_1\left({\displaystyle \frac{{\rho }_{s1}}{{\rho }_f}}\right)+{\varnothing }_2\left({\displaystyle \frac{{\rho }_{s2}}{{\rho }_f}}\right)\right] \\ {A}_3=\left[(1-\left({\varnothing }_1+{\varnothing }_2\right)+{\varnothing }_1{\displaystyle \frac{{\left(\rho c_p\right)}_{s1}}{{\left(\rho c_p\right)}_f}}+{\varnothing }_2{\displaystyle \frac{{\left(\rho c_p\right)}_{s2}}{{\left(\rho c_p\right)}_f}}\right];A_4={\displaystyle \frac{k_{hnf}}{k_f}} \end{gathered}$$

(16)

Equation (16) includes several dimensionless parameters that describe the hybrid nanofluid flow and heat transfer characteristics. Pr represents the ratio of momentum diffusivity to thermal diffusivity, indicating the relative thickness of the velocity and thermal boundary layers. α is the ratio of thermal conductivity to heat capacity. λ quantifies the thermal penetration depth, while M represents the magnetic field parameter, influencing the flow through its interaction with the fluid’s electrical conductivity. The parameters ξ and β account for the contribution of nanoparticles to flow behavior and thermal conductivity enhancement, respectively. Sc, the Schmidt number, links viscosity to solute diffusion, and C_r reflects the concentration gradient in the fluid. The R parameter quantifies the effect of thermal radiation on the system. Finally, A₁, A₂, and A₃ represent the interaction effects of nanoparticles, considering their volume fraction, density, and specific heat capacity, while A₄ indicates the thermal conductivity ratio between the hybrid nanofluid and the base fluid. Also, ${\varnothing }_1$ represents the nanoparticle volume fraction of CuO, and ${\varnothing }_2$ represents the nanoparticle volume fraction of Au. These parameters collectively define the hybrid nanofluid’s dynamic and thermal transport properties.

The thermophysical properties of hybrid nanofluid (μ_hnf, ${\rho }_{hnf}$, ${\alpha }_{hnf}$, k_hnf, ${\left(\rho c_p\right)}_{hnf}$, and ${\sigma }_{hnf}$) and the base fluid $({\nu }_f$) are defined in Equation (17).

$$\begin{array}{c}\hfill {\mu }_{hnf}=\frac{{\mu }_f}{{\left(1-\left({\varnothing }_1+{\varnothing }_2\right)\right)}^{2.5}} ; {\rho }_{hnf}=\left(1-\left({\varnothing }_1+{\varnothing }_2\right)\right){\rho }_f+ {\varnothing }_1{\left(\rho \right)}_{s1}+{\varnothing }_2{\left(\rho \right)}_{s2} ; \\ \hfill {\left(\rho c_p\right)}_{hnf}=\left(1-\left({\varnothing }_1+{\varnothing }_2\right)\right)\rho {c_p}_f+{\varnothing }_1{\left(\rho c_p\right)}_{s1}+{\varnothing }_2{\left(\rho c_p\right)}_{s2};\\ \hfill k_{hnf}=k_{nf}^{\ast }\left({\displaystyle \frac{k_{s2}+2k_{nf}-2{\varnothing }_2\left(k_{nf}-k_{s2}\right)}{k_{s2}+2k_{nf}+{\varnothing }_2\left(k_{nf}-k_{s2}\right)}}\right); k_{nf}=k_f^{\ast }\left({\displaystyle \frac{k_{s1}+2k_f-2{\varnothing }_2\left(k_f-k_{s1}\right)}{k_{s1}+2k_f+{\varnothing }_2\left(k_f-k_{s1}\right)}}\right)\end{array}$$

(17)

Expressions for the local skin friction coefficient $(C_{fx})$, Nusselt ($N{u}_x)$, and Sherwood ($S{h}_x)$ numbers to evaluate the local friction, heat transfer, and mass transfer rates are defined in the following equation.

$$\begin{gathered} C_{fx}={\displaystyle \frac{T_w}{\rho U_w^2}} ;N{u}_x={\displaystyle \frac{x{q}_w}{k_f\left(T_w-T_{\infty }\right)}} ; S{h}_x={\displaystyle \frac{x{q}_m}{D_B\left(C_w-C_{\infty }\right)}};{\tau }_w={\mu }_{hnf}{\left({\displaystyle \frac{\partial u}{\partial y}}\right)}_{y=0}; \\ {q}_w=-k_{hnf}{\left({\displaystyle \frac{\partial T}{\partial y}}\right)}_{y=0} ;q_m=-D_B{\left({\displaystyle \frac{\partial C}{\partial y}}\right)}_{y=0} \end{gathered}$$

(18)

Using the similarity variables, Equation (18) takes the form shown in Equation (19).

$$R{e}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}} C_{fx}={\displaystyle \frac{1}{{\left(1-\left({\varnothing }_1+{\varnothing }_2\right)\right)}^{2.5}}} f^{″}\left(0\right); R{e}^{{\displaystyle \raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}} N{u}_x=-\left(1+R\right)A_4 {\theta }^{\prime }\left(0\right);$$

(19)

where $Re=\left({\displaystyle \frac{x{U}_w}{v_f}}\right)$ is the Reynolds number.

3. Methodology

The current research aimed to solve nonlinear ODEs and analyze the results using FEM and neural network models to attain precise numerical solutions for the system of equations and study key parameters affecting the behavior of hybrid nanofluids, as shown in Figure 2.

3.1. Finite Element Method

The nonlinear ODE system, as derived from Equations (12)–(14), presented significant challenges for analytical solutions. To overcome these, the FEM was chosen for its ability to efficiently handle complex nonlinear systems [23]. The computational domain was discretized into 10,000 quadratic elements, resulting in 20,001 nodes. Each element within this domain corresponded with a set of functions, denoted as f, h, and g, that were assessed at each individual node within the mesh. For numerical integration, the Gaussian quadrature method was employed, which is widely recognized for its accuracy in handling integrals over polynomial functions. This integration process contributed to the formation of a system of 80,004 nonlinear equations. These equations represented the discretized version of the ODE system across the entire computational domain. To apply the necessary boundary conditions and solve the resulting system of equations, Gaussian elimination was employed, with an error tolerance of 0.00001. This ensured that the solutions were accurate to the desired level of precision.

3.2. Neural Network Integration

Once the FEM results were obtained, including C_fx, Nu_x, and $S{h}_x$, the data were further analyzed using a neural network model. The study focused on the use of CuO and Au NP–water hybrid nanoliquids, with a stretching sheet geometry applied as the model’s configuration. An advanced Levenberg–Marquardt neural network algorithm was utilized to train the model. This method was chosen due to its fast convergence and ability to efficiently handle complex datasets. The neural network model, implemented in MATLAB R2017b (version 9.3), was trained to predict and analyze the behavior of the nanofluids under various conditions. The inputs to the network included parameters such as the nanoparticle volume fraction (ϕ₁ and ϕ₂), Reynolds number (Re), Prandtl number (Pr), and other relevant thermophysical properties of the nanofluids.

4. Results and Discussion

This study investigated the impact of slip conditions on the heat transfer coefficient in CuO and AuNP–water hybrid nanofluid flows over a stretching sheet. The findings, supported by Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 and

Table 2. Numerical values of the skin friction coefficient for varying ϕ₁, ϕ₂, and M values.

Parameter				Steady CuO/Au NP–Water	Unsteady CuO/Au NP–Water
ϕ1	ϕ2	M	Pr	f″(0)	f″(0)
0.01	0.01	0.5	6.2	1.372138	1.346720
0.05	0.01	0.5	6.2	1.321664	1.309245
0.1	0.01	0.5	6.2	1.247370	1.192776
0.15	0.01	0.5	6.2	1.163431	1.153442
0.2	0.01	0.5	6.2	1.072726	0.992441
0.01	0.01	0.5	6.2	0.915454	0.853442
0.01	0.05	0.5	6.2	1.151526	0.956524
0.01	0.1	0.5	6.2	1.334509	1.231175
0.01	0.15	0.5	6.2	1.466438	1.341558
0.01	0.2	0.5	6.2	1.551390	1.496571
0.01	0.01	0.1	6.2	0.839528	0.793258
0.01	0.01	0.5	6.2	0.967951	0.854203
0.01	0.01	1.0	6.2	1.078820	0.988270
0.01	0.01	1.5	6.2	1.190422	0.994428
0.01	0.01	2.0	6.2	1.278324	1.104919
0.01	0.01	0.5	6.2	1.723130	1.694609
0.01	0.01	0.5	7.2	1.919324	1.899942
0.01	0.01	0.5	8.2	2.264549	2.160990
0.01	0.01	0.5	9.2	2.533846	2.453244
0.01	0.01	0.5	10.2	2.730954	2.692230

, offered a comprehensive analysis of the temperature and velocity profiles as influenced by key parameters. In Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, the solid line represents the steady-state case, while the dotted line represents the unsteady case. We also clarified that parameters such as ϕ₂ = 0.01, V₀ = 0.5, Pr = 6.2, β = 0.4, R = 1.0, M = 0.5, Cr = 0.1, Sc = 1.0, and ξ = 0.5 were held constant, while ϕ₁ varied from 0.01 to 0.2.

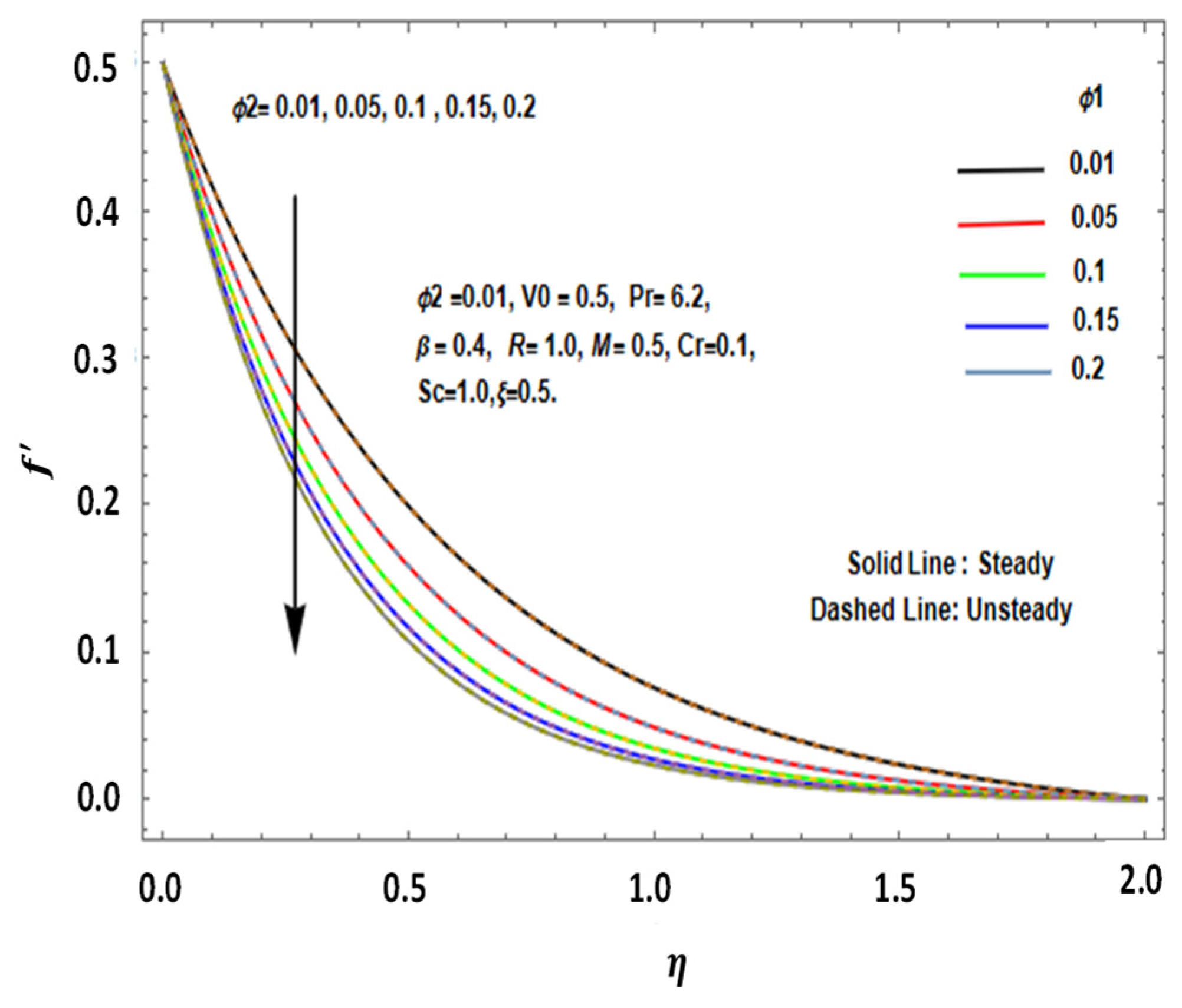
Figure 3, Figure 4, Figure 5 and Figure 6 depict the influence of nanoparticle volume fractions (ϕ₁ and ϕ₂) on the temperature and velocity profiles of CuO and Au NP–water hybrid nanofluids. The results revealed that as ϕ₁ increased, the velocity of the nanofluid rose, whereas an increase in ϕ₂ reduced the velocity, especially under transient conditions. This trend could be attributed to the distinct interactions of CuO and AuNP particles with the fluid medium. CuO NPs, being smaller and having higher thermal conductivity, enhance momentum transfer, leading to an increase in nanofluid velocity. In contrast, AuNPs, which are denser, tend to resist motion due to their higher mass and lower thermal conductivity, thereby reducing velocity. These effects are further accentuated under transient conditions due to dynamic adjustments in the flow structure, where the fluid’s inertia and thermal properties come into play. These findings are consistent with Kodi et al. [24], who reported that nanoparticle interactions significantly influence the flow behavior of hybrid nanofluids, with CuO and Au NPs having contrasting effects due to their differing sizes and thermal conductivities.

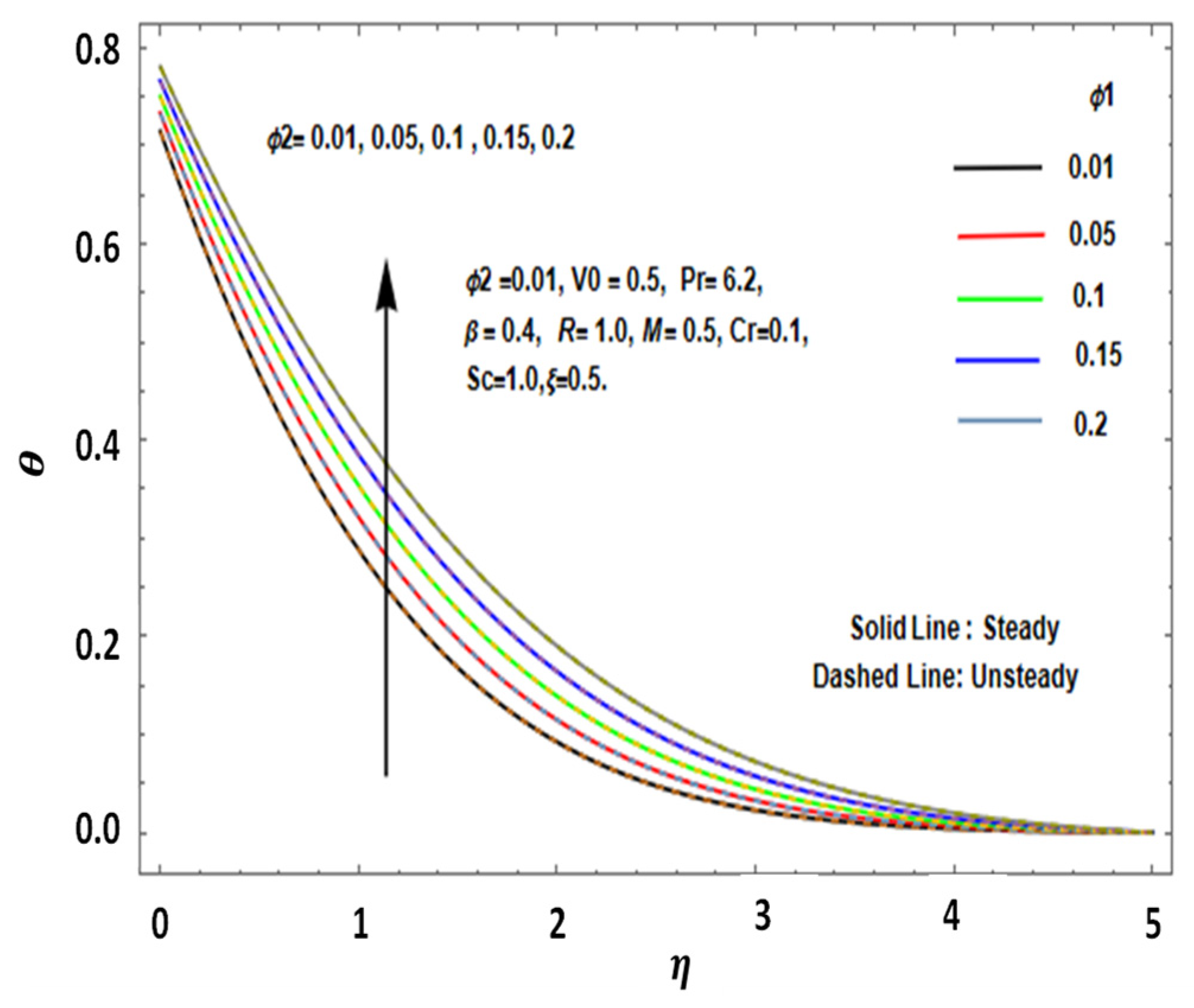
The temperature profiles, as shown in Figure 4 and Figure 6, demonstrated an increase with rising ϕ₁ and ϕ₂ values in both steady and unsteady states. The temperature increase was more pronounced in the transient state, which could be attributed to the thickening of the thermal boundary layer as the NP concentration increased. An enhanced thermal boundary layer facilitates better heat retention and promotes more efficient heat transfer, as the nanoparticles contribute to better thermal conductivity and heat storage. This is particularly evident for hybrid nanofluids with CuO NPs, which are more thermally conductive than Au NPs. Such findings align with previous studies, such as those by Jyothi et al. [15], who highlighted the role of hybrid nanofluids in improving thermal transport properties due to the synergistic effects of different NPs.

Figure 7 demonstrates that as the magnetic field strength (M) increased, the velocity of the hybrid nanofluid decreased for both constant and fluctuating scenarios. This reduction was more pronounced in the fluctuating case under both steady and transient conditions. The observed behavior was consistent with the damping effect of magnetic fields, which exert a Lorentz force that resists the motion of conductive fluids, particularly in the presence of nanoparticles with high conductivity. This effect is more noticeable in hybrid nanofluids that combine conductive nanoparticles such as CuO and Au. Previous studies, such as those by Jyothi et al. [16], corroborate these findings, emphasizing the retarding effect of magnetic fields on electrically conductive fluids, where the Lorentz force opposes the fluid motion, thus lowering the velocity.

In Figure 8, the temperature behavior of hybrid nanofluids with varying Prandtl (Pr) numbers under both constant and fluctuating conditions is explored. Higher Pr values resulted in a significant reduction in temperature, with the effect being more pronounced in fluctuating scenarios. This could be attributed to the higher thermal diffusivity of fluids with a low Pr, which accelerates heat dissipation and reduces the thermal boundary layer thickness. As a result, the fluid temperature decreases more rapidly. This behavior is consistent with established thermal transport theories, where higher Pr fluids, due to their lower thermal diffusivity, exhibit thicker thermal boundary layers and higher temperatures. Earlier numerical studies, including those by Konda et al. [25], also suggest that fluids with higher Prandtl numbers experience reduced thermal boundary layer thickness, thereby lowering the temperature.

Table 2 presents the effects of the ϕ₁ and ϕ₂ volume fraction parameters, magnetic field (M), and Prandtl number (Pr) on the dimensionless mass transfer rates and velocity. The results revealed a consistent decrease in the skin friction coefficient (C_fx) with increasing values of these parameters in both steady and unsteady states, with a more pronounced reduction in the steady state. This behavior could be attributed to the combined influence of magnetic damping, increased thermal resistance, and nanoparticle-induced drag forces, which collectively reduced the fluid’s momentum and hindered heat transfer efficiency. These findings are consistent with previous experimental and numerical studies that highlight the intricate interactions between magnetic and thermal parameters in hybrid nanofluid dynamics. For the ϕ₁ volume fraction parameter, the skin friction coefficient (f″(0)) decreased in both steady and unsteady states, with a more significant reduction in the unsteady state. On the other hand, for the ϕ₂ volume fraction parameter, an increasing trend was observed for both steady and unsteady cases [22]. Furthermore, as the magnetic field parameter (M) increased, the skin friction coefficient rose in both the steady and unsteady cases for CuO and AuNP–water hybrid nanofluid flows over a stretching sheet [23]. Lastly, an increase in the Prandtl number (Pr) resulted in slightly higher skin friction coefficient values in the steady state compared with the unsteady state [24], with both states showing a similar overall trend.

The second part of Section 4 focuses on the outcomes generated using a neural network implemented in MATLAB. This analysis examined the Nusselt number, Sherwood number, and skin friction coefficients for various parameters, including ϕ₁, ϕ₂, M, and Pr. The study applied a neural network model to CuO and Au NP–water hybrid nanoliquids over a stretching sheet as a geometry. The datasets included the skin friction coefficients of various parameters for further analysis. The advanced Levenberg neural network model was employed to yield superior outcomes, as illustrated in Figure 9 and discussed in detail.

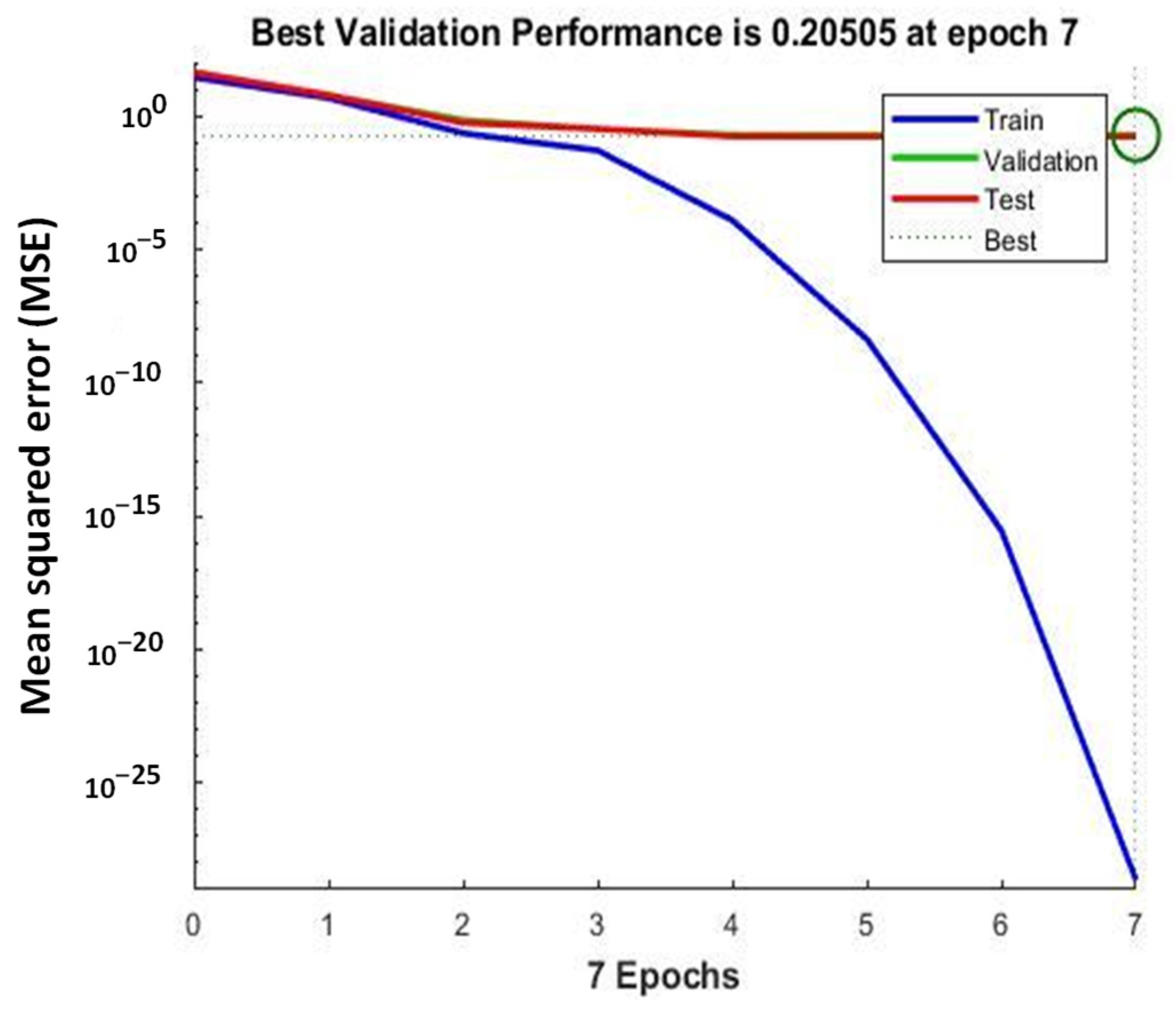
Figure 10 shows the best training performance achieved at 7 epochs, demonstrating notable accuracy and reliable findings. The model’s peak validation performance of 0.20505 at epoch 7 indicates that it quickly reached its optimal predictive capability for the skin friction coefficient.

Figure 11 illustrates the infinitesimal gradient value of 1.3553 × 10⁻¹⁴ at epoch 7, representing minimal parameter variations and signifying that the model was approaching the optimal loss function. This reflected the forthcoming convergence of the training process. Although the gradient remained slightly positive, its small magnitude indicated a significant reduction in the learning rate as the model neared a stable and definitive solution. The parameter μ likely represented the damping factor or learning rate in the optimization process, as employed in the Levenberg–Marquardt algorithm, which controlled the extent of the parameter adjustments during each iteration.

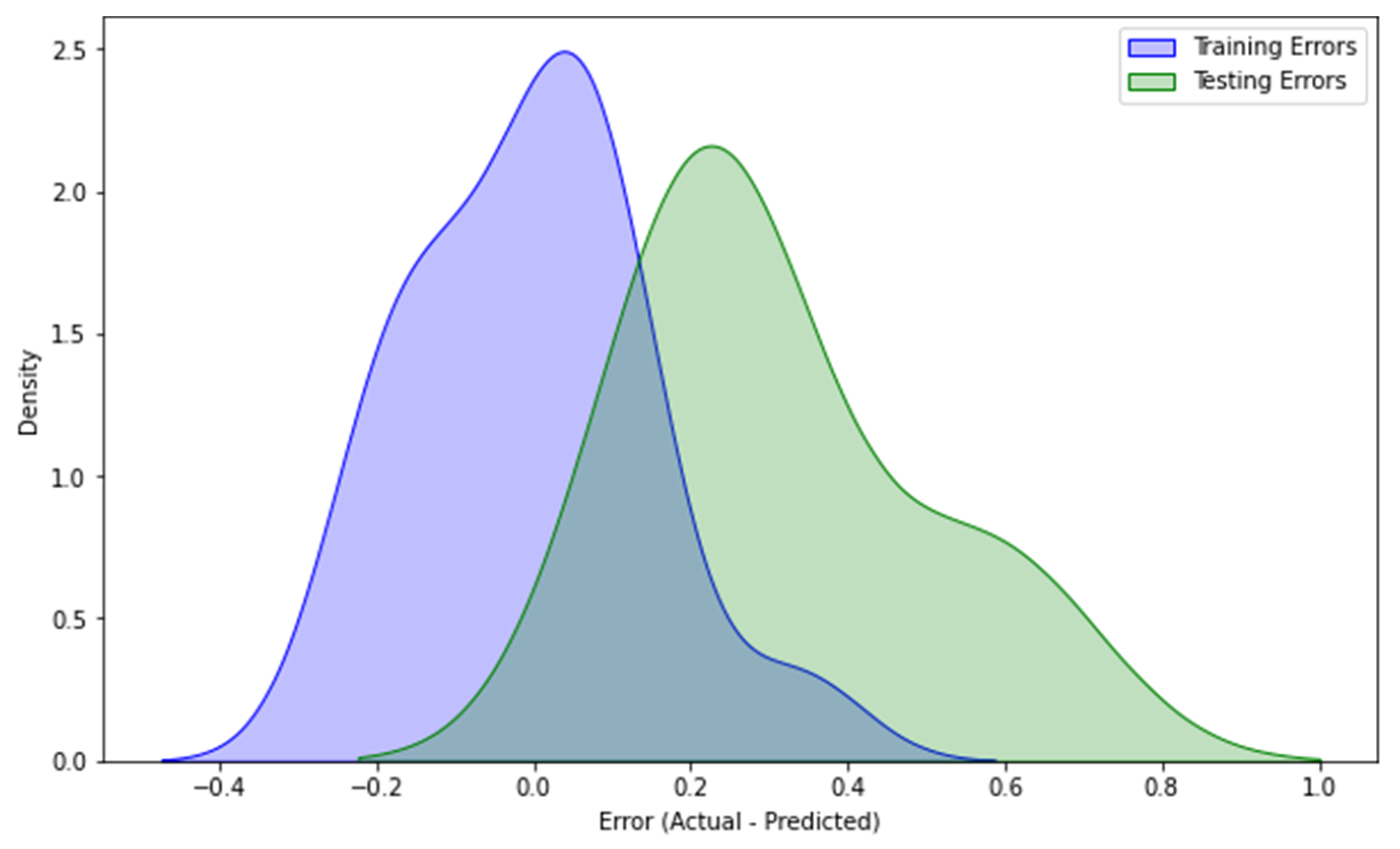
Figure 12 illustrates the error distributions for a model’s performance on the training and testing datasets. The blue curve represents the training errors, which were tightly clustered and shifted toward lower error values, indicating that the model performed well on the data it was trained on. In contrast, the green curve represents the testing errors, which were more spread out and shifted toward slightly higher error values. This indicates that the model faced greater challenges when generalizing unseen data. The overlap between the two curves suggests that the model generalized reasonably well, with a moderate similarity between training and testing performance. However, the broader spread of the testing curve highlights variability in the model’s performance on new data. Although the overall results imply a decent balance between training and testing accuracy, the slight gap between the two curves may indicate a very minor degree of overfitting.

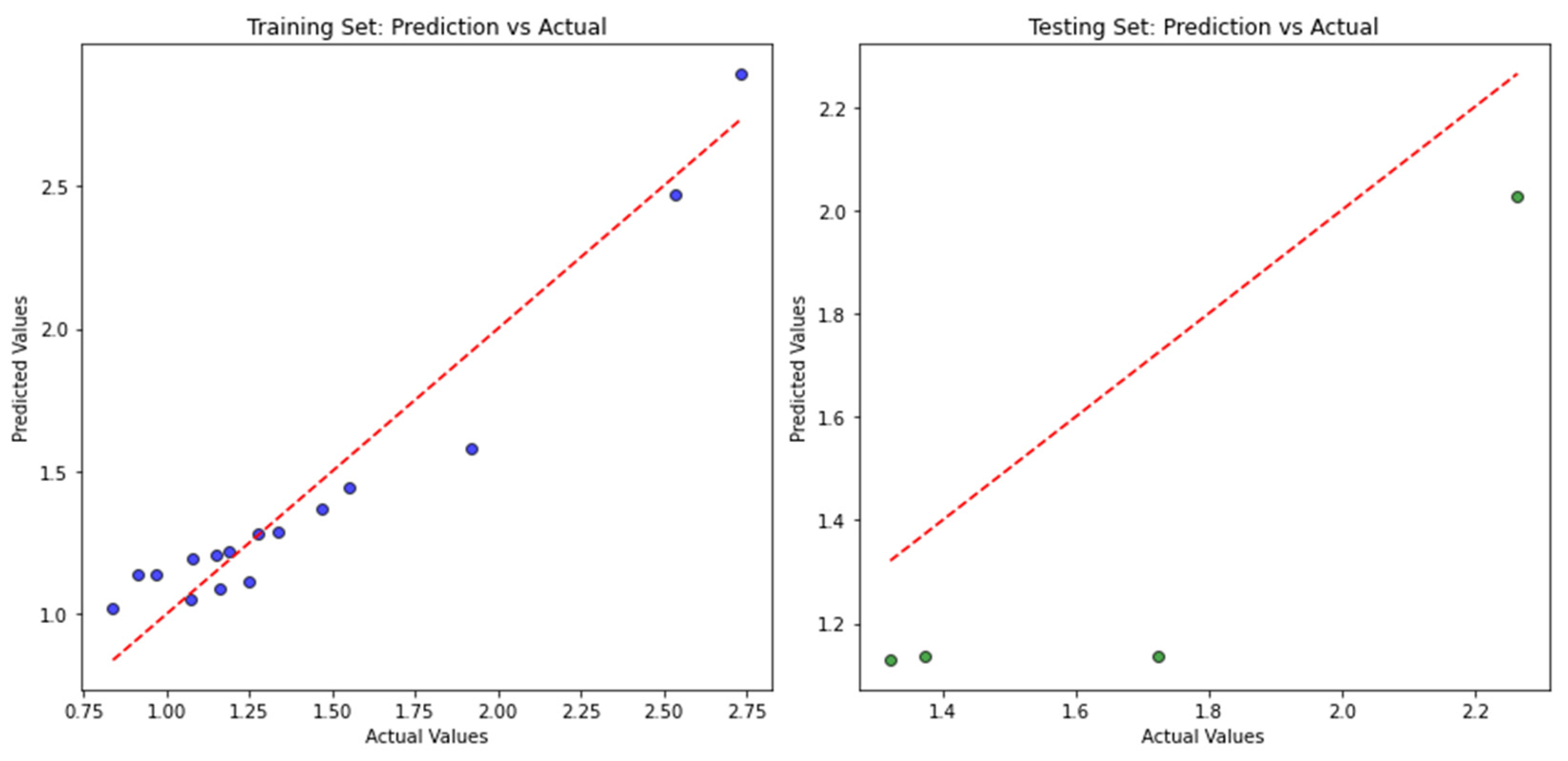
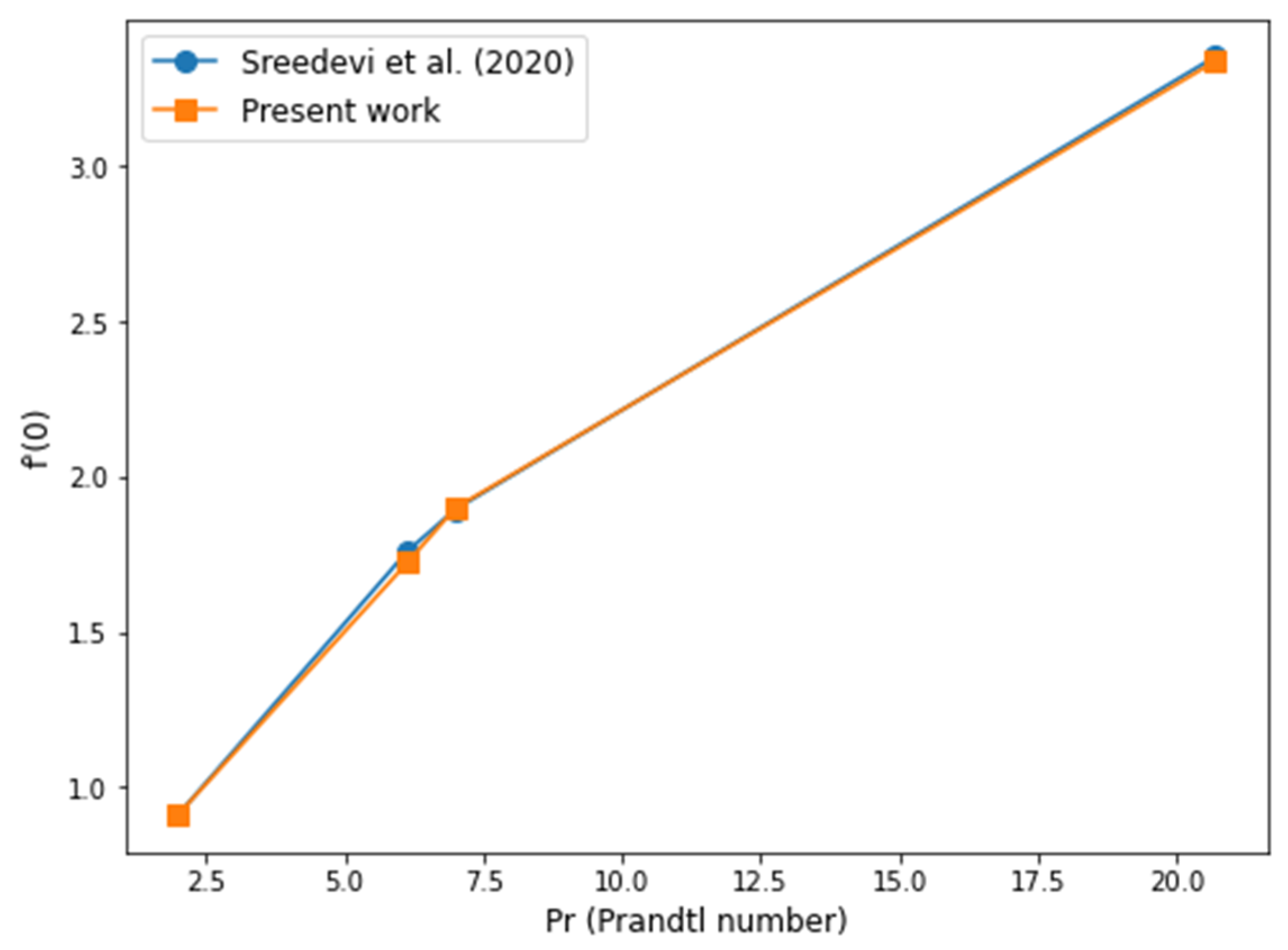
Figure 13a,b show the training and testing results, illustrating the model’s ability to explain the variance in the training data, indicating a strong fit. For the training set, R² = 0.99, demonstrating an exceptional fit. However, for the test set, R² = 0.79, which indicates good alignment with the data but also suggests potential overfitting due to the small dataset. The results were validated by comparing them with published literature (Sreedevi et al. [4]), showing good agreement, as depicted in Figure 14.

5. Conclusions

This research examined the heat and mass transfer behavior of a CuO and Au NP–water hybrid nanofluid flowing over a stretching sheet, considering the effects of velocity slip, temperature slip, chemical reactions, and thermal radiation on the hybrid nanofluid flow dynamics. The key findings revealed that increasing the volume fraction parameters ϕ₁ and ϕ₂ resulted in a thicker thermal boundary layer in both steady and unsteady states. Higher values of ϕ₁ and ϕ₂ enhanced the ϕ₁ velocity profile while reducing the ϕ₂ velocity profile for both states. Furthermore, $C_{fx}$ decreased with increasing ϕ₁ and ϕ₂ values, with a pronounced reduction for high values of M. High Pr values led to a notable decrease in the temperature profile. The neural network model demonstrated exceptional accuracy in predicting the system behavior when $R^2=0.99$. These findings contribute to the advancement of thermal management and material processing technologies, offering promising applications in fields such as heat exchangers, aerospace systems, and other engineering domains requiring efficient heat transfer and fluid flow control.

Although this study provides valuable insights into hybrid nanofluid dynamics and highlights the influence of parameter variations on flow behavior, the model’s application is constrained by the assumptions made regarding the fluid properties. Further research is needed to explore the impact of nanoparticle concentration, aggregation, and sedimentation on hybrid nanofluid stability and long-term performance, especially in complex geometries. Future studies could also focus on the experimental validation of the results and examine the effects of additional parameters, such as the influence of different base fluids or temperature-dependent properties, to enhance the understanding of hybrid nanofluid behavior. Additionally, potential approaches such as sensitivity analyses and explainable AI techniques could be explored to improve the interpretability of the model.