Assessment of the Influences of Numerical Models on Aerodynamic Performances in Hypersonic Nonequilibrium Flows
Abstract
1. Introduction
2. Numerical Approach
2.1. Nonequilibrium N-S Equations
2.2. Wall Boundary Conditions
2.3. Chemical Kinetic Model
3. Physical Model and Grid Convergence
3.1. Physical Model
3.2. Grid Convergence
4. Results and Discussion
4.1. Code Validation
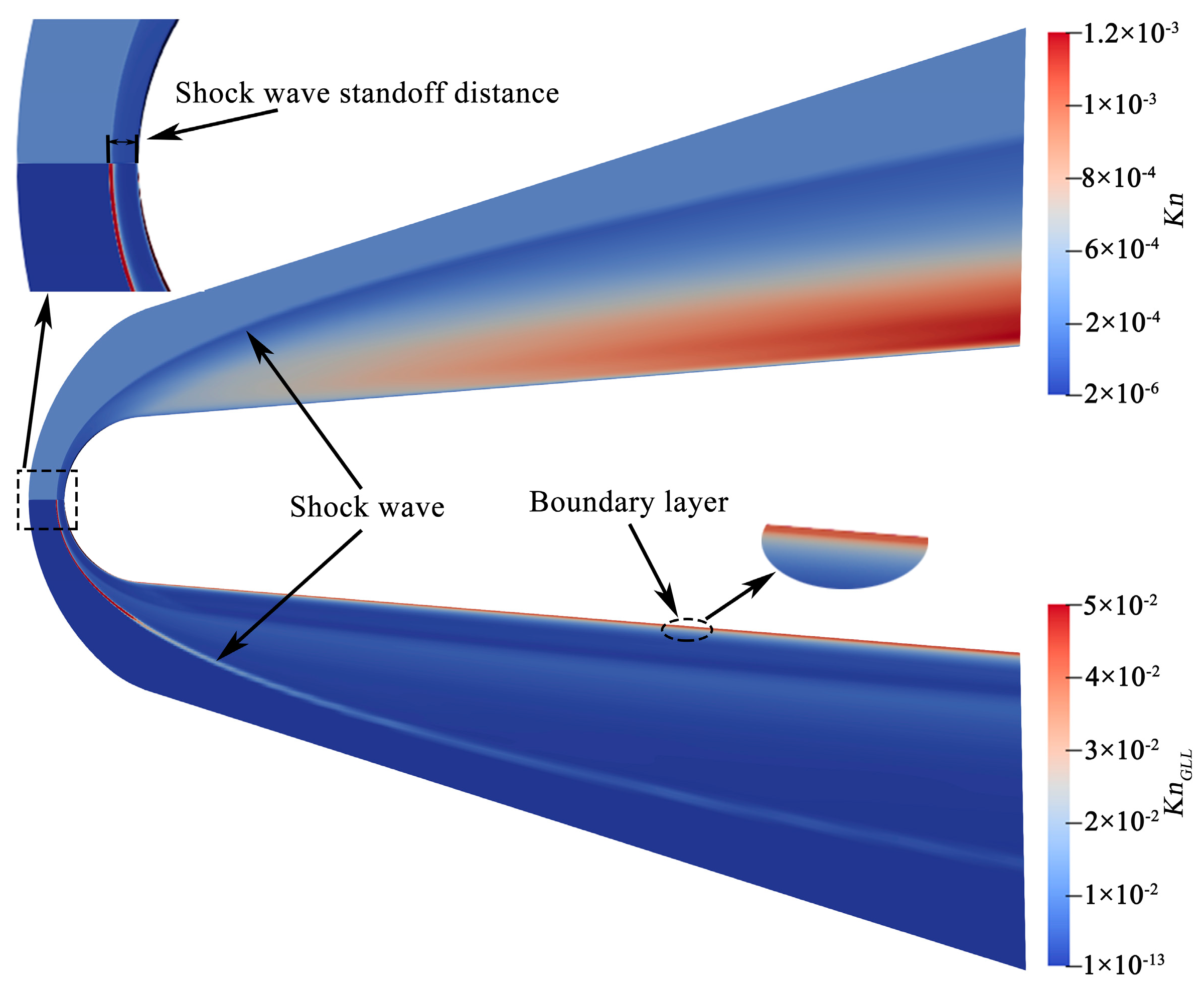
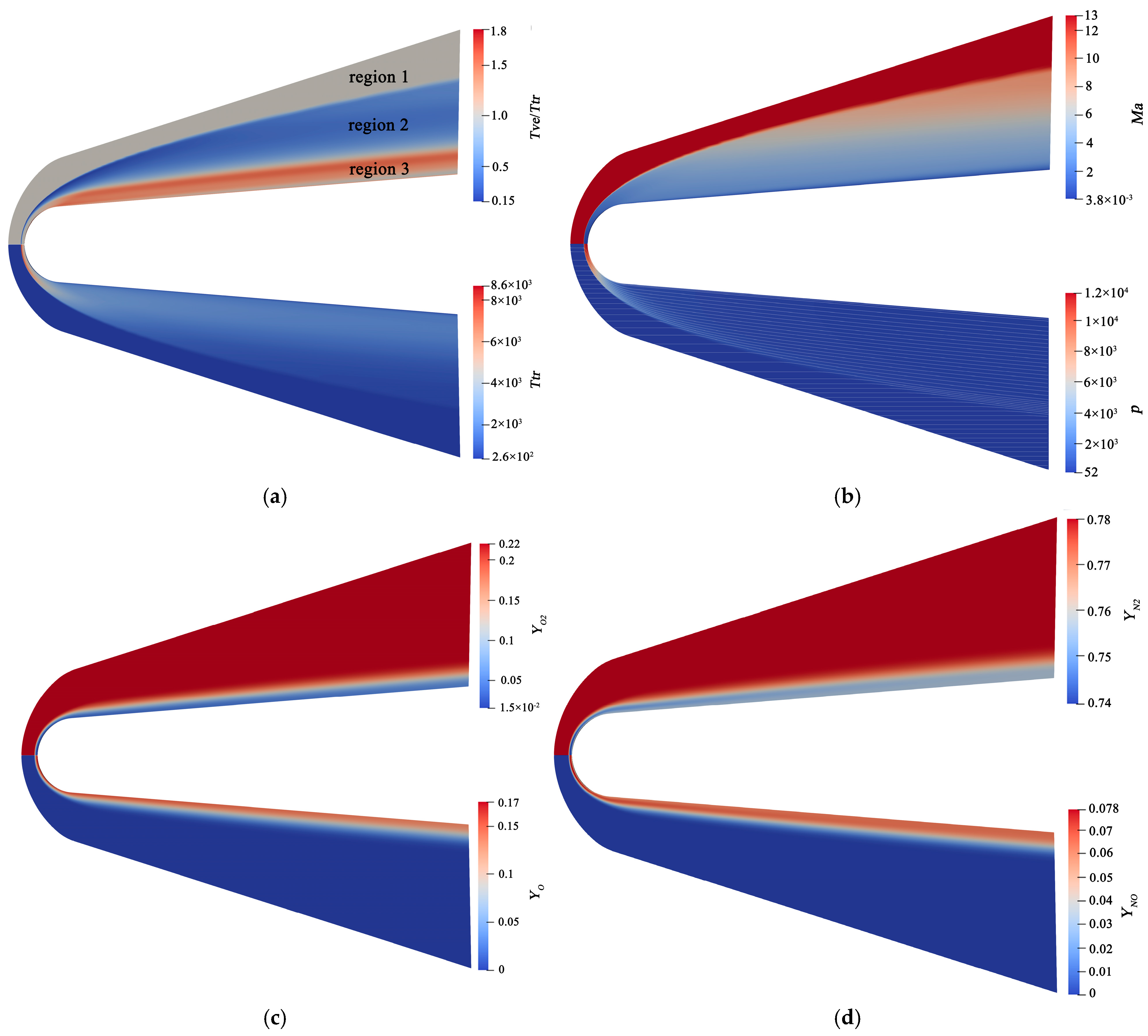
4.2. Flow Features
4.3. Aerodynamic Performances
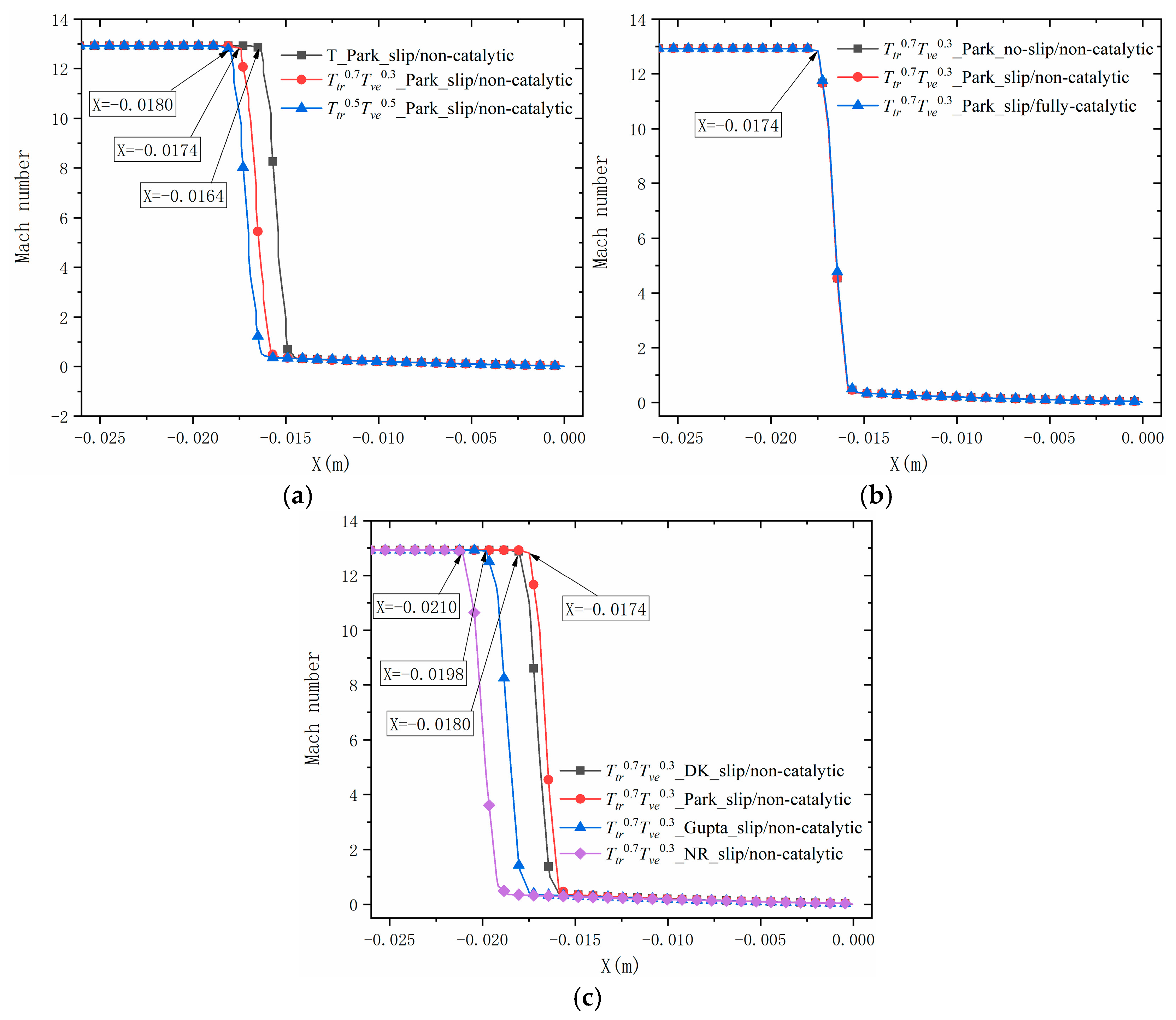
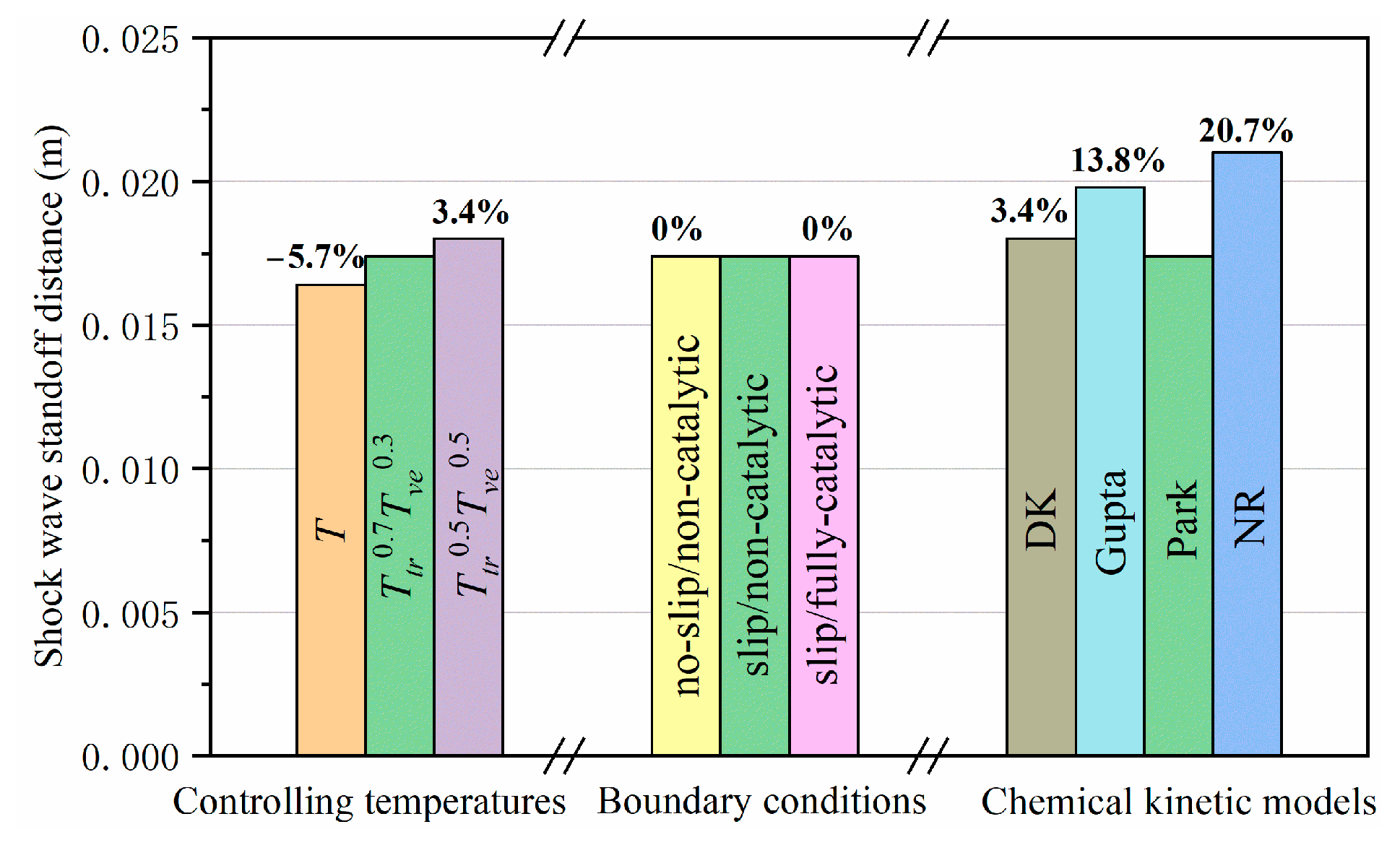
4.3.1. Shock Wave Standoff Distance
4.3.2. Heat Flux
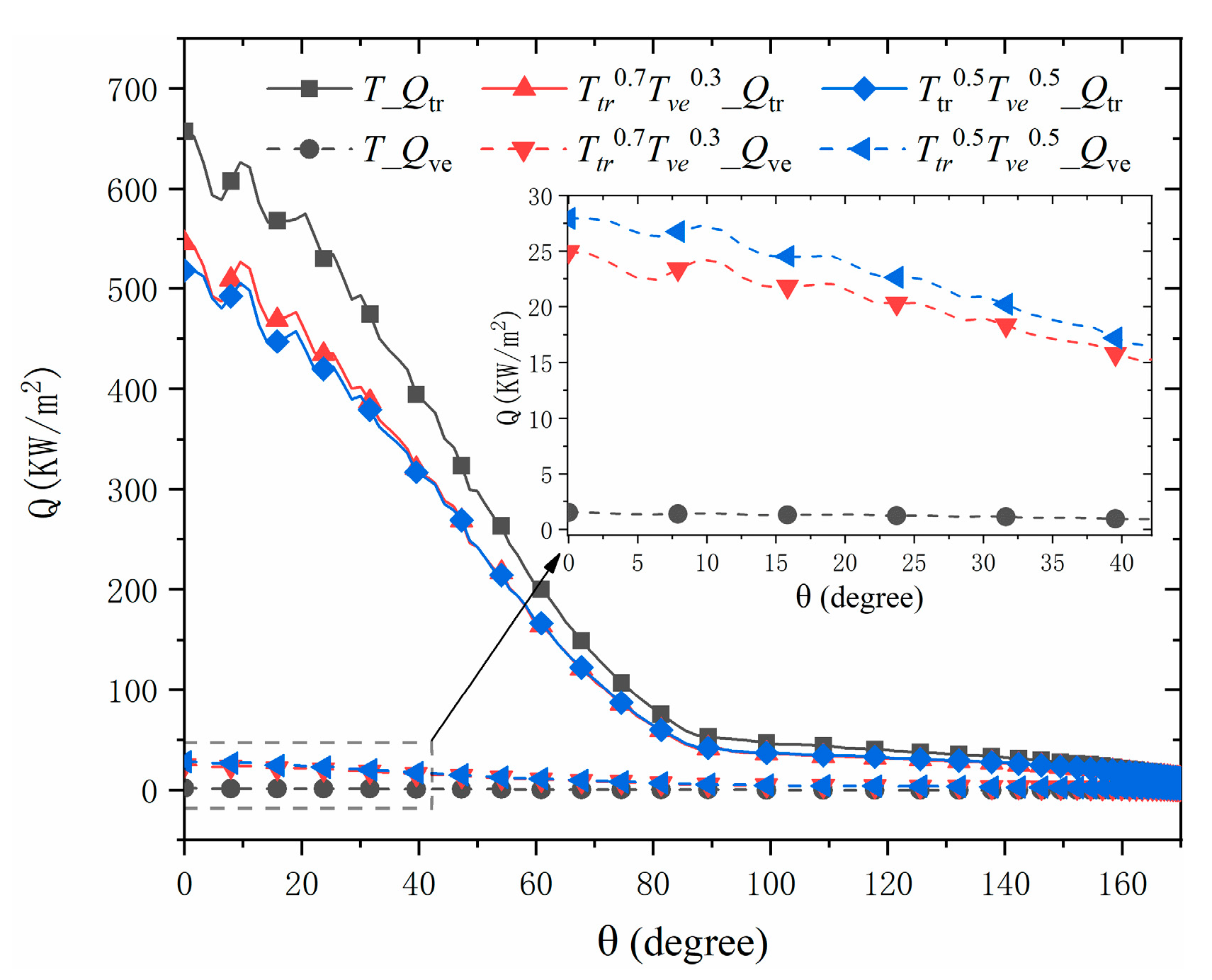
4.4. Discussion the Influence of Numerical Models on the Heat Flux
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Longo, J.M.A.; Hannemann, K.; Hannemann, V. The challenge of modeling high speed flows. In Proceedings of the EUROSIM 2007, Ljubljana, Slovenia, 9–13 September 2007. [Google Scholar]
- Schwartzentruber, T.E.; Boyd, I.D. Progress and future prospects for particle-based simulation of hypersonic flow. Prog. Aerosp. Sci. 2015, 72, 66–79. [Google Scholar] [CrossRef]
- Karpenko, M.; Stosiak, M.; Šukevičius, Š.; Skačkauskas, P.; Urbanowicz, K.; Deptuła, A. Hydrodynamic Processes in Angular Fitting Connections of a Transport Machine’s Hydraulic Drive. Machines 2023, 11, 355. [Google Scholar] [CrossRef]
- Lee, J.H. Basic governing equations for the flight regimes of aeroassisted orbital transfer vehicles. In Proceedings of the AlAA 19th Thermophysics Conference, Snowmass, CO, USA, 25–28 June 1984. [Google Scholar]
- Park, C. Assessment of two-temperature kinetic model for ionizing air. J. Thermophys. Heat Transf. 1989, 3, 233–244. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Wang, X.; Su, T. A review of the mathematical modeling of equilibrium and nonequilibrium hypersonic flows. Adv. Aerodyn. 2022, 4, 38. [Google Scholar] [CrossRef]
- Muylaert, J.; Walpot, L.; Haeuser, J.; Sagnier, P.; Devezeaux, D.; Papirnyk, O.; Lourme, D. Standard model testing in the European High Enthalpy Facility F4 andextrapolation to flight. In Proceedings of the AIAA 17th Aerospace Ground Testing Conference, Nashville, TN, USA, 6–8 July 1992. [Google Scholar]
- Hao, J.; Wang, J.; Lee, C. Numerical study of hypersonic flows over reentry configurations with different chemical nonequilibrium models. Acta Astronaut. 2016, 126, 1–10. [Google Scholar] [CrossRef]
- Niu, Q.; Yuan, Z.; Dong, S.; Tan, H. Assessment of nonequilibrium air-chemistry models on species formation in hypersonic shock layer. Int. J. Heat Mass Transf. 2018, 127, 703–716. [Google Scholar] [CrossRef]
- Kim, J.G.; Kang, S.H.; Park, S.H. Thermochemical nonequilibrium modeling of oxygen in hypersonic air flows. Int. J. Heat Mass Transf. 2020, 148, 119059. [Google Scholar] [CrossRef]
- Harvey, J.K.; Holden, M.S.; Wadhams, T.P. Code validation study of laminar shock/boundary layer and shock/shock interactions in hypersonic flow Part B: Comparison with Navier-Stokes and DSMC Solutions. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar]
- MacLean, M.; Holden, M.A. Dufrene, Comparison Between CFD and Measurements for Real-Gas Effects on Laminar Shock Wave Boundary Layer Interaction. In Proceedings of the AIAA Aviation 44th AIAA Fluid Dynamics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Holden, M.; Wadhams, T.; Harvey, J.; Candler, G. Comparisons between Dsmc and Navier-Stokes Solutions and Measurements in Regions of Laiviinar Shock Wave Boundary Layer Interaction in Hypersonic Flows, NATO RTO-TR-AVT-007-V3. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Candler, G.V.; Nompelis, I.; Druguet, M.-C.; Holden, M.S.; Wadhams, T.P.; CUBRC, B.N.; Boyd, I.D.; Wang, W.-L. CFD Validation for Hypersonic Flight: Hypersonic Double-Cone Flow Simulations. In Proceedings of the 40th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar]
- Nompelis, I.; Candler, G.V.; Holden, M.S. Effect of Vibrational Nonequilibrium on Hypersonic Double-Cone Experiments. AIAA J. 2003, 41, 2162–2169. [Google Scholar] [CrossRef]
- Hao, J.; Wang, J.; Lee, C. Numerical Simulation of High-Enthalpy Double-Cone Flows. AIAA J. 2017, 55, 2471–2475. [Google Scholar] [CrossRef]
- Kianvashrad, N.; Knight, D. Simulation of Hypersonic Shock-Wave–Laminar-Boundary-Layer Interaction on Hollow Cylinder Flare. AIAA J. 2017, 55, 322–326. [Google Scholar] [CrossRef]
- Wang, X.Y.; Yan, C.; Zheng, Y.K.; Li, E.L. Assessment of chemical kinetic models on hypersonic flow heat transfer. Int. J. Heat Mass Transf. 2017, 111, 356–366. [Google Scholar] [CrossRef]
- Holloway, M.E.; Hanquist, K.M.; Boyd, I.D. Effect of Thermochemistry Modeling on Hypersonic Flow Over a Double Cone. In Proceedings of the AIAA SciTech Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Dobrov, Y.; Gimadiev, V.; Karpenko, A.; Volkov, K. Numerical simulation of hypersonic flow with non-equilibrium chemical reactions around sphere. Acta Astronaut. 2022, 194, 468–479. [Google Scholar] [CrossRef]
- Schouler, M.; Prévereaud, Y.; Mieussens, L. Survey of flight and numerical data of hypersonic rarefied flows encountered in earth orbit and atmospheric reentry. Prog. Aerosp. Sci. 2020, 118, 100638. [Google Scholar] [CrossRef]
- Lofthouse, A.J.; Scalabrin, L.C.; Boyd, I.D. Velocity Slip and Temperature Jump in Hypersonic Aerothermodynamics. J. Thermophys. Heat Transf. 2008, 22, 38–49. [Google Scholar] [CrossRef]
- Massuti-Ballester, B.; Pidan, S.; Herdrich, G.; Fertig, M. Recent catalysis measurements at IRS. Adv. Space Res. 2015, 56, 742–765. [Google Scholar] [CrossRef]
- MacLean, M.; Holden, M. Catalytic Effects on Heat Transfer Measurements for Aerothermal Studies with CO2. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Viviani, A.; Pezzella, G. Catalytic Effects on Non-Equilibrium Aerothermodynamics of a Reentry Vehicle. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Yang, J.; Liu, M. Numerical analysis of hypersonic thermochemical non-equilibrium environment for an entry configuration in ionized flow. Chin. J. Aeronaut. 2019, 32, 2641–2654. [Google Scholar] [CrossRef]
- Needels, J.T.; Duzel, U.; Hanquist, K.M.; Alonso, J.J. Sensitivity Analysis of Gas-Surface Modeling in Nonequilibrium Flows. In Proceedings of the AIAA SciTech Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Yang, Y.; Sethuraman, V.R.P.; Kim, H.; Kim, J.G. Determination of surface catalysis on copper oxide in a shock tube using thermochemical nonequilibrium CFD analysis. Acta Astronaut. 2022, 193, 75–89. [Google Scholar] [CrossRef]
- Bechina, A.I.; Kustova, E.V. Rotational Energy Relaxation Time for Vibrationally Excited Molecules, Vestnik St. Petersburg University. Mathematics 2019, 52, 117–129. [Google Scholar]
- Casseau, V.; Scanlon, T.J.; John, B.; Emerson, D.R.; Brown, R.E. Hypersonic simulations using open-source CFD and DSMC solvers. AIP Conf. Proc. 1786, 050006. [Google Scholar] [CrossRef]
- Casseau, V. An Open-Source CFD Solver for Planetary Entry; University of Strathclyde: Glasgow, UK, 2017. [Google Scholar]
- Candler, G.V.; Nompelis, I. Computational Fluid Dynamics for Atmospheric Entry, NATO RTO-EN-AVT-162. 2009. Available online: https://docslib.org/doc/13466456/computational-fluid-dynamics-for-atmospheric-entry (accessed on 19 November 2024).
- Alkandry, H.; Boyd, I.; Martin, A. Comparison of Models for Mixture Transport Properties for Numerical Simulations of Ablative Heat-Shields. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Park, C. Nonequilibrium Hypersonic Aerothermodynamics; Wiley International: New York, NY, USA, 1990. [Google Scholar]
- Blottner, F.G.; Johnson, M.; Ellis, M. Chemically Reacting Viscous Flow Program for Multicomponent Gas Mixture; Report no. SC-RR-70-754; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 1971. [Google Scholar]
- Armaly, B.F.; Rolla, M.; Sutton, K. Viscosity of Multicomponent Partially Ionized Gas Mixtures. In Proceedings of the AlAA 15th thermophysics conference, Snowmass, CO, USA, 14–16 July 1980. [Google Scholar]
- Greenshields, C.J.; Reese, J.M. Rarefied hypersonic flow simulations using the Navier–Stokes equations with non-equilibrium boundary conditions. Prog. Aerosp. Sci. 2012, 52, 80–87. [Google Scholar] [CrossRef]
- Maxwell, J.C. On Stresses in Rarified Gases Arising from Inequalities of Temperature. Philos. Trans. R. Soc. Lond. 1879, 170, 231–256. [Google Scholar]
- Yuan, Z.; Huang, S.; Gao, X.; Liu, J. Effects of Surface-Catalysis Efficiency on Aeroheating Characteristics in Hypersonic Flow. J. Aerosp. Eng. 2016, 30, 04016086. [Google Scholar] [CrossRef]
- Dunn, M.G.; Kang, S. Theoretical and Experimental Studies of Reentry Plasmas; NASA CR-2232; NASA: Washington, DC, USA, 1973. [Google Scholar]
- Gupta, R.N.; Yos, J.M.; Thompson, R.A. A review of reaction rates and thermodynamic and transport properties for the 11-species air model for chemical and thermal nonequilibrium calculations to 30000 K, NASA RP-1232 1990, 1–86. Available online: https://ntrs.nasa.gov/api/citations/19900017748/downloads/19900017748.pdf (accessed on 19 November 2024).
- Park, C. Review of Chemical-Kinetic Problems of Future NASA Missions, I: Earth Entries. J. Thermophys Heat Transf. 1993, 7, 385–398. [Google Scholar] [CrossRef]
- Qu, F.; Chen, J.; Sun, D.; Bai, J.; Zuo, G. A grid strategy for predicting the space plane’s hypersonic aerodynamic heating loads. Aerosp. Sci. Technol. 2019, 86, 659–670. [Google Scholar] [CrossRef]
- Boyd, I.D.; Chen, G.; Candler, G.V. Predicting failure of the continuum fluid equations in transitional hypersonic flows. Phys. Fluids 1995, 7, 210–219. [Google Scholar] [CrossRef]
- Wang, W.-L.; Boyd, I.D. Predicting continuum breakdown in hypersonic viscous flows. Phys. Fluids 2003, 15, 91–100. [Google Scholar] [CrossRef]
- Istomin, V.A.; Oblapenko, G.P. Transport coefficients in high-temperature ionized air flows with electronic excitation. Phys. Plasmas 2018, 25, 013514. [Google Scholar] [CrossRef]
- Hu, Y.; Huang, H.; Guo, J. Shock wave standoff distance of near space hypersonic vehicles. Sci. China Technol. Sci. 2017, 60, 1123–1131. [Google Scholar] [CrossRef]
- Du, Y.-W.; Sun, S.-R.; Tan, M.-J.; Zhou, Y.; Chen, X.; Meng, X.; Wang, H.-X. Non-equilibrium simulation of energy relaxation for earth reentry utilizing a collisional-radiative model. Acta Astronaut. 2022, 193, 521–537. [Google Scholar] [CrossRef]
- Yang, X.; Gui, Y.; Xiao, G.; Du, Y.; Liu, L.; Wei, D. Reacting gas-surface interaction and heat transfer characteristics for high-enthalpy and hypersonic dissociated carbon dioxide flow. Int. J. Heat Mass Transf. 2020, 146, 118869. [Google Scholar] [CrossRef]
- Gimelshein, S.F.; Wysong, I.J. Gas-Phase Recombination Effect on Surface Heating in Nonequilibrium Hypersonic Flows. J. Thermophys. Heat Transf. 2019, 33, 638–646. [Google Scholar] [CrossRef]








| No | Reaction | DK | Gupta | Park | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Af | Bf | Ta | Ab | Bb | Tb | Af | Bf | Ta | Af | Bf | Ta | ||
| 1 | 3.60 × 1018 | −1.0 | 59,500 | 3.0 × 1015 | −0.5 | 0 | 3.61 × 1018 | −1.00 | 59,500 | 1.0 × 1022 | −1.5 | 59,500 | |
| 2 | 3.60 × 1018 | −1.0 | 59,500 | 3.0 × 1015 | −0.5 | 0 | 3.61 × 1018 | −1.00 | 59,500 | 2.0 × 1021 | −1.5 | 59,500 | |
| 3 | 9.00 × 1019 | −1.0 | 59,500 | 7.5 × 1016 | −0.5 | 0 | 3.61 × 1018 | −1.00 | 59,500 | 1.0 × 1022 | −1.5 | 59,500 | |
| 4 | 3.24 × 1019 | −1.0 | 59,500 | 2.7 × 1016 | −0.5 | 0 | 3.61 × 1018 | −1.00 | 59,500 | 2.0 × 1021 | −1.5 | 59,500 | |
| 5 | 7.20 × 1018 | −1.0 | 59,500 | 6.0 × 1015 | −0.5 | 0 | 3.61 × 1018 | −1.00 | 59,500 | 2.0 × 1021 | −1.5 | 59,500 | |
| 6 | 1.90 × 1017 | −0.5 | 1.13 × 105 | 1.1 × 1016 | −0.5 | 0 | 1.92 × 1017 | −0.50 | 113,100 | 7.0 × 1021 | −1.6 | 113,200 | |
| 7 | 1.90 × 1017 | −0.5 | 1.13 × 105 | 1.1 × 1016 | −0.5 | 0 | 1.92 × 1017 | −0.50 | 113,100 | 3.0 × 1022 | −1.6 | 113,200 | |
| 8 | 4.085 × 1022 | −1.5 | 1.13 × 105 | 2.27 × 1021 | −1.5 | 0 | 4.15 × 1022 | −1.50 | 113,100 | 3.0 × 1022 | −1.6 | 113,200 | |
| 9 | 4.7 × 1017 | −0.5 | 1.13 × 105 | 2.72 × 1016 | −0.5 | 0 | 1.92 × 1017 | −0.50 | 113,100 | 7.0 × 1021 | −1.6 | 113,200 | |
| 10 | 7.8 × 1020 | −1.5 | 75,500 | 2.0 × 1020 | −1.5 | 0 | 3.97 × 1020 | −1.50 | 75,600 | 1.1 × 1017 | 0.0 | 75,500 | |
| 11 | 3.9 × 1020 | −1.5 | 75,500 | 1.0 × 1020 | −1.5 | 0 | 3.97 × 1020 | −1.50 | 75,600 | 5.0 × 1015 | 0.0 | 75,500 | |
| 12 | 3.2 × 109 | 1.0 | 19,700 | 1.3 × 1010 | 1.0 | 3580 | 3.18 × 109 | 1.0 | 19,700 | 8.4 × 1012 | 0.0 | 19,450 | |
| 13 | 7.0 × 1013 | 0.0 | 38,000 | 1.56 × 1013 | 0.0 | 0 | 6.75 × 1013 | 0.0 | 37,500 | 6.4 × 1017 | −1.0 | 38,400 | |
| Boundary Conditions | Freestream | ELECTRE Surface | ||
|---|---|---|---|---|
| No-Slip/Non-Catalytic | Slip/Non-Catalytic | Slip/Fully-Catalytic | ||
| Velocity (m/s) | 4230 | 0 | slip | slip |
| Static pressure (Pa) | 52.8 | |||
| Static temperature (K) | 265 | 343 | slip | slip |
| Species | 78% N2, 22% O2 | non-catalytic | non-catalytic | fully-catalytic |
| ywall | Rewall | NI | NJ | |
|---|---|---|---|---|
| grid 1 | 1e-4 | 18.33 | 100 | 153 |
| grid 2 | 5e-5 | 9.17 | 100 | 203 |
| grid 3 | 6e-6 | 1.10 | 180 | 203 |
| grid 4 | 3e-6 | 0.55 | 250 | 253 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhang, Z.; Yang, H. Assessment of the Influences of Numerical Models on Aerodynamic Performances in Hypersonic Nonequilibrium Flows. Processes 2024, 12, 2629. https://doi.org/10.3390/pr12122629
Zhang W, Zhang Z, Yang H. Assessment of the Influences of Numerical Models on Aerodynamic Performances in Hypersonic Nonequilibrium Flows. Processes. 2024; 12(12):2629. https://doi.org/10.3390/pr12122629
Chicago/Turabian StyleZhang, Wenqing, Zhijun Zhang, and Hualin Yang. 2024. "Assessment of the Influences of Numerical Models on Aerodynamic Performances in Hypersonic Nonequilibrium Flows" Processes 12, no. 12: 2629. https://doi.org/10.3390/pr12122629
APA StyleZhang, W., Zhang, Z., & Yang, H. (2024). Assessment of the Influences of Numerical Models on Aerodynamic Performances in Hypersonic Nonequilibrium Flows. Processes, 12(12), 2629. https://doi.org/10.3390/pr12122629






