Quality Control of Electro-Discharge Texturing of Rolls Through Six Sigma

Abstract

This article presents the implementation of the Six Sigma methodology in the electro-discharge texturing process of cold mill work rolls. The final surface quality of sheet metal must meet the specific demands of car body part producers, which require a specific surface texture described by surface microgeometry parameters: the average roughness and the peak density. The requirements for the surface microgeometry of sheet metal are mainly related to improving the formability and adhesion of the paint in the body painting process. These microgeometry parameters can be controlled by the texture of work rolls: this texture is transferred onto the sheet metal surface. The electro-discharge texturing process allows for control of the average roughness and peak density according to individual customer specifications. In this study, a model is proposed to predict the average roughness based on the input parameters of the electro-discharge texturing process: current, voltage, and time. Compared to previous models, this model includes more input parameters. The process suitability was analyzed using control charts, capability indices, and Z scores. The modified weighted product method was used to create a purpose function describing the relationships between the input and output quality parameters. Based on the agreement of the target quality characteristics and the calculated values according to the models obtained, an algorithm to control the texturing process of the work rolls was designed. The proposed model was also validated on results published by other authors and demonstrated good agreement. This study should contribute to the philosophy of continuously improving the surface quality of cold-rolled sheet metal.

1. Introduction

Customers often perceive the quality of cars through the attractiveness of the design, color, and gloss of the body paint. These quality features are closely related to the sheet metal texture, the production quality of the car body surface parts made of this sheet metal, the accuracy of the assembly of these parts, etc. [1]. The rolling process used to make the sheet metal determines its manufacturing qualities, including its formability, glued joint strength, and suitability for paint application [2,3]. Automobile companies specify requirements for texture characteristics—roughness average (Ra), peak density (Pc), and waviness (Wa)—of the sheet metal surface for visible body parts [4,5,6,7]. For these car body parts, carmakers prefer the roughness (Ra) of the sheet metal surface to range from 1.0 μm to 1.6 μm; for the inner parts, it can be higher [2,3]. For example, Škoda Auto, in its specifications, states roughness values of Ra from 1.1 to 1.6 μm and peak density Pc ≥ 40 cm⁻¹; Ford requires roughness Ra from 1.1 to 1.7 μm and peak density Pc ≥ 50 cm⁻¹; Volkswagen requires roughness Ra from 1.1 to 1.6 μm and maximum peak density Pc ≥ 60 cm⁻¹; and Renault requires roughness Ra from 0.7 to 1.3 μm and peak density Pc ≥ 110 cm⁻¹ [4,8].

The manufacturability of car body parts by cold forming—their formability—is greatly affected by the friction between the contact surfaces of the tool and the sheet metal. With a suitable sheet metal surface texture, lubricant accumulates in close pockets on the surface of the sheet metal. This lubricant is pushed out of these pockets during the movement of the material (during forming) and forms a continuous layer between the contact surfaces. The created lubricant layer prevents abrasion (sticking) of softer material (sheet metal) on the contact surfaces of the tool and contributes to reducing frictional forces and improving formability. On the contrary, with an inappropriate texture, the pressure on the contact surfaces increases several times when the sheet moves between the contact surfaces of the tool. As a result of a local increase in pressure on the contact surfaces, especially on the drawing edge of the drawbar, an insufficient amount of lubricant is captured in the shallow pockets. An adequate amount of lubricant is required to create a continuous layer. It has been found that the combination of smaller Ra and greater Pc values is not the most suitable because when the material is moved between the contact surfaces of the tool, the peaks on the surface of the sheet metal wear and are pushed into the depths on the surface of the sheet metal. On the other hand, a more significant increase in the roughness Ra will cause the surface of the tool to be matte after painting [2,3].

The sheet metal surface texture specified by individual car manufacturers can be achieved via controlled formation of the surface texture of cold mill work rolls and rolling parameters (rolling speed, thickness reduction, rolling force, etc.) [9,10]. Thus, the texture from the surface of the cold mill work rolls is transferred to the sheet metal surface [11,12].

Texturing of the work rolls’ surface can be carried out using different methods. In shot blast texturing (SBT) with fine-grained granules, the roll surface quality depends on the shot shape and bulk, the kinetic energy of blast shots, and the surface quality before texturing. Even though the process is simple, highly productive, and relatively low-cost, the surface roughness that it produces is not homogeneous and has low roughness retention compared to other texturing methods [13,14]. Electric discharge texturing (EDT) has been proven to be a reliable method of providing the required surface microtopography [15]. The process consists of the formation of minute surface craters through the discharge of electrical energy between two metal electrodes that are separated by a dielectric fluid. The resultant surface integrity of the roll can be achieved through regulation of the amount of peak current, pulse on/off time, capacitance, polarity, tool electrode material, etc. [16]. Laser beam texturing (LBT) methods, such as Pomini digital texturing, allow good control of the surface texture matrix by means of software, thus resulting in a wide range of surfaces, ranging from deterministic to stochastic, that can be produced. Using this method, it is possible to alter the spacing parameters, density, crater overlap, and various combinations of effects such as fixed crater size and random placement (or variable crater sizes with fixed placement) [5,17]. Electron beam texturing (EBT), similar to laser beam texturing, creates craters with a solid collar when the roll turns into a vacuum chamber and moves along the axis. The distribution of the craters can be controlled by the roll speed and the frequency of beam irradiation; in addition, both may be synchronized. However, the texture obtained is not the most desirable in terms of tribological conditions on contact surfaces of the die since worsened sheet formability can be expected as a result [15]. The Topocrom process creates convex hemispheres on the roll surface that offer an opportunity for a wide range of different resulting topographies, thus achieving the required surfaces by adapting the mean radius, size distribution, and the number of these hemispheres per unit area. This hard chromium electroplating process improves the life of the surface textures created via conventional processes (SBT, EDT, EBT) [15,17]. As Gorbunov and Colak summarized, textures created with EDT, LBT, EBT, and Topocrom technologies show a good correlation between Ra and Pc. Even though the rolls produced via the Topocrom process were found to have a life that was roughly ten times longer than others, high Pc may occur on the surface rolls. The LBT process produces rolls with a very high roughness retention property, but the texturing process is time-consuming, which is a big disadvantage [15,17].

When applying EDT, the texture of the surface and the properties of the surface layer of the work rolls change due to electric discharges. The amount of material reduction in EDT depends on the erosion effect of the electrical discharge between two electrodes that are separated by a dielectric liquid and exposed to the electrical discharge E_DP [9,10,11,18]. The E_DP can be expressed by Relation (1):

$$E_{DP}=U_p.I_p.T_{on},$$

(1)

while

$$Q_{DP}=I_p.T_{on},$$

(2)

where U_p is the peak voltage of the discharge; I_p is the peak current; T_on is the pulse on-time; and Q_DP is the pulse charge.

It can be seen from Relation (1) that the amount of material reduction depends on the parameters of the EDT process, i.e., voltage U_p, current I_p, and discharge duration T_on [9,10,11,18]. To track non-conforming products, control tables are used during data collection to evaluate whether the product passes (OK) or fails (N-OK). Based on these data, the DPMO can be evaluated [19]. The number of defective parts (defects per million opportunities, DPMO) can be determined using Relation (3) [20,21,22]:

$$DPMO={\displaystyle \frac{D}{N.O}}.{10}^6,$$

(3)

where DPMO is defects per million opportunities; D is the total number of defective parts; N is the total number of verified parts; and O is the number of opportunities per unit.

Another sign of process quality is the Six Sigma (Z) level. In the case of continuous data, Z can be calculated according to Relations (4) and (5):

$$Z_U={\displaystyle \frac{UCL-\overline{X}}{\sigma }},$$

(4)

$$Z_L={\displaystyle \frac{\overline{X}-LCL}{\sigma }},$$

(5)

where Z_U is the sigma level for the upper specification limit; Z_L is the sigma level for the lower specification limit; $\overline{X}$ is the measured average value of the quality characteristic; σ is the standard deviation of the quality characteristic; UCL is the upper control limit of the quality characteristic specified by the customer; and LCL is the lower control limit of the quality characteristic specified by the customer.

Requirements of car manufacturers for the quality of the surface of the body parts and the elimination of the waste of resources force the steel industry to produce sheet metals of high surface quality [20,21]. Therefore, steel companies are taking measures to continuously improve the surface texturing processes of work rolls. One possible measure is to reduce the variability of the input parameters of the roll texturing process. According to the International Organization for Standardization, one possibility is the application of Six Sigma principles. Six Sigma tools make it possible to identify the causes of variability and subsequently manage them in order to gradually eliminate the number of non-conforming parts (defective or N-OK parts) with the specification (see Figure 1) [22,23,24,25,26]. The Six Sigma level (Z) can also be calculated on the basis of DPMO using Relation (6):

$$Z=1.5\ast {\sigma }^{-1}\ast \left({\displaystyle \frac{DPMO}{{10}^6}}\right),$$

(6)

or read from

Table 1. Six Sigma conversion table.

Capability Index Cpk min	1	1.13	1.33	1.49	1.667	1.75	1.83	2
Six Sigma level (Zmin score)	3	3.39	4	4.5	5	5.25	5.5	6
DPMO	660,807	30,396	6210	1350	233	88	32	3
Cost of poor quality COPQ	25% to 45%		15% to 25%		5% to 15%

.

Reducing the number of defective products and deviations from the required value of the monitored quality parameter of a given product is the basis for achieving process stability. As mentioned previously, the level of process perfection can be expressed as the maximum number of defects per million opportunities (DPMOs). Using DPMOs as a quality measure in the product creation process can also sensitively reflect the economic aspects of the process. The occurrence of defects always represents, in the final sense, an increase in the cost of poor quality, which ultimately has a negative impact on profit generation. Table 1 shows the relationship between the number of defects, the Six Sigma level, and the cost of quality (cost of poor quality, COPQ) [27].

The aim of this study is to assess the ability of EDT to achieve the specified characteristics (Ra and Pc) of the surface texture of cold mill work rolls on the basis of control diagrams, C_pk, and Z scores. Furthermore, in this study, we aim to carry out a regression analysis of the dependence of the Ra and Pc quality characteristics on the EDT input parameters U_p, I_p, T_on, and T_off and propose an algorithm for gradual improvement of the output parameters of the Ra and Pc.

2. Materials and Methods

The Six Sigma method offers several techniques that can be used to achieve continuous process improvement. One of them is DMAIC. According to this methodology, the procedure needs to be divided into five phases: define, measure, analyze, improve, and control [21,22].

Define: When defining the process, the following assumptions were made:

• When texturing with EDT technology, there is a very good correlation between the roughness Ra and the peak density Pc [4,5,28];
• Prior results show that, depending on the rolling force, it is possible to achieve a 10% to 50% texture transfer from the rolls of the rolling mill to the sheet surface [2,4];
• On the EDT 2100/4500 device, it is possible to repeatedly create a texture on the surface of rolls with roughness Ra in the range from 1.5 μm to 3.8 μm and with peak density Pc > 40 cm⁻¹.

Measure: The rolls were textured on EDT 2100/4500 equipment in an oil dielectric BP250 with eight copper electrodes and using three different plans (PE 1, PE 2, and PE 3; see

Table 2. Plan of experiments—input values.

	PE 1 TRa1 = 1.5 (μm)	PE 2 TRa2 = 2.5 (μm)	PE 3 TRa3 = 3.8 (μm)
Texture current Ip (A)	4	18	19
Lower voltage limit UPL (V)	5	10	15
Upper voltage limit UPH (V)	8	20	25
Pulse duration Ton (μs)	4	14	29
Technological break duration Toff (μs)	6	16	38
Electrode diameter d (mm)	8	8	8

Note: PE 1—plan of experiment 1; PE 2—plan of experiment 2; PE 3—plan of experiment 3; T_Ra,1—target value in PE 1; T_Ra,2—target value in PE 2; T_Ra,3—target value in PE 3.

). The measurement of the output parameters of the work rolls’ surface roughness was carried out with a Hommel Tester T 1000 roughness meter (JENOPTIK Industrial metrology, Villingen-Schwenningen, Germany) according to DIN EN ISO 4288 [29]. Roughness measurements Ra and Pc were taken three times on the left side, three times in the middle, and three times on the right side along the rolls when the rolls were turned at angles of 0°, 90°, 180°, and 270° (see Figure 2). The average Ra values of the work rolls are shown in

Table 3. Measured values in the variation range VR_Ra = CL_Ra,RR ± VR_Ra,SS—first step.

Measure Value	PE 1		PE 2		PE 3
	Ra (μm)	Pc (cm−1)	Ra (μm)	Pc (cm−1)	Ra (μm)	Pc (cm−1)
Average value $\overline{Ra}$	1.548	161	2.5	99	3.845	68
Standard deviation SD	0.06	7	0.06	3	0.04	3
Upper-level Six Sigma ZU	3.38	-	4.49	-	2.25	-
Lower-level Six Sigma ZL	4.98	18.6	4.48	21.1	7.53	10.0
CpKU	1.13	-	1.50	-	1.75	-
CpKL	1.66	6.2	1.49	7.05	2.51	-
DPMO	30,396	0	1350	0	88	3.36

.

3. Results and Discussion

Analysis: In the first phase, variability was analyzed based on the records of the number of non-conforming parts. Out of 175 inspected rolls, 17 were out of specification. Using Relation (3), the value of DPMO ≈ 30,396 was calculated, and a Six Sigma level of 3.39 was subtracted from Table 1. Defects were identified on work rolls, such as burning of the rolls, shine-through of the textured surface of the rolls, strips around the perimeter of the rolls, strips from rolls (aluminations), and texture parameters Ra and Pc.

Burning of the work rolls can be caused by the short duration of the technological T_off, during which there is no interruption of the pulse. Roll burnout can also occur if the circumferential speed of the roll rotation is low. In this case, impurities are not removed from the dielectric liquid, and as a result, the electric arc between the electrode and the workpiece (roll) recurs.

Defects on the textured surface of the roll can be caused by imperfect grinding of the roll. When taking over the rolls from the supplier, precise grinding of the rolls is required. Another cause of defects in the roll texture is damage to the roll pins.

Bands around the circumference of the roll can be caused by an incorrect setting of the texturing I_p. The occurrence of this error is permissible within a certain interval; otherwise, the input values of the texturing current I_p need to be adjusted. Other causes of these strips are poorly ground pins, a worn bearing, an unseated support on the base, and bad centering in the chrome plating bath. These errors can be eliminated by taking measures related to the acceptance procedure from the producer, following technological procedures when setting the rolls in the device, and regular maintenance of the electrospark device.

When analyzing the stability of the process, control diagrams are used, in which it is necessary to mark the following control limits of quality indicators:

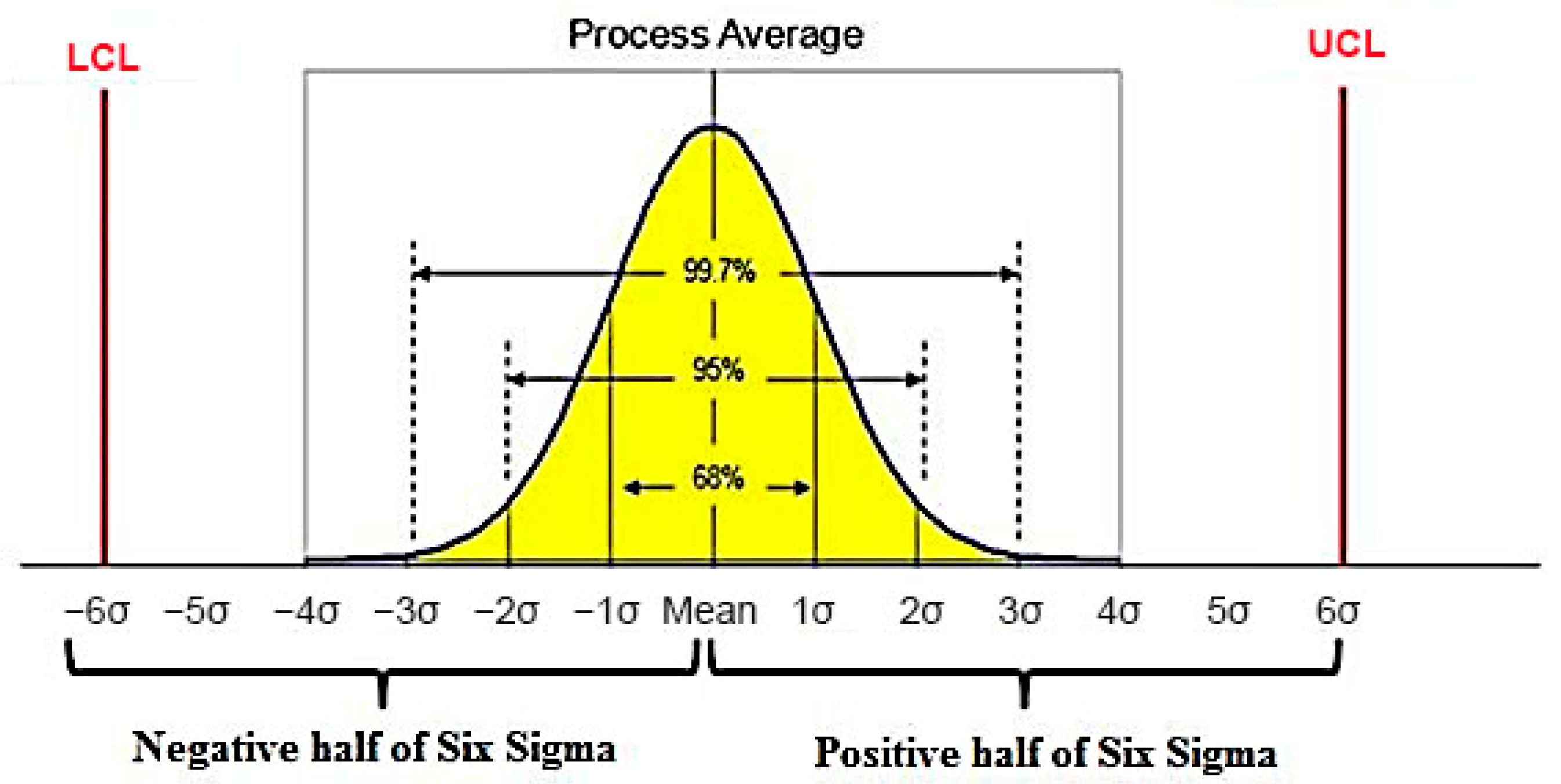
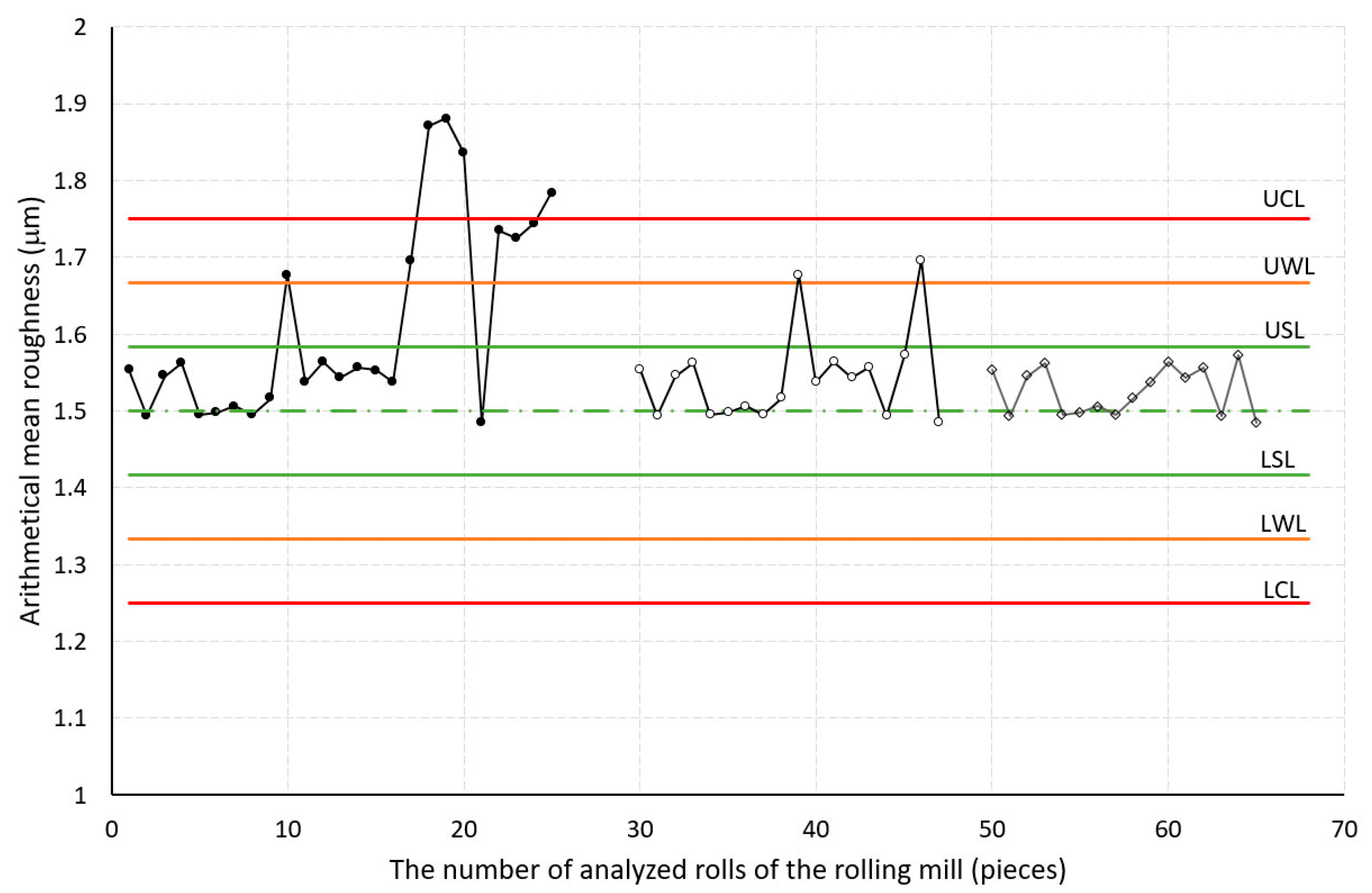
• CL, the central line, or the target value (CL ≈ TV) of the regulated roughness characteristic.
• UCL, the upper control limit, is calculated from the range of variation (VR) of the regulated quality indicator (UCL = CL + VR/2). If the measured values are above the UCL, the process is not stable.
• LCL, the lower control limit, is calculated from the VR range of the regulated quality indicator (UCL = CL − VR/2). If the measured values are below the LCL, the process is not stable.
• UWL, the upper warning limit, is calculated from twice the VR (UWL = CL + 2.VR/6).
• LWL, the lower warning limit, is calculated from twice the VR (UWL = CL − 2.VR/6).
• USL, the upper safe limit, is calculated from a multiple of the VR (USL = CL + VR/6).
• LSL, the lower safe limit, is calculated from a multiple of the VR (USL = CL − VR/6).

Regulation diagram creation was based on the requirement specifications of the Volkswagen car company for the roughness of the sheet metal surface (Ra_SS) for the external parts of the car body (Ra_max = 1.6 μm and Ra_min = 1.1 μm). The variation range (VR_Ra,SS) of the sheet metal surface roughness was determined by Relation (7):

$${VR}_{Ra,SS}={Ra}_{max}-{Ra}_{min},$$

(7)

For the work rolls, UCL_Ra,FR and VR_Ra,FR were determined based on the variation range of roughness VR_RA,SS specified by the automobile company Volkswagen for the sheet surface according to Relations (8) and (9):

$${UCL}_{Ra,FR}={CL}_{Ra,FR}+{\displaystyle \frac{{VR}_{Ra,SS}}{2}},$$

(8)

$${LCL}_{Ra,FR}={CL}_{Ra,FR}-{\displaystyle \frac{{VR}_{Ra,SS}}{2}},$$

(9)

where CL_Ra,FR = TV_Ra,FR is the target value of the quality sign Ra of the finishing rolls, and VR_Ra,SS is the variation range of the Ra quality sign of the sheet metal.

In the first step of the analysis phase, the following were indicated in the control diagram: CL_Ra,FR = TV_Ra,FR, UCL_Ra,FR, LCL_Ra,FR, UW_Ra,FR, LWL_Ra,FR, UCL_Ra,FR, and LCL_Ra,FR. Attention was focused first on identifying data that were out of the regulatory field CL_Ra,FR ± 0.25 μm; see Figure 3 (samples from 1 to 20, which are outside the regulatory boundaries, represent an unstable process). Data on these parts were excluded from further analysis because they are unstable processes. In the second phase, the Ra roughness data were analyzed; these were within the specified control limits (these are samples at x from 20 to 40 in Figure 3). It is assumed that the variability arose as a result of common (predictable) events, which the regulation of texturing process parameters can retain within the specified limits of UCL_Ra,FR and LCL_Ra,FR. If the statistical process is stabilized, i.e., definable causes are identified and analyzed, it is necessary to propose measures preventing their recurrence and, subsequently, propose measures for improvement. To assess the stability of the production process, it is possible to use the capability index C_pk, which is calculated according to Relations (10) and (11):

$$C_{Pk,U}={\displaystyle \frac{UCL-\overline{X}}{3.\sigma }}>1.33,$$

(10)

$$C_{Pk,L}={\displaystyle \frac{\overline{X}-LCL}{3.\sigma }}>1.33,$$

(11)

where C_pk,U is the process capability index calculated for the j-th texture quality sign UCL_j;$\overline{X}$ is the average value from the measured data of the j-th sign of texture quality; σ is the standard deviation of the measured data of the j-th sign of texture quality; and C_pk,L is the process capability index calculated for the j-th texture quality sign LCL_j.

If the C_pk value is less than 1.0, the process is not capable. If the C_pk value is between 1.0 and 1.33, the process is considered barely capable, and if the C_pk value is greater than 1.33, the process is considered capable. If possible, it is necessary to aim for the highest possible C_pk value (greater than 2). If both the C_pk,U and C_pk,L values are greater than 1.33, the process is capable, and the process is under statistical control. In cases where one or both of the C_pk,U and C_pk,L values are smaller than 1.33, the process is not capable, and the process is not under statistical control.

Table 3 shows the Ra values measured in the zone between UCL_Ra and LCL_Ra (in the edge zone). From Table 3, it can be seen that the capability indexes C_pk,URa and C_pkLRa for both the PE2 and PE3 experiment plans are greater than 1.33. This means that the PE2 and PE3 EDT processes are capable. For the EDT according to plan PE1, the value of C_pkU = 1.13. This means that the process under this plan is not capable. However, measures need to be taken to improve it, as it is less than 1.33, and the projected number of non-compliant DPMO_L,Ra products would be approximately 30,396 out of 1 million possibilities.

Table 4. Measured values in the variation range VR_Ra = CL_Ra,RR/3 ± VR_Ra,SS—second step.

Measure Value	PE 1		PE 2		PE 3
	Ra (μm)	Pc (cm−1)	Ra (μm)	Pc (cm−1)	Ra (μm)	Pc (cm−1)
Average value $\overline{Ra}$	1.526	158	2.495	99	3.83	68
Standard deviation SD	0.03	7	0.05	3	0.02	3
Upper-level Six Sigma ZU	7.19	-	4.73	-	10.0	-
Lower-level Six Sigma ZL	8.88	18.1	4.56	21.1	12.91	9.59
CpKU	2.40	-	1.58	-	3.34	-
CpKL	2.96	6.0	1.52	7.05	4.31	3.20
DPMO	0	0	1350	0	0	0

shows the results after filtering out the data that were in the marginal area. The capability indexes’ values were greater than 1.33 in all three plans. This means that the processes in plans PE1, PE2, and PE3 are capable after filtering out data from the marginal area, and the predicted number of DPMO_Ra of non-conforming products would be 1350 in the case of PE2, and ≈0 in the cases of PE1 and PE3. For illustration, a stepwise data filtering procedure is shown in Figure 3 for PE1. Data within the range 0–25 are from before the filtering out was performed (raw data), data within the range 30–45 are from after filtering out the data outside the UCL and LCL, and data in the range 50–65 are from after filtering out the data outside UWL-UCL and LWL-LCL.

In the case of Pc, only the lower limit value (LCL_Pc = 40 cm⁻¹) is defined. Assuming that the lower control limit (LCL_Pc) is determined using Relation (12):

$${LCL}_{Pc}={CL}_{Pc}-k.{\sigma }_{PC},$$

(12)

Then, after adjusting Equation (12), we obtain Equation (13):

$${CL}_{Pc}={LCL}_{Pc}+k.{\sigma }_{PC},$$

(13)

where k is a multiple of the standard deviation of the distance of the upper control limit from the center line (k = 3).

In our case, the maximum value of the directional deviation is equal to 7. This means that CL = 40 + 3 × 7 = 61 cm⁻¹ (see Figure 4). It follows from this figure that the values of Pc determined from records PE1, PE2, and PE3 are higher than the lower LCL_Pc limit value. This means that the EDT processes PE1, PE2, and PE3 are capable of producing Pcs according to specifications without the need to take corrective action.

Control: Managing the process (object) by means of trial and error is ineffective. By purposefully controlling the process aimed at achieving a specified goal, it is possible to gradually set the input parameters using the purpose function [30]. The objective function of multicriteria optimization describing the relationships between input parameters Xi and output quality features S_Qj [22] was created by modifying the weighted product method (WPM) in the form of Equation (14):

$$S_{Qi}={\displaystyle \frac{1}{n}}{\sum }_1^n\left(x_1.w_1+x_2.w_2\dots +x_n.w_n\right)\pm {∆}_{Qj},$$

(14)

where S_Qj represents the output quality feature; x₁, x₂, … x_n represent the input independent factors of the process; w_i represents the criterion weight; j represents a sign of quality; n represents the number of process input parameters; and ∆_Qj represents the accuracy or uncertainty.

It can be seen from Figure 5, Figure 6, Figure 7 and Figure 8 that the dependences of Ra on the discharge energy, or the texturing process parameters I_p, U_p, and T_on, show a good correlation, and the regression equations (Equations (15)–(17)) describe them with very high accuracy:

$${Ra}_{Ip}=1.476\ast \ln \left(I_p\right)-0.5262; {\mathrm{R}}^2=0.99$$

(15)

$${Ra}_{Up}=0.1244\ast U_p; {\mathrm{R}}^2=0.99$$

(16)

$${Ra}_{Ton}=0.0915\ast T_{on}+1.19; {\mathrm{R}}^2=0.99$$

(17)

One of the problems of multicriteria decision-making tasks is that individual criteria (characteristics of quality) or input parameters are expressed in different measurement units [22]. For this reason, it is convenient to transform them into a common unit so that they can be added. The method of relative parameters—planning assistance through technical evaluation of relevance number, PATTERN—is used in the technical, technological, and economic fields. This means that the change in the input parameters (I_p, U_p, and T_on) and the quality sign Q_j can be expressed as a ratio of the value of the Q_j-th parameter to the value of the basic parameter Q_j0 according to Relation (18):

$${IQ}_{ji}={\displaystyle \frac{Q_{ji}}{Q_{ji0}}},$$

(18)

where IQ_ji is the degree of change in quality signs (Ra and Pc) according to the i-th process parameter; w_i is the weight (significance) of the i-th process parameter; and n is the number of i-th process parameters.

If we substitute the individual indices of the change in quality Ra into Equation (14), we obtain

$$S_{QRa}={\displaystyle \frac{1}{n}}{\sum }_1^3\left({IQ}_{Ra\left(Ip\right)}.w_{Ra\left(Ip\right)}+{IQ}_{Ra\left(Up\right)}.w_{Ra\left(Up\right)}+{IQ}_{Ra\left(Ton\right)}.w_{Ra\left(Ton\right)}\right),$$

(19)

After substituting into Equation (18), the change indices, depending on the input parameters of the texturing process, take the following form:

$${IQ}_{Ra\left(Ip\right)}={\displaystyle \frac{Q_{Ra\left(Ip\right)}}{Q_{Ra0\left(Ip\right)}=4}}={\displaystyle \frac{(1.4763\ast \ln (I_p)-0.0526)}{\left(1.4763\ast \ln (4\right)-0.0526)}},$$

(20)

$${IQ}_{Ra\left(up\right)}={\displaystyle \frac{Q_{Ra\left(Up\right)}}{Q_{Ra\left(Up\right)}=6.5}}={\displaystyle \frac{(0.1244\ast U_{p)}+0.7)}{\left(0.1244\ast 6.5\right)+0.7)}},$$

(21)

$${IQ}_{Ra\left(Ton\right)}={\displaystyle \frac{Q_{Ra\left(Ton\right)}}{Q_{Ra0\left(Ton\right)}=6.5}}={\displaystyle \frac{(0.0915\ast T_{on}+1.1942)}{\left(0.0915\ast 6.5\right)+1.1942)}},$$

(22)

In the scalar multicriteria objective function, the approximation function (Figure 6, Figure 7 and Figure 8) with weight value w_i is expressed in Equations (15)–(17) by coefficients for individual variables (w_Ra(Ip) = 1.476, w_Ra(Up) = 0.1244, w_Ra(Ton) = 0.0915) so that no influence of the considered process parameters is preferred. After substituting Equations (20)–(22) into Equation (19), we obtain the overall effect of the texturing process parameters on the Ra quality sign:

$$S_{QRa}={\displaystyle \frac{1}{3}}\left[\ln \left(I_{I,Ra}+I_{U,Ra}+I_{Ton,Ra}\right)\right]\pm {∆}_{QRa},$$

(23)

Figure 9 shows the dependence between the total value of the quality feature S_QRa and the calculated roughness values Y_QRa according to Relation (23), which is described by regression Equation (24):

$$Y_{QRa}=1.526\ast S_{QRa}+0.0091\pm {∆}_{QRa},$$

(24)

After modifying Model (23) into a simpler form, we obtain

$$Y_{QRa}=0.494\ast \ln \left(I_p\right)+0.0424\ast U_p+0.0298\ast T_{on}+0.437\pm {∆}_{QRa},$$

(25)

Model (25) was subsequently tested for target roughness values TV_Ra1 = 1.5 μm, TV_Ra2 = 2.5 μm, and TV_Ra3 = 3.8 μm. The presented model allows one to predict the roughness Y_QRra based on the pulse current I_p, the gap voltage U_p and the pulse on-time T_on.

Table 5. Results of prediction Model (25) and its testing using data from ref. [28].

	Input Data				Calculated Data
Plan	IP (A)	UP (V)	Ton (μs)	TVRa (μm)	YQRa (μm)	ΔRa (μm)	S.D.Ra (μm)	Cpk (μm)	DPMO (Pieces)
PE 1	4	6.5	4	1.5	1.514	0.014		1.311	≈6200
PE 2	8	15	14	2.5	2.511	0.011	0.06	1.325	≈6200
PE 3	19	25	29	3.8	3.806	0.006		1.355	≈4300
After improvement Ton-1
PE 1	4	6.5	3	1.5	1.484	−0.016		1477	≈4300
PE 2	8	15	13	2.5	2.482	−0.018	0.06	1491	≈4300
PE 3	19	25	28	3.8	3.776	−0.024		1522	≈4300
Verification of Model (25) acc. to input parameters of [28]
[28]	20	-	12	3.0	3.103	0.103	0.06	0.818	≈190,000
After improvement Ton-2 and Ip-1
[28]	19	-	10	3.0	2.979	−0.003	0.06	1.373	≈4300

compares the calculated Y_QRa values from Model (25) with the target values TV_Ra1 = 1.5 μm, TV_Ra2 = 2.5 μm, and TV_Ra2 = 3.8 μm.

The comparison shows that there was good agreement between the calculated values according to Model (25) and the target values: for target value TV_Ra1 = 1.5 μm, ΔRa = 0.014 μm and capability index C_pkRa1 = 1.311; for target value TV_Ra2 = 2.5 μm, ΔRa = 0.011 μm and capability index C_pkRa2 = 1.325; and for target value TV_Ra3 = 3.8 μm, ΔRa = 0.006 μm and capability index C_pkRa3 = 1.355. This means that the texturing process for plans PE1 and PE2 is ineligible because the capability index is C_pk < 1.33. When T_on was changed by 1 μs, the C_pkRa capability indices were assumed to be greater than 1.33 when PE 1, PE2, and PE 3 plans were applied. This implies that texturing with these plans should be eligible. Reducing the Six Sigma level by one level, from four to five, will reduce the cost of poor quality by 10%. Thus, it is necessary to change the process parameters to achieve a change in the standard deviation from 0.06 to 0.048.

The proposed model was also tested using the parameters presented in [28], as they are closely related to the results in this paper. Since the authors of [28] only investigated the effect of pulse current I_p and pulse on-time T_on, Model (23) was modified as follows:

$$Y_{QRa}=0.745\ast \ln \left(I_p\right)+0.045T_{on}+0.331\pm {∆}_{QRa},$$

(26)

The difference is that the authors of [28] tested their prediction model for the target roughness value TV_Ra = 3 μm only for the input texturing parameters I_p = 20 A and T_on = 12 μs. In this case, the capability index C_pkRa was 0.818. When T_on was changed by 2 μs and I_p by 1 A, the capability index was 1.373.

The deviation (inaccuracy) ∆Ra was calculated from the difference between the calculated YQ_Ra values and the specified target values CL_Ra,FR = TV_Ra,FR:

$${∆}_{Ra}=Y_{QRa}-{CL}_{Ra,FR},$$

(27)

In the analyzed interval of texturing parameters I_p, U_p, and T_on, the values of ∆R were ±0.015 μm. Similar to [4,28], the assumption was confirmed in our case that a very good correlation (R² = 0.989) was recorded between the roughness Ra and the peak density Pc at the output of the EDT rolls (see Figure 9 and Figure 10). This dependence was described by the regression equation, Equation (28):

$$Y_{QPc}={233.6\ast Y}_{QRa}^{-0.923},$$

(28)

$${∆}_{Pc}=Y_{QPc}-{CL}_{Pc},$$

(29)

The decision process (process control) of texturing was described by the following algorithm (see Figure 11):

The sequence of steps followed in this algorithm is as follows:

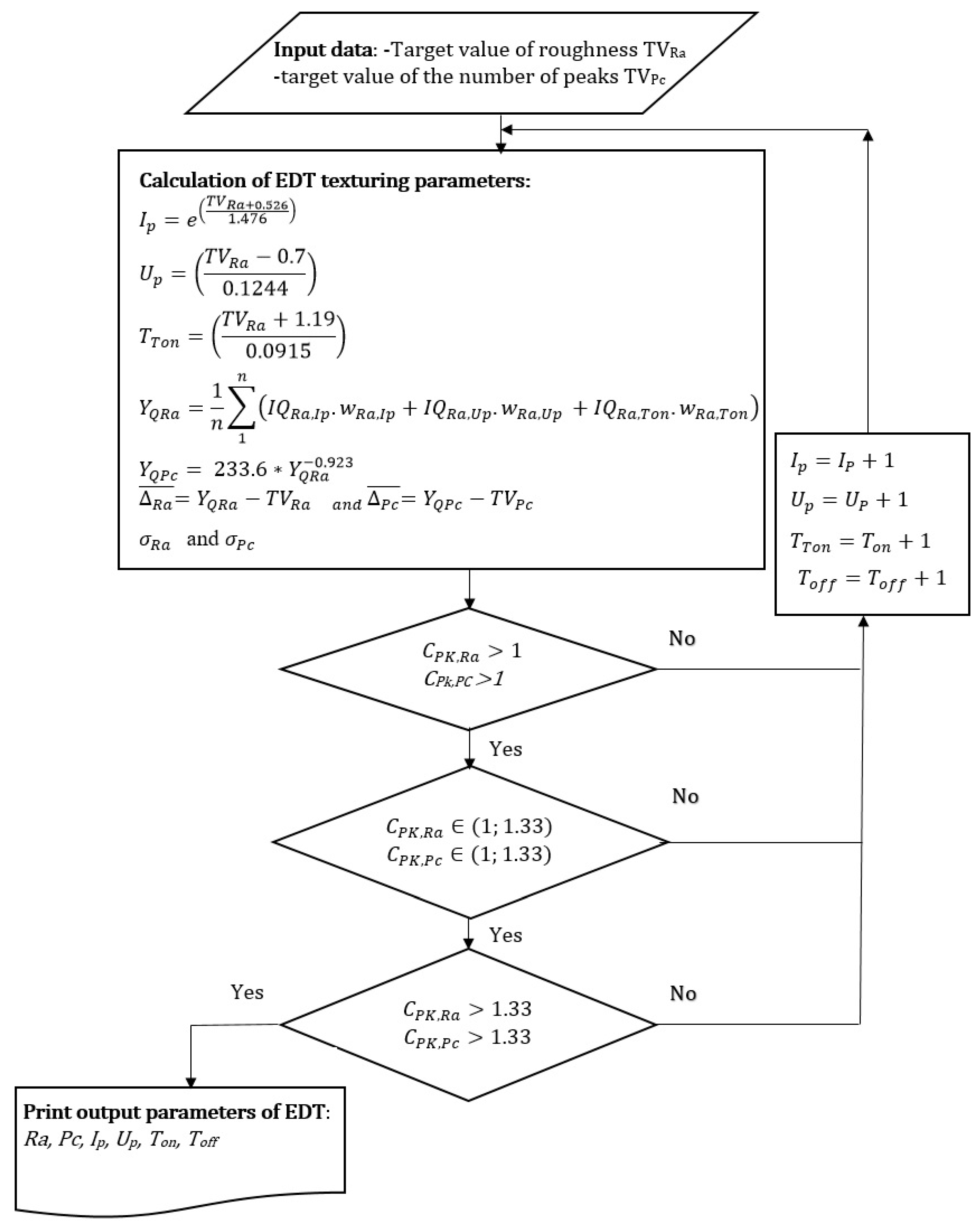
• 1. Step: defining the target values of quality characteristics TV_Ra and TV_Pc.
• 2. Step: Assignment of input parameters of the EDT process (I_p, U_p, T_on, and T_off) to defined target values TV_Ra and TV_Pc according to Formulas (30)–(33):

$${Pc}_{Ip}=322.24 I_P^{-0.539}; {\mathrm{R}}^2=0.97$$

(30)

$${Pc}_{Up}=512.74U_p^{-0.621}; {\mathrm{R}}^2=0.98$$

(31)

$${Pc}_{Ton}=287.87T_{on}^{-0.421}, {\mathrm{R}}^2=0.98$$

(32)

$${Pc}_{Toff}=357.33T_{off}^{-0.459}, {\mathrm{R}}^2=0.99$$

(33)

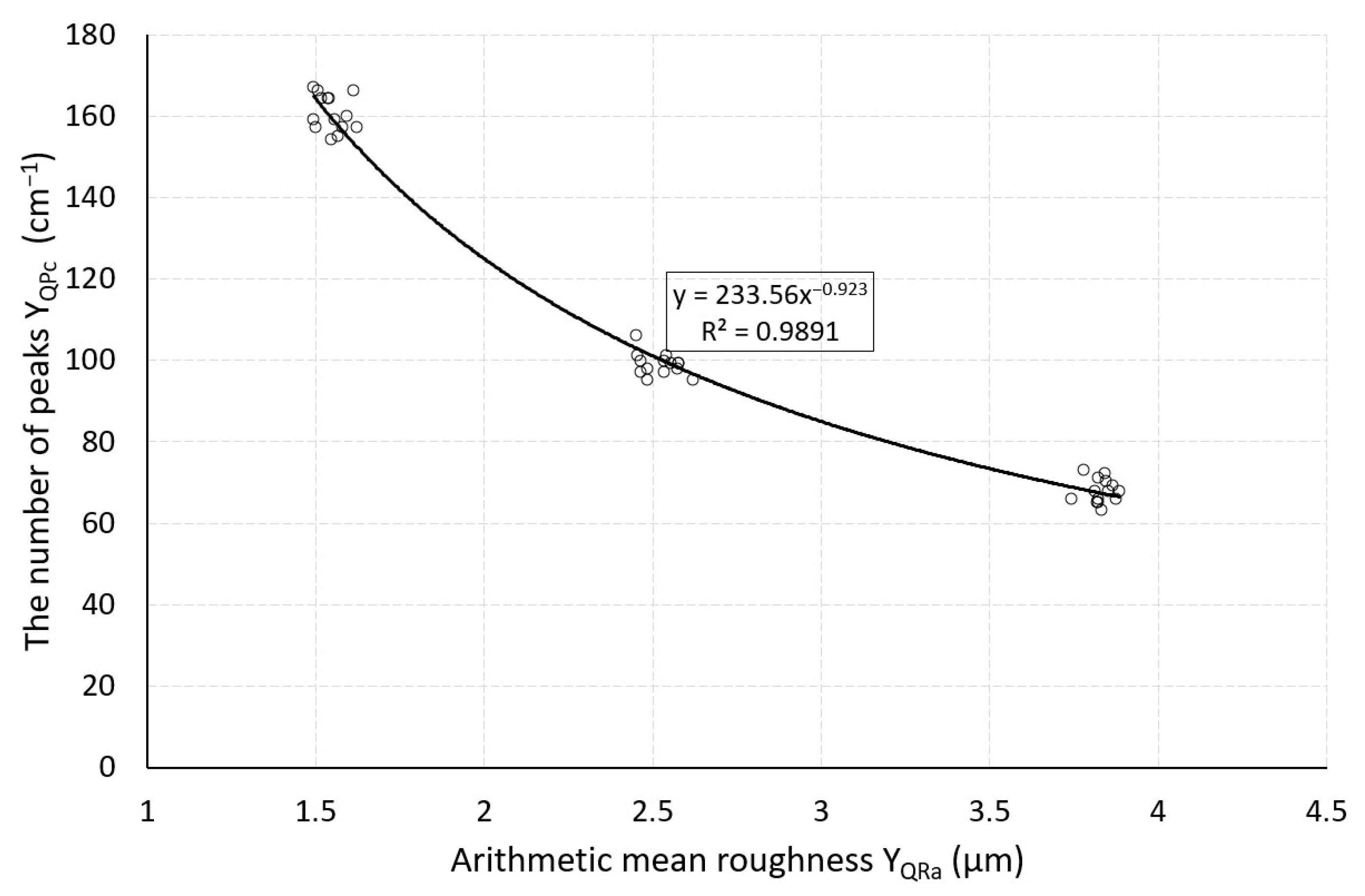
• 3. Step: Calculation of the values of qualitative characteristics Y_QRa and Y_QPc according to Formulas (25) and (28), calculation of ∆Ra and ∆Pc according to Formulas (27) and (29), and calculation of indices C_pkL and C_pkU according to Formulas (10) and (11). Thus, for C_pk ≥ 1.33, the standard deviation after adjustment of the equations is

$$\sigma ={\displaystyle \frac{UCL-\overline{∆Ra}}{3\ast 1.33}}={\displaystyle \frac{0.25-0}{3\ast 1.33}}=0.06$$

(34)

• 4. Step: Comparison of calculated values of C_pkRa and C_pkPC with the limit value 1. If the calculated values of C_pkRa and C_pkPc are less than 1, the process is not capable, and it is necessary to adjust the input parameters.
• 5. Step: If the calculated values of C_pkRa and C_pkPC are in the interval from 1 to 1.33, the process is capable, but the compliance rate is low, so it is recommended to take measures to improve the stability of the process.
• 6. Step: If the calculated C_pkRa and C_pkPC values are greater than 1.33, the compliance rate is high, and no process improvement measures need to be taken.
• 7. Step: Printing of output parameters of the quality characteristics Ra, Pc, and the input parameters of the EDT process I_p, U_p, T_on, and T_off.

4. Conclusions

Based on the results of the analyses, the following conclusions were formulated:

• On the basis of control diagrams, C_pk capability indices, and Z scores, it is possible to take measures to improve the quality characteristics Ra and Pc of the surface textures of the rolls in rolling mills.
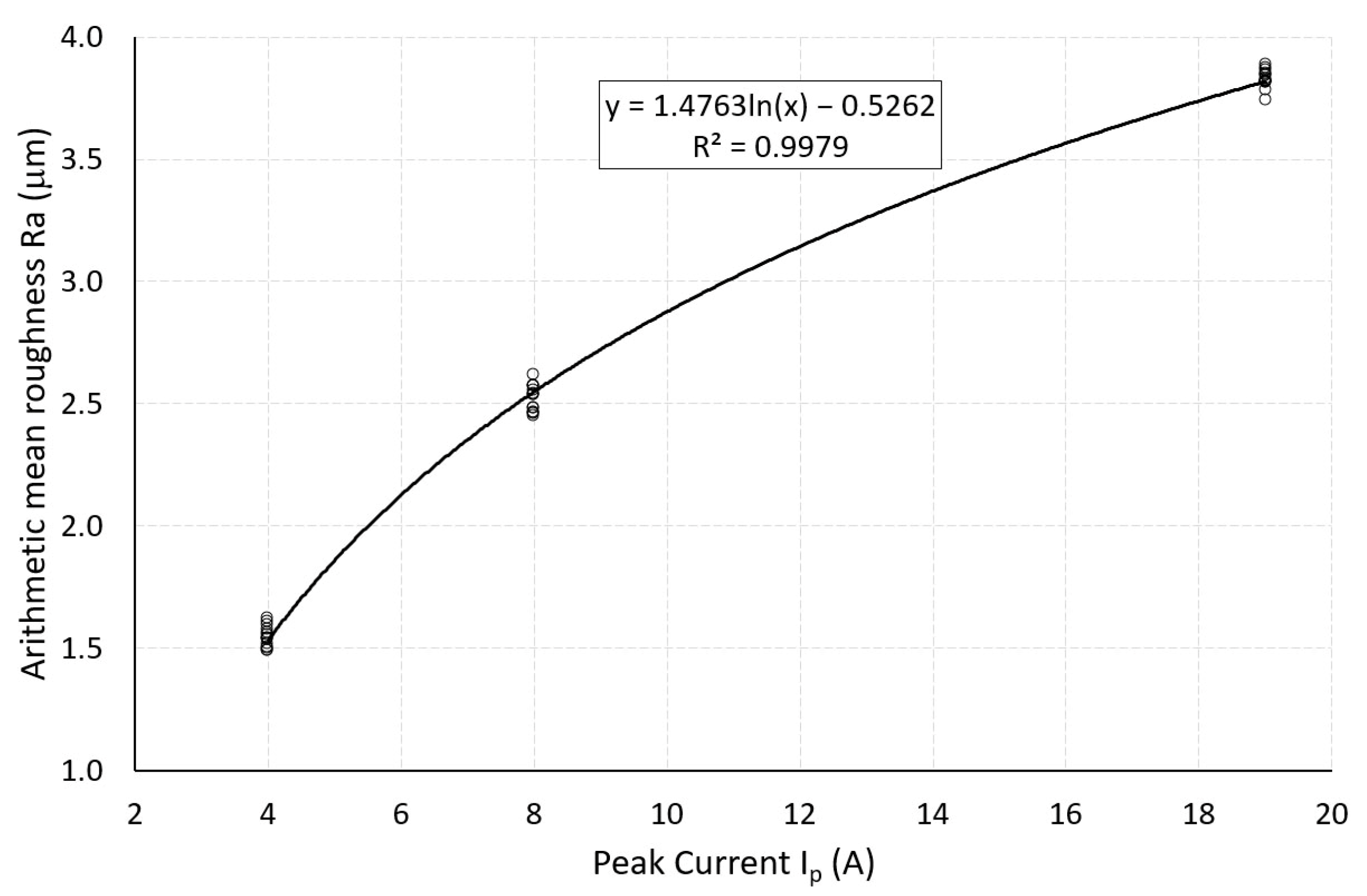
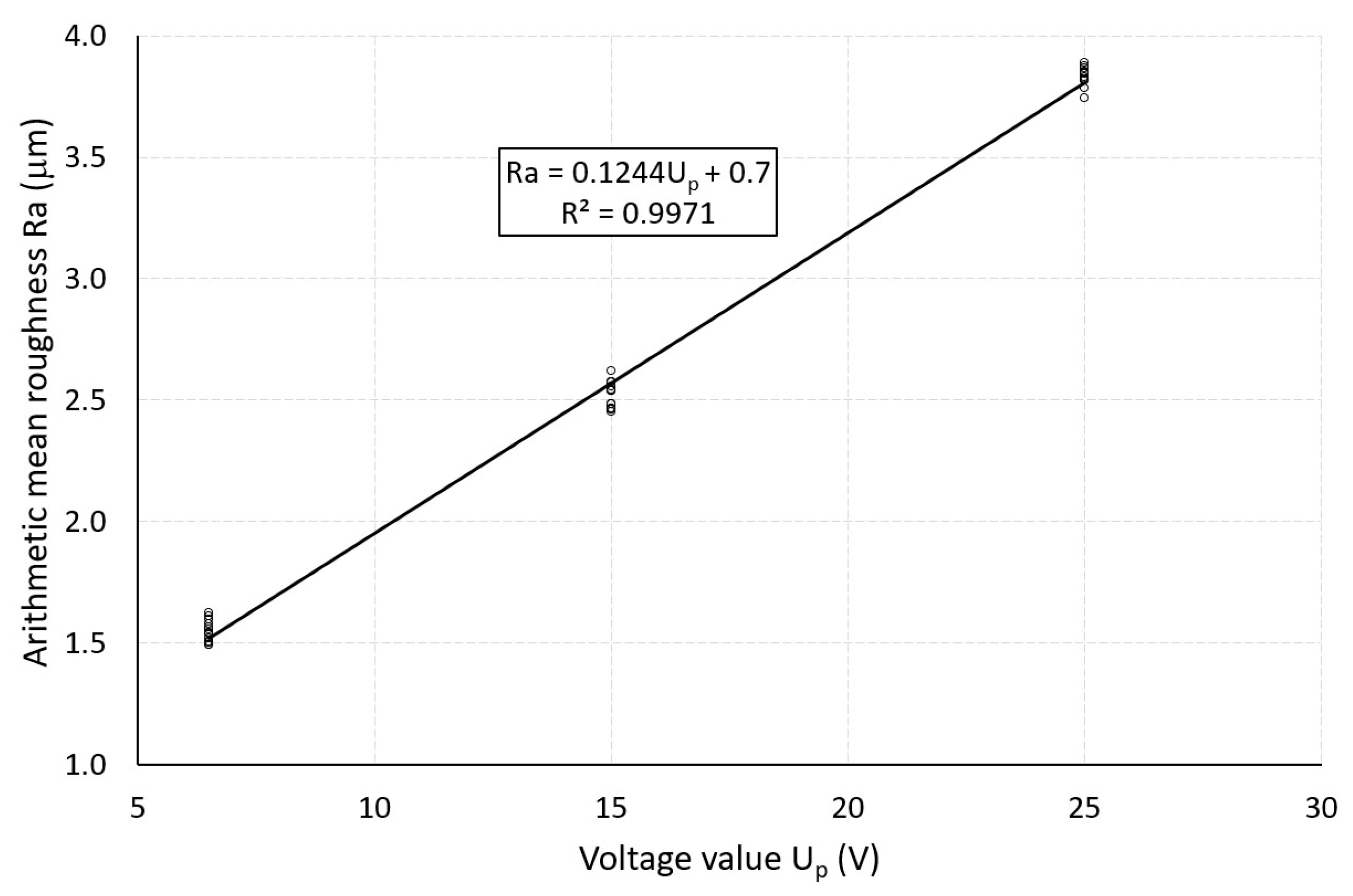
• The results obtained by means of regression analysis indicate that the roughness Ra created during EDT is strongly dependent on the discharge energy. The coefficient of determination R² reached values greater than 0.99.
• The parameters I_p, U_p, and T_on of the EDT process have a major influence on the roughness Ra. An increase in these parameters of the texturing process leads to an increase in Ra values.
• Using regression analysis, the dependences of Ra on I_p were described by a logarithmic regression equation, and the dependences of Ra on both U_p and T_on were described by linear regression equations. The regression models showed a strong correlation (R² > 0.9).
• Using the obtained dependencies, a purpose function was created and verified. This function allows one to predict the roughness Ra with an accuracy of ± 0.02 μm in the analyzed interval of texturing parameters I_p, U_p, and T_on.
• The regression equation of the dependence of the peak density Pc on T_off was used to predict the peak density. The R² coefficient was greater than 0.98.
• Based on the comparison of the conformity of the C_pk capability indices with the limit values, an algorithm was designed, which allows step-by-step decisions to be made to improve the EDT process of rolling mill rolls.

The design of a procedure for taking corrective actions to improve the roughness Ra of EDT rolls based on the C_pkRa capability index also allows the prediction of the amount of non-conforming products out of one million DPMO cases compared to other procedures. Thus, by controlling the texturing process on the cold mill work roll surface based on the proposed algorithm, the number of non-conforming products can be minimized. Future efforts will be focused on verification of the roughness Ra of work rolls ranging from 1.1 μm to 1.6 μm, as presented in a previous work [31]. Furthermore, future studies will also verify whether both the required values of TV_Ra and TV_Pc are achieved on the surface of the sheet metal.