Structural Engineering of π-Linker Aromaticity in Anthanthrene-Based Dyes with D–π–A Configuration: DFT Investigation to Enhance Charge Transfer in DSSCs
Abstract
1. Introduction
2. Methods
3. Results and Discussion
3.1. Dyes Before Adsorption
3.1.1. Degree of Planarity
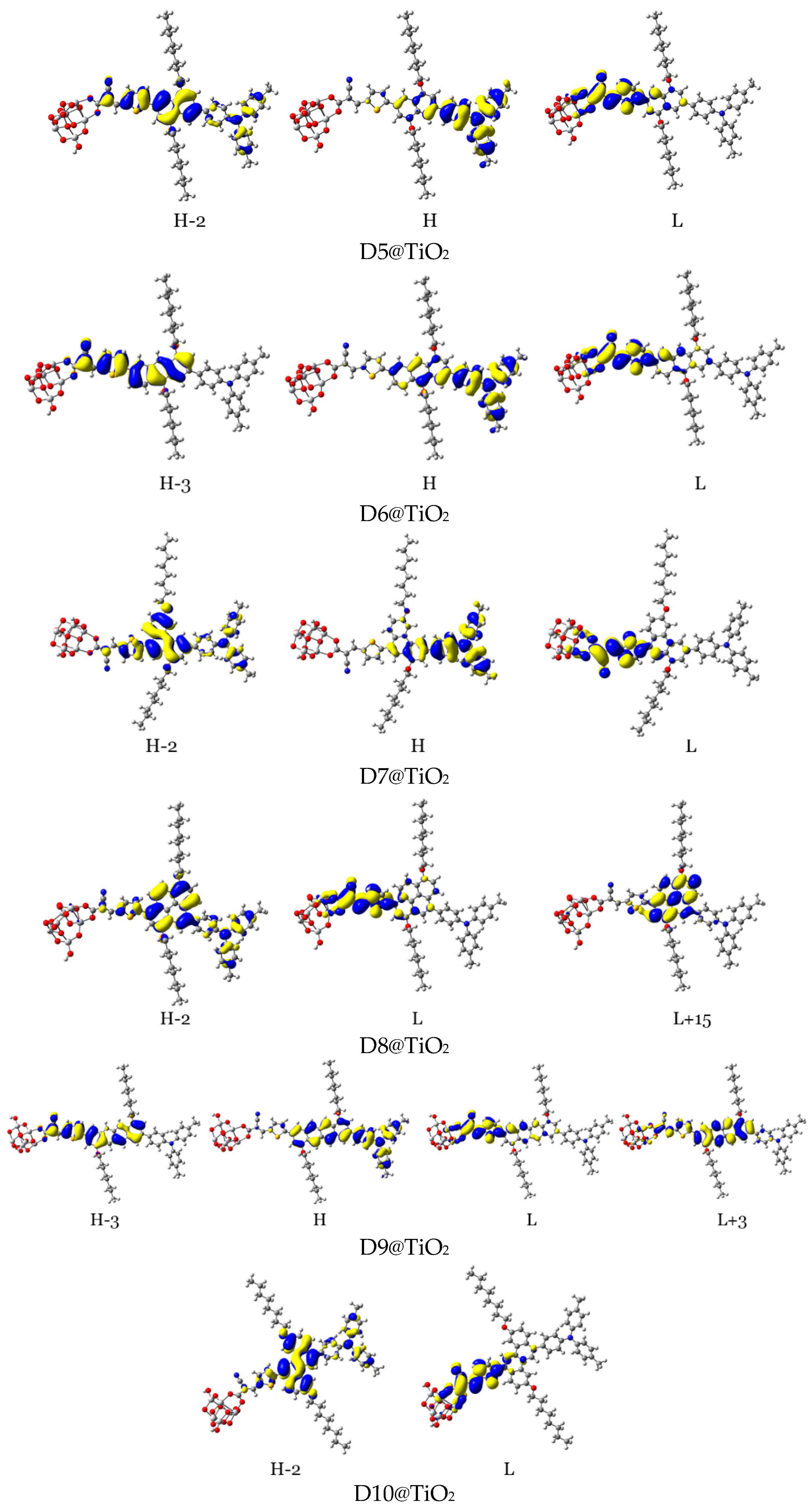
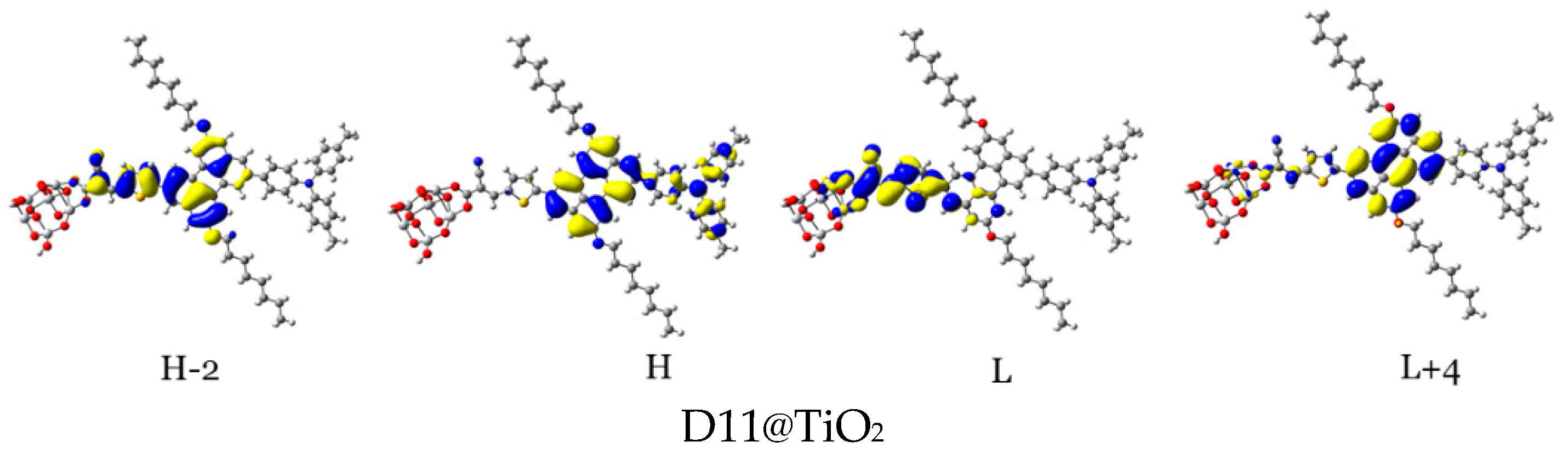
3.1.2. Frontier Molecular Orbitals (FMOs)
3.1.3. UV-Vis Spectroscopic Properties
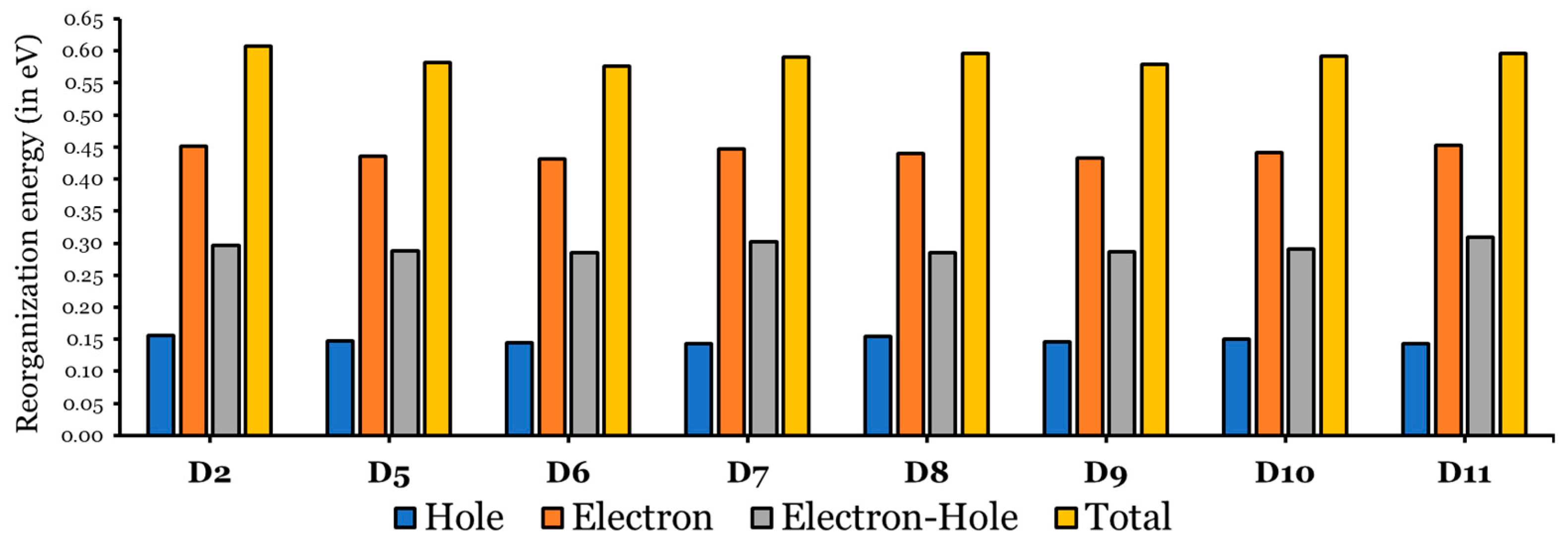
3.1.4. Reorganization Energies, Transfer Integrals, and Intrinsic Mobility
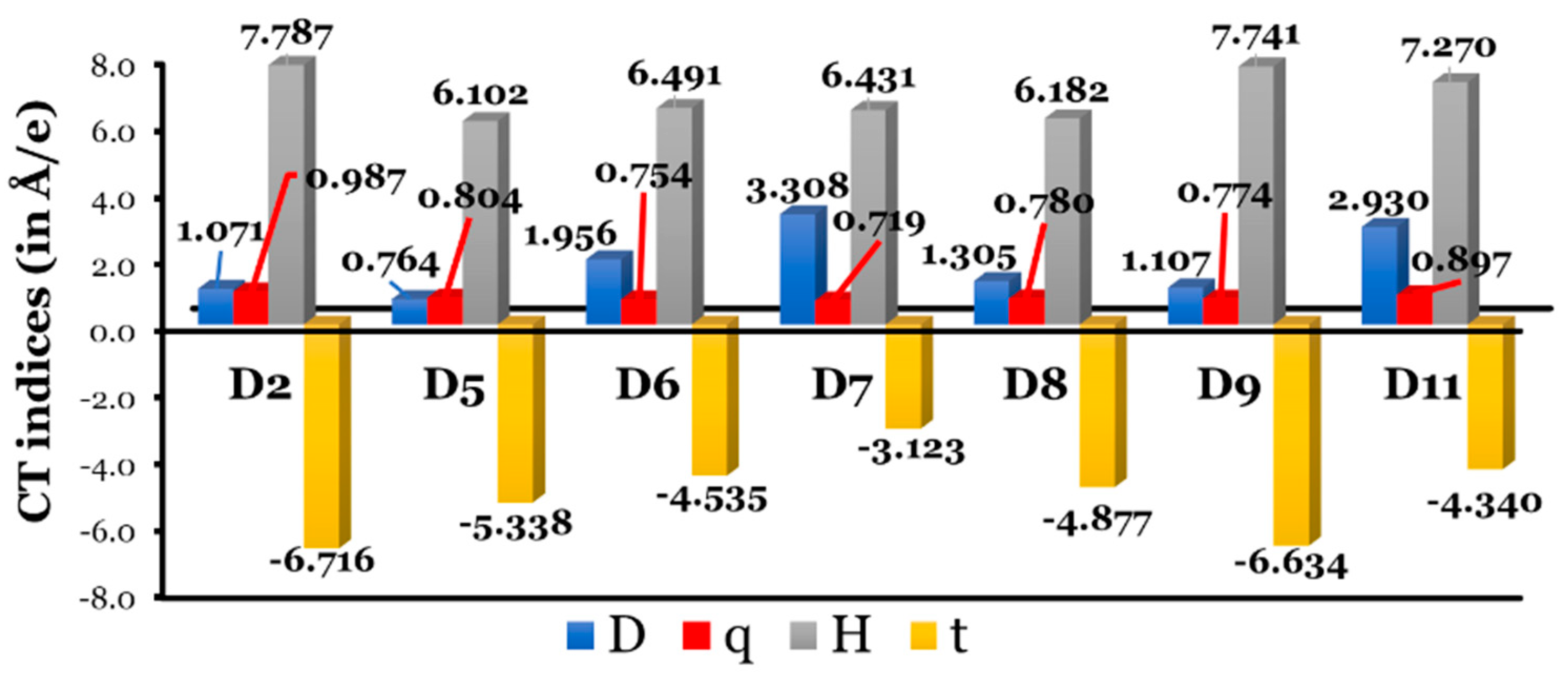
3.1.5. Le Bahers’ Intramolecular Charge-Transfer Indices
3.1.6. Electron Injection and Dye Regeneration Free Energies
3.2. Dyes After Adsorption on TiO2 Clusters
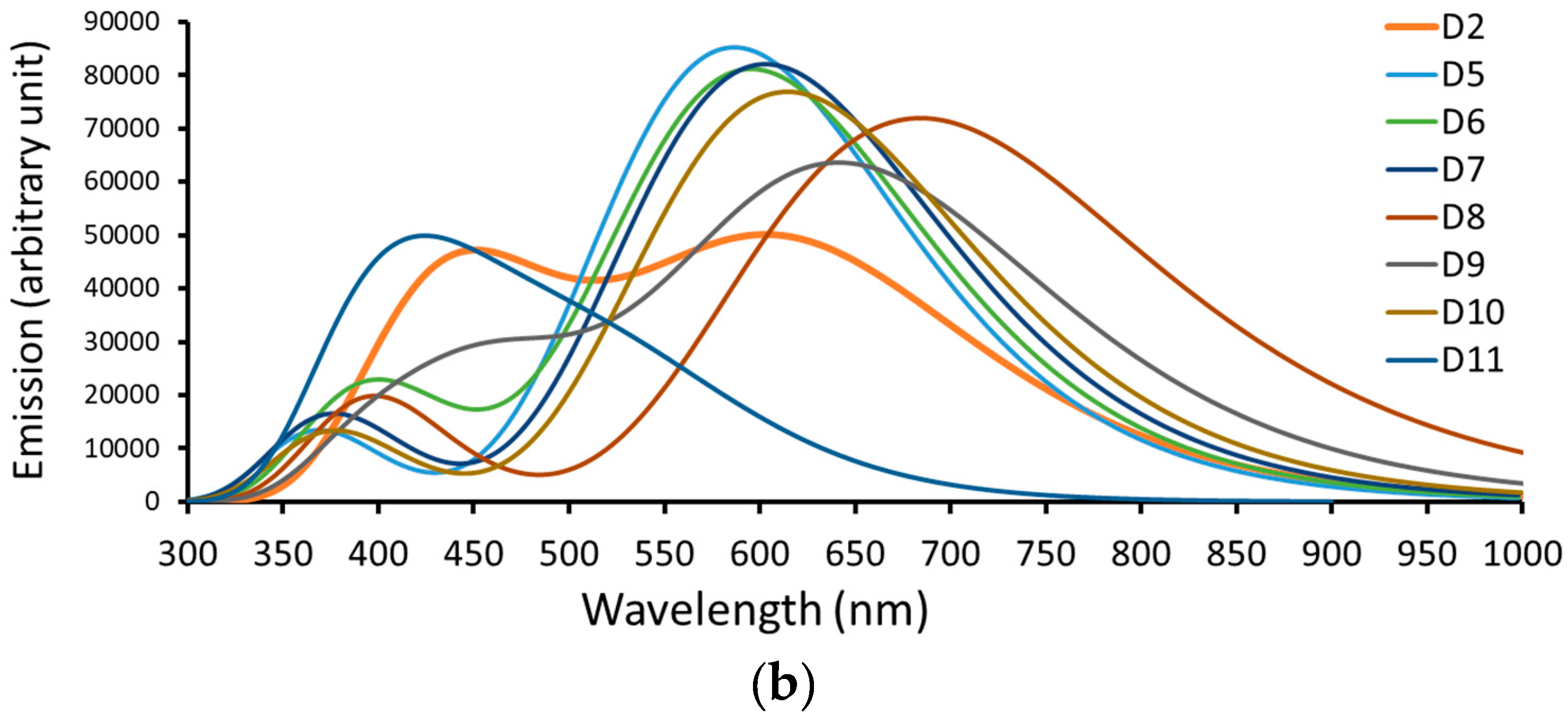
3.2.1. Optical Properties
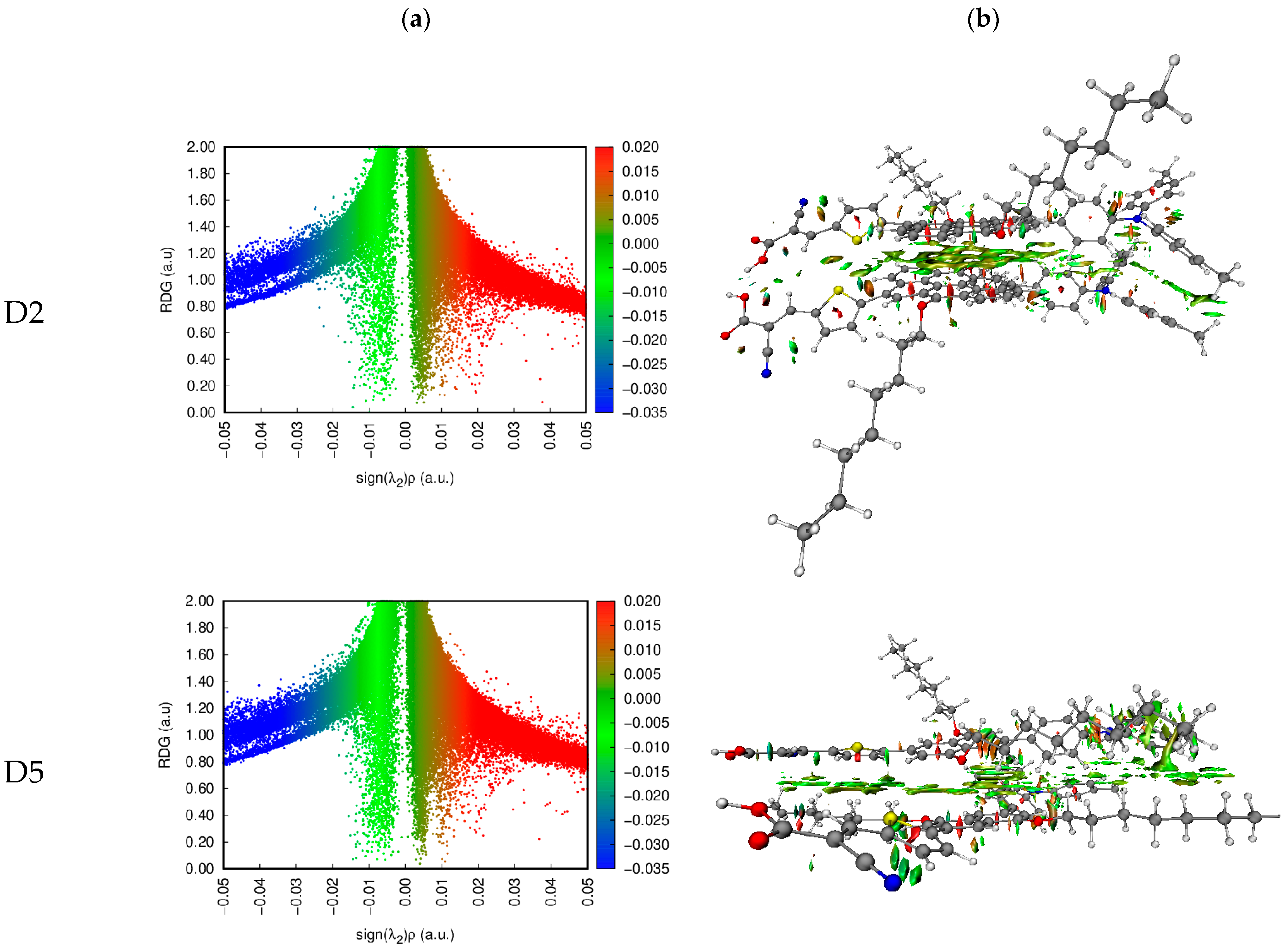
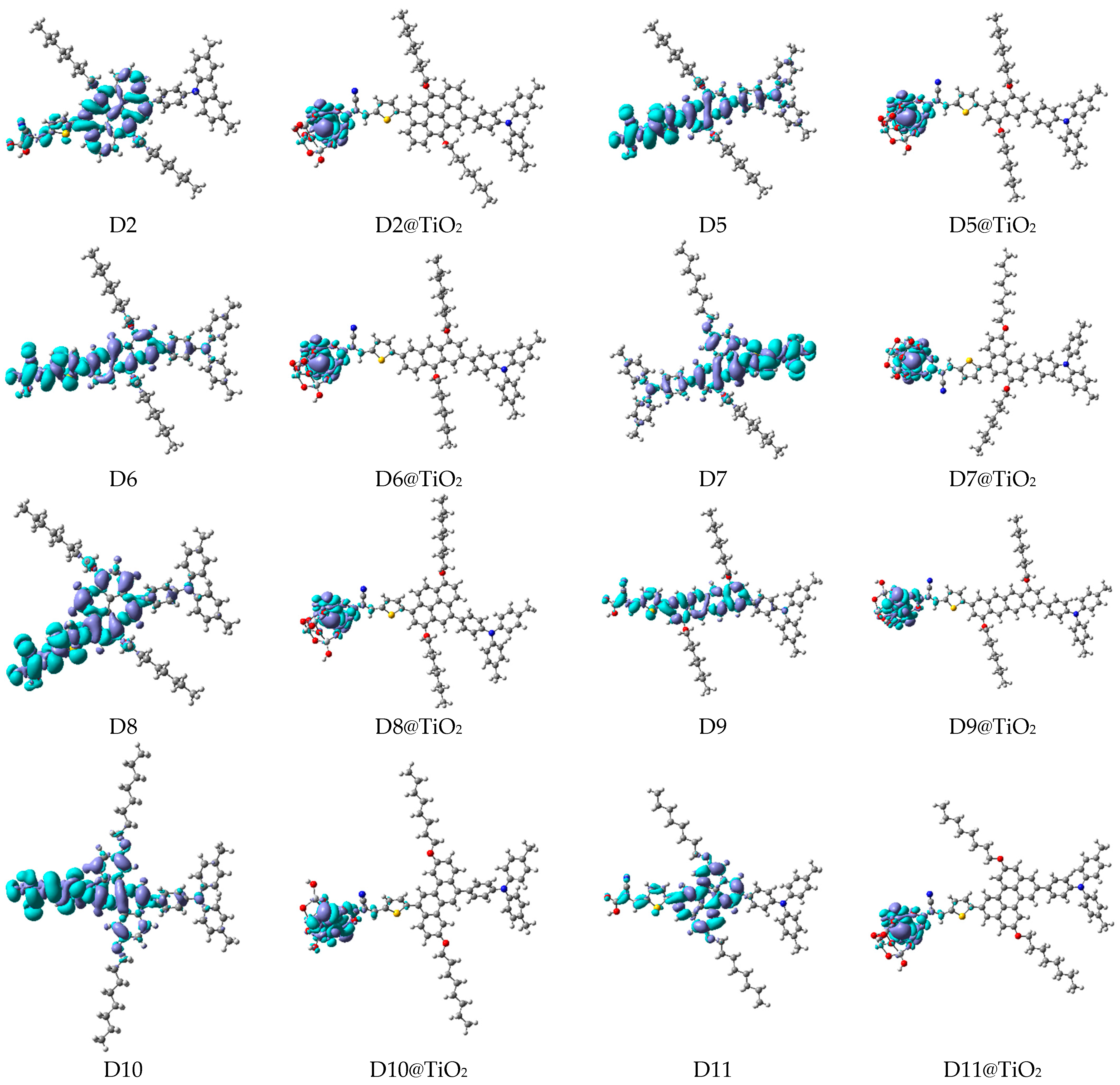
3.2.2. Maps of Molecular Electrostatic Potential and Electron Density Difference
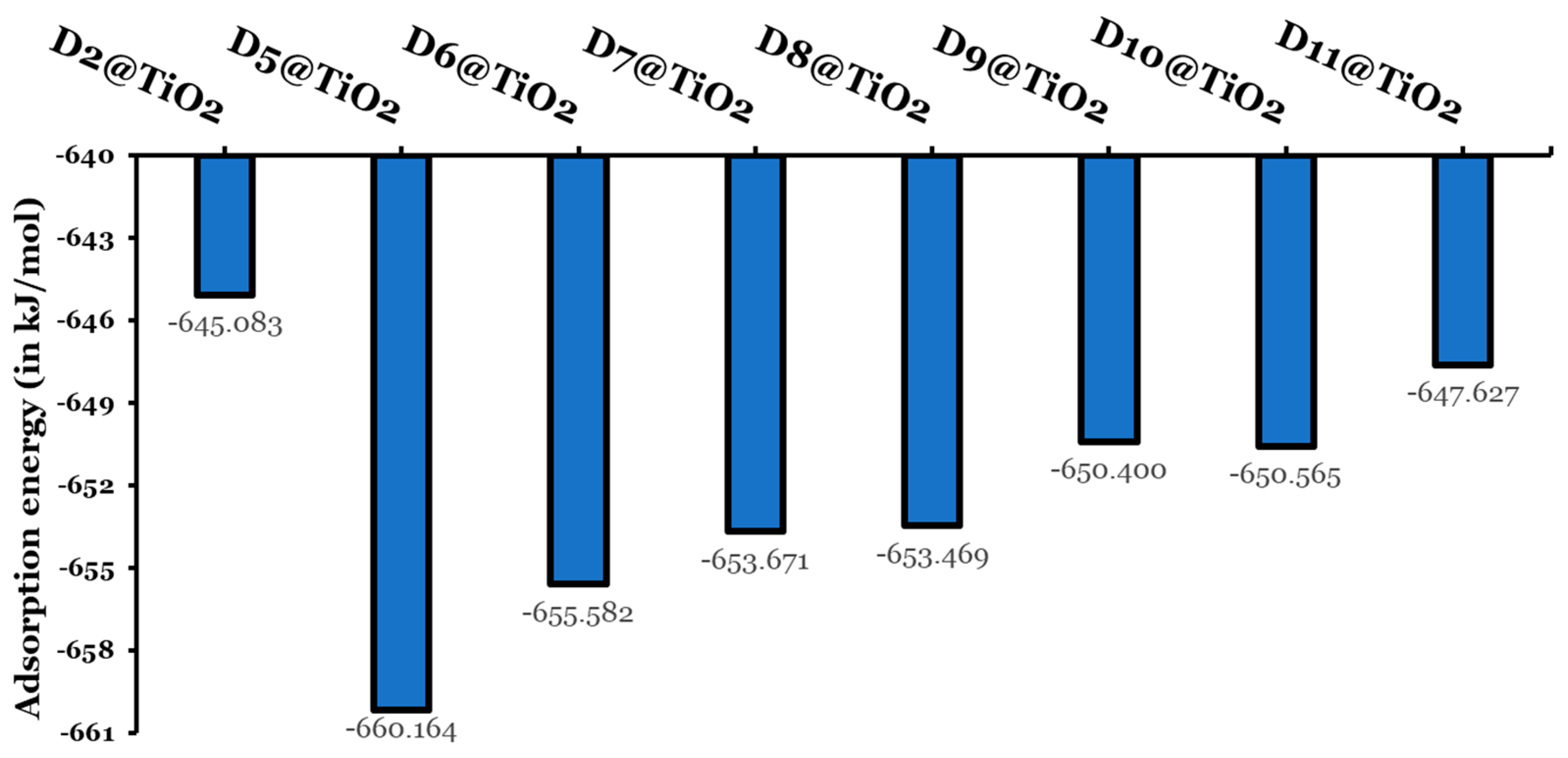
3.2.3. Overall Performance of the Designed Dyes
4. Conclusions
- Although the designed dyes exhibit similar properties to D2 in energy-level alignment and molecular electrostatic potentials (MESPs), D2 outperformed the others by its higher HOMO energy.
- D6 and D9, with lower resonance energies and greater planarity than D2, show smaller energy gaps, facilitating easier electron excitation and longer wavelength absorption.
- All designed dyes demonstrate high LHEs (95–99%).
- The designed dyes (isolated and adsorbed) absorb light at longer wavelengths due to increased resonance energies of the aromatic rings, with most exhibiting greater and values compared to D2, suggesting enhanced dye regeneration and electron injection processes.
- Most of the designed dyes demonstrate favorable electron–hole transport properties, reducing reorganization energy and mitigating recombination.
- All dyes bind chemically to the TiO2 cluster, with the designed dyes showing stronger adsorption and red/blue shifts in absorbance spectra.
- D9, with a naphthacene core, shows moderate resonance energy, achieving balanced mobilities and reduced energy gaps for excellent charge-transfer characteristics.
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
References
- Tyagi, H.; Chakraborty, P.R.; Powar, S.; Agarwal, A.K. (Eds.) Solar Energy: Systems, Challenges, and Opportunities, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2020; p. 423. [Google Scholar]
- Archer, D. Global Warming: Understanding the Forecast; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- O’Regan, B.; Grätzel, M. A low-cost, high-efficiency solar cell based on dye-sensitized colloidal TiO2 films. Nature 1991, 353, 737–740. [Google Scholar] [CrossRef]
- Muñoz-García, A.B.; Benesperi, I.; Boschloo, G.; Concepcion, J.J.; Delcamp, J.H.; Gibson, E.A.; Meyer, G.J.; Pavone, M.; Pettersson, H.; Hagfeldt, A.; et al. Dye-sensitized solar cells strike back. Chem. Soc. Rev. 2021, 50, 12450–12550. [Google Scholar] [CrossRef]
- Borges-Martínez, M.; Alvarez, D.; Montenegro-Pohlhammer, N.; Menéndez, M.I.; López, R.; Cárdenas-Jirón, G. Assessment of BODIPY–Oxasmaragdyrin Dyads for Dye-Sensitized Solar Cells: Aromaticity, Photosensitization Capability, and Charge Transport. J. Phys. Chem. C 2019, 123, 19362–19375. [Google Scholar] [CrossRef]
- He, J.; Wang, B.; Chang, S.; Chen, T. Ruthenium-Based Photosensitizers for Dye-Sensitized Solar Cells. In Organometallics and Related Molecules for Energy Conversion; Wong, W.-Y., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 91–114. [Google Scholar]
- Aksakal, N.E.; Kazan, H.H.; Eçik, E.T.; Yuksel, F. A novel photosensitizer based on a ruthenium(ii) phenanthroline bis(perylenediimide) dyad: Synthesis, generation of singlet oxygen and in vitro photodynamic therapy. New J. Chem. 2018, 42, 17538–17545. [Google Scholar] [CrossRef]
- Al Mogren, M.M.; Ahmed, N.M.; Hasanein, A.A. Molecular modeling and photovoltaic applications of porphyrin-based dyes: A review. J. Saudi Chem. Soc. 2020, 24, 303–320. [Google Scholar] [CrossRef]
- Obasuyi, A.R.; Glossman-Mitnik, D.; Flores-Holguín, N. Electron injection in anthocyanidin and betalain dyes for dye-sensitized solar cells: A DFT approach. J. Comput. Electron. 2019, 18, 396–406. [Google Scholar] [CrossRef]
- Dhar, A.; Kumar, N.S.; Paul, P.K.; Roy, S.; Vekariya, R.L. Influence of tagging thiophene bridge unit on optical and electrochemical properties of coumarin based dyes for DSSCs with theoretical insight. Org. Electron. 2018, 53, 280–286. [Google Scholar] [CrossRef]
- Ayare, N.N.; Sharma, S.; Sonigara, K.K.; Prasad, J.; Soni, S.S.; Sekar, N. Synthesis and computational study of coumarin thiophene-based D-π-A azo bridge colorants for DSSC and NLOphoric application. J. Photochem. Photobiol. A Chem. 2020, 394, 112466. [Google Scholar] [CrossRef]
- Pounraj, P.; Mohankumar, V.; Pandian, M.S.; Ramasamy, P. The effect of different π-bridge configuration on bi-anchored triphenylamine and phenyl modified triphenylamine based dyes for dye sensitized solar cell (DSSC) application: A theoretical approach. J. Mol. Graph. Model. 2018, 79, 235–253. [Google Scholar] [CrossRef]
- Al-Temimei, F.; Mraity, H. DFT/TD-DFT investigation of novel D–π–A configuration dyes for improving solar cell efficiency. Struct. Chem. 2022, 33, 859–869. [Google Scholar] [CrossRef]
- Wazzan, N. Theoretical investigation of anthanthrene-based dyes in dye-sensitized solar cell applications: Effect of nature of alkyl-substitutions and number of anchoring groups. Arab. J. Chem. 2022, 15, 103969. [Google Scholar] [CrossRef]
- Geng, Y.; Yi, C.; Bircher, M.P.; Decurtins, S.; Cascella, M.; Grätzel, M.; Liu, S.-X. Anthanthrene dye-sensitized solar cells: Influence of the number of anchoring groups and substitution motif. RSC Adv. 2015, 5, 98643–98652. [Google Scholar] [CrossRef]
- Giguère, J.-B.; Verolet, Q.; Morin, J.-F. 4,10-Dibromoanthanthrone as a New Building Block for p-Type, n-Type, and Ambipolar π-Conjugated Materials. Chem.—A Eur. J. 2013, 19, 372–381. [Google Scholar] [CrossRef]
- Venkatraman, R.; Panneer, S.V.K.; Varathan, E.; Subramanian, V. Aromaticity–Photovoltaic Property Relationship of Triphenylamine-Based D-π-A Dyes: Leads from DFT Calculations. J. Phys. Chem. A 2020, 124, 3374–3385. [Google Scholar] [CrossRef] [PubMed]
- Pino-Rios, R.; Montenegro-Pohlhammer, N.; Cárdenas-Jirón, G. Assessment of New Expanded Porpholactones as UV/Vis/NIR Chromophores for Dye-Sensitized Solar Cell Applications. J. Phys. Chem. A 2021, 125, 2267–2275. [Google Scholar] [CrossRef]
- Silva López, C.; Nieto Faza, O. 2—Overview of the computational methods to assess aromaticity. In Aromaticity; Fernandez, I., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 41–71. [Google Scholar]
- Prajapat, K.; Dhonde, M.; Sahu, K.; Bhojane, P.; Murty, V.V.S.; Shirage, P.M. The evolution of organic materials for efficient dye-sensitized solar cells. J. Photochem. Photobiol. C Photochem. Rev. 2023, 55, 100586. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li–F. J. Comput. Chem 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Josa, D.; Rodríguez-Otero, J.; Cabaleiro-Lago, E.M.; Rellán-Piñeiro, M. Analysis of the performance of DFT-D, M05-2X and M06-2X functionals for studying π⋯π interactions. Chem. Phys. Lett. 2013, 557, 170–175. [Google Scholar] [CrossRef]
- Walker, M.; Harvey, A.J.A.; Sen, A.; Dessent, C.E.H. Performance of M06, M06-2X, and M06-HF Density Functionals for Conformationally Flexible Anionic Clusters: M06 Functionals Perform Better than B3LYP for a Model System with Dispersion and Ionic Hydrogen-Bonding Interactions. J. Phys. Chem. A 2013, 117, 12590–12600. [Google Scholar] [CrossRef]
- Delgado-Montiel, T.; Soto-Rojo, R.; Baldenebro-López, J.; Glossman-Mitnik, D. Theoretical Study of the Effect of Different π Bridges Including an Azomethine Group in Triphenylamine-Based Dye for Dye-Sensitized Solar Cells. Molecules 2019, 24, 3897. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Li, Y.; Zhang, J.; Guo, X.; Wang, L.; Ågren, H. Theoretical modelling of metal-based and metal-free dye sensitizers for efficient dye-sensitized solar cells: A review. Sol. Energy 2024, 277, 112748. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Cossi, M.; Rega, N.; Scalmani, G.; Barone, V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003, 24, 669–681. [Google Scholar] [CrossRef]
- Wazzan, N.; Irfan, A. Theoretical study of triphenylamine-based organic dyes with mono-, di-, and tri-anchoring groups for dye-sensitized solar cells. Org. Electron. 2018, 63, 328–342. [Google Scholar] [CrossRef]
- Syzgantseva, O.A.; Gonzalez-Navarrete, P.; Calatayud, M.; Bromley, S.; Minot, C. Theoretical Investigation of the Hydrogenation of (TiO2)N Clusters (N = 1–10). J. Phys. Chem. C 2011, 115, 15890–15899. [Google Scholar] [CrossRef]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Frisch, M.J. Gaussian 09 Programmer’s Reference; Gaussian: Wallingford, England, 2009. [Google Scholar]
- Dennington, R.; Keith, T.; Millam, J. GaussView; Version 5; Semichem Inc.: Shawnee, KS, USA, 2009. [Google Scholar]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminformatics 2012, 4, 17. [Google Scholar] [CrossRef]
- Deogratias, G.; Al-Qurashi, O.S.; Wazzan, N.; Pogrebnaya, T.; Pogrebnoi, A. Effects of heteroatoms in π-conjugated linkers on the optical and electronic properties of modified triphenylamine based dyes: Towards DSSCs’ applications. J. Mol. Model. 2020, 26, 288. [Google Scholar] [CrossRef] [PubMed]
- Lu, T. Simple, reliable, and universal metrics of molecular planarity. J. Mol. Model. 2021, 27, 263. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Bai, Y.; Li, R.; Shi, D.; Wenger, S.; Zakeeruddin, S.M.; Grätzel, M.; Wang, P. Employ a bisthienothiophene linker to construct an organic chromophore for efficient and stable dye-sensitized solar cells. Energy Environ. Sci. 2009, 2, 92–95. [Google Scholar] [CrossRef]
- Cahen, D.; Hodes, G.; Grätzel, M.; Guillemoles, J.F.; Riess, I. Nature of Photovoltaic Action in Dye-Sensitized Solar Cells. J. Phys. Chem. B 2000, 104, 2053–2059. [Google Scholar] [CrossRef]
- Som, N.N.; Sampath, P.M.W.P.; Dabhi, S.D.; Mankad, V.; Shinde, S.; Attygalle, M.L.C.; Jha, P.K. Strain and layer modulated electronic and optical properties of low dimensional perovskite methylammonium lead iodide: Implications to solar cells. Sol. Energy 2018, 173, 1315–1322. [Google Scholar] [CrossRef]
- Martsinovich, N.; Troisi, A. Theoretical studies of dye-sensitised solar cells: From electronic structure to elementary processes. Energy Environ. Sci. 2011, 4, 4473–4495. [Google Scholar] [CrossRef]
- Lin, J.T.; Chen, P.-C.; Yen, Y.-S.; Hsu, Y.-C.; Chou, H.-H.; Yeh, M.-C.P. Organic Dyes Containing Furan Moiety for High-Performance Dye-Sensitized Solar Cells. Org. Lett. 2009, 11, 97–100. [Google Scholar] [CrossRef]
- Bora, S.R.; Kalita, D.J. Tuning the charge transfer and optoelectronic properties of tetrathiafulvalene based organic dye-sensitized solar cells: A theoretical approach. RSC Adv. 2021, 11, 39246–39261. [Google Scholar] [CrossRef]
- Hilborn, R.C. Einstein coefficients, cross sections, f values, dipole moments, and all that. Am. J. Phys. 1982, 50, 982–986. [Google Scholar] [CrossRef]
- Marcus, R.A. Electron transfer reactions in chemistry. Theory and experiment. Rev. Mod. Phys. 1993, 65, 599–610. [Google Scholar] [CrossRef]
- Wazzan, N.A. A DFT/TDDFT investigation on the efficiency of novel dyes with ortho-fluorophenyl units (A1) and incorporating benzotriazole/benzothiadiazole/phthalimide units (A2) as organic photosensitizers with D–A2–π–A1 configuration for solar cell applications. J. Comput. Electron. 2019, 18, 375–395. [Google Scholar] [CrossRef]
- Marcus, R.A. Chemical and Electrochemical Electron-Transfer Theory. Annu. Rev. Phys. Chem. 1964, 15, 155–196. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; He, Z.; Xu, Y.; Yu, W. Theoretical investigations on charge transport properties of tetrabenzo[a,d,j,m]coronene derivatives using different density functional theory functionals (B3LYP, M06-2X, and wB97XD). J. Chem. Res. 2019, 43, 293–303. [Google Scholar] [CrossRef]
- Wazzan, N.; El-Shishtawy, R.M.; Irfan, A. DFT and TD–DFT calculations of the electronic structures and photophysical properties of newly designed pyrene-core arylamine derivatives as hole-transporting materials for perovskite solar cells. Theor. Chem. Acc. 2017, 137, 9. [Google Scholar] [CrossRef]
- Alongamo, C.I.L.; Tasheh, S.N.; Nkungli, N.K.; Bine, F.K.; Ghogomu, J.N. Structural, Electronic, and Charge Transport Properties of New Materials based on 2-(5-Mercapto-1,3,4-Oxadiazol-2-yl) Phenol for Organic Solar Cells and Light Emitting Diodes by DFT and TD-DFT. J. Chem. 2022, 2022, 1802826. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
- Le Bahers, T.; Adamo, C.; Ciofini, I. A Qualitative Index of Spatial Extent in Charge-Transfer Excitations. J. Chem. Theory Comput. 2011, 7, 2498–2506. [Google Scholar] [CrossRef]
- Ali, B.A.; Allam, N.K. Propping the optical and electronic properties of potential photo-sensitizers with different π-spacers: TD-DFT insights. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 188, 237–243. [Google Scholar] [CrossRef]
- Li, P.; Cui, Y.; Song, C.; Zhang, H. A systematic study of phenoxazine-based organic sensitizers for solar cells. Dye. Pigm. 2017, 137, 12–23. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, T.; Wu, C.; Guan, W.; Yan, L.; Su, Z. A theoretical design and investigation on Zn-porphyrin-polyoxometalate hybrids with different π-linkers for searching high performance sensitizers of p-type dye-sensitized solar cells. Dye. Pigm. 2016, 130, 168–175. [Google Scholar] [CrossRef]
- Wei, S.; Li, K.; Lu, X.; Zhao, Z.; Shao, Y.; Dang, Y.; Li, S.; Guo, W. Theoretical insight into electronic structure and optoelectronic properties of heteroleptic Cu(I)-based complexes for dye-sensitized solar cells. Mater. Chem. Phys. 2016, 173, 139–145. [Google Scholar] [CrossRef]
- Zanjanchi, F.; Beheshtian, J. Natural pigments in dye-sensitized solar cell (DSSC): A DFT-TDDFT study. J. Iran. Chem. Soc. 2019, 16, 795–805. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Li, X.; Xu, Y. Boosting the photoelectric conversion efficiency of DSSCs through graphene quantum dots: Insights from theoretical study. Mater. Chem. Front. 2021, 5, 5814–5825. [Google Scholar] [CrossRef]
- Al-Qurashi, O.S.; Wazzan, N.A.; Obot, I. Exploring the effect of mono-and di-fluorinated triphenylamine-based molecules as electron donors for dye-sensitised solar cells. Mol. Simul. 2020, 46, 41–53. [Google Scholar] [CrossRef]
- Costa, R.; Al-Qurashi, O.S.; Wazzan, N.; Pogrebnoi, A.; Pogrebnaya, T. Designed complexes based on betanidin and L0 Dyes for DSSCs: Thermodynamic and optoelectronic properties from DFT study. Mol. Simul. 2022, 48, 647–661. [Google Scholar] [CrossRef]
- Irfan, A.; Chaudhry, A.R.; Jin, R.; Al-Sehemi, A.G.; Muhammad, S.; Tang, S. Exploring the charge transfer nature and electro-optical properties of anthracene based sensitizers @TiO2 cluster. J. Taiwan Inst. Chem. Eng. 2017, 80, 239–246. [Google Scholar] [CrossRef]
- Soria, F.A.; Daldossi, C.; Di Valentin, C. Tuning the electron injection mechanism by changing the adsorption mode: The case study of Alizarin on TiO2. Mater. Today Energy 2022, 28, 101085. [Google Scholar] [CrossRef]
- Britel, O.; Fitri, A.; Touimi Benjelloun, A.; Slimi, A.; Benzakour, M.; McHarfi, M. Theoretical design of new carbazole based organic dyes for DSSCs applications. A DFT/TD-DFT insight. J. Photochem. Photobiol. A Chem. 2022, 429, 113902. [Google Scholar] [CrossRef]
- Horn, M.; Schwerdtfeger, C.F.; Meagher, E.P. Refinement of the structure of anatase at several temperatures. Z. Für Krist. 1972, 136, 273. [Google Scholar] [CrossRef]
- Bates, S.P.; Kresse, G.; Gillan, M.J. The adsorption and dissociation of ROH molecules on TiO2(110). Surf. Sci. 1998, 409, 336–349. [Google Scholar] [CrossRef]
- Al-Qurashi, O.S.; Wazzan, N. Prediction of Power Conversion Efficiencies of Diphenylthienylamine-Based Dyes Adsorbed on the Titanium Dioxide Nanotube. ACS Omega 2021, 6, 8967–8975. [Google Scholar] [CrossRef] [PubMed]
- Dette, C.; Pérez-Osorio, M.A.; Kley, C.S.; Punke, P.; Patrick, C.E.; Jacobson, P.; Giustino, F.; Jung, S.J.; Kern, K. TiO2 anatase with a bandgap in the visible region. Nano Lett. 2014, 14, 6533–6538. [Google Scholar] [CrossRef]
- Jin, X.; Sun, L.; Li, D.; Wang, C.-L.; Bai, F.-Q. Efficiency difference between furan- and thiophene-based D–π–A dyes in DSSCs explained by theoretical calculations. RSC Adv. 2018, 8, 29917–29923. [Google Scholar] [CrossRef] [PubMed]
- Dualeh, A.; Angelis, F.; Fantacci, S.; Moehl, T.; Yi, C.; Kessler, F.; Baranoff, E.; Nazeeruddin, M.; Graetzel, M. Influence of Donor Groups of Organic D−π–A Dyes on Open-Circuit Voltage in Solid-State Dye-Sensitized Solar Cells. J. Phys. Chem. C 2012, 116, 1572–1578. [Google Scholar] [CrossRef][Green Version]
- Heng, P.; Mao, L.; Guo, X.; Wang, L.; Zhang, J. Accurate estimation of the photoelectric conversion efficiency of a series of anthracene-based organic dyes for dye-sensitized solar cells. J. Mater. Chem. C 2020, 8, 2388–2399. [Google Scholar] [CrossRef]
- He, L.-J.; Chen, J.; Bai, F.-Q.; Jia, R.; Wang, J.; Zhang, H.-X. Fine-tuning π-spacer for high efficiency performance DSSC: A theoretical exploration with D−π−A based organic dye. Dye. Pigment. 2017, 141, 251–261. [Google Scholar] [CrossRef]
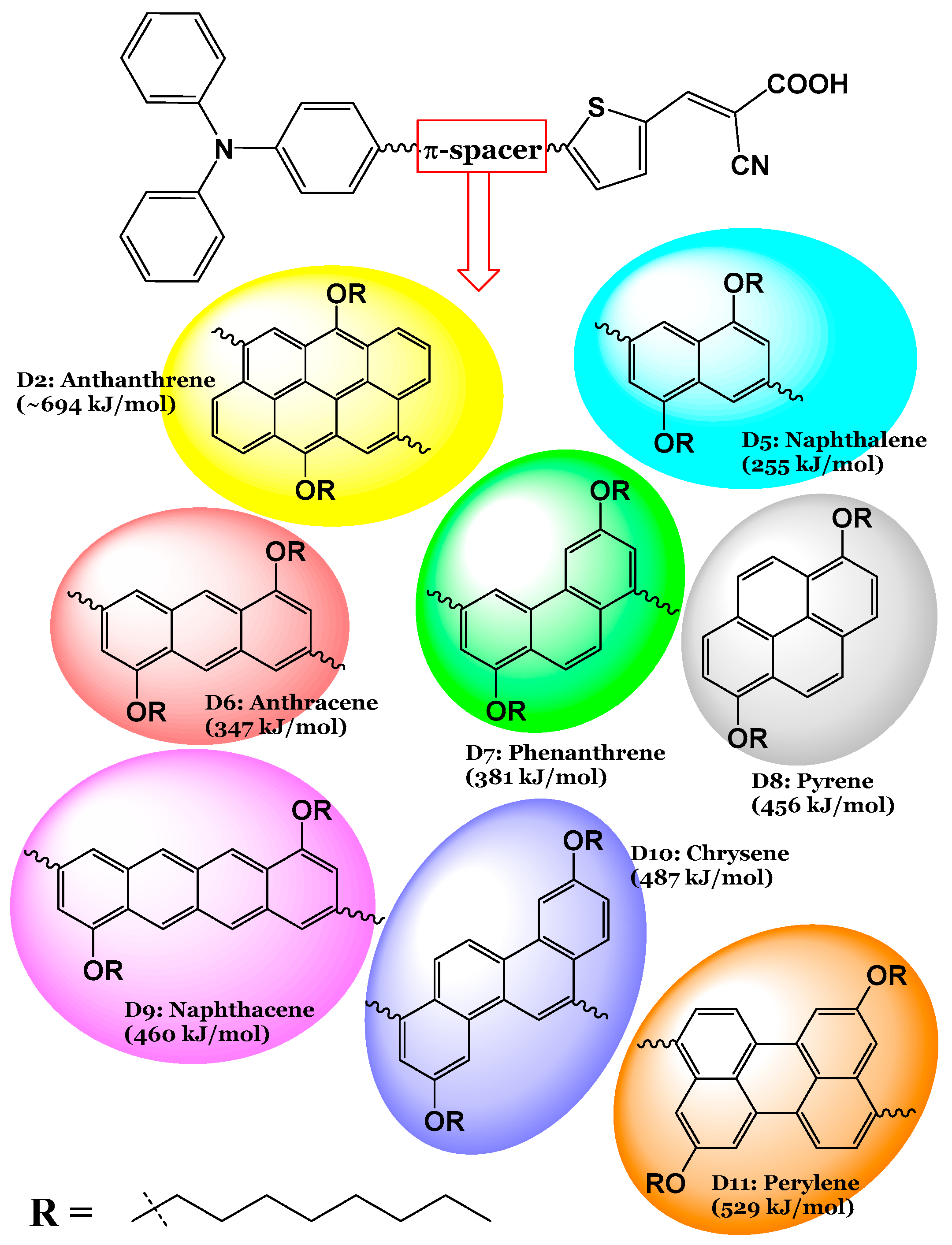
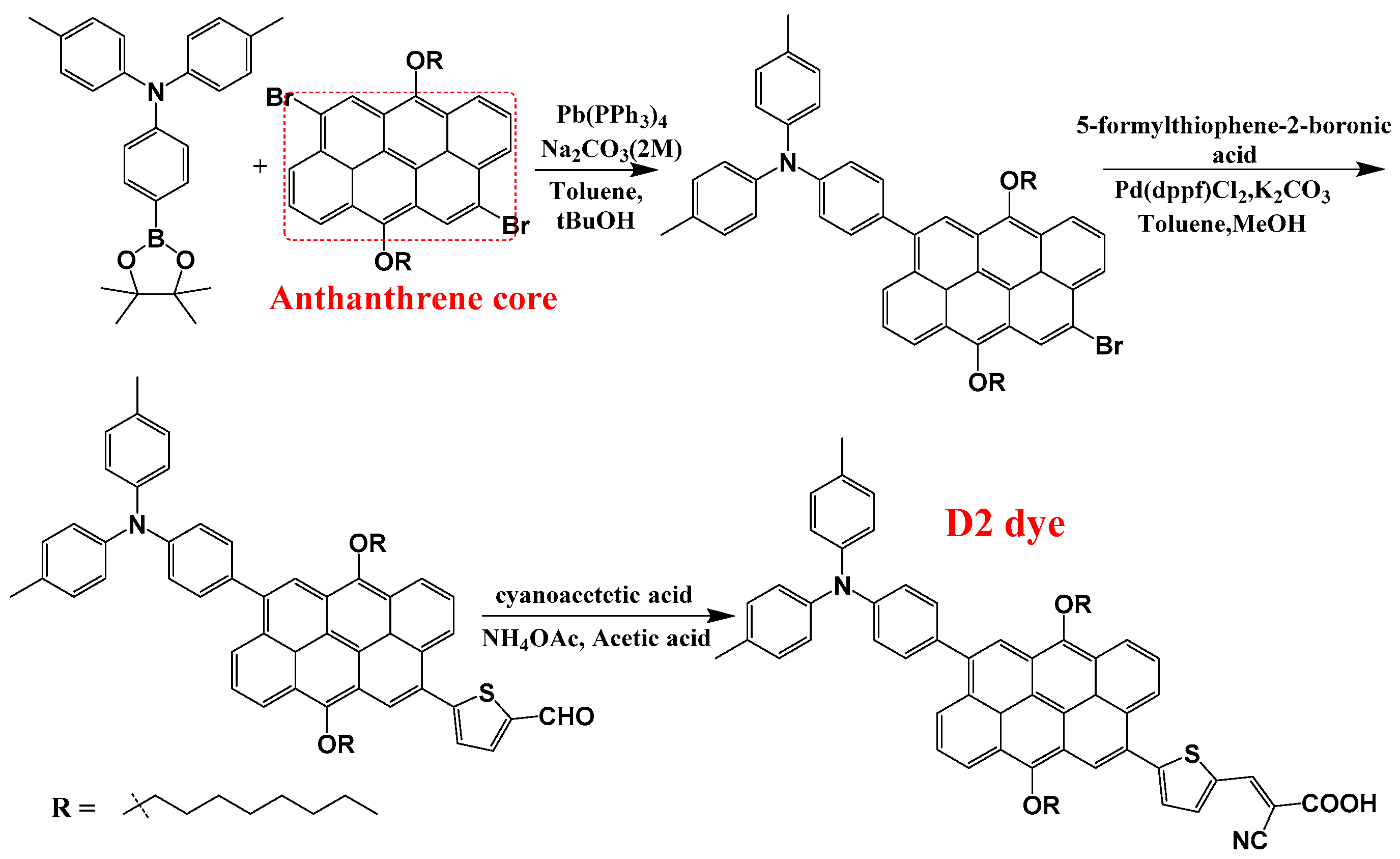
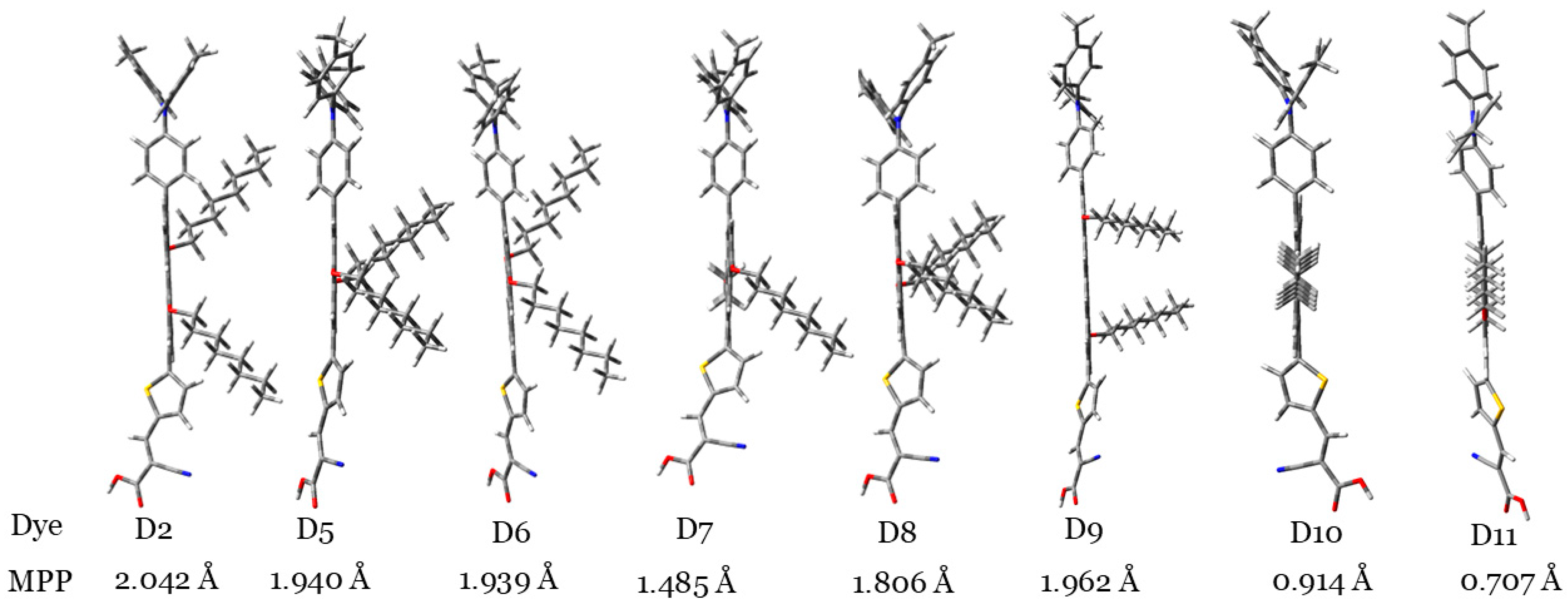
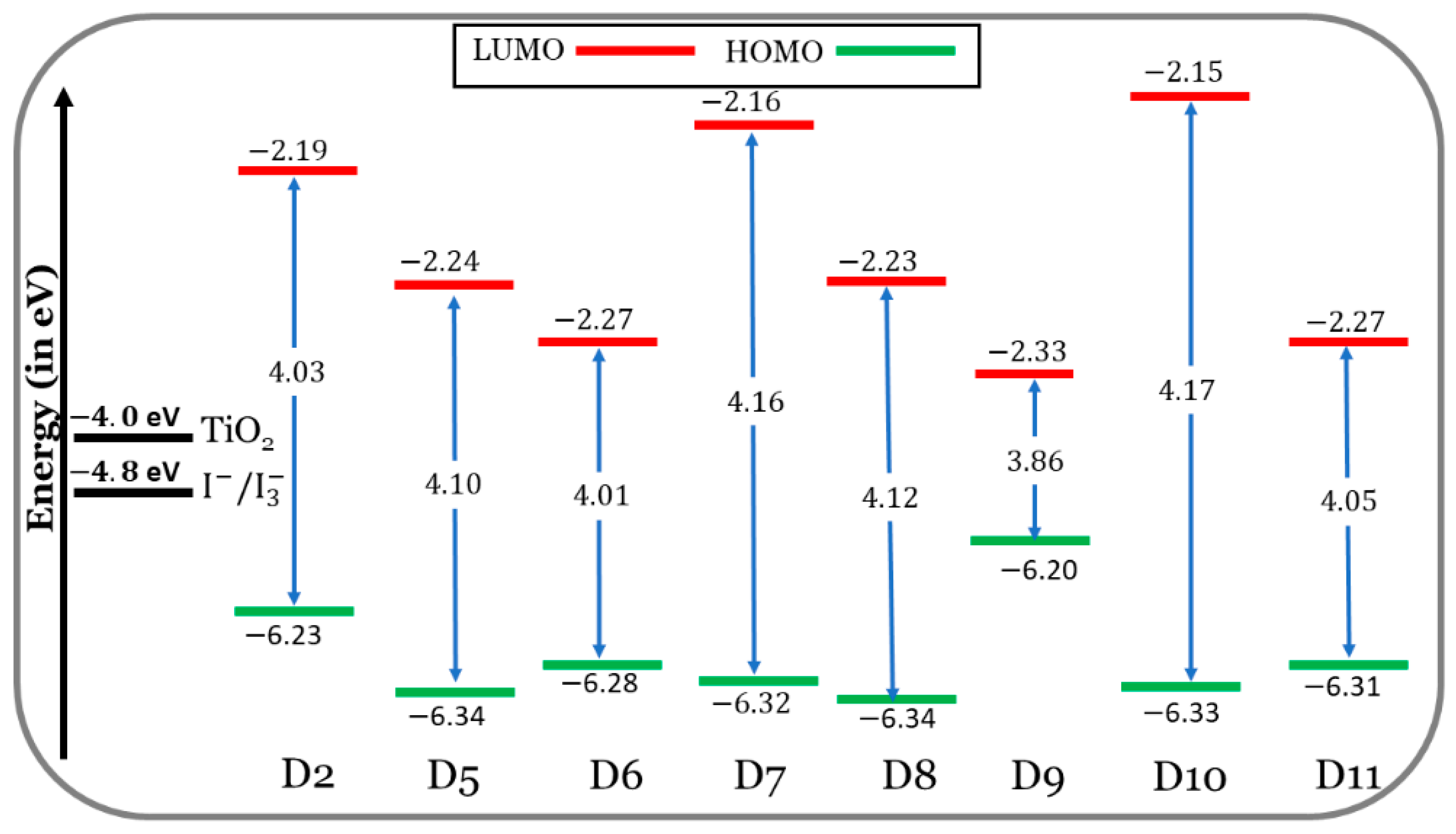





| Aromatic Core (Dye) | DA1 (TPA) | DA2 (TPH) | DA3 (ALKY1) | DA4 (ALKY2) |
|---|---|---|---|---|
| Anthanthrene (D2) | 54.12 | 56.73 | 90.98 | 91.13 |
| Naphthalene (D5) | 35.40 | 25.61 | 92.34 | 90.97 |
| Anthracene (D6) | 35.22 | 25.66 | 91.82 | 93.71 |
| Phenanthrene (D7) | 36.21 | 56.21 | 179.21 | 88.77 |
| Pyrene (D8) | 52.63 | 46.95 | 86.64 | 91.85 |
| Naphthacene (D9) | 35.19 | 25.33 | 91.79 | 92.45 |
| Chrysene (D10) | 52.43 | 56.90 | 179.52 | 179.38 |
| Perylene (D11) | 36.44 | 28.10 | 179.15 | 179.30 |
| Dye | (in nm/eV) | Transition | Transition Character | LHE | Iso-Density | |
|---|---|---|---|---|---|---|
| D2 | 451.36/ 2.75 | 1.001 | S0 → S1 | H → L + 1 (49%) | 0.900 |  |
| 350.77/ 3.53 | 1.490 | S0 → S4 | H-2 → L (47%) | 0.968 |  | |
| D5 | 418.47/ 2.96 | 1.899 | S0 → S1 | H-1 → L (50%) | 0.987 | 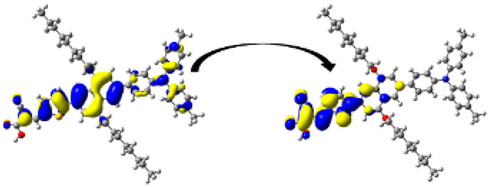 |
| 299.41/ 4.14 | 0.4512 | S0 → S6 | H-1 → L + 1 (38%) | 0.646 | 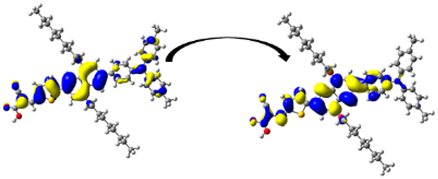 | |
| D6 | 436.19/ 2.84 | 1.447 | S0 → S1 | H-1 → L (44%) | 0.964 | 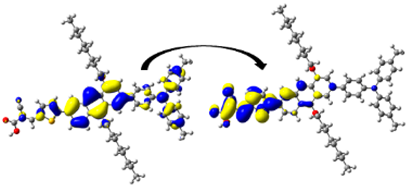 |
| 348.16/ 3.56 | 0.693 | S0 → S3 | H-2 → L (34%) | 0.797 | 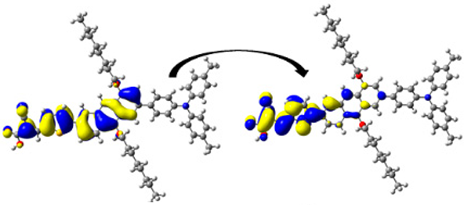 | |
| D7 | 393.40/ 3.15 | 1.421 | S0 → S1 | H-1 → L (47%) | 0.962 | 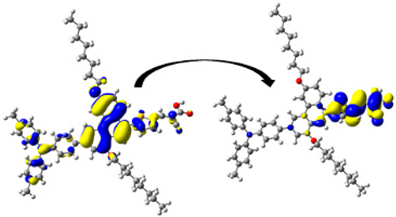 |
| 320.55/ 3.87 | 0.863 | S0 → S3 | H-3 → L (32%) | 0.863 | 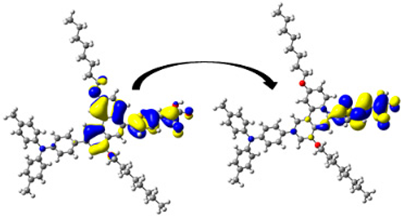 | |
| D8 | 428.01/ 2.90 | 1.571 | S0 → S1 | H-1 → L (50%) | 0.973 | 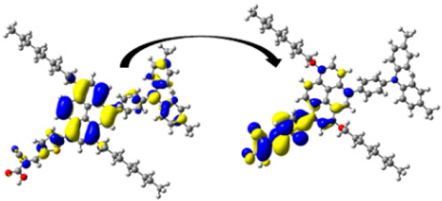 |
| 315.51/ 3.93 | 0.830 | S0 → S5 | H-2 → L (27%) | 0.852 |  | |
| D9 | 413.38/ 3.00 | 1.289 | S0 → S2 | H → L + 1 (41%) | 0.949 |  |
| 368.70/ 3.36 | 1.118 | S0 → S3 | H-1 → L (33%) | 0.924 | 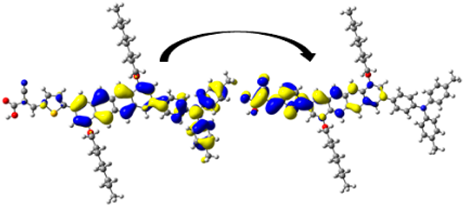 | |
| D10 | 401.63/ 3.09 | 1.306 | S0 → S1 | H-1 → L (47%) | 0.951 | 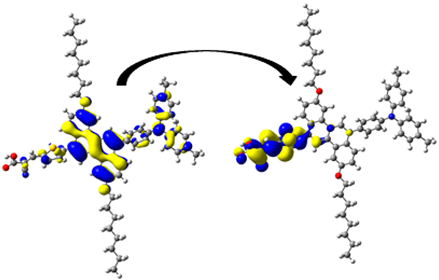 |
| 281.66/ 4.40 | 0.822 | S0 → S10 | H-2 → L (39%) | 0.849 |  | |
| D11 | 400.40/ 3.10 | 1.210 | S0 → S2 | H-1 → L (34%) | 0.938 | 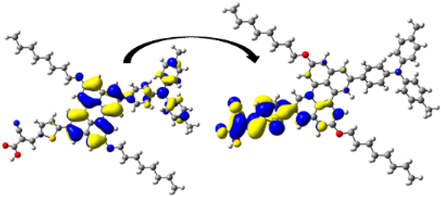 |
| 352.90/ 3.51 | 0.623 | S0 → S4 | H → L + 1 (44%) | 0.762 |  |
| Dye | (in nm/eV) | (in nm) | τ (in ns) | |
|---|---|---|---|---|
| D2 | 616.27/2.01 | 1.1659 | 165 | 4.817 |
| D5 | 586.50/2.11 | 2.1031 | 134 | 2.428 |
| D6 | 595.63/2.08 | 2.0038 | 159 | 2.623 |
| D7 | 602.82/2.06 | 2.0263 | 209 | 2.644 |
| D8 | 684.28/1.81 | 1.7785 | 256 | 3.902 |
| D9 | 646.00/1.92 | 1.5433 | 233 | 3.996 |
| D10 | 614.64/2.02 | 1.8978 | 213 | 2.936 |
| D11 | 531.15/2.33 | 0.5762 | 131 | 7.268 |
| Dye | l | ||||||
|---|---|---|---|---|---|---|---|
| D2 | 0.114 | 0.066 | 12.127 | 0.135 | 3.437 | 2.791 | 0.031 |
| D5 | 0.053 | 0.064 | 2.886 | 0.152 | 6.216 | 2.172 | 0.114 |
| D6 | 0.030 | 0.068 | 0.970 | 0.179 | 3.755 | 0.266 | 0.049 |
| D7 | 0.056 | 0.068 | 3.419 | 0.152 | 4.523 | 1.362 | 0.061 |
| D8 | 0.070 | 0.027 | 4.617 | 0.026 | 3.557 | 1.138 | 0.006 |
| D9 | 0.023 | 0.119 | 0.539 | 0.535 | 3.843 | 0.155 | 0.154 |
| D10 | 0.021 | 0.005 | 20.560 | 0.158 | 3.783 | 5.732 | 0.044 |
| D11 | 0.015 | 0.028 | 0.238 | 0.026 | 6.965 | 0.225 | 0.023 |
| Dye@TiO2 | (in nm/eV) | f | Transition | Transition Character | LHE |
|---|---|---|---|---|---|
| D2@TiO2 | 442.53/2.802 | 0.863 | S0 → S9 | H → L (51%) | 0.863 |
| 357.25/3.471 | 0.726 | S0 → S16 | H−3 → L (45%) | 0.812 | |
| D5@TiO2 | 415.65/2.983 | 1.9869 | S0 → S10 | H−2 → L (48%) | 0.990 |
| 307.09/4.037 | 0.3834 | S0 → S20 | H → L (38%) | 0.586 | |
| D6@TiO2 | 434.58/2.853 | 1.6115 | S0 → S9 | H → L (43%) | 0.976 |
| 347.24/3.571 | 0.5086 | S0 → S9 | H−3 → L (41%) | 0.690 | |
| D7@TiO2 | 415.73/2.982 | 1.5539 | S0 → S10 | H−2 → L (46%) | 0.972 |
| 313.00/3.961 | 0.9301 | S0 → S9 | H → L (30%) | 0.883 | |
| D8@TiO2 | 431.15/2.876 | 1.5860 | S0 → S10 | H−2 → L (47%) | 0.974 |
| 315.21/3.933 | 0.4721 | S0 → S19 | H−2 → L+15 (28%) | 0.663 | |
| D9@TiO2 | 409.02/3.031 | 1.0321 | S0 → S11 | H → L+3 (40%) | 0.907 |
| 366.16/3.386 | 1.0507 | S0 → S15 | H−3 → L (33%) | 0.911 | |
| D10@TiO2 | 410.60/3.020 | 1.2562 | S0 → S10 | H−2 → L (45%) | 0.945 |
| 319.47/3.881 | 0.7682 | S0 → S18 | H−2 → L (35%) | 0.829 | |
| D11@TiO2 | 397.18/3.122 | 1.4398 | S0 → S13 | H−1 → L+4 (35%) | 0.964 |
| 365.14/3.396 | 0.4673 | S0 → S19 | H−3 → L (46%) | 0.659 |
| Dye | Aromatic Core | (kJ/mol) | MPP | (eV) | LHE (%) | (eV) | (eV) | (eV) | (eV) | (kJ/mol) |
|---|---|---|---|---|---|---|---|---|---|---|
| D2 | Anthracene | 694 | 2.042 | 4.030 | 97 | 0.50 | 1.45 | 0.607 | 0.296 | −645.08 |
| D5 | Naphthalene | 255 | 1.940 | 4.099 | 99 | 0.58 | 1.58 | 0.582 | 0.288 | −660.16 |
| D6 | Anthracene | 347 | 1.939 | 4.012 | 96 | 0.52 | 1.52 | 0.576 | 0.286 | −655.58 |
| D7 | Phenanthrene | 381 | 1.485 | 4.161 | 96 | 0.79 | 1.56 | 0.590 | 0.303 | −653.67 |
| D8 | Pyrene | 456 | 1.806 | 4.115 | 97 | 0.52 | 1.58 | 0.595 | 0.286 | −653.47 |
| D9 | Naphthacene | 460 | 1.962 | 3.863 | 95 | 0.76 | 1.44 | 0.579 | 0.286 | −650.40 |
| D10 | Chrysene | 487 | 0.914 | 4.174 | 95 | 0.72 | 1.57 | 0.592 | 0.291 | −650.57 |
| D11 | Perylene | 529 | 0.707 | 4.048 | 94 | 0.75 | 1.55 | 0.596 | 0.310 | −647.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wazzan, N. Structural Engineering of π-Linker Aromaticity in Anthanthrene-Based Dyes with D–π–A Configuration: DFT Investigation to Enhance Charge Transfer in DSSCs. Processes 2025, 13, 418. https://doi.org/10.3390/pr13020418
Wazzan N. Structural Engineering of π-Linker Aromaticity in Anthanthrene-Based Dyes with D–π–A Configuration: DFT Investigation to Enhance Charge Transfer in DSSCs. Processes. 2025; 13(2):418. https://doi.org/10.3390/pr13020418
Chicago/Turabian StyleWazzan, Nuha. 2025. "Structural Engineering of π-Linker Aromaticity in Anthanthrene-Based Dyes with D–π–A Configuration: DFT Investigation to Enhance Charge Transfer in DSSCs" Processes 13, no. 2: 418. https://doi.org/10.3390/pr13020418
APA StyleWazzan, N. (2025). Structural Engineering of π-Linker Aromaticity in Anthanthrene-Based Dyes with D–π–A Configuration: DFT Investigation to Enhance Charge Transfer in DSSCs. Processes, 13(2), 418. https://doi.org/10.3390/pr13020418









