Physics-Constrained Graph Attention Networks for Distribution System State Estimation Under Sparse and Noisy Measurements

Abstract

Accurate state estimation is essential for the real-time operation and control of modern distribution systems characterized by high renewable energy penetration, bidirectional power flows, and volatile loads. Conventional model-driven approaches such as the Weighted Least Squares (WLS) exhibit limited robustness under noisy and sparse measurements, while existing data-driven methods often neglect critical physical constraints inherent to power systems. To address these limitations, this paper proposes a physics-constrained Graph Attention Network (GAT) framework for distribution system state estimation (DSSE) that synergistically integrates data-driven learning with physical domain knowledge. The proposed method comprises three key components: (1) a Gaussian Mixture Model (GMM)-based data augmentation strategy that captures the stochastic characteristics of loads and distributed generation to generate synthetic samples consistent with actual operating distributions; (2) a GAT-based feature extractor with topology-aware admittance matrix embedding that effectively learns spatial dependencies and structural relationships among network nodes; and (3) a physics-constrained loss function that incorporates nodal power and voltage limit penalties to enforce operational feasibility. Comprehensive evaluations on the real-world 141-bus test system demonstrate that the proposed method achieves mean absolute error (MAE) reductions of 52.4% and 45.5% for voltage magnitude and angle estimation, respectively, compared to conventional Graph Convolutional Network (GCN)-based approaches. These results validate the superior accuracy, robustness, and adaptability of the proposed framework under challenging measurement conditions.

1. Introduction

Distribution systems serve as a critical link in the power system infrastructure, responsible for delivering electrical energy from high-voltage transmission systems to end-use consumers. In recent years, the widespread deployment of Distributed Generation (DG) units, electric vehicles, energy storage systems, and advanced demand-side management technologies has fundamentally transformed the operational landscape of the distribution systems [1]. This evolution has introduced new operational challenges, characterized by high renewable energy penetration, bidirectional power flows, and pronounced load variability. Concurrently, legacy distribution system infrastructure continues to suffer from aging equipment, sparse sensor deployment, and suboptimal operational control strategies [2], thereby imposing stringent requirements on system safety, reliability, and economic efficiency.

State estimation constitutes a foundational capability for the real-time monitoring and control of distribution systems. By continuously processing streaming measurement data, state estimators provide accurate estimates of critical operational variables, including nodal voltages, branch power flows, and nodal power injections. These estimates enable enhanced situational awareness, accelerated fault detection and localization, optimized dispatch decisions, and maximized renewable energy integration [3]. Consequently, developing robust and efficient state estimation techniques is essential for realizing intelligent and adaptive distribution system management.

State estimation methods can be categorized into model-driven and data-driven approaches based on their underlying modeling strategies. The Weighted Least Squares (WLS) method, a widely used model-driven approach, formulates state estimation as a weighted least-squares optimization problem to minimize the sum of squared weighted measurement residuals [4,5]. However, WLS exhibits poor robustness when dealing with noisy measurements or outliers, demonstrates strong dependency on network observability, and frequently encounters convergence difficulties [6]. Although several variants incorporating robust estimation techniques [7] or bad data detection mechanisms [8] have been proposed, these approaches remain computationally expensive and suffer from slow convergence, thereby limiting their applicability to real-time operations.

Data-driven approaches overcome these limitations by offering superior feature extraction capabilities and computational efficiency, making them particularly well-suited for complex distribution systems characterized by incomplete measurement coverage. Representative works include: Ref. [9], which employs spiking neural networks to synthesize pseudo-measurements for three-phase state estimation; Ref. [10], which proposes a correlation-aware weight initialization strategy to accelerate training convergence in large-scale systems; and Ref. [11], which leverages a Gaussian Mixture Model (GMM) within a Bayesian framework to characterize the probabilistic distribution of load power and predict conditional expectations of state variables. Extending this line of research, Ref. [12] incorporates the residuals of power flow equations into the loss function, significantly improving the accuracy of state estimation.

GNNs have recently emerged as a promising paradigm for modeling non-Euclidean network structures, including power systems [13,14]. Ref. [15] utilizes message-passing mechanisms to facilitate information propagation among neighboring nodes, effectively capturing topology-dependent state relationships. Ref. [16] augments the Graph Attention Network (GAT) framework with global multi-head attention modules to enhance robustness to measurement noise. Additionally, Ref. [17] investigates weakly supervised GNN-based learning by integrating physical priors, thereby reducing the reliance on high-quality labeled data. Despite their strong real-time performance, existing data-driven state estimation methods typically overlook the physical constraints inherent in distribution systems, leading to reduced accuracy and limited generalization under sparse measurement conditions.

To address the challenges imposed by sparse measurements and frequent topological changes in distribution systems, this study proposes a physics-constrained GNN approach for distribution system state estimation (DSSE). Firstly, a GMM-based probabilistic data augmentation strategy is introduced to model the stochastic behavior of loads and DG, enabling the generation of realistic synthetic samples under data-scarce scenarios. Secondly, a GAT-based spatial feature learning module with topological feature embedding is designed to effectively capture spatial dependencies and structural correlations among nodes. Finally, a physics-constrained regularization mechanism is developed by incorporating operational limits on nodal power and voltage magnitudes into the loss function, ensuring physical consistency throughout model training. Extensive experiments conducted on the real-world 141-bus system verify that the proposed approach outperforms existing data-driven methods in terms of estimation accuracy, robustness, and generalization ability.

The main contributions of this work are summarized as follows:

• We develop a GMM-based probabilistic data augmentation framework that explicitly models the stochastic variability of loads and distributed generation units.This strategy not only generates realistic synthetic samples to mitigate data scarcity during training but also covers corner cases arising from loads and DG volatility, thereby ensuring model robustness against the high stochasticity inherent in modern distribution networks.
• We construct a GAT learning module with topology-aware admittance matrix embedding to capture fine-grained spatial correlations and structural coupling inherent in distribution systems.
• We propose a physics-constrained loss regularization strategy that incorporates nodal power and voltage inequality constraints, ensuring physical feasibility and significantly enhancing estimation accuracy and robustness in low-observability conditions.

The remainder of this paper is organized as follows: Section 2 presents a comprehensive review of existing state estimation methods for distribution systems, including both non-graph-based and graph-based approaches. Section 3 introduces the methodology of GMM-based data augmentation and the proposed physics-constrained GAT-based state estimation model. Section 4 details the experimental validation, including effectiveness analysis and robustness analysis across multiple test scenarios. Finally, Section 5 concludes the paper with a summary of key findings.

2. Related Works

2.1. Non-Graph-Based Methods for DSSE

Non-graph-based methods, including traditional model-driven and early data-driven approaches, form the foundation of distribution system state estimation. These methods rely primarily on mathematical modeling or machine learning without explicitly exploiting network topology information.

The WLS method, introduced by Schweppe et al. [4,5], remains the classical model-driven approach, estimating system states by minimizing weighted measurement residuals. However, its sensitivity to noise, strong observability requirements, and limited robustness under bad data have been widely reported [6,18]. To enhance robustness, extensions such as the Weighted Least Absolute Value (WLAV) estimator [19] and exponential objective functions [8] were proposed, yet these methods remain computationally demanding. Distributed frameworks, such as the multi-area state estimation by Korres [20] and the robust ADMM-based approach by Kekatos and Giannakis [21], improved scalability but introduced boundary inconsistency and synchronization issues.

Dynamic estimation based on the Kalman Filter (KF) and its variants integrates temporal evolution of system states. The Extended Kalman Filter (EKF) [22] and Unscented Kalman Filter (UKF) [23] improved nonlinear modeling accuracy, while adaptive implementations [24] addressed noise sensitivity. Nevertheless, their high computational complexity limits real-time applicability.

With the rise of data analytics, non-graph-based data-driven methods emerged to learn mappings between measurements and system states without relying on explicit physical models. Zamzam et al. [25] integrated shallow neural networks to initialize WLS estimation, enhancing convergence, whereas Mestav et al. [11] proposed a Bayesian neural estimator using GMM to represent load uncertainty. Liang et al. [26] further introduced physics-guided neural estimation, embedding power flow constraints to improve interpretability and accuracy. While effective under partial observability, these methods lack explicit representation of structural dependencies across network nodes, motivating the development of graph-based learning frameworks.

2.2. Graph-Based Methods for DSSE

Graph-based learning methods explicitly model the spatial and topological dependencies of electrical networks, offering significant improvements in accuracy and interpretability over non-graph-based approaches.

Huang et al. [15] introduced a message-passing GNN framework that enables localized information exchange between neighboring nodes, capturing the coupling between topology and electrical states. Hu et al. [16] extended this approach by employing a GAT, utilizing its multi-head attention mechanism to enhance robustness against noisy and incomplete measurements.

Furthermore, several approaches have emerged that integrate physical information with Graph Neural Networks. For instance, to reduce dependence on labeled data, Habib et al. [17] proposed a weakly supervised GNN that incorporates physical priors into the training process. Ref. [27] introduced a hybrid state estimation method combining a physics-informed GNN with Bayesian probabilistic weighted averaging. More recently, Ref. [28] developed a deep learning framework incorporating cross-modal attention modeling and power flow constraints, demonstrating significant improvements in both accuracy and computational speed for state estimation in low-observability distribution networks. These advancements highlight the capability of graph-based learning to unify physical interpretability, spatial correlation modeling, and real-time computational efficiency in DSSE.

3. Methodology

3.1. Overview of the State Estimation Problem

In distribution system state estimation, the goal is to determine the optimal system state variables by integrating known network topology information with sparse and noisy measurement data. The measurement model can be expressed as [29]:

$$\mathbf{z}=h\left(\mathbf{x}\right)+\mathbf{v}$$

(1)

where $\mathbf{z}=\lfloor z_1,z_2,\dots ,z_m\rfloor$ denotes the measurement vector, typically including branch power or current measurements as well as nodal power or voltage measurements. m represents the total number of measurements. $\mathbf{x}=\lfloor x_1,x_2,\dots ,x_n\rfloor$ denotes the state vector, usually composed of the voltage magnitudes and phase angles at all nodes, with dimension n. $\mathbf{v}=\lfloor v_1,v_2,\dots ,v_m\rfloor$ represents the measurement error, which is commonly assumed to follow a Gaussian distribution with zero mean and variance ${\sigma }_i^2$. The nonlinear function $h(·)$ characterizes the relationship between the system’s state variables and measurements based on underlying electrical network equations.

Within a data-driven framework, the DSSE task can be reformulated as a supervised regression problem, where a functional mapping between measurement data and system states is learned from historical records:

$$\widehat{\mathbf{x}}=f\left(\mathbf{z}\right)$$

(2)

where $f(·)$ denotes the data-driven model. $\widehat{\mathbf{x}}$ represents the estimated state vector.

Data-driven state estimation methods offer advantages in terms of estimation accuracy and computational efficiency [18]. However, their performance often suffers from limited availability of historical operational data, which restricts the size and diversity of training samples. Moreover, purely data-driven models tend to disregard physical constraints embedded in power systems, leading to poor interpretability and limited generalization [27]. To address these challenges, this study proposes a physics-constrained data-driven framework that introduces a probabilistic data augmentation strategy and embeds two categories of physical information—the network admittance matrix and operational constraints—into the neural network architecture. This integration enhances both the physical fidelity and the generalization capability of the learned DSSE model.

3.2. Gmm-Based Data Augmentation Method

The GMM is a classical generative modeling approach that expresses complex distributions as a weighted combination of multiple Gaussian components. By estimating these Gaussian parameters from data, GMMs can effectively capture multimodal characteristics within heterogeneous datasets, such as diverse load and distributed generation patterns. When the observed variable y follows a mixture of Gaussian distributions, its probability density function can be defined as [11,12]:

$$p\left(\mathbf{y}\right)=\sum _{k=1}^K{\pi }_k,N\left(\mathbf{y}\right|{\mathit{\mu }}_k,{\mathbf{\Sigma }}_k)$$

(3)

where K represents the total number of Gaussian distributions. ${\pi }_k$ denotes the mixing coefficient of the k-th Gaussian component, satisfying $0\le {\pi }_k\le 1$. $N\left(\mathbf{y}\right|{\mathit{\mu }}_k,{\mathbf{\Sigma }}_k)$ denotes a multivariate Gaussian distribution with mean vector ${\mu }_k$ and covariance matrix ${\mathrm{\Sigma }}_k$. It can be expressed as

$$N\left(\mathbf{y}\right|{\mathit{\mu }}_k,{\mathbf{\Sigma }}_k)={\displaystyle \frac{1}{{\left(2\pi \right)}^{d/2}{\left|{\mathbf{\Sigma }}_k\right|}^{1/2}}}exp\left[-{\displaystyle \frac{1}{2}}{(\mathbf{y}-{\mathit{\mu }}_k)}^T{\mathbf{\Sigma }}_k^{-1}(\mathbf{y}-{\mathit{\mu }}_k)\right]$$

(4)

where $\mathbf{d}$ denotes the dimensionality of $\mathbf{y}$.

To estimate the parameters $\theta ={\{{\pi }_k,{\mu }_k,{\Sigma }_k\}}_{k=1}^K$ using the GMM, the Expectation–Maximization (EM) algorithm [30] is typically employed. The algorithm iteratively alternates between the Expectation (E) step and the Maximization (M) step until convergence is achieved [31].

In the E-step, the posterior probability that the i-th sample ${\mathbf{x}}_i$ belongs to the k-th Gaussian component is computed as:

$${\gamma }_{ik}=P(z_i=k,|,{\mathbf{x}}_i,{\mathit{\theta }}^{\left(t\right)})={\displaystyle \frac{{\pi }_k^{\left(t\right)}N({\mathbf{x}}_i|{\mathit{\mu }}_k^{\left(t\right)},\mathbf{\Sigma }{k}^{\left(t\right)})}{\sum {j=1}^K{\pi }_j^{\left(t\right)}N({\mathbf{x}}_i|{\mathit{\mu }}_j^{\left(t\right)},{\mathbf{\Sigma }}_j^{\left(t\right)})}}$$

(5)

where ${\mathbf{z}}_i$ is the latent class indicator variable, $\mathbf{t}$ denote the iteration index. To formulate the optimization objective of the EM algorithm, the complete-data log-likelihood function of the GMM can be written as:

$$lnp(\mathbf{x},\mathbf{z}|\mathit{\theta })=\sum _{i=1}^{Num}\sum _{k=1}^K{z}_{ik}\left(ln{\pi }_k+lnN\left({\mathbf{x}}_i\right|{\mathit{\mu }}_k,{\mathbf{\Sigma }}_k)\right)$$

(6)

where ${\mathbf{z}}_{ik}$ is a binary variable, equal to 1 if $z_i=k$, and 0 otherwise.

During the M-step, the goal is to maximize the expected complete log-likelihood with respect to parameters ${\theta }^{\left(t\right)}$ under the current posterior distribution of the latent variable:

$$Q\left(\mathit{\theta }\right|{\mathit{\theta }}^{\left(t\right)})={\mathbb{E}}_{p\left(\mathbf{z}\right|\mathbf{x},{\mathit{\theta }}^{\left(t\right)})}\left[lnp(\mathbf{x},\mathbf{z}|\mathit{\theta })\right]$$

(7)

Substituting the posterior probability ${\gamma }_{ik}$ into the expectation, we obtain:

$${\pi }_k^{(t+1)}={\displaystyle \frac{1}{Num}}\sum _{i=1}^{Num}{\gamma }_{ik},{\mu }_k^{(t+1)}={\displaystyle \frac{1}{{\sum }_{i=1}^{Num}{\gamma }_{ik}}}\sum _{i=1}^{Num}{\gamma }_{ik}{x}_i$$

(8)

$${\mathbf{\Sigma }}_k^{(t+1)}={\displaystyle \frac{1}{{\sum }_{i=1}^{Num}{\gamma }_{ik}}}\sum _{i=1}^{Num}{\gamma }_{ik}(x_i-{\mu }_k^{(t+1)}){(x_i-{\mu }_k^{(t+1)})}^T$$

(9)

The EM algorithm alternates between the E-step and M-step until convergence. The resulting mixture distribution effectively captures the probabilistic structure of real-world data, outperforming simplistic unimodal Gaussian assumptions in terms of flexibility and representational capacity.

By learning the joint probabilistic distribution of stochastic load and DG behavior, the trained GMM serves as a realistic data generator for producing augmented samples. These synthesized samples are subsequently used to expand the training dataset of the neural state estimation model, enhancing learning robustness, mitigating data scarcity, and improving generalization across varying operating scenarios.

3.3. Physics-Constrained GAT-Based Distribution System State Estimation Model

3.3.1. Node Feature Learning Module Based on GAT

The GAT is a neural architecture that integrates attention mechanisms into graph learning frameworks [32]. By adaptively assigning different weights to neighboring nodes, GAT effectively captures complex correlations and feature dependencies between nodes in graph-structured data. Benefiting from its self-attention formulation, GAT alleviates the limitations of fixed, predefined adjacency matrices and enhances the model’s ability to learn topological relationships relevant to distribution systems.

Given an input feature vector $h_i\in R^d$ for node i, where d represents the feature dimension, GAT applies a shared linear transformation followed by a multi-head attention mechanism to perform feature aggregation and update node representations. The linear transformation is expressed as

$$\widetilde{h_i}=\mathbf{W}{h}_i$$

(10)

where $\mathbf{W}$ represents learnable weight matrix.

The attention mechanism quantifies the importance of neighbor node j to node i through the attention coefficient ${\alpha }_{ij}$, which is normalized by the Softmax function [33]:

$$e_{ij}={\mathbf{a}}^T\mathrm{LeakyReLU}({\mathbf{W}}_a\widetilde{h_i}\oplus {\mathbf{W}}_a\widetilde{h_j})$$

(11)

$${\alpha }_{ij}={\displaystyle \frac{exp\left(e_{ij}\right)}{{\sum }_{k\in \mathcal{N}\left(i\right)}exp\left(e_{ik}\right)}}$$

(12)

where ${\mathbf{e}}_{ij}$ is the unnormalized attention weight from i to j. ${\mathbf{a}}^T$ is the learnable attention weight vector. ${\mathbf{W}}_a$ is the weight matrix for attention computation. ⊕ denotes the concatenation of vectors. LeakyReLU is the Leaky Rectified Linear Unit activation function that prevents neuron sparsity. $\mathcal{N}\left(i\right)$ represents the neighbor set of node i.

The aggregated feature of node i is then updated through a weighted summation of transformed neighbor features:

$${\mathbf{h}}_i^{\prime }=\sigma \left(\sum _{j\in \mathcal{N}\left(i\right)}\left({\alpha }_{ij}{\tilde{\mathbf{h}}}_j\right)\right)$$

(13)

This attention-based scheme adaptively quantifies the relative contribution of neighboring nodes during feature aggregation, enabling the model to focus on the most informative spatial dependencies.

To enhance representational richness and prevent overfitting, GAT commonly employs a multi-head attention strategy. In this case, K independent attention heads perform separate feature transformations and then aggregate their outputs. Multi-head attention reduces computational complexity by averaging the attention outputs across heads as follows:

$${\mathbf{h}}_i^{\prime }=\sigma \left({\displaystyle \frac{1}{K}}\sum _{k=1}^K\sum _{j\in \mathcal{N}\left(i\right)}{\alpha }_{ij}^{\left(k\right)}{\mathbf{W}}_m^{\left(k\right)}{\tilde{\mathbf{h}}}_j\right)$$

(14)

where the weight matrix of the k-th attention head is denoted as ${\mathbf{W}}_m^{\left(k\right)}$.

This section constructs a node feature learning module based on the GAT. For a distribution system topology graph G containing N nodes, the active power, reactive power, and voltage magnitude measurements $\mathbf{z}$ are used as node input features. By leveraging the advantage of GAT in capturing inter-node dependencies, the distribution system state estimation problem is reformulated as a node-level regression task. The node feature learning module based on GAT is therefore defined as follows:

$${\mathbf{x}}_{GAT}=\sigma \left(f_{GAT}(G,z)\right)$$

(15)

where ${\mathbf{x}}_{GAT}\in {\mathbb{R}}^{N\times m}$ is the output node feature vector. $\mathbf{m}$ denotes the feature dimension. $f_{GAT}(·)$ represents the GAT network.

GAT performs feature transformation, attention coefficient computation, and information-weighted aggregation to adaptively model the correlation between nodal features and the underlying topological structure of the distribution system. When the network topology changes, traditional data-driven models must be retrained to adapt to the new configuration. In contrast, GAT dynamically computes attention weights during each feature aggregation step, making the model less dependent on a static adjacency matrix and instead enabling it to adaptively update message-passing pathways according to the neighbor node features. This property allows GAT to maintain strong adaptability in scenarios with dynamic or evolving network structures.

Additionally, the attention mechanism of GAT provides inherent noise resilience. As illustrated in Equation (12), attention coefficients are computed dynamically based on the similarity between node feature representations. When nodal features are distorted by noise or pseudo-measurement errors, their similarity to the target node decreases, and consequently, their attention weights are reduced during aggregation. This feature-similarity-based weighting mechanism effectively mitigates the influence of noise on feature learning and promotes robust state estimation performance.

Moreover, the local information aggregation mechanism of GAT alleviates the effect of missing node measurements. As shown in Equation (14), when certain node data are unavailable, the feature update process not only depends on the node’s own information but also integrates information from its neighboring nodes. Consequently, missing data primarily affect only local estimates rather than propagating large-scale errors across the graph structure, ensuring stable performance under incomplete or imperfect measurement conditions.

3.3.2. Topological Feature Embedding Module

Traditional data-driven state estimation models are typically developed for a fixed distribution system topology. When the network structure changes, these models must be retrained to accommodate the new topology, resulting in reduced generalization capability. Although GAT inherently provides some degree of adaptability to topological variation, their ability to incorporate explicit physical topology remains limited. To address this issue, this study introduces a topological feature embedding module that incorporates structural information from the distribution system admittance matrix. Through this mechanism, the model captures essential topological correlations between nodes, enabling a unified representation that enhances the robustness and interpretability of the estimation process.

Specifically, the input to this module is derived from the admittance matrix-based topological encoding, denoted as ${\mathbf{Y}}_{bus}\in {\mathbb{R}}^{N\times N}$. The topological features are extracted by a two-layer linear transformation, starting with linear topological feature extraction:

$${\mathbf{Y}}_{\mathrm{stage}1}={\mathbf{W}}_1{\mathbf{Y}}_{\mathrm{bus}}+{\mathbf{b}}_1$$

(16)

where $W_1\in {\mathbb{R}}^{N\times N}$ and ${\mathbf{b}}_1$ denote the learnable weight matrix and bias vector of the first layer, respectively. The output $Y_{stage1}\in {\mathbb{R}}^{N\times N}$ represents the intermediate features.

A second linear transformation is applied to generate higher-level topological embeddings:

$${\mathbf{Y}}_{\mathrm{stage}2}={\mathbf{W}}_2{\mathbf{Y}}_{\mathrm{stage}1}+{\mathbf{b}}_2$$

(17)

where ${\mathbf{W}}_2\in {\mathbb{R}}^{1\times N}$ and ${\mathbf{b}}_2$ denote the weight matrix and bias vector for the second layer. The ${\mathbf{Y}}_{\mathrm{stage}2}\in {\mathbb{R}}^{1\times N}$ represents the resulting topological features.

To enhance the nonlinear representation capacity and ensure that the topological feature coefficients remain within a reasonable range, a hyperbolic tangent activation function is applied:

$${\mathbf{Y}}_{\mathrm{embedding}}=tanh\left({\mathbf{Y}}_{\mathrm{stage}2}\right)$$

(18)

$$tanh\left(x\right)={\displaystyle \frac{e^x-e^{-x}}{e^x+e^{-x}}}$$

(19)

Finally, the extracted topological feature matrix ${\mathbf{Y}}_{\mathrm{embedding}}\in {\mathbb{R}}^{1\times N}$ embedding is fused with the nodal feature matrix obtained from the GAT layer through feature fusion:

$${\mathbf{x}}_{\mathrm{embedding}}={\mathbf{x}}_{\mathrm{GAT}}\otimes {\widehat{\mathbf{Y}}}_{\mathrm{embedding}}$$

(20)

where ${\mathbf{x}}_{\mathrm{embedding}}\in {\mathbb{R}}^{N\times m}$ represents the topology-embedded node features, ${\widehat{\mathbf{Y}}}_{embedding}\in {\mathbb{R}}^{N\times 1}$ represents the transpose of ${\mathbf{Y}}_{embedding}$; ⊗ denotes element-wise multiplication.

The feature fusion enables the model to jointly encode electrical topology and nodal physical characteristics, thereby capturing the inherent coupling between network connectivity and operational states. Thus, the embedded representation ${\mathbf{x}}_{\mathrm{embedding}}$ reflects both electrical dependencies and graph-based information, serving as an enriched input for the subsequent regression stage.

The final output of the topological embedding module is then expressed as

$${\mathbf{y}}_{\mathrm{out}}={\mathbf{x}}_{\mathrm{embedding}}{\mathbf{W}}_3+{\mathbf{b}}_3$$

(21)

where ${\mathbf{W}}_3\in {\mathbb{R}}^{m\times 2}$ and ${\mathbf{b}}_3$ are the weight matrix and bias vector of the output linear layer.

3.3.3. Operational Constraint Embedding Module

Data-driven state estimation methods can achieve high estimation accuracy. However, their outputs often lack physical interpretability, as they may deviate from the inherent physical constraints of power systems [17]. To address this limitation, this study incorporates operational constraints of the distribution system into the training process by introducing a physics-constrained penalty mechanism. This approach ensures that model outputs not only minimize prediction error but also comply with the physical and operational laws of the system.

Specifically, a penalty-based optimization framework is formulated to embed operational constraints into the loss function. The Mean Absolute Error (MAE) loss is used to quantify estimation accuracy, while constraint violation terms are added to reflect physical feasibility. The penalty terms enforce limits on system variables, including active and reactive power flows as well as voltage magnitude bounds. The penalty loss function is defined as follows:

$$\begin{array}{cc}{\mathcal{L}}_{\mathrm{pen}}\hfill & ={\displaystyle \frac{1}{M}}{\displaystyle \sum _{i=1}^M}[{\displaystyle \frac{{\alpha }_P}{L}}max(0,P_i-P^{max})\hfill \\ \hfill & +{\displaystyle \frac{{\alpha }_Q}{L}}max(0,Q_i-Q^{max})\hfill \\ \hfill & +{\displaystyle \frac{{\alpha }_V}{N}}max(0,V_i-V^{max})\hfill \\ \hfill & +{\displaystyle \frac{{\alpha }_V}{N}}max(0,V^{min}-V_i)]\hfill \end{array}$$

(22)

where ${\mathbf{P}}_i$ and ${\mathbf{Q}}_i$ denote the active and reactive power at node $\mathbf{i}$, respectively. ${\mathbf{V}}_i$ is the nodal voltage magnitude. ${\mathbf{P}}^{max}$ and ${\mathbf{Q}}^{max}$ represent the upper limits of active and reactive power. ${\mathbf{V}}^{min}$ and ${\mathbf{V}}^{max}$ are the permissible voltage boundaries.

By combining the MAE loss and the penalty term, the overall objective function is defined as

$$\mathcal{L}=(1-\lambda ){\mathcal{L}}_{\mathrm{MAE}}+\lambda {\mathcal{L}}_{\mathrm{pen}}$$

(23)

$${\mathcal{L}}_{\mathrm{MAE}}={\displaystyle \frac{1}{M}}\sum _{i=1}^M|{\widehat{x}}_i-x_i|$$

(24)

where $\lambda$ is a balance coefficient that regulates the trade-off between prediction accuracy and constraint compliance.

3.3.4. Overall Model Framework

In summary, the overall structure of the proposed model is illustrated in Figure 1. First, the distribution system measurement data and the adjacency matrix are fed into the GAT-based node feature learning module. Through multiple layers of graph convolutions, the model extracts high-dimensional node feature representations that capture spatial and electrical relationships among network nodes.

Meanwhile, the network admittance matrix is linearly transformed to obtain the topological feature embeddings, which encapsulate the physical connectivity and coupling characteristics of the distribution grid.

Subsequently, the node feature representations are fused with the topological embeddings, and the fused result is processed through a linear mapping layer to generate the model’s output. This design allows the model to integrate both learned feature dependencies and physically informed structural information.

Finally, the loss function incorporates an operational constraint penalty term to ensure that the estimated results adhere to the physical laws and operating limits of the distribution system. The model parameters are optimized via backpropagation, and after multiple training iterations, the final distribution system state estimation model is obtained, providing accurate and physically consistent estimation performance.

4. Experiment

4.1. Experimental Setup

To validate the effectiveness of the proposed method, experiments were conducted on the real-world 141-bus distribution system [34], with the network topology depicted in Figure 2. In this test system, the distribution lines are modeled using the standard $\pi$-equivalent circuit model. Furthermore, all load and DG buses are modeled as constant power (PQ) nodes; specifically, DG units are treated as negative PQ injections to accurately reflect their active power generation characteristics. The simulations utilized real-world time-series data for load consumption and DG outputs, sourced from a European region [35], to serve as nodal power injection profiles. The dataset features a temporal resolution of 15 min, capturing realistic distribution network operational variability.

The data generation process comprises three steps designed to emulate realistic operating conditions. First, to account for scenarios involving frequent topological changes in distribution networks, five distinct network topology configurations were constructed by altering the line connectivity relationships. Second, a GMM was employed to learn the probabilistic distributions of load demands and DG outputs from 7000 original historical samples. Leveraging this learned distribution, 14,000 augmented nodal power injection samples were subsequently generated via Monte Carlo sampling. Finally, the generated power injection samples were mapped onto the five distinct distribution network topologies, and power flow analyses were performed to obtain the corresponding system operating states. This process yielded an augmented dataset comprising 14,000 distribution system operating snapshots.

In this framework, real-time measurements include nodal power injections and voltage magnitudes. For nodes not equipped with real-time metering devices, pseudo-measurements were employed to substitute for the missing injection data. Typically, these pseudo-values are derived from load forecasting results or historical load distribution models [36]. For voltage at these pseudo-measurement nodes, the input values were set to 0 to represent the absence of direct measurements. The detailed measurement parameter configurations are presented in

Table 1. Measurement parameter settings.

Measurement Information	Parameter Setting
Pseudo-measurement description	Nodal power injection
Pseudo-measurement nodes	All nodes
Pseudo-measurement noise	50% Gaussian-distributed noise
Real-time measurement description	Nodal power injection, Voltage Magnitude and Angle
Real-time measurement nodes	Nodes 1, 8, 13, 21, 27, 34, 37, 44, 51, 56, 61, 65, 68, 72, 75, 79, 83, 87, 94, 100, 105, 109, 112, 117, 124, 129, 133, 136, 139
Real-time measurement noise	1% Gaussian-distributed noise

.

In this study, the nodal active power, reactive power, voltage magnitude, and voltage angle were selected as input features for the proposed model. The dataset was divided into training and testing subsets in a ratio of 80% to 20%, respectively. To ensure fair performance comparison, all models were optimized using a grid-based hyperparameter search strategy. The search ranges and configuration details are summarized in

Table 2. Hyperparameter settings.

Parameter Name	Search Range
Number of hidden layers	2, 3, 4, 5
Hidden layer dimension	16, 32, 64, 128
Number of GAT attention heads	2, 4, 6, 8
Learning rate	[0.0001, 0.01]
Batch size	32, 64, 128, 256
Penalty coefficients	[0.001, 1]

.

To comprehensively evaluate the performance of the distribution system state estimation, the Mean Absolute Percentage Error (MAPE) and Root Mean Square Error (RMSE) were employed as evaluation metrics, in addition to the MAE metric. The formulations for MAPE and RMSE are defined as follows:

$$\mathrm{MAPE}={\displaystyle \frac{100\%}{M}}\sum _{i=1}^M\left|{\displaystyle \frac{{\widehat{x}}_i-x_i}{x_i}}\right|,$$

(25)

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{M}}\sum _{i=1}^M{({\widehat{x}}_i-x_i)}^2},$$

(26)

where ${\widehat{\mathbf{x}}}_{\mathbf{i}}$ and ${\mathbf{x}}_{\mathbf{i}}$ denote the estimated and actual values, respectively. The MAE metric is computed using the same method as described in Equation (24).

4.2. Experimental Analysis

To verify the effectiveness of the proposed method, comparative experiments were conducted against representative benchmarks and ablation variants. The comparison includes a GCN-based state estimation method, a GAT-based method trained without the proposed GMM-based data augmentation using only the original dataset (denoted as GAT-g), and a GAT-based variant excluding both the topological feature and operational constraint embedding modules (denoted as GAT-p). The quantitative performance comparison of all four approaches is presented in

Table 3. Performance comparison of different methods on the real-world 141-bus system.

Methods	Metrics	Voltage Phase Angle		Voltage Magnitude
		Value	Unit	Value	Unit
GCN	MAE	7.2215	(${10}^{-3}$)	29.218	(${10}^{-3}$)
	MAPE	0.7502	(%)	17.015	(%)
	RMSE	8.9358	(${10}^{-3}$)	35.546	(${10}^{-3}$)
GAT-g	MAE	5.8263	(${10}^{-3}$)	22.544	(${10}^{-3}$)
	MAPE	0.6071	(%)	12.689	(%)
	RMSE	7.4731	(${10}^{-3}$)	28.115	(${10}^{-3}$)
GAT-p	MAE	3.9550	(${10}^{-3}$)	19.011	(${10}^{-3}$)
	MAPE	0.4117	(%)	11.032	(%)
	RMSE	4.9834	(${10}^{-3}$)	24.611	(${10}^{-3}$)
Proposed Method	MAE	3.4372	(${10}^{-3}$)	15.915	(${10}^{-3}$)
	MAPE	0.3583	(%)	8.5727	(%)
	RMSE	4.4092	(${10}^{-3}$)	20.885	(${10}^{-3}$)

.

As shown in Table 3, the proposed method achieves higher estimation accuracy in large-scale distribution systems. Compared with the second-best method, GAT-p, the proposed model reduces the MAE of voltage magnitude and phase angle by 13.1% and 16.3%, respectively, and also exhibits performance improvements in terms of MAPE and RMSE. It can also be observed that the GCN method performs worse than all three GAT-based methods, with voltage magnitude and phase angle MAE values that are 2.10 and 1.84 times those of the proposed approach. This is because GCN aggregates neighbor information with uniform weights, failing to reflect the relative importance of different nodes, which limits its capability for feature extraction in large-scale distribution systems characterized by sparse and complex connectivity. In contrast, GAT improves the representation learning process by assigning adaptive attention weights to neighboring nodes, thereby enhancing its ability to extract key measurement features.

To provide an intuitive comparison, one test case from the dataset was selected. Figure 3 and Figure 4 illustrate the estimated voltage magnitudes and phase angles of the 141-node system. As seen from the figures, the estimation results obtained using the proposed method are closer to the ground truth than those of the comparative methods, demonstrating superior state estimation performance.

Furthermore, a topology generalization test was performed on four additional distribution system configurations from the 141-node dataset.

Table 4. Description of topology generalization test.

Topology	Connected Branches	Disconnected Branches
T1	7–37	6–37
T2	51–85	50–85
T3	89–101	91–101
T4	132–122	121–12

describes the line connection relationships of different topologies, and

Table 5. Results of topology generalization test.

Methods	Metrics	MAE (${10}^{-3}$)
		T1	T2	T3	T4
GCN	Voltage magnitude (p.u.)	7.2305	7.2910	7.4405	7.2709
	Phase angle (deg)	29.411	30.784	29.597	31.094
GAT-g	Voltage magnitude (p.u.)	5.9266	6.1196	5.9739	6.0814
	Phase angle (deg)	23.236	23.983	23.662	24.365
GAT-p	Voltage magnitude (p.u.)	4.1630	4.3747	4.1920	4.2983
	Phase angle (deg)	20.108	20.804	20.455	21.072
Proposed Method	Voltage magnitude (p.u.)	3.5522	3.9088	3.5910	3.6444
	Phase angle (deg)	16.124	17.576	16.435	16.964

presents the corresponding generalization test results. As indicated in Table 5, the proposed method consistently achieves the best performance across all four topological structures, with estimation accuracy comparable to that under the initial topology. These results confirm that training with multi-topology data endows the proposed method with strong generalization capability in large-scale distribution systems, enabling reliable and stable state estimation across varying network configurations after a single training process.

4.3. Robustness Analysis

To evaluate the capability of the proposed method in handling real-time measurement loss, three test cases were designed. In Case 1, real-time measurements at nodes 13 and 21 were removed; in Case 2, measurements at nodes 61 and 65 were omitted; and in Case 3, measurements at nodes 13, 21, 61, and 65 were simultaneously missing. The estimation results for the missing-measurement scenarios are illustrated in Figure 5 and Figure 6. Taking Case 3 as an example, compared with the complete-measurement scenario, the MAE of voltage magnitude and phase angle in the proposed method increased by $1.78\times {10}^{-3}$ and $6.70\times {10}^{-3}$, respectively, representing smaller increments than those observed for the second-best method, GAT-p, whose increases were $2.99\times {10}^{-3}$ and $9.45\times {10}^{-3}$. This superior performance can be attributed to the incorporation of the grid admittance matrix within the proposed framework and the inclusion of an operational constraint regularization term in the loss function to guide the model training process. These enhancements effectively embed physical prior knowledge into the learning model, enabling it to maintain high estimation accuracy even when partial measurement data are unavailable.

To further assess noise resistance, four levels of Gaussian noise—2%, 3%, 4%, and 5%—were added to simulate different measurement noise scenarios. The results of the noise robustness tests are summarized in

Table 6. Results of noise robustness test.

Methods	Metrics	MAE (${10}^{-3}$)
		2%	3%	4%	5%
GCN	Voltage magnitude (p.u.)	8.2421	8.8744	10.897	12.144
	Phase angle (deg.)	31.584	34.443	35.255	36.365
GAT-g	Voltage magnitude (p.u.)	6.5954	7.8630	8.9230	9.8292
	Phase angle (deg.)	24.533	27.087	32.374	37.046
GAT-p	Voltage magnitude (p.u.)	5.7227	6.3465	8.0600	8.5678
	Phase angle (deg.)	23.793	27.028	30.492	34.717
Proposed Method	Voltage magnitude (p.u.)	4.3615	5.3943	6.4019	7.2438
	Phase angle (deg.)	18.032	22.602	26.920	31.073

. Under the 5% noise level, the proposed method achieved reductions in voltage magnitude MAE by 40.4%, 26.3%, and 15.5% compared to GCN, GAT-g, and GAT-p, respectively. For voltage phase angle MAE, the reductions were 14.6%, 16.1%, and 10.5%, respectively. These results demonstrate that the proposed approach preserves high estimation accuracy even under severe noise conditions, indicating strong robustness and resistance to disturbances in real-time measurement data.

5. Conclusions

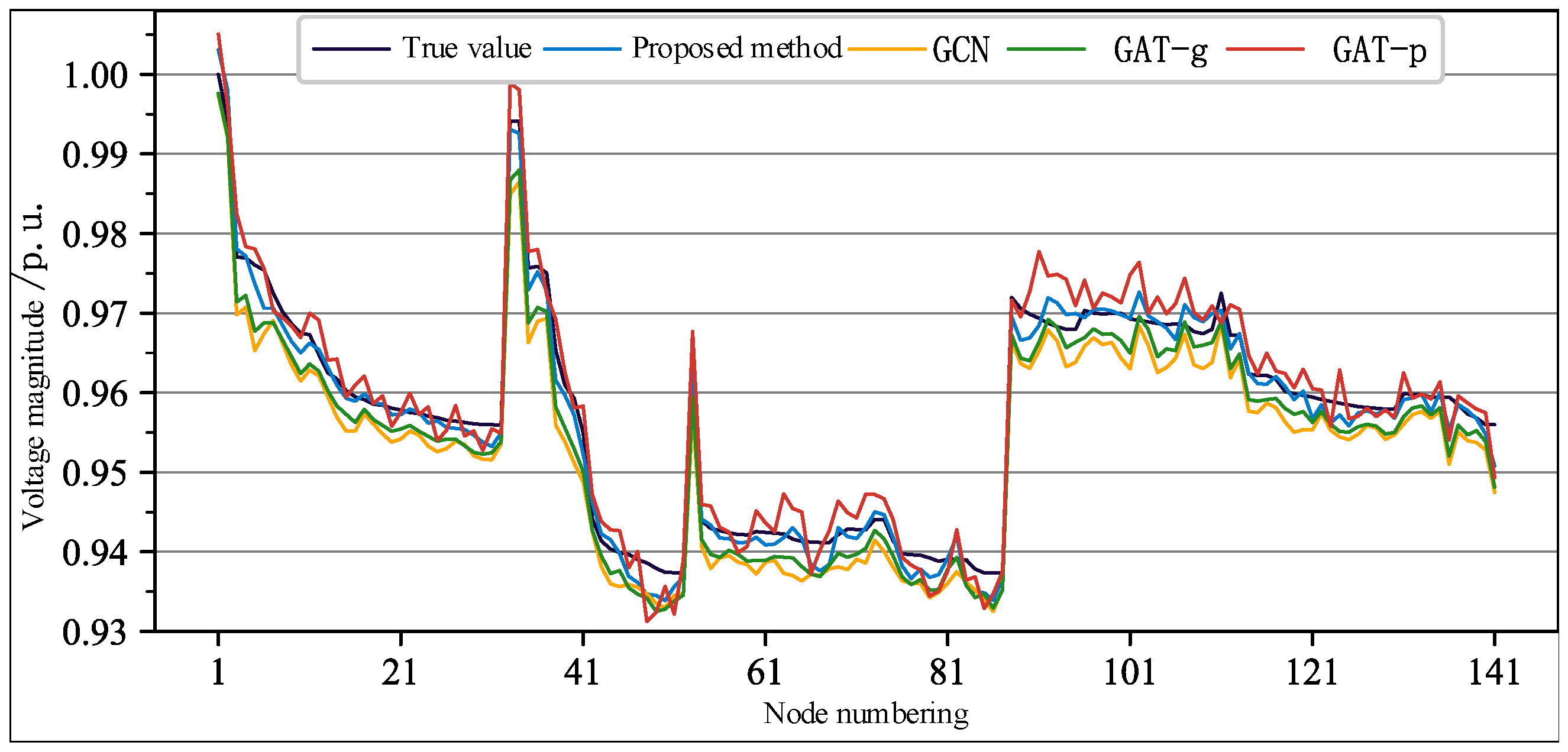
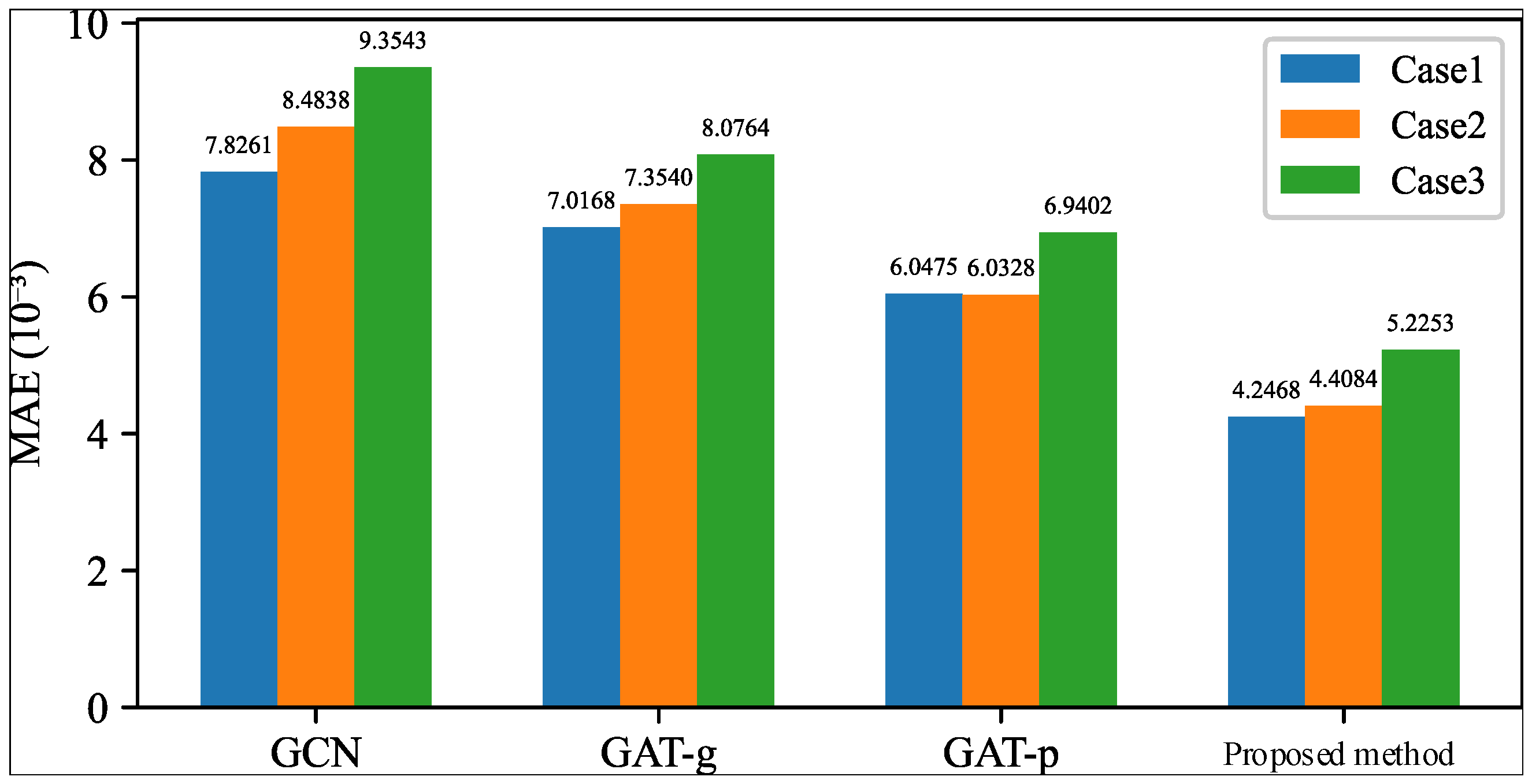
To address the challenges of insufficient training data and inadequate utilization of physical information in existing data-driven state estimation methods, this paper proposes a novel distribution system state estimation approach that integrates physical constraints with a GAT. The method targets scenarios with limited deployment of real-time measurement devices across nodes. First, a GMM-based data augmentation technique is developed to expand the training dataset by learning the probabilistic distribution of nodal power injections and generating synthetic samples. Second, a GAT-based node feature learning module is designed to effectively capture the mapping between measurement information and system states. Furthermore, a topology feature embedding module is introduced to extract and regulate node features using the network admittance matrix. In addition, an operational constraint embedding module is incorporated into the loss function, adding penalties for power flow and voltage limit violations to guide model optimization in a physically consistent manner. The proposed method is validated on the real-world 141-bus test system. Experimental results demonstrate that, compared with data-driven baselines such as GCN, the proposed method achieves a 13.1–52.4% reduction in voltage magnitude MAE and a 16.3–45.5% reduction in voltage phase angle MAE. Moreover, by jointly training with datasets of multiple network topologies, the model maintains consistent estimation performance under various structural configurations, enabling adaptability to dynamic grid topology changes. Additionally, the proposed method exhibits robustness against data quality issues, sustaining stable estimation accuracy in scenarios with missing measurements and noisy data, which confirms its effectiveness and reliability in practical distribution system environments.

Despite the promising results, this study is subject to certain limitations. First, the proposed framework has been validated primarily on simulated datasets derived from standard test systems, while its performance on large-scale, real-world distribution networks remains to be further verified. Second, although the model exhibits a degree of robustness against measurement noise, the impact of extreme scenarios, such as bad data and false data injection attacks, has not been explicitly considered. Future work will focus on addressing these challenges to enhance the practical applicability of the proposed method.